Developing CRS iterative methods for periodic Sylvester matrix equation

Abstract

In this paper, by applying Kronecker product and vectorization operator, we extend two mathematical equivalent forms of the conjugate residual squared (CRS) method to solve the periodic Sylvester matrix equation

$$\begin{aligned} A_{j} X_{j} B_{j} + C_{j} X_{j+1} D_{j} = E_{j} \quad \text{for } j=1,2, \ldots ,\lambda . \end{aligned}$$

We give some numerical examples to compare the accuracy and efficiency of the matrix CRS iterative methods with other methods in the literature. Numerical results validate that the proposed methods are superior to some existing methods and that equivalent mathematical methods can show different numerical performance.

1 Introduction

We consider the iterative solution of the periodic Sylvester matrix equation

$$\begin{aligned} A_{j} X_{j} B_{j} + C_{j} X_{j+1} D_{j} = E_{j} \quad \text{for }j=1,2, \ldots , \end{aligned}$$

(1.1)

where the coefficient matrices $A_{j}, B_{j}, C_{j}, D_{j}, E_{j} \in \mathbf{R}^{m\times m}$ and the solutions $X_{j} \in \mathbf{R} ^{m\times m}$ are periodic with period λ, that is, $A_{j+\lambda } = A_{j}$, $B_{j+\lambda } = B_{j}$, $C_{j+\lambda } = C _{j}$, $D_{j+\lambda } = D_{j}$, $E_{j+\lambda } = E_{j}$, and $X_{j+ \lambda } = X_{j}$. The periodic Sylvester matrix equation (1.1) attracts considerable attention because it comes from a variety of fields of control theory and applied mathematics [1,2,3,4,5,6,7,8,9,10,11,12].

In recent years, many efficient iterative methods have been proposed to solve the periodic Sylvester matrix equation (1.1). For example, Hajarian [13, 14] developed the conjugate gradient squared (CGS), biconjugate gradient stabilized (BiCGSTAB) and biconjugate residual methods for solving the periodic Sylvester matrix equation (1.1). Lv and Zhang [15] proposed a new kind of iterative algorithm for constructing the least square solution for the periodic Sylvester matrix equation. Hajarian [16] studied the biconjugate A-orthogonal residual and conjugate A-orthogonal residual squared (CORS) methods for solving coupled periodic Sylvester matrix equation, and so forth; see [17,18,19,20,21,22,23,24,25,26,27,28] and the references therein.

As we know, by applying Kronecker product and vectorization operator, some iterative algorithms for solving linear system $Ax=b$ can be extended to solve linear matrix equations. Recently, Sogabe et al. [29] proposed a conjugate residual squared (CRS) method for solving linear systems $Ax=b$ with nonsymmetric coefficient matrix. Independently, Zhang et al. [30] presented another form of CRS method. It can be proved that these CRS methods are mathematically equivalent. Chen and Ma [31] used the matrix CRS iterative method to solve a class of coupled Sylvester-transpose matrix equations. In this work, we obtain a matrix form of the CRS methods for solving the periodic Sylvester matrix equation (1.1).

The rest of this paper is organized as follows. In Sect. 2, we extend the CRS methods to solve the periodic Sylvester matrix equation (1.1). We give some numerical examples and comparison results in Sect. 3. In Sect. 4, we draw a brief conclusion.

Throughout this paper, we use the following notations. The set of all real m-vectors and the set of all $m\times n$ real matrices are denoted by $\mathbf{R}^{m}$ and $\mathbf{R}^{m\times n}$, respectively. The usual inner product in $\mathbf{R}^{m}$ is denoted by $(u,v)$ for $u, v\in \mathbf{R}^{m}$. For a matrix $A \in \mathbf{R}^{m\times n}$, we denote its trace and transpose by $\operatorname{tr}(A)$ and $A^{T}$, respectively. The inner product of $A \in \mathbf{R}^{m\times n}$ and $B \in \mathbf{R}^{m\times n}$ is defined by $\langle A,B\rangle = \operatorname{tr}(B^{T}A)$. Then the norm of a matrix generated by this inner product is the matrix Frobenius norm $\|\cdot \|$. For a matrix $A\in \mathbf{R}^{m\times n}$, the vectorization operator is defined as $\operatorname{vec}(A) = (a_{1}^{T}\ a_{2}^{T}\ \cdots\ a_{n}^{T})^{T}$, where $a_{i}$ is the ith column of A. The Kronecker product of matrices $A = [a_{ij}] \in \mathbf{R}^{m\times n}$ and $B \in \mathbf{R}^{p \times q}$ is defined as $A \otimes B = [a_{ij}B] \in \mathbf{R}^{mp \times nq}$. For matrices A, B, and X of appropriate dimensions, we have the following well-known property related to the Kronecker product and vectorization operator:

$$\begin{aligned} \operatorname{vec} (A X B) = \bigl(B^{T} \otimes A\bigr) \operatorname{vec} (X). \end{aligned}$$

2 Matrix forms of the CRS iterative methods

In this section, we first briefly recall the CRS iterative methods for solving a large sparse nonsymmetric linear system $A x = b$, where $A \in \mathbf{R}^{N\times N}$ and $x, b \in \mathbf{R}^{N}$. As described in the introduction, the CRS iterative methods are presented in [29] and [30], which are summarized as the following Algorithms 2.1 and 2.2, respectively. For more detail about the CRS methods, see [32,33,34].

Algorithm 2.1

(The first form of CRS method (CRS1) [29])

• 1. $x_{0}$ is an initial guess; $r_{0} = b - A x_{0}$; choose $r_{0}^{*}$ (for example, $r_{0}^{*} =r_{0}$).

• 2. Set $e_{0} = r_{0}$, $d_{0} = A e_{0}$, $\beta _{-1} = 0$. Let $t = A^{T} r_{0}^{*}$.

• 3. For $n = 0,1,\ldots$ , until convergence Do:

  $$\begin{aligned} &s_{n} = d_{n} + \beta _{n-1}(f_{n-1}+ \beta _{n-1} s_{n-1}); \\ &\alpha _{n} = (t, r_{n})/(t, s_{n}); \\ &h_{n} = e_{n} - \alpha _{n} s_{n}; \\ &f_{n} = d_{n} - \alpha _{n} A s_{n}; \\ &x_{n+1} = x_{n} + \alpha _{n} (e_{n} + h_{n}); \\ &r_{n+1} = r_{n} - \alpha _{n} (d_{n} + f_{n}); \\ &\beta _{n} = (t, r_{n+1})/(t, r_{n}); \\ &e_{n+1} = r_{n+1} + \beta _{n} h_{n}; \\ &d_{n+1} = A r_{n+1} + \beta _{n} f_{n}; \end{aligned}$$

• 4. EndDo.

Algorithm 2.2

(The second form of CRS method (CRS2) [30])

• 1. Compute $r_{0} = b - Ax_{0}$; choose $r_{0}^{*}$ such that $(A r_{0}, r_{0}^{*})\neq 0$ (for example, $r_{0}^{*} = r_{0}$).

• 2. Set $p_{0} = u_{0} = r_{0}$. Let $t = A^{T} r_{0}^{*}$.

• 3. For $n = 0,1,\ldots$ , until convergence Do:

  $$\begin{aligned} &\alpha _{n} = (t, r_{n})/(t, A p_{n}); \\ &q_{n} = u_{n} - \alpha _{n} A p_{n}; \\ &x_{n+1} = x_{n} + \alpha _{n} (u_{n} + q_{n}); \\ &r_{n+1} = r_{n} - \alpha _{n} A (u_{n} + q_{n}); \\ &\beta _{n} = (t, r_{n+1})/(t, r_{n}); \\ &u_{n+1} = r_{n+1} + \beta _{n} q_{n}; \\ &p_{n+1} = u_{n+1} + \beta _{n} (q_{n} + \beta _{n} p_{n}); \end{aligned}$$

• 4. EndDo.

Let

$$\begin{aligned} h_{n} \leftrightarrow q_{n}, \qquad e_{n} \leftrightarrow u_{n}, \qquad s_{n} \leftrightarrow A p_{n}, \qquad d_{n} \leftrightarrow A u_{n}, \qquad f_{n} \leftrightarrow A q_{n}. \end{aligned}$$

Then we can verify that CRS1 and CRS2 are mathematically equivalent. The CRS methods were proposed mainly to avoid using the transpose of A in the BiCR algorithm and gain a faster convergence for roughly the same computational costs [30]. Indeed, in many cases, the CRS methods converge twice as fast as the BiCR method [33, 35]. On the other hand, the BiCR method can be derived from the preconditioned conjugate residual (CR) method [36]. Furthermore, the CR and conjugate gradient (CG) methods exhibit typically similar convergence [37]. In exact arithmetic, they terminate after a finite number of iterations. In conclusion, we can expect that the CRS methods also terminate after a finite number of iterations in exact arithmetic.

In the following, we want to use the CRS algorithms to solve the periodic Sylvester matrix equations (1.1). For this purpose, we can easily show that the periodic Sylvester matrix equation (1.1) is equivalent to the following generalized Sylvester matrix equation [13]:

$$ \mathbf{A}\mathbf{X}\mathbf{B}+\mathbf{C}\mathbf{X}\mathbf{D}= \mathbf{E}, $$

(2.1)

where

$$\begin{aligned} &\mathbf{A} = \begin{bmatrix} 0&\cdots &0&A_{1} \\ A_{2}&&&0 \\ &\ddots &&\vdots \\ 0&&A_{\lambda }&0 \end{bmatrix}, \qquad \mathbf{B}= \begin{bmatrix} 0&B_{2}&&0 \\ \vdots &&\ddots & \\ 0&&&B_{\lambda } \\ B_{1}&0&\cdots &0 \end{bmatrix}, \\ &\mathbf{C}=\operatorname{diag} [C_{1},C_{2},\ldots ,C_{\lambda } ], \qquad \mathbf{D} =\operatorname{diag} [D_{1},D_{2}, \ldots ,D_{\lambda } ], \\ &\mathbf{E}=\operatorname{diag} [E_{1},E_{2},\ldots ,E_{\lambda } ], \qquad \mathbf{X}=\operatorname{diag} [X_{2},X_{3}, \ldots ,X_{\lambda },X_{1} ]. \end{aligned}$$

Then we need to transform the generalized Sylvester matrix equations (2.1) into a linear system $Ax=b$. We should mention that the following derivation borrows much of that used in [13].

By applying the Kronecker product and vectorization operator we can change the generalized Sylvester matrix equations (2.1) into the following linear system of equations:

$$\begin{aligned} \bigl(\mathbf{B}^{T}\otimes \mathbf{A}+ \mathbf{D}^{T}\otimes \mathbf{C}\bigr) \operatorname{vec}(\mathbf{X})= \operatorname{vec}(\mathbf{E}). \end{aligned}$$

(2.2)

Denote

$$ A:=\mathbf{B}^{T}\otimes \mathbf{A}+\mathbf{D}^{T}\otimes \mathbf{C},\qquad x:= \operatorname{vec}(\mathbf{X}),\qquad b:=\operatorname{vec}( \mathbf{E}). $$

Then (2.2) can be written as

$$ Ax=b, $$

where $A\in R^{\lambda ^{2} m^{2}\times \lambda ^{2} m^{2}}$ and $x, b\in R^{\lambda ^{2} m^{2}}$. Then we are in position to present the matrix forms of Algorithms 2.1 and 2.2 for solving the generalized Sylvester matrix equation (2.1), and we just discuss Algorithm 2.1 in detail since the discussion of Algorithm 2.2 is similar.

From Algorithm 2.1 and the linear system of equation (2.2) we have

$$\begin{aligned} & r_{0}=b-Ax_{0}\rightarrow r_{0}=\operatorname{vec}(\mathbf{E})- \bigl(\mathbf{B} ^{T} \otimes \mathbf{A}+\mathbf{D}^{T}\otimes \mathbf{C} \bigr) x_{0}, \end{aligned}$$

(2.3)

$$\begin{aligned} & d_{0}=Ae_{0}\rightarrow d_{0}= \bigl(\mathbf{B}^{T}\otimes \mathbf{A}+ \mathbf{D}^{T}\otimes \mathbf{C} \bigr) e_{0}, \end{aligned}$$

(2.4)

$$\begin{aligned} &t=A^{T}r_{0}^{*}\rightarrow t= \bigl(\mathbf{B}\otimes \mathbf{A} ^{T}+\mathbf{D}\otimes \mathbf{C}^{T} \bigr) r_{0}^{*}, \end{aligned}$$

(2.5)

$$\begin{aligned} &As_{n}\rightarrow \bigl(\mathbf{B}^{T} \otimes \mathbf{A}+\mathbf{D} ^{T}\otimes \mathbf{C} \bigr)s_{n}, \end{aligned}$$

(2.6)

$$\begin{aligned} &A r_{n+1} \rightarrow \bigl(\mathbf{B}^{T} \otimes \mathbf{A}+ \mathbf{D}^{T}\otimes \mathbf{C} \bigr)r_{n+1}. \end{aligned}$$

(2.7)

According to (2.3)–(2.7), we define

$$\begin{aligned} &x_{n}=\operatorname{vec}\bigl(\mathbf{X}(n)\bigr), \qquad r_{n}=\operatorname{vec}\bigl(\mathbf{R}(n)\bigr), \qquad s_{n}=\operatorname{vec}\bigl(\mathbf{S}(n)\bigr), \end{aligned}$$

(2.8)

$$\begin{aligned} &h_{n}=\operatorname{vec}\bigl(\mathbf{H}(n)\bigr), \qquad f_{n}=\operatorname{vec}\bigl(\mathbf{F}(n)\bigr), \qquad e_{n}=\operatorname{vec}\bigl(\mathbf{E}(n)\bigr), \end{aligned}$$

(2.9)

$$\begin{aligned} &d_{n}=\operatorname{vec}\bigl(\mathbf{D}(n)\bigr), \qquad r_{0}^{*}=\operatorname{vec}\bigl( \mathbf{R}^{*}(0)\bigr), \qquad t=\operatorname{vec}(\mathbf{T}), \end{aligned}$$

(2.10)

where $\mathbf{X}(n),\mathbf{R}(n),\mathbf{S}(n),\mathbf{H}(n), \mathbf{F}(n),\mathbf{E}(n), \mathbf{D}(n),\mathbf{R}^{*}(0), \mathbf{T}\in \mathbf{R}^{\lambda m\times \lambda m}$ for $n=0,1,2, \ldots$ . Substituting (2.8)–(2.10) into (2.3)–(2.7), we get

$$\begin{aligned} &\operatorname{vec}\bigl(\mathbf{R}(0)\bigr) =\operatorname{vec}(\mathbf{E})- \bigl(\mathbf{B}^{T}\otimes \mathbf{A}+\mathbf{D}^{T}\otimes \mathbf{C} \bigr) \operatorname{vec}\bigl(\mathbf{X}(0)\bigr), \\ &\operatorname{vec}\bigl(\mathbf{D}(0)\bigr) = \bigl(\mathbf{B}^{T} \otimes \mathbf{A}+ \mathbf{D}^{T}\otimes \mathbf{C} \bigr) \operatorname{vec}\bigl(\mathbf{E}(0)\bigr), \\ &\operatorname{vec}(\mathbf{T}) = \bigl(\mathbf{B}\otimes \mathbf{A}^{T}+ \mathbf{D}\otimes \mathbf{C}^{T} \bigr) \operatorname{vec}\bigl( \mathbf{R}^{*}(0)\bigr), \\ &As_{n} = \bigl(\mathbf{B}^{T}\otimes \mathbf{A}+ \mathbf{D}^{T} \otimes \mathbf{C} \bigr) \operatorname{vec}\bigl( \mathbf{S}(n)\bigr), \end{aligned}$$

and

$$\begin{aligned} Ar_{n+1}= \bigl(\mathbf{B}^{T}\otimes \mathbf{A}+ \mathbf{D}^{T} \otimes \mathbf{C} \bigr) \operatorname{vec}\bigl( \mathbf{R}(n+1)\bigr). \end{aligned}$$

In addition, for the parameters $\alpha _{n}$ and $\beta _{n}$, we have

$$\begin{aligned} \alpha _{n}=\bigl\langle \mathbf{R}(n),\mathbf{T}\bigr\rangle /\bigl\langle \mathbf{V}(n),\mathbf{T}\bigr\rangle \end{aligned}$$

and

$$\begin{aligned} \beta _{n}=\bigl\langle \mathbf{R}(n+1),\mathbf{T}\bigr\rangle /\bigl\langle \mathbf{R}(n),\mathbf{T}\bigr\rangle . \end{aligned}$$

From this discussion it follows that the matrix form of CRS1 method for solving the generalized Sylvester matrix equation (2.1) can be constructed as the following Algorithm 2.3. Analogously, the matrix form of CRS1 method for solving the generalized Sylvester matrix equation (2.1) is summarized as Algorithm 2.4.

Algorithm 2.3

(Matrix CRS1 method for solving (2.1))

• 1. Compute $\mathbf{R}(0) = \mathbf{E} - \mathbf{A} \mathbf{X}(0) \mathbf{B} - \mathbf{C} \mathbf{X}(0) \mathbf{D}$ for an initial guess $\mathbf{X}(0) \in \mathbf{R}^{\lambda m\times \lambda m}$. Set $\mathbf{R}^{*}(0) = \mathbf{E}(0) = \mathbf{R}(0)$ and $\mathbf{D}(0)= \mathbf{A} \mathbf{E}(0) \mathbf{B} + \mathbf{C} \mathbf{E}(0) \mathbf{D}$. Let $\beta _{-1}=0$.

• 2. Set $\mathbf{T} = \mathbf{A}^{T} \mathbf{R}^{*}(0) \mathbf{B}^{T} + \mathbf{C}^{T} \mathbf{R}^{*}(0) \mathbf{D}^{T}$.

• 3. For $n=0,1,\ldots$ , until convergence Do:

  $$\begin{aligned} &\mathbf{S}(n) = \mathbf{D}(n) + \beta _{n-1} \bigl(\mathbf{F}(n-1) + \beta _{n-1} \mathbf{S}(n-1) \bigr); \\ &\alpha _{n} = \bigl\langle \mathbf{R}(n), \mathbf{T}\bigr\rangle / \bigl\langle \mathbf{S}(n),\mathbf{T}\bigr\rangle ; \\ &\mathbf{H}(n) = \mathbf{E}(n)-\alpha _{n} \mathbf{S}(n); \\ &\mathbf{F}(n) = \mathbf{D}(n)-\alpha _{n} \bigl(\mathbf{A} \mathbf{S}(n) \mathbf{B} + \mathbf{C} \mathbf{S}(n) \mathbf{D}\bigr); \\ &\mathbf{X}(n+1) = \mathbf{X}(n) + \alpha _{n}\bigl(\mathbf{E}(n)+ \mathbf{H}(n)\bigr); \\ &\mathbf{R}(n+1) = \mathbf{R}(n) - \alpha _{n} \bigl(\mathbf{D}(n)+ \mathbf{F}(n)\bigr); \\ &\beta _{n} = \bigl\langle \mathbf{R}(n+1), \mathbf{T}\bigr\rangle / \bigl\langle \mathbf{R}(n),\mathbf{T}\bigr\rangle ; \\ &\mathbf{E}(n+1)=\mathbf{R}(n+1)+\beta _{n}\mathbf{H}(n); \\ &\mathbf{D}(n+1) = \mathbf{A} \mathbf{R}(n+1) \mathbf{B} + \mathbf{C} \mathbf{R}(n+1) \mathbf{D}) + \beta _{n} \mathbf{F}(n); \end{aligned}$$

• 4. EndDo.

Algorithm 2.4

(Matrix CRS2 method for solving (2.1))

• 1. Compute $\mathbf{R}(0) = \mathbf{E} - \mathbf{A} \mathbf{X}(0) \mathbf{B} - \mathbf{C} \mathbf{X}(0) \mathbf{D}$ for an initial guess $\mathbf{X}(0) \in \mathbf{R}^{\lambda m\times \lambda m}$. Set $\mathbf{R}^{*}(0) = \mathbf{P}(0) = \mathbf{U}(0) = \mathbf{R}(0)$.

• 2. Set $\mathbf{T} = \mathbf{A}^{T} \mathbf{R}^{*}(0) \mathbf{B}^{T} + \mathbf{C}^{T} \mathbf{R}^{*}(0) \mathbf{D}^{T}$.

• 3. For $n=0,1,\ldots$ , until convergence Do:

  $$\begin{aligned} &\mathbf{V}(n) = \mathbf{A} \mathbf{P}(n) \mathbf{B} + \mathbf{C} \mathbf{P}(n) \mathbf{D}; \\ &\alpha _{n} = \bigl\langle \mathbf{R}(n), \mathbf{T}\bigr\rangle / \bigl\langle \mathbf{V}(n),\mathbf{T}\bigr\rangle ; \\ &\mathbf{Q}(n)=\mathbf{U}(n)-\alpha _{n}\mathbf{V}(n); \\ &\mathbf{X}(n+1)=\mathbf{X}(n)+\alpha _{n}\bigl(\mathbf{U}(n)+ \mathbf{Q}(n)\bigr); \\ &\mathbf{W}(n) = \mathbf{A} \bigl(\mathbf{U}(n)+\mathbf{Q}(n)\bigr) \mathbf{B} + \mathbf{C} \bigl(\mathbf{U}(n) + \mathbf{Q}(n)\bigr)\mathbf{D}; \\ &\mathbf{R}(n+1)=\mathbf{R}(n)-\alpha _{n} \mathbf{W}(n); \\ &\beta _{n} = \bigl\langle \mathbf{R}(n+1), \mathbf{T}\bigr\rangle / \bigl\langle \mathbf{R}(n),\mathbf{T}\bigr\rangle ; \\ &\mathbf{U}(n+1)=\mathbf{R}(n+1)+\beta _{n}\mathbf{Q}(n); \\ &\mathbf{P}(n+1) = \mathbf{U}(n+1) + \beta _{n} \bigl(\mathbf{Q}(n) + \beta _{n} \mathbf{P}(n)\bigr); \end{aligned}$$

• 4. EndDo.

From Algorithms 2.3 and 2.4 by using the equivalent relationships of periodic Sylvester matrix equation (1.1) and generalized Sylvester matrix equation (2.1) we can derive the CRS methods for solving periodic Sylvester matrix equation (1.1) as Algorithms 2.5 and 2.6, respectively.

Algorithm 2.5

(Matrix CRS1 method for solving (1.1))

• 1. Choose $X_{j}(0)\in \mathbf{R}^{m \times m}$ for $j=1,2,\ldots , \lambda$ and set $X_{\lambda +1}(0) = X_{1}(0)$.

• 2. Compute $R_{j} (0) = E_{j} - A_{j} X_{j} (0) B_{j} - C_{j} X_{j+1}(0) D_{j}$ and set $R_{j}^{*}(0) = E_{j}(0) = R_{j}(0)$ for $j=1,2,\ldots ,\lambda$. Let $E_{\lambda +1}(0) = E_{1}(0)$ and $R_{\lambda +1} ^{*}(0) = R_{1}^{*}(0)$. Set $D_{j}(0)= A_{j} E_{j}(0) B_{j} + C_{j} E _{j+1}(0) D_{j}$. Let $\beta _{-1}=0$.

• 3. Set $T_{j} = A_{j}^{T} R_{j}^{*}(0) B_{j}^{T} + C_{j}^{T} R_{j+1} ^{*}(0) D_{j}^{T}$ for $j=1,2,\ldots ,\lambda$.

• 4. For $n=0,1,\ldots$ , until convergence Do:

  $$\begin{aligned} &S_{j}(n) = D_{j}(n) + \beta _{n-1} \bigl(F_{j}(n-1) + \beta _{n-1} S_{j}(n-1) \bigr) \quad \mbox{for }j=1,2,\ldots ,\lambda . \\ &\mbox{Let }S_{\lambda +1}(n) = S_{1}(n); \\ &\alpha _{n} = \Biggl(\sum_{j=1}^{\lambda } \bigl\langle R_{j}(n), T _{j}\bigr\rangle \Biggr)\biggm/ \Biggl( \sum_{j=1}^{\lambda }\bigl\langle S_{j}(n),T _{j}\bigr\rangle \Biggr); \\ &H_{j}(n) = E_{j}(n)-\alpha _{n} S_{j}(n)\quad \mbox{for }j=1,2,\ldots , \lambda ; \\ &F_{j}(n) = D_{j}(n)-\alpha _{n} (A_{j} S_{j}(n) B_{j} + C_{j} S _{j+1}(n) D_{j}\quad \mbox{for }j=1,2,\ldots ,\lambda ; \\ &X_{j}(n+1) = X_{j}(n) + \alpha _{n} \bigl(E_{j}(n)+H_{j}(n)\bigr)\quad \mbox{for } j=1,2,\ldots ,\lambda ; \\ &R_{j}(n+1) = R_{j}(n) - \alpha _{n} \bigl(D_{j}(n)+F_{j}(n)\bigr)\quad \mbox{for } j=1,2,\ldots ,\lambda ; \\ &\mbox{Let }R_{\lambda +1}(n+1) = R_{1}(n+1); \\ &\beta _{n} = \Biggl(\sum_{j=1}^{\lambda } \bigl\langle R_{j}(n+1), T _{j}\bigr\rangle \Biggr)\biggm/ \Biggl( \sum_{j=1}^{\lambda }\bigl\langle R_{j}(n),T _{j}\bigr\rangle \Biggr); \\ &E_{j}(n+1)=R_{j}(n+1)+\beta _{n}H_{j}(n) \quad \mbox{for }j=1,2,\ldots , \lambda ; \\ &D_{j}(n+1) = A_{j} R_{j}(n+1) B_{j} + C_{j} R_{j+1}(n+1) D _{j}) + \beta _{n} F_{j}(n)\quad \mbox{for }j=1,2,\ldots ,\lambda ; \end{aligned}$$

• 5. EndDo.

Algorithm 2.6

(Matrix CRS2 method for solving (1.1))

• 1. Choose $X_{j}(0)\in \mathbf{R}^{m \times m}$ for $j=1,2,\ldots , \lambda$ and set $X_{\lambda +1}(0) = X_{1}(0)$.

• 2. Compute $R_{j} (0) = E_{j} - A_{j} X_{j} (0) B_{j} - C_{j} X_{j+1}(0) D_{j}$ and set $R_{j}^{*}(0) = P_{j}(0) = U_{j}(0) = R_{j}(0)$ for $j=1,2,\ldots ,\lambda$. Let $R_{\lambda +1}^{*}(0) = R_{1}^{*}(0)$.

• 3. Set $T_{j} = A_{j}^{T} R_{j}^{*}(0) B_{j}^{T} + C_{j}^{T} R_{j+1} ^{*}(0) D_{j}^{T}$ for $j=1,2,\ldots ,\lambda$.

• 4. For $n=0,1,\ldots$ , until convergence Do:

  $$\begin{aligned} &\mbox{Let }P_{\lambda +1}(n) = P_{1}(n); \\ &V_{j}(n) = A_{j} P_{j}(n) B_{j} + C_{j} P_{j+1}(n) D_{j}\quad \mbox{for } j=1,2, \ldots ,\lambda ; \\ &\alpha _{n} = \Biggl(\sum_{j=1}^{\lambda } \bigl\langle R_{j}(n), T _{j}\bigr\rangle \Biggr)\biggm/ \Biggl( \sum_{j=1}^{\lambda }\bigl\langle V_{j}(n),T _{j}\bigr\rangle \Biggr); \\ &Q_{j}(n)=U_{j}(n)-\alpha _{n} V_{j}(n)\quad \mbox{for }j=1,2,\ldots , \lambda ; \\ &X_{j}(n+1)=X_{j}(n)+\alpha _{n} \bigl(U_{j}(n)+Q_{j}(n)\bigr)\quad \mbox{for } j=1,2,\ldots ,\lambda ; \\ &\mbox{Let }U_{\lambda +1}(n) = U_{1}(n)\quad \mbox{and}\quad Q_{\lambda +1}(n) = Q _{1}(n); \\ &W_{j}(n) = A_{j} \bigl(U_{j}(n)+Q_{j}(n) \bigr) B_{j} + C_{j} \bigl(U_{j+1}(n) + Q_{j+1}(n)\bigr)D_{j}\quad \mbox{for }j=1,2,\ldots ,\lambda ; \\ &R_{j}(n+1)=R_{j}(n)-\alpha _{n} W_{j}(n)\quad \mbox{for }j=1,2,\ldots , \lambda ; \\ &\beta _{n} = \Biggl(\sum_{j=1}^{\lambda } \bigl\langle R_{j}(n+1), T _{j}\bigr\rangle \Biggr)\biggm/ \Biggl( \sum_{j=1}^{\lambda }\bigl\langle R_{j}(n),T _{j}\bigr\rangle \Biggr); \\ &U_{j}(n+1)=R_{j}(n+1)+\beta _{n}Q_{j}(n) \quad \mbox{for }j=1,2,\ldots , \lambda ; \\ &P_{j}(n+1) = U_{j}(n+1) + \beta _{n} \bigl(Q_{j}(n) + \beta _{n} P _{j}(n)\bigr)\quad \mbox{for }j=1,2,\ldots ,\lambda ; \end{aligned}$$

• 5. EndDo.

Based on the earlier discussion, we know that Algorithms 2.5 and 2.6 are just the matrix forms of the original CRS method. Hence, generally speaking, Algorithms 2.5 and 2.6 have the same properties as Algorithms 2.1 and 2.2. For instance, in exact arithmetic, Algorithms 2.5 and 2.6 will also terminate after a finite number of iterations.

3 Numerical experiments

In this section, we present two numerical examples to show the accuracy and efficiency of the proposed methods. We compare the performances of CRS methods to those of the CGS, BiCGSTAB [13], and CORS [16] methods.

In our experiments, all runs are started from the zero initial guess and implemented in MATLAB(R2014b) with a machine precision 10⁻¹⁶ on a personal computer with Intel(R) Core(TM) i7-6500U CPU 2.50 GHz 2.60 GHz, 16.0 GB memory.

Example 3.1

([13])

Consider the periodic Sylvester matrix equation

$$\begin{aligned} X_{j}+C_{j}X_{j+1}D_{j}=E_{j} \quad \text{for }j=1,2 \end{aligned}$$

with parameters

$$\begin{aligned} &C_{1} =\operatorname{tril}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(2+\operatorname{diag}\bigl(\operatorname{rand}(m)\bigr) \bigr), \\ &D_{1} =\operatorname{triu}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(1.75+\operatorname{diag}\bigl(\operatorname{rand}(m) \bigr)\bigr), \\ &C_{2} =\operatorname{triu}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(1.75+\operatorname{diag}\bigl(\operatorname{rand}(m) \bigr)\bigr), \\ &D_{2} =\operatorname{tril}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(2+\operatorname{diag}\bigl(\operatorname{rand}(m)\bigr) \bigr), \\ &E_{1} =E_{2}=\operatorname{rand}(m,m). \end{aligned}$$

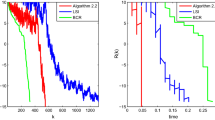
In this example, we set $m=20$. The numerical results are shown in Fig. 1, where

$$\begin{aligned} r_{n}=\log _{10}\sqrt{ \bigl\Vert E_{1}-X_{1}(n)-C_{1}X_{2}(n)D_{1} \bigr\Vert ^{2}+ \bigl\Vert E _{2}-X_{2}(n)-C_{2}X_{1}(n)D_{2} \bigr\Vert ^{2}}. \end{aligned}$$

From Fig. 1 we find that the CRS1 and CRS2 methods are superior to the CGS and CORS methods, and the BiCGSTAB method is the best among them for Example 3.1. In addition, the residual history of the CRS1 method seems smoother than that of the CRS2 method.

Figure 1

The residual for Example 3.1

Example 3.2

([16])

Consider the periodic Sylvester matrix equations

$$\begin{aligned} X_{j}+C_{j}X_{j+1}D_{j}=E_{j}, \quad \text{for }j=1,2 \end{aligned}$$

with parameters

$$\begin{aligned} &C_{1} =-\operatorname{triu}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(1.75+\operatorname{diag}\bigl(\operatorname{rand}(m) \bigr)\bigr), \\ &D_{1} =\operatorname{tril}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(1.25+\operatorname{diag}\bigl(\operatorname{rand}(m) \bigr)\bigr), \\ &C_{2} =\operatorname{triu}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(1.75+\operatorname{diag}\bigl(\operatorname{rand}(m) \bigr)\bigr), \\ &D_{2} =\operatorname{tril}\bigl(\operatorname{rand}(m,m),1\bigr)+ \operatorname{diag}\bigl(2+\operatorname{diag}\bigl(\operatorname{rand}(m)\bigr) \bigr), \\ &E_{1} =E_{2}=\operatorname{rand}(m,m). \end{aligned}$$

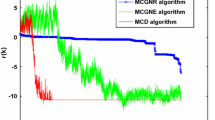
In this example, let $m=40$. The numerical results are shown in Fig. 2, where

$$\begin{aligned} r_{n}=\log _{10}\sqrt{ \bigl\Vert E_{1}-X_{1}(n)-C_{1}X_{2}(n)D_{1} \bigr\Vert ^{2}+ \bigl\Vert E _{2}-X_{2}(n)-C_{2}X_{1}(n)D_{2} \bigr\Vert ^{2}}. \end{aligned}$$

From Fig. 2, for Example 3.2, we see that the CRS2 method is the best one among the five methods mentioned. The BiCGSTAB method can achieve higher accuracy than the CGS, CORS, and CRS1 methods.

Figure 2

The residual for Example 3.2

4 Conclusions

In this paper, we present two matrix forms of the CRS iterative method for solving the periodic Sylvester matrix equation (1.1). Numerical examples and comparison with the CGS, BiCGSTAB, and CORS methods have illustrated that the CRS methods can work quite well in some situations. In addition, numerical results show that the CRS1 and CRS2 methods show different numerical performance, though they are mathematically equivalent.