1 Introduction

Time delay is one of sources of instability and poor performance, so that dynamic systems with time delay have received extensive attention and research. Meanwhile, fractional-order systems have gained considerable importance because of many advantages of fractional derivatives. The especially important advantages are that researchers have more degrees of freedom in the model and that memories of various materials and processes are included in the model; see [1,2,3]. There are different definitions of fractional derivatives [4], among which the most commonly used definition is the Caputo definition. In the literature, it is called a smooth fractional derivative because it is suitable to be treated by the Laplace transform technique. Analysis of equations generated by different fractional derivatives has been done; see [5].

Caputo and Fabrizio (CF) proposed a new fractional derivative without a singular kernel [6] in 2015. Its advantages are mainly shown in the following aspects: First, it is less affected by the past; second, the asymptotic behavior of the new derivative, in contrast to the Caputo derivative, for the larger of the variable, is linearly increasing and diverging. A lot of results about this new derivative are reviewed. In [7, 8] the properties of the CF derivative and fractional integral associated with the CF derivative are studied. Boundary value problems with CF derivatives have been studied in [9, 10]. In [11] a linear fuzzy model with CF operator is studied, and the \((i,\alpha )\) and \((\mathit{ii},\alpha )\) differentiable solutions of the model are obtained. In [12], some good examples presented, which justify that CF derivatives are much more needed to describe real problems. In [13, 14] the kernel and no-index property of CF derivative separately are studied, which helps us to know more information on the derivative and its links to other fractional derivatives and real problems.

In this paper, we establish a new fractional-order system by combining new fractional derivative and time delay and study the stability and robust stability of the new system. By using the Laplace transform we establish a characteristic equation and provide some brief sufficient stability conditions. Finally, we give examples to demonstrate the effectiveness of results.

2 Problem formulation and preliminaries

In this paper, by \({}_{\mathrm{CF}}D_{t}^{\alpha }\) we denote the new derivative of order α:

$$ {}_{\mathrm{CF}}D_{t}^{\alpha }x(t)=\frac{{d^{\alpha }x(t)}}{{dt^{\alpha }}}= \frac{1}{ {1-\alpha }} \int _{0}^{t}\exp \biggl(-\frac{\alpha }{{1-\alpha }}(t- \tau ) \biggr)\dot{x}(\tau )\,d\tau , \quad 0< \alpha \leq 1. $$

We mainly consider the following fractional linear system:

$$ {}_{\mathrm{CF}}D^{\alpha }x(t)=\frac{{d^{\alpha }x(t)}}{{dt^{\alpha }}}=Ax(t)+Bx(t- \tau ), $$
(1)

where \(x(t)\in \mathbb{R}^{n}\), \(A,B\in \mathbb{R}^{n\times n}\), and \(0<\alpha <1\).

Throughout this article, the following conventions are used:

$$ \begin{aligned} &\mu (A), \quad \text{the matrix measure of a matrix } A, \text{i.e.}, \mu (A)=\frac{1}{2}\lambda _{\max }\bigl(A+A^{*} \bigr). \\ &\rho (A), \quad \text{the spectral radius of a matrix } A. \\ & \Vert A \Vert , \quad \text{the spectral norm of a matrix } A; \Vert A \Vert = \sqrt{\lambda _{\max } \bigl(A^{*} A\bigr)}. \\ &A^{*}, \quad \text{the conjugate transpose of a matrix } A. \end{aligned} $$
(2)

3 Main results

Lemma 3.1

([15])

Let \(A, B, C \in {\mathbb{C}^{n \times n}}\) and \(\vert A\vert \le V\). Then

$$ \begin{gathered} (1)\quad \mathbb{R}e\bigl(\lambda _{j}(A) \bigr)\leq \mu (A), \quad j\in {1,2,\ldots,n}; \\ (2)\quad \mu (A+B)\leq \mu (A)+\mu (B); \\ (3)\quad \mu (A)\leq \Vert A \Vert , \quad\quad \rho (A)\leq \Vert A \Vert . \end{gathered} $$
(3)

Lemma 3.2

([16])

Let \(C\in {\mathbb{C}^{n \times n}}\), \(\Vert C\Vert <1\). Then \((I-C)^{-1}\) exists, and \(\Vert (I-C)^{-1}\Vert \leq \frac{1}{(1-\Vert C\Vert )}\).

Lemma 3.3

([17])

For a matrix \(B\in {\mathbb{C}^{n \times n}}\) and a positive constant τ,

$$ \mu \bigl(Be^{-s\tau }\bigr)\leq \sqrt{{\rho ^{2}} {(B_{u})} + {\rho ^{2}} {(B _{l})}}, \quad \mathbb{R}e(s)\geq 0, $$
(4)

where \(B_{u}=\frac{1}{2}(B+B^{*})\), \(B_{l}=\frac{i}{2}(B-B^{*})\), and \(i^{2}=-1\).

Definition 3.1

System (1) with \(x(t_{0})=x_{0}\) is said to be stable if and only if \(\lim_{t\to +\infty }\Vert x(t)\Vert =0\).

Next, the stability of system (1) is studied. First, using the Laplace transform to system (1) for a given initial condition \(x(t_{0})=x_{0}\), we obtain

$$ L \bigl({}_{CF}D_{t}^{\alpha }x(t) \bigr)=L \bigl(Ax(t) \bigr) \quad \Leftrightarrow \quad \frac{1}{{1 - \alpha }} \biggl( { \frac{1}{{s + \beta }}\bigl(sX(s) - x_{0}\bigr)} \biggr) = AX(s)+Be^{-s\tau }X(s), $$
(5)

where \(sX(s)=L{(x(t))}\), \(\beta =\frac{\alpha }{1-\alpha }\), and \(L(x(t-\tau ))=e^{-s\tau }X(s)\). Simplifying (5), we get

$$ \bigl\{ {s\bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)- \alpha \bigl(A+Be^{-s\tau }\bigr)} \bigr\} X(s)= x(0). $$
(6)

Setting \(\Delta (s)\triangleq s(I-(1-\alpha )(A+Be^{-s\tau }))-\alpha (A+Be^{-s\tau })\), equation (6) can be written as

$$ \Delta (s) X(s)= x(0). $$
(7)

The distribution of eigenvalues of \(\Delta (s)\) totally determine the stability of system (1), so the following definition is obvious.

Definition 3.2

The characteristic equation of system (1) is \(\det (\Delta (s) )=0\).

Theorem 3.1

System (1) is asymptotically stable if and only if the real parts of roots to the characteristic equation are negative.

Proof

According to (7) and paper [18], this result is easily obtained. □

Remark 3.1

Next, let us make a simple comparison with the traditional Caputo characteristic equations. Obviously, the characteristic equation of the same system described by the Caputo derivative is

$$ \det \bigl(s^{\alpha }I-A-Be^{-s\tau } \bigr)=0, $$
(8)

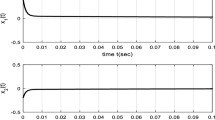
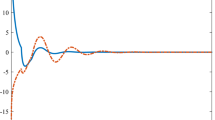
which is difficult to solve since this is a fractional-order equation. In addition, without loss of generality, let \(A = \operatorname{diag}(-9.47, -9.47)\) and \(B=\operatorname{diag}(1.05, 1.05)\). Figures 1 and 2 illustrate that our new characteristic equation \(\det (\Delta (s) )=0\) is less affected by α and τ corresponding to the traditional Caputo characteristic equation (8). Therefore the result described by the new derivative is better than that described by the Caputo derivative.

Figure 1
figure 1

Relations between \(\mathbb{R}e(s)\) and α when \(\tau =1\) (left is \(\det (\Delta (s) )=0\), right is Eq. (8))

Full size image
Figure 2
figure 2

Relations between \(\mathbb{R}e(s)\) and τ when \(\alpha =0.2\) (left is \(\det (\Delta (s) )=0\), right is Eq. (8))

Full size image

Theorem 3.2

System (1) is asymptotically stable if the following inequalities hold:

$$ \begin{gathered} (\mathrm{a}) \quad (1-\alpha ) \bigl( \Vert A \Vert + \Vert B \Vert \bigr)< 1; \\ (\mathrm{b}) \quad \mu (A)+\sqrt{{\rho ^{2}} {(B_{u})}+{ \rho ^{2}} {(B_{l})}}+(1-\alpha )\frac{ { \Vert {A^{2}} \Vert + \Vert AB+BA \Vert + \Vert {B^{2}} \Vert }}{{1-(1-\alpha )( \Vert A \Vert + \Vert B \Vert )}}< 0. \end{gathered} $$
(9)

Proof

According to Theorem 3.1, system (1) is asymptotically stable if and only if all roots of the equation \(\det (\Delta (s) )=0\) lie in the open left half complex plane, and hence we consider system (1) in \(\mathbb{R}e(s) \geq 0\). In this restricted area, \(0< e^{-s\tau }<1\). If inequality (a) holds, then from Lemma 3.1 we have

$$ \begin{aligned} \rho \bigl((1-\alpha ) \bigl(A+Be^{-s\tau }\bigr) \bigr)&\leq (1-\alpha ) \rho \bigl(A+Be^{-s\tau } \bigr)\leq (1-\alpha ) \bigl\Vert \bigl(A+Be^{-s\tau }\bigr) \bigr\Vert \\ &\leq (1-\alpha ) \bigl( \Vert A \Vert + \bigl\Vert Be^{-s\tau } \bigr\Vert \bigr)\leq (1-\alpha ) \bigl( \Vert A \Vert + \Vert B \Vert \bigr)< 1. \end{aligned} $$

From Lemma (3.2) we further know that \(N= (I-(1- \alpha )(A+Be^{-s\tau }) )^{-1}\) exists, and after premultiplication of \(\det (\Delta (s) )\neq 0\) by N, we have

$$ \det \bigl(sI-\alpha \bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr) \bigr)^{-1}\bigl(A+Be^{-s \tau }\bigr) \bigr)\neq 0,\quad \mathbb{R}e(s)\geq 0. $$

Employing the well-known relation

$$ \bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr) \bigr)^{-1}=I+\bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr) \bigr)^{-1}(1- \alpha ) \bigl(A+Be^{-s\tau }\bigr), $$

we obtain

$$ \begin{aligned}[b]& \det \bigl(sI-\alpha \bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1}\bigl(A+Be^{-s \tau }\bigr) \bigr) \\ & \quad =\det \bigl(sI-\bigl(\alpha \bigl(A+Be^{-s\tau }\bigr)+ \alpha (1- \alpha ) \bigl(I -(1- \alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1} \bigl(A+Be^{-s\tau }\bigr)^{2}\bigr) \bigr) \\ & \quad =\det\bigl(sI-\bigl(\alpha \bigl(A+Be^{-s\tau }\bigr)+\alpha (1-\alpha ) \bigl(I -(1-\alpha ) \bigl(A+Be ^{-s\tau }\bigr)\bigr)^{-1} \\ & \quad\quad{} \cdot \bigl(A^{2}+(AB+BA)e^{-s\tau }+B^{2}e^{-2s\tau } \bigr)\bigr)\bigr)\neq 0,\quad \mathbb{R}e(s)\geq 0, \end{aligned} $$
(10)

which is equivalent to

$$ \begin{aligned} &s\neq \lambda _{j}\bigl(\alpha \bigl(A+Be^{-s\tau }\bigr)+ \alpha (1-\alpha ) \bigl(I -(1- \alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1} \\ &\hphantom{s\neq}{} \cdot \bigl(A^{2}+(AB+BA)e^{-s\tau }+B^{2}e^{-2s\tau } \bigr)\bigr), \\ &\quad \mathbb{R}e(s)\geq 0, j\in 1,2,\ldots,n. \end{aligned} $$

Since \(0<\alpha <1\), if we have that

$$ \begin{gathered} \mathbb{R}e\bigl(\lambda _{j}\bigl( \bigl(A+Be^{-s\tau }\bigr)+(1-\alpha ) \bigl(I -(1-\alpha ) \bigl(A+Be ^{-s\tau }\bigr)\bigr)^{-1} \\ \quad{} \cdot \bigl(A^{2}+(AB+BA)e^{-s\tau }+B^{2}e^{-2s\tau } \bigr)\bigr)\bigr)< 0, \end{gathered} $$

then we can prove that \(\det (\Delta (s) )\neq 0\) for \(\mathbb{R}e(s)\geq 0\).

In fact, by Lemmas 3.1 and 3.3 and inequality (b) in this theorem we get

$$\begin{aligned}& \mathbb{R}e\bigl(\lambda _{j}\bigl(\bigl(A+Be^{-s\tau }\bigr)+(1- \alpha ) \bigl(I-(1-\alpha ) \bigl(A+Be ^{-s\tau }\bigr)\bigr)^{-1} \bigl(A^{2}+(AB+BA)e^{-s\tau }+B^{2}e^{-2s\tau }\bigr) \bigr)\bigr) \\& \quad \leq \mu \bigl(\bigl(A+Be^{-s\tau }\bigr)+ (1-\alpha ) \bigl(I -(1- \alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1}\bigl(A ^{2}+(AB+BA)e^{-s\tau }+B^{2}e^{-2s\tau }\bigr)\bigr) \\& \quad \leq \mu (A)+\mu \bigl(Be^{-s\tau }\bigr) \\& \quad \quad{} +(1-\alpha ) \bigl\Vert \bigl(I -(1-\alpha ) \bigl(A+Be^{-s \tau }\bigr)\bigr)^{-1} \bigl(A^{2}+(AB+BA)e^{-s\tau }+B^{2}e^{-2s\tau }\bigr) \bigr\Vert \\& \quad \leq \mu (A)+\sqrt{{\rho ^{2}} {(B_{u})}+{\rho ^{2}} {(B_{l})}} \\& \quad \quad{} +(1-\alpha ) \bigl\Vert \bigl(I -(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1} \bigr\Vert \cdot \bigl\Vert \bigl(A^{2}+(AB+BA)e ^{-s\tau }+B^{2}e^{-2s\tau } \bigr) \bigr\Vert \\& \quad \leq \mu (A)+\sqrt{{\rho ^{2}} {(B_{u})}+{\rho ^{2}} {(B_{l})}} +(1- \alpha ) \frac{{ \Vert {A^{2}} \Vert + \Vert AB+BA \Vert + \Vert {B^{2}} \Vert }}{{1-(1-\alpha )( \Vert A \Vert + \Vert B \Vert )}}< 0. \end{aligned}$$
(11)

Thus the proof is completed. □

Using simple matrix theory, the following corollaries can be easily proved.

Corollary 3.1

System (1) is asymptotically stable if the following inequalities hold:

$$ \begin{gathered} (\mathrm{a}) \quad (1-\alpha ) \bigl( \Vert A \Vert + \Vert B \Vert \bigr)< 1; \\ (\mathrm{b}) \quad \mu (A)+\sqrt{{\rho ^{2}} {(B_{u})}+{ \rho ^{2}} {(B_{l})}}+(1-\alpha )\frac{ { \Vert {A^{2}} \Vert + \Vert AB \Vert + \Vert BA \Vert + \Vert {B^{2}} \Vert }}{{1-(1-\alpha )( \Vert A \Vert + \Vert B \Vert )}}< 0. \end{gathered} $$
(12)

Corollary 3.2

System (1) is asymptotically stable if there exists an invertible matrix \(P\in \mathbb{C}^{n\times n}\) such that the following inequalities hold:

$$ \begin{gathered} (\mathrm{a}) \quad (1-\alpha ) \bigl( \Vert A \Vert + \Vert B \Vert \bigr)< 1; \\ (\mathrm{b}) \quad \mu \bigl(P^{-1}AP\bigr) +\sqrt{{\rho ^{2}} {\bigl(P^{-1}B_{u}P\bigr)}+{\rho ^{2}} {\bigl(P^{-1}B _{l}P\bigr)}} \\ \hphantom{(\mathrm{b}) \quad}\quad {}+(1-\alpha )\frac{{ \Vert P^{-1} \Vert ( \Vert {A^{2}} \Vert + \Vert AB+BA \Vert + \Vert {B^{2}} \Vert ) \Vert P \Vert }}{{1-(1-\alpha )( \Vert A \Vert + \Vert B \Vert )}}< 0. \end{gathered} $$
(13)

Corollary 3.2 is better when matrices A, \(B_{u}\), \(B_{l}\) are similar to diagonal matrices.

Remark 3.2

Theorem 3.1 means that all eigenvalues of the matrix

$$ \bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1} \bigl(A+Be^{-s\tau }\bigr) $$

are negative. By this way, the LMI

$$ \bigl(\bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1} \bigl(A+Be^{-s\tau }\bigr) \bigr) ^{T}P+P \bigl(\bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr)\bigr)^{-1}\bigl(A+Be^{-s\tau }\bigr) \bigr)< 0, $$

where \(P=P^{T}>0\), can be used for analysis of the stability of system (1). It is not easy since there exists \(e^{s\tau }\) in this LMI, but some work can be done to get some stability conditions. LMI may also be used by Lyapunov theory, but unfortunately, there do not exist the corresponding theorems for fractional systems described by the Caputo–Fabrizio derivatives. Next, we discuss this problem for system (1) with input \(u(t)\):

$$ {}_{\mathrm{CF}}D^{\alpha }x(t)=\frac{{d^{\alpha }x(t)}}{{dt^{\alpha }}}=Ax(t)+Bx(t- \tau )+Cu(t), $$
(14)

where \(u(t)\in \mathbb{R}^{m}\) and \(C\in \mathbb{R}^{n\times m}\).

Using the Laplace transform, we have

$$ \bigl\{ {s\bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }\bigr) \bigr)-\alpha \bigl(A+Be^{-s\tau }\bigr)} \bigr\} X(s)= x(0)+s(1-\alpha )CU(s)+\alpha CU(s), $$
(15)

where \(U(s)=L(u(t))\). If \(u(t)=Kx(t)\), then \(U(s)=L(u(t))=L(Kx(t))=KX(s)\), so that equation (15) becomes

$$ \bigl\{ {s\bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }+CK\bigr) \bigr)-\alpha \bigl(A+Be^{-s\tau }+CK\bigr)} \bigr\} X(s)= x(0). $$
(16)

The characteristic equation of system (14) is

$$ \det \bigl(\Delta (s) \bigr)=\det \bigl(s\bigl(I-(1-\alpha ) \bigl(A+Be^{-s\tau }+CK\bigr)\bigr)- \alpha \bigl(A+Be^{-s\tau }+CK\bigr) \bigr)=0. $$

Using the same method, we can easily obtain following theorems.

Theorem 3.3

System (5) is asymptotically stable if and only if the real parts of roots to the characteristic equation of system (5) are negative.

Theorem 3.4

System (5) is asymptotically stable if the following inequalities hold:

$$ \begin{gathered} (\mathrm{a}) \quad (1-\alpha ) \bigl( \Vert A+CK \Vert + \Vert B \Vert \bigr)< 1; \\ (\mathrm{b}) \quad \mu (A+CK)+\sqrt{{\rho ^{2}} {(B_{u})}+{ \rho ^{2}} {(B_{l})}} \\ \hphantom{(\mathrm{b}) \quad}\quad{} +(1-\alpha )\frac{{ \Vert {(A+CK)^{2}} \Vert + \Vert (A+CK)B+B(A+CK) \Vert + \Vert {B^{2}} \Vert }}{{1-(1- \alpha )( \Vert A+CK \Vert + \Vert B \Vert )}}< 0. \end{gathered} $$
(17)

4 Numerical examples

Example 4.1

Consider the stability of the following fractional-order system with time delay:

$$ {}_{\mathrm{CF}}D^{\alpha }x(t)=\frac{{d^{\alpha }x(t)}}{{dt^{\alpha }}}=Ax(t)+Bx(t- \tau ), $$
(18)

where \(\alpha =0.960\), and

A= ( − 9.1473 2.4510 − 2.4510 − 9.1473 ) ,B= ( 1.0142 − 0.2718 0.2718 1.0142 ) .

A Matlab program was written to help us to validate the conditions in Theorem 3.2. By computing we have

$$ \begin{gathered} (1-\alpha ) \bigl( \Vert A \Vert + \Vert B \Vert \bigr)=0.4208< 1, \\ \mu (A)+\sqrt{{\rho ^{2}} {(B_{u})}+{\rho ^{2}} {(B_{l})}}+(1-\alpha )\frac{ { \Vert {A^{2}} \Vert + \Vert AB+BA \Vert + \Vert {B^{2}} \Vert }}{{1-(1-\alpha )( \Vert A \Vert + \Vert B \Vert )}}=-0.4544< 0. \end{gathered} $$

Therefore from Theorem 3.2 we have that the fractional system (18) is asymptotically stable. In fact, we further get that this system is stable for all \(\alpha \in [0.960, 1)\).

5 Conclusions

In summary, this paper mainly presents a necessary and sufficient stability condition and some brief sufficient stability conditions for fractional-order described by the Caputo–Fabrizio derivative linear system with time delay. The proposed method is quite different from the other in the literature. Numerical experiments demonstrate that this method is feasible.