Sliding-mode ${H_{\infty}}$ synchronization for complex dynamical network systems with Markovian jump parameters and time-varying delays

Abstract

This paper is devoted to the investigation of the sliding-mode controller design problem for a class of complex dynamical network systems with Markovian jump parameters and time-varying delays. On the basis of an appropriate Lyapunov–Krasovskii functional, a set of new sufficient conditions is developed which not only guarantee the stochastic stability of the sliding-mode dynamics, but also satisfy the ${H_{\infty}}$ performance. Next, an integral sliding surface is designed to guarantee that the closed-loop error system reach the designed sliding surface in a finite time. Finally, an example is given to illustrate the validity of the obtained theoretical results.

1 Introduction

In recent years, increasing attention has been drawn to the problem of complex networks due to their potential applications in many real-world systems, such as biological systems, chemical systems, social systems and technological systems. In particular, the synchronization phenomena in complex dynamical networks system have attracted rapidly increasing interests, which mean that all nodes can reach a common state. Several famous network models, such as the scale-free model [1] and the small-word model [2, 3], which accurately characterize some important natural structures, have been researched. Complex dynamical network are prominent in describing the sophisticated collaborative dynamics in many fields of science and engineering [4,5,6].

The feature of time delay exists extensively in many real-world systems. It is well known that the existence of time delay in a network can make system instable and degrade its performance. In recent decades, considerable attention has been devoted to the time-delay systems due to their extensive applications in practical systems including circuit theory, neural network [7,8,9,10] and complex dynamical networks system [11,12,13,14,15,16] etc. Thus, synchronization for complex dynamical networks with time delays in the dynamical nodes and coupling has become a key and significant topic. Some researchers have proposed some results in this area. In [11], the author proposed pinning control scheme to achieve synchronization for singular complex networks with mixed time delays. Based on impulsive control method, the authors in [12, 13] studied projective synchronization between general complex networks with coupling time-varying delay and multiple time-varying delays [14], respectively. Based on sampled-data control [15], the authors proposed a method with finite-time ${H_{\infty}}$ synchronization in Markovian jump complex networks with time-varying delays. Based on pinning impulsive control [17], the problem of exponential synchronization of Lur’e complex dynamical network with delayed coupling was studied.

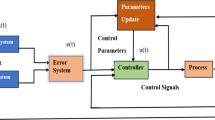
The dynamical behaviors of all nodes in complex dynamical networks are not always the same. Thus, many authors have studied the characteristics of all nodes in CDNs with the help of digital controllers, such as pinning control [18,19,20,21], sampled-data control [22, 23], impulsive control [24,25,26] and sliding control [27,28,29,30] and so on. Under an important pinning control approach, by a minimum number of controllers, the system can reached the predetermined goal. Under a sampled-data controller, the states of the control systems at sampling instants are adjusted continuously by using zero-order holder. Under an impulsive controller, states of the control systems are adjusted at discrete-time sampling instants. Under sliding control, in the design of the sliding surface, a set of specified matrices are employed to establish the connections among sliding surface corresponding to every mode. No matter what control strategy is adopted, the ultimate goal is to make the system stable and achieve our intended results. In this paper, the goal is to select suitable sliding control to synchronize complex networks with Markovian jump parameters and time delays.

The sliding-mode control methods were initiated in the former Soviet Union about 40 years ago, and since then the sliding-mode control methodology has been receiving much more attention within the last two decades. Sliding-mode control is widely adopted in lots of complex and engineering systems, including time delays [31,32,33] stochastic systems [34, 35], singular systems [36,37,38], Markovian jumping systems [39,40,41], and fuzzy systems [42,43,44]. As is well known, system performance may be degraded by the affection of the presence of nonlinearities and external disturbances. In [32], a sliding-mode approach is proposed for the exponential ${H_{\infty}}$ synchronization problem of a class of master–slave time-delay systems with both discrete and distributed time delays. In [34], the authors were concerned with event-triggered sliding-mode control for an uncertain stochastic system subject to limited communication capacity. In [38], this paper is concerned with non-fragile sliding-mode control of discrete singular systems with external disturbance. In [41], the authors considered sliding-mode control design for singular stochastic Markovian jump systems with uncertainties. The main advantage of the sliding mode is low sensitivity to plant parameter variation and disturbance, which eliminate the necessity of exact modeling.

Markovian jump systems including time-evolving and event-driven mechanisms have the advantage of better representing physical systems with random changes in both structure and parameters. Much recent attention has been paid to the investigation of these systems. When complex dynamical networks systems experience abrupt changes in their structure, it is natural to model them by Markovian jump complex networks systems. A great deal of literature has been published to study the Markovian jump complex networks systems; see [11, 14, 15, 19, 23, 28] for instance.

Up to now, unfortunately, there have only been few papers related to the topic of synchronization of complex dynamical networks with Markovian jump parameters and time-varying delays coupling in the dynamical nodes. So it is challenging to solve this synchronization problem for complex dynamical networks. Motivated by the aforementioned discussion, this paper aims to study the ${H_{\infty}}$ synchronization of complex dynamical network system. To achieve the ${H_{\infty}}$ synchronization of complex dynamical networks with Markovian jump parameter, the integral sliding surface is designed, and a novel sliding-mode controllers is proposed. The main contributions of this article are summarized as follows: (1) This paper extends previous work on the synchronization problem for complex dynamical network systems with Markovian jump parameters and time-varying delays and derives some new theoretical results. (2) An appropriate integral sliding-mode surface is constructed such that the reduced-order equivalent sliding motion can adjust the effect of the chattering phenomenon. (3) Using a Lyapunov–Krasovskii functional and a sliding-mode controller, we establish new sufficient conditions in terms of LMIs to ensure the stochastic stability and the ${H_{\infty}}$ performance condition.

Notation

${R^{n}}$ denotes the n dimensional Euclidean space; ${R^{m \times n}}$ represents the set of all $m \times n$ real matrices. For a real asymmetric matrix X and Y, the notation $X \geqslant Y$ (respectively, $X > Y$ ) means $X - Y$ is semi-positive definite (respectively, positive definite). The superscript T denotes matrix transposition. Moreover, in symmetric block matrices, ∗ is used as an ellipsis for the terms that are introduced by asymmetry and $\operatorname{diag} \{ \cdots \}$ denotes a block-diagonal matrix. The notation $A \otimes B$ stands for the Kronecker product of matrices A and B. $\Vert \, { \cdot }\, \Vert$ stands for the Euclidean vector norm. ${\mathcal {E}}$ stands for the mathematical expectation. If not explicitly stated, matrices are assumed to have compatible dimensions.

2 System description and preliminary lemma

Let $\{ r(t)\ (t \ge0)\}$ be a right-continuous Markovian chain on the probability space $(\varOmega,F, {\{ {F_{t}}\} _{t \ge0}},P)$ taking a value in the finite space ${\mathcal {S}} = \{ 1,2, \ldots,m\}$, with generator $\varPi = {\{ {\pi_{ij}}\} _{m \times m}}$ ($i,j \in {\mathcal {S}}$) given as follows:

$$\operatorname{Pr} ({r_{t + \Delta t}} = j|{r_{t}} = i) = \textstyle\begin{cases} {\pi_{ij}}\Delta t + o(\Delta t),& i \ne j, \\ 1 + {\pi_{ij}}\Delta t + o(\Delta t),& i = j, \end{cases} $$

where $\Delta t > 0$, $\lim_{\Delta t \to0} (o\Delta t/\Delta t) = 0$, and ${\pi_{ij}}$ is the transition rate from mode i to mode j satisfying ${\pi_{ij}} \ge0$ for $i \ne j$ with ${\pi_{ij}} = - \sum_{j = 1\, j \ne i}^{m} {{\pi _{ij}}}$ ($i,j \in{\mathcal {S}}$).

The following complex dynamical network systems of N identical nodes is considered, in which each node consists of an n-dimensional dynamical subsystem with Markovian jump parameter and time delay:

$$ \textstyle\begin{cases} {{\dot{x}}_{k}} ( t ) = A ( {r ( t )} ){x_{k}} ( t ) + C ( {r ( t )} )f ( {{x_{k}} ( t )} ) + {\sigma_{1}}\sum_{j = 1}^{N} {{g_{kj}}{\varGamma_{1}} ( {r ( t )} ){x_{j}} ( t )} \\ \hphantom{{{\dot{x}}_{k}} ( t ) ={}}{} + {\sigma_{2}}\sum_{j = 1}^{N} {{g_{kj}}{\varGamma_{2}} ( {r ( t )} ){x_{j}} ( {t - \tau ( t )} )} + D ( {r ( t )} ){w_{k}} ( t ) + B ( {r ( t )} ){u_{k}} ( t ), \\ {z_{k}} ( t ) = E ( {r ( t )} ){x_{k}} ( t ) ,\quad k = 1,2, \ldots,N, \end{cases} $$

(1)

where ${x_{k}} ( t ) = ( {{x_{k1}},{x_{k2}}, \ldots ,{x_{kn}}} )^{T} \in{R^{n}}$ represents the state vector of the kth node of the complex dynamical system; ${u_{k}} ( t )$ denote the control input and ${w_{k}} ( t )$ is the disturbance; $f ( {{x_{k}} ( t )} )$ is for vector-valued nonlinear functions; $A ( {r ( t )} )$, $C ( {r ( t )} )$, $D ( {r ( t )} )$ and $B ( {r ( t )} )$ are matrix functions of the random jumping process $\{ {r ( t )} \}$; ${\varGamma_{1}} ( {r ( t )} )$ and ${\varGamma_{2}} ( {r ( t )} )$ represent the inner coupling matrix of the complex networks; ${\sigma_{1}}$ and ${\sigma_{2}} > 0$ denote the non-delayed and delayed coupling strengths. $G = { ( {{g_{kj}}} )_{N \times N}}$ is the out-coupling matrix representing the topological structure of the complex networks, in which ${g_{kj}}$ is defined as follows: if there exists a connection between node k and node j (${k \ne j}$), then ${g_{kj}} = {g_{jk}} = 1$, otherwise, ${g_{kj}} = {g_{jk}} = 0$ (${k \ne j}$). The row sums of G are zero, that is, $\sum_{j = 1}^{N} {{g_{kj}}} = - {g_{kk}}$, $k = 1,2, \ldots,N$. The bounded function $\tau ( t )$ represents unknown discrete-time delays of the system. The time delay $\tau ( t )$ is assumed to satisfy the condition as follows:

$$ 0 \le\tau ( t ) \le\tau,\qquad 0 \le\dot{\tau}( t ) \le\bar{\tau}, $$

(2)

where τ and τ̄ are given nonnegative constants.

Assumption 2.1

For all $x,y \in{R^{n}}$, the nonlinear function $f ( \cdot )$ is continuous and assumed to satisfy the following sector-bounded nonlinearity condition:

$$ { \bigl[ {f ( x ) - f ( y ) - {U_{1}} ( {x - y} )} \bigr]^{T}} \bigl[ {f ( x ) - f ( y ) - {U_{2}} ( {x - y} )} \bigr] \le0, $$

(3)

where ${U_{1}}$ and ${U_{2}} \in{R^{n \times n}}$ are known constant matrices with ${U_{2}} - {U_{1}} > 0$. For presentation simplicity and without loss of generality, it is assumed that $f ( 0 ) = 0$.

Definition 2.1

([41])

The complex dynamical network systems (1) is said to be stochastically stable, if any $e ( 0 ) \in{R^{n}}$ and ${r_{0}} \in{\mathcal {S}}$ there exists a scalar$\tilde{M} ( {e ( 0 ),{r_{0}}} ) > 0$ such that

$$\lim_{t \to\infty} {\mathcal {E}} \biggl\{ { \int_{0}^{t} {{e^{T}} \bigl( {s,e ( 0 ),{r_{0}}} \bigr)e \bigl( {s,e ( 0 ),{r_{0}}} \bigr)} } \biggr\} \le\tilde{M} \bigl( {e ( 0 ),{r_{0}}} \bigr), $$

where $e ( {t,e ( 0 ),{r_{0}}} )$ denotes the solution under the initial condition $e ( 0 )$ and ${r_{0}}$. And ${e_{k}} ( t ) = {x_{k}} ( t ) - s ( t )$ is the synchronization error of the complex dynamical network system, and $s ( t ) \in{R^{n}}$ can be an equilibrium point, or a (quasi-)periodic orbit, or an orbit of a chaotic attractor, which satisfies $\dot{s} ( t ) = A ( {r ( t )} )s ( t ) + C ( {r ( t )} )f ( {s ( t )} )$.

Definition 2.2

([32])

The ${H_{\infty}}$ performance measure of the systems (1) is defined as

$${J_{\infty}} = {\mathcal {E}} \biggl( { \int_{0}^{\infty}{{z_{e}} {{ ( t )}^{T}} {z_{e}} ( t ) - {\gamma^{2}} {w^{T}} ( t )w ( t )\,dt} } \biggr), $$

where the positive scalar γ is given.

Lemma 2.1

(Jensen’s inequality)

For a positive matrix M, scalar ${h_{U}} > {h_{L}} > 0$ the following integrations are well defined:

• (1) $- ({h_{U}} - {h_{L}})\int_{t - {h_{U}}}^{t - {h_{L}}} {{x^{T}}(s)} Mx(s)\,ds \le - (\int_{t - {h_{U}}}^{t - {h_{L}}} {{x^{T}}(s)\,ds} )M(\int_{t - {h_{U}}}^{t - {h_{L}}} {{x^{T}}(s)\,ds} )$,

• (2) $- (\frac{{h_{U}^{2} - h_{L}^{2}}}{2})\int_{t - {h_{U}}}^{t - {h_{L}}} {\int_{s}^{t} {{x^{T}}(u)Mx(u)} } \,du\,ds \le - (\int_{t - {h_{U}}}^{t - {h_{L}}} {\int_{s}^{t} {{x^{T}}(u)} } \,du\,ds)M(\int _{t - {h_{U}}}^{t - {h_{L}}} {\int_{s}^{t} {x(u)} } \,du\,ds)$.

Lemma 2.2

([11])

If for any constant matrix $R \in R{^{m \times m}}$, $R = {R^{T}} > 0$, scalar $\gamma > 0$ and a vector function $\phi:[0,\gamma] \to R{^{m}}$ such that the integrations concerned are well defined, the following inequality holds:

$$-\gamma {\int }_{t-\gamma }^t{\dot{\varphi }}^T(s)R\dot{\varphi }(s)ds\le {\left(\begin{array}{c}\varphi (t)\\ \varphi (t-\gamma )\end{array}\right)}^T\left(\begin{array}{cc}-R& R\\ \ast & -R\end{array}\right)\left(\begin{array}{c}\varphi (t)\\ \varphi (t-\gamma )\end{array}\right).$$

Lemma 2.3

([45])

Let ⊗ denote the Kronecker product. A, B, C and D are matrices with appropriate dimensions. The following properties hold:

• (1) $( {cA} ) \otimes B = A \otimes ( {cB} )$, for any constant c,

• (2) $( {A + B} ) \otimes C = A \otimes C + B \otimes C$,

• (3) $( {A \otimes B} ) ( {C \otimes D} ) = ( {AC} ) \otimes ( {BD} )$,

• (4) ${ ( {A \otimes B} )^{T}} = {A^{T}} \otimes{B^{T}}$,

• (5) ${ ( {A \otimes B} )^{ - 1}} = ( {{A^{ - 1}} \otimes{B^{ - 1}}} )$.

For the sake of simplicity, when $r ( t ) = i$, we denote ${A_{i}}$, ${C_{i}}$, ${B_{i}}$, ${D_{i}}$, ${\varGamma_{1i}}$, ${\varGamma_{2i}}$ as $A ( {r ( t )} )$, $C ( {r ( t )} )B ( {r ( t )} )$, $D ( {r ( t )} )$, ${\varGamma_{1}} ( {r ( t )} )$, ${\varGamma_{2}} ( {r ( t )} )$. Let $e ( t ) = x ( t ) - s ( t )$ be the synchronization error of system from the initial mode ${r_{0}}$. Then the error dynamical, namely, the synchronization error system can be expressed by

$$ \textstyle\begin{cases} {{\dot{e}}_{k}} ( t ) = {A_{i}}{e_{k}} ( t ) + {C_{i}}g ( {{e_{k}} ( t )} ) + {\sigma_{1}}\sum_{j = 1}^{N} {{g_{kj}}{\varGamma_{1i}}{e_{j}} ( t )} + {\sigma_{2}}\sum_{j = 1}^{N} {{g_{kj}}{\varGamma_{2i}}{e_{j}} ( {t - d ( t )} )} \\ \hphantom{{{\dot{e}}_{k}} ( t ) ={}}{}+ {B_{i}}{u_{k}} ( t ) + {D_{i}}{w_{k}} ( t ) , \\ {z_{k}} ( t ) = {E_{i}}{e_{k}} ( t ),\quad k = 1,2, \ldots,N, \end{cases} $$

(4)

where $g ( {{e_{k}} ( t )} ) = f ( {{x_{k}} ( t )} ) - f ( {{s_{k}} ( t )} )$.

Now, the original synchronization problem can be replace by the equivalent problem of the stability the system (4) by a suitable choice of the sliding-mode control. In the following, the sliding-mode controller will be designed using variable structure control and sliding-mode control methods [46]. Let us introduce the sliding surface as

$$\begin{aligned} {S_{k}} ( {t,i} ) =& {V_{i}} {e_{k}} ( t ) - {V_{i}} \int _{0}^{t} \Biggl[ ( {{A_{i}} - {B_{i}} {K_{i}}} ){e_{k}} ( s ) + { \sigma_{1}}\sum_{j = 1}^{N} {{g_{kj}} {\varGamma_{1i}} {e_{k}} ( s )} \\ &{} + {\sigma_{2}}\sum_{j = 1}^{N} {{g_{kj}} {\varGamma_{2i}} {e_{k}} \bigl( {s - d ( s )} \bigr)} \Biggr]\,ds. \end{aligned}$$

(5)

${V_{i}} \in{R^{m \times n}}$, ${K_{i}} \in{R^{r \times n}}$ are real matrices to be designed. ${V_{i}}$ is designed such that ${V_{i}}{B_{i}}$ is non-singular. It is clear that ${\dot{S}_{k}} ( {t,i} ) = 0$ is a necessary condition for the state trajectory to stay on the switching surface ${S_{k}} ( {t,i} ) = 0$. Therefore, by ${\dot{S}_{k}} ( {t,i} ) = 0$ and (4), we get

$$ 0 = {V_{i}} {B_{i}} {K_{i}} {e_{k}} ( t ) + {V_{i}} {C_{i}}g \bigl( {{e_{k}} ( t )} \bigr) + {V_{i}} {B_{i}} {u_{k}} + {V_{i}} {D_{i}} {w_{k}} ( t ). $$

(6)

Solving Eq. (6) for ${u_{k}} ( t )$

$$ {u_{keq}} ( t ) = - {K_{i}} {e_{k}} ( t ) - {\hat{V}_{i}} {C_{i}}g \bigl( {{e_{k}} ( t )} \bigr) - {\hat{V}_{i}} {D_{i}} {w_{k}} ( t ), $$

(7)

where ${\hat{V}_{i}} = { ( {{V_{i}}{B_{i}}} )^{ - 1}}{V_{i}}$.

Substituting (7) into (4), the error dynamics with sliding mode is given as follows:

$$ \textstyle\begin{cases} {{\dot{e}}_{k}} ( t ) = ( {{A_{i}} - {B_{i}}{K_{i}}} ){e_{k}} ( t ) + ( {{C_{i}} - {B_{i}}{{\hat{V}}_{i}}{C_{i}}} )g ( {{e_{k}} ( t )} ) \\ \hphantom{{{\dot{e}}_{k}} ( t ) ={}}{} + {\sigma_{1}}\sum_{j = 1}^{N} {{g_{kj}}{\varGamma_{1i}}{e_{j}} ( t )} + {\sigma_{2}}\sum_{j = 1}^{N} {{g_{kj}}{\varGamma_{2i}}{e_{j}} ( {t - d ( t )} )} + ( {I - {B_{i}}{{\hat{V}}_{i}}} ){D_{i}}{w_{k}} ( t ) , \\ {z_{k}} ( t ) = {E_{i}}{e_{k}} ( t ) . \end{cases} $$

(8)

Or equivalently

$$ \textstyle\begin{cases} e ( t ) = ( {{I_{N}} \otimes ( {{A_{i}} - {B_{i}}{K_{i}}} )} )e ( t ) + ( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}}{{\hat{V}}_{i}}{C_{i}}} )} )g ( {e ( t )} ) \\ \hphantom{e ( t ) ={}}{} + {\sigma_{1}} ( {G \otimes{\varGamma_{1i}}} )e ( t ) + {\sigma_{2}} ( {G \otimes{\varGamma_{2i}}} )e ( t ) + ( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}}{{\hat{V}}_{i}}{D_{i}}} )} )w ( t ) , \\ z ( t ) = ( {{I_{N}} \otimes{E_{i}}} )e ( t ). \end{cases} $$

(9)

The problem to be addressed in this paper is formulated as follows: given the complex dynamical network system (1) with Markovian jump parameters and time delays, finding a mode-dependent sliding mode stochastically stable and ${H_{\infty}}$ synchronization control $u ( t )$ with any $r ( t ) = i \in{\mathcal {S}}$ for the error system (4) is stochastically stable and satisfies an ${H_{\infty}}$ norm bound γ, i.e. ${J_{\infty}} < 0$.

3 Main results

The purpose of this section is to solve the problem of ${H_{\infty}}$ synchronization. More specifically, we will establish LMI conditions to check whether the sliding-mode dynamics have ideal properties, such as being stochastically stable and ${H_{\infty}}$ synchronization. The relevant conclusion of the stability analysis is provided in the following theorem.

3.1 Stability analysis

Theorem 3.1

Let the matrices ${V_{i}}$, ${K_{i}}$ (${i = 1,2, \ldots,N}$) with $\det ( {{V_{i}}{B_{i}}} ) \ne0$ be given. The complex dynamical network system (1) with Markovian jump parameter is stochastically stable and shows ${H_{\infty}}$ synchronization in the sense of Definition 2.1 and Definition 2.2, if there exist some positive definite matrices ${P_{i}}$, ${Q_{1}}$, ${Q_{2}}$, ${X_{\iota}}$ (${\iota = 1,2,3}$) such that the following matrix holds for any $i \in{\mathcal {S}}$:

$${\Phi }_i=\left[\begin{array}{ccccccc}{\Phi }_{11}& {\Phi }_{12}& -X_2& \frac{2}{\tau }{X}_3& {\Phi }_{15}& {\Phi }_{16}& {\Phi }_{17}\\ \ast & -(1-\overline{\tau })Q_1& 0& 0& 0& {\Phi }_{26}& 0\\ \ast & \ast & -Q_2+X_2& 0& 0& 0& 0\\ \ast & \ast & \ast & -\frac{X_1}{\tau }-\frac{2X_3}{{\tau }^2}& 0& 0& 0\\ \ast & \ast & \ast & \ast & -\epsilon I& {\Phi }_{56}& 0\\ \ast & \ast & \ast & \ast & \ast & {\Phi }_{66}& {\Phi }_{67}\\ \ast & \ast & \ast & \ast & \ast & \ast & -e^{-2\alpha \tau }{\gamma }^2\end{array}\right]<0,$$

(10)

where

$$\begin{aligned}& \begin{aligned} {\varPhi_{11}} &= \operatorname{sym} \bigl( { ( {{I_{N}} \otimes{P_{i}}} ) \bigl( {{I_{N}} \otimes ( {{A_{i}} - {B_{i}} {K_{i}}} )} \bigr)} \bigr) + \operatorname{sym} \bigl( { ( {{I_{N}} \otimes{P_{i}}} ) ( {G \otimes {\varGamma_{1i}}} )} \bigr) \\ &\quad {}+ {Q_{1}} + {Q_{2}}+ \tau{X_{1}} + {X_{2}} - 2{X_{3}} - \varepsilon\bar{R} + \varLambda_{1}^{T} \bigl( {{I_{N}} \otimes ( {{A_{i}} - {B_{i}} {K_{i}}} )} \bigr) \\ &\quad {}+ {\sigma_{1}}\varLambda_{1}^{T} ( {G \otimes{\varGamma_{1i}}} ) + {e^{ - 2\alpha\tau}} { ( {{I_{N}} \otimes E} )^{T}} ( {{I_{N}} \otimes E} ) , \end{aligned} \\& {\varPhi_{12}} = {\sigma_{2}} ( {{I_{N}} \otimes{P_{i}}} ) ( {G \otimes{\varGamma_{2i}}} ) + {\sigma _{2}}\varLambda_{1}^{T} ( {G \otimes{ \varGamma_{2i}}} ), \\& {\varPhi_{15}} = ( {{I_{N}} \otimes{P_{i}}} ) \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{\hat{V}}_{i}} {C_{i}}} )} \bigr) + \varLambda_{1}^{T} \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{ \hat{V}}_{i}} {C_{i}}} )} \bigr) - \varepsilon\bar{S}, \\& {\varPhi_{16}} = - \varLambda_{1}^{T} + { \bigl( {{I_{N}} \otimes ( {{A_{i}} - {B_{i}} {K_{i}}} )} \bigr)^{T}} {\varLambda_{2}} + {\sigma _{1}} { ( {G \otimes{\varGamma_{1i}}} )^{T}} { \varLambda_{2}}, \\& {\varPhi_{17}} = ( {{I_{N}} \otimes{P_{i}}} ) \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{\hat{V}}_{i}} {D_{i}}} )} \bigr) + \varLambda_{1}^{T} \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{ \hat{V}}_{i}} {D_{i}}} )} \bigr), \\& {\varPhi_{26}} = {\sigma_{2}} { ( {G \otimes{ \varGamma_{2i}}} )^{T}} {\varLambda_{2}}, \\& {\varPhi_{56}} = - \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{\hat{V}}_{i}} {C_{i}}} )} \bigr){\varLambda_{2}}, \\& {\varPhi_{66}} = {\tau^{2}} {X_{2}} + \frac{{{\tau^{2}}}}{2}{X_{3}} - 2\varLambda_{2}^{T}, \\& {\varPhi_{67}} = \varLambda_{2}^{T} \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{\hat{V}}_{i}} {D_{i}}} )} \bigr). \end{aligned}$$

Proof

Design the following positive definition functional for the system:

$$ V \bigl( {e ( t ),i,t} \bigr) = {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) + {V_{2}} \bigl( {e ( t ),i,t} \bigr) + {V_{3}} \bigl( {e ( t ),i,t} \bigr), $$

(11)

where

$$\begin{aligned}& {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) = \sum _{k = 1}^{N} {e_{k}^{T} ( t ){P_{i}} {e_{k}} ( t )} , \end{aligned}$$

(12)

$$\begin{aligned}& {V_{2}} \bigl( {e ( t ),i,t} \bigr) = \int_{t - \tau ( t )}^{t} {{e^{T}} ( s ){Q_{1}}e ( s )\,ds} + \int_{t - \tau}^{t} {e^{T}} ( s ){Q_{2}}e ( s )\,ds, \end{aligned}$$

(13)

$$\begin{aligned}& \begin{aligned}[b] {V_{3}} \bigl( {e ( t ),i,t} \bigr) &= \int_{ - \tau}^{t} { \int _{t + \theta}^{t} {{e^{T}} ( s ){X_{1}}e ( s )\, ds\, d\theta } } + \tau \int_{ - \tau}^{0} { \int_{t + \theta}^{t} {{{\dot{e}}^{T}} ( s ){X_{2}}\dot{e} ( s )\, ds\, d\theta} } \\ &\quad {}+ \int_{ - \tau}^{0} { \int_{\upsilon}^{0} { \int_{t + \theta}^{t} {{{\dot{e}}^{T}} ( s ){X_{3}}e ( s )} } }\, ds\, d\theta \, d\upsilon. \end{aligned} \end{aligned}$$

(14)

By the definition of the infinitesimal operator ${\mathcal {L}}$ of the stochastic Lyapunov–Krasovskii functional in [47], we obtain

$$\begin{aligned} {\mathcal {L}}V\bigl(e(t),i,t\bigr)& = \lim_{\Delta t \to0} \frac{1}{\Delta } \bigl[ {{\mathcal {E}} \bigl[ {V\bigl(e(t + \Delta),{r_{i + \Delta}},t + \Delta\bigr)} \bigr]\left \vert {x(t),{r_{t = i}}} \right .} \bigr] - V\bigl(x(t),i,t\bigr) \\ & = {V_{t}} \bigl( {e ( t ),i,t} \bigr) + {{\dot{e}}^{T}} ( t ){V_{e}} \bigl( {e ( t ),i,t} \bigr) + \sum _{j = 1}^{m} {{\pi_{ij}}V} \bigl( {e ( t ),i,t} \bigr) . \end{aligned}$$

(15)

Calculating the infinitesimal generator of $V ( {e ( t ),i,t} )$ along the trajectory of the error sliding-mode dynamics (8) and (9), we obtain

$$\begin{aligned}& {\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) = 2 \sum_{k = 1}^{N} {e_{k}^{T} ( t ){P_{i}} {{\dot{e}}_{k}} ( t )} \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr)} = 2\sum_{k = 1}^{N} {e_{k}^{T} ( t ){P_{i}} ( {{A_{i}} - {B_{i}} {K_{i}}} ){e_{k}} ( t )} \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{} + 2\sum_{k = 1}^{N} {e_{k}^{T} ( t ){P_{i}} ( {{C_{i}} - {B_{i}} {{\hat{V}}_{i}} {C_{i}}} )g \bigl( {e ( t )} \bigr)} \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{}+ 2{\sigma_{1}}\sum_{k = 1}^{N} {e_{k}^{T} ( t ){P_{i}}\sum _{j = 1}^{N} {{g_{kj}} {\varGamma_{1i}} {e_{j}} ( t )} } \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{} + 2{\sigma_{2}}\sum_{k = 1}^{N} {e_{k}^{T} ( t ){P_{i}}\sum _{j = 1}^{N} {{g_{kj}} {\varGamma_{2i}} {e_{j}} \bigl( {t - \tau ( t )} \bigr)} } \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{} + 2\sum_{k = 1}^{N} {e_{k}^{T} ( t ){P_{i}} ( {{D_{i}} - {B_{i}} {{\hat{V}}_{i}} {D_{i}}} ){w_{k}} ( t )} \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr)} = 2{e^{T}} ( t ) ( {{I_{N}} \otimes{P_{i}}} ) \bigl( {{I_{N}} \otimes ( {{A_{i}} - {B_{i}} {K_{i}}} )} \bigr)e ( t ) \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{} + 2{e^{T}} ( t ) ( {{I_{N}} \otimes{P_{i}}} ) \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{\hat{V}}_{i}} {C_{i}}} )} \bigr)g \bigl( {e ( t )} \bigr) \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{} + 2{\sigma_{1}} {e^{T}} ( t ) ( {{I_{N}} \otimes{P_{i}}} ) ( {G \otimes{ \varGamma_{1i}}} )e ( t ) \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{} + 2{\sigma_{2}} {e^{T}} ( t ) ( {{I_{N}} \otimes{P_{i}}} ) ( {G \otimes{ \varGamma_{2i}}} )e \bigl( {t - \tau ( t )} \bigr) \\& \hphantom{{\mathcal {L}} {V_{1}} \bigl( {{e_{k}} ( t ),i,t} \bigr) ={}}{} + 2{e^{T}} ( t ) ( {{I_{N}} \otimes{P_{i}}} ) \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{\hat{V}}_{i}} {D_{i}}} )} \bigr)w ( t ), \end{aligned}$$

(16)

$$\begin{aligned}& \begin{aligned}[b] {\mathcal {L}} {V_{2}} \bigl( {e ( t ),i,t} \bigr) &= {e^{T}} ( t ) ( {{Q_{1}} + {Q_{2}}} )e ( t ) - \bigl( {1 - \dot{\tau}( t )} \bigr){e^{T}} \bigl( {t - \tau ( t )} \bigr){Q_{1}}e \bigl( {t - \tau ( t )} \bigr) \\ &\quad {} - {e^{T}} ( {t - \tau} ){Q_{2}}e ( {t - \tau} ) \\ &\le{e^{T}} ( t ) ( {{Q_{1}} + {Q_{2}}} )e ( t ) - ( {1 - \bar{\tau}} ){e^{T}} \bigl( {t - \tau ( t )} \bigr){Q_{1}}e \bigl( {t - \tau ( t )} \bigr) \\ &\quad {}- {e^{T}} ( {t - \tau} ){Q_{2}}e ( {t - \tau} ), \end{aligned} \end{aligned}$$

(17)

$$\begin{aligned}& \begin{aligned}[b] {\mathcal {L}} {V_{3}} \bigl( {e ( t ),i,t} \bigr) &= \tau {e^{T}} ( t ){X_{1}}e ( t ) - \int_{t - \tau}^{t} {{e^{T}} ( t ){X_{1}}e ( t )\,ds} + {\tau^{2}} {{\dot{e}}^{T}} ( t ){X_{2}}\dot{e} ( t ) \\ &\quad {}- \tau \int_{t - \tau}^{t} {{{\dot{e}}^{T}} ( t ){X_{2}}\dot{e} ( t )\,ds} + \int_{ - \tau}^{0} { \int_{\upsilon}^{0} {{{\dot{e}}^{T}} ( t ){X_{3}}\dot{e} ( t )\,d\theta \,d\upsilon} } \\ &\quad {}- \int_{ - \tau}^{0} { \int_{t + \upsilon}^{t} {{{\dot{e}}^{T}} ( t ){X_{3}}\dot{e} ( t )\,ds\,d\upsilon} } \\ &= \tau{e^{T}} ( t ){X_{1}}e ( t ) + {{\dot{e}}^{T}} ( t ) \biggl( {{\tau^{2}} {X_{2}} + \frac{{{\tau^{2}}}}{2}{X_{3}}} \biggr)\dot{e} ( t ) \\ &\quad {}- \int_{t - \tau}^{t} {{e^{T}} ( t ){X_{1}}e ( t )\,ds}- \tau \int_{t - \tau}^{t} {{{\dot{e}}^{T}} ( t ){X_{2}}\dot{e} ( t )\,ds} \\ &\quad {}- \int_{ - \tau}^{0} \int_{t + \upsilon}^{t} {{\dot{e}}^{T}} ( t ){X_{3}}\dot{e} ( t )\,ds\,d\upsilon. \end{aligned} \end{aligned}$$

(18)

According to Lemma 2.1 and Lemma 2.2, we have

$$\begin{aligned}& - \int_{t - \tau}^{t} {{e^{T}} ( s ){X_{1}}e ( s )\,ds} \le - \frac{1}{\tau}{ \biggl( { \int_{t - \tau}^{t} {e ( s )\,ds} } \biggr)^{T}} {X_{1}} \biggl( { \int_{t - \tau}^{t} {e ( s )\,ds} } \biggr), \end{aligned}$$

(19)

$$-\tau {\int }_{t-\tau }^t{\dot{e}}^T(s)X_2\dot{e}(s)ds\le {\left(\begin{array}{c}e(t)\\ e(t-\tau )\end{array}\right)}^T\left(\begin{array}{cc}-X_2& X_2\\ \ast & -X_2\end{array}\right)\left(\begin{array}{c}e(t)\\ e(t-\tau )\end{array}\right),$$

(20)

$$\begin{aligned}& - \int_{ - \tau}^{0} { \int_{t + \upsilon}^{t} {{{\dot{e}}^{T}} ( t ){X_{3}}\dot{e} ( t )\,ds\,d\upsilon} } \\& \quad \le - \frac{2}{{{\tau^{2}}}}{ \biggl( { \int_{ - \tau}^{0} { \int_{t + \upsilon}^{t} {\dot{e} ( t )\,ds\,d\upsilon} } } \biggr)^{T}} {X_{3}} \biggl( { \int_{ - \tau}^{0} { \int_{t + \upsilon}^{t} {\dot{e} ( t )\,ds\,d\upsilon} } } \biggr) \\& \quad = - \frac{2}{{{\tau^{2}}}}{ \biggl( {\tau e ( t ) - \int_{t - \tau}^{t} {e ( s )\,ds} } \biggr)^{T}} {X_{3}} \biggl( {\tau e ( t ) - \int_{t - \tau}^{t} {e ( s )\,ds} } \biggr) . \end{aligned}$$

(21)

For any matrices ${\varLambda_{1}}$ and ${\varLambda_{2}}$ with appropriate dimensions, the following equations hold:

$$\begin{aligned} 0 =& 2 \bigl[ {{e^{T}} ( t )\varLambda_{1}^{T} + {{ \dot{e}}^{T}} ( t )\varLambda_{2}^{T}} \bigr] \\ &{} \times\bigl[ - \dot{e} ( t ) + \bigl( {{I_{N}} \otimes ( {{A_{i}} - {B_{i}} {K_{i}}} )} \bigr)e ( t ) + \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{ \hat{V}}_{i}} {C_{i}}} )} \bigr)g \bigl( {e ( t )} \bigr) \\ &{} + {\sigma_{1}} ( {G \otimes{\varGamma_{1i}}} )e ( t ) + { \sigma_{2}} ( {G \otimes{\varGamma_{2i}}} )e \bigl( {t - \tau ( t )} \bigr) + \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{\hat{V}}_{i}} {D_{i}}} )} \bigr)w ( t ) \bigr]. \end{aligned}$$

(22)

It can be deduced from Assumption 2.1 that, for the matrices ${U_{1}}$ and ${U_{2}}$, the following inequalities hold:

$$y(t)=\epsilon {\left(\begin{array}{c}e(t)\\ g(e(t))\end{array}\right)}^T\left(\begin{array}{cc}\overline{R}& \overline{S}\\ \ast & I\end{array}\right)\left(\begin{array}{c}e(t)\\ g(e(t))\end{array}\right)\le 0,$$

(23)

where

$$\begin{aligned}& \bar{R} = \frac{{{{ ( {{I_{N}} \otimes{U_{1}}} )}^{T}} ( {{I_{N}} \otimes{U_{2}}} ) + ( {{I_{N}} \otimes{U_{2}}} ){{ ( {{I_{N}} \otimes{U_{1}}} )}^{T}}}}{2} , \\& \bar{S} = \frac{{{{ ( {{I_{N}} \otimes{U_{2}}} )}^{T}} + {{ ( {{I_{N}} \otimes{U_{1}}} )}^{T}}}}{2} . \end{aligned}$$

On the other hand, for a prescribed $\gamma > 0$, under zero initial condition, ${J_{\infty}}$ can be rewritten as

$$\begin{aligned} {J_{\infty}} \le&{\mathcal {E}}\biggl( { \int_{0}^{\infty}{{e^{ - 2\alpha t}} \bigl[ {{z^{T}} ( t )z ( t ) - {\gamma ^{2}} {w^{T}} ( t )w ( t )} \bigr]\,dt} + V \bigl( {e ( t ),i,t} \bigr)| {_{t \to\infty}}} \\ &{} - V \bigl( {e ( t ),i,t} \bigr)| {_{t = 0}} \biggr) \\ \le&{\mathcal {E}} \biggl( { \int_{0}^{\infty}{{e^{ - 2\alpha t}} \bigl[ {{z^{T}} ( t )z ( t ) - {\gamma^{2}} {w^{T}} ( t )w ( t )} \bigr] + {\mathcal {L}}V \bigl( {e ( t ),i,t} \bigr)\,dt} } \biggr) . \end{aligned}$$

(24)

From the obtained derivation terms in Eqs. (16)–(21) and adding Eqs. (22)–(23) into (24)

$$ {J_{\infty}} \le{\mathcal {E}} \biggl( { \int_{0}^{\infty}{{\xi^{T}} ( t ){ \varPhi_{i}}\xi ( t )\,dt} } \biggr), $$

(25)

where

$$\xi (t)={\left[\begin{array}{cccccc}{e}^T(t)& e^T(t-\tau )& e^T(t-\tau (t)){({\int }_{t-\tau }^{t}e(s)ds)}^T& g^T(e(t))& {\dot{e}}^T(t)& w^T(t)\end{array}\right]}^T.$$

According to the condition (10) in Theorem 3.1, it means that the condition ${J_{\infty}} < 0$ is satisfied. Moreover, ${J_{\infty}} < 0$ for $w ( t ) = 0$ implies ${\mathcal {E}} \{ {{\mathcal {L}}V ( {e ( t ),i,t} )} \} < 0$. Then we have

$$ {\mathcal {E}} \bigl\{ {{\mathcal {L}}V \bigl( {e ( t ),i,t} \bigr)} \bigr\} < - {a_{1}} {\mathcal {E}} \bigl\{ {{e^{T}} ( t )e ( t )} \bigr\} , $$

(26)

where ${a_{1}} = \min \{ {{\lambda_{\min}} ( { - {\varPhi _{i}}} ),i \in{\mathcal {S}}} \}$, then ${a_{1}} > 0$. By Dynkin’s formula, we have

$$ {\mathcal {E}} \biggl\{ { \int_{0}^{t} {{e^{T}} ( s )e ( s )\,ds} } \biggr\} \le a_{1}^{ - 1}V \bigl( {e ( 0 ),{r_{0}},0} \bigr) $$

(27)

and

$$ \lim_{t \to\infty} {\mathcal {E}} \biggl\{ { \int_{0}^{t} {{e^{T}} ( s )e ( s )\,ds} } \biggr\} \le a_{1}^{ - 1}V \bigl( {e ( 0 ),{r_{0}},0} \bigr). $$

(28)

Then from Definition 2.1, the sliding-mode dynamical system (9) is stochastically stable. This completes the proof. □

Remark 1

It should be pointed out that Theorem 3.1 provided a sufficient condition of stability for the sliding-mode complex dynamical network systems (9). But the parameter matrix is not given so we cannot apply the LMI toolbox of Matlab to solve them. According to Theorem 3.1 and the Schur complement, the strict LMI conditions will be given in the next theorem.

Theorem 3.2

Under Assumption 2.1, a synchronization law given in the form of Eq. (9) exists such that the Markovian jump synchronization error system (9) with time-varying delays is stochastically stable and an ${H_{\infty}}$ performance level $\gamma > 0$ in the sense of Definition 2.1 and Definition 2.2, if there exist some matrices ${Y_{i}}$, ${\hat{V}_{i}}$ and positive definite matrices ${M_{i}}$ (${i = 1,2, \ldots,s}$), ${\tilde{X}_{\iota}}$ (${\iota = 1,2,3}$), ${Q_{1}}$, ${Q_{2}}$ satisfying the following LMIs:

$$\begin{array}{c}\left[\begin{array}{ccccccccc}{\Sigma }_{11}& {\Sigma }_{12}& -{\tilde{X}}_2& \frac{2}{\tau }{\tilde{X}}_3& {\Sigma }_{15}& {\Sigma }_{16}& {\Sigma }_{17}& {\Sigma }_{18}& {\Sigma }_{19}\\ \ast & -(1-\overline{\tau }){\tilde{Q}}_1& 0& 0& 0& {\Sigma }_{26}& 0& 0& 0\\ \ast & \ast & -{\tilde{Q}}_2+{\tilde{X}}_2& 0& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & -\frac{{\tilde{X}}_1}{\tau }-\frac{2{\tilde{X}}_3}{{\tau }^2}& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & -\epsilon I& {\Sigma }_{56}& 0& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\Sigma }_{66}& {\Sigma }_{67}& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & -e^{-2\alpha \tau }{\gamma }^2& 0& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & -I& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\Sigma }_{99}\end{array}\right]\hfill \\ <0,\hfill \end{array}$$

(29)

$$\begin{aligned}& {\hat{V}_{i}} {B_{i}} = I, \end{aligned}$$

(30)

where

$$\begin{aligned}& \begin{aligned} {\varSigma_{11}} &= \operatorname{sym} \bigl( { \bigl( {{I_{N}} \otimes ( {{A_{i}} {M_{i}} - {B_{i}} {Y_{i}}} )} \bigr)} \bigr) + \operatorname{sym} \bigl( { ( {G \otimes {\varGamma_{1i}}} ) ( {{I_{N}} \otimes{M_{i}}} )} \bigr) + {{\tilde{Q}}_{1}} + {{\tilde{Q}}_{2}} \\ &\quad {}+ \tau{{\tilde{X}}_{1}} + {{\tilde{X}}_{2}} - 2{{ \tilde{X}}_{3}} + \tilde{\varLambda}_{1}^{T} \bigl( {{I_{N}} \otimes ( {{A_{i}} {M_{i}} - {B_{i}} {Y_{i}}} )} \bigr) \\ &\quad {}+ {\sigma_{1}}\tilde{\varLambda}_{1}^{T} ( {G \otimes{\varGamma_{1i}}} ) ( {{I_{N}} \otimes{M_{i}}} ), \end{aligned} \\& {\varSigma_{12}} = {\sigma_{2}} ( {G \otimes{ \varGamma_{2i}}} ) ( {{I_{N}} \otimes{M_{i}}} ) + { \sigma_{2}}\tilde{\varLambda}_{1}^{T} ( {G \otimes{ \varGamma_{2i}}} ) ( {{I_{N}} \otimes{M_{i}}} ), \\& \begin{aligned} {\varSigma_{15}} &= \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{\hat{V}}_{i}} {C_{i}}} )} \bigr) ( {{I_{N}} \otimes{M_{i}}} ) + \tilde{\varLambda}_{1}^{T} \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{\hat{V}}_{i}} {C_{i}}} )} \bigr) \\ &\quad {}- \varepsilon ( {{I_{N}} \otimes{M_{i}}} )\bar{S} , \end{aligned} \\& {\varSigma_{16}} = - \tilde{\varLambda}_{1}^{T} ( {{I_{N}} \otimes {M_{i}}} ) + { \bigl( {{I_{N}} \otimes ( {{A_{i}} {M_{i}} - {B_{i}} {Y_{i}}} )} \bigr)^{T}} {{\tilde{\varLambda}}_{2}} + { \sigma _{1}} ( {{I_{N}} \otimes{M_{i}}} ){ ( {G \otimes{\varGamma _{1i}}} )^{T}} {{\tilde{\varLambda}}_{2}}, \\& {\varSigma_{17}} = \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{\hat{V}}_{i}} {D_{i}}} )} \bigr) + \tilde{\varLambda}_{1}^{T} \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{ \hat{V}}_{i}} {D_{i}}} )} \bigr), \\& {\varSigma_{26}} = {\sigma_{2}} ( {{I_{N}} \otimes{M_{i}}} ){ ( {G \otimes{\varGamma_{2i}}} )^{T}} {{\tilde{\varLambda}}_{2}}, \\& {\varSigma_{56}} = - \bigl( {{I_{N}} \otimes ( {{C_{i}} - {B_{i}} {{\hat{V}}_{i}} {C_{i}}} )} \bigr){{\tilde{\varLambda}}_{2}}, \\& {\varSigma_{66}} = {\tau^{2}} {{\tilde{X}}_{2}} + \frac{{{\tau ^{2}}}}{2}{{\tilde{X}}_{3}} - 2 ( {{I_{N}} \otimes{M_{i}}} )\tilde{\varLambda}_{2}^{T}, \\& {\varSigma_{67}} = \tilde{\varLambda}_{2}^{T} \bigl( {{I_{N}} \otimes ( {{D_{i}} - {B_{i}} {{\hat{V}}_{i}} {D_{i}}} )} \bigr), \\& {\varSigma_{18}} = {e^{ - \alpha\tau}} ( {{I_{N}} \otimes {M_{i}}} ){ ( {{I_{N}} \otimes E} )^{T}}, \\& {\varSigma_{19}} = \bigl[ {\sqrt{{\pi_{i1}}} ( {{I_{N}} \otimes{M_{i}}} ), \sqrt{{\pi_{i2}}} ( {{I_{N}} \otimes {M_{i}}} ), \ldots, \sqrt{{ \pi_{is}}} ( {{I_{N}} \otimes{M_{i}}} )} \bigr], \\& {\varSigma_{99}} = \operatorname{diag} \bigl\{ { - ( {{I_{N}} \otimes{M_{1}}} ), - ( {{I_{N}} \otimes{M_{2}}} ), \ldots, - ( {{I_{N}} \otimes{M_{s}}} )} \bigr\} . \end{aligned}$$

Proof

Using the following diagonal matrix:

$$\operatorname{diag} \bigl\{ {{{ ( {{I_{N}} \otimes{P_{i}}} )}^{ - 1}},{{ ( {{I_{N}} \otimes{P_{i}}} )}^{ - 1}},{{ ( {{I_{N}} \otimes{P_{i}}} )}^{ - 1}}, {{ ( {{I_{N}} \otimes {P_{i}}} )}^{ - 1}},I,{{ ( {{I_{N}} \otimes{P_{i}}} )}^{ - 1}},I} \bigr\} $$

and its transpose, to pre-multiplying and post-multiplying (11), where ${M_{i}} = P_{i}^{ - 1}$, applying Schur complements and Lemma 2.3 and considering ${K_{i}}{M_{i}} = {Y_{i}}$, we can get (29). Thereby the proof of the theorem is completed. □

3.2 Sliding-model control design

The objective now is to study the reachability. In this section, an appropriate control law will be constructed to drive the trajectories of the system (1) into the designed sliding surface ${S_{k}} ( {t,i} ) = 0$ with ${S_{k}} ( {t,i} )$ defined in (6) in finite time and maintain them on the surface afterwards.

Theorem 3.3

Suppose that the sliding function is given in (6) where ${K_{i}}$ and ${M_{i}}$ satisfy (29)–(30). Then the trajectories of the error dynamic system (9) can be driven onto the sliding surface ${S_{k}} ( {t,i} ) = 0$ in finite time and then maintain the sliding motion if the control is designed as follows:

$$ {u_{k}} ( t ) = - {K_{i}} {e_{k}} ( t ) - \bigl[ {{\delta_{ki}} + \bigl\Vert {B_{i}^{ - 1}} \bigr\Vert \bigl( { \bigl\Vert {{C_{i}}g \bigl( {{e_{k}} ( t )} \bigr)} \bigr\Vert + {\rho_{i}} \bigl\Vert {{w_{k}} ( t )} \bigr\Vert } \bigr)} \bigr] \operatorname{sign} \bigl( {B_{i}^{T}V_{i}^{T}S ( {k,i} )} \bigr), $$

(31)

where ${\rho_{i}}: = \max_{i \in{\mathcal {S}}} { ( {{\lambda_{\max}} ( {{D_{i}}D_{i}^{T}} )} )^{0.5}}$.

Proof

Choose the following Lyapunov function:

$$ W \bigl( {{S_{k}} ( {t,i} )} \bigr) = \frac{1}{2}S_{k}^{T} ( {t,i} ){S_{k}} ( {t,i} ). $$

(32)

Calculating the time derivative of the sliding-mode surface ${S_{k}} ( {t,i} )$ along the trajectory of (4), we obtain

$$\begin{aligned} \dot{W} \bigl( {{S_{k}} ( {t,i} )} \bigr) =& S_{k}^{T} ( {t,i} ){{\dot{S}}_{k}} ( {t,i} ) \\ =& S_{k}^{T} ( {t,i} ){V_{i}}\Biggl\{ {{\dot{e}}_{k}} ( t ) - \Biggl[ { ( {{A_{i}} - {B_{i}} {K_{i}}} ){e_{k}} ( t ) + {\sigma_{1}}\sum _{j = 1}^{N} {{g_{kj}} { \varGamma_{1i}} {e_{j}} ( t )} } \\ &{} + {\sigma_{1}}\sum_{j = 1}^{N} {{g_{kj}} {\varGamma _{2i}} {e_{j}} \bigl( {t - d ( t )} \bigr)} \Biggr] \Biggr\} \\ =& S_{k}^{T} ( {t,i} ){V_{i}} \bigl[ {{B_{i}} {K_{i}} {e_{k}} ( t ) + {C_{i}}g \bigl( {{e_{k}} ( t )} \bigr) + {B_{i}} {u_{k}} ( t ) + {D_{i}} {w_{k}} ( t )} \bigr] \\ =& S_{k}^{T} ( {t,i} ){V_{i}} {B_{i}} \bigl[ {{u_{k}} ( t ) + {K_{i}} {e_{k}} ( t ) + B_{i}^{ - 1}{C_{i}}g \bigl( {{e_{k}} ( t )} \bigr) + B_{i}^{ - 1}{D_{i}} {w_{k}} ( t )} \bigr] \\ \le& S_{k}^{T} ( {t,i} ){V_{i}} {B_{i}} \bigl[ {{u_{k}} ( t ) + {K_{i}} {e_{k}} ( t )} \bigr] \\ &{} + \bigl\Vert {B_{i}^{ - 1}} \bigr\Vert \bigl( { \bigl\Vert {{C_{i}}g \bigl( {{e_{k}} ( t )} \bigr)} \bigr\Vert + {\rho_{i}} \bigl\Vert {{w_{k}} ( t )} \bigr\Vert } \bigr) \bigl\Vert {B_{i}^{T}V_{i}^{T}{S_{k}} ( {t,i} )} \bigr\Vert . \end{aligned}$$

(33)

Substituting (31) into (33) implies that

$$ \dot{W} \bigl( {{S_{k}} ( {t,i} )} \bigr) \le - {\delta _{ki}} \bigl\Vert {B_{i}^{T}V_{i}^{T}{S_{k}} ( {t,i} )} \bigr\Vert \le- \sqrt{2} {\delta_{ki}} { \lambda_{\min}} ( {{V_{i}} {B_{i}}} ){W^{0.5}} \bigl( {{S_{k}} ( {t,i} )} \bigr). $$

(34)

Then, letting ${S_{k}} ( {{t_{0}} = 0,{r_{0}}} ) = {S_{k0}}$ and integrating from $0 \to t$, one obtains

$$ {\mathcal {E}} { \bigl\{ {W \bigl( {{S_{k}} ( {t,i} )} \bigr) \vert {{S_{k0}},{r_{0}}} } \bigr\} ^{0.5}} \le - \frac{{\sqrt{2} }}{2}{\delta_{ki}} { \lambda_{\min}} ( {{V_{i}} {B_{i}}} )t + {W^{0.5}} ( {{S_{k0}},{r_{0}}} ). $$

(35)

The left-hand side of (35) is nonnegative; we can judge that $W ( {{S_{k}} ( {t,i} )} )$ reaches zero in finite time for each mode $i \in{\mathcal {S}} = \{ {1,2, \ldots,m} \}$, and the finite time ${t^{*} }$ is estimated by

$$ {t^{*} } \le\frac{{\sqrt{2W ( {{S_{k0}},{r_{0}}} )} }}{{{\delta_{ki}}{\lambda_{\min}} ( {{V_{i}}{B_{i}}} )}}. $$

(36)

Therefore, it is shown from (36) that the system trajectories can be driven onto the predefined sliding surface in finite time. In other words, the sliding-mode surface ${S_{k}} ( {t,i} )$ must be reachable. □

Remark 2

In order to eliminate the chattering caused by $\operatorname{sign} ( {B_{i}^{T}V_{i}^{T}S ( {k,i} )} )$, a boundary layer is introduced around each switch surface by replace $\operatorname{sign} ( {B_{i}^{T}V_{i}^{T}S ( {k,i} )} )$ in (31) by saturation function. Hence, the control law (31) can be expressed as

$$ {u_{k}} ( t ) = - {K_{i}} {e_{k}} ( t ) - \bigl[ {{\delta_{ki}} + \bigl\Vert {B_{i}^{ - 1}} \bigr\Vert \bigl( { \bigl\Vert {{C_{i}}g \bigl( {{e_{k}} ( t )} \bigr)} \bigr\Vert + {\rho _{i}} \bigl\Vert {{w_{k}} ( t )} \bigr\Vert } \bigr)} \bigr]\operatorname{sat} \biggl( {\frac{{B_{i}^{T}V_{i}^{T}S ( {k,i} )}}{\kappa}} \biggr). $$

(37)

The jth element of $\operatorname{sat} ( B_{i}^{T}V_{i}^{T}S ( {k,i} ) / \kappa )$ is described as

$$ \operatorname{sat} \biggl( {\frac{{{{ [ {V_{i}^{T}B_{i}^{T}{S_{k}} ( {t,i} )} ]}_{j}}}}{{{\kappa_{j}}}}} \biggr) = \textstyle\begin{cases} { [ {\operatorname{sign} ( {V_{i}^{T}B_{i}^{T}{S_{k}} ( {t,i} )} )} ]_{j}}, &\mbox{if }{ [ {V_{i}^{T}B_{i}^{T}{S_{k}} ( {t,i} )} ]_{j}} > \kappa_{j}, \\ \frac{{{{ [ {V_{i}^{T}B_{i}^{T}{S_{k}} ( {t,i} )} ]}_{j}}}}{{{\kappa_{j}}}}, &\mbox{otherwise}, \end{cases} $$

(38)

where $j = 1,2, \ldots,m$, ${\kappa_{j}}$ is a measure of the boundary layer thickness around the jth switching surface.

4 Example

In this section, an example is provided to demonstrate that the proposed method is effective.

Example 1

Consider complex dynamical networks systems (1) with three nodes and mode ${\mathcal {S}} = \{ {1,2} \}$. The relevant parameters are given as follows.

Mode 1:

$$\begin{array}{c}{A}_1=\left[\begin{array}{cc}-0.1& 0.1\\ 0& -0.2\end{array}\right],B_1=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right],C_1=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],\hfill \\ D_1=\left[\begin{array}{cc}-0.1& 0.1\\ 0.1& -0.2\end{array}\right],{\Gamma }_{11}=\left[\begin{array}{cc}0.8& 0\\ 0& 0.8\end{array}\right],{\Gamma }_{21}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],E_1=\left[\begin{array}{cc}1& 0\end{array}\right].\hfill \end{array}$$

Mode 2:

$$\begin{array}{c}{A}_2=\left[\begin{array}{cc}-0.1& 0.1\\ -0.1& 0.2\end{array}\right],B_2=\left[\begin{array}{cc}0& 1\\ 1& 1\end{array}\right],C_2=\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right],D_2=\left[\begin{array}{cc}-0.1& 0.1\\ -0.1& -0.2\end{array}\right],\hfill \\ {\Gamma }_{12}=\left[\begin{array}{cc}0.3& 0\\ 0& 0.3\end{array}\right],{\Gamma }_{22}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],E_2=\left[\begin{array}{cc}1& 1\end{array}\right].\hfill \end{array}$$

In addition, the transition rate matrix is given by $\pi =\left[\begin{array}{cc}-2& 2\\ 3& -3\end{array}\right]$.

And the outer coupling matrix is given as

$$G=\left[\begin{array}{ccc}-1& 1& 0\\ 1& -2& 1\\ 1& 1& -2\end{array}\right].$$

The nonlinear function $f ( {{x_{i}} ( t )} )$ is taken as

$$f(x_i(t))=\left[\begin{array}{c}-0.5x_{i1}(t)-tanh(0.2x_{i1}(t))+0.2x_{i2}(t)\\ 0.65x_{i2}(t)-tanh(0.45x_{i2}(t))\end{array}\right].$$

Let us take the matrices ${U_{1}}$ and ${U_{2}}$ as follows: $U_1=\left[\begin{array}{cc}-0.5& 0.2\\ 0& 0.65\end{array}\right]$, $U_2=\left[\begin{array}{cc}-0.3& 0.2\\ 0& 0.45\end{array}\right]$.

The time-varying delay is chosen as $\tau ( t ) = 0.9 + 0.01\sin ( {40t} )$. According, one has $\tau = 0.91$, $\bar{\tau}= 0.4$. Let us consider the coupling strength ${\sigma_{1}} = 0.2$, ${\sigma_{2}} = 0.5$. The coefficient of free weight matrix $\varepsilon = 0.1$, and $\alpha = 0.6$. The exogenous input $\omega ( t ) = \frac{1}{{1 + {t^{2}}}}$.

The LMIs (29) in Theorem 3.2 are solved by Matlab LMI toolbox, and obtained $\gamma = 8.4702\mathrm{e} {+} 04$.

$$\begin{array}{c}{M}_1=\left[\begin{array}{cc}127.0802& 3.3343\\ 3.3343& 120.4664\end{array}\right],M_2=\left[\begin{array}{cc}72.6259& -7.6644\\ -7.6644& 371.9771\end{array}\right],\hfill \\ Y_1=1.0\mathrm{e}+04\ast \left[\begin{array}{cc}-1.8445& -0.0364\\ -0.0364& -4.2983\end{array}\right],Y_2=1.0e+04\ast \left[\begin{array}{cc}-2.3288& 3.1836\\ 3.1836& -0.6094\end{array}\right],\hfill \\ {\tilde{X}}_1=1.0\mathrm{e}+04\ast \left[\begin{array}{cccccc}2.6572& 0.0178& 0.0007& 0.0005& 0.0007& -0.0067\\ 0.0178& 2.6863& -0.0004& 0.0066& -0.0015& 0.0091\\ 0.0007& -0.0004& 2.6572& 0.0197& 0.0010& -0.0024\\ 0.0005& 0.0066& 0.0197& 2.6325& 0.0009& 0.0272\\ 0.0007& -0.0015& 0.0010& 0.0009& 2.5636& -0.0356\\ -0.0067& 0.0091& -0.0024& 0.0272& -0.0356& 2.6089\end{array}\right],\hfill \\ {\tilde{X}}_2=\left[\begin{array}{cccccc}38.0472& -1.1333& -0.0541& -0.4213& -0.1619& 0.4567\\ 0.9337& 72.0648& -0.3623& 6.1533& -2.7151& -10.2644\\ 0.1775& 0.3276& 38.0115& -1.0913& 0.1921& 0.3917\\ 0.3648& -4.4085& 1.0863& 68.9744& -0.6696& 4.2949\\ 0.4862& 2.7744& 0.0387& 0.6443& 37.6727& -2.6762\\ -0.3795& 11.3680& -0.3935& -1.8270& 2.2792& 86.5689\end{array}\right],\hfill \\ {\tilde{X}}_3=\left[\begin{array}{cccccc}75.9386& -2.2126& -0.0752& -0.8326& -0.0613& 0.3964\\ 1.7490& 143.3691& 0.1992& 10.0380& -5.0827& -20.6567\\ 0.3153& -0.2654& 75.8670& -1.4096& 0.5290& 0.9310\\ 0.7231& -6.7185& 1.3070& 137.5655& -1.1323& 7.1219\\ 0.7064& 5.1990& -0.0751& 1.0765& 75.1961& -5.2959\\ -0.2254& 22.8512& -0.9253& -2.5126& 4.6910& 172.5156\end{array}\right],\hfill \\ Q_1=1.0\mathrm{e}+04\ast \left[\begin{array}{cccccc}3.8856& 0.0424& -0.0020& 0.0017& -0.0001& -0.0156\\ 0.0424& 3.9816& -0.0011& 0.0059& -0.0041& 0.0181\\ -0.0020& -0.0011& 3.8928& 0.0451& -0.0080& -0.0050\\ 0.0017& 0.0059& 0.0451& 3.8696& 0.0012& 0.0447\\ -0.0001& -0.0041& -0.0080& 0.0012& 3.8835& -0.0819\\ -0.0156& 0.0181& -0.0050& 0.0447& -0.0819& 3.8253\end{array}\right],\hfill \\ Q_2=1.0\mathrm{e}+04\ast \left[\begin{array}{cccccc}2.8470& 0.0225& 0.0009& 0.0005& 0.0009& 0.0083\\ 0.0225& 2.8972& -0.0006& 0.0086& -0.0020& 0.0118\\ 0.0009& -0.0006& 2.8469& 0.0247& 0.0013& -0.0030\\ 0.0005& 0.0087& 0.0247& 2.8285& 0.0011& 0.0349\\ 0.0009& -0.0020& 0.0013& 0.0011& 2.8424& -0.0443\\ -0.0083& 0.0118& -0.0030& 0.0349& -0.0443& 2.8071\end{array}\right].\hfill \end{array}$$

The gain matrices ${K_{1}}$, ${K_{2}}$ can be obtained by simple calculation,

$$K_1=Y_1{M}_1^{-1}=\left[\begin{array}{cc}-145.1707& 0.9965\\ 6.0522& -356.9849\end{array}\right],K_2=Y_2{M}_2^{-1}=\left[\begin{array}{cc}-0.1108& 0.0346\\ 0.1891& 0.0000\end{array}\right].$$

Moreover, by (5), setting ${V_{i}} = {\hat{V}_{i}}$ the switching surface function can be computed as

$$\begin{aligned}& \begin{aligned} {S_{k}} ( {t,1} ) &= {V_{1}} {e_{k}} ( t ) - {V_{1}} \int _{0}^{t} \Biggl[ ( {{A_{1}} - {B_{1}} {K_{1}}} ){e_{k}} ( s ) + { \sigma_{1}}\sum_{j = 1}^{3} {{g_{kj}} {\varGamma_{11}} {e_{k}} ( s )} \\ &\quad {}+ {{\sigma_{2}}\sum_{j = 1}^{3} {{g_{kj}} {\varGamma_{21}} {e_{k}} \bigl( {s - d ( s )} \bigr)} } \Biggr]\,ds, \end{aligned} \\& \begin{aligned} {S_{k}} ( {t,2} ) &= {V_{2}} {e_{k}} ( t ) - {V_{2}} \int _{0}^{t} \Biggl[ { ( {{A_{2}} - {B_{2}} {K_{2}}} ){e_{k}} ( s ) + { \sigma_{1}}\sum_{j = 1}^{3} {{g_{kj}} {\varGamma_{12}} {e_{k}} ( s )} } \\ &\quad {} + {\sigma_{2}}\sum_{j = 1}^{3} {{g_{kj}} {\varGamma _{22}} {e_{k}} \bigl( {s - d ( s )} \bigr)} \Biggr]\,ds, \end{aligned} \end{aligned}$$

where $k = 1,2,3$.

The simulation results are presented in Figs. 1–4. It can be seen from Figs. 1 and 2 that the synchronization error converges to zero in mode 1 and mode 2, respectively. Figures 3 and 4 demonstrate the sliding-mode surface function in mode 1 and mode 2, respectively.

Figure 1

The state estimation error trajectories ${e_{ki}} ( t )$ ($k = 1,2,3$) ($i = 1$)

Figure 2

The state estimation error trajectories ${e_{ki}} ( t )$ ($k = 1,2,3$) ($i = 2$)

Figure 3

The sliding-mode surface function ${S_{k}} ( t )$ ($k = 1,2,3$) in mode 1

Figure 4

The sliding-mode surface function ${S_{k}} ( t )$ ($k = 1,2,3$) in mode 2

5 Conclusion

In this paper, we have shown a sliding-mode design method to solve the ${H_{\infty}}$ synchronization problem for complex dynamical network systems with Markovian jump parameters and time-varying delays. A novel integral sliding-mode controller was proposed. On the basis of Lyapunov stability theory, it has been shown that the Markovian jump complex dynamical network systems via sliding-mode control can be guaranteed to show synchronization and satisfy ${H_{\infty}}$ performance. An example was given to shown the effectiveness of the obtained methods.

It would be interesting to extend the results obtained to multiple complex dynamical networks with multiple coupling delays. This topic will be considered in future work.