1 Introduction

Hematopoiesis (blood cell production) is an extremely complex process. As we know, all blood cells come from the hematopoietic stem cells (HSCs) which can differentiate mature blood cells into the blood circulatory system so as to maintain the normal blood environment. The process of differentiation is called hematopoiesis. Over the past few decades, many researchers have studied hematopoiesis dynamics from the perspective of anatomy, physiology, and mathematics. In 1977, Mackey and Glass studied the density of mature blood cell in a hematopoietic system and proposed a nonlinear delay differential equation model (Hematopoiesis Model, HM) describing the dynamics of hematopoiesis [1, 2]. In 1991, by using a variable replacement method, Gyori and Ladas obtained sufficient conditions for the global attractivity of the unique positive equilibrium point of HM [3]. In Ref. [4], authors extended the HM to a general nonlinear delayed differential equation and proved the sufficient conditions for the existence of a periodic positive solution based on cone fixed point theorem. In Ref. [5], authors proved the existence of a unique positive almost periodic solution of a generalized model hematopoiesis with delays and impulses. In Ref. [6], Ding et al. presented several existence and uniqueness results about positive almost periodic solutions for a class of hematopoiesis model. Hereafter, some extended hematopoiesis models were also proposed, the existence and stability of a positive periodic solution of the models were discussed [7–12]. Some stability condition and control methods were put forward. In Ref. [13], authors presented a feedback control method for the global attractivity of a positive almost-periodic solution of the model of hematopoiesis. In Refs. [14–17], the authors pointed out that the hematopoiesis can be controlled by the gene regulation or drugs.

All of the above models and studies of hematopoiesis are based on a single hematopoietic organ. However, there are multiple organs or tissues with hematopoietic function, including bone marrow, lymph node, liver, spleen, etc. Moreover, bone marrow is also located in different parts of the body, and there do exist connections and effects among them. For example, the damage of a hematopoietic organ can cause other organs to increase the production of blood cells. Therefore, a normal blood circulatory system should be the synergy result of these hematopoietic organs or tissues. In this work, we consider the mathematical model of hematopoiesis with the coexistence of multiple hematopoietic organs or tissues.

The progress of complex networks theory and modeling, along with access to new data, enables humans to achieve true predictive power in areas never before imagined. In recent years, complex networks theory is widely used in biology research [18, 19]. In Ref. [20], Zemanova et al. studied relationship between the cluster structure and the function in complex brain networks based on the cluster synchronization method. In Ref. [21], Chen et al. suggested that there is an extensive network of TET2-Targeting MicroRNAs regulating malignant hematopoiesis. In Ref. [22], Swiersa et al. proposed an approach to program the HSCs and erythroid lineage specification by using genetic regulatory networks.

Motivated by the above discussions, we propose a nonlinear time-delay differential system as a model of a coupled hematopoiesis network which reflects the interactions of multiple hematopoiesis organs. The existence of a unique positive periodic solution of the model is proved rigorously, and the sufficient conditions of asymptotic stability of the periodic solution are presented and verified through theoretical analysis and numerical simulations, respectively. Furthermore, in the case of non-asymptotic stability of the periodic solution, a feedback controller is designed to ensure the stability of the system.

The rest of the paper is organized as follows. In Sect. 2, the model and mathematical preliminaries are introduced. The existence and asymptotic stability of the positive periodic solutions are proved in Sect. 3. A feedback control scheme is proposed in Sect. 4. An example and some numerical simulations are provided to verify the theoretical results in Sect. 5. Finally, a brief conclusion is given in Sect. 6.

2 Model and preliminaries

The general hematopoiesis model with a single hematopoietic system is described by [1, 4]

$$ \dot{x}(t)=-a(t)x(t)+\frac{b(t)}{1+x^{m}(t-\delta)}, $$
(1)

where \(x(t)\) denotes the density of mature cells in blood circulation at time t, the delay \(\delta>0\) is the time delay between the production of immature cells in the hematopoietic organs and their maturation for release in the circulating bloodstreams, \(m>0\) is the disturbing parameter, and the disturbing functions \(a(t)\) and \(b(t)\) are continuous and ϖ-periodic.

Here, considering the synergy of the multiple hematopoietic organs or tissues, we extend the model (1) to a complex dynamical network model with multiple coupled hematopoiesis, which is described in nonlinear differential equations as follows:

$$ \dot{x}_{i}(t)=-a_{i}(t)x_{i}(t)+ \sum^{n}_{j=1}b_{ij} \frac{\beta_{ij}(t)}{1+x^{m}_{j}(t)} +\sum^{n}_{j=1}c_{ij} \frac{w_{ij}(t)}{1+x^{m}_{j}(t-\delta)},\quad i=1,2,\ldots,n, $$
(2)

where \(x_{i}(t)\in(0,\infty)\) represents the density of mature cells in the ith organ, the parameters \(b_{ij}\), \(c_{ij}\) are the connection weight and the delay connection weight between organ i and organ j, respectively. Model (2) can be rewritten in a vector form as follows:

$$ \dot{X}(t)=-A(t)X(t)+B\beta(t)G\bigl(X(t)\bigr)+CW(t)G\bigl(X(t- \delta)\bigr), $$
(3)

where \(X(t)=[x_{1}(t),x_{2}(t),\ldots,x_{n}(t)]^{T} \in(R^{+})^{n}\), \(x_{i}(t)\in(0,\infty)\) is the ith state variable of equations (2) (\(i=1,2,\ldots,n\)). \(G(X(t))=[\frac{1}{1+x^{m}_{1}(t)},\frac{1}{1+x^{m}_{2}(t)},\ldots,\frac {1}{1+x^{m}_{n}(t)}]^{T} \), and \(G(\cdot)\) is a real continuous vector function in the Euclidean space. The matrices \(A(t)=\operatorname{diag}\{a_{1}(t),a_{2}(t),\ldots,a_{n}(t)\}\), \(\beta (t)=(\beta_{ij} (t))_{n\times n}\), and \(W(t)=(w_{ij}(t))_{n\times n}\) are continuous positive ϖ-periodic function matrices. The matrices \(B=(b_{ij})_{n\times n}\) and \(C=(c_{ij})_{n\times n}\) are non-negative constant matrices which represent the coupling and delay coupling strength among n organs, respectively.

The main purpose of this paper is to prove the existence and asymptotic stability of a unique periodic positive solution of system (2) under certain conditions. Then we propose a feedback control method to ensure the stability of system (2) when the above conditions do not hold.

In order to derive our results, the definition of normal cone and a lemma are given below.

Definition 1

([23])

Let κ be a real Banach space. A nonempty convex closed set \(P\subset\kappa\) is called a cone if it satisfies the following two conditions: (i) \(x \in P\), \(\lambda\geq0\) implies \(\lambda x \in P\); (ii) \(x \in P\), \(-x \in P\) implies \(x=\theta\) (where θ denotes the zero element of κ). P is said to be normal if there exists a positive constant M such that, for all \(x,y\in P\), \(\theta\preceq x \preceq y\) implies \(\| x \| \leq M \| y \|\).

Lemma 1

([24])

Let κ be a real Banach space and ℓ is a cone in κ. Suppose that

  1. (i)

    cone ℓ is normal, \(\wp: \ell\rightarrow\ell\) is a completely continuous operator;

  2. (ii)

    for \(\forall X_{0} \in\ell\), there exists \(\epsilon_{0}>0\) such that \(\| \wp(X_{0})\|>\| X_{0}\|\), \(\| \wp^{2}(X_{0})\|\ge\epsilon_{0}\| \wp(X_{0})\|\);

  3. (iii)

    for any \(0<\mu<1\) and \(X \in\ell\) satisfying \(\| X_{0}\|<\| X \|<\| \wp(X_{0})\|\), there exists \(\eta(X,\mu)>0\) such that \(\|\wp(\mu X)\|\leq [\mu(1+\eta)]^{-1}\| \wp(X)\|\).

Then the operator ℘ has a unique fixed point X̃. Furthermore, for any initial \(X_{0} \in\ell\) and an iterated sequence \(X_{k}=\wp(X_{k-1})\) (\(k=1,2,3,\ldots\)), we have \(\lim_{k \rightarrow\infty}\| X_{k}-\widetilde{X}\|=0\).

3 Existence and asymptotic stability of the positive periodic solution

In this section, we address the existence and asymptotic stability of the positive periodic solution of model (3).

Theorem 1

For the differential equation (3), there exists a unique positive periodic solution \(\widetilde{X}(t)\) if \(\| \Lambda(s)\|<1\) for \(s \in(0,\infty)\), where \(\Lambda(s)=\operatorname{diag}\{\frac{\mu+\mu x_{1}^{m}(s)}{1+\mu^{m} x_{1}^{m}(s)},\frac{\mu+\mu x_{2}^{m}(s)}{1+\mu^{m} x_{2}^{m}(s)}, \ldots,\frac{\mu+\mu x_{n}^{m}(s)}{1+\mu^{m} x_{n}^{m}(s)}\}\), \(0<\mu<1\).

Proof

Let us set \(H(t,s)=(e^{\int^{\varpi}_{0} A(u)\,du}-I)^{-1}e^{\int^{s}_{t} A(u)\,du}\), \(s\in[t,t+\varpi]\). Let \(\ell=\{X(t): X(t+\varpi)=X(t),\| X(t)\|=\operatorname{Max}_{[1\le k\le n]}\{\operatorname{Max}_{s\in [t,t+\varpi]}\{|x_{k}(s)|\}\}\}\) denotes a continuous function set. Obviously ℓ is a cone of Banach space. For \(X(t): \| X(t)\|=\operatorname{Max}_{[1\le k\le n]}\{\operatorname{Max}_{s\in [t,t+\varpi]}\{|x_{k}(s)|\}\}\) and \(Y(t): \| Y(t)\|=\operatorname{Max}_{[1\le k\le l]}\{\operatorname{Max}_{s\in [t,t+\varpi]}\{|x_{k}(s)|\}\}\), where \(n< l\), we have \(\theta\preceq X(t) \preceq Y(t)\), which implies \(\| X(t) \| \leq\| Y(t) \|\). So ℓ is a normal cone.

Construct the following operator ℘:

$$\wp\bigl(X(t)\bigr)= \int^{t+\varpi}_{t}H(t,s)\bigl[B\beta (s)G\bigl(X(s) \bigr)+CW(s)G\bigl(X(s-\delta)\bigr)\bigr]\,ds. $$

Obviously, \(\wp(X(t+\varpi))=\wp(X(t))\), that is, \(\wp :\ell\rightarrow\ell\).

Then we obtain

$$\begin{aligned}& \dot{\wp}\bigl(X(t)\bigr)=-A(t)\wp\bigl(X(t)\bigr)+B\beta (t)G\bigl(X(t) \bigr)+CW(t)G\bigl(X(t-\delta)\bigr), \\& \bigl\Vert \dot{\wp}\bigl(X(t)\bigr) \bigr\Vert \le \bigl\Vert A(t)\wp \bigl(X(t)\bigr) \bigr\Vert + \bigl\Vert B\beta(t)G\bigl(X(t)\bigr) \bigr\Vert + \bigl\Vert CW(t)G\bigl(X(t-\delta)\bigr) \bigr\Vert . \end{aligned}$$

Because \(A(t), \beta(t)\), and \(W(t)\) are ϖ-periodic function matrices, we have

$$\begin{aligned}& \bigl\Vert A(t) \bigr\Vert \le M_{1},\qquad \bigl\Vert \beta(t) \bigr\Vert \le M_{2},\qquad \bigl\Vert W(t) \bigr\Vert \le M_{3}, \\& \bigl\Vert G\bigl(X(t)\bigr) \bigr\Vert \le1,\qquad \bigl\Vert G\bigl(X(t-\delta)\bigr) \bigr\Vert \le1. \end{aligned}$$

Thus

$$ \bigl\Vert \wp\bigl(X(t)\bigr) \bigr\Vert \le\varpi \bigl\Vert H(t,s) \bigr\Vert \bigl( \Vert B \Vert M_{2}+ \Vert C \Vert M_{3}\bigr). $$
(4)

Therefore, \(\| \dot{\wp}(X(t))\|\) and \(\| \wp(X(t))\|\) are bounded. Based on the Arzela–Ascoli theorem [25], the operator \(\wp: \ell\rightarrow\ell\) is a completely continuous operator. Furthermore, for \(X_{0}(t) \in\ell\), we readily obtain \(\| \wp(X_{0}(t))\| \ge\| X_{0}(t)\|\). Since matrices B and C are non-negative matrices, from (4), we have

$$\bigl\Vert G \bigl(\wp\bigl(X(s)\bigr)\bigr) \bigr\Vert \ge\bigl[1+\bigl( \varpi \bigl\Vert H(t,s) \bigr\Vert \bigl( \Vert B \Vert M_{2}+ \Vert C \Vert M_{3}\bigr)\bigr)^{m}\bigr]^{-1} $$

and

$$\bigl\Vert G \bigl(\wp\bigl(X(s-\delta)\bigr)\bigr) \bigr\Vert \ge\bigl[1+ \bigl(\varpi \bigl\Vert H(t,s) \bigr\Vert \bigl( \Vert B \Vert M_{2}+ \Vert C \Vert M_{3}\bigr)\bigr)^{m} \bigr]^{-1}. $$

Because

$$\begin{aligned} \bigl\Vert \wp^{2}\bigl(X_{0}(t)\bigr) \bigr\Vert =& \biggl\Vert \int^{t+\varpi}_{t}H(t,s)\bigl[B\beta (s)G\bigl(\wp \bigl(X_{0}(s)\bigr)\bigr)+CW(s)G\bigl(\wp\bigl(X_{0}(s- \delta)\bigr)\bigr)\bigr]\,ds \biggr\Vert \\ \ge&\bigl[1+\bigl(\varpi \bigl\Vert H(t,s) \bigr\Vert \bigl( \Vert B \Vert M_{2}+ \Vert C \Vert M_{3}\bigr) \bigr)^{m}\bigr]^{-1} \\ &{}\times \biggl\Vert \int^{t+\varpi}_{t}H(t,s)\bigl[B\beta (s)G \bigl(X_{0}(s)\bigr)+CW(s)G\bigl(X_{0}(s-\delta)\bigr)\bigr] \,ds \biggr\Vert \\ =&\bigl[1+\bigl(\varpi \bigl\Vert H(t,s) \bigr\Vert \bigl( \Vert B \Vert M_{2}+ \Vert C \Vert M_{3}\bigr) \bigr)^{m}\bigr]^{-1} \bigl\Vert \wp\bigl(X_{0}(t) \bigr) \bigr\Vert , \end{aligned}$$

there exists \(\epsilon_{0}=[1+(\varpi\| H(t,s)\|(\| B\| M_{2}+\| C\| M_{3}))^{m}]^{-1}>0\) such that \(\|\wp^{2}(X_{0}(t))\| \ge \epsilon_{0} \|\wp(X_{0}(t))\|\).

If, for any \(X(t)\in\ell\), there is \(\| X_{0}(t)\|<\| X(t)\|\), then for \(0<\mu<1\), we can obtain

$$\begin{aligned} \wp\bigl(\mu X(t)\bigr) =& \int^{t+\varpi}_{t}H(t,s)\bigl[B\beta(s)G\bigl(\mu X(s) \bigr)+CW(s)G\bigl(\mu X(s-\delta)\bigr)\bigr]\,ds \\ =&\frac{1}{\mu} \int^{t+\varpi}_{t}H(t,s)\bigl[B\beta (s)\Lambda(s)G\bigl( X(s)\bigr)+CW(s)\Lambda(s-\delta)G\bigl(X(s-\delta)\bigr)\bigr] \,ds, \end{aligned}$$
(5)

where

$$\Lambda(s)=\operatorname{diag}\biggl\{ \frac{\mu+\mu x_{1}^{m}(s)}{1+\mu^{m} x_{1}^{m}(s)},\frac{\mu+\mu x_{2}^{m}(s)}{1+\mu^{m} x_{2}^{m}(s)}, \ldots,\frac{\mu+\mu x_{n}^{m}(s)}{1+\mu^{m} x_{n}^{m}(s)}\biggr\} . $$

And because

$$ \mu^{1-m}< \bigl\Vert \Lambda(s) \bigr\Vert < \mu \quad(0< m < 1);\qquad \mu \le \bigl\Vert \Lambda(s) \bigr\Vert < \mu^{1-m}\quad(m \ge1). $$
(6)

Combining (5) and (6), we obtain

$$\bigl\Vert \wp\bigl(\mu X(t)\bigr) \bigr\Vert \le\frac{1}{\mu} \bigl\Vert \Lambda(s) \bigr\Vert \cdot \biggl\Vert \int^{t+\varpi}_{t}H(t,s)\bigl[B\beta(s)G\bigl( X(s) \bigr)+CW(s)G\bigl(X(s-\delta)\bigr)\bigr]\,ds \biggr\Vert . $$

Then

$$\bigl\Vert \wp\bigl(\mu X(t)\bigr) \bigr\Vert \le\frac{1}{\mu}\bigl[1+ \bigl( \bigl\Vert \Lambda(s) \bigr\Vert ^{-1}-1\bigr) \bigr]^{-1} \bigl\Vert \wp\bigl(X(t)\bigr) \bigr\Vert . $$

By Lemma 1, when \(\|\Lambda(s)\|<1 \), \(s \in(0,\infty)\), the operator \(\wp:\ell\rightarrow\ell\) has a unique positive fixed point \(\widetilde{X}(t) \in\ell\). Furthermore, for the iteration \(X_{k+1}(t)=\wp(X_{k}(t))\), \(k\in N^{+}\), we have \(\lim_{k\rightarrow\infty}\| X_{k}(t)-\widetilde{X}(t)\|=0\) for any initial value \(X_{0}(t) \in\ell\). So \(\widetilde{X}(t)=\wp(\widetilde{X}(t))\), and

$$\begin{aligned} \dot{\widetilde{X}}(t) =&\dot{\wp}\bigl(\widetilde{X}(t)\bigr)=-A(t)\wp\bigl( \widetilde {X}(t)\bigr)+B\beta(t)G\bigl(\widetilde{X}(t)\bigr)+CW(t)G\bigl( \widetilde{X}(t-\delta )\bigr) \\ =&-A(t)\widetilde{X}(t)+B\beta (t)G\bigl(\widetilde{X}(t)\bigr)+CW(t)G\bigl( \widetilde{X}(t-\delta)\bigr). \end{aligned}$$
(7)

That is, \(\widetilde{X}(t)\) is a unique positive periodic solution of equation (3). Thus the proof is completed. □

Theorem 2

Assume that there exist positive constants \(\alpha, \beta, \gamma>0\), and a positive definite matrix P satisfying

$$ H^{T}(t)P+PH(t) \geq\alpha I $$
(8)

and

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} (\alpha-\beta) I & PE(t-\delta)\\ E^{T}(t-\delta)P & \beta I \end{array}\displaystyle \right )>\gamma, $$
(9)

where \(H(t)=A(t)+B\beta(t) J_{0}(\widetilde{X}(t))\), \(E(t-\delta)=CW(t) J_{0}(\widetilde{X}(t-\delta))\), and \(\widetilde{X}(t)\) is the periodic solution of equation (3). Then \(\widetilde{X}(t)\) is asymptotically stable.

Proof

From (3) and (7), we have

$$\textstyle\begin{cases} \dot{X}(t)=-A(t)X(t)+B\beta (t)G(X(t))+CW(t)G(X(t-\delta)), \\ \dot{\widetilde{X}}(t)=-A(t)\widetilde{X}(t)+B\beta (t)G(\widetilde{X}(t))+CW(t)G(\widetilde{X}(t-\delta)). \end{cases} $$

Let \(y(t)=X(t)-\widetilde{X}(t)\), we obtain

$$ \dot{y}(t)=-A(t)y(t)+F_{1}\bigl(t,y(t) \bigr)+F_{2}\bigl(t,y(t-\delta)\bigr), $$
(10)

where

$$\begin{aligned}& F_{1}\bigl(t,y(t)\bigr)=B\beta (t)\bigl[G\bigl(\widetilde{X}(t)+y(t) \bigr)-G\bigl(\widetilde{X}(t)\bigr)\bigr], \\& F_{2}\bigl(t,y(t-\delta)\bigr)=CW(t)\bigl[G\bigl(\widetilde{X}(t- \delta)+y(t-\delta )\bigr)-G\bigl(\widetilde{X}(t-\delta)\bigr)\bigr]. \end{aligned}$$

Obviously, \(y(t)=0\) is the equilibrium point of (10). Linearizing \(F_{1}\) and \(F_{2}\) at the equilibrium, we have

$$\begin{aligned}& F_{1}\bigl(t,y(t)\bigr)\doteq-B\beta(t)J_{0}\bigl( \widetilde{X}(t)\bigr)y(t), \\& F_{2}\bigl(t,y(t-\delta)\bigr)\doteq-CW(t) J_{0}\bigl( \widetilde{X}(t-\delta)\bigr)y(t-\delta)), \end{aligned}$$

where

$$\begin{aligned}& J_{0}\bigl(\widetilde{X}(t)\bigr)=\operatorname{diag}\biggl\{ \frac{m{\widetilde {x}_{1}}^{m-1}(t)}{(1+{\widetilde{x}_{1}}^{m}(t))^{2}}, \frac{m{\widetilde{x}_{2}}^{m-1}(t)}{(1+{\widetilde{x}_{2}}^{m}(t))^{2}},\ldots ,\frac{m{\widetilde{x}_{n}}^{m-1}(t)}{(1+{\widetilde{x}_{n}}^{m}(t))^{2}}\biggr\} , \\& J_{0}\bigl(\widetilde{X}(t-\delta)\bigr)=\operatorname{diag}\biggl\{ \frac{m{\widetilde {x}_{1}}^{m-1}(t-\delta)}{(1+{\widetilde{x}_{1}}^{m}(t-\delta))^{2}}, \frac{m{\widetilde{x}_{2}}^{m-1}(t-\delta)}{(1+{\widetilde {x}_{2}}^{m}(t-\delta))^{2}},\ldots ,\frac{m{\widetilde{x}_{n}}^{m-1}(t-\delta)}{(1+{\widetilde {x}_{n}}^{m}(t-\delta))^{2}}\biggr\} . \end{aligned}$$

The linearization of (10) is

$$\begin{aligned} \dot{y}(t) =&-A(t)y(t)-B\beta(t) J_{0}\bigl(\widetilde{X}(t) \bigr)y(t)-CW(t) J_{0}\bigl(\widetilde{X}(t-\delta)\bigr)y(t-\delta)) \\ =&-\bigl[A(t)+B\beta(t) J_{0}\bigl(\widetilde{X}(t)\bigr) \bigr]y(t)-CW(t) J_{0}\bigl(\widetilde{X}(t-\delta)\bigr)y(t-\delta)). \end{aligned}$$

Then we obtain

$$ \dot{y}(t)=-H(t)y(t)-E(t-\delta))y(t-\delta)). $$
(11)

Taking the Lyapunov function

$$V(t)=y^{T}(t)Py(t)+\beta \int_{t-\delta}^{t} y^{T}(s)y(s)\,ds, $$

we have

$$\begin{aligned} \dot{V}(t) =&-\bigl[H(t)y(t)+E(t-\delta))y(t-\delta )\bigr]^{T}Py(t)-y^{T}(t)P \bigl[H(t)y(t)+E(t-\delta))y(t-\delta)\bigr] \\ &{}+\beta y^{T}(t)y(t)-\beta y^{T}(t-\delta)y(t-\delta) \\ =&-y^{T}(t)\bigl[H^{T}(t)P+PH(t)\bigr]y(t)+\beta y^{T}(t)y(t)-y^{T}(t-\delta)E^{T}(t- \delta)Py(t) \\ &{}-y^{T}(t)PE(t-\delta))y(t-\delta )-\beta y^{T}(t- \delta)y(t-\delta). \end{aligned}$$

According to (8) and (9), we obtain

$$\begin{aligned} \dot{V}(t) \leq& -\alpha y^{T}(t)y(t)+\beta y^{T}(t)y(t)-y^{T}(t- \delta)E^{T}(t-\delta)Py(t) \\ &{}-y^{T}(t)PE(t-\delta))y(t-\delta )- \beta y^{T}(t-\delta)y(t-\delta) \\ =&-\bigl(y^{T}(t),y^{T}(t-\delta)\bigr) \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} (\alpha-\beta) I & P E(t-\delta)\\ E^{T}(t-\delta)P & \beta I \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} y(t) \\ y(t-\delta) \end{array}\displaystyle \right ) \\ \leq&-\gamma\bigl(y^{T}(t),y^{T}(t-\delta)\bigr)\left ( \textstyle\begin{array}{@{}c@{}} y(t)\\ y(t-\delta) \end{array}\displaystyle \right ). \end{aligned}$$

It is obvious that \(\dot{V}(t)=0\) if and only if \(y(t)=0\). Let S be the set of all points where \(\dot{V}(t)=0\), that is, \(S=\{\dot{V}(t)=0\}=\{y(t)=0\}\). From (10), the largest invariant set of S is \(M=\{y(t)=0\}\). According to LaSalles invariance principle [26], starting with any initial values, the trajectories of system (10) will converge to M asymptotically, which implies that \(y(t)\rightarrow0\) (\(t\rightarrow\infty\)). That is, the periodic solution \(\widetilde{X}(t)\) of (3) is asymptotically stable. Now the proof is completed. □

Remark 1

It is worth noting that, conditions (8) and (9) in Theorem 2 are quite conservative and would be difficult to achieve. Fortunately, a human organ system has the ability to adjust and maintain balance. In the following section, we will discuss the feedback control law to ensure the stability of system (3).

4 Feedback control

According to Theorem 2, the asymptotic stability of \(\widetilde{X}(t)\) is not guaranteed when condition (8) or (9) is not met. In this section, a feedback control method is proposed to guarantee the asymptotic stability of the periodic solution \(\widetilde{X}(t)\). By employing a controller U, the controlled system (3) can be rewritten as

$$ \dot{X}(t)=-A(t)X(t)+B\beta (t)G\bigl(X(t)\bigr)+CW(t)G\bigl(X(t- \delta)\bigr)+U. $$
(12)

Theorem 3

Consider system (12) with a linear feedback controller \(U=-ky(t)\), where k is a sufficiently large positive constant. Assume that there exist constants \(\alpha, \beta, \gamma >0\), and a positive definite matrix P satisfying

$$ H^{T}(t)P+PH(t)\geq\alpha I $$
(13)

and

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} (k+\alpha-\beta) I & PE(t-\delta)\\ E^{T}(t-\delta)P & \beta I \end{array}\displaystyle \right )>\gamma. $$
(14)

Then system (12) can be stabilized to the periodic solution \(\widetilde{X}(t)\) of equation (3).

Proof

Let \(y(t)=X(t)-\tilde{X}(t)\).

Combining (12) and (7), we have

$$\dot{y}(t)=-A(t)y(t)+F_{1}\bigl(t,y(t)\bigr)+F_{2} \bigl(t,y(t-\delta)\bigr)-ky(t). $$

By linearizing the above equation, we obtain

$$\dot{y}(t)=-A(t)y(t)-B\beta(t) J_{0}\bigl(\widetilde{X}(t) \bigr)y(t)-CW(t) J_{0}\bigl(\widetilde{X}(t-\delta)\bigr)y(t- \delta))-ky(t), $$

that is,

$$ \dot{y}(t)=-\bigl(H(t)+kI\bigr)y(t)-E(t-\delta))y(t-\delta)). $$
(15)

The rest of the proof is similar to that of Theorem 2. Therefore, the equilibrium point \(y(t)=0\) of (15) is asymptotically stable, that is, \(\lim_{t\rightarrow0} y(t)=0\). Thus, an arbitrary solution \(X(t)\) of (12) is stabilized to the periodic solution \(\tilde{X}(t)\) of equation (3). The proof is thus completed. □

Remark 2

Comparing (14) with (9), one can see that the application scope of theory condition is broadened by adding a feedback controller U. It implies that a living organism is more likely to reach a steady state via appropriate feedback adjustment.

5 Example and numerical simulations

In this section, an example and some numerical simulations are provided to verify the existence and the asymptotic stability of the unique positive periodic solution of equation (3), as well as the effectiveness of the control method.

First, we provide an example of model (2) (or equation (3)) whose solution is asymptotically stable.

We take \(n=3\), \(\delta=20\), \(m=2\), and the matrices are as follows:

$$\begin{aligned}& A_{1}(t)= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \sin(0.1t)+1& 0& 0 \\ 0 &\cos(0.1t)+1& 0\\ 0 & 0 &\cos(0.2t)+1 \end{array}\displaystyle \right ], \\& B_{1}= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.9542&0.6627 & 0.7111\\ 0.0319 &0.2815 & 0.6246\\ 0.3569 & 0.2304 & 0.5906 \end{array}\displaystyle \right ], \\& \beta_{1}(t)= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \sin(0.1t)+1& 0& 0 \\ 0 &\sin(0.2t)+1& 0\\ 0 & 0 &\sin(0.3t)+1 \end{array}\displaystyle \right ], \\& C_{1}= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.6604 & 0.4513 & 0.8562\\ 0.0476 & 0.2409 & 0.2815\\ 0.3488 & 0.7151 & 0.7311 \end{array}\displaystyle \right ], \\& W_{1}(t)= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \cos(0.1t)+1& 0& 0 \\ 0 &\cos(0.2t)+1& 0\\ 0 & 0 &\cos(0.3t)+1 \end{array}\displaystyle \right ]. \end{aligned}$$

So the differential equation is

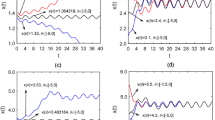
$$ \dot{X}(t)=-A_{1}(t)X(t)+B_{1} \beta_{1} (t)G\bigl(X(t)\bigr)+C_{1}W_{1}(t)G \bigl(X(t-20)\bigr). $$
(16)

Figure 1 displays the stability of the unique positive periodic solution of equation (16). Figure 1(a) displays the evolution of each component \(x_{k}(t)\) (\(k=1,2,3\)) of solution \(X(t)\) with different initial values, and Fig. 1(b) is the phase diagram of solution \(X(t)\). It is obvious that the unique positive periodic solution \(\widetilde{X}(t)\) is asymptotically stable.

Figure 1
figure 1

The asymptotic stability of the unique periodic positive solution of equation (16)

Full size image

Next, we give an example to verify the effectiveness of the feedback control method.

Let us take \(\bar{C_{1}}=10C_{1}\) in equation (16), then we have

$$ \dot{X}(t)=-A_{1}(t)X(t)+B_{1} \beta_{1} (t)G\bigl(X(t)\bigr)+\bar{C_{1}}W_{1}(t)G \bigl(X(t-20)\bigr). $$
(17)

Figure 2 shows that the unique positive periodic solution \(\widetilde{X}(t)\) of equation (17) is non-asymptotically stable.

Figure 2
figure 2

The non-asymptotic stability of the periodic solution \(\tilde{X}(t)\) of equation (17)

Full size image

Then we employ a linear feedback controller U in (17), the equation is rewritten as

$$ \dot{X}(t)=-A_{1}(t)X(t)+B_{1} \beta_{1} (t)G\bigl(X(t)\bigr)+\bar{C_{1}}W_{1}(t)G \bigl(X(t-20)\bigr)+U. $$
(18)

Here, we take the feedback gain \(k=8\), that is, \(U=-8y(t)\). As is shown in Fig. 3(a), each component \(x_{k}(t)\) (\(k=1,2,3\)) of the solution \(X(t)\) starting from different initial values tends to be the same. That is, the unique positive periodic solution \(\widetilde{X}(t)\) of the controlled system (18) is asymptotically stable. The phase diagram of solution \(X(t)\) in Fig. 3(b) displays the same result. This shows that our feedback control method is effective.

Figure 3
figure 3

The asymptotic stability of the periodic solution \(\tilde{X}(t)\) of equation (18)

Full size image

6 Conclusion

In this paper, we have studied the stability and feedback control of the hematopoiesis network model with nonlinear differential equations. On the one hand, we proved the existence and asymptotic stability of the unique positive periodic solution of the system under certain conditions. On the other hand, we designed appropriate feedback controller to stabilize an arbitrary solution of the model to the unique positive periodic solution. The result reveals that, when the hematopoietic system becomes chaotic, a living organism can return to stable states by means of appropriate physical adjustment.