Abstract
In this paper, a three-species delayed food chain system with mutual interference and impulses is established. By utilizing the continuation theorem, the comparison theorem, some analysis techniques, and constructing a suitable Lyapunov functional, some sufficient conditions for the existence of positive periodic solutions, permanence, and global attractivity of the system are obtained. The conditions obtained are related to the mutual interference constant m, prey refuge constant θ, delays, and impulses. An example is given to show the feasibility of the results.
Similar content being viewed by others
1 Introduction
Impulsive differential equations are used for the mathematical simulation of processes which are subject to impulses during their evolution. Such processes can be observed in numerous fields of science and technology: control theory, population dynamics, biotechnologies, industrial robotics, etc. [1]. In population dynamics, many evolution processes in nature are characterized by the fact that, at certain moments of time, they experience some abrupt changes of state. Examples include annual harvesting and stocking of species as well as annual immigration. The theory of impulsive and delay differential equations is emerging as an important area of investigation [1–10]. For instance, Wang et al. [4] studied a delayed prey–predator system with mutual interference and impulses as follows:
In 1971, Hassell [11] proposed the concept of mutual interference of predator species and introduced the mutual interference constant m (\(0 < m \le 1\)). In recent years, mutual interference of predator has been studied extensively by some researchers [11–13]. Wang [12] and He [13] studied several kinds of predator–prey systems with mutual interference and obtained some sufficient conditions which guaranteed the permanence and globally asymptotic stability of the systems.
However, in the real world, prey species often make use of refuges to decrease predation risk. Here refuges mean some places or situations where predation risk is somehow reduced. Examples include spatial refuges, temporal refuges, and so on. During the last decade, numerous works have been published and much essential progress has been pushed on this direction [14–16]. González-Olivares and Ramos-Jiliberto [15] proposed a predator–prey system with Holling type II functional response and a prey refuge. They showed that there was a trend from limit cycles through non-zero stable points up to predator extinction and prey stabilizing at high densities. In reference [16], Ma et al. were interested in the interplay between the stabilizing effects of mutual interference and the destabilizing effects of prey refuge:
where m (\(0 < m \le 1\)) is a constant of mutual interference. θ (\(0 < \theta \le 1\)) is a constant number of prey using refuges.
Furthermore, there are three rudimentary and important ecological systems that are predator–prey system, competitive system, and cooperative system in mathematical biology. The predator–prey model, such as three-species predator–prey system and food-chain system, is the most popular population model and has extremely rich dynamics [8–10, 12–14]. Recently, the dynamic behaviors of predator–prey system with different kinds of functional responses have been extensively investigated [9, 10, 12–19]. For example, the authors [18] gave the following non-linear functional response:
where \(c_{i}\) is the rate of a predator searching for the prey x, α is a positive constant, \(\beta = h_{1}c_{1}\), \(\gamma = h_{2}c_{2}\), \(h_{i}\) represents the expected handling time spent with the prey x to y. Obviously, if β or γ tends to zero, it will be Holling type-II functional response [19]. For example, Do proposed and studied a constant periodic releasing for top predator or periodic impulsive immigration for top predator—a three-species food chain system with impulsive control and Beddington–DeAngelis functional response [9].
Motivated by these facts, in this paper, we are concerned with the following delayed three-species Beddington-type food chain system with mutual interference and impulsive control methods. The model is described by the following differential equations:
with the initial conditions
where \(x(t)\), \(y(t)\), \(z(t)\) represent the densities of prey and mid-level predator and top predator, respectively. \(\Delta x(t_{k}) = x(t_{k}^{ +} ) - x(t_{k})\), \(\Delta y(t_{k}) = y(t_{k}^{ +} ) - y(t_{k})\) and \(\Delta z(t_{k}) = z(t_{k}^{ +} ) - z(t_{k})\) represent the regular harvest or death from spraying pesticide of the populations \(x(t)\), \(y(t)\), and \(z(t)\) at time \(t_{k}\), respectively. \(Z^{ +} = \{ 1,2, \ldots \}\) and \(0 \le t_{0} < t_{1} < t_{2} < \cdots < t_{k} < \cdots\) are fixed points with \(t_{k} \to + \infty\) as \(k \to + \infty\).
For the sake of generality and convenience, we assume that the following conditions hold.
(I) \(a_{i}(t)\), \(b_{i}(t)\), \(i = 1,2,3\), \(d_{i}(t)\), \(i = 1,2\), \(c_{i}(t)\), \(i = 1,2,3,4\), are all positive, continuous, and ω-periodic functions, and \(\tau_{1}\), \(\tau_{2}\), and \(\tau_{3}\) are non-negative constants.
(II) \(- 1 < d_{1k} \le 0\), \(- 1 < d_{2k} \le 0\), \(- 1 < d_{3k} \le 0\) are constants for \(k \in Z^{ +} \) and there exists a positive integer q such that \(t_{k + q} = t_{k} + \omega\), \(d_{1,(k + q)} = d_{1k}\), \(d_{2,(k + q)} = d_{2k}\), \(d_{3,(k + q)} = d_{3k}\), and \(t_{k} - \tau_{1}\), \(t_{k} - \tau_{2}\), \(t_{k} - \tau_{3} \ne t_{m}\).
Without loss of generality, we assume that \(t_{k} \ne 0\), ω, and \([0,\omega ] \cap \{ t_{k}\} = \{ t_{1},t_{2}, \ldots,t_{q}\}\), and let
The rest of this article is organized as follows. In Sect. 2, we present the result on the existence of positive periodic solutions of system (1.2). In Sect. 3, we study the permanence of system (1.2). In Sect. 4, we investigate the global attractivity of system (1.2). In Sect. 5, an example is given to show the feasibility of our results by means of simulation. In the last section, we conclude this paper.
2 Existence of periodic solution
In order to prove the existence of positive solutions of system (1.2), we first introduce the following coincidence degree theorem.
Let X, Y be real Banach spaces, \(L:\operatorname{Dom}L\subset X\to Y\) be a linear operator. The operator L will be called a Fredholm operator of index zero if \(\operatorname{dim}\operatorname{Ker}L=\operatorname{co}\operatorname{dim}\operatorname{Im}L<+\infty\) and ImL is closed in Y. If L is a Fredholm operator of index zero, there exist continuous projectors \(P:X\to X\) and \(Q:Y\to Y\) such that \(\operatorname{Im}P=\operatorname{Ker}L\), \(\operatorname{Ker}Q=\operatorname{Im}L=\operatorname{Im}(I-Q)\). It follows that \(L|_{\operatorname{Dom}L\cap \operatorname{Ker}P}:(I-P)X\to \operatorname{Im}L\) is invertible. We denote the inverse of that operator by \(K_{P}\). If Ω is an open bounded subset of X and \(N:\bar{\Omega}\to Y\) is a continuous operator, the operator N will be called L-compact on Ω̄ if \(QN(\bar{\Omega})\) is bounded and \(K_{P}(I-Q)N:\bar{\Omega}\to X\) is compact. Since ImQ is isomorphic to KerL, there exists isomorphism \(\Phi:\operatorname{Im} Q \to \operatorname{Ker}L\).
Lemma 2.1
(see [20])
Let \(\Omega\subset X\) be an open bounded set, let L be a Fredholm operator of index zero and N be L-compact on Ω̄. Suppose that
-
(i)
for each \(\lambda\in(0,1)\), every solution x of \(Lx=\lambda Nx\) is such that \(x\notin \partial\Omega\);
-
(ii)
\(QNx \neq 0\) for each \(x\in \partial\Omega \cap \operatorname{Ker} L\);
-
(iii)
\(\operatorname{deg}(\Phi QN,\Omega\cap\operatorname{Ker}L,0)\neq 0\).
Then the equation \(Lx=Nx\) has at least one solution in \(\bar{\Omega}\cap\operatorname{Dom}L\).
Theorem 2.1
If \(\int_{0}^{T} a_{1}(t)\,dt + \sum_{k = 1}^{q} \ln (1 + d_{1k}) > 0\) and the following algebraic equation
has finite solutions \((u^{*},v^{*},w^{*})\), then system (2.1) has at least one positive ω-periodic solution.
Proof
Let \((x(t),y(t),z(t)) \in R^{3}\) be an arbitrary positive ω-periodic solution of system (1.2). Set \(x(t) = e^{u(t)}\), \(y(t) = e^{v(t)}\), \(z(t) = e^{w(t)}\), then it follows from system (1.2) that
Let \(S = \{ x(t) \in \mathit{PC}^{1}([0,\omega ],R)|x(\omega ) = x(0)\}\), where \(\mathit{PC}^{1}([0,\omega ],R)=\{x \in \mathit{PC}([0,\omega ],R)| [4]x(t)\mbox{ is continuous, differentiable at }t\neq t_{k}, x'(t_{k}^{ +} ), x'(t_{k}^{ -} )\mbox{ exist, and }x'(t_{k}^{ -} )=x'(t_{k}), k=1,2,\ldots, [4]q\}\); \(\mathit{PC}([0,\omega ],R) = \{ x:[0,\omega ] \to R|x(t)\mbox{ is continuous at }t\neq t_{k}, x(t_{k}^{ +} ), x(t_{k}^{ -} )\mbox{ exist, and }x(t_{k}^{ -} ) = x(t_{k}^{ +} ), k=1,2,\ldots,q\}\). Let \(X = S \times S \times S\). For \(\xi(t)=(u(t),v(t),w(t))\in X\), we define
Let \(Y=X\times R^{q}\times R^{q}\times R^{q}\). For \(h=(\xi,e_{1},e_{2},e_{3})\in Y\), \(\xi\in X\), \(e_{1}\in R^{q}\), \(e_{2}\in R^{q}\), \(e_{3}\in R^{q}\), we define \(\Vert h \Vert_{Y} =\Vert \xi\Vert_{X}+\Vert e_{1}\Vert +\Vert e_{2}\Vert +\Vert e_{3}\Vert\), then X and Y are Banach spaces.
For convenience, we denote
Let \(\operatorname{Dom}L = X\), \(L:\operatorname{Dom} L \to Y\),
Let \(N:X \to Y\),
then
ImL is closed in Y, \(\dim \operatorname{Ker}L = \operatorname{co}\dim \operatorname{Im} L = 3\). So L is a Fredholm operator of index zero. Let
It is easy to know that P, Q are continuous projectors and \(\operatorname{Im} P = \operatorname{Ker}L\), \(\operatorname{Ker}Q = \operatorname{Im} L = \operatorname{Im} (I - Q)\).
Therefore, the inverse \(K_{P}\) exists and it has the following form: \(K_{P}:\operatorname{Im} L \to \operatorname{Ker}P \cap \operatorname{Dom}L\),
Clearly, QN and \(K_{P}(I - Q)N\) are continuous. Let Ω be any open bounded set in X. It is easy to verify that \(QN(\Omega )\) is uniformly bounded, \(K_{P}(I - Q)N(\bar{\Omega} )\) is equicontinuous and uniformly bounded. By Ascoli–Arzela theorem we know that \(K_{P}(I - Q)N\) is compact on Ω̄. Thus, N is L-compact on Ω̄.
Now, it needs to show that there exists a domain Ω that satisfies all the requirements given in Lemma 2.1. Corresponding to operator equation \(L\xi = \lambda N\xi\), \(\lambda \in (0,1)\). Assume that \(\xi (t) = (u(t),v(t),w(t)) \in X\) is a solution of this operator equation, then we have
Integrating (2.2) over \([0,\omega]\), we get
Since \(\xi (t) = (u(t),v(t),w(t)) \in X\), there exist \(\xi_{1},\xi_{2},\xi_{3} \in [0,\omega ]\) such that \(\min_{t \in [0,\omega ]}u(t) = u(\xi_{1})\), \(\min_{t \in [0,\omega ]}v(t) = v(\xi_{2})\), \(\min_{t \in [0,\omega ]}w(t) = w(\xi_{3})\).
It follows from (2.3) that
Thus
Similarly, it follows from (2.4) that
Thus
It follows from (2.5) that
Thus
On the other hand, from the fact of \(\xi (t) = (u(t),v(t),w(t)) \in X\), we know that \(\sup_{t \in [0,\omega ]}u(t)\) exists, and there exists \(\eta_{1} \in [0,\omega ]\) such that \(u(\eta_{1}^{ +} ) = \sup_{t \in [0,\omega ]}u(t)\) (\(u(\eta_{1}^{ +} ) = u(\eta_{1})\) for \(\eta_{1} \ne t_{k}\); \(u(\eta_{1}^{ +} ) = u(t_{k}^{ +} )\) for \(\eta_{1} = t_{k}\)).
Hence, from (2.3) we get
Similarly, there exist \(\eta_{2},\eta_{3} \in [0,\omega ]\), \(v(\eta_{2}^{ +} ) = \sup_{t \in [0,\omega ]}v(t)\), \(w(\eta_{3}^{ +} ) = \sup_{t \in [0,\omega ]}w(t)\). From (2.4) we can get
Thus,
From (2.5) we can get
Thus,
Hence,
This implies that any solution \(\xi (t)\) of the operator equation \(L\xi = \lambda N\xi\) satisfies \(\Vert \xi \Vert \le \sqrt{H_{1}^{2} + H_{2}^{2} + H_{3}^{2}} = H\).
Now we consider the system of algebraic equations with respect to u, v, w (\((u,v,w) \in R^{3}\) is a constant vector):
where \(\mu \in [0,1]\). By the above similar deduction steps, we know
This implies that any constant solution \((u,v,w)\) of (2.6) always satisfies \(\sqrt{u^{2} + v^{2} + w^{2}} \le H\). (It is independent of μ).
We know that system (2.6) can be changed into the following system (2.7):
For any \(\mu \in [0,1]\), any solution \((u,v,w)\) of (2.7) always satisfies \(\sqrt{u^{2} + v^{2} + w^{2}} \le H\).
Let \(\mu = 1\), then any solution \((u,v,w)\) of the following system (2.8) satisfies \(\sqrt{u^{2} + v^{2} + w^{2}} \le H\).
Let \(M^{*} = H + \delta\) (\(\delta > 0\), δ is sufficiently large). Let \(\Omega = \{ \xi = (u(t),v(t),w(t)) \in X \vert \Vert \xi \Vert < M^{*} \}\), then condition (i) of Lemma 2.1 is satisfied.
For any constant vector \(\xi_{0} = (u_{0},v_{0},w_{0}) \in \partial \Omega\), \(\sqrt{u_{0}^{2} + v_{0}^{2} + w_{0}^{2}} = M^{*}\).
Hence, condition (ii) of Lemma 2.1 is satisfied.
Let \(\Phi:\operatorname{Im} Q \to \operatorname{Ker}L\),
Let \(F(\xi,\mu ) = \mu \Phi QN\xi + (1 - \mu )\Phi G\xi\), where \(\mu \in [0,1]\), \(\xi = (u,v,w) \in R^{3}\),
For \(\xi \in \partial \Omega \cap \operatorname{Ker}L\), \(\xi = (u,v,w)\) is a constant vector, and \(\sqrt{u^{2} + v^{2} + w^{2}} = M^{*}\).
From (2.7) we know \(F(\xi,\mu ) \ne 0\) (\(\xi \in \partial \Omega \cap \operatorname{Ker}L\)).
It is easy to verify that the following system of equations has a unique solution \(\xi^{*} = (u^{*},v^{*},w^{*})\).
Thus,
(where \(J_{\Phi G}\) is the Jacobian determinant of ΦG). Hence condition (iii) of Lemma 2.1 is satisfied.
Thus, by Lemma 2.1, we know that the operator equation \(L\xi = N\xi\) has at least one solution in \(\bar{\Omega} \cap \operatorname{Dom}L\). Therefore system (2.1) has at least one-periodic solution \((u^{*}(t),v^{*}(t),w^{*}(t))\). So system (1.2) has at least one ω-periodic solution \((x^{*}(t),y^{*}(t),z^{*}(t)) = (e^{u^{*}(t)},e^{v^{*}(t)},e^{w^{*}(t)})\). The proof of Theorem 2.1 is completed. □
From Theorem 2.1, if we let \(\theta = 0\), \(\alpha_{i} = 1\), \(\beta_{i} = 0\), \(\gamma_{i} = 0\) (\(i = 1,2\)), \(z(t) = 0\), then we can get the following corollary.
Corollary 2.1
If \(\int_{0}^{T} a_{1}(t)\,dt + \sum_{k = 1}^{q} \ln (1 + d_{1k}) > 0\) and the following algebraic equation set
has finite solutions \((u^{*},v^{*})\), then system (2.1) has at least one positive ω-periodic solution.
Remark 2.1
Corollary 2.1 is the same as Theorem 2.1 of [4]. Their model is the special case of (1.2). In this sense, we generalize or improve their results.
3 Permanence
Definition 3.1
System (1.2) is said to be permanent if there exist positive constants T, \(G_{i}\), \(g_{i}\), \(i = 1,2,3\), such that any solution \((x(t),y(t),z(t))^{T}\) of system (1.2) satisfies \(g_{1} \le x(t) \le G_{1}\), \(g_{2} \le y(t) \le G_{2}\), \(g_{3} \le z(t) \le G_{3}\) for \(t \ge T\).
Lemma 3.1
(see [20])
If \(a > 0\), \({b} > 0\), and \(\xi (t) \ge ( \le )b - a\xi (t)\) for \(t \ge 0\), \(z(0) > 0\), then \(\xi (t) \ge ( \le )\frac{b}{a} + [\xi (0) - \frac{b}{a}]\exp \{ - at \}\).
Lemma 3.2
If \(a > 0\), \({b} > 0\), \(\tau \ge 0\), then:
-
(1)
If \(y'(t) \le y(t)[b - ay(t - \tau )]\), then there exists a constant \(T > 0\) such that \(y(t) \le \frac{a}{b}\exp \{ b\tau \}\) for \(t \ge T\).
-
(2)
If \(y'(t) \ge y(t)[b - ay(t - \tau )]\), and there exist positive constants T and G such that \(y(t) < G\) for \(t \ge T\), then for any small constant \(\varepsilon > 0\) there exists a constant \(T^{*} > T\) such that \(y(t) \ge \min \{ \frac{b}{a}\exp \{ (b - aM)\tau \},\frac{b}{a} - \varepsilon \}\) for \(t \ge T^{*}\). In [21], the value of the above ε is \(b/2a\).
Consider the following non-impulsive functional differential system:
Lemma 3.3
If \((x(t),y(t),z(t))\) is a solution of system (1.2) on \([0, + \infty )\), then \((u(t),v(t),w(t)) = (\Lambda_{d_{1}}^{ - 1}x(t),\Lambda_{d_{2}}^{ - 1}y(t),\Lambda_{d_{3}}^{ - 1}z(t))\) is a solution of system (3.1) on \([0, + \infty )\).
Lemma 3.4
If \((u(t),v(t),w(t))\) is a solution of system (3.1) on \([0, + \infty)\), then \((x(t),y(t),z(t)) = (\Lambda_{d_{1}}u(t),\Lambda_{d_{2}}v(t),\Lambda_{d_{3}}w(t))\) is a solution of system (1.2) on \([0, + \infty)\).
The proofs of the above two lemmas are similar to that of Theorem 1 in [6], so we omit them here.
Lemma 3.5
There exists a positive constant \(T_{0}\) such that the solution \((u(t),v(t),w(t))\) of system (3.1) satisfies \(0 < u(t) \le G_{1}\), \(0 < v(t) \le G_{2}\), and \(0 < w(t) \le G_{3}\) for \(t \ge T_{0}\), where
Proof
It follows from system (3.1) that
The first inequality of (3.3) and Lemma 3.2 yield that there exists a positive constant \(T_{1}\) such that
which, together with the second inequality of (3.3), yields
and the third inequality of (3.3) yields
Thus from Lemma 3.1 we know that, for any small positive constant ε, there exists a positive constant \(T_{0} \ge T_{1}\) such that \(v(t) \le G_{2}\), \(w(t) \le G_{3}\) for \(t \ge T_{0}\). □
Lemma 3.6
If \(\Delta_{1} > 0\), \(\Delta_{2} > 0\), and \(\Delta_{3} > 0\), then there exists a positive constant \(T^{*}\) such that the solution \((u(t),v(t),w(t))\) of system (3.1) satisfies
where ε is a small enough positive constant, and
Proof
It follows from Lemma 3.5 and system (3.1) that, for \(t \ge T_{0}\),
which, together with Lemmas 3.1 and 3.2, implies that there exists a positive constant \(T^{*} \ge T_{0}\) such that \(u(t) \ge g_{1}\), \(v(t) \ge g_{2}\), and \(w(t) \ge g_{3}\) for \(t \ge T^{*}\). □
From Lemmas 3.5 and 3.6 we can get the following result on the permanence of system (3.1), which, together with Lemmas 3.3 and 3.4, yields the permanence of system (1.2).
Theorem 3.1
If \(\Delta_{1} > 0\), \(\Delta_{2} > 0\), and \(\Delta_{3} > 0\), then system (1.2) is permanent and enters eventually into the region
From Theorem 3.1, if we let \(\theta = 0\), \(\alpha_{i} = 1\) (\(i = 1,2\)), \(z(t) = 0\), then we can get the following corollary.
Corollary 3.1
If \(\Delta_{1} > 0\) and \(\Delta_{2} > 0\), then system (1.2) is permanent and enters eventually into the region
Remark 3.1
Corollary 3.1 is the same as Theorem 3.1 of [4]. Their model is the special case of (1.2). In this sense, we generalize or improve their results.
4 Stability
Definition 4.1
System (1.2) is called globally attractive if
for any three positive solutions \((x(t),y(t),z(t))\) and \((\hat{x}(t),\hat{y}(t),\hat{z}(t))\) of system (1.2).
Theorem 4.1
If \(\Delta_{1} > 0\), \(\Delta_{2} > 0\), and \(\Delta_{3} > 0\) and
then system (1.2) is globally attractive, where
Proof
Let \((\hat{x}(t),\hat{y}(t),\hat{z}(t))\) and \((x(t),y(t),z(t))\) be any two positive solutions of system (1.2); then \((\hat{u}(t),\hat{v}(t),\hat{w}(t)) = (\Lambda_{d_{1}}^{ - 1}\hat{x}(t),\hat{y}_{d_{2}}^{ - 1}(t),\hat{z}_{d_{3}}^{ - 1}(t))\) and \((u(t),v(t),w(t)) = (\Lambda_{d_{1}}^{ - 1}x(t),y_{d_{2}}^{ - 1}(t),z_{d_{3}}^{ - 1}(t))\) are positive solutions of system (3.1). It follows from Lemmas 3.5 and 3.6 that there exist positive constants \(g_{i}\), \(G_{i}\), and \(T^{*}\) (defined in Lemma 3.5 and Lemma 3.6, respectively) such that
Define a function
By calculating its upper right derivative along the solution of system (3.1), we get
which, together with
and
and
yields
Define further
and
We choose the Lyapunov functional as follows: \(V(t) = V_{1}(t) + \kappa V_{2}(t) + V_{3}(t) + V_{4}(t) + V_{5}(t)\).
Thus, for \(t \ge T^{*}\),
It follows from \(\Phi^{L} > 0\), \(\Psi^{L} > 0\), and \(\mathrm{E}^{L} > 0\) that
Integrating both sides of the above inequality gives
which, together with the boundedness of \(u'(t)\), \(v'(t)\), and \(w'(t)\), yields that \(|u(s) - \hat{u}(s)|\), \(|v(s) - \hat{v}(s)|\), and \(|w(s) - \hat{w}(s)|\) are uniformly continuous on \([T^{*}, + \infty)\). By Barbalat’s lemma [22], we have
which yields \(\lim_{t \to + \infty} (|x(s) - \hat{x}(s)| + |y(s) - \hat{y}(s)| + |z(s) - \hat{z}(s)|) = 0\). The proof is now finished. □
From Theorem 3.1, if we let \(\theta = 0\), \(\alpha_{i} = 1\) (\(i = 1,2\)), \(z(t) = 0\), then we can get the following corollary.
Corollary 4.1
If \(\Delta_{1} > 0\) and \(\Delta_{2} > 0\),
then system (1.2) is globally attractive, where
Remark 4.1
Corollary 4.1 is the same as Theorem 4.1 of [4]. Their model is the special case of (1.2). In this sense, we generalize or improve their results.
5 Examples and simulation
In this section, we give some examples and numerical simulations to verify the feasibility of our theoretical results, and further study the complexity and variety of system (1.2).
In order to verify the feasibility of our results, we consider the following system:
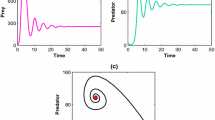
We take, corresponding to system (3.1), \(a_{1} = 10 + 0.1\sin (t)\), \(a_{2} = 2.3 - 0.1\sin (t)\), \(a_{3} = 2 - 0.1\sin (t)\), \(B_{1}(t) = 10\), \(B_{2}(t) = 0.4\), \(B_{3}(t) = 0.1\), \(C_{1}(t) = 1 + 0.29\sin (t)\), \(C_{2}(t) = 2 + 0.1\sin (t)\), \(C_{3}(t) = 0.1 + 0.29\sin (t)\), \(C_{4}(t) = 3 + 0.1\sin (t)\), \(\alpha_{1}(t) = \alpha_{2}(t) = 1.1\), \(\beta_{1}(t) = \beta_{2}(t) = 1\), \(\gamma_{1}(t) = \gamma_{2}(t) = 1\), \(\tau_{1} = \tau_{2} = \tau_{3} = 0.002\), \(T = 1\), \(d_{1k} = 0.15\), \(d_{2k} = 0.005\), \(d_{3k} = 0.001\), \(m = 0.1\), \(\theta = 0.4\), and let \(\sum_{k = 1}^{q} \ln (1 + d_{1k}) \ge - 10\). By direct computation we have \(\int_{0}^{T} a_{1}(t)\,dt \approx 10.045969769\), \(\Delta_{1} = 9.2434 > 0\), \(\Delta_{2} = 0.2053 > 0\), \(\Delta_{3} = 0.0748 > 0\), \(\lim_{t \to + \infty} \inf \{ \Phi (t),\Psi (t), \mathrm{E}(t) \} \approx [4] 0.1936 > 0\). By verification, these parameters satisfy the conditions of Theorems 2.1, 3.1, 4.1 that system (1.2) is permanent and has positive T-periodic solution, which is globally attractive. In order to see these dynamic properties clearly, we drew the figures for the evolution of the solutions of system (1.2) by using the function dde23 in Matlab; see Figs. 1(a)–1(b). If we change the mutual interference of the predator m and the prey refuge constant θ, the other parameters are the same as in Fig. 1, then we get another dynamic portrait that is very different from Fig. 1. We give examples for \(m = 0.8\) and \(\theta = 0.7\), see Fig. 1(c) and Fig. 1(d), respectively. Figure 1(c) and Fig. 1 (d) show that the mutual interference of the predator m and the prey refuge constant θ affects the dynamic behaviors of system (1.2).
The dynamic behavior of system (1.2) with initial values of \(x(0)=1\), \(y(0)=1\), \(z(0)=1\), (a) time series of \(x(t)\), \(y(t)\), \(z(t)\), which are simulated 100 cycles in the interval \([0,200]\). (b) phase portrait of \(x(t)\), \(y(t)\), \(z(t)\), the solution goes gradually into the stable state from the initial point \([1,1,1]\). (c) dynamic behavior of system (1.2) with the mutual interference of the predator \(m=0.8\) and the prey refuge \(\theta=0.7\), (d) phase portrait of \(x(t)\), \(y(t)\), \(z(t)\), other parameters are the same as in Fig. 1(a)
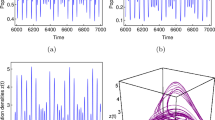
In order to show the complex dynamic behaviors of system (1.2), we choose another set of parameters as \(a_{1} = 1\), \(a_{2} = 0.1\), \(a_{3} = 0.1\), \(b_{1}(t) = 0.35\), \(b_{2}(t) = 0.1\), \(b_{3}(t) = 0.45\), \(c_{1}(t) = 1\), \(c_{2}(t) = 0.8\), \(c_{3}(t) = 1\), \(c_{4}(t) = 0.8\), \(\alpha_{1}(t) = \alpha_{2}(t) = 1\), \(\beta_{1}(t) = \beta_{2}(t) = 0.5\), \(\gamma_{1}(t) = \gamma_{2}(t) = 0.5\), \(\tau_{1} = \tau_{2} = \tau_{3} = 0.01\), \(d_{1k} = 0.05\), \(d_{2k} = 0.05\), \(d_{3k} = 0.05\), \(m = 0.9\), \(\theta = 0.1\). The bifurcation diagrams of \(x(t)\), \(y(t)\), and \(z(t)\) with respect to parameter T in range \([0,6]\) are shown in Fig. 2. Figure 2(a)–(c) are bifurcation diagrams of \(x(t)\), \(y(t)\), and \(z(t)\), respectively. From these diagrams, we can see that impulsive period T heavily affects the dynamic behaviors. For example, Fig. 2(a) shows the complex dynamic behaviors of x. Figure 3 shows the magnified parts of Fig. 2(a). From Fig. 3(a) we can see, when impulsive period \(T < 0.43\), it is stable; if \(T \in [2.62,3.31]\), we found that system (1.2) exhibits stable solutions, chaos, bifurcations, stable periodic solutions, and so on (see Fig. 3(c)); it seems more chaotic on the interval (see Figs. 3(a), 3(b), and 3(d)) when \(T \in [043,2.62] \cup [3.31,6]\); when \(T > 5.35\), it is stable. These phenomena support strongly that system (1.2) has rich and complicated behavior.
Bifurcation diagrams of system (1.2) with \(x(0) = 0.5\), \(y(0) = 0.9\), \(z(0) = 0.7\). The system exhibits stable solution, periodic doubling bifurcation, and chaotic phenomenon corresponding with different T. (a) is the bifurcation diagram of population \(x(t)\). (b) is the bifurcation diagram of population \(y(t)\). (c) is the bifurcation diagram of population \(z(t)\)
The magnified parts of Fig. 2(a) of dynamic behavior of x
6 Conclusion
In this paper, the dynamic behaviors of a delayed impulsive food chain system with prey refuge and mutual inference of predator are investigated and numerical simulations are given. Conditions for the existence and globally asymptotic stability of periodic solution of system (1.2) are obtained in Theorem 2.1 and Theorem 3.1, respectively. Theorem 4.1 gives the sufficient conditions of the permanence of this system (1.2). By computer simulation, the abundant dynamic behaviors of system (1.2) are exhibited.
Theorem 2.1, Theorem 3.1, Theorem 4.1, and simulations show that dynamic properties of (1.2) depend on the mutual interference of the predator m, the prey refuge θ, delays \(\tau_{i}\) (\(i = 1,2,3\)), and the parameter \(d_{i}\) (\(i = 1,2,3\)) of pests or predator which represent the regular harvest or deaths from spraying pesticide. Figure 1(c)–(d) imply that different values of mutual interference of predator m and the prey refuge θ bring different dynamic properties for system (1.2). Figure 2 and Fig. 3 show that impulsive period T heavily affects the dynamic behavior of system (1.2). As T changes, periodic behaviors, bifurcations, and chaotic phenomenon appear, respectively. Hence, we can choose a moderate value of T for some different control strategies.
In addition, model (1.2) generalizes the model of reference [4]. In reference [4], Wang did not consider the prey refuge θ, the Beddington–DeAngelis functional response, and the case that a predator (\(y(t)\)) also has a natural enemy (\(z(t)\)) for understanding and investigating more complex food-chain system. In reference [9], Do studied a three-species food chain system with impulsive control and Beddington–DeAngelis functional response, but he did not consider the prey refuge θ, mutual inference of predator m, and he considered the periodic pulse system. In reference [10], the author studied the existence and global asymptotic stability of positive periodic solutions of periodic n-species Lotka–Volterra impulsive systems with several deviating arguments. In part 4.4 of reference [1], the authors investigated the existence of almost periodic solutions of the impulsive n-species Lotka–Volterra type system. But they did not study the persistence and numerical simulation of the system. However, this paper makes a comprehensive study of the above factors. Our main results generalize or improve their corresponding results in this sense. All above results show that the dynamic behaviors of system (1.2) become more complex than those of system (1.1).
References
Stamova, I., Stamov, G.: Applied Impulsive Mathematical Models. Springer, Berlin (2016)
Shao, Y., Dai, B., Luo, Z.: The dynamics of an impulsive one-prey multi-predators system with delay and Holling-type II functional response. Appl. Math. Comput. 217(6), 2414–2424 (2010)
Ma, X., Shao, Y., Wang, Z., Luo, M., Fang, X., Ju, Z.: An impulsive two-stage predator–prey model with stage-structure and square root functional responses. Math. Comput. Simul., 119, 91–107 (2016)
Wang, K., Zhu, Y.: Periodic solutions, permanence and global attractivity of a delayed impulsive prey–predator system with mutual interference. Nonlinear Anal., Real World Appl. 14(2), 1044–1054 (2013)
He, X.Z.: Stability and delays in a predator–prey system. J. Math. Anal. Appl. 198(2), 355–370 (1996)
Yan, J., Zhao, A.: Oscillation and stability of linear impulsive delay differential equations. J. Math. Anal. Appl. 227(1), 187–194 (1998)
Zhou, X., Liu, X., Zhong, S.: Stability of delayed impulsive stochastic differential equations driven by a fractional Brown motion with time-varying delay. Adv. Differ. Equ. 2016(1), 328 (2016)
Lu, G., Lu, Z.: Non-permanence for three-species Lotka–Volterra cooperative difference systems. Adv. Differ. Equ. 2017(1), 152 (2017)
Do, Y., Baek, H., Kim, D.: Impulsive perturbations of a three-species food chain system with the Beddington-DeAngelis functional response. Discrete Dyn. Nat. Soc. 2012, 417–437 (2012)
Stamova, I.M.: Existence and global asymptotic stability of positive periodic solutions of n-species delay impulsive Lotka–Volterra type systems. J. Biol. Dyn. 5(6), 619–635 (2011)
Hassell, M.P.: Mutual interference between searching insect parasites. J. Anim. Ecol. 40(2), 473–486 (1971)
Wang, Z., Shao, Y., Fang, X., Ma, X.: An impulsive three-species model with square root functional response and mutual interference of predator. Discrete Dyn. Nat. Soc. 2016, Article ID 3897234 (2016)
He, D., Huang, W., Xu, Q.: The dynamic complexity of an impulsive Holling II predator–prey model with mutual interference. Appl. Math. Model. 34(9), 2654–2664 (2010)
Baek, H.: A food chain system with Holling type IV functional response and impulsive perturbations. Comput. Math. Appl. 60(5), 1152–1163 (2010)
González-Olivares, E., Ramos-Jiliberto, R.: Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecol. Model. 166(166), 135–146 (2001)
Ma, Z., Chen, F., Wu, C., Chen, W.: Dynamic behaviors of a Lotka–Volterra predator–prey model incorporating a prey refuge and predator mutual interference. Appl. Math. Comput. 219(15), 7945–7953 (2013)
Chen, L., Chen, F., Wang, Y.: Influence of predator mutual interference and prey refuge on Lotka–Volterra predator–prey dynamics. Commun. Nonlinear Sci. Numer. Simul. 18(11), 3174–3180 (2013)
Yang, K.: Basic properties of mathematical population models. J. Biomath. 26(2), 129–142 (2002)
Gakkhar, S., Naji, R.K.: Order and chaos in a food web consisting of a predator and two independent preys. Commun. Nonlinear Sci. Numer. Simul. 10(2), 105–120 (2005)
Gaines, R.E., Mawhin, J.L.: Coincidence Degree, and Nonlinear Differential Equations. Springer, Berlin (1977)
Chao, C., Chen, F.: Conditions for global attractivity of multispecies ecological competition-predator system with Holling III type functional response. J. Biomath. 19(2), 136–140 (2004)
Barbălat, I.: Systèmes d’équations différentielles d’oscillations non linéaires. Rev. Math. Pures Appl. 4, 267–270 (1959)
Acknowledgements
This paper is supported by the Natural Science Foundation of Guangxi (2016GXNSFAA380194), National Natural Science Foundation of China (11161015).
Authors’ information
SZ is now studying for the M.S. degree at Guilin University of Technology, Guilin, China. Her research interest is the study of dynamical behaviors and simulation analysis of periodic impulsive differential equations. YS received Ph.D. degree in mathematics from Central South University, Changsha, China. He is a professor of School of Science, Guilin University of Technology, Guilin, China. His research interests are differential equations and dynamical systems. He is mainly engaged in qualitative studies of complex dynamical systems. QL and ZW are now studying for the M.S. degree at Guilin University of Technology, Guilin, China. Their research interests are stability analysis and numerical simulation of impulsive systems.
Author information
Authors and Affiliations
Contributions
All authors contributed equally in this article. They read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhou, S., Shao, Y., Liu, Q. et al. A delayed impulsive food chain system with prey refuge and mutual inference of predator. Adv Differ Equ 2018, 137 (2018). https://doi.org/10.1186/s13662-018-1586-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1586-y