1 Introduction

In recent several decades, cellular neural networks (CNNs) have attracted much attentions from many scholars since they have been applied in numerous areas, for example, they can be applied to image processing, pattern recognition, psychophysics, etc. [1–6]. A great deal of achievement on the dynamics of CNNs has been made. For instance, Abbas and Xia [7] studied the attractivity of k-almost automorphic solution of CNNs with delay, Balasubramaniam et al. [8] considered the global asymptotic stability of BAM FCNNs with mixed delays, Qin et al. [9] considered the convergence and attractivity of memristor-based delayed CNNs. For additional explanation, one can refer to [10–15].

We know that FCNNs possess fuzzy logic between template input and/or output. A lot of authors think that the FCNNs play a key role in image processing aspects [16]. In addition, leakage delay has a great effect on the dynamical nature of neural networks [17–21]. For instance, leakage delay can destabilize a model [22]. In [23], the authors believed that the appearance of the equilibrium has no contact with initial value and delay. Moreover, the proportional delay of neural networks can be expressed by \(\xi(s)=s-rs, 0< r<1, s>0\). In real life, proportional delay plays a huge role in many areas such as quality of web, current collection [24] and so on. Since the applications of CNNs have an important relation with the global exponential convergence behaviors [25–37]. Therefore we think that it is meaningful to analyze the global exponential convergence of neural networks with proportional delays and leakage delays. But now there is no existing work as regards the global exponential convergence of FCNNs with proportional delays and leakage delays.

Inspired by the viewpoint, it is necessary for us to study the existence and global attractivity for neural networks with proportional delays and leakage delays. In this paper, we will discuss the following neural network model:

$$ \textstyle\begin{cases} \dot{z}_{i}(t)=-\alpha_{i}(t)z_{i}(t-\delta_{i}(t))+\sum_{j=1}^{n}A_{ij}(t)h_{j}(z_{j}(t))+\sum_{j=1}^{n}B_{ij}(t)v_{j}(t)+G_{i}(t)\\ \phantom{ \dot{z}_{i}(t)=}{} +\bigwedge_{j=1}^{n}C_{ij}(t)h_{j}(z_{j}(\theta _{ij}t))+\bigvee_{j=1}^{n}D_{ij}(t)h_{j}(z_{j}(\theta_{ij}t))\\ \phantom{ \dot{z}_{i}(t)=}{} +\bigwedge_{j=1}^{n}E_{ij}(t)v_{j}(t)+\bigvee_{j=1}^{n}F_{ij}(t)v_{j}(t),\quad t\geq\bar{t}\geq0, i\in\Lambda=\{1,2,\ldots,n\}, \end{cases} $$
(1.1)

where \(\alpha_{i}(t)\) is a rate coefficient, \(A_{ij}(t)\ (B_{ij}(t)) \) denotes the feedback (feedforward) template; \(C_{ij}(t)\ (D_{ij}(t))\) stands for fuzzy feedback MIN (MAX) template, \(E_{ij}(t)\ (F_{ij}(t))\) means fuzzy feedforward MIN (MAX) template. \(\bigwedge\ (\bigvee)\) stand for the fuzzy AND (OR) operation, \(z_{i}(t), v_{i}(t)\) and \(G_{i}(t)\) denote the state, input and bias of the ith neuron, respectively; \(h(\cdot)\) is the activation function; \(\delta_{i}(t)\) is the transmission delay. \(\theta _{ij}, i, j\in\Lambda\) stand for proportional delays and satisfy \(0<\theta_{ij}\leq1\), and \(\theta_{ij}t=t-(1-\theta_{ij})t\), in which \(\tau_{ij}(t)=(1-\theta_{ij})t\) is the transmission delay function, and \((1-\theta_{ij})t\rightarrow\infty\) as \(\theta_{ij}\neq1, t\rightarrow\infty\), \(t-\delta_{i}(t)>\bar{t}\) \(\forall t\geq\bar{t}\).

The initial values of (1.1) take the form

$$ z_{i}(s)=\psi_{i}(s),\quad s\in[ \varsigma_{i} \bar{t}, \bar{t}],i\in\Lambda, $$
(1.2)

where \(\varsigma_{i}=\min_{i,j\in\Lambda}\{\theta_{ij}\}\), and \(\psi _{i}(t)\in R\) represents a continuous function, where \(t\in[\varsigma_{i} \bar{t}, \bar{t}]\).

Set

$$l^{+}=\sup_{t\in[\bar{t},+\infty)} \bigl\vert l(t) \bigr\vert ,\qquad l^{-}=\inf_{t\in [\bar{t},+\infty)} \bigl\vert l(t) \bigr\vert , $$

where l stands for a bounded and continuous function. Let \(z=(z_{1},z_{2},\ldots,z_{n})^{T}\in R^{n}\), \(\vert z \vert =( \vert z_{1} \vert , \vert z_{2} \vert ,\ldots, \vert z_{n} \vert )^{T}\) and \(\Vert z \Vert =\max_{i\in\Lambda} \vert z_{i} \vert \). We assume that \(d_{i}, A_{ij}, B_{ij},C_{ij},D_{ij}, E_{ij},F_{ij},G_{i},v_{i}: [\bar{t},+\infty)\rightarrow R\) and \(\delta_{i}: [\bar{t},+\infty)\rightarrow[0,+\infty)\) are bounded and continuous functions.

Lemma 1.1

([38])

If \(z_{j}\) and \(q_{j}\) are two states of (1.1), then

$$\begin{aligned} &\Bigl\vert \bigwedge C_{ij}(t)h_{j}(z_{j})- \bigwedge C_{ij}(t)h_{j}(q_{j}) \Bigr\vert \leq \sum_{j=1}^{n} \bigl\vert C_{ij}(t) \bigr\vert \bigl\vert h_{j}(z_{j})-h_{j}(q_{j}) \bigr\vert , \\ &\Bigl\vert \bigvee D_{ij}(t)h_{j}(z_{j})- \bigvee D_{ij}(t)h_{j}(q_{j}) \Bigr\vert \leq\sum_{j=1}^{n} \bigl\vert D_{ij}(t) \bigr\vert \bigl\vert h_{j}(z_{j})-h_{j}(q_{j}) \bigr\vert . \end{aligned}$$

Now we also give some assumptions as follows:

  1. (Q1)

    \(\exists \alpha_{i}^{*}:[t_{0},+\infty)\rightarrow(0,+\infty)\) and a constant \(\eta_{i}>0\) which satisfy \(e^{-\int_{s}^{t}\alpha_{i}(\theta)\,d\theta }\leq \eta_{i}e^{-\int_{s}^{t}\alpha_{i}^{*}(\theta)\,d\theta}\), \(\forall t,s\in R, i\in\Lambda\) and \(t-s\geq0\), where \(\alpha_{i}^{*}\) is a bounded and continuous function.

  2. (Q2)

    ∃ constants \(L_{j}\geq0\) which satisfy \(\vert h_{j}(t_{1})-h_{j}(t_{2}) \vert \leq L_{j} \vert t_{1}-t_{2} \vert , h_{j}(0)=0\) \(\forall t_{1},t_{2}\in R, i\in\Lambda\).

  3. (Q3)

    ∃ constants \(\mu_{1}>0,\mu_{2}>0,\ldots,\mu_{n}>0\) and \(\gamma^{*}>0\) which satisfy

    $$\begin{aligned} & \sup_{t\geq\bar{t}}\Biggl\{ -\alpha_{i}^{*}(t)+ \eta_{i}\Biggl[ \bigl\vert \alpha _{i}(t) \bigr\vert \delta_{i}^{*}(t)e^{\gamma^{*}\delta_{i}^{+}}+\mu_{i}^{-1}\sum _{j=1}^{n} \bigl\vert A_{ij}(t) \bigr\vert L_{j}\mu_{j} \\ & \quad{}+\mu_{i}^{-1}\sum_{j=1}^{n} \bigl\vert C_{ij}(t) \bigr\vert L_{j}\mu_{j} e^{\gamma^{*}(1-\theta _{ij})t}+\mu_{i}^{-1}\sum _{j=1}^{n} \bigl\vert D_{ij}(t) \bigr\vert L_{j}\mu_{j}e^{\gamma^{*}(1-\theta _{ij})t}\Biggr]\Biggr\} < 0, \\ & \sup_{t\geq\bar{t}}\Biggl\{ \bigl\vert \alpha_{i}(t) \bigr\vert +\eta_{i}\Biggl[ \bigl\vert \alpha _{i}(t) \bigr\vert \delta_{i}(t)e^{\gamma^{*}\delta_{i}^{+}}+\mu_{i}^{-1} \sum_{j=1}^{n} \bigl\vert A_{ij}(t) \bigr\vert L_{j}\mu_{j} \\ & \quad{}+\mu_{i}^{-1}\sum_{j=1}^{n} \bigl\vert C_{ij}(t) \bigr\vert L_{j} \mu_{j}e^{\gamma^{*}(1-\theta _{ij})t}+\mu_{i}^{-1}\sum _{j=1}^{n} \bigl\vert D_{ij}(t) \bigr\vert L_{j}\mu_{j}e^{\gamma^{*}(1-\theta _{ij})t}\Biggr]\Biggr\} < 1, \end{aligned}$$

    and \(G_{i}(t)+(B_{ij}(t)+E_{ij}(t)+F_{ij}(t))v_{j}=O(e^{-\gamma^{*}t})\) as \(t\rightarrow+\infty\), where \(i,j\in\Lambda\).

The pivotal achievements of this article consist of three points: (i) the global exponential convergence of FCCNs with leakage delays and proportional delays is firstly considered; (ii) a new sufficient criterion guaranteeing the global exponential convergence of model (1.1) is presented; (iii) the analytic predictions of this article are more common and the analysis method of this article can be applied to the investigation of some other related network systems.

2 Main findings

Now we will give the important findings on the global exponential convergence for (1.1).

Theorem 2.1

For (1.1), if (Q1)–(Q3) hold, then ∃ a constant \(\gamma>0\) such that, for every \(z=(z_{1},z_{2},\ldots,z_{n})^{T}\), \(z_{i}(t)=O(e^{-\gamma t})\) when \(t\rightarrow+\infty, i\in\Lambda\).

Proof

In order to prove \(z_{i}(t)=O(e^{-\gamma t})\) when \(t\rightarrow+\infty, i\in\Lambda\), we need prove that there exists a constant \(M>0\) such that \(z_{i}(t)=M e^{-\gamma t} \) when \(t\rightarrow+\infty, i\in\Lambda\). For convenience, we firstly establish an equivalent form of the original system by applying a suitable variable substitution. By way of contradiction and the differential inequality strategies, we obtain the results of the theorem. In the following, we will given the detailed proofs.

Assume that \(z(t)=(z_{1}(t),z_{2}(t),\ldots, z_{n}(t))^{T}\) is an arbitrary solution of (1.1) and the initial value is \(\psi=(\psi_{1},\psi_{2},\ldots,\psi_{n})^{T}\). Set

$$ w(t)=\bigl(w_{1}(t),w_{2}(t),\ldots, w_{n}(t)\bigr)^{T}=\bigl(\mu_{1}^{-1}z_{1}(t), \mu_{2}^{-1}z_{2}(t),\ldots, \mu_{n}^{-1}z_{n}(t) \bigr)^{T}. $$
(2.1)

Then (1.1) becomes

$$ \textstyle\begin{cases} \dot{w}_{i}(t)=-\alpha_{i}(t)w_{i}(t-\delta_{i}(t))+\mu_{i}^{-1}\sum_{j=1}^{n}A_{ij} (t)h_{j}(\mu_{j}w_{j}(t))\\ \phantom{\dot{w}_{i}(t)=}{} +\mu_{i}^{-1}\sum_{j=1}^{n}B_{ij}(t)v_{j}(t)+\mu_{i}^{-1}I_{i}(t)\\ \phantom{\dot{w}_{i}(t)=}{} +\mu_{i}^{-1}\bigwedge_{j=1}^{n}C_{ij}(t)h_{j}(\mu _{j}w_{j}(\theta_{ij}t))+\mu_{i}^{-1}\bigvee_{j=1}^{n}D_{ij}(t)h_{j}(\mu _{j}w_{j}(\theta_{ij}t))\\ \phantom{\dot{w}_{i}(t)=}{} +\mu_{i}^{-1}\bigwedge_{j=1}^{n}E_{ij}(t)v_{j}(t)+\mu _{i}^{-1}\bigvee_{j=1}^{n}F_{ij}(t)v_{j}(t),\quad i\in\Lambda=\{1,2,\ldots,n\}. \end{cases} $$
(2.2)

By (Q3), we can find a \(\gamma\in(0,\min\{\gamma^{*},\min_{i\in\Lambda}\inf_{t\geq t_{0}}\alpha_{i}^{*}(t)\})\) which satisfies

$$\begin{aligned} &\sup_{t\geq\bar{t}}\Biggl\{ \gamma-\alpha_{i}^{*}(t)+ \eta_{i}\Biggl[ \bigl\vert \alpha _{i}(t) \bigr\vert \delta_{i}^{*}(t)e^{\gamma^{*}\delta_{i}^{+}} \\ &\quad{}+\mu_{i}^{-1}\sum _{j=1}^{n} \bigl\vert A_{ij}(t) \bigr\vert L_{j}\mu_{j} +\mu_{i}^{-1}\sum_{j=1}^{n} \bigl\vert C_{ij}(t) \bigr\vert L_{j}\mu_{j} e^{\gamma^{*}(1-\theta _{ij})t} \\ & \quad{}+\mu_{i}^{-1}\sum _{j=1}^{n} \bigl\vert D_{ij}(t) \bigr\vert L_{j}\mu_{j}e^{\gamma^{*}(1-\theta _{ij})t}+\gamma\Biggr]\Biggr\} < 0, \quad i\in\Lambda, \end{aligned}$$
(2.3)
$$\begin{aligned} & \sup_{t\geq\bar{t}}\Biggl\{ \bigl\vert \alpha_{i}(t) \bigr\vert +\eta_{i}\Biggl[ \bigl\vert \alpha _{i}(t) \bigr\vert \delta_{i}(t)e^{\gamma^{*}\delta_{i}^{+}}+ \mu_{i}^{-1}\sum_{j=1}^{n} \bigl\vert A_{ij}(t) \bigr\vert L_{j}\mu_{j} \\ & \quad{}+\mu_{i}^{-1}\sum_{j=1}^{n} \bigl\vert C_{ij}(t) \bigr\vert L_{j} \mu_{j}e^{\gamma^{*}(1-\theta _{ij})t} \\ & \quad{}+\mu_{i}^{-1}\sum _{j=1}^{n} \bigl\vert D_{ij}(t) \bigr\vert L_{j}\mu_{j}e^{\lambda^{*}(1-\theta _{ij})t}+\gamma\Biggr]\Biggr\} < 1, \quad i\in\Lambda. \end{aligned}$$
(2.4)

Set

$$ \Vert \psi \Vert _{\mu}=\max_{i\in\Lambda} \Bigl\{ \mu_{i}^{-1}\max_{t\in[\varsigma_{i}\bar {t},\bar{t}]} \bigl\vert \psi_{i}(t) \bigr\vert \Bigr\} . $$
(2.5)

For \(\epsilon>0\), one has

$$ \bigl\vert w_{i}(t) \bigr\vert < \bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(t-\bar{t})}< \chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(t-\bar{t})} $$
(2.6)

\(\forall t\in[\varsigma_{i}\bar{t},\bar{t}]\), where \(\chi=\max_{i\in\Lambda}\eta_{i}+1\) which satisfies

$$ \bigl\vert \mu _{i}^{-1} \bigl(B_{ij}(t)v_{j}(t)+G_{i}(t)+E_{ij}(t)v_{j}(t)+F_{ij}(t)v_{j}(t) \bigr) \bigr\vert < \gamma \chi\bigl( \Vert \psi \Vert _{\mu}+ \epsilon\bigr)e^{-\gamma(t-\bar{t})} $$
(2.7)

\(\forall t\geq\bar{t}, i\in\Lambda\). In the sequel, we will prove that

$$ \bigl\vert w_{i}(t) \bigr\vert < \chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(t-\bar{t})} $$
(2.8)

\(\forall t\geq\bar{t}, i\in\Lambda\). Assume that (2.8) does not hold, then we can find \(i\in\Lambda\) and \(t^{*}>\bar{t}\) which satisfies

$$ \bigl\vert w_{i}\bigl(t^{*}\bigr) \bigr\vert =\chi \bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(t^{*}-\bar{t})} $$
(2.9)

and

$$ \bigl\vert w_{j}(t) \bigr\vert =\chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(t-\bar{t})} $$
(2.10)

\(\forall t\in[\varsigma_{j}\bar{t},t^{*}],j\in\Lambda\).

In addition

$$ \textstyle\begin{cases} \dot{w}_{i}(s)+\alpha_{i}(s)w_{i}(s)\\ \quad{}=\alpha_{i}(s)\int_{s-\delta _{i}(s)}^{s}\dot{w}_{i}(\theta)\,d\theta+\mu_{i}^{-1}\sum_{j=1}^{n}A_{ij}(s)h_{j}(\mu _{j}w_{j}(s))+\mu_{i}^{-1}\sum_{j=1}^{n}B_{ij}(s)v_{j}(s)\\ \qquad{} +\mu_{i}^{-1}\bigwedge_{j=1}^{n}C_{ij}(s)h_{j}(\mu_{j}w_{j}(\theta_{ij}s))+\mu_{i}^{-1}\bigvee_{j=1}^{n}D_{ij}(s)h_{j}(\mu_{j}w_{j}(\theta_{ij}s))\\ \qquad{} +\mu_{i}^{-1}\bigwedge_{j=1}^{n}E_{ij}(s)v_{j}(s)+\mu_{i}^{-1}\bigvee_{j=1}^{n}F_{ij}(s)v_{j}(s)+\mu _{i}^{-1}G_{i}(s), \end{cases} $$
(2.11)

where \(s\in[\bar{t},t],t\in[\bar{t},t^{*}],i\in\Lambda\).

In view of (2.11), one has

$$ \textstyle\begin{cases} \dot{w}_{i}(t)=\alpha_{i}(\bar{t})e^{-\int_{\bar{t}}^{t}\alpha _{i}(v)\,dv}+\int_{\bar{t}}^{t}e^{-\int_{s}^{t}\alpha_{i}(v)\,dv}[d_{i}(s)\int _{s-\delta_{i}(s)}^{s}\dot{w}_{i}(v)\,dv\\ \phantom{\dot{w}_{i}(t)=}{} +\mu_{i}^{-1}\sum_{j=1}^{n}A_{ij}(s)h_{j}(\mu _{j}w_{j}(s))+\mu_{i}^{-1}\sum_{j=1}^{n}B_{ij}(s)v_{j}(s)\\ \phantom{\dot{w}_{i}(t)=}{} +\mu_{i}^{-1}\bigwedge_{j=1}^{n}C_{ij}(s)h_{j}(\mu _{j}w_{j}(\theta_{ij}s))+\mu_{i}^{-1}\bigvee_{j=1}^{n}D_{ij}(s)h_{j}(\mu _{j}w_{j}(\theta_{ij}s))\\ \phantom{\dot{w}_{i}(t)=}{} +\mu_{i}^{-1}\bigwedge_{j=1}^{n}E_{ij}(s)v_{j}(s)+\mu _{i}^{-1}\bigvee_{j=1}^{n}F_{ij}(s)v_{j}(s)+\mu_{i}^{-1}G_{i}(s)]\,ds. \end{cases} $$
(2.12)

According to (2.3), (2.7) and (2.10), we get

$$\begin{aligned} \bigl\vert \dot{w}_{i}\bigl(t^{*}\bigr) \bigr\vert ={}&\Biggl\vert \alpha_{i}(\bar{t})e^{-\int_{\bar{t}}^{t^{*}}\alpha _{i}(v)\,dv}+ \int_{\bar{t}}^{t^{*}} e^{-\int_{s}^{t^{*}} \alpha_{i}(v)\,dv} \Biggl[ \alpha_{i}(s) \int_{s-\delta_{i}(s)}^{s}\dot{w}_{i}(v)\,dv \\ & {}+\mu_{i}^{-1}\sum_{j=1}^{n}A_{ij}(s)h_{j} \bigl(\mu_{j}w_{j}(s)\bigr)+\mu_{i}^{-1} \sum_{j=1}^{n}B_{ij}(s)v_{j}(s) \\ & {}+\mu_{i}^{-1}\bigwedge_{j=1}^{n}C_{ij}(s)h_{j} \bigl(\varrho_{j}w_{j}(\theta _{ij}s)\bigr)+ \mu_{i}^{-1}\bigvee_{j=1}^{n}D_{ij}(s)h_{j} \bigl(\mu_{j}w_{j}(\theta _{ij}s)\bigr) \\ & {}+\mu_{i}^{-1}\bigwedge_{j=1}^{n}E_{ij}(s)v_{j}(s)+ \mu_{i}^{-1}\bigvee_{j=1}^{n}F_{ij}(s)v_{j}(s)+ \mu_{i}^{-1}G_{i}(s)\Biggr]\,ds\Biggr\vert \\ \leq{}&\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr) \eta_{i}e^{-\int_{\bar{t}}^{t^{*}} \alpha_{i}^{*}(v)\,dv}+ \int_{\bar{t}}^{t^{*}} e^{-\int_{s}^{t^{*}} \alpha_{i}^{*}(v)\,dv} \eta_{i} \\ &{}\times\Biggl[ \bigl\vert \alpha_{i}(s) \bigr\vert \delta_{i}(s)\chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon \bigr)e^{-\gamma(s-\delta_{i}(s)-\bar{t})}+\mu_{i}\sum_{j=1}^{n} \bigl\vert A_{ij}(s) \bigr\vert L_{j}\mu _{j} \bigl\vert w_{j}(s) \bigr\vert \\ & {}+\mu_{i}\sum_{j=1}^{n} \bigl\vert C_{ij}(s) \bigr\vert L_{j}\mu_{j} \bigl\vert w_{j}(\theta_{ij}s) \bigr\vert +\mu_{i} \sum_{j=1}^{n} \bigl\vert D_{ij}(s) \bigr\vert L_{j}\mu_{j} \bigl\vert w_{j}(\theta_{ij}s) \bigr\vert \\ & {}+ \Biggl\vert \mu_{i}^{-1}\sum _{j=1}^{n}B_{ij}(s)v_{j}(s)+ \mu_{i}^{-1}\bigwedge_{j=1}^{n}E_{ij}(s)v_{j}(s)+ \mu_{i}^{-1}\bigvee_{j=1}^{n}F_{ij}(s)v_{j}(s)+ \mu _{i}^{-1}G_{i}(s) \Biggr\vert \Biggr]\,ds \\ \leq{}&\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr) \eta_{i}e^{-\int_{\bar{t}}^{t^{*}} \alpha_{i}^{*}(v)\,dv}+ \int_{\bar{t}}^{t^{*}} e^{-\int_{s}^{t^{*}} \alpha_{i}^{*}(v)\,dv} \eta_{i} \\ &{}\times\Biggl[ \bigl\vert \alpha_{i}(s) \bigr\vert \delta_{i}(s)\chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon \bigr)e^{-\gamma(s-\delta_{i}^{+}-\bar{t})} \\ &{}+\mu_{i}\sum_{j=1}^{n} \bigl\vert A_{ij}(s) \bigr\vert L_{j}\mu _{j} \chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(s-\bar{t})} \\ & {}+\mu_{i}\sum_{j=1}^{n} \bigl\vert C_{ij}(s) \bigr\vert L_{j}\mu_{j}\chi \bigl( \Vert \psi \Vert _{\mu}+\epsilon \bigr)e^{-\gamma(\theta_{ij}s-\bar{t})} \\ &{} + \mu_{i}\sum_{j=1}^{n} \bigl\vert D_{ij}(s) \bigr\vert L_{j}\mu_{j}\chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon \bigr)e^{-\gamma(\theta_{ij}s-\bar{t})} \\ & {}+\gamma\chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon \bigr)e^{-\gamma(\theta_{ij}s-\bar {t})}\Biggr]\,ds \\ \leq{}&\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr) \eta_{i}e^{-\int_{\bar{t}}^{t^{*}} \alpha_{i}^{*}(v)\,dv}+ \int_{\bar{t}}^{t^{*}} e^{-\int_{s}^{t^{*}} (\alpha_{i}^{*}(v)-\gamma)\,dv} \eta_{i} \Biggl[ \bigl\vert d_{i}(s) \bigr\vert \delta_{i}(s)e^{\gamma\delta_{i}^{+}} \\ & {}+\mu_{i}\sum_{j=1}^{n} \bigl\vert A_{ij}(s) \bigr\vert L_{j}\mu_{j}+ \mu_{i}\sum_{j=1}^{n} \bigl\vert C_{ij}(s) \bigr\vert L_{j}\mu_{j}e^{\gamma(1-\theta_{ij})s} \\ & {}+\mu_{i}\sum_{j=1}^{n} \bigl\vert D_{ij}(s) \bigr\vert L_{j}\mu_{j}e^{\gamma(1-\theta _{ij})s}+ \gamma\Biggr]\,ds \chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon \bigr)e^{-\gamma(t^{*}-\bar {t})} \\ \leq{}&\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr) \eta_{i}e^{-\int_{\bar{t}}^{t^{*}} \alpha_{i}^{*}(v)\,dv} \\ &{}+ \int_{\bar{t}}^{t^{*}} e^{-\int_{s}^{t^{*}} (\alpha_{i}^{*}(v)-\gamma)\,dv} \bigl[ \alpha_{i}^{*}(s)-\gamma\bigr] \,ds \chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(t^{*}-\bar {t})} \\ ={}& \chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon \bigr)e^{-\gamma(t^{*}-\bar{t})} \biggl[\biggl(\frac{\eta_{i}}{\chi}-1\biggr) e^{-\int_{\bar{t}}^{t^{*}} (\alpha_{i}^{*}(v)-\gamma)\,dv}+1\biggr] \\ < {}&\chi\bigl( \Vert \psi \Vert _{\mu}+\epsilon\bigr)e^{-\gamma(t^{*}-\bar{t})}. \end{aligned}$$
(2.13)

By (2.9), we know that (2.8) holds. Therefore \(z_{i}(t)=O(e^{-\gamma t})\) when \(t\rightarrow+\infty, i\in\Lambda\). □

Remark 2.1

In [39], the authors studied the finite-time synchronization of delayed neural networks. This paper does not involve proportional delay and leakage delay. In [40] the authors analyzed the finite-time synchronization for neural networks with proportional delays, this article does not consider the leakage delays. Huang [41] considered the exponential stability of delayed neural networks, but he also did not consider the effect of proportional delays and leakage delays. moreover, all authors of [39–41] did not investigate the global exponential convergence of systems. In this article, we study the global exponential convergence of FCNNs with leakage delays and proportional delays. All the theoretical findings in [39–41] cannot be applied to (1.1) to ensure the global exponential convergence of (1.1). Up to now, there are no results on the global exponential convergence of FCNNs with leakage delays and proportional delays. From this viewpoint, our results on global exponential convergence for FCNNs are essentially innovative and complete several earlier publications.

3 Examples

Considering the following model:

$$ \textstyle\begin{cases} \dot{z}_{1}(t)=-\alpha_{1}(t)z_{1}(t-\delta_{1}(t))+\sum_{j=1}^{2}A_{1j}(t)h_{j}(z_{j}(t))\\ \phantom{\dot{z}_{1}(t)=}{}+\sum_{j=1}^{2}B_{ij}(t)u_{j}(t)+\bigwedge_{j=1}^{2}C_{1j}(t)h_{j}(z_{j}(\theta_{1j}t))\\ \phantom{\dot{z}_{1}(t)=}{} +\bigvee_{j=1}^{2}D_{1j}(t)h_{j}(z_{j}(\theta _{1j}t))+\bigwedge_{j=1}^{2}E_{1j}(t)v_{j}(t)+\bigvee_{j=1}^{2}F_{1j}(t)v_{j}(t)+G_{1}(t),\\ \dot{z}_{2}(t)=-\alpha_{2}(t)z_{2}(t-\delta_{2}(t))\\ \phantom{\dot{z}_{1}(t)=}{}+\sum_{j=1}^{2}A_{2j}(t)h_{j}(z_{j}(t))+\sum_{j=1}^{2}B_{2j}(t)v_{j}(t)+\bigwedge_{j=1}^{2}C_{2j}(t)h_{j}(z_{j}(\theta_{2j}t))\\ \phantom{\dot{z}_{2}(t)=}{} +\bigvee_{j=1}^{2}D_{2j}(t)h_{j}(z_{j}(\theta _{2j}t))+\bigwedge_{j=1}^{2}E_{2j}(t)v_{j}(t)+\bigvee_{j=1}^{2}F_{2j}(t)v_{j}(t)+G_{2}(t), \end{cases} $$
(3.1)

where \(h_{1}(v)=h_{2}(v)=0.5(| v+1|-| v-1| )\) and

$$\begin{aligned} & \left[ \begin{matrix} \alpha_{1}(t) & \delta_{1}(t) \\ \alpha_{2}(t) & \delta_{2}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.1(1+0.5\sin t) & 0.01 \vert \sin t \vert \\ 0.1(1+0.5\sin t) & 0.01 \vert \cos t \vert \end{matrix} \right], \\ & \left[ \begin{matrix} A_{11}(t) & A_{12}(t) \\ A_{21}(t) & A_{22}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.01 \vert \sin(25\pi t) \vert & 0.01 \vert \sin(25\pi t) \vert \\ 0.01 \vert \cos(20\pi t) \vert & 0.01 \vert \cos(20\pi t) \vert \end{matrix} \right], \\ & \left[ \begin{matrix} B_{11}(t) & B_{12}(t) \\ B_{21}(t) & B_{22}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.01 \vert \sin(24\pi t) \vert & 0.01 \vert \sin(24\pi t) \vert \\ 0.01 \vert \cos(12\pi t) \vert & 0.02 \vert \sin(15\pi t) \vert \end{matrix} \right], \\ & \left[ \begin{matrix} C_{11}(t) & C_{12}(t) \\ C_{21}(t) & C_{22}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.01 \vert \sin(22\pi t) \vert & 0.02 \vert \cos(18\pi t) \vert \\ 0.03 \vert \sin(15\pi t) \vert & 0.03 \vert \cos(18\pi t) \vert \end{matrix} \right], \\ & \left[ \begin{matrix} D_{11}(t) & D_{12}(t) \\ D_{21}(t) & D_{22}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.01 \vert \cos(20\pi t) \vert & 0.02 \vert \sin(15\pi t) \vert \\ 0.02 \vert \sin(20\pi t) \vert & 0.01 \vert \cos(15\pi t) \vert \end{matrix} \right], \\ & \left[ \begin{matrix} E_{11}(t) & E_{12}(t) \\ E_{21}(t) & E_{22}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.04 \vert \sin(30\pi t) \vert & 0.05 \vert \sin(28\pi t) \vert \\ 0.07 \vert \sin(30\pi t) \vert & 0.05 \vert \sin(28\pi t) \vert \end{matrix} \right], \\ & \left[ \begin{matrix} F_{11}(t) & F_{12}(t) \\ F_{21}(t) & F_{22}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.03 \vert \sin(26\pi t) \vert & 0.02 \vert \sin(24\pi t) \vert \\ 0.01 \vert \cos(26\pi t) \vert & 0.02 \vert \cos(24\pi t) \vert \end{matrix} \right], \\ & \left[ \begin{matrix} V_{1}(t) & G_{1}(t) \\ V_{2}(t) & G_{2}(t) \end{matrix} \right]=\left[ \begin{matrix} 0.21 \vert \sin(13\pi t) \vert & 0.24 \vert \cos(20\pi t) \vert \\ 0.34 \vert \sin(16\pi t) \vert & 0.25 \vert \cos(20\pi t) \vert \end{matrix} \right], \\ & \left[ \begin{matrix} \theta_{11} & \theta_{12} \\ \theta_{21} & \theta_{22} \end{matrix} \right]=\left[ \begin{matrix} 0.01 & 0.01 \\ 0.02 & 0.02 \end{matrix} \right]. \end{aligned}$$

Then \(L_{1}=L_{2}=1\). Let \(\alpha_{i}^{*}(t)=0.1, \eta_{i}=e^{\frac{1}{10}}\), then \(e^{-\int_{s}^{t}\alpha_{i}(\theta)\,d\theta}\leq e^{\frac{1}{10}}e^{-(t-s)},i=1,2,t\geq s\). Let \(\mu_{1}=\mu_{2}=1, \gamma^{*}=1\). So

$$\begin{aligned} & \sup_{t\geq\bar{t}}\Biggl\{ -\alpha_{1}^{*}(t)+ \eta_{1}\Biggl[ \bigl\vert \alpha _{1}(t) \bigr\vert \delta_{1}^{*}(t)e^{\gamma^{*}\delta_{1}^{+}}+\mu_{1}^{-1}\sum _{j=1}^{2} \bigl\vert A_{1j}(t) \bigr\vert L_{j}\mu_{j} \\ & \quad{}+\mu_{1}^{-1}\sum_{j=1}^{2} \bigl\vert C_{1j}(t) \bigr\vert L_{j}\mu_{j} e^{\gamma^{*}(1-\theta _{1j})t}+\mu_{1}^{-1}\sum _{j=1}^{2} \bigl\vert D_{1j}(t) \bigr\vert L_{j}\mu_{j}e^{\gamma^{*}(1-\theta _{1j})t}\Biggr]\Biggr\} =-0.0432< 0, \\ & \sup_{t\geq\bar{t}}\Biggl\{ \bigl\vert \alpha_{1}(t) \bigr\vert +\eta_{1}\Biggl[ \bigl\vert \alpha _{1}(t) \bigr\vert \delta_{1}(t)e^{\gamma^{*}\delta_{1}^{+}}+\mu_{1}^{-1} \sum_{j=1}^{2} \bigl\vert A_{1j}(t) \bigr\vert L_{j}\mu_{j} \\ & \quad{}+\mu_{1}^{-1}\sum_{j=1}^{2} \bigl\vert C_{1j}(t) \bigr\vert L_{j} \mu_{j}e^{\gamma^{*}(1-\theta _{1j})t}+\mu_{1}^{-1}\sum _{j=1}^{2} \bigl\vert D_{1j}(t) \bigr\vert L_{j}\mu_{j}e^{\gamma^{*}(1-\theta _{1j})t}\Biggr]\Biggr\} =0.3511< 1, \\ & \sup_{t\geq\bar{t}}\Biggl\{ -\alpha_{2}^{*}(t)+ \eta_{2}\Biggl[ \bigl\vert \alpha _{2}(t) \bigr\vert \delta_{2}^{*}(t)e^{\gamma^{*}\delta_{2}^{+}}+\mu_{2}^{-1}\sum _{j=1}^{2} \bigl\vert A_{2j}(t) \bigr\vert L_{j}\mu_{j} \\ & \quad{}+\mu_{2}^{-1}\sum_{j=1}^{2} \bigl\vert C_{2j}(t) \bigr\vert L_{j}\mu_{j} e^{\gamma^{*}(1-\theta _{2j})t}+\mu_{2}^{-1}\sum _{j=1}^{2} \bigl\vert D_{2j}(t) \bigr\vert L_{j}\mu_{j}e^{\gamma^{*}(1-\theta _{2j})t}\Biggr]\Biggr\} =-0.04628< 0, \\ & \sup_{t\geq\bar{t}}\Biggl\{ \bigl\vert \alpha_{2}(t) \bigr\vert +\eta_{2}\Biggl[ \bigl\vert \alpha _{2}(t) \bigr\vert \delta_{2}(t)e^{\gamma^{*}\delta_{2}^{+}}+\mu_{2}^{-1} \sum_{j=1}^{2} \bigl\vert A_{2j}(t) \bigr\vert L_{j}\mu_{j} \\ & \quad{}+\mu_{2}^{-1}\sum_{j=1}^{2} \bigl\vert C_{2j}(t) \bigr\vert L_{j} \mu_{j}e^{\gamma^{*}(1-\theta _{2j})t}+\mu_{i}^{-1}\sum _{j=1}^{2} \bigl\vert D_{2j}(t) \bigr\vert L_{j}\mu_{j}e^{\gamma^{*}(1-\theta _{2j})t}\Biggr]\Biggr\} =0.4516< 1. \end{aligned}$$

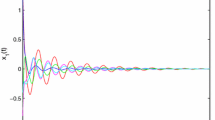
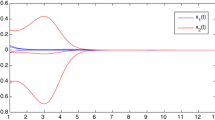
Therefore (Q1)–(Q3) of Theorem 2.1 hold true, then all solutions of (3.1) have global exponential convergence. This result can be shown in Fig. 1 and Fig. 2.

Figure 1
figure 1

Diagram of relationship of \(t-z_{1}\) for (3.1)

Full size image
Figure 2
figure 2

Diagram of relationship of \(t-z_{2}\) for (3.1)

Full size image

4 Conclusions

In this article, we have discussed neural networks with leakage delays and proportional delays. With the aid of inequality strategies and fuzzy differential equation approach, a sufficient criterion ensuring the global exponential convergence of neural networks with leakage delays and proportional delays is derived. The sufficient condition can be tested by algebraic manipulation without difficulty. The derived results complement parts of earlier work (for instance, [39–41]). In addition, the method of this article can be used to discuss some other similar network models.