1 Introduction

Infectious disease population dynamics is often influenced by different types of environmental noise, in which white noise is the most typical one. The effects of white noise on epidemic models have already been considered by many authors (e.g. [1–4]). In this literature the extinction and persistence of the disease were discussed. In reference [4], the authors assumed that the environmental white noises mainly influence the natural death rates μ of the populations. That is, \(\mu \to \mu +\sigma \dot{B}(t)\), where \(B(t)\) is a standard Brownian motion, \(\sigma^{2}\) represents the intensity of white noise. By replacing \(\mu \,{\mathrm{d}}t\) by \(\mu \,{\mathrm{d}}t+ \sigma\, {\mathrm{d}}B(t)\) in the deterministic SIR model with saturated incidence, the authors obtained a stochastic SIR model, which takes the form of

$$ \textstyle\begin{cases} dS(t)= ( \Lambda -\frac{\beta S(t)I(t)}{1+\alpha I(t)}-\mu S(t) ) \,dt- \sigma S(t)\,dB(t),\\ dI(t)= ( \frac{\beta S(t)I(t)}{1+\alpha I(t)}-( \mu +\varepsilon +\gamma )I(t) ) \,dt-\sigma I(t)\,dB(t). \end{cases} $$
(1.1)

In this model, \(S(t)\) and \(I(t)\) denote the number of susceptible and infected individuals at time t, respectively. The influx of individuals into the susceptibles is given by a constant Λ. The natural death rate is denoted by constant μ and individuals in \(I(t)\) suffer an additional death due to disease with rate constant ε; β and γ represent the disease transmission coefficient and the rate of recovery from infection, respectively; α is the saturated coefficient. Since the dynamics of compartment R has no effect on the disease transmission dynamics, it was omitted from the classical SIR model. In [4] the authors analyzed the long-time behavior of densities of the distributions of the solution and proved that the densities can converge in \(L^{1}\) to an invariant density.

In reality, except for white noise there is another important environmental noise: color noise, which can cause the population system to switch from one environmental regime to another. Such a switching is usually described by a continuous-time Markov chain \(r(t)\), \(t\geq 0\) with a finite state space \(\mathbb{S}=\{1,2,\ldots,N\}\). And the generator \(\Gamma =(\gamma_{ij})_{N\times N}\) of \(r(t)\) is given by

$$ \mathbb{P} \bigl\{ r(t+\delta )=j|r(t)=i \bigr\} = \textstyle\begin{cases} \gamma_{ij}\delta +o(\delta ) &\text{if }i\neq j,\\ 1+\gamma_{ii} \delta +o(\delta ) &\text{if } i= j, \end{cases} $$

where \(\gamma_{ij}\geq 0\) for \(i,j=1,\ldots,N\) with \(j\neq i\) and \(\gamma_{ii}=-\sum_{j\neq i}\gamma_{ij}\) for each \(i=1,\ldots,N\). Assume Markov chain \(r(t)\) is independent of Brownian motion. For convenience, throughout this paper we assume

$$ \gamma_{ij}> 0\quad \text{for }i,j=1,\ldots,N\text{ with }j\neq i. $$

This assumption ensures that the Markov chain \(r(t)\) is irreducible. Consequently, there exists a unique stationary distribution \(\pi =\{\pi_{1},\pi_{2},\ldots,\pi_{N}\}\) of \(r(t)\) which satisfies \(\pi \Gamma =0\), \(\sum_{i=1}^{N}\pi_{i}=1\) and \(\pi_{i}>0\), \(\forall i \in \mathbb{S}\).

Incorporating color noise into system (1.1), we get a regime-switching diffusion model:

$$ \textstyle\begin{cases} dS(t)= ( \Lambda (r(t))- \frac{\beta (r(t)) S(t)I(t)}{1+\alpha (r(t))I(t)}-\mu (r(t)) S(t) ) \,dt- \sigma (r(t)) S(t)\,dB(t),\\ dI(t)= ( \frac{\beta (r(t)) S(t)I(t)}{1+ \alpha (r(t))I(t)}-(\mu (r(t))+\varepsilon (r(t))+\gamma (r(t)))I(t) ) \,dt- \sigma (r(t))I(t)\,dB(t), \end{cases} $$
(1.2)

where \(\Lambda (i)\), \(\beta (i)\), \(\mu (i)\), \(\varepsilon (i)\), \(\gamma (i)\), \(\alpha (i)\) and \(\sigma (i)\), \(i\in \mathbb{S}\), are all positive constants.

In the earlier literature, regime switching was introduced into population models; see e.g. [5–8]. Due to the important effect of color noise on disease transmission, many author considered deterministic epidemic model with Markovian switching [9, 10].

Recently, much literature considered asymptotic behavior of stochastic epidemic model under regime switching, e.g. [11–14]. In this literature the uniform ellipticity condition is necessary when proving the ergodicity of stochastic system. But for system (1.2) the diffusion matrix of system (1.2) is given by \(A_{i}=\sigma^{2}(i) \bigl ( {\scriptsize\begin{matrix}{} S^{2} & SI \cr SI & I^{2}\end{matrix}} \bigr ) \), \(i\in \mathbb{S}\). Obviously \(A_{i}\) is degenerate, the uniform ellipticity condition is no longer satisfied. System (1.2) with \(\alpha =\varepsilon =\gamma =0\) has been considered by Liu [12], but the author ignored the fact that a degenerate diffusion matrix cannot ensure uniform ellipticity.

Throughout this paper, if A is a vector or matrix, we use \(A'\) to denote its transpose; set \(\hat{g}=\min_{k\in \mathbb{S}}\{g(k)\}\) and \(\check{g}=\max_{k\in \mathbb{S}}\{g(k)\}\) for any vector \(g=(g(1),\ldots,g(N))\); set

$$ \mathcal{R}_{i}:=\nu_{i}\Lambda (i)-\mu (i)-\varepsilon (i)-\gamma (i)-\frac{ \sigma^{2}(i)}{2},\quad i\in \mathbb{S}\quad \text{and}\quad \mathcal{R} ^{s}=\sum_{i=1}^{N} \pi_{i}\mathcal{R}_{i}, $$

where \(\boldsymbol{\nu} =(\nu_{1},\ldots,\nu_{N})'\) is the unique positive solution of linear equation

$$ \bigl(\operatorname{diag} \bigl\{ \mu (1),\ldots,\mu (N) \bigr\} -\Gamma \bigr)x= \bigl(\beta (1),\ldots, \beta (N) \bigr)'. $$
(1.3)

Remark 1.1

The existence of the unique solution of (1.3) is given by Lemma 2.1 in [12].

By using similar arguments to Theorem 2.1 of [14], it follows that, for any \((S(0),I(0), r(0))\in \mathbb{R}^{2}_{+} \times \mathbb{S}\), system (1.2) has a unique global solution, which remain in \(\mathbb{R}^{2}_{+}\) with probability 1.

The aim of this paper is to consider the long-time behavior of system (1.2). We prove that the disease becomes extinct exponentially if \(\mathcal{R}^{s}<0\); whereas if \(\mathcal{R}^{s}>0\) and \(\beta (i)>\alpha (i)(\varepsilon (i)+ \gamma (i))\), \(i\in \mathbb{S}\), system (1.2) has a stable stationary distribution.

The rest of this paper is organized as follows. In Section 2, we present the sufficient condition for the extinction of the disease. In Section 3 the conditions for the existence of a stable stationary distribution are given. Finally, we draw a conclusion.

2 Extinction of the disease

In this section, we present the sufficient condition for the extinction of the disease.

Theorem 2.1

If \(\mathcal{R}^{s}<0\), the disease \(I(t)\) tends to zero exponentially.

Proof

Consider the following system:

$$ dX(t)= \bigl(\Lambda \bigl(r(t) \bigr)-\mu \bigl(r(t) \bigr)X(t) \bigr)\,dt+ \sigma \bigl(r(t) \bigr)X(t)\,dB(t). $$

By the stochastic comparison theorem, it follows that \(S(t)\leq X(t)\) a.s. if \(S(0)=X(0)>0\). According to Corollary 4.1 in [12], we have

$$ \lim_{t\to \infty }\frac{1}{t} \int_{0}^{t}\beta \bigl(r(s) \bigr)X(s)\,ds= \sum _{i\in \mathbb{S}}\pi_{i}\Lambda (i)\nu_{i}. $$
(2.1)

By using the generalized Itó formula, it follows from (1.2) that

$$\begin{aligned}& \frac{\ln I(t)-\ln I(0)}{t} \\& \quad =\frac{1}{t} \int_{0}^{t}\frac{\beta (r(s)) S(s)}{1+\alpha (r(t))I(s)}\,ds- \frac{1}{t} \int_{0}^{t} \biggl( \mu \bigl(r(t) \bigr)+ \varepsilon \bigl(r(t) \bigr)+\gamma \bigl(r(t) \bigr)+\frac{ \sigma^{2}(r(s))}{2} \biggr) \,ds \\& \quad \quad{} +\frac{1}{t} \int_{0}^{t}\sigma \bigl(r(s) \bigr)\,dB(s) \\& \quad \leq \frac{1}{t} \int_{0}^{t} \biggl( \beta \bigl(r(s) \bigr)X(s)-\mu \bigl(r(s) \bigr)-\varepsilon \bigl(r(s) \bigr)-\gamma \bigl(r(s) \bigr)- \frac{\sigma^{2}(r(s))}{2} \biggr) \,ds \\& \quad \quad{} +\frac{1}{t} \int_{0}^{t}\sigma \bigl(r(s) \bigr)\,dB(s). \end{aligned}$$

Taking \(t\to \infty \), in view of (2.1), it follows that

$$ \limsup_{t\to \infty } \frac{\ln I(t)}{t}\leq \sum _{i=1}^{N}\pi_{i} \mathcal{R}_{i}= \mathcal{R}^{s}< 0. $$

The proof is complete. □

3 Existence of stationary distribution and its stability

Let \(x(t)=\ln S(t)\) and \(y(t)=\ln I(t)\), system (1.2) becomes

$$ \textstyle\begin{cases} dx(t)= ( \Lambda (r(t))e^{-x(t)}-\frac{\beta (r(t)) e^{y(t)}}{1+ \alpha (r(t))e^{y(t)}}-c_{1}(r(t)) ) \,dt-\sigma (r(t))\,dB(t),\\ dy(t)= ( \frac{\beta (r(t)) e^{x(t)}}{1+\alpha (r(t))e^{y(t)}}-c_{2}(r(t)) ) \,dt- \sigma (r(t))\,dB(t), \end{cases} $$
(3.1)

where \(c_{1}(i):=\mu (i)+\frac{\sigma^{2}(i)}{2}\), \(c_{2}(i):=\mu {(i)}+\varepsilon (i)+\gamma (i)+\frac{\sigma^{2}(i)}{2}\).

In order to investigate the existence of stationary distribution of system (1.2) and its stability, it suffices to consider the corresponding property for system (3.1).

Theorem 3.1

Let \((x(t),y(t))\) be a solution of system (3.1) with initial value \((x(0),y(0),r(0))\in \mathbb{R}^{2}\times \mathbb{S}\). Then for every \(t>0\) the distribution of \((x(t),y(t),r(t))\) has a density \(u(t,x,y,i)\). If \(\mathcal{R}^{s}>0\) and \(\beta (i)>\alpha (i)(\varepsilon (i)+\gamma (i))\), \(i\in \mathbb{S}\), then there exists a unique density \(u_{*}(x,y,i)\) such that

$$ \lim_{t\to \infty }\sum_{i=1}^{N} \iint_{\mathbb{R}^{2}} \bigl\vert u(t,x,y,i)-u _{*}(x,y,i) \bigr\vert \,dx\,dy=0. $$

Next, we will prove this theorem by Lemmas 3.1–3.2.

Let \((x^{(i)}(t),y^{(i)}(t))\) be a solution of system

$$ \textstyle\begin{cases} dx^{(i)}(t)= ( \Lambda (i)e^{-x^{(i)}(t)}-\frac{\beta (i) e^{y ^{(i)}(t)}}{1+\alpha (i)e^{y^{(i)}(t)}}-c_{1}(i) ) \,dt-\sigma (i)\,dB(t), \\ dy^{(i)}(t)= ( \frac{\beta (i) e^{x^{(i)}(t)}}{1+\alpha (i)e ^{y^{(i)}(t)}}-c_{2}(i) ) \,dt-\sigma (i)\,dB(t). \end{cases} $$
(3.2)

Denote by \({\mathcal{A}}_{i}\) the differential operators

$$ {\mathcal{A}}_{i}f=\frac{\sigma^{2}(i)}{2} \biggl[ \frac{\partial^{2}f}{ \partial x^{2}}+2 \frac{\partial^{2}f}{\partial x \partial y}+\frac{ \partial^{2}f}{\partial y^{2}} \biggr] -\frac{\partial (h_{i}^{1} f)}{ \partial x}- \frac{\partial (h_{i}^{2} f)}{\partial y}, \quad f\in L ^{1} \bigl(\mathbb{R}^{2}, \mathcal{B} \bigl(\mathbb{R}^{2} \bigr),m \bigr), $$

where \(\mathcal{B}(\mathbb{R}^{2})\) is the σ-algebra of Borel subsets of \(\mathbb{R}^{2}\), m is the Lebesgue measure on \((\mathbb{R}^{2},\mathcal{B}(\mathbb{R}^{2}))\) and

$$ h^{1}_{i}(x,y)=\Lambda (i)e^{-x}- \frac{\beta ({i}) e^{y}}{1+\alpha (i)e ^{y}}-c_{1}(i) ,\quad\quad h^{2}_{i}(x,y)= \frac{\beta (i) e^{x}}{1+\alpha (i)e^{y}}-c_{2}(i). $$

According to Lemma 3.3 and Lemma 3.5 in [4], we know that for any \(i\in \mathbb{S}\) the operator \({\mathcal{A}}_{i}\) generates an integral Markov semigroup \(\{{\mathcal{T}}_{i}(t)\}_{t \geq 0}\) on the space \(L^{1}(\mathbb{R}^{2},\mathcal{B}(\mathbb{R} ^{2}),m)\) and

$$ \int_{0}^{\infty }{\mathcal{T}}_{i}(t)f\,dt>0, \quad \textit{a.e. }\text{on } \mathbb{R}^{2}. $$
(3.3)

Let \((x(t),y(t))\) be the unique solution of system (3.1) with \((x(0),y(0),r(0))\in \mathbb{R}^{2}\times \mathbb{S}\), then \((x(t),y(t),r(t))\) constitutes a Markov process on \(\mathbb{R}^{2} \times \mathbb{S}\). In view of Lemma 5.5 in [15], for \(t>0\) the distribution of the process \((x(t),y(t), r(t))\) is absolutely continuous and its density \(u=(u_{1},u_{2},\ldots,u_{N})\) (where \(u_{i}:=u(t,x,y,i)\)) satisfies the following master equation:

$$ \frac{\partial u}{\partial t}=\Gamma ' u+{\mathcal{A}}u, $$
(3.4)

where \({\mathcal{A}}u=({\mathcal{A}}_{1}u_{1},{\mathcal{A}}_{2}u_{2},\ldots,{\mathcal{A}}_{N}u_{N})'\).

Let \(X=\mathbb{R}^{2}\times \mathbb{S}\), Σ be the σ-algebra of Borel subsets of X, and m̂ be the product measure on \((X,\Sigma )\) given by \(\hat{m}(B\times {i})=m(B)\) for each \(B\in \mathcal{B}(\mathbb{R}^{2})\) and \(i\in \mathbb{S}\). Obviously, \({\mathcal{A}}u\) generates a Markov semigroup \(\{{\mathcal{T}}(t)\} _{t\geq 0}\) on the space \(L^{1}(X,\Sigma ,\hat{m})\), which is given by

$$ {\mathcal{T}}(t)f= \bigl({\mathcal{T}}_{1}(t)f(x,y,1),\ldots,{ \mathcal{T}} _{N}(t)f(x,y,N) \bigr)', \quad f\in L^{1}(X,\Sigma ,\hat{m}). $$

Let λ be a constant such that \(\lambda >\max_{1\leq i\leq N} \{-\gamma_{ii}\}\) and \(Q=\lambda^{-1}\Gamma '+I\). Then (3.4) becomes

$$ \frac{\partial u}{\partial t}=\lambda Qu-\lambda u+{\mathcal{A}}u. $$
(3.5)

Obviously, Q is also a Markov operator on \(L^{1}(X,\Sigma ,\hat{m})\).

From the Philips perturbation theorem [16], (3.5) with the initial condition \(u(0,x,y,k)=f(x,y,k)\) generates a Markov semigroup \(\{\mathcal{{P}}(t)\} _{t\geq 0}\) on the space \(L^{1}(X)\) given by

$$ {\mathcal{{P}}}(t)f=e^{-\lambda t}\sum _{n=0}^{\infty }\lambda^{n} S^{(n)}(t)f, $$
(3.6)

where \(S^{(0)}(t)={\mathcal{T}}(t)\) and

$$ S^{(n+1)}(t)f= \int_{0}^{t} S^{(0)}(t-s)QS^{(n)}(s)f \,ds, \quad n\geq 0. $$
(3.7)

Lemma 3.1

If \(\beta (i)>\alpha (i)(\varepsilon (i)+\gamma (i))\), \(i\in \mathbb{S}\), then the semigroup \(\{\mathcal{P}(t)\}_{t\geq 0}\) is asymptotically stable or is sweeping with respect to compact sets.

Proof

Since \(\{\mathcal{T}(t)\}_{t\geq 0}\) is an integral Markov semigroup, \(\{\mathcal{P}(t)\}_{t\geq 0}\) is a partially integral Markov semigroup. In view of (3.3), (3.7) and \(Q_{ij}>0\) (\(i \neq j\)), we know that, for every nonnegative \(f\in L^{1}(X)\) with \(\Vert f \Vert =1\),

$$ \int_{0}^{\infty }{\mathcal{P}}(t)f\,dt>0,\quad \textit{a.e. }\text{on } X. $$

By using similar arguments to Corollary 1 in [17], it follows that \(\{\mathcal{P}(t)\}_{t\geq 0}\) is asymptotically stable or is sweeping with respect to compact sets. □

Remark 3.1

A density \(f_{*}\) is called invariant if \(\mathcal{{P}}(t)f_{*}=f_{*}\) for each \(t>0\). The Markov semigroup \(\{\mathcal{{P}}(t)\}_{t\geq 0}\) is called asymptotically stable if there is an invariant density \(f_{*}\) such that

$$ \lim_{t\to \infty } \bigl\Vert {\mathcal{{P}}}(t)f-f_{*} \bigr\Vert =0\quad \text{for }f \in D, $$

where \(D=\{f\in L^{1}(X):f\geq 0, \Vert f \Vert =1\}\).

A Markov semigroup \(\{\mathcal{{P}}(t)\}_{t\geq 0}\) is called sweeping with respect to a set \(A\in \Sigma \) if for every \(f\in D\)

$$ \lim_{t\to \infty } \int_{A} {\mathcal{P}}(t)f(x){\hat{m}}(dx)=0. $$

Lemma 3.2

If \({\mathcal{R}}^{s}>0\) and \(\beta (i)>\alpha (i)(\varepsilon (i)+ \gamma (i))\), \(i\in \mathbb{S}\), then the semigroup \(\{\mathcal{{P}}(t)\} _{t\geq 0}\) is asymptotically stable.

Proof

We will construct a nonnegative \(C^{2}\)-function V and a closed set \(U\in \mathcal{B}(\mathbb{R}^{2})\) (which lies entirely in \(\mathbb{R}^{2}\)) such that, for any \(i\in \mathbb{S}\),

$$ \sup_{(x,y)\in \mathbb{R}^{2}\backslash U}\mathscr{A}^{*}V(x,y,i)< 0, $$

where

$$ \begin{aligned}[b] \mathscr{A}^{*}V(x,y,i)= {}& \frac{\sigma^{2}(i)}{2} \biggl[ \frac{\partial ^{2}V}{\partial x^{2}}+2\frac{\partial^{2}V}{\partial x \partial y}+ \frac{ \partial^{2}V}{\partial y^{2}} \biggr] +h^{1}_{i}\frac{\partial V}{ \partial x}+h_{i}^{2} \frac{\partial V}{\partial y} \\ &{}+ \sum_{j\in \mathbb{S}}\gamma_{ij}V(x,y,j) \end{aligned} $$
(3.8)

and

$$ h^{1}_{i}(x,y)=\Lambda (i)e^{-x}- \frac{\beta (i) e^{y}}{1+\alpha (i)e ^{y}}-c_{1}(i),\quad\quad h^{2}_{i}(x,y)= \frac{\beta (i) e^{x}}{1+\alpha (i)e ^{y}}-c_{2}(i). $$

In fact, \(\mathscr{A}^{*}\) is the adjoint operator of the infinitesimal generator of the semigroup \(\{\mathcal{{P}}(t)\}_{t\geq 0}\).

Since the matrix Γ is irreducible, there exists \(\varpi =( \varpi_{1},\varpi_{2},\ldots,\varpi_{N})\) that is a solution of the Poisson system (see [18], Lemma 2.3) such that

$$ \Gamma \varpi -{\mathcal{R}}=-\sum_{i=1}^{N} \pi_{i}{\mathcal{R}}_{i} {\mathbf{{1}}}, $$

where \({\mathcal{R}}=({\mathcal{R}}_{1},{\mathcal{R}}_{2},\ldots, {\mathcal{R}}_{N})'\) and \(\mathbf{{1}}=(1,1,\ldots,1)'\). That is, for any \(i\in \mathbb{S}\),

$$ \sum_{j\in \mathbb{S}}\gamma_{ij} \varpi_{j}-{\mathcal{R}}_{i}=-\sum _{i=1}^{N}\pi_{i}{\mathcal{R}}_{i}=-{ \mathcal{R}}^{s}. $$
(3.9)

Take \(\theta \in (0,1)\) and \(r>0\) such that

$$ \hat{\mu }- \frac{\theta }{2}\check{\sigma }_{1}^{2}>0, \quad\quad \hat{\mu }+\hat{\varepsilon }+\hat{\gamma }-\frac{\theta }{2} \check{ \sigma }_{2}^{2}>0\quad \text{and}\quad \max _{x\in [0,\infty )}f(x)-r {\mathcal{R}}^{s}\leq -2, $$
(3.10)

where the function \(f(x)\) is given in (3.11).

Define a \(C^{2}\)-function V as follows:

$$\begin{aligned} &V (x,y,i) =\frac{1}{\theta +1} \bigl(e^{x}+e^{y} \bigr)^{\theta +1}-x-r \bigl( y+\nu _{i} \bigl(e^{x}+e^{y} \bigr) \bigr) +r \bigl(\varpi_{i}+ \vert \varpi \vert \bigr),\quad (x,y)\in \mathbb{R}^{2}. \end{aligned}$$

Next we will find a closed set \(U\subset \mathbb{R}^{2}\) such that \(\mathscr{A}^{*}V(x,y,i)\leq -1\), \((x,y)\in \mathbb{R}^{2}-U\).

Denote

$$ V_{1}=\frac{1}{\theta +1} \bigl(e^{x}+e^{y} \bigr)^{\theta +1},\quad\quad V_{2}=-y-\nu _{i} \bigl(e^{x}+e^{y} \bigr)+ \bigl(\varpi_{i}+ \vert \varpi \vert \bigr),\quad\quad V_{3}=-x. $$

Then

$$ \mathscr{A}^{*}V=\mathscr{A}^{*}V_{1}+r \mathscr{A}^{*}V_{2}+ \mathscr{A}^{*}V_{3}. $$

Direct calculation implies that

$$\begin{aligned}& \begin{aligned} \mathscr{A}^{*}V_{1} &= \bigl(e^{x}+e^{y} \bigr)^{\theta } \bigl(\Lambda (i)-\mu (i) e ^{x}- \bigl(\mu (i)+ \varepsilon (i)+\gamma (i) \bigr)e^{y} \bigr)+\frac{\sigma^{2}(i) \theta }{2} \bigl(e^{x}+e^{y} \bigr)^{\theta -1} \bigl(e^{2x}+e^{2y} \bigr) \\ &\leq 2^{\theta }\Lambda (i) \bigl(e^{\theta x} +e^{\theta y} \bigr)-\mu (i) e ^{(1+\theta )x}- \bigl(\mu (i)+\varepsilon (i)+\gamma (i) \bigr)e^{(1+\theta )y} \\ &\quad{} +\frac{ \theta }{2}\sigma^{2}(i) \bigl(e^{(1+\theta )x}+e^{(1+\theta )y} \bigr) \\ &= 2^{\theta }\Lambda (i) \bigl(e^{\theta x} +e^{\theta y} \bigr)- \biggl(\mu (i)- \frac{ \theta }{2}\sigma^{2}(i) \biggr)e^{(1+\theta )x} \\ &\quad{} - \biggl(\mu (i)+\varepsilon (i)+ \gamma (i)-\frac{\theta }{2} \sigma^{2}(i) \biggr)e^{(1+\theta )y}, \end{aligned} \\& \mathscr{A}^{*}V_{3}=-\Lambda (i)e^{-x}+ \frac{\beta (i) e^{y}}{1+ \alpha (i)e^{y}}+c_{1}(i), \end{aligned}$$

and

$$\begin{aligned} \mathscr{A}^{*}V_{2} &=-\frac{\beta (i) e^{x}}{1+\alpha (i)e^{y}}+c _{2}(i)-\nu_{i}\Lambda (i)+\nu_{i}\mu (i)e^{x}+\nu_{i} \bigl(\mu (i)+\varepsilon (i)+\gamma (i) \bigr)e^{y} \\ & \quad{} -\sum_{j\in \mathbb{S}}\gamma_{ij}\nu_{j} \bigl(e^{x}+e^{y} \bigr)+ \sum _{j\in \mathbb{S}} \gamma_{ij}\varpi_{j} \\ &=- \biggl( \beta (i)-\nu_{i}\mu (i)+\sum _{j\in \mathbb{S}}\gamma_{ij} \nu_{j} \biggr) e^{x}+ \biggl( \nu_{i} \bigl(\mu (i)+\varepsilon (i)+\gamma (i) \bigr)- \sum_{j\in \mathbb{S}}\gamma_{ij} \nu_{j} \biggr) e^{y} \\ & \quad{} -\mathcal{R}_{i}+\sum_{j\in \mathbb{S}} \gamma_{ij}\varpi_{j}+\frac{ \beta (i)\alpha (i)e^{x+y}}{1+\alpha (i)e^{y}} \\ &=-{\mathcal{R}}^{s}+ \bigl(\beta (i)+\nu_{i} \bigl( \varepsilon (i)+\gamma (i) \bigr) \bigr)e ^{y}+\frac{\beta (i)\alpha (i)e^{x+y}}{1+\alpha (i)e^{y}}, \end{aligned}$$

where equations (1.3) and (3.9) are used. Hence,

$$ \mathscr{A}^{*}V\leq f(x)+g(y)-r{\mathcal{R}}^{s}+r \frac{\beta (i) \alpha (i)e^{x+y}}{1+\alpha (i)e^{y}}, $$

where

$$ \begin{gathered} f(x)=2^{\theta }\check{\Lambda } e^{\theta x}- \biggl( \hat{\mu }- \frac{ \theta }{2}\check{\sigma }^{2} \biggr)e^{(1+\theta )x}-{ \hat{\Lambda }} {e ^{-x}}+\check{c}_{1}, \\ g(y)=2^{\theta }\check{\Lambda } e^{\theta y}- \biggl(\hat{\mu }+ \hat{ \varepsilon }+\hat{\gamma }-\frac{\theta }{2}\check{\sigma }^{2} \biggr)e ^{(1+\theta )y} +r \bigl(\check{\beta }+\check{\nu }(\check{\varepsilon }+ \check{\gamma }) \bigr) e^{y}. \end{gathered} $$
(3.11)

In view of (3.10), we can obtain

$$ f(x)+\max_{y\in [0,\infty )}g(y)-r{\mathcal{R}}^{s}+r{\check{ \beta }}e ^{x}\to -\infty , \quad \text{as }x\to \pm \infty . $$

Take \(\kappa \in (0,\infty )\) large enough such that

$$ \mathscr{A}^{*}V\leq f(x)+\max_{y\in [0,\infty )}g(y)-r{ \mathcal{R}} ^{s}+r{\check{\beta }}e^{x}\leq -1,\quad \text{on }\mathbb{R}^{2}-U _{1}, $$
(3.12)

where \(U_{1}=\{(x,y)\in \mathbb{R}^{2}:x\in [-\kappa ,\kappa ]\}\).

For \((x,y)\in U_{1}\), according to (3.10) we have

$$ \mathscr{A}^{*}V\leq \max_{x\in [0,\infty )}f(x)+g(y)-r{ \mathcal{R}} ^{s}+r{\check{\beta }} {\check{\alpha }}e^{\kappa +y}\to -\infty , \quad \text{as } y\to +\infty , $$

and

$$ \mathscr{A}^{*}V\leq \max_{x\in [0,\infty )}f(x)+g(y)-r{ \mathcal{R}} ^{s}+r{\check{\beta }} {\check{\alpha }}e^{\kappa +y} \to \max_{x\in [0,\infty )}f(x)-r{\mathcal{R}}^{s}\leq -2, \quad \text{as }y\to -\infty . $$

Taking \(\rho \in (0,\infty )\) large enough such that

$$ \mathscr{A}^{*}V\leq -1,\quad \text{on }U_{1}-U_{2}, $$
(3.13)

where \(U_{2}=\{(x,y)\in \mathbb{R}^{2}:x\in [-\kappa ,\kappa ], y \in [-\rho ,\rho ]\}\). Noting \(U_{2}\subset U_{1}\), we obtain \((\mathbb{R}^{2}-U_{1})\cup (U_{1}-U_{2})=\mathbb{R}^{2}-U_{2}\). Combining (3.12) and (3.13), it follows that, for any \(i\in \mathbb{S}\),

$$ \mathscr{A}^{*}V(x,y,i)< -1, \quad (x,y)\in \mathbb{R}^{2}-U_{2}. $$

Such a function V is called a Khasminskiĭ function. By using similar arguments to those in [19], the existence of a Khasminskiĭ function implies that the semigroup is not sweeping from the set \(U_{2}\). According to Lemma 3.1, the semigroup \(\{\mathcal{{P}}(t)\}_{t\geq 0}\) is asymptotically stable, which completes the proof. □

4 Conclusion

In this paper, we consider the long-time behavior of a regime-switching SIR epidemic model. Since the diffusion is degenerate we employ the Markov semigroup theory to study the long-time behavior of system (1.2). We prove that if \(\mathcal{R}^{s}<0\), the disease becomes extinct exponentially; whereas if \(\mathcal{R}^{s}>0\) and \(\beta (i)>\alpha (i)(\varepsilon (i)+ \gamma (i))\), \(i\in \mathbb{S}\), the densities of the distributions of the solution can converge in \(L^{1}\) to an invariant density. In some sense, \(\mathcal{R}^{s}\) is the threshold determining that the disease does or does not occur.

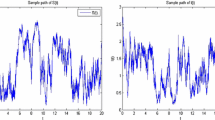
Let \(\mathbb{S}=\{1,2\}\), \(\Gamma = \bigl [{\scriptsize\begin{matrix}{} -2 & 2 \cr 1 & -1 \end{matrix}} \bigr ] \). Obviously, \(\pi =(1/3, 2/3)\). Take \(S(0)=2\), \(I(0)=1\) and

$$\begin{aligned} &\Lambda (1)=0.9,\quad\quad \mu (1)=0.2,\quad\quad \varepsilon (1)=0.2,\quad\quad \gamma (1)=0.3, \\ &\beta (1)=0.3,\quad\quad \alpha (1)=0.1, \quad\quad \sigma (1)=0.1, \\ &\Lambda (2)=1.0,\quad\quad \mu (2)=0.2,\quad\quad \varepsilon (2)=0.1,\quad\quad \gamma (2)=0.4, \\ &\beta (2)=0.1,\quad\quad \alpha (2)=0.15,\quad\quad \sigma (2)=0.2. \end{aligned}$$

It is easy to check that the disease persists and becomes extinct in fixed environments 1 and 2, respectively. However, in the regime-switching case, we get \(\mathcal{R}^{s}=0.1042>0\). According to Theorem 3.1, the disease is persistent (see Figure 1). In fact, the condition \(\beta (i)>\alpha (i)(\varepsilon (i)+\gamma (i))\), \(i\in \mathbb{S}\) is not necessary (see Figure 2). In the proof of Theorem 3.1, such a condition is mainly used to ensure that the support of the invariant measure (if it exists) in each fixed environment is \(\mathbb{R}^{2}_{+}\), which can make the proof of the main result easier.

Figure 1
figure 1

The sample path of \(I(t)\) with \(S(0)=2\), \(I(0)=1\). Here \(\alpha (1)=0.1\) and \(\alpha (2)=0.15\). In this case, \(\beta (i)> \alpha (i)(\varepsilon (i)+\gamma (i))\), \(i\in \mathbb{S}\)

Full size image
Figure 2
figure 2

The sample path of \(I(t)\) with \(S(0)=2\), \(I(0)=1\). Here \(\alpha (1)=0.7\) and \(\alpha (2)=0.3\). In this case, \(\beta (i)< \alpha (i)(\varepsilon (i)+\gamma (i))\), \(i\in \mathbb{S}\)

Full size image

References [20, 21] provided another skeleton to prove the ergodicity of stochastic population systems and rates of convergence can also be estimated. In the future, we may continue our research in this direction. In addition, delay is a common phenomenon in the natural world; then it is interesting to consider stochastic models with delay (see e.g. [22, 23]), which can lead to further investigation of along the line of the present paper.