1 Introduction

There has been a dramatic increase in studying chaos and systems with chaotic behavior in the past decades [1–3]. Applications of chaos have been witnessed in various areas ranging from path planning generator [4], secure communications [5–7], audio encryption scheme [8], image encryption [9–11], to truly random number generator [12, 13]. Many three-dimensional (3D) autonomous chaotic systems have been found and reported in the literature [14]. It has previously been observed that common 3D autonomous chaotic systems, such as Lorenz system [15], Chen system [16], Lü system [17], or Yang’s system [18, 19], have one saddle and two unstable saddle-foci. However, recent evidence suggests that chaos can be observed in 3D autonomous systems with stable equilibria [20, 21].

Several attempts have been made to investigate chaotic systems with stable equilibria. Yang and Chen proposed a chaotic system with one saddle and two stable node-foci [20]. In spite of the fact that the Yang-Chen system connected the original Lorenz system and the original Chen system, it was not diffeomorphic with the original Lorenz and Chen systems. Yang et al. found an unusual Lorenz-like chaotic system with two stable node-foci [21]. By using the center manifold theory and normal form method, Wei investigated delayed feedback on such a chaotic system with two stable node-foci [22]. A six-term system with stable equilibria was presented in [23]. Interestingly, the six-term system with stable equilibria exhibited a double-scroll chaotic attractor [23]. In addition, the generalized Sprott C system with only two stable equilibria was introduced in [24, 25]. It is worth noting that systems with stable equilibria are systems with ‘hidden attractors’ [26–29]. Hidden attractors have received considerable attention recently because of their roles in theoretical and practical problems [30–38].

Different definitions and main properties of fractional calculus have been reported in the literature [47–50]. The fractional derivatives play important roles in the field of mathematical modeling of numerous models such as fractional model of regularized long-wave equation [51], Lienard’s equation [52], fractional model of convective radial fins [53], modified Kawahara equation [54], etc. In recent years, there has been an increasing interest in the stability of fractional systems [55–57]. Moreover, it is worth noting that local fractional derivatives with special functions have received significant attention in different areas [58–60]. Authors have focused on local fractional diffusion equations in fractal heat transfer [61], fractal LC-electric circuit [62], and new rheological models [63, 64]. When considering the effects of fractional derivatives on systems with hidden attractors, a few fractional-order forms of systems with hidden attractors have been introduced [39]. Fractional-order forms of systems without equilibrium were reported in [39–41, 43, 44], while fractional-order forms of systems with an infinite number of equilibrium points were presented in [42, 45, 46]. Sifeu et al. investigated the fractional-order form of a three-dimensional chaotic autonomous system with only one stable equilibrium [65]. In order to determine chaos synchronization between such fractional-order systems, some synchronization schemes were constructed as summarized in Table 1. Authors have tended to synchronize fractional systems with the same orders. Therefore, studies on synchronization of such fractional systems with different orders should be considered further.

Table 1 Synchronization schemes used for fractional-order forms of chaotic systems with hidden attractors
Full size table

The aim of this study is to examine the fractional-order form of a 3D system with stable equilibria and its full-state hybrid projective synchronization schemes. The model of the fractional system and its chaotic behavior are presented in Section 2. Different types of full-state hybrid projective synchronization schemes are investigated in Section 3. Section 4 presents results and discussions. Finally, the concluding remarks are drawn in the last section.

2 Fractional-order form of the system with stable equilibria

We consider the three-dimensional autonomous system with six terms described by

$$ \begin{gathered} \dot{x} = a(z-x), \\ \dot{y} = -xz + e, \\ \dot{z} = xy - bz, \end{gathered} $$
(1)

in which x, y, z are state variables, while a, b, e are positive parameters (\(a, b, e > 0\)). It is easy to see that system (1) has two following equilibrium points:

$$ {E_{1}} = (\sqrt {e} ,b,\sqrt {e} ),\qquad {E_{2}} = ( - \sqrt {e} ,b, - \sqrt {e} ). $$
(2)

According to the Routh-Hurwitz stability criterion, the equilibrium points of system (1) are stable for \(b > a\). In other words, we can obtain a system with two stable equilibrium points for \(b > a\).

Interestingly, for \(a = 14.1\), \(b = 15\), and \(e = 90\), system (1) with two stable equilibria exhibits chaos as shown in Figure 1. It is simple to verify that system (1) with two stable equilibria belongs to a new class of systems with hidden attractors [26–29].

Figure 1
figure 1

Chaotic attractor of the 3D system with two stable equilibrium points for \(\pmb{a = 14.1}\) , \(\pmb{b = 15}\) , \(\pmb{e = 90}\) , and the initial conditions \(\pmb{(x(0),y(0),z(0))=(1.1,15,-1)}\) .

Full size image

Previous studies have introduced different definitions of fractional-order derivative. However, Grunwald-Letnikov, Riemann-Liouville, and Caputo definitions are commonly used ones [47–50]. In this section, we utilize the Caputo definition:

$$ {}_{0}D_{t}^{q}f ( t ) = \textstyle\begin{cases} \frac{1}{{\Gamma ( {m - q} )}}\int_{0}^{t} \frac{{{f^{ ( m )}} ( \tau )}}{{{{ ( {t - \tau} )}^{q + 1 - m}}}}\,d\tau,& m - 1 < q < m, \\ \frac{{{d^{m}}}}{{d{t^{m}}}}f ( t ),& q = m. \end{cases} $$
(3)

In (3), m is the first integer which is not less than q \(( {m = \lceil q \rceil} )\) and Γ is the gamma function defined by

$$ \Gamma ( z ) = \int_{0}^{\infty}{{t^{z - 1}} {e^{ - t}}\,dt.} $$
(4)

Derived from integer-order system (1), we consider the fractional-order form of (1) given by

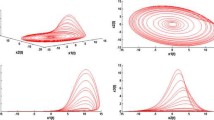
$$ \begin{gathered} D_{t}^{q_{1}}x = a ( {z - x} ), \\ D_{t}^{q_{2}}y = - xz + e, \\ D_{t}^{q_{3}}z = xy - bz, \end{gathered} $$
(5)

in which the derivative orders are \(q_{1}\), \(q_{2}\), \(q_{3}\) satisfying \(0< q_{1}, q_{2},q_{3} <1 \). In fractional-order system (5), x, y, z are state variables, while a, b, e are positive parameters (\(a, b, e > 0\)). Here, the Caputo definition of fractional-order derivative has been used. In order to find the numerical solutions of fractional-order system (5), we have applied the Adams-Bashforth-Moulton predictor-corrector method [66, 67]. As a result, we have found the chaotic behavior in fractional system (5) for the incommensurate orders \(q_{1}=0.98\) and \(q_{2}=q_{3}=0.99\). Chaotic behavior of fractional-order system (5) is illustrated in Figure 2. In the next section, we will study two state hybrid projective synchronization schemes for such a 3D fractional-order system.

Figure 2
figure 2

Chaotic attractor of fractional-order system ( 5 ) for \(\pmb{a = 14.1}\) , \(\pmb{b = 15}\) , \(\pmb{e = 90}\) , the initial conditions \(\pmb{(x(0),y(0),z(0))=(1.1,15,-1)}\) and \(\pmb{q_{1}=0.98}\) , \(\pmb{q_{2}=q_{3}=0.99}\) .

Full size image

3 Synchronization schemes of the 3D fractional-order chaotic system

Among all types of chaos synchronization schemes, full-state hybrid projective synchronization (FSHPS) is one of the most noticeable types. It has been widely used in the synchronization of fractional chaotic (hyperchaotic) systems [68]. In this type of synchronization, each slave system state achieves synchronization with linear combination of master system states. Recently, an interesting scheme has been introduced [69], where each master system state synchronizes with a linear constant combination of slave system states. Since master system states and slave system states have been inverted with respect to the FSHPS, the new scheme has been called the inverse full-state hybrid projective synchronization (IFSHPS). Obviously, the problem of IFSHPS is more difficult than the problem of FSHPS. Studying the inverse problems of synchronization which produce new types of chaos synchronization is an attractive research topic. Based on fractional-order Lyapunov approach, this section first analyzes the FSHPS between the 3D fractional chaotic system (5) and a 4D fractional chaotic system with an infinite number of equilibrium points. Successively, the IFSHPS is proved between the 3D fractional chaotic system (5) and a 4D fractional chaotic system without equilibrium points.

3.1 Fractional-order Lyapunov method

Lemma 1

The trivial solution of the following fractional-order system [70]

$$ D_{t}^{p}X ( t ) =F \bigl( X ( t ) \bigr) , $$
(6)

where \(D_{t}^{p}= [ D_{t}^{p},D_{t}^{p},\ldots,D_{t}^{p} ] \), \(0< p\leq 1\), and \(F:\mathbf{R}^{n}\rightarrow\mathbf{R}^{n}\), is asymptotically stable if there exists a positive definite Lyapunov function \(V ( X ( t ) ) \) such that \(D_{t}^{p}V ( X ( t ) ) <0\) for all \(t>0\).

Lemma 2

([71])

\(\forall X(t)\in\mathbf{R}^{n}\), \(\forall p\in [ 0,1 ] \), and \(\forall t>0\)

$$ \frac{1}{2}D_{t}^{p} \bigl( X^{T}(t)X(t) \bigr) \leq X^{T}(t)D_{t}^{p} \bigl( X(t) \bigr) . $$
(7)

3.2 Full-state hybrid projective synchronization (FSHPS) and inverse full-state hybrid projective synchronization (IFSHPS)

The master system and the slave system can be described in the following forms:

$$\begin{aligned}& D_{t}^{p_{i}}x_{i}(t)=F_{i} \bigl( X ( t ) \bigr) ,\quad i=1,2,\ldots,n, \end{aligned}$$
(8)
$$\begin{aligned}& D_{t}^{q_{i}}y_{i} ( t ) =G_{i} \bigl( Y ( t ) \bigr) +u_{i},\quad i=1,2,\ldots,m, \end{aligned}$$
(9)

where \(X(t)= ( x_{i} ) _{1\leq i\leq n}\), \(Y(t)= ( y_{i} ) _{1\leq i\leq m}\) are the states of the master system and the slave system, respectively, \(D_{t}^{p_{i}}\), \(D_{t}^{q_{i}}\) are the Caputo fractional derivatives of order \(p_{i}\) and \(q_{i}\), respectively, \(0< p_{i}<1\), \(F_{i}:\mathbf{R}^{n}\rightarrow\mathbf{R}\) (\(i=1,2,\ldots,n \)), \(G_{i}:\mathbf{R}^{m}\rightarrow\mathbf{R}\) (\(i=1,2,\ldots,m\)), and \(u_{i}\) (\(i=1,2,\ldots,m \)) are controllers.

In the next, we present the definitions of FSHPS and IFSHPS for the master system (8) and the slave system (9).

Definition 1

The master system (8) and the slave system (9) are in full-state hybrid projective synchronization (FSHPS) when there are controllers \(u_{i}\), \(i=1,2,\ldots,m\), and given real numbers \(( \alpha _{ij} ) _{m\times n}\) such that the synchronization errors

$$ e_{i} ( t ) =y_{i} ( t ) -\sum _{j=1}^{n}\alpha _{ij}x_{j}(t), \quad i=1,2,\ldots,m, $$
(10)

satisfy that \(\lim_{t\rightarrow+\infty}e_{i} ( t ) =0\).

Definition 2

The master system (8) and the slave system (9) are in inverse full-state hybrid projective synchronization (IFSHPS) when there are controllers \(u_{i}\), \(i=1,2,\ldots,m\), and given real numbers \(( \beta_{ij} ) _{n\times m}\) such that the synchronization errors

$$ e_{i} ( t ) =x_{i} ( t ) -\sum _{j=1}^{m}\beta _{ij}y_{j}(t), \quad i=1,2,\ldots,n, $$
(11)

satisfy that \(\lim_{t\rightarrow+\infty}e_{i} ( t ) =0\).

3.3 FSHPS between the 3D fractional chaotic system and 4D fractional chaotic system with an infinite number of equilibrium points

Here, the master system is described as follows:

$$ \begin{gathered} D_{t}^{p_{1}}x_{1} = a ( x_{3}-x_{1} ) , \\ D_{t}^{p_{2}}x_{2} = -x_{1}x_{3}+c, \\ D_{t}^{p_{3}}x_{3} = x_{1}x_{2}-bx_{3}, \end{gathered} $$
(12)

where \((a,b,c)=(14.1,15,90)\) and \((p_{1},p_{2},p_{3})=(0.98,0.99,0.99)\).

The slave system is defined as

$$ \begin{gathered} D_{t}^{0.95}y_{1} = 10 ( y_{2}-y_{1} ) +y_{4}+u_{1}, \\ D_{t}^{0.95}y_{2} = 15y_{1}-y_{1}y_{3}+u_{2}, \\ D_{t}^{0.95}y_{3} = 4y_{1}^{2}-2.5y_{3}+u_{3}, \\ D_{t}^{0.95}y_{4} = -10y_{2}-y_{4}+u_{4}, \end{gathered} $$
(13)

where \(U=(u_{1},u_{2},u_{3},u_{4})^{T}\) is the vector controller. It is noted that the uncontrolled system (13) is a chaotic system with an infinite number of equilibrium points [42].

According to the definition of FSHPS, the errors between the master system (12) and the slave system (13) are defined as follows:

$$ {e_{i}} = {y_{i}} - \sum _{j = 1}^{3} {{\alpha_{ij}} {x_{j}}}, \quad i=1,2,3,4, $$
(14)

where

$$ (\alpha_{ij})_{4\times3}=\left ( \begin{matrix} 1 & -2 & 3 \\ -2 & 1 & -1 \\ 3 & 0 & 4 \\ 3 & 1 & 2\end{matrix} \right ) . $$
(15)

The error system (14) can be derived as

$$ \begin{gathered} D_{t}^{0.95}e_{1} = 10 ( y_{2}-y_{1} ) +y_{4}+{u_{1}}-D_{t}^{0.95} ( x_{1}-2x_{2}+3x_{3} ) , \\ D_{t}^{0.95}e_{2} = 15y_{1}-y_{1}y_{3}+{u_{2}}-D_{t}^{0.95} ( -2x_{1}+x_{2}-x_{3} ) , \\ D_{t}^{0.95}e_{3} = 4y_{1}^{2}-2.5y_{3}+u_{3}-D_{t}^{0.95} ( 3x_{1}+4x_{3} ) , \\ D_{t}^{0.95}e_{4} = -10y_{2}-y_{4}+u_{4}-D_{t}^{0.95} ( 3x_{1}+x_{2}+2x_{3} ) . \end{gathered} $$
(16)

The error system (16) can be written as follows:

$$ D_{t}^{0.95}e=Be+U+R, $$
(17)

where \(e= ( e_{1},e_{2},e_{3},e_{4} ) ^{T}\), \(U= ( u_{1},u_{2},u_{3},u_{4} ) ^{T}\),

$$ B=\left ( \begin{matrix} -10 & 10 & 0 & 1 \\ 15 & 0 & 0 & 0 \\ 0 & 0 & -2.5 & 0 \\ 0 & -10 & 0 & -1\end{matrix} \right ) $$
(18)

and \(R= ( R_{1},R_{2},R_{3},R_{4} ) ^{T}\), where

$$ \begin{gathered} R_{1} = -D_{t}^{0.95} ( x_{1}-2x_{2}+3x_{3} ) , \\ R_{2} = -y_{1}y_{3}-D_{t}^{0.95} ( -2x_{1}+x_{2}-x_{3} ) , \\ R_{3} = 4y_{1}^{2}-D_{t}^{0.95} ( 3x_{1}+4x_{3} ) , \\ R_{4} = -D_{t}^{0.95} ( 3x_{1}+x_{2}+2x_{3} ) . \end{gathered} $$
(19)

Theorem 1

The master system (12) and the slave system (13) are globally FSHP synchronized under the following control law:

$$ ( u_{1},u_{2},u_{3},u_{4} ) ^{T}=- ( R+Ce ) , $$
(20)

where

$$ C=\left ( \begin{matrix} 0 & 10 & 0 & 1 \\ 15 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & -10 & 0 & 0\end{matrix} \right ) . $$
(21)

Proof

Applying the control law given in Eq. (20) to Eq. (17) yields the resulting error dynamics as follows:

$$ \begin{gathered} D_{t}^{0.95}e_{1} = -10e_{1}, \\ D_{t}^{0.95}e_{2} = -e_{2}, \\ D_{t}^{0.95}e_{3} = -2.5e_{3}, \\ D_{t}^{0.95}e_{4} = -e_{4}. \end{gathered} $$
(22)

If a Lyapunov function candidate is chosen as \(V ( e_{1},e_{2},e_{3},e_{4} ) =\sum_{i=1}^{4}\frac{1}{2}e_{i}^{2}\), then the time Caputo fractional derivative of order 0.95 of V along the trajectory of system (22) is as follows:

$$ D_{t}^{0.95}V ( e_{1},e_{2},e_{3},e_{4} ) =\sum_{i=1}^{4}D_{t}^{0.95} \frac{1}{2}e_{i}^{2}. $$
(23)

Using Lemma 2 in Eq. (23), we get

$$\begin{aligned} D_{t}^{0.95}V ( e_{1},e_{2},e_{3},e_{4} ) & \leq \sum _{i=1}^{4}e_{i}D_{t}^{0.95}e_{i} \\ & =- \bigl( 10e_{1}^{2}+e_{2}^{2}+2.5e_{3}^{2}+e_{4}^{2} \bigr) < 0.\end{aligned} $$

Thus, from Lemma 1, it is immediate that the zero solution of system (22) is globally asymptotically stable; and therefore, systems (12) and (13) are FSHP synchronized. □

In order to illustrate the correction of the proposed synchronization scheme, numerical simulations have been implemented. Figure 3 displays the synchronization errors between the master system (12) and the slave system (13) in 4D. Obviously, Figure 3 indicates that we have achieved the synchronization between the master system (12) and the slave system (13).

Figure 3
figure 3

Time series of the synchronized error signals between the master system ( 12 ) and the slave system ( 13 ) in 4D.

Full size image

3.4 IFSHPS between the 3D fractional system and the 4D fractional chaotic system without equilibrium points

Now, the master system is taken as system (12), and the slave system is defined as

$$ \begin{gathered} D_{t}^{q}y_{1} = 5 ( y_{2}-y_{1} ) +y_{4}+u_{1}, \\ D_{t}^{q}y_{2} = -y_{1}y_{3}+u_{2}, \\ D_{t}^{q}y_{3} = -90+y_{1}y_{2}+u_{3}, \\ D_{t}^{q}y_{4} = -10y_{1}+u_{4}, \end{gathered} $$
(24)

where \(U=(u_{1},u_{2},u_{3},u_{4})^{T}\) is the vector controller. It is worth noting that the uncontrolled system (24) is a chaotic system without equilibrium points [41].

Based on the definition of IFSHPS, the errors between the master system (12) and the slave system (24) are given as follows:

$$ {e_{i}} = {x_{i}} - \sum_{j = 1}^{4} {{\beta_{ij}} {y_{j}}}, \quad i=1,2,3, $$
(25)

where

$$ (\beta_{ij})_{3\times4}=\left ( \begin{matrix} 1 & 0 & 0 & -1 \\ 0 & 2 & 0 & 5 \\ 0 & 0 & -3 & 4\end{matrix} \right ) . $$
(26)

The error system (25) can be derived as

$$ \begin{gathered} D_{t}^{0.9}e_{1} = -u_{1}+u_{4}+T_{1}, \\ D_{t}^{0.9}e_{2} = -2u_{2}-5u_{4}+T_{2}, \\ D_{t}^{0.9}e_{3} = 3u_{3}-4u_{4}+T_{3}, \end{gathered} $$
(27)

where

$$ \begin{gathered} T_{1} = D_{t}^{0.9}x_{1}-a ( y_{2}-y_{1} ) -y_{4}-cy_{1}, \\ T_{2} = D_{t}^{0.9}x_{2}-2y_{1}y_{3}+5cy_{1}, \\ T_{3} = D_{t}^{0.9}x_{3}-3b+3y_{1}y_{2}+4cy_{1}. \end{gathered} $$
(28)

Theorem 2

The master system (12) and the slave system (24) are globally IFSHP synchronized under the following control law:

$$ ( u_{1},u_{2},u_{3} ) ^{T}= \operatorname{diag} \biggl( -1,-\frac {1}{2},\frac{1}{3} \biggr) \times \bigl( \operatorname{diag} ( -l_{1}e_{1},-l_{2}e_{2},-l_{3}e_{3} ) -T \bigr) $$
(29)

and

$$ u_{4}=0, $$
(30)

where \(T= ( T_{1},T_{2},T_{3} ) ^{T}\) and \(( l_{i} ) _{1\leq i\leq3}\) are control positive constants.

Proof

By using Eq. (30), the error system (27) can be described as

$$ \bigl( D_{t}^{0.9}e_{1},D_{t}^{0.9}e_{2},D_{t}^{0.9}e_{3} \bigr) ^{T}=\operatorname{diag} ( -1,-2,3 ) \times ( u_{1},u_{2},u_{3} ) ^{T}+T, $$
(31)

and by substituting the control law (29) into Eq. (31), the error system can be written as

$$ \bigl( D_{t}^{0.9}e_{1},D_{t}^{0.9}e_{2},D_{t}^{0.9}e_{3} \bigr) ^{T}=-\operatorname{diag} ( l_{1}e_{1},l_{2}e_{2},l_{3}e_{3} ) . $$
(32)

If a Lyapunov function candidate is chosen as \(V ( e_{1},e_{2},e_{3} ) =\sum_{i=1}^{3}\frac{1}{2}e_{i}^{2}\), then the time Caputo fractional derivative of order 0.9 of V along the trajectory of system (32) is as follows:

$$ D_{t}^{0.9}V ( e_{1},e_{2},e_{3} ) =\sum_{i=1}^{3}D_{t}^{0.9} \frac{1}{2}e_{i}^{2}. $$
(33)

Using Lemma 2 in Eq. (33), we get

$$\begin{aligned} D_{t}^{0.95}V ( e_{1},e_{2},e_{3},e_{4} ) & \leq \sum _{i=1}^{3}e_{i}D_{t}^{0.9}e_{i} \\ & =- \bigl( l_{1}e_{1}^{2}+l_{2}e_{2}^{2}+l_{3}e_{3}^{2} \bigr) < 0.\end{aligned} $$

Thus, from Lemma 1, it is easy to see that the zero solution of system (32) is globally asymptotically stable; and therefore, systems (12) and (24) are IFSHP synchronized. □

For the numerical simulations, the control constants are chosen as \(l_{1}=1\), \(l_{2}=2\), and \(l_{3}=3\). As can be seen in Figure 4, the synchronization occurs between the master system (12) and the slave system (24) in 3D.

Figure 4
figure 4

Time series of the synchronized error signals between the master system ( 12 ) and the slave system ( 24 ) in 3D.

Full size image

4 Results and discussion

Figure 1 displays the chaotic attractor of three-dimensional autonomous system (1). Interestingly, system (1) has two stable equilibrium points, and attractors in this system are ‘hidden attractors’ because the basin of attraction for a hidden attractor is not connected with any unstable fixed point [27–29]. Recently, a hidden attractor has been discovered in different systems such as Chua’s system [27], model of drilling system [32], extended Rikitake system [36], and DC/DC converter [38]. The identification of hidden attractors in practical applications is important to avoid the sudden change to undesired behavior [29]. Previous research has established that derivatives are important in the field of mathematical modeling [51–54]. Fractional-order system (5) involving derivative orders is a generalization of autonomous system (1). Fractional system (5) exhibits chaos for the incommensurate orders \(q_{1}=0.98\), and \(q_{2}=q_{3}=0.99\) as shown in Figure 2. In addition, we have found that fractional system (5) also can generate chaotic behavior for commensurate orders.

Researchers have shown an increased interest in control and synchronization of fractional-order systems [55–57, 68–70]. We have studied the synchronization of fractional systems with different orders. Figure 3 illustrates the FSHPS between the considered 3D fractional chaotic system (5) and the 4D fractional chaotic system with an infinite number of equilibrium points. Figure 4 indicates the IFSHPS between the introduced 3D fractional system and the 4D fractional chaotic system without equilibrium. The complexity of proposed synchronization schemes can be used in secure communication and chaotic encryption schemes. In our future works, we will use the recent stability results of fractional systems [55–57] for discrete fractional systems and their synchronization.

5 Conclusions

In this work, the fractional-order form of a 3D chaotic system with two stable equilibrium points has been studied. Remarkably, the fractional system can display chaotic behavior. Moreover, we have studied two types of synchronization for such a 3D fractional system: full-state hybrid projective synchronization and inverse full-state hybrid projective synchronization. By using the proposed synchronization schemes, we have obtained the synchronization between the 3D fractional-order system and the 4D fractional-order system with an infinite number of equilibrium points as well as the 4D fractional-order system without equilibrium. Further studies regarding practical applications of this fractional system will be carried out in our next works.