Abstract
This paper investigates the aperiodically intermittent synchronization for a class of directed complex networks with switching network topologies. The assumption that all of the switching topologies contain a directed spanning tree is removed which is necessary in the previous related literature. That is, only some switching topologies contain a directed spanning tree when zero-in-degree nodes are pinned. By using M-matrix theory and constructing multiple Lyapunov functions, some sufficient conditions are derived to achieve the aperiodically intermittent synchronization of switching complex networks. Finally, some numerical simulations are given to demonstrate the theoretical results.
Similar content being viewed by others
1 Introduction
In the past few years, the study of complex networks has attracted an increasing interest from various research areas. The main reason is that many systems in nature and human society can be described as complex networks such as World Wide Web [1], epidemic spreading networks [2], collaborative networks [3], biological neural networks [4], and so on. In complex networks, one of the interesting phenomena is synchronization, which is very important in many research and application fields [5–12].
However, complex networks are not always able to synchronize by themselves. Hence, various effective control protocols have been proposed to achieve synchronization, such as feedback control [13–15], adaptive control [16, 17], impulsive control [18, 19], pinning control [20, 21] and intermittent control [22, 23] and so on. Compared with the continuous control, intermittent control is more economic and it has attracted great interests [24, 25]. In [26], the synchronization problem for a class of complex delayed dynamical networks is investigated by periodically intermittent control. The topology structure of the considered complex networks is time-invariant and the intermittent controller is periodical. In [27], synchronization problem for nonlinear coupled networks is investigated via aperiodically intermittent pinning control. Both an aperiodically constant intermittent control strategy and an aperiodically adaptive intermittent control strategy are designed. However, the network topology considered is undirected and time-invariant. In most of the aforementioned works, it is commonly assumed that the network topology contains a directed spanning tree. There is very little research on switching complex networks containing no directed spanning tree.
Unfortunately, the common assumption that each possible network topology contains a directed spanning tree is not always satisfied. In [28], the common assumption is removed. It is theoretically shown that the global pinning synchronization in such switching complex networks can be ensured if some nodes are appropriately pinned and the coupling is carefully selected. Nevertheless, the switching signal is periodical and the zero-in-degree nodes are pinned all the time. It should be pointed out that, to the best of our knowledge, there have been few results about the switching complex networks containing no directed spanning tree via aperiodically intermittent control, which is the motivation of this paper.
This paper aims to solve the challenging issue of pinning synchronization for a class of switching complex networks via aperiodically intermittent control. By using tools from M-matrix theory and constructing multiple Lyapunov functions, the global pinning synchronization can be realized if the coupling strength and the switching time are satisfied some inequations.
The main contributions of this paper can be highlighted as follows. Firstly, the assumption that all of the switching topologies contain a directed spanning tree is removed which is necessary in the previous related literature. That is, only some switching topologies contain a directed spanning tree when zero-in-degree nodes are pinned. Secondly, there is no node pinned when the switching topologies contain no directed spanning tree. The pinned nodes are time-varying, which are dependent on the switching topologies. Moreover, all the possible topologies switch aperiodically. That is, the zero-in-degree nodes are pinned aperiodically intermittently.
The remainder of the paper is organized as follows. In Section 2, some preliminaries on graph theory and the problem formulation are provided. In Section 3, by using M-matrix theory and constructing multiple Lyapunov functions, some sufficient conditions are derived to achieve the aperiodically intermittent synchronization of switching complex networks. Numerical simulations are given to demonstrate the effectiveness of the main results in Section 4. Finally, Section 5 concludes the whole work.
Notation
Let N, R, \(\mathbf{R}^{N}\), \(\mathbf{R}^{N\times N}\) be the sets of nonnegative integers, real numbers, N-dimensional real column vectors and \(N\times N\) real matrices, respectively. \(1_{N}\) represents the N-dimensional column vector with each element being 1. The superscript T means the transpose for matrices. Notation \(\operatorname{diag}\{x_{1},\ldots,x_{n}\}\) represents a diagonal matrix with \(x_{i}\) (\(i=1,\ldots,n\)), being its ith diagonal element. ⊗ and \(\Vert \cdot \Vert \) denote the Kronecker product and the Euclidean norm, respectively. For a real symmetric matrix Q, \(\lambda _{\min }(Q)\) represents the smallest eigenvalue of Q.
2 Preliminaries and problem formulation
In this section, we provide some useful preliminaries on algebraic graph theory and matrix theory.
Let \(\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{A})\) be a weighted directed graph of order N, where \(\mathcal{V}=\{v_{1},v_{2},\ldots ,v_{N}\}\) is the set of nodes, \(\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V} \) is the set of edges, and \(\mathcal{A}=[a_{ij}]_{N\times N}\) with \(a_{ij}\geq 0\) (\(i,j=1,2,\ldots,N\)) is a weighted adjacency matrix. An edge of \(\mathcal{G}\) is denoted by \(e_{ij}=(v_{i},v_{j}) \), where \(v_{i}\) and \(v_{j}\) are called the tail and head of the edge, and \(e_{ij}\in \mathcal{E}\) if and only if \(a_{ij}>0 \). Moreover, only simple graph is considered in this paper, that is, self-loops and multiple links are not allowed in \(\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{A})\). Correspondingly, the Laplacian matrix of \(\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{A})\) is defined as \({L}=[l_{ij}]_{N\times N}\), where \(l _{ij}=-a_{ij}\), \(i\neq j\) and \(l_{ii}=\sum_{k=1,k\neq i}^{N}a_{ik}\) for \(i=1,2,\ldots,N\). A directed path is an order sequence of vertices such that any two consecutive vertices are an edge of digraph. If there is a directed path from every node to every other node, the graph is said to be strongly connected for directed graph. A digraph has a directed spanning tree if it has N vertices and \(N-1\) edges and there exists a root vertex with directed paths to all other vertices and the Laplacian matrix L with a directed spanning tree has the following properties.
Lemma 1
[29]
Suppose that the directed graph \(\mathcal{G}\) contains a directed spanning tree. Then 0 is a simple eigenvalue of its Laplacian matrix L, and all the other eigenvalues of L have positive real parts.
Definition 1
[30]
Let \(\mathbf{Z}_{N}=\{L=[l_{ij}]_{N\times N}\in \mathbf{R}^{N\times N}:l_{ij}\leq 0 \mbox{ if } i\neq j, i,j=1,2,\ldots,N\}\) denote the set of real matrices whose off-diagonal elements are all non-positive.
Definition 2
[30]
A matrix \(L\in \mathbf{R}^{{N\times N}}\) is called a nonsingular M-matrix if \(L\in \mathbf{Z}_{N}\) and all the leading principal minors of L are positive.
Lemma 2
[30]
Suppose that matrix \(L=[l_{ij}]_{N\times N}\in \mathbf{R}^{N\times N}\) has \(l_{ij}\leq 0\), for all \(i\neq j\), \(i,j=1,2,\ldots,N\). Then the following statements are equivalent.
-
(1)
L is a nonsingular M-matrix;
-
(2)
There exists a positive definite diagonal matrix \(\Phi =\operatorname{diag}\{\phi _{1},\phi _{2},\ldots,\phi _{n}\}\in \mathbf{R}^{N\times N}\) such that \(L^{T}\Phi +\Phi L>0\);
-
(3)
All the eigenvalues of L have positive real parts.
Definition 3
[31]
The function \(f(\cdot )\) is said to satisfy \(f(\cdot )\in \operatorname{QUAD}(P,\Delta )\), if there exist two positive definite diagonal matrices \(P=\operatorname{diag}(p_{1},\ldots,p_{n})\) and \(\Delta =\operatorname{diag}(\delta _{1},\ldots,\delta _{n})\), such that, for any \(x,y\in \mathbf{R}^{n}\), the following condition holds: \((x-y)^{T}P(f(x)-f(y)-\Delta x+\Delta y)\leq 0\).
The QUAD assumption can be satisfied for several well-known chaotic oscillators, such as cellular neural networks, the Lorenz system, and so on. Furthermore, it is easy to verify that the QUAD assumption holds if the nonlinear function f satisfies the global Lipschitz condition.
In [27], the authors have investigated the aperiodically intermittent control for the time-invariant network and the pinning control was only imposed on the first node with a constant control gain. The model in [27] was described as
where \(x_{i}(t)=(x_{i1},x_{i2},\ldots,x_{in})^{T}\in \mathbf{R}^{n}\), \(f(x_{i}(t))=(f_{1}(x_{i1}(t)),f_{2}(x_{i2}(t)),\ldots,f_{n}(x_{in}(t)))^{T}\), \(c>0\) is the coupling strength, \(\Gamma =\operatorname{diag}(\gamma _{1},\ldots,\gamma _{n})\in \mathbf{R}^{n\times n}\) is a positive semi-definite matrix denoting the inner coupling matrix, \(A=[a_{ij}]_{N\times N}\) is the outer coupling matrix reflecting the network topology, the network topology is time-invariant and \(\pi (t)\) is the target trajectory satisfying \(\dot{\pi }(t)=f(\pi (t))\).
From a practical viewpoint, it is impossible that the network topology is time-invariant forever and it is inevitable some links may be lost or added as the networked systems evolve with time. Then the directed complex networks with switching topologies considered in this paper are more significant than [27]. Now, we firstly introduce an aperiodically switching signal \(r(t):[0,+\infty )\rightarrow \{1,2,\ldots,p\}\) to describe the evolution of the network topologies. Suppose there exists an infinite sequence \(\{\bar{t}_{\rho },\rho =0,1,2,\ldots\}\) with \(\bar{t}_{0}=0\), \(\omega _{1}>\bar{t}_{\rho +1}-\bar{t}_{\rho }>\omega _{0}>0\), and \([\bar{t}_{\rho },\bar{t}_{\rho +1})\), \(\rho \in \mathbf{N}\) are uniformly bounded non-overlapping time intervals where \(\bar{t}_{\rho }\) denotes the switching time. For each \(\rho \in \mathbf{N}\), the network topology is time-invariant for all \(t\in [\bar{t}_{\rho },\bar{t}_{\rho +1})\). Take \(\pi (t)\) as a virtual root into consider and let \(\mathcal{G}(\bar{\mathcal{A}}^{r(t)})\) denote the augmented interaction graph consisting of \(N+1\) nodes. \(\overline{\mathcal{G}}=\{\mathcal{G}(\bar{\mathcal{A}}^{1}),\mathcal{G}(\bar{\mathcal{A}}^{2}),\ldots,\mathcal{G}(\bar{\mathcal{A}}^{p})\}\) is the set of all possible augmented interaction graph. It is not necessary that each possible network topologies contains a directed spanning tree with the virtual root. Suppose \(\widehat{\mathcal{G}}=\{\mathcal{G}(\bar{\mathcal{A}}^{\varsigma _{1}}),\mathcal{G}(\bar{\mathcal{A}}^{\varsigma _{2}}),\ldots,\mathcal{G}(\bar{\mathcal{A}}^{\varsigma _{q}})\}\) is the set of augmented interaction graphs containing a directed spanning tree with \(\{\varsigma _{1},\ldots,\varsigma _{q}\}=\mathcal{Q}\subseteq \mathcal{P}=\{1,2,\ldots,p\}\). In general, it is assumed that the directed network topology contains a directed spanning tree at the beginning and some links will be lost or added as the network topology evolves with time.
In order to observe the switching time, we introduce a function \(h:\mathcal{P}\rightarrow \{0,1\}\) as follows:
Obviously, if the image of h equals the set \(\{1\}\), each possible network topology contains a directed spanning tree, that is, \(\mathcal{Q}=\mathcal{P}\), if h maps into \(\{0\}\), each possible network topology does not have any directed spanning tree, that is, \(\mathcal{Q}=\Phi \). In fact, the function h can be regarded as an observer to measure the switching network topologies containing a directed spanning tree. Without loss of generality, we assume \(h(\cdot )\) does not always equal 0 or 1, that is, \(\mathcal{Q}\subset \mathcal{P}\). Then, using the function h, we can get a time sequence:
and for \(k\geq 0\),
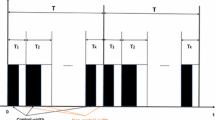
It is easy to see that \(\{\tilde{t}_{k},k\geq 0\}\) is the set of switching time containing directed spanning tree and \(\{\tilde{s}_{k},k\geq 0\}\) is the set of switching time when the directed network does not contain any directed spanning tree. That is, for all \(t\in [\tilde{t}_{k},\tilde{s}_{k})\), the network topologies contain a directed spanning tree, and for all \(t\in [\tilde{s}_{k},\tilde{t}_{k+1})\), the network topologies contain no directed spanning tree. Moreover, \([\tilde{t}_{k},\tilde{s}_{k})\) and \([\tilde{s}_{k},\tilde{t}_{k+1})\) have no multiple switching. Suppose \(\tilde{t}_{k}=\tilde{t}_{k}^{1}<\tilde{t}_{k}^{2}<\cdots<\tilde{t}_{k}^{\theta _{k}+1} =\tilde{s}_{k}\) and \(\tilde{s}_{k}=\tilde{s}_{k}^{1}<\tilde{s}_{k}^{2}<\cdots<\tilde{s}_{k}^{\vartheta _{k}+1} =\tilde{t}_{k+1}\) where \(\tilde{t}_{k}^{j}\) (\(j=1,\ldots,\theta _{k}, \theta _{k}\leq q\)) and \(\tilde{s}_{k}^{j}\) (\(j=1,\ldots,\vartheta _{k}, \vartheta _{k}\leq p-q\)) are all switching time in \([\tilde{t}_{k},\tilde{s}_{k})\) and \([\tilde{s}_{k},\tilde{t}_{k+1})\), respectively (see Figure 1).
Now, we introduce the switching network model with aperiodically intermittent pinning control. The dynamics of the ith node are described as
where \(x_{i}(t)\), \(f(x_{i}(t))\), Γ and c are the same as defined in (1), \(r(t)\in \mathcal{Q}\) represents the mode at time t, \(A^{r(t)}=[a_{ij}^{r(t)}]_{N\times N}\) is the outer coupling matrix reflecting the switched network topology at mode \(r(t)\), \(D^{r(t)}=\operatorname{diag}\{d_{1}^{r(t)},d_{2}^{r(t)},\ldots,d_{N}^{r(t)}\}\), \(d_{i}^{r(t)}\in \{0,1\}\) and \(d_{i}^{r(t)}=1\) if and only if the ith node is pinned at mode \(r(t)\). \(\pi (t)\) is the target trajectory satisfying \(\dot{\pi }(t)=f(\pi (t))\). \(\pi (t)\) may be an equilibrium point, a periodic orbit, or even a chaotic orbit. Our aim in this paper is to pin some nodes with zero in-degree in some switching topologies via aperiodically intermittent control such that all the nodes can approach \(\pi (t)\) as time t approaches +∞, that is, \(\lim_{t\rightarrow +\infty }\Vert x_{i}(t)-\pi (t) \Vert =0\), \(i=1,2,\ldots,N\).
Remark 1
Although aperiodically intermittent control has been investigated in [27], the network topology was time-invariant and the pinning control was only imposed on the first node all the time. In this paper, we investigate switching complex networks and choose the pinned nodes with zero in-degree in \(\mathcal{G}(\bar{\mathcal{A}}^{\varsigma _{i}})\) (\(i=1,\ldots,q\)) by using Tarjan’s algorithm [32]. Moreover, the nodes which are pinned may be different at different modes. The pinned nodes are controlled aperiodically intermittently only in some topologies which contain a directed spanning tree, while in other topologies no node is pinned. Our model (3) is more general than the model in [27].
Let \(e_{i}(t)=x_{i}(t)-\pi (t)\) (\(i=1,2,\ldots,N\)) denote the synchronization error and \(E(t)=(e_{1}^{T}(t),e_{2}^{T}(t),\ldots,e_{N}^{T}(t))^{T}\). Then we can get the synchronization error systems as follows:
where \({F}(E(t))=(({f}(x_{1}(t))-f(\pi (t)))^{T},({f}(x_{2}(t))-f(\pi (t)))^{T},\ldots,({f}(x_{N}(t))-f(\pi (t)))^{T})^{T}\), \(\widehat{L}^{r(t)}=L^{r(t)}+cD^{r(t)}\). According to the above statement and Lemma 2, it is found that \(\widehat{L}^{r(t)}\) (\(t\in [\tilde{t}_{k}^{j},\tilde{t}_{k}^{j+1}), j=1,\ldots,\theta _{k}\)) is a nonsingular M-matrix. Then, using Theorem 2.3 of [30], we can get the following result.
Lemma 3
For \(t\in [\tilde{t}_{k}^{j},\tilde{t}_{k}^{j+1})\), \(j\in \{1,2,\ldots,\theta _{k}\}\), \(k\in \mathbf{N}\), there exist positive vectors \(\xi ^{r(\tilde{t}_{k}^{j})}=(\xi _{1}^{r(\tilde{t}_{k}^{j})},\xi _{2}^{r(\tilde{t}_{k}^{j})},\ldots, \xi _{N}^{r(\tilde{t}_{k}^{j})})^{T}\in \mathbf{R}^{N}\), such that \((\widehat{L}^{r(\tilde{t}_{k}^{j})})^{T}\xi ^{r(\tilde{t}_{k}^{j})}=\mathbf{1}_{N}\) and \(\Xi ^{r(\tilde{t}_{k}^{j})}\widehat{L}^{r(\tilde{t}_{k}^{j})}+(\widehat{L}^{r(\tilde{t}_{k}^{j})})^{T}\Xi ^{r(\tilde{t}_{k}^{j})}>0\), where \(\Xi ^{r(\tilde{t}_{k}^{j})}=\operatorname{diag}\{1/\xi _{1}^{r(\tilde{t}_{k}^{j})},1/\xi _{2}^{r(\tilde{t}_{k}^{j})}, \ldots,1/\xi _{N}^{r(\tilde{t}_{k}^{j})}\}\).
For notational convenience, denote \(\mu _{k}=\tilde{s}_{k}-\tilde{t}_{k}\) and \(\eta _{k}=\tilde{t}_{k+1}-\tilde{s}_{k}\) as the ith control width and the ith rest width, respectively. Let \(\lambda _{0}^{r(\tilde{t}_{k}^{j})}=\lambda _{\min }^{r(\tilde{t}_{k}^{j})}\xi _{\min }^{r(\tilde{t}_{k}^{j})}\), where \(\lambda _{\min }^{r(\tilde{t}_{k}^{j})}\) is the smallest eigenvalue of \(\Xi ^{r(\tilde{t}_{k}^{j})}\widehat{L}^{r(\tilde{t}_{k}^{j})}+(\widehat{L}^{r(\tilde{t}_{k}^{j})})^{T} \Xi ^{r(\tilde{t}_{k}^{j})}\), \(\xi _{\min }^{r(\tilde{t}_{k}^{j})}=\min_{i=1,2,\ldots ,N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), \(\xi ^{r(\tilde{t}_{k}^{j})}=(\xi _{1}^{r(\tilde{t}_{k}^{j})},\xi _{2}^{\tilde{t}_{k}^{j}},\ldots, \xi _{N}^{\tilde{t}_{k}^{j}})^{T}\) is defined in Lemma 3, and \(\chi _{k}=\min_{1\leq j\leq \vartheta _{k}}\tilde{\lambda }^{r(\tilde{s}_{k}^{j})}\) where \(\tilde{\lambda }_{\min }^{r(\tilde{s}_{k}^{j})}\) is the smallest eigenvalue of \((\Xi ^{r(\tilde{t}_{k}^{\theta _{k}})})^{-1}(\Xi ^{r(\tilde{t}_{k}^{\theta _{k}})}{L}^{r(\tilde{s}_{k}^{j})} +({L}^{r(\tilde{s}_{k}^{j})})^{T} \Xi ^{r(\tilde{t}_{k}^{\theta _{k}})})\).
Assumption 1
For any \(k\in \mathbf{N}\), there is no repetitively switching topology in \([\tilde{t}_{k},\tilde{s}_{k})\) or \([\tilde{s}_{k},\tilde{t}_{k+1})\). The switching times in \([\tilde{t}_{k},\tilde{s}_{k})\) and \([\tilde{s}_{k},\tilde{t}_{k+1})\) are not more than q and \(p-q\), respectively.
Lemma 4
[33]
Suppose that \(P\in \mathbf{R}^{N\times N}\) is a positive definite matrix and \(M\in \mathbf{R}^{N\times N}\) is symmetric. Then, for any vector \(x\in \mathbf{R}^{N}\), the following inequality holds:
where \(\lambda _{\min }(P^{-1}M)\) and \(\lambda _{\max }(P^{-1}M)\) are the minimum and maximum eigenvalues of \(P^{-1}M\), respectively.
3 Main results
In the following section, we aim to find some sufficient synchronization criteria for synchronizing all the nodes in the switching networks (3) with the target trajectory \(\pi (t)\).
Theorem 1
Under the QUAD assumption, the pinning synchronization in switching networks (3) with target trajectory \(\pi (t)\) could be achieved if there exists a positive scalar \(\varepsilon _{0}\) such that, for each \(k\in \mathbf{N}\), \(j=1,2,\ldots,\theta _{k}\), the following conditions are satisfied.
-
(1)
\({\lambda }_{0}^{r(\tilde{t}_{k}^{j})}>2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{j})}\),
-
(2)
\(\sum_{j=1}^{\theta _{k}}\alpha ^{r(\tilde{t}_{k}^{j})} (\tilde{t}_{k}^{j+1}-\tilde{t}_{k}^{j})>{\sum_{j=1}^{\vartheta _{k}} \beta ^{r(\tilde{s}_{k}^{j})}(\tilde{s}_{k}^{j+1}-\tilde{s}_{k}^{j})}+p\ln\zeta _{k}+\varepsilon _{0}\),
where \(\alpha ^{r(\tilde{t}_{k}^{j})}={\lambda }_{0}^{r(\tilde{t}_{k}^{j})}-2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{j})}\), \(\beta ^{r(\tilde{s}_{k}^{j})}=2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{\theta _{k}})}-\tilde{\lambda }_{\min }^{r(\tilde{s}_{k}^{j})}\), \(\lambda _{0}^{r(\tilde{t}_{k}^{j})}=\lambda _{\min }^{r(\tilde{t}_{k}^{j})} \xi _{\min }^{r(\tilde{t}_{k}^{j})}\), \(\delta _{\max }=\max_{1\leq i\leq n}\delta _{i}\), \(\zeta ^{r(\tilde{t}_{k}^{j})}=\xi _{\max }^{r(\tilde{t}_{k}^{j})}/\xi _{\min }^{r(\tilde{t}_{k}^{j})}\), \(\xi _{\max }^{r(\tilde{t}_{k}^{j})}=\max_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), and \(\xi _{\min }^{r(\tilde{t}_{k}^{j})}=\min_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), \(\zeta _{k}=\max \{\varsigma _{1,k},\varsigma _{2,k}\}\), \(\varsigma _{1,k}=\max_{1\leq j\leq \theta _{k}}\{\zeta ^{r(\tilde{t}_{k}^{j})}\}\), \(\varsigma _{2,k}=\max_{1\leq j\leq \vartheta _{k}}\{\zeta ^{r(\tilde{s}_{k}^{j})}\}\).
Proof
Note that global pinning synchronization of the switching networks (3) with the target trajectory \(\pi (t)\) is achieved if and only if the zero equilibrium point of the error systems (4) is globally attractive.
For each \(\tilde{t}_{k}^{j}\), \(j=1,\ldots,\theta _{k}\), \(k\in \mathbf{N}\), the interaction digraph \(\mathcal{G}(\bar{\mathcal{A}}^{r(\tilde{t}_{k}^{j})})\) contain a directed spanning tree rooted at the virtual node. Thus, there exists a positive definite matrix \(\Xi ^{r(\tilde{t}_{k}^{j})}\) as defined in Lemma 3 such that \(\Xi ^{r(\tilde{t}_{k}^{j})}\widehat{L}^{r(\tilde{t}_{k}^{j})}+ (\widehat{L}^{r(\tilde{t}_{k}^{j})})^{T}\Xi ^{r(\tilde{t}_{k}^{j})}>0\). Then we construct the following multiple Lyapunov functions for the switching systems (4):
For \(t\in [\tilde{t}_{k}^{j},\tilde{t}_{k}^{j+1})\), \(j=1,\ldots,\theta _{k}\), \(k\in \mathbf{N}\), the derivative of \(V(t)\) with respect to time t along with solutions of (4) can be calculated as follows:
Using Lemma 4, it follows from (6) that
where \(\delta _{\max }=\max_{1\leq i\leq n}\delta _{i}\), \(\zeta ^{r(\tilde{t}_{k}^{j})}=\xi _{\max }^{r(\tilde{t}_{k}^{j})}/\xi _{\min }^{r(\tilde{t}_{k}^{j})}\), \(\xi _{\max }^{r(\tilde{t}_{k}^{j})}=\max_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), and \(\xi _{\min }^{r(\tilde{t}_{k}^{j})} = \min_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), \(\tilde{\lambda }_{0}^{r(\tilde{t}_{k}^{j})}\) is the smallest eigenvalue of \((\Xi ^{r(\tilde{t}_{k}^{j})})^{-1}(\Xi ^{r(\tilde{t}_{k}^{j})}\widehat{L}^{r(\tilde{t}_{k}^{j})}+ (\widehat{L}^{r(\tilde{t}_{k}^{j})})^{T}\Xi ^{r(\tilde{t}_{k}^{j})})\). Note that, for each \(\tilde{t}_{k}^{j}\), \(j=1,\ldots,\theta _{k}\), the following inequality is always satisfied: \(\tilde{\lambda }_{0}^{r(\tilde{t}_{k}^{j})}\geq \lambda _{\min }^{r(\tilde{t}_{k}^{j})} \xi _{\min }^{r(\tilde{t}_{k}^{j})}\), where \(\lambda _{\min }^{r(\tilde{t}_{k}^{j})}\) is the smallest eigenvalue of \(\Xi ^{r(\tilde{t}_{k}^{j})}\widehat{L}^{r(\tilde{t}_{k}^{j})}+(\widehat{L}^{r(\tilde{t}_{k}^{j})})^{T} \Xi ^{r(\tilde{t}_{k}^{j})}\), \(\xi _{\min }^{r(\tilde{t}_{k}^{j})}=\min_{i=1,2,\ldots, N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), \(\xi ^{r(\tilde{t}_{k}^{j})}=(\xi _{1}^{r(\tilde{t}_{k}^{j})},\xi _{2}^{\tilde{t}_{k}^{j}},\ldots, \xi _{N}^{\tilde{t}_{k}^{j}})^{T}\) is defined in Lemma 3. Then we find that
where \(\alpha ^{r(\tilde{t}_{k}^{j})}={\lambda }_{0}^{r(\tilde{t}_{k}^{j})}-2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{j})}\), \(\lambda _{0}^{r(\tilde{t}_{k}^{j})}=\lambda _{\min }^{r(\tilde{t}_{k}^{j})} \xi _{\min }^{r(\tilde{t}_{k}^{j})}\). It can be seen from condition (1) that \(\alpha ^{r(\tilde{t}_{k}^{j})}>0\), \(j=1,\ldots,\theta _{k}\), \(k\in \mathbf{N}\).
Therefore,
On the other hand, it follows from (5) that
where \(t\in [\tilde{t}_{k}^{j},\tilde{t}_{k}^{j+1})\), \(j=1,\ldots,\theta _{k}, k\in \mathbf{N}\). Then we have
where \(\varsigma _{1,k}=\max_{1\leq j\leq \theta _{k}}\{\zeta ^{r(\tilde{t}_{k}^{j})}\}\).
For \(t\in [\tilde{s}_{k}^{j},\tilde{s}_{k}^{j+1}), j=1,\ldots,\vartheta _{k}, k\in \mathbf{N}\), we get
where \(\beta ^{r(\tilde{s}_{k}^{j})}=2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{\theta _{k}})}-\tilde{\lambda }_{\min }^{r(\tilde{s}_{k}^{j})}\), \(\tilde{\lambda }_{\min }^{r(\tilde{s}_{k}^{j})}\) is the smallest eigenvalue of
Similarly, we get
where \(\varsigma _{2,k}=\max_{1\leq j\leq \vartheta _{k}}\{\zeta ^{r(\tilde{s}_{k}^{j})}\}\).
Therefore,
where \(\zeta _{k}=\max \{\varsigma _{1,k},\varsigma _{2,k}\}\), \(\varsigma _{1,k}=\max_{1\leq j\leq \theta _{k}}\{\zeta ^{r(\tilde{t}_{k}^{j})}\}\), \(\varsigma _{2,k}=\max_{1\leq j\leq \vartheta _{k}}\{\zeta ^{r(\tilde{s}_{k}^{j})}\}\).
Then it can be directly found from (14) and the condition (2) that
for any given \(k\in \mathbf{N}\). Furthermore, we can obtain by recursion that
Used to the dwell time \(\omega _{0}>0\), we know that there is no Zeno behavior as the switching networks evolve with time [34]. Thus, for any given time \(t>0\), there exists a positive integer m such that \(\tilde{t}_{m}< t\leq \tilde{t}_{m+1}\).
When \(t\in [0,\tilde{t}_{1}^{2})\), we get
where \(\alpha ^{r(\tilde{t}_{1}^{1})}=\lambda _{0}^{r(\tilde{t}_{1}^{1})}-2\delta _{\max }\zeta ^{r(\tilde{t}_{1}^{1})}>0\).
When \(t\in [\tilde{t}_{1}^{\theta _{1}},\tilde{t}_{1}^{\theta _{1}+1})\), it can be found that
When \(t\in [\tilde{s}_{1}^{1},\tilde{s}_{1}^{2})\), it can be similarly calculated that
When \(t\in [\tilde{s}_{1}^{\vartheta _{1}},\tilde{s}_{1}^{\vartheta _{1}+1})\), we get
When \(t\in [\tilde{t}_{m}^{j},\tilde{t}_{m}^{j+1})\), \(j=1,2,\ldots,\theta _{m}, m\geq 2\), we have
where \(\hat{\iota }_{0}=\max_{1\leq k\leq m}\{\mu _{k}+\eta _{k}\}\).
When \(t\in [\tilde{s}_{m}^{l},\tilde{s}_{m}^{l+1})\), \(l=1,2,\ldots,\vartheta _{m}\), \(m\geq 2\), we have
Combining with (21) and (22), we have the following. As time \(t\rightarrow +\infty \), \(V(t)\rightarrow 0\). Then \(e_{i}(t)\rightarrow 0\), \(j=1,\ldots,N\). That is pinning synchronization of the switched networks (3) with the target trajectory \(\pi (t)\) could be realized. The proof is completed. □
Remark 2
From the above analysis, we can see that the network topologies contain a directed spanning tree in the time periods \([\tilde{t}_{k}^{j},\tilde{t}_{k}^{j+1})\subseteq [\tilde{t}_{k},\tilde{s}_{k})\), \(j=1,2,\ldots,\theta _{k}\), \(k\in \mathbf{N}\) when zero-in-degree nodes are pinned. While \(t\in [\tilde{s}_{k}^{l},\tilde{s}_{k}^{l+1})\subseteq [\tilde{s}_{k},\tilde{t}_{k+1})\), \(l=1,2,\ldots\vartheta _{k}, k\in \mathbf{N}\), no node is pinned and the network topologies contain no directed spanning tree. Moreover, \([\tilde{t}_{k}^{j},\tilde{t}_{k}^{j+1})\) are called control spans benefitial to pinning synchronization, thus they are as long as possible; while the rest spans \([\tilde{s}_{k}^{l},\tilde{s}_{k}^{l+1})\), harmful to synchronization, should be as short as possible.
Remark 3
It is easy to see that c plays a very important role which affect the realization of the conditions in Theorem 1. Given the network topology, the bigger c the bigger the value of \({\lambda }_{0}^{r(\tilde{t}_{k}^{j})}\), then the second condition is easier to be satisfied. Moreover, the control spans become shorter and the rest spans become longer.
Remark 4
In [28], the topologies switch periodically and some nodes are pinned all the time though the topologies contain no directed spanning tree. In this paper, all the topologies switch aperiodically and there exist no two topologies simultaneously which is different from jointly connected graphs [35]. Moreover, no node is pinned when the topologies contain no directed spanning tree and the pinned nodes are dependent on the topologies. Our method is more reasonable than [28].
When all the possible switching topologies contain a directed spanning tree, some nodes with zero in-degree are pinned all the time though the pinned nodes may be different in different modes.
Corollary 1
Under the QUAD assumption, if all the network topologies contain a directed spanning tree, that is, \(\mathcal{P}=\mathcal{Q}\), the global pinning synchronization of switching networks (3) with the target trajectory \(\pi (t)\) can be achieved if \({\lambda }_{0}^{r(\tilde{t}_{k}^{j})}>2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{j})}\), where \(\delta _{\max }=\max_{1\leq i\leq n}\delta _{i}\), \(\zeta ^{r(\tilde{t}_{k}^{j})}=\xi _{\max }^{r(\tilde{t}_{k}^{j})}/\xi _{\min }^{r(\tilde{t}_{k}^{j})}\), \(\xi _{\max }^{r(\tilde{t}_{k}^{j})}=\max_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), and \(\xi _{\min }^{r(\tilde{t}_{k}^{j})}=\min_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), \(\tilde{\lambda }_{0}^{r(\tilde{t}_{k}^{j})}\) is the smallest eigenvalue of \((\Xi ^{r(\tilde{t}_{k}^{j})})^{-1}(\Xi ^{r(\tilde{t}_{k}^{j})}\widehat{L}^{r(\tilde{t}_{k}^{j})}+ (\widehat{L}^{r(\tilde{t}_{k}^{j})})^{T}\Xi ^{r(\tilde{t}_{k}^{j})})\).
Remark 5
Since the controller is dependent on the topologies according to (3), the controller becomes continuous instead of the aperiodically intermittent controller when \(\mathcal{P}=\mathcal{Q}\). The conditions (2) in Theorem 1 is apparently satisfied. Then, provided the conditions (1) in Theorem 1 could be satisfied under some \(c>0\), the switching network (3) can synchronize with the target trajectory \(\pi (t)\). Although the controller becomes continuous when \(\mathcal{P}=\mathcal{Q}\), different nodes are pinned in different topologies, not as in [36].
Corollary 2
Suppose function \(f\in \operatorname{QUAD}(P,\Delta )\) and \(\mathcal{P}\subset \mathcal{Q}\). The global pinning synchronization of switched networks (3) with the target trajectory \(\pi (t)\) can be achieved if there exists a positive scalar \(\varepsilon _{k}\) for each \(k\in \mathbf{N}\), such that the following conditions hold.
-
(1)
\({\lambda }_{0}^{r(\tilde{t}_{k}^{j})}>2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{j})}\),
-
(2)
\(\sum_{j=1}^{\theta _{k}}\alpha ^{r(\tilde{t}_{k}^{j})}(\tilde{t}_{k}^{j+1}-\tilde{t}_{k}^{j})>{\sum_{j=1}^{\vartheta _{k}} \beta ^{r(\tilde{s}_{k}^{j})}(\tilde{s}_{k}^{j+1}-\tilde{s}_{k}^{j})}+p\ln\zeta _{k}+\varepsilon _{k}\),
where \(\alpha ^{r(\tilde{t}_{k}^{j})}={\lambda }_{0}^{r(\tilde{t}_{k}^{j})}-2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{j})}\), \(\beta ^{r(\tilde{s}_{k}^{j})}=2\delta _{\max }\zeta ^{r(\tilde{t}_{k}^{\theta _{k}})}-\tilde{\lambda }_{\min }^{r(\tilde{s}_{k}^{j})}\), \(\lambda _{0}^{r(\tilde{t}_{k}^{j})}=\lambda _{\min }^{r(\tilde{t}_{k}^{j})} \xi _{\min }^{r(\tilde{t}_{k}^{j})}\), \(\delta _{\max }=\max_{1\leq i\leq n}\delta _{i}\), \(\zeta ^{r(\tilde{t}_{k}^{j})}=\xi _{\max }^{r(\tilde{t}_{k}^{j})}/\xi _{\min }^{r(\tilde{t}_{k}^{j})}\), \(\xi _{\max }^{r(\tilde{t}_{k}^{j})}=\max_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), and \(\xi _{\min }^{r(\tilde{t}_{k}^{j})}=\min_{1\leq i\leq N}\xi _{i}^{r(\tilde{t}_{k}^{j})}\), \(\zeta _{k}=\max \{\varsigma _{1,k},\varsigma _{2,k}\}\), \(\varsigma _{1,k}=\max_{1\leq j\leq \theta _{k}}\{\zeta ^{r(\tilde{t}_{k}^{j})}\}\), \(\varsigma _{2,k}=\max_{1\leq j\leq \vartheta _{k}}\{\zeta ^{r(\tilde{s}_{k}^{j})}\}\).
Remark 6
In this paper, if the switching topologies become periodic, that is, \(\tilde{s}_{k}-\tilde{t}_{k}=\varpi \) and \(\tilde{t}_{k+1}-\tilde{t}_{k}=\omega\) (\(k=1,2,\ldots\)), where ϖ and ω are positive scalars, the obtained results still hold. Then it becomes periodically intermittent pinning synchronization.
4 An illustrative example
In this section, some numerical simulations are provided to illustrate the effectiveness of the obtained theoretical results.
Assume the target trajectory \(\pi (t)\) is given by a 3-D cellular neural network as follows:
where \(\pi (t)=(\pi _{1}(t),\pi _{2}(t),\pi _{3}(t))^{T}\), \(L(\pi (t))=(l(\pi _{1}(t)),l(\pi _{2}(t)),l(\pi _{3}(t)))^{T}\), \(l(v)=(\vert v+1 \vert -\vert v-1 \vert )/2\). This neural network has a double-scrolling chaotic attractor shown in Figure 2, which is the same as in [37]. It is easy to see that the function \(f(\cdot )\) satisfies Assumption 1 [38]. Moreover, let \(\Gamma =I\).
Suppose the switching time as in Figure 1. According to Figure 1, we can see that \(\overline{\mathcal{G}}=\{\mathcal{G}(\bar{\mathcal{A}^{1}}),\mathcal{G}(\bar{\mathcal{A}^{2}}),\mathcal{G}(\bar{\mathcal{A}^{3}}),\mathcal{G}(\bar{\mathcal{A}^{4}})\}\) and \(\widehat{\mathcal{G}}=\{\mathcal{G}(\bar{\mathcal{A}^{1}}),\mathcal{G}(\bar{\mathcal{A}^{2}})\}\). The four switching topologies are given in Figures 3 and 4 where the weight on each edge is assumed to be one. In Figures 3 and 4, the neighboring relationships between the nodes in network (3) and the single target node (labeled node 9) are depicted by dashed lines with arrows.
Choose \(c=19.25\), we can obtain from Theorem 1 that the aperiodically intermittent synchronization of switching complex networks dependent on topology structure can be ensured with the target trajectory \(\pi (t)\). The synchronization errors of the switching networks (4) are, respectively, shown in Figures 5, 6 and 7. Let \(\Vert e(t) \Vert =1/8(\sum_{i=1}^{8}\Vert x_{i}(t)-\pi (t) \Vert ^{2})^{1/2}\) denote the synchronization error of the considered network. It can be seen from Figure 8 that the global pinning synchronization problem is indeed solved.
5 Conclusions
In this paper, event-triggered schemes and self-triggered schemes are investigated to realize the exponential synchronization of the networked dynamical systems. The coupled information under these schemes is updated only when the triggering conditions are violated. The next observation time these nodes is predicted only based on the latest observations of their neighborhood and the virtual leader. Thus, continuous communication can be avoided and the quantity of information transmission is largely reduced. Moreover, a positive lower bound for inter-event intervals is achieved and the Zeno behavior can be excluded. Finally, two numerical simulation examples are provided to illustrate the effectiveness of the proposed results. In the future, we will focus on the related applications of the event-triggered scheme in the coupled neural networks with time-delays and quantization.
References
Huberman, BA, Adamic, LA: Internet: growth dynamics of the world-wide web. Nature 401(6749), 131 (1999)
Pastor-Satorras, R, Vespignani, A: Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86(14), 3200 (2001)
Wang, F, Sun, Y: Self-organizing peer-to-peer social networks. Comput. Intell. 24(3), 213-233 (2008)
Selverston, A: Model Neural Networks and Behavior. Springer, Berlin (2013)
Lu, J, Ho, DW: Globally exponential synchronization and synchronizability for general dynamical networks. IEEE Trans. Cybern. 40(2), 350-361 (2010)
Chen, Y, Yu, W, Li, F, Feng, S: Synchronization of complex networks with impulsive control and disconnected topology. IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process. 60(5), 292-296 (2013)
Yang, X, Wu, Z, Cao, J: Finite-time synchronization of complex networks with nonidentical discontinuous nodes. Nonlinear Dyn. 73(4), 2313-2327 (2013)
Yang, X, Ho, DW: Synchronization of delayed memristive neural networks: Robust analysis approach. IEEE Trans. Cybern. 46(12), 3377-3387 (2015). doi:10.1109/TCYB.2015.2505903
Gao, J, Zhu, P: Global exponential synchronization of networked dynamical systems under event-triggered control schemes. Adv. Differ. Equ. 2016(1), 286 (2016). doi:10.1186/s13662-016-1006-0
Cao, Y, Zhang, L, Li, C, Chen, MZ: Observer-based consensus tracking of nonlinear agents in hybrid varying directed topology. IEEE Trans. Cybern. 47(8), 2212-2222 (2017). doi:10.1109/TCYB.2016.2573138
Gao, J, Zhu, P, Xiong, W, Cao, J, Zhang, L: Asymptotic synchronization for stochastic memristor-based neural networks with noise disturbance. J. Franklin Inst. 353(13), 3271-3289 (2016)
Gao, J, Zhu, P, Alsaedi, A, Alsaadi, FE, Hayat, T: A new switching control for finite-time synchronization of memristor-based recurrent neural networks. Neural Netw. 86, 1-9 (2017). doi:10.1016/j.neunet.2016.10.008
Li, X, Wang, X, Chen, G: Pinning a complex dynamical network to its equilibrium. IEEE Trans. Circuits Syst. I, Regul. Pap. 51(10), 2074-2087 (2004)
Zhou, Q, Shi, P, Xu, S, Li, H: Adaptive output feedback control for nonlinear time-delay systems by fuzzy approximation approach. IEEE Trans. Fuzzy Syst. 21(2), 301-313 (2013)
Shi, Y, Zhu, P: Finite-time synchronization of stochastic memristor-based delayed neural networks. Neural Comput. Appl. 21(2), 1-9 (2016). doi:10.1007/s00521-016-2546-7
Yu, W, Chen, G, Lü, J, Kurths, J: Synchronization via pinning control on general complex networks. SIAM J. Control Optim. 51(2), 1395-1416 (2013)
Su, H, Rong, Z, Chen, MZ, Wang, X, Chen, G, Wang, H: Decentralized adaptive pinning control for cluster synchronization of complex dynamical networks. IEEE Trans. Cybern. 43(1), 394-399 (2013)
Lu, J, Kurths, J, Cao, J, Mahdavi, N, Huang, C: Synchronization control for nonlinear stochastic dynamical networks: pinning impulsive strategy. IEEE Trans. Neural Netw. Learn. Syst. 23(2), 285-292 (2012)
Yang, X, Cao, J, Lu, J: Stochastic synchronization of complex networks with nonidentical nodes via hybrid adaptive and impulsive control. IEEE Trans. Circuits Syst. I, Regul. Pap. 59(2), 371-384 (2012)
Porfiri, M, Di Bernardo, M: Criteria for global pinning-controllability of complex networks. Automatica 44(12), 3100-3106 (2008)
Song, Q, Liu, F, Cao, J, Yu, W: Pinning-controllability analysis of complex networks: an m-matrix approach. IEEE Trans. Circuits Syst. I, Regul. Pap. 59(11), 2692-2701 (2012)
Huang, T, Li, C, Liu, X: Synchronization of chaotic systems with delay using intermittent linear state feedback. Chaos 18(3), 033122 (2008)
Yang, X, Cao, J: Stochastic synchronization of coupled neural networks with intermittent control. Phys. Lett. A 373(36), 3259-3272 (2009)
Zhang, G, Shen, Y: Exponential stabilization of memristor-based chaotic neural networks with time-varying delays via intermittent control. IEEE Trans. Neural Netw. Learn. Syst. 26(7), 1431-1441 (2015)
Yang, S, Li, C, Huang, T: Exponential stabilization and synchronization for fuzzy model of memristive neural networks by periodically intermittent control. Neural Netw. 75, 162-172 (2016)
Xia, W, Cao, J: Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos 19(1), 013120 (2009)
Liu, X, Chen, T: Synchronization of nonlinear coupled networks via aperiodically intermittent pinning control. IEEE Trans. Neural Netw. Learn. Syst. 26(1), 113-126 (2015)
Wen, G, Yu, W, Hu, G, Cao, J, Yu, X: Pinning synchronization of directed networks with switching topologies: a multiple Lyapunov functions approach. IEEE Trans. Neural Netw. Learn. Syst. 26(12), 3239-3250 (2015)
Ren, W, Beard, RW: Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 50(5), 655-661 (2005)
Berman, A, Plemmons, RJ: Nonnegative Matrices in the Mathematical Sciences. SIAM, Philadelphia (1994)
Lu, W, Chen, T: New approach to synchronization analysis of linearly coupled ordinary differential systems. Physica D 213(2), 214-230 (2006)
Tarjan, R: Depth-first search and linear graph algorithms. SIAM J. Comput. 1(2), 146-160 (1972)
Bernstein, DS: Matrix Mathematics: Theory, Facts, and Formulas. Princeton University Press, Princeton (2009)
Zhang, J, Johansson, KH, Lygeros, J, Sastry, S: Zeno hybrid systems. Int. J. Robust Nonlinear Control 11(5), 435-451 (2001)
Lin, P, Jia, Y: Consensus of a class of second-order multi-agent systems with time-delay and jointly-connected topologies. IEEE Trans. Autom. Control 55(3), 778-784 (2010)
Liu, X, Chen, T: Cluster synchronization in directed networks via intermittent pinning control IEEE Trans. Neural Netw. 22(7), 1009-1020 (2011)
Liu, X, Chen, T: Synchronization of complex networks via aperiodically intermittent pinning control. IEEE Trans. Autom. Control 60(12), 3316-3321 (2015)
Wu, W, Chen, T: Global synchronization criteria of linearly coupled neural network systems with time-varying coupling IEEE Trans. Neural Netw. 19(2), 319-332 (2008)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (11501391, 11601449) and supported by Key Program of Sichuan Provincial Department of Education (16ZA0066).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Jie Gao and Jinde Cao contributed equally to this work.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gao, J., Cao, J. Aperiodically intermittent synchronization for switching complex networks dependent on topology structure. Adv Differ Equ 2017, 244 (2017). https://doi.org/10.1186/s13662-017-1261-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1261-8