1 Introduction

Generally speaking, it is not an easy task to seek the fundamental matrix for linear differential delay systems due to the memory accumulated by the long-tail effects that the time-delay term introduces. In the theory of linear systems, it is necessary to find an explicit form of the desired fundamental matrix for the stability analysis. In fact, some easily used criteria for the stability results involve the fundamental matrix. In the past decade, there has been a rapid development on the representation of solutions, which lead to results on asymptotic stability, finite time stability and control problems for linear/nonlinear continuous delay systems and discrete delay systems or fractional order delay systems. For more results on matrix representation of the solution to a delay differential and discrete systems and their stability analysis and control problems, one can refer to [1–21] and the references therein.

The concept of finite time stability of delay differential equations arises from the fields of multibody mechanics, automatic engines and physiological systems as introduced by Dorato [22], which characterizes the system state by not exceeding a certain bounded for a given finite time interval and this seems more appropriate from practical considerations. Concerning the finite time stability, Ulam’s stability and stable manifolds of linear systems, impulsive systems and fractional systems, the methods of fundamental matrix, linear matrix inequality, algebraic inequality and integral inequality are often used to deal with this issue. For more recent contributions, one can see [23–37].

After reviewing, the criteria for linear delay differential systems are established by characterizing the eigenpolynomial distribution in the previous literature; it is not difficult to see that the procedure of the proof is complicated and the threshold for the desired delay systems is not easy to determine in practical problems. Thus it will be better to analyze the stability of delay differentia systems by using the representation of the solutions directly.

In this paper, we study the finite time stability of the following second order linear differential equations with a pure delay term:

$$\begin{aligned} \textstyle\begin{cases} \ddot{x}(t)+\Omega^{2}x(t-\tau)=0, & \tau>0,t\in J:=[0,T],\\ x(t)\equiv\varphi(t), \dot{x}(t)\equiv\dot{\varphi}(t), & -\tau\leq t\leq0, \end{cases}\displaystyle \end{aligned}$$
(1)

where \(x\in \mathbb {R}^{n}\), τ is the time delay, φ is an arbitrary twice continuously differentiable vector function, T is a pre-fixed positive number and Ω is a \(n\times n\) nonsingular matrix.

Recently, Khusainov et al. [2] gave a new representation of the solution for (1) as follows:

$$\begin{aligned} & x(t)=\cos_{\tau}\Omega t\varphi(-\tau)+ \Omega^{-1}\sin_{\tau}\Omega t\dot{\varphi}(-\tau)+ \Omega^{-1} \int^{0}_{-\tau}\sin_{\tau}\Omega (t-\tau-s) \ddot{\varphi}(s)\,ds, \end{aligned}$$
(2)

where \(\cos_{\tau}\Omega t\) is called the delayed matrix cosine of polynomial degree 2k (see [2], Definition 1) on the intervals \((k-1)\tau\leq t< k\tau\) formulated by

$$\begin{aligned} \cos_{\tau}\Omega t=\textstyle\begin{cases} \Theta, & -\infty< t< -\tau,\\ I, & -\tau \leq t< 0,\\ I-\Omega^{2}\frac{t^{2}}{2!}, & 0\leq t< \tau,\\ \vdots & \vdots \\ I-\Omega^{2}\frac{t^{2}}{2!}+\Omega^{4}\frac{(t-\tau)^{4}}{4!}+\cdots +(-1)^{k}\Omega^{2k}\frac{[t-(k-1)\tau]^{2k}}{(2k)!}, & (k-1)\tau\leq t< k\tau, \end{cases}\displaystyle \end{aligned}$$
(3)

and \(\sin_{\tau}\Omega t\) is called a delayed matrix sine of polynomial degree \(2k+1\) (see [2], Definition 2) on the intervals \((k-1)\tau\leq t< k\tau\) formulated by

$$\begin{aligned}& \sin_{\tau}\Omega t= \textstyle\begin{cases} \Theta, & -\infty < t< -\tau,\\ \Omega(t+\tau ), & -\tau\leq t< 0,\\ \Omega(t+\tau)-\Omega^{3}\frac{t^{3}}{3!},& 0\leq t< \tau,\\ \vdots & \vdots \\ \Omega(t+\tau)-\Omega^{3}\frac{t^{3}}{3!}+\cdots+(-1)^{k}\Omega ^{2k+1}\frac{[t-(k-1)\tau]^{2k+1}}{(2k+1)!}, & (k-1)\tau\leq t< k\tau, \end{cases}\displaystyle \end{aligned}$$
(4)

respectively, and Θ and I are the zero and identity matrices. Delayed matrix cosine and sine of polynomial degrees play an important role in studying second order delay differential equations since they can act as the fundamental matrix to seeking some possible representation of solutions to the problem by using a variation of constants formula. For more properties of a delayed matrix cosine and sine of polynomial degrees, one can see [2], Lemmas 1-6.

Obviously, when \(\tau=0\), \(\cos_{\tau}\Omega t\) and \(\sin_{\tau}\Omega t\) reduce to the matrix cosine function \(\cos\Omega t\) and matrix sine function \(\sin\Omega t\), respectively, which are given by the formal matrix series

$$\cos\Omega t=1-\Omega^{2}\frac{t^{2}}{2!}+\cdots+(-1)^{k} \Omega^{2k}\frac {t^{2k}}{(2k)!}+\cdots $$

and

$$\sin\Omega t=\Omega\frac{t}{1!}-\Omega^{3}\frac{t^{3}}{3!}+ \cdots +(-1)^{k}\Omega^{2k+1}\frac{t^{2k+1}}{(2k+1)!}+\cdots. $$

By Gantmakher [38], p.123,

$$x(t)=x_{0}\cos\Omega t+\Omega^{-1}\dot{x}_{0}\sin \Omega t,\quad\mbox{provided } \Omega^{-1} \mbox{ exists,} $$

is a solution of a second order differential system \(\ddot{x}(t)+\Omega^{2}x(t)=0, t\geq0, x(0)=x_{0}\in \mathbb {R}^{n}, \dot {x}(0)=\dot{x}_{0}\in \mathbb {R}^{n}\).

Motivated by [2], we prefer to adopt the method of the delayed matrix cosine and sine of polynomial degree to study the stability of the second order delay differential system (1). Compared with the method of the eigenpolynomial distribution, we do not need to solve an equation of the fourth degree. We give stability criteria by establishing the desired inequalities via using the norm estimation of the delayed matrix cosine and sine of polynomial degree.

The rest of this paper is organized as follows. In Section 2, we give two other possible formulas of solutions for the current systems by adopting the methods of integration by parts. Two very important lemmas, which present the estimation of the delayed matrix sine and cosine of polynomial degrees, is given. In Section 3, we present three sufficient conditions to guarantee the finite time stability results. In Section 4, an example is given to demonstrate the applicability of our main results for the linear case. In the final section, we extend the study of the finite time stability of the delay differential equation with nonlinearity by using a Gronwall inequality under a linear growth condition.

2 Preliminaries

Denote by \(C(J, \mathbb{R}^{n})\) the metric space of vector-value continuous functions from \(J\rightarrow\mathbb{R}^{n}\) endowed with the norm \(\|x\| =\sum^{n}_{i=1}|x_{i}(t)|\), and consider its \(\|x\|_{C}=\max_{t\in J}\| x(t)\|\). We introduce a space \(C^{1}(J, \mathbb {R}^{n})=\{x\in C(J, \mathbb {R}^{n}): \dot{x}\in C(J, \mathbb {R}^{n}) \}\). For \(A: \mathbb {R}^{n}\to \mathbb {R}^{n}\), we consider its matrix norm \(\|A\|=\max_{\|z\|=1}\|Az\|\) generated by \(\|\cdot\|\). In addition, we note \(\|\varphi\|_{C}=\max_{s\in[-\tau, 0]}\|\varphi(s)\|\).

We need the following rules of differentiation for the delayed matrix cosine of polynomial degree 2k on the interval \([(k-1)\tau,k\tau)\) and sine of polynomial degree \(2k+1\) on the interval \([(k-1)\tau,k\tau)\) defined in (3) and (4), respectively.

Lemma 2.1

see [2], Lemmas 1 and 2

The following rules of differentiation are true for the matrix functions (3) and (4):

$$\begin{aligned}& \frac{d}{dt}\cos_{\tau}\Omega t=-\Omega\sin_{\tau} \Omega(t-\tau),\qquad \frac{d}{dt}\sin_{\tau}\Omega t=\Omega \cos_{\tau}\Omega t. \end{aligned}$$

Remark 2.2

For simplification of the next computation, one can divide the term \(\int^{0}_{-\tau}\sin_{\tau}\Omega(t-\tau-s)\ddot{\varphi}(s)\,ds\) in (2) into the following form according to the subintervals \([(k-1)\tau,k\tau)\):

$$\begin{aligned}& \int^{0}_{-\tau}\sin_{\tau}\Omega(t-\tau-s) \ddot{\varphi}(s)\,ds \\& \quad= \int^{t-k\tau}_{-\tau}\sin_{\tau}\Omega(t-\tau-s) \ddot{\varphi }(s)\,ds+ \int^{0}_{t-k\tau}\sin_{\tau}\Omega(t-\tau-s) \ddot{\varphi}(s)\,ds. \end{aligned}$$

Obviously, \(\sin_{\tau}\Omega(t-\tau-s)\) has different formulas in different subintervals \([(k-1)\tau,k\tau)\) by (4).

By Remark 2.2, the solution (2) of system (1) can be expressed in the following form:

$$\begin{aligned} x(t) =&\cos_{\tau}\Omega t\varphi(-\tau)+ \Omega^{-1}\sin_{\tau}\Omega t\dot{\varphi}(-\tau)+ \Omega^{-1} \int^{t-k\tau}_{-\tau}\sin_{\tau }\Omega(t-\tau-s) \ddot{\varphi}(s)\,ds \\ &{}+\Omega^{-1} \int^{0}_{t-k\tau}\sin_{\tau}\Omega(t-\tau-s)\ddot {\varphi}(s)\,ds \end{aligned}$$
(5)

for \((k-1)\tau\leq t\leq k\tau\).

Observing the solution (2) involves φ̈, which seems a requirement that is a bit stronger to the initial conditions.

Remark 2.3

In order to obtain some alternative formulas, one can apply integration by parts via Lemma 2.1 to derive that

$$\begin{aligned}& \int^{0}_{-\tau}\sin_{\tau}\Omega(t-\tau-s) \ddot{\varphi }(s)\,ds \\& \quad=\sin_{\tau}\Omega(t-\tau)\dot{\varphi}(0)-\sin_{\tau} \Omega t\dot {\varphi}(-\tau)+\Omega \int^{0}_{-\tau}\cos_{\tau}\Omega(t-\tau-s)\dot {\varphi}(s)\,ds, \end{aligned}$$

then the solution (2) can be expressed as

$$\begin{aligned}& x(t)=\cos_{\tau}\Omega t\varphi(-\tau)+ \Omega^{-1}\sin_{\tau}\Omega (t-\tau)\dot{\varphi}(0)+ \int^{0}_{-\tau}\cos_{\tau}\Omega(t-\tau -s) \dot{\varphi}(s)\,ds. \end{aligned}$$
(6)

If we take integration by parts again for the integral part of (6), then we have

$$\begin{aligned}& \int^{0}_{-\tau}\cos_{\tau}\Omega(t-\tau-s)\dot{ \varphi }(s)\,ds \\& \quad=\cos_{\tau}\Omega(t-\tau)\varphi(0)-\cos_{\tau}\Omega t \varphi(-\tau )-\Omega \int^{0}_{-\tau}\sin_{\tau}\Omega(t-2\tau-s) \varphi(s)\,ds, \end{aligned}$$

which implies that (6) can be expressed as

$$\begin{aligned}& x(t)=\cos_{\tau}\Omega(t-\tau)\varphi(0)+ \Omega^{-1}\sin_{\tau}\Omega (t-\tau)\dot{\varphi}(0)-\Omega \int^{0}_{-\tau}\sin_{\tau}\Omega (t-2\tau-s) \varphi(s)\,ds. \end{aligned}$$
(7)

Definition 2.4

see [24], Definitions 2.1

The system (1) satisfying the initial conditions \(x(t)\equiv \varphi(t)\) and \(\dot{x}(t)\equiv\dot{\varphi}(t)\) for \(-\tau\leq t\leq 0\) is finite time stable with respect to \(\{0,J,\delta,\epsilon,\tau\} \), if and only if

$$\begin{aligned}& \gamma< \delta \end{aligned}$$
(8)

implies

$$\bigl\Vert x(t) \bigr\Vert < \epsilon, \quad\forall t\in J, $$

where \(\gamma=\max\{\|\varphi\|_{C},\|\dot{\varphi}\|_{C},\|\ddot {\varphi}\|_{C}\}\) denotes the initial time of observation of the system. In addition, δ, ϵ are real positive numbers.

Using the form of \(\cos_{\tau}\Omega t\) and \(\sin_{\tau}\Omega t\) one can prove the following two lemmas, which will be widely used in the sequel.

Lemma 2.5

For any \(t\in[(k-1)\tau,k\tau)\), \(k=0,1,\ldots,n\), the following formula is true:

$$\begin{aligned}& \Vert \cos_{\tau}\Omega t \Vert \leq\cosh\bigl( \Vert \Omega \Vert t\bigr). \end{aligned}$$

Proof

Using the form of (3), one can calculate that

$$\begin{aligned} \Vert \cos_{\tau}\Omega t \Vert \leq&1+ \Vert \Omega \Vert ^{2}\frac{t^{2}}{2!}+ \Vert \Omega \Vert ^{4} \frac{(t-\tau)^{4}}{4!}+\cdots+ \Vert \Omega \Vert ^{2k} \frac{[t-(k-1)\tau ]^{2k}}{(2k)!} \\ \leq& 1+ \Vert \Omega \Vert ^{2}\frac{t^{2}}{2!}+ \Vert \Omega \Vert ^{4}\frac {t^{4}}{4!}+\cdots+ \Vert \Omega \Vert ^{2k}\frac{t^{2k}}{(2k)!} \\ \leq& \sum_{k=0}^{\infty}\frac{( \Vert \Omega \Vert t)^{2k}}{(2k)!}= \cosh\bigl( \Vert \Omega \Vert t\bigr). \end{aligned}$$

The proof is completed. □

Lemma 2.6

For any \(t\in[(k-1)\tau,k\tau)\), \(k=0,1,\ldots,n\), the following formula is true:

$$\begin{aligned}& \Vert \sin_{\tau}\Omega t \Vert \leq\sinh\bigl[ \Vert \Omega \Vert (t+\tau)\bigr]. \end{aligned}$$

Proof

Using the form of (4), we get

$$\begin{aligned} \Vert \sin_{\tau}\Omega t \Vert \leq& \Vert \Omega \Vert (t+ \tau)+ \Vert \Omega \Vert ^{3}\frac {t^{3}}{3!}+\cdots+ \Vert \Omega \Vert ^{2k+1}\frac{[t-(k-1)\tau ]^{2k+1}}{(2k+1)!} \\ \leq& \Vert \Omega \Vert (t+\tau)+ \Vert \Omega \Vert ^{3} \frac{(t+\tau)^{3}}{3!}+\cdots+ \Vert \Omega \Vert ^{2k+1} \frac{(t+\tau)^{2k+1}}{(2k+1)!} \\ \leq&\sum_{k=0}^{\infty}\frac{[ \Vert \Omega \Vert (t+\tau )]^{2k+1}}{(2k+1)!}= \sinh\bigl[ \Vert \Omega \Vert (t+\tau)\bigr]. \end{aligned}$$

The proof is finished. □

Remark 2.7

When \(t\in(-\infty,-\tau)\), we can get \(\|\cos_{\tau }\Omega t\|=\|\sin_{\tau}\Omega t\|=0\) by the form (3) and (4).

As is well known, the exponential form of hyperbolic functions cosht and sinht are defined as follows:

$$\cosh t=\frac{e^{t}+e^{-t}}{2},\qquad \sinh t=\frac{e^{t}-e^{-t}}{2},\quad t\in \mathbb{R}. $$

Then, for all \(t\in\mathbb{R}\), we have the fact that \(\sinh t\leq\cosh t\) holds and the larger the value of t, the closer cosht and sinht. When \(t\rightarrow+\infty\), we get \(\cosh t=\sinh t\). In addition, both cosht and sinht are nonnegative, monotone increasing functions for \(t\geq0\).

Obviously, the derivatives of \(\cosh(\cdot)\) and \(\sinh(\cdot)\) are

$$\begin{aligned}& \frac{d}{dt}\cosh t=\sinh t,\qquad \frac{d}{dt}\sinh t=\cosh t. \end{aligned}$$
(9)

Next, we give an example to verify the results of Lemmas 2.5 and 2.6 and also show the images of a delayed cosine function and delayed sine function.

Example 2.8

Set \(\tau=0.4\), \(\Omega=2\), \(\Omega\in \mathbb {R}^{1}\). By (3) and (4) we derive that \(\cos_{0.4}2t\) and \(\sin_{0.4}2t\) are as follows:

$$ \cos_{0.4}2t= \textstyle\begin{cases} 1, & t\in[-0.4,0),\\ 1-2^{2}\frac{t^{2}}{2}, & t\in[0,0.4),\\ 1-2^{2}\frac{t^{2}}{2}+2^{4}\frac{(t-0.4)^{4}}{4!}, & t\in[0.4,0.8),\\ 1-2^{2}\frac{t^{2}}{2}+2^{4}\frac{(t-0.4)^{4}}{4!}-2^{6}\frac {(t-0.8)^{6}}{6!}, & t\in[0.8,1.2],\\ \vdots \end{cases} $$
(10)

and

$$ \sin_{0.4}2t=\textstyle\begin{cases} 2(t+0.4), & t\in[-0.4,0),\\ 2(t+0.4)-2^{3}\frac{t^{3}}{3!}, & t\in[0,0.4),\\ 2(t+0.4)-2^{3}\frac{t^{3}}{3!}+2^{5}\frac{(t-0.4)^{5}}{5!}, & t\in [0.4,0.8),\\ 2(t+0.4)-2^{3}\frac{t^{3}}{3!}+2^{5}\frac{(t-0.4)^{5}}{5!}-2^{7}\frac {(t-0.8)^{7}}{7!}, & t\in[0.8,1.2],\\ \vdots \end{cases} $$
(11)

It follows from Figure 1 and Figure 2 that the inequalities in Lemma 2.5 and Lemma 2.6 hold.

Figure 1
figure 1

\(\pmb{\|\cos_{0.4}2t\|}\) and \(\pmb{\cosh(2t)}\) .

Full size image
Figure 2
figure 2

\(\pmb{\|\sin_{0.4}2t\|}\) and \(\pmb{\sinh[2(t+0.4)]}\) .

Full size image

The images of delayed cosine \(\cos_{0.4}2t\) and delayed sine \(\sin_{0.4}2t\) are shown in Figure 3 and Figure 4, respectively. Obviously, we can see that the delayed cosine and delayed sine do have some similar properties of the classical cosine and sine functions such as a wave line, monotonicity and periodicity.

Figure 3
figure 3

The delayed cosine function \(\pmb{\cos_{0.4}2t}\) .

Full size image
Figure 4
figure 4

The delayed sine function \(\pmb{\sin_{0.4}2t}\) .

Full size image

However, the differences between delayed cosine and delayed sine and cosine and sine are that the delayed cosine and delayed sine appear in the interval segment \([-\tau,0]\) and with the increasing of variables t, the upper and lower bounds of delayed cosine and delayed sine are also increasing. When the delay \(\tau=0\), by (3) and (4), the delayed cosine and delayed sine coincide with the cosine and sine functions.

3 Finite time stability results for linear case

In this section, we present some sufficient conditions for finite time stability results for the desired system (1) by using three possible formulas of solutions, which do enrich the design methods in the practical problem.

Now we are ready to present the first theorem by using the classical representation of solution (2) derived by Khusainov et al. [2].

Theorem 3.1

The system (1) is finite time stable with respect to \(\{ 0,J,\delta,\epsilon,\tau\}\), if

$$ \cosh\bigl( \Vert \Omega \Vert T\bigr)< \frac{\epsilon-\delta(1+\tau) \Vert \Omega ^{-1} \Vert \sinh[ \Vert \Omega \Vert (T+\tau)]}{\delta}, $$
(12)

where δ and ϵ are defined in Definition 2.4.

Proof

By using equation (2) via some fundamental computations, one can get

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert =& \biggl\Vert \cos_{\tau}\Omega t\varphi(-\tau)+\Omega^{-1}\sin _{\tau} \Omega t\dot{\varphi}(-\tau)+\Omega^{-1} \int^{0}_{-\tau}\sin _{\tau}\Omega(t-\tau-s) \ddot{\varphi}(s)\,ds \biggr\Vert \\ \leq& \Vert \cos_{\tau}\Omega t \Vert \bigl\Vert \varphi(-\tau) \bigr\Vert + \bigl\Vert \Omega^{-1} \bigr\Vert \Vert \sin _{\tau}\Omega t \Vert \bigl\Vert \dot{\varphi}(-\tau) \bigr\Vert \\ &{}+ \biggl\Vert \Omega^{-1} \int^{0}_{-\tau}\sin_{\tau}\Omega(t-\tau-s)\ddot {\varphi}(s)\,ds \biggr\Vert \\ \leq& \Vert \cos_{\tau}\Omega t \Vert \bigl\Vert \varphi(-\tau) \bigr\Vert + \bigl\Vert \Omega^{-1} \bigr\Vert \Vert \sin _{\tau}\Omega t \Vert \bigl\Vert \dot{\varphi}(-\tau) \bigr\Vert \\ &{}+ \bigl\Vert \Omega^{-1} \bigr\Vert \int^{0}_{-\tau} \bigl\Vert \sin_{\tau} \Omega(t-\tau-s) \bigr\Vert \bigl\Vert \ddot{\varphi}(s) \bigr\Vert \,ds. \end{aligned}$$
(13)

From (8) and (13), we have

$$\begin{aligned}& \bigl\Vert x(t) \bigr\Vert \leq\delta \Vert \cos_{\tau}\Omega t \Vert +\delta \bigl\Vert \Omega^{-1} \bigr\Vert \Vert \sin _{\tau}\Omega t \Vert +\delta \bigl\Vert \Omega^{-1} \bigr\Vert \int^{0}_{-\tau} \bigl\Vert {{\sin_{\tau} \Omega(t-\tau-s)}} \bigr\Vert \,ds. \end{aligned}$$

Next, according to Lemmas 2.5 and 2.6, we obtain

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq\delta\cosh\bigl( \Vert \Omega \Vert t\bigr)+\delta \bigl\Vert \Omega^{-1} \bigr\Vert \sinh \bigl[ \Vert \Omega \Vert (t+\tau)\bigr]+\delta\tau \bigl\Vert \Omega^{-1} \bigr\Vert {{\sinh\bigl[ \Vert \Omega \Vert (t+\tau) \bigr]}}, \end{aligned}$$
(14)

where we use the fact

$$\begin{aligned} & \bigl\Vert \sin_{\tau}\Omega(t-\tau-s) \bigr\Vert \leq\sinh \bigl[ \Vert \Omega \Vert (t-s) \bigr]\leq\sinh\bigl[ \Vert \Omega \Vert (t+\tau)\bigr],\quad -\tau\leq s\leq0, t\in J. \end{aligned}$$
(15)

Since sinht and cosht are both monotonically increasing functions when \(t\geq0\), \(\|x(t)\|<\epsilon\) for \(\forall t\in J\) can be obtained by combining (12) and (14).

Thus, the system (1) is finite time stable by Definition 2.4. □

Next, we use a new alternative representation of solution (6) to derive the following result.

Theorem 3.2

The system (1) is finite time stable with respect to \(\{ 0,J,\delta,\epsilon,\tau\}\), if

$$\begin{aligned} & \cosh\bigl( \Vert \Omega \Vert T\bigr)< \frac{\epsilon-\delta \Vert \Omega^{-1} \Vert \sinh( \Vert \Omega \Vert T)-\delta\tau{{\lambda}}}{\delta}, \end{aligned}$$
(16)

where \(\lambda:=\max\{\cosh(\|\Omega\|\tau), \cosh(\| \Omega\|T)\}\).

Proof

Similar to Theorem 3.1, we estimate the norm \(\|\cdot\|\) of the solution formula (6),

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq& \Vert \cos_{\tau} \Omega t \Vert \bigl\Vert \varphi(-\tau) \bigr\Vert + \bigl\Vert \Omega^{-1} \bigr\Vert \bigl\Vert \sin_{\tau}\Omega(t-\tau) \bigr\Vert \bigl\Vert \dot{\varphi}(0) \bigr\Vert \\ &{}+ \biggl\Vert \int^{0}_{-\tau}\cos_{\tau}\Omega(t-\tau-s)\dot{ \varphi }(s)\,ds \biggr\Vert \\ \leq& \Vert \cos_{\tau}\Omega t \Vert \bigl\Vert \varphi(-\tau) \bigr\Vert + \bigl\Vert \Omega^{-1} \bigr\Vert \bigl\Vert \sin _{\tau}\Omega(t-\tau) \bigr\Vert \bigl\Vert \dot{\varphi}(0) \bigr\Vert \\ &{}+ \int^{0}_{-\tau} \bigl\Vert \cos_{\tau} \Omega(t-\tau-s) \bigr\Vert \bigl\Vert \dot{\varphi}(s) \bigr\Vert \,ds. \end{aligned}$$
(17)

By (8), the inequality (17) implies

$$\begin{aligned} & \bigl\Vert x(t) \bigr\Vert \leq\delta \Vert \cos_{\tau}\Omega t \Vert +\delta \bigl\Vert \Omega^{-1} \bigr\Vert \bigl\Vert \sin _{\tau}\Omega(t-\tau) \bigr\Vert +\delta \int^{0}_{-\tau} \bigl\Vert \cos_{\tau}\Omega (t-\tau-s) \bigr\Vert \,ds. \end{aligned}$$

Then, according to Lemmas 2.5 and 2.6, one can get

$$\begin{aligned} & \bigl\Vert x(t) \bigr\Vert \leq\delta\cosh\bigl( \Vert \Omega \Vert t\bigr)+\delta \bigl\Vert \Omega^{-1} \bigr\Vert \sinh \bigl( \Vert \Omega \Vert t\bigr)+\delta\tau{{\lambda}}, \end{aligned}$$
(18)

where we use the fact

$$\begin{aligned} & \bigl\Vert \cos_{\tau}\Omega(t-\tau-s) \bigr\Vert \leq\cosh \bigl[ \Vert \Omega \Vert (t-\tau -s) \bigr]\leq\lambda, \quad-\tau\leq s \leq0, t\in J. \end{aligned}$$

Linking (16) and (18), we obtain \(\|x(t)\|<\epsilon , \forall t\in J\). Thus, the system (1) is finite time stable. □

Finally, we adopt another representation of solution (7) to derive another new result.

Theorem 3.3

The system (1) is finite time stable with respect to \(\{ 0,J,\delta,\epsilon,\tau\}\), if

$$\begin{aligned} \theta< \frac{\epsilon-\delta( \Vert \Omega^{-1} \Vert +\tau \Vert \Omega \Vert )\sinh( \Vert \Omega \Vert T)}{\delta}, \end{aligned}$$
(19)

where \(\theta:=\max\{\cosh( \Vert \Omega \Vert \tau), \cosh( \Vert \Omega \Vert T-\tau)\}\).

Proof

By Lemmas 2.5, 2.6 and taking the norm on both sides of (7) via (8), we have

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq& \bigl\Vert \cos_{\tau}\Omega(t-\tau) \bigr\Vert \bigl\Vert \varphi(0) \bigr\Vert + \bigl\Vert \Omega ^{-1} \bigr\Vert \bigl\Vert \sin_{\tau}\Omega(t-\tau) \bigr\Vert \bigl\Vert \dot{\varphi}(0) \bigr\Vert \\ &{}+ \| \Omega\| \biggl\Vert \int^{0}_{-\tau}\sin_{\tau}\Omega(t-2\tau-s) \varphi (s)\,ds \biggr\Vert \\ \leq& \bigl\Vert \cos_{\tau}\Omega(t-\tau) \bigr\Vert \bigl\Vert \varphi(0) \bigr\Vert + \bigl\Vert \Omega^{-1} \bigr\Vert \bigl\Vert \sin _{\tau}\Omega(t-\tau) \bigr\Vert \bigl\Vert \dot{ \varphi}(0) \bigr\Vert \\ &{}+ \Vert \Omega \Vert \bigl\Vert \varphi(s) \bigr\Vert \int^{0}_{-\tau} \bigl\Vert \sin_{\tau} \Omega(t-2\tau -s) \bigr\Vert \,ds. \end{aligned}$$
(20)

Note that \(\sin_{\tau}\Omega t=\Theta\) if \(t\in(-\infty ,-\tau)\). For \(-\tau\leq s\leq0\), we get \(\|\sin_{\tau}\Omega(t-2\tau -s)\|=0\) when \(t-2\tau-s<-\tau\), by Lemma 2.6, we get \(\|\sin _{\tau}\Omega(t-2\tau-s)\|\leq\sinh[\|\Omega\|(t-\tau-s)]\leq\sinh(\| \Omega\|t)\) when \(t-2\tau-s\geq-\tau\). In the end, we can obtain

$$\begin{aligned} & \bigl\Vert \sin_{\tau}\Omega(t-2\tau-s) \bigr\Vert \leq\sinh\bigl( \Vert \Omega \Vert t\bigr),\quad -\tau\leq s\leq 0, t\in J. \end{aligned}$$
(21)

From (8), (20), (21), Lemmas 2.5 and 2.6, we can get

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq&\delta\cosh\bigl[ \Vert \Omega \Vert (t-\tau)\bigr]+\delta \bigl\Vert \Omega^{-1} \bigr\Vert \sinh \bigl( \Vert \Omega \Vert t\bigr)+\delta\tau \Vert \Omega \Vert \sinh\bigl( \Vert \Omega \Vert t\bigr) \\ \leq&\delta\theta+\delta\bigl( \bigl\Vert \Omega^{-1} \bigr\Vert + \tau \Vert \Omega \Vert \bigr)\sinh\bigl( \Vert \Omega \Vert t\bigr). \end{aligned}$$
(22)

Substituting (19) into (22), we can finally obtain \(\Vert x(t) \Vert <\epsilon, \forall t\in J\). Thus, the system (1) is finite time stable. □

Remark 3.4

By the results in Theorems 3.1-3.3, we can analyze that when \(\alpha<\beta\) and \(\alpha<\rho\), the result of Theorem 3.1 is the optimal. When \(\beta<\alpha\) and \(\beta<\rho\), the result of Theorem 3.2 is the optimal. When \(\rho<\alpha\) and \(\rho<\beta\), the result of Theorem 3.3 is the optimal. And

$$\begin{aligned} \alpha :=&\delta\cosh\bigl( \Vert \Omega \Vert T\bigr)+\delta \bigl\Vert \Omega^{-1} \bigr\Vert \sinh\bigl[ \Vert \Omega \Vert (T+\tau) \bigr]+\delta\tau \bigl\Vert \Omega^{-1} \bigr\Vert \sinh\bigl[ \Vert \Omega \Vert (T+\tau)\bigr], \\ \beta :=&\delta\cosh\bigl( \Vert \Omega \Vert T\bigr)+\delta \bigl\Vert \Omega^{-1} \bigr\Vert \sinh\bigl( \Vert \Omega \Vert T\bigr)+ \delta\tau\lambda, \\ \rho :=&\delta\theta+\delta\bigl( \bigl\Vert \Omega^{-1} \bigr\Vert +\tau \Vert \Omega \Vert \bigr)\sinh\bigl( \Vert \Omega \Vert T \bigr). \end{aligned}$$

Remark 3.5

We have studied the finite time stability of system (1) in Theorems 3.1-3.3. Now we analyze the stability of solution (2) to system (1) when \(t\rightarrow\infty\). In fact,

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq & \Vert \cos_{\tau}\Omega t \Vert \bigl\Vert \varphi(-\tau) \bigr\Vert \\ &{}+ \bigl\Vert \Omega^{-1} \bigr\Vert \bigl\Vert \sin_{\tau}\Omega t\dot{\varphi}(-\tau) \bigr\Vert + \bigl\Vert \Omega^{-1} \bigr\Vert \int^{0}_{-\tau } \bigl\Vert \sin_{\tau} \Omega(t-\tau-s)\ddot{\varphi}(s) \bigr\Vert \,ds, \end{aligned}$$

which implies that it is impossible to guarantee that \(\Vert x(t) \Vert \rightarrow0\) when \(t\rightarrow\infty\) since the first term \(\Vert \cos _{\tau}\Omega t \Vert \Vert \varphi(-\tau) \Vert \leq\cosh( \Vert \Omega \Vert t) \Vert \varphi (-\tau) \Vert =\frac{e^{ \Vert \Omega \Vert t}+e^{- \Vert \Omega \Vert t}}{2} \Vert \varphi(-\tau) \Vert \rightarrow\infty\) when \(t\rightarrow\infty\) even we put the strong condition on \(\Vert \Omega^{-1} \Vert \leq e^{-\nu(t+\tau)},\nu> \Vert \Omega \Vert \), to guarantee the second and third terms tend to zero due to \(\Vert \sin _{\tau}\Omega t \Vert \leq\sinh[ \Vert \Omega \Vert (t+\tau)]\leq e^{ \Vert \Omega \Vert (t+\tau)}\).

In the next section, we give an example of the stability of system (1) to verify Theorems 3.1-3.3.

4 A numerical example

Example 4.1

In this part, we consider the finite time stability of the following second order differential equations:

$$\begin{aligned} & \textstyle\begin{cases} \ddot{x}(t)+\Omega^{2}x(t-0.5)=0,& x\in \mathbb {R}^{2}, t\in J:=[0,1],\\ \varphi(t)=(0.1t^{2},0.2t)^{\mathrm{T}}, \dot{\varphi }(t)=(0.2t,0.2)^{\mathrm{T}}, \ddot{\varphi}(t)=(0.2,0)^{\mathrm{T}}, & -0.5\leq t\leq0, \end{cases}\displaystyle \end{aligned}$$
(23)

where \(\tau=0.5\), \(T=1\), \(n=2\),

$$\begin{aligned} & \Omega= \begin{pmatrix} 2 & 0\\ 1 & 2 \end{pmatrix},\qquad \Omega^{-1}= \begin{pmatrix} 0.5 & 0\\ -0.25 & 0.5 \end{pmatrix}. \end{aligned}$$

By (5), we get the solution of system (23) as follows:

$$\begin{aligned} x(t) =&\cos_{0.5}\Omega t\varphi(-0.5)+ \Omega^{-1}\sin_{0.5}\Omega t\dot {\varphi}(-0.5) \\ &{}+\Omega^{-1} \int^{t-0.5}_{-0.5}\sin_{0.5}\Omega(t-0.5-s) \ddot{\varphi }(s)\,ds \\ &{}+\Omega^{-1} \int^{0}_{t-0.5}\sin_{0.5}\Omega(t-0.5-s)\ddot{ \varphi}(s)\,ds, \end{aligned}$$
(24)

where \(0\leq t\leq0.5 \) and

$$\begin{aligned} x(t) =&\cos_{0.5}\Omega t\varphi(-0.5)+ \Omega^{-1}\sin_{0.5}\Omega t\dot {\varphi}(-0.5) \\ &{}+\Omega^{-1} \int^{t-1}_{-0.5}\sin_{0.5}\Omega(t-0.5-s) \ddot{\varphi }(s)\,ds \\ &{}+\Omega^{-1} \int^{0}_{t-1}\sin_{0.5}\Omega(t-0.5-s)\ddot{ \varphi}(s)\,ds, \end{aligned}$$
(25)

where \(0.5\leq t\leq1\).

Next, we get

$$\begin{aligned} \cos_{0.5}\Omega t= \begin{pmatrix} \cos_{0.5}2t & 0 \\ \cos_{0.5}t & \cos_{0.5}2t \end{pmatrix},\qquad \sin_{0.5}\Omega t= \begin{pmatrix} \sin_{0.5}2t & 0 \\ \sin_{0.5}t & \sin_{0.5}2t \end{pmatrix}, \end{aligned}$$

by (3) and (4), we obtain

$$\begin{aligned}& \cos_{0.5}t=\textstyle\begin{cases} 1, & t\in[-0.5,0),\\ 1-\frac{t^{2}}{2}, & t\in[0,0.5),\\ 1-\frac{t^{2}}{2}+\frac{(t-0.5)^{4}}{4!}, & t\in[0.5,1),\\ \vdots \end{cases}\displaystyle \\& \sin_{0.5}t= \textstyle\begin{cases} (t+0.5), & t\in[-0.5,0),\\ (t+0.5)-\frac{t^{3}}{3!}, & t\in[0,0.5),\\ (t+0.5)-\frac{t^{3}}{3!}+\frac{(t-0.5)^{5}}{5!}, & t\in[0.5,1),\\ \vdots \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned} \cos_{0.5}2t= \textstyle\begin{cases} 1, & t\in[-0.5,0),\\ 1-2^{2}\frac{t^{2}}{2}, & t\in[0,0.5),\\ 1-2^{2}\frac{t^{2}}{2}+2^{4}\frac{(t-0.5)^{4}}{4!}, & t\in[0.5,1),\\ \vdots \end{cases}\displaystyle \\ \sin_{0.5}2t= \textstyle\begin{cases} 2(t+0.5), & t\in[-0.5,0),\\ 2(t+0.5)-2^{3}\frac{t^{3}}{3!}, & t\in[0,0.5),\\ 2(t+0.5)-2^{3}\frac{t^{3}}{3!}+2^{5}\frac{(t-0.5)^{5}}{5!}, & t\in [0.5,1),\\ \vdots \end{cases}\displaystyle \end{aligned}$$

When \(0\leq t\leq0.5\), by (24) we get

$$\begin{aligned} x(t) =& \begin{pmatrix} \cos_{0.5}2t & 0 \\ \cos_{0.5}t & \cos_{0.5}2t \end{pmatrix} \begin{pmatrix} 0.025\\ -0.1 \end{pmatrix} \\ &{}+ \begin{pmatrix} 0.5 & 0\\ -0.25 & 0.5 \end{pmatrix} \begin{pmatrix} \sin_{0.5}2t & 0 \\ \sin_{0.5}t & \sin_{0.5}2t \end{pmatrix} \begin{pmatrix} -0.1\\ 0.2 \end{pmatrix} \\ &{}+ \begin{pmatrix} 0.5 & 0\\ -0.25 & 0.5 \end{pmatrix} \begin{pmatrix} \int^{t-0.5}_{-0.5}0.2\sin_{0.5}2(t-0.5-s)\,ds\\ \int^{t-0.5}_{-0.5}0.2\sin_{0.5}(t-0.5-s)\,ds \end{pmatrix} \\ &{}+ \begin{pmatrix} 0.5 & 0\\ -0.25 & 0.5 \end{pmatrix} \begin{pmatrix} \int^{0}_{t-0.5}0.2\sin_{0.5}2(t-0.5-s)\,ds\\ \int^{0}_{t-0.5}0.2\sin_{0.5}(t-0.5-s)\,ds \end{pmatrix} = \begin{pmatrix} x_{1}(t)\\ x_{2}(t) \end{pmatrix}. \end{aligned}$$

Through a basic calculation one can obtain

$$\begin{aligned} x_{1}(t) =&0.025\cos_{0.5}2t-0.05\sin_{0.5}2t+0.5 \int ^{t-0.5}_{-0.5}0.2\sin_{0.5}2(t-0.5-s)\,ds \\ &{}+0.5 \int^{0}_{t-0.5}0.2\sin_{0.5}2(t-0.5-s)\,ds \end{aligned}$$

and

$$\begin{aligned} x_{2}(t) =&0.025\cos_{0.5}t-0.1\cos_{0.5}2t+0.125 \sin_{0.5}2t-0.05\sin _{0.5}t \\ &{}-0.25 \int^{t-0.5}_{-0.5}0.2\sin_{0.5}2(t-0.5-s) \,ds+0.5 \int ^{t-0.5}_{-0.5}0.2\sin_{0.5}(t-0.5-s)\,ds \\ &{}-0.25 \int^{0}_{t-0.5}0.2\sin_{0.5}2(t-0.5-s)\,ds+0.5 \int ^{0}_{t-0.5}0.2\sin_{0.5}(t-0.5-s)\,ds. \end{aligned}$$

When \(0.5\leq t\leq1\), by (25) in the same way we get

$$\begin{aligned} x(t) =& \begin{pmatrix} \cos_{0.5}2t & 0 \\ \cos_{0.5}t & \cos_{0.5}2t \end{pmatrix} \begin{pmatrix} 0.025\\ -0.1 \end{pmatrix} \\ &{}+ \begin{pmatrix} 0.5 & 0\\ -0.25 & 0.5 \end{pmatrix} \begin{pmatrix} \sin_{0.5}2t & 0 \\ \sin_{0.5}t & \sin_{0.5}2t \end{pmatrix} \begin{pmatrix} -0.1\\ 0.2 \end{pmatrix} \\ &{}+ \begin{pmatrix} 0.5 & 0\\ -0.25 & 0.5 \end{pmatrix} \begin{pmatrix} \int^{t-1}_{-0.5}0.2\sin_{0.5}2(t-0.5-s)\,ds\\ \int^{t-1}_{-0.5}0.2\sin_{0.5}(t-0.5-s)\,ds \end{pmatrix} \\ &{}+ \begin{pmatrix} 0.5 & 0\\ -0.25 & 0.5 \end{pmatrix} \begin{pmatrix} \int^{0}_{t-1}0.2\sin_{0.5}2(t-0.5-s)\,ds\\ \int^{0}_{t-1}0.2\sin_{0.5}(t-0.5-s)\,ds \end{pmatrix} = \begin{pmatrix} x_{1}(t)\\ x_{2}(t) \end{pmatrix}, \end{aligned}$$

then one can obtain

$$\begin{aligned} x_{1}(t) =&0.025\cos_{0.5}2t-0.05\sin_{0.5}2t+0.5 \int ^{t-1}_{-0.5}0.2\sin_{0.5}2(t-0.5-s)\,ds \\ &{}+0.5 \int^{0}_{t-1}0.2\sin_{0.5}2(t-0.5-s)\,ds \end{aligned}$$

and

$$\begin{aligned} x_{2}(t) =&0.025\cos_{0.5}t-0.1\cos_{0.5}2t+0.125 \sin_{0.5}2t-0.05\sin _{0.5}t \\ &{}-0.25 \int^{t-1}_{-0.5}0.2\sin_{0.5}2(t-0.5-s) \,ds+0.5 \int ^{t-1}_{-0.5}0.2\sin_{0.5}(t-0.5-s)\,ds \\ &{}-0.25 \int^{0}_{t-1}0.2\sin_{0.5}2(t-0.5-s)\,ds+0.5 \int^{0}_{t-1}0.2\sin _{0.5}(t-0.5-s)\,ds. \end{aligned}$$

By calculating we obtain \(\gamma=\max\{\|\varphi\|_{C},\|\dot{\varphi}\| _{C},\|\ddot{\varphi}\|_{C}\}=0.3\), \(\|\Omega\|=3\), \(\|\Omega^{-1}\| =0.75\), then we set \(\delta=0.31>0.3=\gamma\).

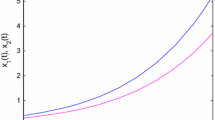
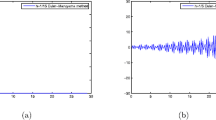
Figure 5 shows the state response \(x(t)\) of (23) and Figure 6 shows the norm \(\|x(t)\| \) of (23). By Theorems 3.1-3.3, we can calculate that \(\|x(t)\|\leq18.8158\), \(\|x(t)\|\leq7.0106\) and \(\|x(t)\|\leq 7.7167\), we just only take \(\epsilon=18.82, 7.02, 7.72\), respectively. The data is shown in Table 1.

Figure 5
figure 5

The state response \(\pmb{x(t)}\) of ( 23 ).

Full size image
Figure 6
figure 6

The norm \(\pmb{\|x(t)\|}\) of ( 23 ).

Full size image
Table 1 Finite time stable results of ( 23 ) by Theorems 3.1 - 3.3
Full size table

We can see \(\|x(t)\|<\epsilon\) for \(\forall t\in J\) through Figure 6 and Table 1, the system (23) is finite time stable with respect to \(\{0,J,\delta,\epsilon,\tau\}\) under Theorems 3.1-3.3. We can also obtain \(\alpha=18.8158, \beta=7.0106,\rho=7.7167\). The result of Theorem 3.2 is the optimal in this example.

5 Extension to delay system with nonlinear term

In this section, we consider the following delay differential equations with nonlinear term:

$$\begin{aligned}& \textstyle\begin{cases} \ddot{x}(t)+\Omega^{2}x(t-\tau)=f(x(t)), & \tau>0,t\in J,\\ x(t)\equiv\varphi(t), \dot{x}(t)\equiv\dot{\varphi}(t), & -\tau\leq t\leq0, \end{cases}\displaystyle \end{aligned}$$
(26)

where \(f\in C(\mathbb {R}^{n},\mathbb {R}^{n})\).

Definition 5.1

see [39], Definitions 2

The system (26) satisfying initial conditions \(x(t)\equiv \varphi(t)\) and \(\dot{x}(t)\equiv\dot{\varphi}(t)\) for \(-\tau\leq t\leq 0\) are finite time stable with respect to \(\{0,J,\delta,\epsilon,\tau\} \), if and only if

$$\begin{aligned}& \gamma^{2}< \delta \end{aligned}$$
(27)

implies

$$\bigl\Vert x(t) \bigr\Vert ^{2}< \epsilon, \quad\forall t\in J, $$

where \(\gamma=\max\{\|\varphi\|_{C},\|\dot{\varphi}\|_{C},\|\ddot {\varphi}\|_{C}\}\) denotes the initial time of observation of the system. In addition, δ, ϵ are real positive numbers.

The following Gronwall inequality will be used to derive the finite time stability for our problem.

Lemma 5.2

see [40], p.12

Let \(u(t)\), \(k(t,s)\) and its partial derivative \(k_{t}(t,s)\) be nonnegative continuous functions for \(t_{0}< s< t\), and suppose

$$\begin{aligned} u(t)\leq a+ \int^{t}_{t_{0}}k(t,s)u(s)\,ds,\quad t\geq t_{0}, \end{aligned}$$

where \(a\geq0\) is a constant. Then

$$\begin{aligned} u(t)\leq a\exp \biggl( \int_{t_{0}}^{t}k(t,s)\,ds \biggr),\quad t\geq t_{0}. \end{aligned}$$

Now we are ready to state our main result in the section.

Theorem 5.3

Suppose that \(f\in C(\mathbb {R}^{n},\mathbb {R}^{n})\) and there exists \(P>0\) such that \(\| f(x)\|\leq P\|x\|\) for all \(x\in \mathbb {R}^{n}\). The system (26) is finite time stable with respect to \(\{ 0,J,\delta,\epsilon,\tau\}\) provided that

$$\begin{aligned} e^{ P \Vert \Omega^{-1} \Vert \Vert \Omega \Vert ^{-1} [\cosh( \Vert \Omega \Vert t)-1 ] }< \frac{\sqrt{\epsilon}}{a}, \quad\forall t\in J, \end{aligned}$$
(28)

where

$$\begin{aligned} {{a=\sqrt{\delta}\cosh\bigl( \Vert \Omega \Vert T\bigr)+\sqrt{ \delta}(\tau+1) \bigl\Vert \Omega^{-1} \bigr\Vert \sinh\bigl[ \Vert \Omega \Vert (T+\tau)\bigr]}}. \end{aligned}$$
(29)

Proof

By [2], Theorem 2, equation (14), the solution of (26) has the form

$$\begin{aligned} x(t) =&\cos_{\tau}\Omega t\varphi(-\tau)+ \Omega^{-1}\sin_{\tau}\Omega t\dot{\varphi}(-\tau)+ \Omega^{-1} \int^{0}_{-\tau}\sin_{\tau}\Omega (t-\tau-s) \ddot{\varphi}(s)\,ds \\ &{}+\Omega^{-1} \int^{t}_{0}\sin_{\tau}\Omega(t-\tau-s)f \bigl(x(s)\bigr)\,ds, \end{aligned}$$
(30)

where the matrix Ω is nonsingular. Taking the norm for (30), we obtain

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq& \Vert \cos_{\tau} \Omega t \Vert \bigl\Vert \varphi(-\tau) \bigr\Vert + \bigl\Vert \Omega^{-1} \bigr\Vert \Vert \sin_{\tau}\Omega t \Vert \bigl\Vert \dot{\varphi}(-\tau) \bigr\Vert \\ &{}+ \bigl\Vert \Omega^{-1} \bigr\Vert \int^{0}_{-\tau} \bigl\Vert \sin_{\tau} \Omega(t-\tau-s) \bigr\Vert \bigl\Vert \ddot{\varphi}(s) \bigr\Vert \,ds \\ &{}+ \bigl\Vert \Omega^{-1} \bigr\Vert \int^{t}_{0} \bigl\Vert \sin_{\tau} \Omega(t-\tau-s) \bigr\Vert \bigl\Vert f\bigl(x(s)\bigr) \bigr\Vert \,ds. \end{aligned}$$
(31)

From (27) and (31), we have

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq&\sqrt{\delta} \Vert \cos_{\tau} \Omega t \Vert +\sqrt{\delta} \bigl\Vert \Omega ^{-1} \bigr\Vert \Vert \sin_{\tau}\Omega t \Vert +\sqrt{\delta} \bigl\Vert \Omega^{-1} \bigr\Vert \int ^{0}_{-\tau} \bigl\Vert \cos_{\tau} \Omega(t-\tau-s) \bigr\Vert \,ds \\ &{}+ \bigl\Vert \Omega^{-1} \bigr\Vert \int^{t}_{0} \bigl\Vert \sin_{\tau} \Omega(t-\tau-s) \bigr\Vert \bigl\Vert f\bigl(x(s)\bigr) \bigr\Vert \,ds. \end{aligned}$$

Next, according to Lemmas 2.5, 2.6 and (15), we obtain

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq&\sqrt{\delta}\cosh\bigl( \Vert \Omega \Vert t\bigr)+\sqrt{\delta} \bigl\Vert \Omega ^{-1} \bigr\Vert \sinh\bigl[ \Vert \Omega \Vert (t+\tau)\bigr]+\sqrt{\delta}\tau \bigl\Vert \Omega^{-1} \bigr\Vert {{\sinh\bigl[ \Vert \Omega \Vert (t+\tau)\bigr]}} \\ &{}+ \int^{t}_{0} \bigl\Vert \Omega^{-1} \bigr\Vert \bigl\Vert f\bigl(x(s)\bigr) \bigr\Vert \sinh\bigl[ \Vert \Omega \Vert (t-s)\bigr]\,ds. \end{aligned}$$
(32)

Note that \(\|f(x)\|\leq P\|x\|\) for all \(x\in \mathbb {R}^{n}\), then the inequality (32) becomes that

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq a+ \int^{t}_{0}k(t,s) \bigl\Vert x(s) \bigr\Vert \,ds, \end{aligned}$$
(33)

where a is defined in (29) and \(k(t,s)=P \Vert \Omega^{-1} \Vert \sinh [ \Vert \Omega \Vert (t-s) ]\).

Calculating the partial derivative \(k_{t}(t,s)\) via (9), we obtain

$$\begin{aligned} k_{t}(t,s)=P \bigl\Vert \Omega^{-1} \bigr\Vert \Vert \Omega \Vert \cosh \bigl[ \Vert \Omega \Vert (t-s) \bigr],\quad {{0\leq s\leq t}}. \end{aligned}$$

Note that \(\Vert x(t) \Vert \), \(k(t,s)\) and its partial derivative \(k_{t}(t,s)\) are all nonnegative continuous functions and a is a constant. Thus, the conditions in Lemma 5.2 are satisfied, then by Lemma 5.2 we get

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq ae^{ \int_{0}^{t}k(t,s)\,ds }, \quad t\in J. \end{aligned}$$
(34)

Next,

$$\begin{aligned} \int_{0}^{t}k(t,s)\,ds= \int_{0}^{t}P \bigl\Vert \Omega^{-1} \bigr\Vert \sinh \bigl[ \Vert \Omega \Vert (t-s) \bigr]\,ds=P \bigl\Vert \Omega^{-1} \bigr\Vert \Vert \Omega \Vert ^{-1} \bigl[ \cosh\bigl( \Vert \Omega \Vert t\bigr)-1 \bigr]. \end{aligned}$$
(35)

Submitting (35) into (34) and by (28) we obtain

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert \leq ae^{ P \Vert \Omega^{-1} \Vert \Vert \Omega \Vert ^{-1} [\cosh( \Vert \Omega \Vert t)-1 ] }< \sqrt{\epsilon}, \end{aligned}$$

which implies that \(\Vert x(t) \Vert ^{2}<\epsilon, t\in J\). The proof is finished. □