Dynamic analysis of effects of phytoplankton dispersal on zooplankton

Abstract

In this paper, we formulate a delayed phytoplankton-zooplankton model with impulsive diffusion on phytoplankton. Using the discrete dynamical system determining the stroboscopic map, we obtain the zooplankton-extinction periodic solution which is globally attractive. The conditions of the permanence are given by using the theory on the delay and impulsive differential equation. Finally, some numerical simulations are presented to illustrate the results.

1 Introduction

Plankton, including phytoplankton and zooplankton, are an important food source for organisms in an aquatic environment. Phytoplankton perform a great service for the earth by absorbing the carbon dioxide from the surrounding environments and releasing the oxygen into the atmosphere [1, 2]. As a primary producer, phytoplankton are most favorable food sources for fish and other aquatic animals [3]. An obvious feature of the phytoplankton is a rapid appearance and disappearance resulting in the formation of bloom, which causes a great harm to the human health and zooplankton population [4, 5]. Therefore, it is necessary to investigate the effect of zooplankton and phytoplankton on the occurrence of bloom.

Many mathematical models have been formulated to describe the dynamical interaction between zooplankton and phytoplankton [6–10]. In [6], deterministic and stochastic models of nutrient-phytoplankton-zooplankton interaction are proposed to investigate the impact of toxin-producing phytoplankton upon persistence of the populations. The author of [7] formulated a toxin-producing phytoplankton-zooplankton model with stochastic perturbation and investigated the global stability of the positive equilibrium by means of constructing suitable Lyapunov functions. Chowdhury et al. [9] proposed a mathematical model of NTP-TPP-zooplankton with constant and variable zooplankton migration. The asymptotic dynamics of the system around the biologically feasible equilibria was explored through local stability analysis. The authors of [11] analyzed a mathematical model for the interactions between phytoplankton and zooplankton in a periodic environment and obtained the permanent condition.

As we know, population dispersal has a great effect on the dynamics [12–17]. Hong et al. [12] investigated a single species model with intermittent unilateral diffusion in two patches. The global attractivity of positive periodic solution and the extinction of species were established by using Lyapunov function approach. Shao [16] formulated a delayed predator-prey system with impulsive diffusion between two patches:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \textstyle\begin{array}{@{}l} \frac{dx_{1}}{dt}=x_{1}(r_{1}-a_{1}x_{1}-b_{1}y),\\ \frac{dx_{2}}{dt}=x_{2}(r_{2}-a_{2}x_{2}),\\ \frac{dy}{dt}=y(-r_{3}+a_{3}x_{1}(t-\tau_{1})-b_{2}y(t-\tau_{2})), \end{array}\displaystyle & t\neq nT,\\ \textstyle\begin{array}{@{}l} \Delta x_{1}=d_{1}(x_{2}-x_{1}),\\ \Delta x_{2}=d_{2}(x_{1}-x_{2}), \Delta y=0, \end{array}\displaystyle & t=nT, \end{array}\displaystyle \right . $$

(1.1)

with the initial condition

$$\begin{aligned}& x_{1}(s)=\phi_{1}(s),\qquad x_{2}(s)= \phi_{2}(s),\qquad y(s)=\phi_{3}(s), \\& \quad\phi=(\phi_{1},\phi_{2},\phi_{3})\in C \bigl([-\tau, 0], R_{+}^{3} \bigr),\phi_{i}(0)>0,i=1,2,3, \end{aligned}$$

where phytoplankton are structured into two patches connected by impulsive diffusion. Wang and Jia [18] proposed a single species model with impulsive diffusion and pulsed harvesting at the different fixed time as follows:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \textstyle\begin{array}{@{}l} \frac{dx_{1}}{dt}=x_{1}(a_{1}-b_{1}x^{\theta_{1}}_{1}),\\ \frac{dx_{2}}{dt}=x_{2}(a_{2}-b_{2}x^{\theta_{2}}_{2}), \end{array}\displaystyle & t\neq(n+l-1)T, t\neq nT,\\ \textstyle\begin{array}{@{}l} \Delta x_{1}=-p_{1}x_{1},\\ \Delta x_{2}=-p_{2}x_{2}, \end{array}\displaystyle & t=(n+l-1)T,\\ \textstyle\begin{array}{@{}l} \Delta x_{1}=d_{1}(x_{2}-x_{1}),\\ \Delta x_{2}=d_{2}(x_{1}-x_{2}), \Delta y=0, \end{array}\displaystyle & t=nT, \end{array}\displaystyle \right . $$

(1.2)

where the system is composed of two patches connected by diffusion. $x_{i}$ ($i = 1, 2$) is the density of species in the ith patch. Wang et al. [19] proposed a single species model with impulsive diffusion between two patches and obtained a globally stable positive periodic solution by using the discrete dynamical system generated by a monotone, concave map for the population. However, little information is available about the application of impulsive diffusion to plankton model. In this paper, we will formulate a nonlinear modeling of the interaction between phytoplankton and zooplankton with impulsive dispersal on the phytoplankton.

The outline of this paper is as follows: a delayed phytoplankton-zooplankton model with impulsive diffusion is presented in Section 2. In addition, some important lemmas are also given in Section 2. In Sections 3 and 4, we obtain the sufficient conditions for global attractivity of zooplankton-extinction periodic solution and the permanence of the system. Finally, we give some numerical simulations and a brief discussion.

2 Development model and preliminaries

Although phytoplankton are single-celled organisms, they play an important role in the marine ecosystem. To describe the complex effect of the phytoplankton on zooplankton, Roy et al. [20] considered a significant number of species of phytoplankton that have the ability to produce toxic or inhibitory compounds and they formulated the following model:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dP_{1}}{dt}=P_{1}\{r_{1}(1-\frac{P_{1}+\alpha_{1}P_{2}}{K})-\frac {w_{1}Z}{D_{1}+P_{1}}\},\\ \frac{dP_{2}}{dt}=P_{2}\{r_{2}(1-\frac{P_{2}+\alpha_{2}P_{1}}{K})-\frac {w_{2}Z}{D_{2}+P_{2}}\},\\ \frac{dZ}{dt}=Z\{\frac{\xi_{1}P_{1}}{D_{1}+P_{1}}-\frac{\xi_{2}P_{2}}{D_{2}+P_{2}}-c\}. \end{array}\displaystyle \right . $$

(2.1)

Motivated by [16, 18, 19], we are concerned with the effects of the phytoplankton-impulsive diffusion in two patches on the dynamics of a phytoplankton-zooplankton system,

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \textstyle\begin{array}{@{}l} \frac{dP_{1}}{dt}= P_{1}(r_{1}-a_{1}P_{1}^{\theta_{1}})-\alpha_{1}P_{1}Z,\\ \frac{dP_{2}}{dt}=P_{2}(r_{2}- a_{2}P_{2}^{\theta_{2}})-\alpha_{2} P_{2}Z ,\\ \frac{dZ}{dt}= Z( \varrho_{1}P_{1}+\varrho_{2}P_{2}-a_{3}Z(t-\tau)-\mu- \frac {\beta P_{2}}{K+P_{2}}), \end{array}\displaystyle & t\neq nT,\\ \textstyle\begin{array}{@{}l} \Delta P_{1}=d(P_{2}-P_{1}),\\ \Delta P_{2}=d(P_{1}-P_{2}), \Delta Z=0, \end{array}\displaystyle & t= nT, \end{array}\displaystyle \right . $$

(2.2)

with the initial condition

$$ \begin{aligned} &P_{1}(s)=\phi_{1}(s), \qquad P_{2}(s)=\phi_{2}(s),\qquad Z(s)=\phi_{3}(s), \\ &\quad\phi=(\phi_{1},\phi_{2},\phi_{3})\in C \bigl([-\tau, 0], R_{+}^{3} \bigr), \phi_{i}(0)>0,i=1,2,3, \end{aligned} $$

(2.3)

where $P_{1}(t)$ denotes the concentration of the nontoxic phytoplankton (NPP) and $P_{2}(t)$ is the concentration of the toxin-producing phytoplankton (TPP). $Z(t)$ is the concentration of the zooplankton. $r_{1}$ and $r_{2}$ are the intrinsic growth rates of NTP and TPP population, respectively. $\theta_{i}$ ($i=1,2$) present nonlinear measure of intra-species interference. $a_{i}$ ($i=1,2$) are the coefficients of intra-specific competition. $\alpha_{i}$ ($i=1,2$) denote the capturing rates of the zooplankton. $\frac{\varrho_{i}}{\alpha_{i}}$ ($i=1,2$) denote the conversion rate of nutrient into the production rate of the zooplankton. The term $-a_{3}Z(t-\tau)$ denotes the negative feedback of zooplankton crowding. T is the impulsive diffusion because of the external perturbation. d ($0< d<1$) is the diffusion rate. μ is the death rate of zooplankton. The term $\frac{\beta P}{K+P_{2}}$ ($\beta>0$, $K>0$) contributes to the death of zooplankton population, where K is a half-saturation constant, β denotes the rate of toxin liberation by toxin-producing phytoplankton. $\Delta P_{i}(t^{+})=P_{i}(t^{+})-P_{i}(t)$ ($i=1,2$), $\Delta Z(t^{+})=Z(t^{+})-Z(t)$, $n\in N$.

For convenience, we first give some lemmas.

Lemma 2.1

All the solutions $(P_{1}(t),P_{2}(t), Z(t))$ of system (2.2) with the initial conditions are positive for all $t\geq0$.

Lemma 2.2

Let $(P_{1}(t),P_{2}(t), Z(t))$ be any solution of system (2.2), there exists a constant $M>0$, such that $P_{i}(t)\leq M$ ($i=1,2$) and $Z(t)\leq M$ for t large enough.

Proof

Define $V(t)= \frac{\theta_{1}}{\varrho_{1}}P_{1}(t)+\frac{\varrho_{2}}{\alpha_{2}} P_{2}(t)+Z(t)$. When $t\neq nT$, we have

$$\begin{aligned}[b] D^{+}V +\mu V(t)&\leq \frac{\varrho_{1}}{\alpha_{1}}\bigl((r_{1}+ \mu)P_{1}-a_{1}P_{1}^{\theta_{1}}\bigr)+ \frac{\varrho _{2}}{\alpha_{2}}\bigl((r_{2}+\mu)P_{2}-a_{2}P_{2}^{\theta_{2}} \bigr) \\ &\leq\frac{(r_{1}+\mu) \theta_{1}\varrho_{1}}{\alpha_{1}(\theta_{1}+1)}\biggl(\frac{r_{1}+\mu}{a_{1}(\theta _{1}+1)}\biggr)^{\frac{1}{\theta_{1}}}+ \frac{(r_{2}+\mu) \theta_{2}\varrho_{2}}{\alpha_{2}(\theta_{2}+1)}\biggl(\frac{r_{2}+\mu}{a_{2}(\theta _{2}+1)}\biggr)^{\frac{1}{\theta_{2}}} \stackrel{\Delta}{=}\xi. \end{aligned} $$

For $t=nT$, $V(nT^{+}) \leq V(nT)$, hence we obtain

$$V(t)\leq V\bigl(0^{+}\bigr)e^{-\mu t}+\frac{\xi}{\mu}\bigl(1-e^{-\mu t} \bigr)\rightarrow \frac{\xi}{\mu} $$

as $t\rightarrow\infty$, which shows $V(t)$ is uniformly ultimately bounded. Thus, we have $P_{i}(t)\leq M$ ($i=1,2$), $Z(t)\leq M$.

Consider the following system:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \textstyle\begin{array}{@{}l} \frac{dP_{1}}{dt}= P_{1}(r_{1}-a_{1}P_{1}^{\theta_{1}}),\\ \frac{dP_{2}}{dt}=P_{2}(r_{2}-a_{2}P_{2}^{\theta_{2}}), \end{array}\displaystyle & t\neq nT,\\ \textstyle\begin{array}{@{}l} \Delta P_{1}=d(P_{2}-P_{1}),\\ \Delta P_{2}=d(P_{1}-P_{2}), \end{array}\displaystyle & t= nT. \end{array}\displaystyle \right . $$

(2.4)

Integrating system (2.4) on $(nT,(n+1)T]$, we have

$$\begin{aligned} &P_{i}(t)=\biggl( P_{1}^{-\theta_{i}}\bigl(nT^{+} \bigr)e^{-r_{i}\theta_{i}(t-nT)}+\frac{a_{i}}{r_{i}}\bigl( 1-e^{-r_{i}\theta_{i}(t-nT)}\bigr) \biggr)^{-\frac{1}{\theta_{i}}}, \\ &\quad t\in\bigl(nT,(n+1)T\bigr],i=1,2. \end{aligned}$$

(2.5)

Similar to [18], we derive the difference equation at the impulsive moment according to system (2.5).

$$ \left \{ \textstyle\begin{array}{@{}l} P_{1}(n+1)T^{+}= (\frac{P_{1}^{\theta_{1}}(nT^{+})}{\beta_{1}+\gamma_{1} P_{1}^{\theta_{1}}(nT^{+})})^{\frac{1}{\theta_{1}}}+d((\frac{P_{2}^{\theta _{2}}(nT^{+})}{\beta_{2}+\gamma_{2} P_{2}^{\theta_{2}}(nT^{+})})^{\frac{1}{\theta_{2}}} -(\frac{P_{1}^{\theta_{1}}(nT^{+})}{\beta_{1}+\gamma_{1} P_{1}^{\theta _{1}}(nT^{+})})^{\frac{1}{\theta_{1}}}),\\ P_{2}(n+1)T^{+}=(\frac{P_{2}^{\theta_{2}}(nT^{+})}{\beta_{2}+\gamma_{2} P_{2}^{\theta_{2}}(nT^{+})})^{\frac{1}{\theta_{2}}}+d((\frac{P_{1}^{\theta _{1}}(nT^{+})}{\beta_{1}+\gamma_{1} P_{1}^{\theta_{1}}(nT^{+})})^{\frac{1}{\theta_{1}}} -(\frac{P_{2}^{\theta_{2}}(nT^{+})}{\beta_{2}+\gamma_{2} P_{2}^{\theta_{2}}(nT^{+})})^{\frac{1}{\theta_{2}}}), \end{array}\displaystyle \right . $$

(2.6)

where $\beta_{i}=e^{-r_{i}\theta_{i}T}<1$, $\gamma_{i}=\frac{a_{i}}{r_{i}}(1-e^{-r_{i}\theta_{i}T}), i=1,2$. Equation (2.6) presents the phytoplankton concentration between patches after diffusion at the moment $t=nT$.

To investigate the dynamics of system (2.6), we define a continuous map $F: R_{+}^{2}\rightarrow R_{+}^{2}$,

$$ \left \{ \textstyle\begin{array}{@{}l} F_{1}(x)= (\frac{x_{1}^{\theta_{1}}}{\beta_{1}+\gamma_{1} x_{1}^{\theta_{1}} })^{\frac{1}{\theta_{1}}}+d((\frac{x_{2}^{\theta_{2}}}{\beta_{2}+\gamma_{2} x_{2}^{\theta_{2}} })^{\frac{1}{\theta_{2}}} -(\frac{x_{1}^{\theta_{1}}}{\beta_{1}+\gamma_{1} x_{1}^{\theta_{1}} })^{\frac {1}{\theta_{1}}}),\\ F_{2}(x)=(\frac{x_{2}^{\theta_{2}}}{\beta_{2}+\gamma_{2} x_{2}^{\theta_{2}} })^{\frac{1}{\theta_{2}}}+d((\frac{x_{1}^{\theta_{1}}}{\beta_{1}+\gamma_{1} x_{1}^{\theta_{1}} })^{\frac{1}{\theta_{1}}} -(\frac{x_{2}^{\theta_{2}}}{\beta_{2}+\gamma_{2} x_{2}^{\theta_{2}} })^{\frac{1}{\theta_{2}}}). \end{array}\displaystyle \right . $$

(2.7)

 □

Lemma 2.3

[18]

There exists a unique positive fixed point $q=(q_{1},q_{2})$ of map F and for any $x=(x_{1},x_{2})$, we have $F(x)\rightarrow q$ as $n\rightarrow\infty$, which implies $q=(q_{1},q_{2})$ is globally asymptotically stable. Therefore, system (2.4) has a positive periodic solution $(P_{1}^{*}(t),P_{2}^{*}(t))$, where

$$ P_{i}^{*}(t)=\biggl(\frac{a_{i}}{r_{i}}+\biggl(\frac{1}{q_{i}^{\theta_{i}}}- \frac {a_{i}}{r_{i}}\biggr)e^{-r_{i}\theta_{i}(t-nT)}\biggr)^{-\frac{1}{\theta_{i}}},\quad t\in \bigl(nT,(n+1)T\bigr],i=1,2. $$

(2.8)

Thus, system (2.2) has a zooplankton-extinction periodic solution $(P_{1}^{*}(t),P_{2}^{*}(t),0)$.

Lemma 2.4

[16]

Let us consider the following equality:

$$ \frac{dx}{dt}\leq x(t) \bigl(a-bx(t-\tau)\bigr), $$

(2.9)

where $a,b,\tau>0, x(t)>0$ for $t\in[-\tau,0]$. Then we obtain $\frac{a}{b}e^{a-ae^{a\tau}}\leq x(t)\leq \frac{a}{b}e^{a\tau}$ for t large enough.

3 Global attractivity of the zooplankton-extinction periodic solution

Theorem 3.1

The zooplankton-extinction periodic solution $(P_{1}^{*}(t),P_{2}^{*}(t),0)$ is globally attractive if ${\sum_{i=1}^{i=1}}\varrho_{i}(\frac{a_{i}}{r_{i}}+(\frac {1}{q_{i}^{\theta_{i}}}-\frac{a_{i}}{r_{i}})e^{-r_{i}\theta_{i}T})^{-\frac{1}{\theta _{i}}}<\mu$ holds.

Proof

From the first two equations of system (2.1), we have

$$ \begin{aligned} \frac{dP_{1}}{dt}\leq P_{1}(r_{1}-a_{1}P_{1}^{\theta_{1}}),\\ \frac{dP_{2}}{dt}\leq P_{2}(r_{2}-a_{2}P_{2}^{\theta_{2}}). \end{aligned} $$

(3.1)

We consider the comparison system as follows:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \textstyle\begin{array}{@{}l} \frac{du_{1}}{dt}= u_{1}(r_{1}-a_{1}u_{1}^{\theta_{1}}),\\ \frac{du_{2}}{dt}=u_{2}(r_{2}-a_{2}u_{2}^{\theta_{2}}), \end{array}\displaystyle & t\neq nT,\\ \textstyle\begin{array}{@{}l} \Delta u_{1}=d(u_{2}-P_{1}),\\ \Delta u_{2}=d(u_{1}-u_{2}), \end{array}\displaystyle & t= nT. \end{array}\displaystyle \right . $$

(3.2)

From Lemma 2.3, we see that system (3.2) has a periodic solution $(u_{1}^{*}(t),u_{2}^{*}(t))$,

$$ u_{i}^{*}(t)=\biggl(\frac{a_{i}}{r_{i}}+\biggl(\frac{1}{q_{i}^{\theta_{i}}}- \frac {a_{i}}{r_{i}}\biggr)e^{-r_{i}\theta_{i}(t-nT)}\biggr)^{-\frac{1}{\theta_{i}}},\quad t\in \bigl(nT,(n+1)T\bigr],i=1,2, $$

(3.3)

which is globally asymptotically stable. There exist an integer $k_{1}>0$ and $\varepsilon_{1}>0$ such that $P_{i}(t)\leq u_{i}(t)\leq u^{*}_{i}(t)+\varepsilon$ for $kT \leq t\leq(k+1)T$, that is,

$$\begin{aligned} &P_{i}(t)\leq u^{*}_{i}(t)+\varepsilon\leq\biggl( \frac{a_{i}}{r_{i}}+\biggl(\frac{1}{q_{i}^{\theta_{i}}}-\frac {a_{i}}{r_{i}} \biggr)e^{-r_{i}\theta_{i}T}\biggr)^{-\frac{1}{\theta_{i}}}+\varepsilon \stackrel{\Delta}{=} \kappa_{i} \\ &\quad (i=1,2), kT\leq t\leq (k+1)T,k>k_{1}>0. \end{aligned}$$

(3.4)

Again from system (2.2), we have

$$ \frac{dZ}{dt}\leq Z\bigl(\varrho_{1}\kappa_{1}+ \varrho_{2}\kappa_{2}-\mu-a_{3}Z(t-\tau)\bigr), \quad t>k_{1}T+\tau. $$

(3.5)

From the condition of the Theorem 3.1, we have $\theta_{1}\kappa_{1}+ \theta_{2}\kappa_{2}<\mu$ for ε small enough. From system (3.4) and Lemma 2.4, we easily obtain $Z(t)\leq0$ using the comparison theorem of impulsive differential equations. Again from the positivity of $Z(t)$, we derive $\lim_{t\rightarrow\infty}Z(t)=0$. Therefore, there exists an integer $k_{2}>k_{1}$ such that $Z(t)<\varepsilon_{1}$ for $t>k_{2}T$.

From the first equations of system (2.2), we have

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dP_{1}}{dt}\geq P_{1}(r_{1}-\alpha_{1}\varepsilon_{1}- a_{1}P_{1}^{\theta_{1}}),\\ \frac{dP_{2}}{dt}\geq P_{2}(r_{2}-\alpha_{2}\varepsilon_{1}- a_{2}P_{2}^{\theta_{2}}). \end{array}\displaystyle \right . $$

(3.6)

Integrating the comparison system, we have

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \textstyle\begin{array}{@{}l} \frac{du_{3}}{dt}= u_{3}(r_{1}-\alpha_{1}\varepsilon_{1}-a_{1}u_{3}^{\theta_{1}}),\\ \frac{du_{4}}{dt}=u_{4}(r_{2}-\alpha_{2}\varepsilon_{1}-a_{2}u_{4}^{\theta_{2}}), \end{array}\displaystyle & t\neq nT,\\ \textstyle\begin{array}{@{}l} \Delta u_{3}=d(u_{4}-u_{3}),\\ \Delta u_{4}=d(u_{3}-u_{4}), \end{array}\displaystyle & t= nT. \end{array}\displaystyle \right . $$

(3.7)

From Lemma 2.3, we get system (3.7) has a periodic solution $(u^{*}_{3}(t),u^{*}_{4}(t))$ as follows:

$$\begin{aligned} &u^{*}_{i}(t)=\biggl(\frac{a_{i}}{r_{i}-\alpha_{i}\varepsilon_{1}}+\biggl(\frac {1}{{q_{*}}_{i}^{\theta_{i}}}- \frac{a_{i}}{r_{i}-\alpha_{i}\varepsilon _{1}}\biggr)e^{-(r_{i}-\alpha_{i}\varepsilon_{1})\theta_{i}(t-nT)} \biggr)^{-\frac{1}{\theta_{i}}},\\ &\quad t \in\bigl(nT,(n+1)T\bigr]\ (i=3,4), \end{aligned}$$

which is globally asymptotically stable and ${q_{*}}_{i}$ can be computed similar to Lemma 2.3.

By the comparison theorem of impulsive different equations, for any $\varepsilon_{2}>0$, there exists an integer $k_{3}$ ($k_{3}>k_{2}$) such that $P_{1}(t)\geq u^{*}_{3}(t)-\varepsilon_{2}$ and $P_{2}(t)>u^{*}_{4}(t)-\varepsilon_{2}$, $kT< t<(k+1)T$, $k>k_{3}$.

Let $\varepsilon_{1}\rightarrow0$, we have $P_{i}(t)\rightarrow P^{*}_{i}(t),i=1,2$. Therefore, the zooplankton-extinction periodic solution $(P_{1}^{*}(t),P_{2}^{*}(t),0)$ is globally attractive if $\sum_{i=1}^{i=1}\varrho_{i}(\frac{a_{i}}{r_{i}}+(\frac {1}{q_{i}^{\theta_{i}}}-\frac{a_{i}}{r_{i}})e^{-r_{i}\theta_{i}T})^{-\frac{1}{\theta _{i}}}<\mu$ holds. The proof is completed. □

4 Permanence

In this section, we investigate system (2.2) is permanent if the zooplankton population is above a certain threshold level for sufficiently large time.

Theorem 4.1

System (2.2) is permanent if $\theta_{1}a_{1}+\theta_{2}a_{2}>\mu+\frac{\beta M}{K+M}$ holds, where M is a positive constant.

Proof

Let $(P_{1}(t),P_{2}(t),Z(t))$ be any solution of system (2.2) with initial value (2.3). From Lemma 2.2, we obtain $P_{1}(t)< M,P_{2}(t)< M, Z(t)< M$ for $t\rightarrow\infty$. Next, we need to prove there exists a positive constant $m>0$ such that $P_{i}(t)>m$ ($i=1,2$) and $Z(t)>m$ as $t\rightarrow\infty$.

From system (3.4), we have $P_{i}(t)\leq \kappa_{i}$ ($i=1,2$) for t large enough. According to system (2.2), we have $\frac{dZ}{dt}\leq Z(t)(\varrho_{1}\kappa_{1}+\varrho_{2}\kappa_{2}-\mu-a_{3}Z(t-\tau) )$. According to Lemma 2.4, we derive

$$ Z(t)\leq \frac{(\varrho_{1}\kappa_{1}+\varrho_{2}\kappa_{2}-\mu) }{a_{3}}e^{(\varrho_{1}\kappa_{1}+\varrho_{2}\kappa_{2}-\mu)\tau} \stackrel{\Delta}{=}\vartheta. $$

(4.1)

From system (2.2), we get

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dP_{1}}{dt}\geq P_{1}(r_{1}-a_{1}P_{1}^{\theta_{1}}-\alpha_{1}P_{1}\vartheta),\\ \frac{dP_{2}}{dt}\geq P_{2}(r_{2}-a_{2}P_{2}^{\theta_{2}}-\alpha_{2}\vartheta). \end{array}\displaystyle \right . $$

(4.2)

We consider the comparison system:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \textstyle\begin{array}{@{}l} \frac{dv_{1}}{dt}= v_{1}(r_{1}-\alpha_{1}\vartheta-a_{1}v_{1}^{\theta_{1}}),\\ \frac{dv_{2}}{dt}=v_{2}(r_{2}-\alpha_{2}\vartheta-a_{2}v_{2}^{\theta_{2}}), \end{array}\displaystyle & t\neq nT,\\ \textstyle\begin{array}{@{}l} \Delta v_{1}=d(v_{2}-v_{1}),\\ \Delta v_{2}=d(v_{1}-v_{2}), \end{array}\displaystyle & t= nT. \end{array}\displaystyle \right . $$

(4.3)

From Lemma 2.3, we know that system (4.3) has a periodic solution $(v^{*}_{1}(t),v^{*}_{2}(t))$ as follows:

$$ v^{*}_{i}(t)=\biggl(\frac{a_{i}}{r_{i}-\alpha_{i}\vartheta}+\biggl(\frac{1}{{\overline {q}}_{i}^{\theta_{i}}}- \frac{a_{i}}{r_{i}-\alpha_{i}\vartheta}\biggr) e^{-(r_{i}-\alpha_{i}\vartheta)\theta_{i}(t-nT)}\biggr)^{-\frac{1}{\theta _{i}}},\quad i=1,2, $$

(4.4)

which is globally asymptotically stable, where $\overline{q}_{i}$ can be obtained similar to Lemma 2.3. We obtain $P_{i}(t)\geq v_{i}(t)$ ($i=1,2$) for $nT< t\leq(n+1)T$ by using the comparison theorem of the impulsive differential equations. Thus, there exists $\varepsilon_{3}>0$ such that

$$ P_{i}(t)\geq\biggl(\frac{a_{i}}{r_{i}-\alpha_{i}\vartheta}+\biggl(\frac{1}{{\overline {q}}_{i}^{\theta_{i}}}- \frac{a_{i}}{r_{i}-\alpha_{i}\vartheta}\biggr) e^{-(r_{i}-\alpha_{i}\vartheta)\theta_{i}(t-nT)}\biggr)^{-\frac{1}{\theta _{i}}}- \varepsilon_{3}\stackrel{\Delta}{=}m_{i}\quad(i=1,2) $$

(4.5)

for t large enough.

In the following, we will show there exists a positive constant $m_{3}>0$ such that $Z(t)\geq m_{3}$ as $t\rightarrow\infty$.

Again from system (2.2), we get

$$ \frac{dZ}{dt}\geq Z\biggl(\varrho_{1}m_{1}+ \varrho_{2}m_{2}-\mu-\frac{\beta M}{K+M}-a_{3}Z(t- \tau)\biggr). $$

(4.6)

Considering the following comparison system:

$$ \frac{dw}{dt}= w\biggl(\varrho_{1}m_{1}+ \varrho_{2}m_{2}-\mu-\frac{\beta M}{K+M}-a_{3}w(t- \tau)\biggr), $$

(4.7)

we get

$$ Z(t)\geq w(t)\geq \frac{A}{a_{3}}e^{A-Ae^{A\tau}}, $$

(4.8)

where $A=\varrho_{1}m_{1}+\varrho_{2}m_{2}-\mu-\frac{\beta M}{K+M}$.

From system (4.5), we derive

$$ m_{i}>{\overline{q}}_{i}^{\theta_{i}}- \varepsilon_{3}\quad(i=1,2) $$

(4.9)

for t large enough. From system (4.9) and the condition

$$\theta_{1}a_{1}+\theta_{2}a_{2}>\mu+ \frac{\beta M}{K+M}, $$

we obtain $\varrho_{1}m_{1}+\varrho_{2}m_{2}-\mu-\frac{\beta M}{K+M}>0$. Therefore, there exists $\varepsilon_{4}>0$ such that $Z(t)\geq \frac{A}{a_{3}}e^{A-Ae^{A\tau}}-\varepsilon_{4}\stackrel{\Delta}{=}m_{3}$ as $t\rightarrow\infty$. Define $m=\min\{m_{1},m_{2},m_{3}\}$, we have $P_{1}(t)\geq m,P_{2}(t)\geq m, Z(t)\geq m$ holding for $t\rightarrow\infty$. The proof is completed. □

5 Discussion

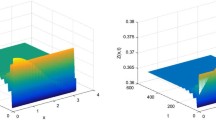
To investigate the effect of the phytoplankton diffusion on the dynamics, we formulate a phytoplankton-zooplankton model with impulsive diffusion. By using impulsive differential equations, we prove the zooplankton-extinction is globally attractive if $\sum_{i=1}^{i=1}\theta_{i} (\frac{a_{i}}{r_{i}}+(\frac{1}{q_{i}^{\theta_{i}}}-\frac {a_{i}}{r_{i}})e^{-r_{i}\theta_{i}T})^{-\frac{1}{\theta_{i}}}<\mu$, which is simulated in Figure 1 with parameters $r_{1}=1.5$, $a_{1}=0.2$, $\alpha_{1}=0.5, \theta_{1}=0.8, \theta_{2}=0.3, r_{2}=6, a_{2}=0.1$, $\alpha_{2}=0.1, \beta=0.7, \varrho_{1}=0.1, \varrho_{2}=0.1, \tau=0, a_{3}=0.8, K=3, \mu=0.8, d=0.01,T=2.42$. The phytoplankton and zooplankton coexist when $\theta_{1}a_{1}+\theta_{2}a_{2}>\mu+\frac{\beta M}{K+M}$. Let parameters be $r_{1}=1.5, a_{1}=0.2, \alpha_{1}=0.8, \theta_{1}=0.8, \theta_{2}=0.3$, $r_{2}=6, a_{2}=0.1, \alpha_{2}=0.1, \beta=0.5, \varrho_{1}=0.1, \varrho_{2}=0.1, \tau=0, a_{3}=0.2, K=3, \mu=0.2, d=0.01$, we can see the phytoplankton and zooplankton oscillate in an impulsive period, which shows phytoplankton and zooplankton are permanent (see Figure 2).

Figure 1

Time series and phase portrait of the zooplankton-extinction periodic solution of system ( 2.2 ) with the parameters $\pmb{r_{1}=1.5}$ , $\pmb{a_{1}=0.2}$ , $\pmb{\alpha_{1}=0.5}$ , $\pmb{\theta_{1}=0.8}$ , $\pmb{\theta_{2}=0.3}$ , $\pmb{r_{2}=6}$ , $\pmb{a_{2}=0.1}$ , $\pmb{\alpha_{2}=0.1}$ , $\pmb{\beta=0.7}$ , $\pmb{\varrho_{1}=0.1}$ , $\pmb{\varrho_{2}=0.1}$ , $\pmb{\tau=0}$ , $\pmb{a_{3}=0.8}$ , $\pmb{K=3}$ , $\pmb{\mu=0.8}$ , $\pmb{d=0.01}$ , $\pmb{T=2.42}$ .

Figure 2

Time series and phase portrait of the permanence of system ( 2.2 ) with the parameters $\pmb{r_{1}=1.5}$ , $\pmb{a_{1}=0.2}$ , $\pmb{\alpha_{1}=0.5}$ , $\pmb{\theta_{1}=0.8}$ , $\pmb{\theta_{2}=0.3}$ , $\pmb{r_{2}=6}$ , $\pmb{a_{2}=0.1}$ , $\pmb{\alpha_{2}=0.1}$ , $\pmb{\beta=0.7}$ , $\pmb{\varrho_{1}=0.1}$ , $\pmb{\varrho_{2}=0.1}$ , $\pmb{\tau=0}$ , $\pmb{a_{3}=0.8}$ , $\pmb{K=3}$ , $\pmb{\mu=0.8}$ , $\pmb{d=0.01}$ , $\pmb{T=2.42}$ .