1 Introduction and statement of the main results

The second part of Hilbert’s 16th problem and its weak version are two open problems in the qualitative theory of real planar differential systems; see [1–4]. Since both problems are difficult, mathematicians try to study particular and simple cases. For example, Smale’s 13th problem restricts Hilbert’s 16th problem to the Liénard systems [5].

In recent years, stimulated by nonsmooth phenomena in the real world, piecewise smooth differential systems have attracted a good deal of attention; see, for instance, [6, 7]. There are several papers [8, 9] considering the limit cycles for piecewise smooth Liénard systems. The authors of [10] studied the Hopf bifurcation for a piecewise smooth planar Hamiltonian system. In the paper [11], the authors considered the Poincaré bifurcation for piecewise smooth Hamiltonian systems and obtained the first-order Melnikov function. Then, they applied the first-order Melnikov function to study the number of limit cycles that bifurcate from the period annulus of the center and obtained some new results. Later, by introducing multiple parameters, in [12], some new formulas are obtained for piecewise smooth systems. In the paper [13], the authors considered the number of limit cycles that bifurcate from the period annulus of the center for a piecewise smooth quadratic isochronous center. Generally speaking, a piecewise smooth system can bifurcate more limit cycles than a smooth one. In a recent paper [9], the authors studied the limit cycles for m-piecewise smooth Liénard system, They conjecture that the number of limit cycles decreases as m increases.

In this paper, we consider the following piecewise smooth perturbed Hamiltonian system:

$$ \begin{pmatrix} \frac{dx}{dt}\\ \frac{dy}{dt} \end{pmatrix} = \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \bigl( {\scriptsize\begin{matrix}{} H_{y}(x,y)+\varepsilon f^{+}(x,y)\cr -H_{x}(x,y)+\varepsilon g^{+}(x,y) \end{matrix}} \bigr), & x>0,\\ \bigl( {\scriptsize\begin{matrix}{} H_{y}(x,y)+\varepsilon f^{-}(x,y)\cr -H_{x}(x,y)+\varepsilon g^{-}(x,y) \end{matrix}} \bigr), & x< 0, \end{array}\displaystyle \right . $$
(1)

where \(f^{\pm}(x,y)\) and \(g^{\pm}(x,y)\) are polynomial functions with respect to x and y.

Note that the unperturbed system \(\mbox{(1)}|_{\varepsilon=0}\) is a Hamiltonian system with the first integral \(H(x,y)\), and there is a family of periodic orbits \(L_{h}=L^{+}_{h}\cup L^{-}_{h}\) surrounding the center, where \(L^{\pm}_{h}:H(x,y)=h,x>0\) (\(x<0\)), \(h\in(h_{1},h_{2})\). Without loss of generality, we suppose that \(L_{h}\) has the clockwise orientation.

In this paper, we try to study the first-order Melnikov function for piecewise smooth system (1). Applying the first-order Melnikov function, we consider the number of limit cycles that bifurcate from the period annulus of the center for unperturbed system \(\mbox{(1)}|_{\varepsilon=0}\) under piecewise smooth polynomial perturbation.

Theorem 1

The first-order Melnikov function of system (1) can be expressed as

$$\begin{aligned} M_{1}(h)={}&{-} \int_{L^{+}_{h}} \biggl( \int _{0}^{x}g_{y}^{+}(x,y)\, \mathrm{d}x+f^{+}(x,y) \biggr)\,\mathrm{d}y \\ &{}- \int_{L^{-}_{h}} \biggl( \int_{0}^{x}g_{y}^{-}(x,y)\, \mathrm {d}x+f^{-}(x,y) \biggr)\,\mathrm{d}y, \end{aligned}$$
(2)

where \(L^{\pm}(h):H(x,y)=h,x>0\) (\(x<0\)), \(h\in(h_{1},h_{2})\), and \(L_{h}=L^{+}_{h}\cup L^{-}_{h}\) has the clockwise orientation.

Moreover, if \(M_{1}(h^{*})=0\) and \(M_{1}^{\prime}(h^{*})\neq0\) for some \(h^{*}\in(h_{1},h_{2})\), then for \(|\varepsilon|>0\) sufficiently small, system (1) has a unique limit cycle near \(L_{h^{*}}\).

Remark 2

If \(f^{+}(x,y)\equiv f^{-}(x,y)\) and \(g^{+}(x,y)\equiv g^{-}(x,y)\), then system (1) is a smooth near-Hamiltonian system, and the first-order Melnikov function is well known; see [3]. Let \(\operatorname{deg} H(x,y)=m\). There are many papers considering the number of limit cycles that bifurcate from the period annulus of the center. See, for instance, \(m=2\) (e.g. [14]), \(m=3\) (e.g. [15]), \(m=4\) (e.g. [16]), \(m=5\) (e.g. [17, 18]), \(m=6\) (e.g. [19]).

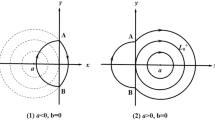
As applications, we study the number of limit cycles for the piecewise smooth perturbation of the global center

$$ \begin{pmatrix} \frac{dx}{dt}\\ \frac{dy}{dt} \end{pmatrix} =\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \bigl({\scriptsize\begin{matrix}{} y+y^{3}+\varepsilon f^{+}(x,y)\cr -x+\varepsilon g^{+}(x,y) \end{matrix}} \bigr), & x> 0,\\ \bigl({\scriptsize\begin{matrix}{} y+y^{3}+\varepsilon f^{-}(x,y)\cr -x+\varepsilon g^{-}(x,y) \end{matrix}} \bigr), & x< 0, \end{array}\displaystyle \right . $$
(3)

and the truncated pendulum

$$ \begin{pmatrix} \frac{dx}{dt}\\ \frac{dy}{dt} \end{pmatrix} =\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \bigl({\scriptsize\begin{matrix}{} y-y^{3}+\varepsilon f^{+}(x,y)\cr -x+\varepsilon g^{+}(x,y) \end{matrix}} \bigr), & x> 0,\\ \bigl({\scriptsize\begin{matrix}{} y-y^{3}+\varepsilon f^{-}(x,y)\cr -x+\varepsilon g^{-}(x,y) \end{matrix}} \bigr), & x< 0, \end{array}\displaystyle \right . $$
(4)

where

$$ \begin{aligned} &f^{+}(x,y)=a_{1}x+a_{2}y+a_{3}x^{2}+a_{4}xy+a_{5}y^{2}+a_{6}x^{3}+a_{7}x^{2}y+a_{8}xy^{2}+a_{9}y^{3}, \\ &g^{+}(x,y)=b_{1}x+b_{2}y+b_{3}x^{2}+b_{4}xy+b_{5}y^{2}+b_{6}x^{3}+b_{7}x^{2}y+b_{8}xy^{2}+b_{9}y^{3}, \\ &f^{-}(x,y)=c_{1}x+c_{2}y+c_{3}x^{2}+c_{4}xy+c_{5}y^{2}+c_{6}x^{3}+c_{7}x^{2}y+c_{8}xy^{2}+c_{9}y^{3}, \\ &g^{-}(x,y)=d_{1}x+d_{2}y+d_{3}x^{2}+d_{4}xy+d_{5}y^{2}+d_{6}x^{3}+d_{7}x^{2}y+d_{8}xy^{2}+d_{9}y^{3}. \end{aligned} $$
(5)

Note that for \(\varepsilon=0\), systems (3) and (4) are Hamiltonian systems. These systems occur in oscillating chemical reactor models and have been studied in several papers; see, for instance, [14, 20].

Applying the first-order Melnikov function given by (2), we consider the number of limit cycles that can bifurcate from the period annuls surrounding the origin of systems (3) and (4) under piecewise smooth cubic polynomial perturbation. Our result is the following theorem.

Theorem 3

There are at least five limit cycles that can bifurcate from the period annulus surrounding the origin of (3) (resp. (4)) by the first-order Melnikov function.

Remark 4

If \(a_{i}=c_{i},b_{i}=d_{i},i=1,2,\ldots,9\), then systems (3) and (4) become smooth near-Hamiltonian systems and have been studied in the papers [14, 20], where the authors obtained that there are at most two limit cycles that bifurcate from the period annulus of the origin for the smooth systems (3) and (4). Our result shows that planar piecewise smooth differential systems (3) and (4) can bifurcate three more limit cycles than the smooth one.

2 Proof of Theorem 1

We need the following lemma derived from [11] to prove Theorem 1.

Lemma 5

Consider the perturbed piecewise smooth Hamiltonian system

$$ \begin{pmatrix} \frac{dx}{dt}\\ \frac{dy}{dt} \end{pmatrix} =\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \bigl({\scriptsize\begin{matrix}{} H^{+}_{y}(x,y)+\varepsilon f^{+}(x,y)\cr -H^{+}_{x}(x,y)+\varepsilon g^{+}(x,y) \end{matrix}} \bigr), & x> 0,\\ \bigl({\scriptsize\begin{matrix}{} H^{-}_{y}(x,y)+\varepsilon f^{-}(x,y)\cr -H^{-}_{x}(x,y)+\varepsilon g^{-}(x,y) \end{matrix}} \bigr), & x< 0, \end{array}\displaystyle \right . $$
(6)

where \(f^{\pm}(x,y)\) and \(g^{\pm}(x,y)\) are analytic functions with respect to \(x,y\). Assume that:

  1. (I)

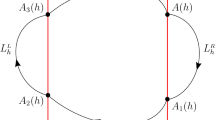
    There exist an interval \(J=(\alpha,\beta)\) and two points \(A(h)=(0,\alpha(h))\) and \(A_{1}(h)=(0,\alpha_{1}(h))\), where \(\alpha(h)\neq\alpha_{1}(h)\), such that, for \(h\in J\), we have

    $$ \begin{aligned} &H^{+} \bigl(A(h) \bigr)=H^{+} \bigl(A_{1}(h) \bigr)=h, \\ &H^{-} \bigl(A(h) \bigr)=H^{-} \bigl(A_{1}(h) \bigr). \end{aligned} $$
    (7)
  2. (II)

    The system has an orbital arc \(L^{+}_{h}\) starting from \(A(h)\) and ending at \(A_{1}(h)\) defined by \(H^{+}(x,y)=h,x>0\). The system has an orbital arc \(L^{-}_{h}\) starting from \(A_{1}(h)\) and ending at \(A(h)\) defined by \(H^{-}(x,y)=h,x\leqslant0\).

Under assumptions (I) and (II), system \(\mbox{(6)}|_{\varepsilon=0}\) has a family of periodic orbits \(L_{h} = L^{+}_{h}\cup L^{-}_{h}\) for \(h\in J\). Each of the closed curves \(L_{h}\) is piecewise smooth in general. Further, without loss of generality, suppose that \(L_{h}\) has a clockwise orientation.

Then the first-order Melnikov function of system (6) can be expressed as

$$\begin{aligned} M_{1}(h)=\frac{H^{+}_{y}(A)}{H^{-}_{y}(A)} \biggl(\frac {H^{-}_{y}(A_{1})}{H^{+}_{y}(A_{1})} \int _{L^{+}_{h}}g^{+}\,\mathrm{d}x-f^{+}\, \mathrm{d}y + \int_{L^{-}_{h}}g^{-}\,\mathrm{d}x-f^{-}\, \mathrm{d}y \biggr). \end{aligned}$$
(8)

Further, if \(M_{1}(h^{*})=0\) and \(M_{1}^{\prime}(h^{*})\neq0\) for some \(h^{*}\in J\), then for \(|\varepsilon|>0\) sufficiently small, system (6) has a unique limit cycle near \(L_{h^{*}}\).

Proof of Theorem 1

Since the unperturbed system \(\mbox{(1)}|_{\varepsilon=0}\) is a Hamiltonian system with first integral \(H(x,y)\), it is obvious that assumptions (I) and (II) are satisfied. Note that \(H^{+}(x,y)\equiv H^{-}(x,y)=H(x,y)\) for system (1). Then

$$ H^{+}_{y} \bigl(A(h) \bigr)=H^{-}_{y} \bigl(A(h) \bigr),\qquad H^{+}_{y} \bigl(A_{1}(h) \bigr)=H^{-}_{y} \bigl(A_{1}(h) \bigr). $$
(9)

Replacing (9) by (8), we have

$$ M_{1}(h)=M^{+}(h)+M^{-}(h), $$
(10)

where

$$ \begin{aligned} &M^{+}(h)= \int_{L^{+}_{h}}g^{+}(x,y)\,\mathrm{d}x-f^{+}(x,y) \,\mathrm{d}y, \\ &M^{-}(h)= \int_{L^{-}_{h}}g^{-}(x,y)\,\mathrm{d}x-f^{-}(x,y) \,\mathrm{d}y. \end{aligned} $$
(11)

Applying Green’s formula two times to the integrals (11), we have

$$\begin{aligned} M^{+}(h)&= \int_{L^{+}_{h}}g^{+}(x,y)\,\mathrm {d}x-f^{+}(x,y) \,\mathrm{d}y \\ &= \int_{L^{+}_{h}}g^{+}(x,y)\,\mathrm{d}x- \int _{L^{+}_{h}}f^{+}(x,y)\,\mathrm{d}y \\ &= \oint_{L^{+}_{h}\cup\overrightarrow {A_{1}A}}g^{+}(x,y)\,\mathrm{d}x- \int _{L^{+}_{h}}f^{+}(x,y)\,\mathrm{d}y \\ &= \iint_{\operatorname{int}(L^{+}_{h}\cup\overrightarrow {A_{1}A})}g_{y}^{+}(x,y)\,\mathrm{d}x\, \mathrm{d}y- \int _{L^{+}_{h}}f^{+}(x,y)\,\mathrm{d}y \\ &= \oint_{L^{+}_{h}\cup\overrightarrow{A_{1}A}} \biggl( \int _{0}^{x}g_{y}^{+}(x,y)\, \mathrm{d}x \biggr)\,\mathrm{d}y- \int _{L^{+}_{h}}f^{+}(x,y)\,\mathrm{d}y \\ &=- \int_{L^{+}_{h}} \biggl( \int_{0}^{x}g_{y}^{+}(x,y)\, \mathrm {d}x+f^{+}(x,y) \biggr)\,\mathrm{d}y, \end{aligned}$$
(12)

where \(L^{+}_{h}: H(x,y)=h,x>0\).

Similarly, we have

$$ M^{-}(h)=- \int_{L^{-}_{h}} \biggl( \int _{0}^{x}g_{y}^{-}(x,y)\, \mathrm{d}x+f^{-}(x,y) \biggr)\,\mathrm{d}y, $$
(13)

where \(L^{-}_{h}: H(x,y)=h,x<0\).

Replacing (12) and (13) by (10), we obtain the first-order Melnikov function (2). According to Lemma 5, every simple zero of the first-order Melnikov function (2) provides a limit cycle of system (1). This completes the proof. □

3 Proof of Theorem 3

In order to estimate the number of the zeros of the first-order Melnikov function, we need the following lemma.

Lemma 6

[21]

Consider \(p+1\) linearly independent analytical functions \(f_{i}: U \rightarrow\mathbb{R}\), \(i=0,1,\ldots,p\), where \(U \in\mathbb{R}\) is an interval. Suppose that there exists \(j \in \{0,1,\ldots,p\}\) such that \(f_{j}\) has constant sign. Then there exist \(p+1\) constants \(C_{i}, i=0,1,\ldots,p\), such that \(f(r)=\sum^{p}_{i=0}C_{i}f_{i}(r)\) has at least p simple zeros in U.

Proof of Theorem 3

First, we consider system (3). From

$$ H(x,y)=\frac{x^{2}}{2}+\frac{y^{2}}{2}+\frac{y^{4}}{4}=h \in(0,+\infty) $$
(14)

we obtain that

$$ L^{\pm}(h):x=\pm\sqrt{2h-y^{2}- \frac{y^{4}}{2}} $$
(15)

and

$$ \alpha(h)=\sqrt{1+h}-1, \qquad\alpha_{1}(h)=- \alpha(h). $$
(16)

According to Theorem 1, the first-order Melnikov function is

$$\begin{aligned} M_{1}(h)={}& \int_{L^{+}_{h}} \biggl( \int _{0}^{x}g_{y}^{+}(x,y)\, \mathrm{d}x+f^{+}(x,y) \biggr)\,\mathrm{d}y \\ &{} + \int_{L^{-}_{h}} \biggl( \int _{0}^{x}g_{y}^{-}(x,y)\, \mathrm{d}x+f^{-}(x,y) \biggr)\,\mathrm{d}y \\ ={}& \int_{L^{+}_{h}} \biggl( \int_{0}^{x}g_{y}^{+}(x,y)\, \mathrm {d}x+f^{+}(x,y) \biggr)\,\mathrm{d}y \\ &{} - \int_{L^{+}_{h}} \biggl( \int _{0}^{-x}g_{y}^{-}(x,y)\, \mathrm{d}x+f^{-}(-x,y) \biggr)\,\mathrm{d}y, \end{aligned}$$
(17)

where \(f^{\pm}(x,y)\) and \(g^{\pm}(x,y)\) are given by (5). □

For simplicity, we define the following functions:

$$ I_{i,j}(h)= \int_{L^{+}_{h}}x^{i}y^{j}\,\mathrm{d}y,\quad h \in(0,+\infty). $$
(18)

Lemma 7

The following equalities hold: 5

  1. (i)

    \(I_{0,1}(h)=I_{1,1}(h)=I_{2,1}(h)=I_{0,3}(h)=0\);

  2. (ii)

    \(I_{0,0}(h),I_{1,0}(h),I_{2,0}(h),I_{0,2}(h),I_{3,0}(h),I_{1,2}(h)\) are linearly independent functions.

Proof

(i) Note that \(L^{+}_{h}:x=\sqrt{2h-y^{2}-\frac{y^{4}}{2}}\) and \(\alpha _{1}(h)=-\alpha(h)\). By symmetry we have

$$ I_{0,1}(h)= \int_{L^{+}_{h}}y\,\mathrm{d}y= \int _{\alpha(h)}^{-\alpha(h)}y\,\mathrm{d}y=0. $$

The equalities \(I_{1,1}(h)=I_{2,1}(h)=I_{0,3}(h)=0\) can be proved similarly.

(ii) In order to prove that \(I_{0,0}(h),I_{1,0}(h),I_{2,0}(h),I_{0,2}(h),I_{3,0}(h),I_{1,2}(h)\) are linearly independent functions, for these functions, we make the following Taylor expansions in the variable h around \(h=0\):

$$ \begin{aligned} &I_{0,0}(h)=-h+\frac{1}{4}h^{2}- \frac{1}{8}h^{3}+O \bigl(h^{4} \bigr), \\ &I_{1,0}(h)=-\sqrt{2}h^{\frac{3}{2}}+\frac{13\sqrt{2}}{48}h^{\frac {5}{2}}- \frac{359\sqrt{2}}{2{,}560}h^{\frac{7}{2}}+O \bigl(h^{\frac{9}{2}} \bigr), \\ &I_{2,0}(h)=-2h^{2}+\frac{7}{12}h^{3}+O \bigl(h^{4} \bigr), \\ &I_{3,0}(h)=-2\sqrt{2}h^{\frac{5}{2}}+\frac{5\sqrt{2}}{8}h^{\frac {7}{2}}+O \bigl(h^{\frac{9}{2}} \bigr), \\ &I_{0,2}(h)=-\frac{1}{12}h^{3}+O \bigl(h^{4} \bigr), \\ &I_{1,2}(h)=-\frac{\sqrt{2}}{12}h^{\frac{7}{2}}+O \bigl(h^{\frac{9}{2}} \bigr). \end{aligned} $$
(19)

Suppose that

$$ F(h)=k_{1}I_{0,0}(h)+k_{2}I_{1,0}(h)+k_{3}I_{2,0}(h)+k_{4}I_{0,2}(h)+k_{5}I_{3,0}(h)+k_{6}I_{1,2}(h) \equiv 0. $$
(20)

In the following, we need to prove that \(k_{i}=0\), \(i=1,2,\ldots,6\).

From \(F^{\prime}(0)=-k_{1}=0\) we have \(k_{1}=0\). Substituting \(k_{1}=0\) into (21), from \(\lim_{h\rightarrow0^{+}}\frac{F(h)}{h^{\frac {3}{2}}}=-\sqrt{2}k_{2}=0\) we have \(k_{2}=0\). Substituting \(k_{1}=k_{2}=0\) into (21), from \(F^{\prime\prime}(0)=-4k_{3}=0\) we have \(k_{3}=0\). Similarly, we can obtain that \(k_{4}=k_{5}=k_{6}=0\). □

Substituting statement (i) of Lemma 7 into (17), we have

$$\begin{aligned} M_{1}(h)={}&(c_{0,0}-a_{0,0})I_{0,0}(h) \\ &{} -(a_{1,0}+b_{0,1}+c_{1,0}+d_{0,1})I_{1,0}(h) \\ &{} - \biggl(a_{2,0}-c_{2,0}+\frac{b_{1,1}}{2}- \frac{d_{1,1}}{2} \biggr)I_{2,0}(h) \\ &{} +(c_{0,2}-a_{0,2})I_{0,2}(h) \\ &{} - \biggl(a_{3,0}+c_{3,0}+\frac{b_{2,1}}{3}+ \frac{d_{2,1}}{3} \biggr)I_{3,0}(h) \\ &{} -(a_{1,2}+3b_{0,3}+c_{1,2}+3d_{0,3})I_{1,2}(h). \end{aligned}$$
(21)

By statement (ii) of Lemma 7 the first-order Melnikov function \(M_{1}(h)\) given by (21) is a linear combination of six linearly independent functions \(I_{0,0}(h),I_{1,0}(h),I_{2,0}(h)\), \(I_{0,2}(h),I_{3,0}(h), I_{1,2}(h)\) with arbitrary coefficients. From Lemma 6 we obtain that \(M_{1}(h)\) has at least five simple zeros in \((0,+\infty)\). According to Theorem 1, we can deduce that there are at least five limit cycles that can bifurcate from the period annulus surrounding the origin of (3) by the first-order Melnikov function.

The proof of Theorem 3 for system (4) is similar. The main difference is that

$$ L^{\pm}(h):x=\pm\sqrt{2h-y^{2}+ \frac{y^{4}}{2}},\quad h\in \biggl(0,\frac{1}{4} \biggr) $$
(22)

and

$$ \alpha(h)=\sqrt{1-\sqrt{1-4h}},\qquad \alpha_{1}(h)=- \alpha(h), $$
(23)

so we omit it.