1 Introduction

In recent years, more and more phenomena of anomalous diffusion were found in physics, biology, and chemistry [1–3]. The theory of diffusion or transport on both disordered systems and fractals has been extensively studied [4–7]. Nevertheless, as a new and effective tool, the fractional derivative is quite suitable for the mathematical modeling of nonlocal processes such as fractional Brown motion [8, 9], non-Newtonian fluid mechanics [10], nonequilibrium thermodynamics [11], complex ecological systems [12], etc. This is also the main advantage of fractional derivatives compared with integer order derivative models. Mathematicians and physicists have established some significant fractional diffusion equations to describe anomalous diffusion [13, 14]. The main idea is continuous time random walks (CTRWs) with long time behavior of the mean square displacement \(\langle x^{2}(t)\rangle\sim t^{\gamma}\), where γ is the diffusion exponent. If \(\gamma=1\), it corresponds to normal diffusion, otherwise, the case \(\gamma<1\) corresponds to sub-diffusion and the case \(\gamma>1\) corresponds to sup-diffusion [14–17]. The classical diffusion equation in Euclidean space with d dimensions can be expressed by

$$ \frac{\partial}{\partial t}u(x,t)=\frac{1}{x^{d-1}}\frac{\partial }{\partial x} \biggl(x^{d-1} \frac{\partial}{\partial x}u(x,t) \biggr) . $$
(1.1)

The probability density of random walker namely the solution of (1.1) is

$$ u(x,t)=t^{-d/2}e^{-\frac{x^{2}}{4t}}. $$
(1.2)

Metzler et al. [18] have considered a random walk on fractal object with \(\gamma=2/d_{\omega}\), where \(d_{\omega}>2\) is the anomalous diffusion exponent. The probability density of the random walker’s asymptotic behavior satisfies

$$ u(x,t)\sim t^{-d_{f}/d_{\omega}}e^{-c(x/ \sigma)^{\mu}} \quad(t \to \infty), $$
(1.3)

where \(d_{f}\) is the fractal Hausdorff dimension and c is a nonzero constant,

$$ \sigma^{2}=\bigl\langle x^{2}(t)\bigr\rangle , \qquad \mu=d_{\omega}/(d_{\omega}-1). $$
(1.4)

This kind of anomalous diffusion on fractals could be characterized by the macroscopical fractional diffusion equation

$$ \frac{\partial^{\frac{2}{d_{\omega}}}}{\partial t^{\frac{2}{d_{\omega }}}}u(x,t)=\frac{1}{x^{d_{s}-1}}\frac{\partial}{\partial x} \biggl(x^{d_{s}-1} \frac{\partial}{\partial x}u(x,t) \biggr), $$
(1.5)

where \(d_{s}=2d_{f}/d_{\omega}\) is called the fractal spectral dimension. The operator \(\partial^{\frac{2}{d_{\omega}}}/\partial t^{\frac{2}{d_{\omega}}}\) is the Riemann-Liouville fractional derivative of order \(2/d_{w}\), which is defined by

$$ \frac{\partial^{\frac{2}{d_{\omega}}}}{\partial t^{\frac{2}{d_{\omega }}}}f(t)=\frac{1}{\Gamma(1-2/d_{\omega})}\frac{d}{dt} \int_{0}^{t}(t-\eta)^{-\frac{2}{d_{\omega}}}f(\eta)\,d\eta. $$
(1.6)

The time fractional diffusion equation (1.5) can be regarded as a generalization of diffusion equation (1.1). If \(d_{\omega}=2\), equation (1.5) is reduced to the normal diffusion equation (1.1). In recent years, a great deal of mathematical effort in analytical and numerical method for fractional differential equations has been devoted to FPDE’s applications, for instance, the Fourier-Laplace transform [19], the Mellin transform [20, 21], the homotopy perturbation method (HPM) [22, 23], the homotopy perturbation Sumudu transform method (HPSTM) [24, 25], the Green’s function [26, 27], the Adomian decomposition method (ADM) [28], etc., but there is not one single method that can be adapted to all fractional equations. The non-locality of the fractional derivative operator makes it difficult for mathematical analysis and numerical computation. The objective of this paper is twofold. The first one is to investigate the singular Sturm-Liouville problem of (1.5) with the Dirichlet boundary condition [29–31], the other is to give an implicit numerical method for fractional diffusion equation with non-homogeneous Dirichlet boundary. Due to the relationship between Caputo and Riemann-Liouville type fractional derivatives [19], we can write the equation as

$$ {}_{0}^{C}D_{t}^{\alpha}u(x,t)= \frac{1}{x^{\beta}}\frac{\partial }{\partial x} \biggl(x^{\beta}\frac{\partial}{\partial x}u(x,t) \biggr)+f(x,t) $$
(1.7)

with the initial and boundary conditions

$$\begin{aligned}& u(x,0)=\psi(x),\quad0< x< L, \end{aligned}$$
(1.8)
$$\begin{aligned}& u(0,t)=u(L,t)=0,\quad0< t< \infty, \end{aligned}$$
(1.9)

where \(\alpha=2/d_{\omega},\beta=d_{s}-1\), and \(0<\alpha,\beta<1\). The Caputo type operator \({}_{0}^{C}D_{t}^{\alpha}\) is defined by

$$ {}_{0}^{C}D_{t}^{\alpha}u(x,t)= \frac{1}{\Gamma(1-\alpha)} \int_{0}^{t}(t-\eta)^{-\alpha} \frac{\partial u(x,\eta)}{\partial\eta}\,d\eta. $$
(1.10)

This paper is organized as follows. In the second part, we deal with the singular Sturm-Liouville problem. In the third part, we discuss the numerical method, which contains a stability and convergence analysis; the numerical results of a concrete example and a robustness analysis are also given.

2 Sturm-Liouville problem

In this section, first of all, we consider the following homogeneous equation:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} {}_{0}^{C}D_{t}^{\alpha}u(x,t)=\frac{1}{x^{\beta}}\frac{\partial }{\partial x} (x^{\beta}\frac{\partial}{\partial x}u(x,t) ),\ & 0< \alpha,\beta< 1,\\ u(x,0)=\psi(x),& 0< x< L, \\ u(0,t)=u(L,t)=0 ,& 0< t< \infty. \end{array}\displaystyle \right . $$
(2.1)

Let \(u(x,t)=X(x)T(t)\), λ denotes the eigenvalue of (2.1). Thus we have

$$ \frac{ (x^{\beta}X'(x) )'}{x^{\beta}X(x)}=\frac {{}_{0}^{C}D_{t}^{\alpha}T(t)}{T(t)}:=-\lambda. $$
(2.2)

Because of the boundary conditions, we have \(X(0)=X(L)=0\). Hence we obtain the S-L problem

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \frac{d}{dx} (x^{\beta}\frac{dX}{dx} )+\lambda x^{\beta} X(x)=0, \\ X(0)=X(L)=0. \end{array}\displaystyle \right . $$
(2.3)

The fractional order differential equation about \(T(t)\) is

$$ {}_{0}^{C}D_{t}^{\alpha}T(t)+\lambda T(t)=0. $$
(2.4)

Let \(p(x)=x^{\beta}\geq0\) and the root of \(p(x)\) belong to \([0,L]\), hence, the S-L problem is singular.

Lemma 2.1

Let \(u(x),v(x) \in C^{2}[0,L]\), for the linear differential operator \(N:=\frac{d}{dx} (p(x)\frac{d}{dx} )\), the following equation ideally holds:

$$ \int_{0}^{L}(v Nu-u Nv)\,dx=p(x)\bigl[u'(x)v(x)-u(x)v'(x) \bigr] \big|_{0}^{L} . $$
(2.5)

In particular, if \(u(x),v(x) \in C_{0}^{2}[0,L]\), we have

$$ \int_{0}^{L}(v Nu-u Nv)\,dx=0. $$
(2.6)

Proof

Applying the formula of the integral by parts to the left side of (2.5), then we can obtain

$$\begin{aligned}& \int_{0}^{L}v N u \,dx=p(x)u'(x)v(x) \big|_{0}^{L}- \int_{0}^{L}p(x)u'(x)v'(x)\,dx, \end{aligned}$$
(2.7)
$$\begin{aligned}& \int_{0}^{L}u N v \,dx=p(x)u(x)v'(x) \big|_{0}^{L}- \int_{0}^{L}p(x)u'(x)v'(x)\,dx . \end{aligned}$$
(2.8)

The conclusion follows from equation (2.7) minus equation (2.8). The lemma is now proved. □

Theorem 2.1

The eigenvalue and eigenvector have the following properties.

  1. (1)

    All of eigenvalues \(\lambda_{j}\) are negative real numbers.

  2. (2)

    Eigenvectors corresponding to different eigenvalues are orthogonal on \([0,L]\), with respect to the weight function \(x^{\beta}\), that is, if \(\lambda_{j}\neq\lambda_{k}\) and \(X_{m}\) \((m=j,k)\) are the corresponding eigenvectors, then we have

    $$\int_{0}^{L}p(x)X_{j}(x)X_{k}(x)=0\quad (j\neq k). $$
  3. (3)

    An orthogonal basis \(\{X_{n}(x)\}\) is a complete orthogonal system in \(L_{2}^{*}[0,L]\), where

    $$L_{2}^{*}[0,L]= \biggl\{ y(x) \Big| \int_{0}^{L}p(x)y^{2}(x)\,dx < \infty \biggr\} . $$

Proof

(1) If there are a complex number λ and \(\eta(x) \in C_{0}^{2}[0,L]\) such that

$$ N\eta(x)-\lambda p(x)\eta(x)=0. $$
(2.9)

The conjugate λ̄ and η̄ satisfy

$$ N\bar{\eta}(x)-\lambda p(x)\bar{\eta}(x)=0. $$
(2.10)

Following from Lemma 2.1, the next equality holds:

$$ \int_{0}^{L}\bar{\eta}N\eta-\eta N\bar{\eta}\,dx=0. $$
(2.11)

That is,

$$ (\lambda-\bar{\lambda}) \int_{0}^{L}p(x)\eta(x)\bar{\eta}(x)\,dx=0. $$
(2.12)

The fact that \(\eta(x)\neq0\) implies that \(\lambda=\bar{\lambda}\). Multiply \(\eta(x)\) at both sides of equation (2.9) and then perform the integral on the interval \([0,L]\), then we have

$$ \lambda \int_{0}^{L}p(x)\eta^{2}(x)\,dx= \int_{0}^{L}p(x)\eta^{\prime2}(x)\,dx. $$
(2.13)

The eigenvalue λ must be a negative real number.

(2) By Lemma 2.1, the eigenfunctions \(X_{j}\) and \(X_{k}\) satisfy

$$ \int_{0}^{L}X_{j}N X_{k}-X_{k}N X_{j}\,dx=0 $$
(2.14)

and

$$ X_{j}N X_{k}=-\lambda_{k}p(x)X_{j}X_{k}; \qquad X_{k}N X_{j}=-\lambda_{j}p(x) X_{j}X_{k}. $$
(2.15)

Therefore,

$$ (\lambda_{j}-\lambda_{k}) \int_{0}^{L}p(x)X_{j}(x)X_{k}(x)\,dx=0. $$
(2.16)

If \(\lambda_{j}\neq\lambda_{k}\), the eigenvectors \(X_{m}\) \((m=j,k)\) are orthogonal in \(L_{2}^{*}[0,L]\).

(3) Let \(f(x)\in H^{1}[0,L]\),

$$ \delta_{N}=f(x)-\sum_{n=1}^{N}f_{n}X_{n}(x). $$
(2.17)

Define

$$\begin{aligned}& H(y,z)= \int_{0}^{L}p(x)y(x)z(x)\,dx; \qquad H(y)=H(y,y), \end{aligned}$$
(2.18)
$$\begin{aligned}& D(y,z)= \int_{0}^{L}p(x)y'(x)z'(x)\,dx; \qquad D(y)=D(y,y). \end{aligned}$$
(2.19)

Then we have \(H (\delta_{N},X_{k})=0\). The Rayleigh quotient of the singular S-L problem

$$ J[\delta_{N}]=\frac{D(\delta_{N})}{H(\delta_{N})} \geq\lambda_{N+1}. $$
(2.20)

By the Sobolev embedding theorem \(H^{1}[0,L] \hookrightarrow C^{1}[0,L]\), \(\lim_{n \to\infty}\lambda_{n}=+\infty\), thus,

$$ H(\delta_{N})=\|\delta_{N}\|_{L_{2}^{*}}\leq \frac{D(r_{N})}{\lambda _{N+1}}\leq\frac{D(f)}{\lambda_{N+1}} \to0\quad(N \to\infty). $$
(2.21)

Since the Hilbert space \(H^{1}\) is dense in \(L_{2}^{*}[0,L]\), the proof is now complete. □

Let \(X(x)=x^{\nu}Y(x)\), where \(\nu=\frac{1-\beta}{2}\), suppose \(X(x)=O(x^{\nu})\), hence equation (2.3) becomes

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} x^{2}Y''(x)+xY'(x)+(\lambda x^{2}-\nu^{2})Y(x)=0, \\ Y(0)< \infty,\qquad Y(L)=0. \end{array}\displaystyle \right . $$
(2.22)

The stretching transformation \(y(x)=Y(\frac{x}{\sqrt{\lambda}})\) is used to convert equation (2.22) into the νth order Bessel equation,

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} x^{2}y''(x)+xy'(x)+(x^{2}-\nu^{2})y(x)=0, \\ y(0)< \infty, \qquad y(\sqrt{\lambda} L)=0. \end{array}\displaystyle \right . $$
(2.23)

The solution of the νth order Bessel equation is

$$ y(x)=C_{1}J_{\nu}(x)+C_{2}J_{-\nu}(x), $$
(2.24)

where \(C_{1}\) and \(C_{2}\) are arbitrary constants. \(J_{\nu}(x)\) and \(J_{-\nu}(x)\) are Bessel functions,

$$ \begin{aligned} &J_{\nu}(x)=\sum_{k=0}^{\infty} \frac{(-1)^{k}}{k!\Gamma(\nu+k+1)} \biggl(\frac{x}{2} \biggr)^{2k+\nu}, \\ &J_{-\nu}(x)=\sum_{k=0}^{\infty} \frac{(-1)^{k}}{k!\Gamma(-\nu+k+1)} \biggl(\frac{x}{2} \biggr)^{2k-\nu }. \end{aligned} $$
(2.25)

Combined with the boundary conditions, set \(\mu_{\nu}^{(n)}\) is the nth solution of the νth order Bessel function [32], and \(0<\mu_{\nu}^{(1)}<\mu_{\nu}^{(2)}<\cdots <\mu _{\nu}^{(n)}<\cdots\), \(\lim_{n \to\infty}\mu_{\nu}^{(n)}=+\infty\). Then, the eigenvalues and eigenfunctions for (2.3) are given by

$$ \lambda_{n}= \biggl(\frac{\mu_{\nu}^{(n)}}{L} \biggr)^{2} ;\qquad X_{n}(x)=x^{\nu}J_{\nu} \biggl(\frac{\mu_{\nu}^{(n)}}{L}x \biggr). $$
(2.26)

Lemma 2.2

Let \(n-1< p\leq n\), the Laplace transform formula for the Caputo fractional derivative is

$$\mathscr{L}\bigl\{ {}_{0}^{C}D_{t}^{p}f(x) \bigr\} =s^{p}F(s)-\sum_{k=0}^{n-1}s^{p-k-1}f^{(k)}(0+). $$

Laplace transform formula for the Mittag-Leffler function is

$$\mathscr{L}\bigl\{ t^{n\alpha+\beta-1}E_{\alpha,\beta}^{(n)}\bigl(-\gamma t^{\alpha }\bigr)\bigr\} =\frac{n!s^{\alpha-\beta}}{(s^{\alpha}+\gamma)^{n+1}}, $$

where \(F(s)\) is the Laplace transform for \(f(x)\), γ is a real number, and the Mittag-Leffler function \(E_{\alpha,\beta}(t)\) is

$$E_{\alpha,\beta}(t)=\sum_{k=0}^{\infty} \frac{t^{k}}{\Gamma(\alpha k+\beta)}. $$

Proof

See [19]. □

By the Laplace transform, Lemma 2.2, and the inverse Laplace transform, the solution of (2.4) is given as

$$ T_{n}(t)=E_{\alpha,1}\bigl(-\lambda_{n}t^{\alpha} \bigr). $$
(2.27)

Hence the general solution of (2.1) is of the form of the following series:

$$ u(x,t)=\sum_{n=1}^{\infty}D_{n}x^{\nu}J_{\nu} \biggl(\frac{\mu_{\nu }^{(n)}}{L}x \biggr)E_{\alpha,1} \biggl(- \biggl( \frac{\mu_{\nu }^{(n)}}{L} \biggr)^{2} t^{\alpha} \biggr). $$
(2.28)

We consider the initial value and Theorem 2.1; \(D_{n}\) can be determined by

$$ D_{n}=\frac{\int_{0}^{L}\psi(x)p(x)X_{n}(x)\,dx}{\|X_{n}(x)\|_{L_{2}^{*}}^{2}}. $$
(2.29)

For the non-homogeneous equation

$$ {}_{0}^{C}D_{t}^{\alpha}u(x,t)= \frac{1}{x^{\beta}}\frac{\partial }{\partial x} \biggl(x^{\beta}\frac{\partial}{\partial x}u(x,t) \biggr)+f(x,t). $$
(2.30)

Let the non-homogeneous term \(f(x,t)\) and the solution \(u(x,t)\) and the initial value \(\psi(x)\) be of the following form of a series expansion:

$$\begin{aligned} &f(x,t)=\sum_{n=1}^{\infty}f_{n}(t)X_{n}(x), \\ &u(x,t)=\sum_{n=1}^{\infty}T_{n}(t)X_{n}(x), \\ &\psi(x)=\sum_{n=1}^{\infty}\psi_{n} X_{n}(x), \end{aligned}$$
(2.31)

where \(f_{n}(t)\) is the general Fourier series of \(f(x,t)\), \(\psi_{n}\) is the general Fourier series of \(\psi(x)\). Insert series (2.31) into the non-homogeneous equation (2.30) and the initial value condition, then we have

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} {}_{0}^{C}D_{t}^{\alpha}T_{n}(t)+\lambda_{n} T_{n}(t)=f_{n}(t), \\ T_{n}(0)=\psi_{n}. \end{array}\displaystyle \right . $$
(2.32)

By the Laplace transform, Lemma 2.2, and the inverse Laplace transform, \(T_{n}(t)\) is given as

$$ T_{n}(t)=\psi_{n} E_{\alpha,1}\bigl(- \lambda_{n}t^{\alpha}\bigr)+ \int_{0}^{t}f_{n}(t-\tau) E_{\alpha,\alpha}\bigl(-\lambda_{n}\tau^{\alpha}\bigr)\,d\tau. $$
(2.33)

Finally, we obtain the solution of the non-homogeneous equation (2.30)

$$ u(x,t)=\sum_{n=1}^{\infty}x^{\nu} \biggl[\psi_{n} E_{\alpha,1}\bigl(-\lambda_{n}t^{\alpha} \bigr)+ \int_{0}^{t}f_{n}(t-\tau) E_{\alpha,\alpha}\bigl(-\lambda_{n}\tau^{\alpha}\bigr)\,d\tau \biggr]J_{\nu} \biggl(\frac{\mu_{\nu }^{(n)}}{L}x \biggr), $$
(2.34)

where the generalized Fourier coefficients are

$$\begin{aligned}& f_{n}(t)=\frac{\int_{0}^{L}f(x,t)p(x)X_{n}(x)\,dx}{\|X_{n}(x)\| _{L_{2}^{*}}^{2}}, \end{aligned}$$
(2.35)
$$\begin{aligned}& \psi_{n}=\frac{\int_{0}^{L}\psi(x)p(x)X_{n}(x)\,dx}{\|X_{n}(x)\| _{L_{2}^{*}}^{2}}. \end{aligned}$$
(2.36)

3 Numerical method

In the section, we propose an implicit numerical method for the Caputo type FPDE.

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} {}_{0}^{C}D_{t}^{\alpha}u(x,t)=\frac{1}{x^{\beta}}\frac{\partial }{\partial x} (x^{\beta}\frac{\partial}{\partial x}u(x,t) )+f(x,t), & 0< \alpha,\beta< 1,\\ u(x,0)=\psi(x),& 0< x< L, \\ u(0,t)=u(L,t)=0,& 0< t< \infty. \end{array}\displaystyle \right . $$
(3.1)

We use a uniform grid for spatial axis with grid spacing \(h=L/M\), the points in the grid \(x_{j}\) are given by

$$ x_{j}=j h,\quad j=0,1,2,\ldots,M. $$
(3.2)

Likewise, we take a grid on the temporal axis with grid spacing τ, the grid points \(t_{n}\) are given by

$$ t_{n}=n\tau, \quad n=0,1,2,\ldots. $$
(3.3)

Let \(u_{j}^{n}\) be the numerical approximation to the solution of (3.1) at the point \((j h,n\tau)\). Similarly, \(f_{j}^{n}=f(j h,n\tau)\). Using the forward difference, we have a finite difference approximation of the Caputo type fractional derivative,

$$\begin{aligned} {}_{0}^{C}D_{t}^{\alpha}u(x,t)\big|_{(x_{j},t_{n})}&= \frac{1}{\Gamma (1-\alpha)} \int_{0}^{t_{n}}(t_{n}-\eta)^{-\alpha} \frac{\partial u(x_{j},\eta)}{\partial\eta}\,d\eta \\ &=\frac{1}{\Gamma(1-\alpha)}\sum_{k=1}^{n} \int_{t_{k-1}}^{t_{k}}(t_{n}-\eta)^{-\alpha} \frac{\partial u(x_{j},\eta )}{\partial\eta}\,d\eta \\ &=\frac{1}{\Gamma(1-\alpha)}\sum_{k=1}^{n} \tau^{-1}\Delta_{t}(x_{j},t_{k-1}) \int_{t_{k-1}}^{t_{k}}(t_{n}-\eta)^{-\alpha}\,d\eta+O(\tau) \\ &\approx\frac{\tau^{-\alpha}}{\Gamma(2-\alpha)}\sum_{k=0}^{n-1} \omega_{k;\alpha}\Delta_{t}u(x_{j},t_{n-k-1}), \end{aligned}$$
(3.4)

where \(\omega_{k;\alpha}=(1+k)^{1-\alpha}-k^{1-\alpha},k=0,1,2,\ldots ,n-1\). The expression of the forward difference \(\Delta _{t}u(x_{j},t_{n-k-1})\) is

$$ \Delta_{t}u(x_{j},t_{n-k-1})=u(x_{j},t_{n-k})-u(x_{j},t_{n-k-1}). $$
(3.5)

According to Abelian summation method by part, we have

$$ \sum_{k=0}^{n}\omega_{k;\alpha}\Delta _{t}u(x_{j},t_{n-k})=u(x_{j},t_{n+1})- \omega_{n;\alpha }u(x_{j},t_{0})+\sum _{k=0}^{n-1}(\omega_{k+1;\alpha}- \omega_{k;\alpha })u(x_{j},t_{n-k}). $$
(3.6)

Using the backward difference for \(\partial u/ \partial x\) and the central difference for \(\partial^{2}u/\partial x^{2}\),

$$\begin{aligned}& \frac{\partial u}{\partial x} \bigg| _{(x_{j},t_{n+1})}=\frac {u(x_{j},t_{n+1})-u(x_{j-1},t_{n+1})}{h}+O(h), \end{aligned}$$
(3.7)
$$\begin{aligned}& \frac{\partial^{2}u}{\partial x^{2}} \bigg|_{(x_{j},t_{n+1})}=\frac {u(x_{j+1},t_{n+1})-2u(x_{j},t_{n+1})+u(x_{j-1},t_{n+1})}{h^{2}}+O\bigl(h^{2} \bigr). \end{aligned}$$
(3.8)

Hence, we obtain a numerical scheme for (3.1)

$$\begin{aligned} &(1+2r-r_{j})u_{j}^{n+1} \\ &\quad=\omega_{n;\alpha}u_{j}^{0}+ \sum_{k=0}^{n-1}(\omega_{k;\alpha}- \omega_{k+1;\alpha })u_{j}^{n-k}+ru_{j+1}^{n+1}+(r-r_{j})u_{j-1}^{n+1}+ \tau^{\alpha}\Gamma(2-\alpha)f_{j}^{n+1}, \end{aligned}$$
(3.9)

where

$$ r=\frac{\tau^{\alpha}\Gamma(2-\alpha)}{h^{2}} ; \qquad r_{j}=\frac{\beta \tau^{\alpha}\Gamma(2-\alpha)}{jh^{2}},\quad j=1,2, \ldots,M, $$
(3.10)

with the initial and boundary conditions

$$ \begin{aligned} &u_{j}^{0}=\psi(jh), \quad j=0,1,2,\ldots,M, \\ &u_{0}^{n}=u_{M}^{n}=0, \quad n=0,1,2,\ldots. \end{aligned} $$
(3.11)

When \(n=0\) the numerical scheme of (3.9) becomes

$$ (1+2r-r_{j})u_{j}^{1}=u_{j}^{0}+ru_{j+1}^{1}+(r-r_{j})u_{j-1}^{1}+ \tau^{\alpha}\Gamma(2-\alpha)f_{j}^{1} . $$
(3.12)

Instead of equations (3.9) and (3.12), the difference scheme can be rewritten in the following matrix form:

$$ \left \{ \textstyle\begin{array}{@{}l@{\quad}l} D \mathbf{u}^{1}=\mathbf{u}^{0}+\tau^{\alpha}\Gamma(2-\alpha)\mathbf {f}^{1}, \\ D \mathbf{u}^{n+1}=\omega_{n;\alpha}\mathbf{u}^{0}+\sum _{k=0}^{n-1}(\omega_{k;\alpha}-\omega_{k+1;\alpha})\mathbf{u}^{n-k}+\tau ^{\alpha}\Gamma(2-\alpha)\mathbf{f}^{n+1}, \quad n \geq1, \end{array}\displaystyle \right . $$
(3.13)

where

$$\begin{aligned}& D = \begin{pmatrix} 1+2r-r_{1} & -r & 0 & \cdots& 0 &0 \\ r_{2}-r&1+2r-r_{2}&-r&\cdots& 0&0\\ 0&r_{3}-r&1+2r-r_{3}&\cdots&0&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&1+2r-r_{M-2}&-r\\ 0&0&0&\cdots&r_{M-1}-r&1+2r-r_{M-1} \end{pmatrix} , \\& \mathbf{u}^{n}= \begin{pmatrix} &u_{1}^{n}&\\ &u_{2}^{n}&\\ &\vdots&\\ &u_{M-2}^{n}&\\ &u_{M-1}^{n}& \end{pmatrix} ,\qquad \mathbf{f}^{n}= \begin{pmatrix} &f_{1}^{n}&\\ &f_{2}^{n}&\\ &\vdots&\\ &f_{M-2}^{n}&\\ &f_{M-1}^{n}& \end{pmatrix} . \end{aligned}$$

We consider the stability of (3.13) in the following supremum norm:

$$ \bigl\| \mathbf{u}^{n+1}\bigr\| _{\infty}=\max_{1\leq j\leq M-1}\bigl|u_{j}^{n+1}\bigr|, \qquad\|\mathbf{f}\|_{\infty}=\max_{0\leq j\leq M,n\geq0}\bigl|f_{j}^{n}\bigr|. $$
(3.14)

Lemma 3.1

The coefficients \(\omega_{k;\alpha},r_{j},r\) satisfy

  1. 1.

    \(r>r_{j}>0, j=1,2,\ldots,M\),

  2. 2.

    \(\omega_{k;\alpha}>0\) and \(\omega_{k;\alpha}^{-1}=O(k^{\alpha}),k \to\infty\),

  3. 3.

    \(\omega_{k;\alpha}>\omega_{k+1;\alpha}, k=0,1,2,\ldots,n-1\).

Proof

See [33, 34]. □

Theorem 3.1

The difference scheme (3.13) satisfies

$$\bigl\| \mathbf{u}^{n+1}\bigr\| _{\infty}\leq\bigl\| \mathbf{u}^{0} \bigr\| _{\infty}+C\|\mathbf{f}\|_{\infty}, $$

where C is a positive constant.

Proof

We use mathematical induction to show it. Suppose that \(|u_{j_{0}}^{1}|=\max\{|u_{1}^{1}|,u_{2}^{1},\ldots, |u_{M-1}^{1}|\}\). Applying Lemma 3.1, we have

$$\begin{aligned} (1+2r-r_{j})\bigl|u_{j_{0}}^{1}\bigr|&=\bigl|\omega_{n;\alpha }u_{j_{0}}^{0}+ru_{j_{0}+1}^{1}+(r-r_{j})u_{j_{0}-1}^{1}+ \tau^{\alpha }\Gamma(2-\alpha)f_{j}^{1}\bigr| \\ &\leq\omega_{n;\alpha }\bigl|u_{j_{0}}^{0}\bigr|+r\bigl|u_{j_{0}+1}^{1}\bigr|+(r-r_{j})\bigl|u_{j_{0}-1}^{1}\bigr| +\tau^{\alpha}\Gamma(2-\alpha)\bigl|f_{j}^{1}\bigr| \\ &\leq\bigl|u_{j_{0}}^{0}\bigr|+r\bigl|u_{j_{0}}^{1}\bigr|+(r-r_{j})\bigl|u_{j_{0}}^{1}\bigr|+ \tau^{\alpha}\Gamma(2-\alpha)\bigl|f_{j}^{1}\bigr| \\ &\leq\bigl\| \mathbf{u}^{0}\bigr\| +(2r-r_{j})\bigl|u_{j_{0}}^{1}\bigr|+ \tau^{\alpha}\Gamma(2-\alpha)\|\mathbf{f}\|_{\infty}. \end{aligned}$$

Hence, we obtain

$$ \bigl\| \mathbf{u}^{1}\bigr\| _{\infty}\leq\bigl\| \mathbf{u}^{0} \bigr\| _{\infty}+C\|\mathbf{f}\|_{\infty}, $$
(3.15)

where the positive constant C is \(\omega_{n}^{-1}\tau^{\alpha}\Gamma (2-\alpha)\). We assume that

$$ \bigl\| \mathbf{u}^{m}\bigr\| _{\infty}\leq\bigl\| \mathbf{u}^{0} \bigr\| _{\infty}+C\|\mathbf{f}\|_{\infty},\quad m=1,2,\ldots,n. $$
(3.16)

We have \(m=n+1\). From (3.9) we obtain

$$\begin{aligned} &(1+2r-r_{j})\bigl\| \mathbf{u}^{n+1}\bigr\| _{\infty} \\ &\quad= \Biggl|\omega_{n;\alpha}u_{j_{0}}^{0} +\sum _{k=0}^{n-1}(\omega_{k;\alpha}- \omega_{k+1;\alpha})u_{j_{0}}^{n-k} +ru_{j_{0}+1}^{n+1}+(r-r_{j})u_{j_{0}-1}^{n+1}+ \tau^{\alpha}\Gamma(2-\alpha)f_{j_{0}}^{n+1}\Biggr| \\ &\quad\leq\bigl|u_{j_{0}}^{0}\bigr|+\sum_{k=0}^{n-1}( \omega_{k;\alpha}-\omega_{k+1;\alpha})\bigl|u_{j_{0}}^{n-k}\bigr| +r\bigl|u_{j_{0}+1}^{n+1}\bigr| +(r-r_{j})\bigl|u_{j_{0}-1}^{n+1}\bigr|+\tau^{\alpha} \Gamma(2-\alpha)\bigl|f_{j_{0}}^{n+1}\bigr| \\ &\quad\leq\bigl\| \mathbf{u}^{0}\bigr\| _{\infty}+\sum _{k=0}^{n-1}(\omega_{k;\alpha }- \omega_{k+1;\alpha})\bigl\| \mathbf{u}^{0}\bigr\| _{\infty}+(2r-r_{j}) \bigl\| \mathbf{u}^{n+1}\bigr\| _{\infty} +\omega_{n;\alpha}^{-1} \tau^{\alpha}\Gamma(2-\alpha)\|\mathbf{f}\| _{\infty} \\ &\quad\leq\bigl\| \mathbf{u}^{0}\bigr\| _{\infty}+(2r-r_{j})\bigl\| \mathbf{u}^{n+1}\bigr\| _{\infty} +\omega_{n;\alpha}^{-1} \tau^{\alpha}\Gamma(2-\alpha)\|\mathbf{f}\| _{\infty}. \end{aligned}$$

Therefore

$$ \bigl\| \mathbf{u}^{n+1}\bigr\| _{\infty}\leq\bigl\| \mathbf{u}^{0} \bigr\| _{\infty}+C\|\mathbf{f}\|_{\infty}. $$
(3.17)

We complete the proof. □

Theorem 3.2

The numerical schemes (3.9) and (3.12) for FPDE are unconditionally stable.

Proof

Suppose that \(\tilde{u}_{j}^{n}\) is an approximate solution of the numerical schemes (3.9) and (3.12). Let \(\varepsilon_{j}^{n}=\tilde{u}_{j}^{n}-u_{j}^{n}\), \(\varepsilon _{j}^{n}\) satisfy

$$ (1+2r-r_{j})\varepsilon_{j}^{n+1}= \omega_{n;\alpha}\varepsilon_{j}^{0}+\sum _{k=0}^{n-1}(\omega_{k;\alpha}- \omega_{k+1;\alpha })\varepsilon_{j}^{n-k}+r \varepsilon_{j+1}^{n+1}+(r-r_{j})\varepsilon _{j-1}^{n+1}. $$
(3.18)

Applying Theorem 3.1, we obtain

$$ \bigl\| {\boldsymbol{\varepsilon}}^{n+1}\bigr\| _{\infty}\leq\bigl\| {\boldsymbol{ \varepsilon}}^{0}\bigr\| _{\infty}. $$
(3.19)

 □

We denote the solution of IBVP (3.1) with \(u(x,t)\) and set \(z_{j}^{n}=u_{j}^{n}-u(j\Delta x,n\Delta t)\), and we see that \(z_{j}^{n}\) satisfies

$$ (1+2r-r_{j})z_{j}^{n+1}=\omega_{n;\alpha }z_{j}^{0}+rz_{j+1}^{n+1}+(r-r_{j})z_{j-1}^{n+1}+O \bigl(\tau^{1+\alpha }\bigr)+O\bigl(\tau^{\alpha}h^{2}\bigr). $$
(3.20)

Using \(\|z^{0}\|_{\infty}=0\) and Theorem 3.1, we have

$$ \bigl\| \mathbf{z}^{n+1}\bigr\| _{\infty}\leq C\tau^{a}\bigl( \tau+h^{2}\bigr). $$
(3.21)

Therefore, we obtain the global convergence theorem.

Theorem 3.3

The difference scheme (3.13) for approximating the partial differential equation (3.1) is a convergent scheme.

Some numerical examples are tested to verify the efficiency and stability of our proposed method.

Example

$$ \left \{ \textstyle\begin{array}{@{}l} {}_{0}^{C}D_{t}^{\alpha}u(x,t)=\frac{1}{x^{\beta}}\frac{\partial }{\partial x} (x^{\beta}\frac{\partial}{\partial x}u(x,t) )+f(x,t), \\ u(x,0)=0, \quad0< x< 1, \\ u(0,t)=u(1,t)=0, \end{array}\displaystyle \right . $$
(3.22)

where the non-homogeneous term \(f(x,t)\) satisfies

$$f(x,t)=\frac{t^{1-\alpha}\sin\pi x}{\Gamma(2-\alpha)}-\pi t \biggl(\frac {\beta}{x}\cos\pi x-\pi\sin\pi x \biggr). $$

The series solution can be yield by equation (2.1) and the exact analytical solution of (3.22) is given by

$$ u(x,t)=t \sin\pi x. $$
(3.23)

While \(\alpha=0\) (i.e., the anomalous diffusion exponent is large enough), the fractional Caputo operator is the identity operator and equation (1.7) is changed into the ordinary differential equation (ODE)

$$ u(x,t)=\frac{1}{x^{\beta}}\frac{\partial}{\partial x} \biggl( x^{\beta } \frac{\partial}{\partial x}u(x,t) \biggr)+f(x,t). $$
(3.24)

The maximum absolute errors between the exact solution and numerical solution

$$ E_{\infty}(\tau,h,\alpha,\beta)=\max_{0\leq j\leq M,n\geq 0}\bigl|u_{j}^{n}-u(x_{j},t_{n})\bigr| $$
(3.25)

are shown in Table 1 and Table 2. From Table 1, we can see that the maximum absolute error increases drastically as the parameter β increases. While in Table 2, the maximum absolute error is almost constant when the fractional order α changes in (3.22). In Figure 1, the numerical results for the time fractional diffusion equation with different parameters \(\tau,h,\beta\) are provided. In Figure 2, the numerical results for the time fractional diffusion equation with different parameters \(\tau,h,\alpha\) are also given. We assume that \(u_{\alpha,\beta}(x,t)\) is the solution of (1.7). The robustness parameter \(\Re_{\alpha}\) used to quantify the shift of the solution \(u_{\alpha,\beta}(x,t)\) at x position t time when α changes then is

$$ \Re_{\alpha}=\frac{\partial u_{\alpha,\beta}(x,t)}{\partial\alpha} . $$
(3.26)

Similarly, \(\Re_{\beta}\) is defined by

$$ \Re_{\beta}=\frac{\partial u_{\alpha,\beta}(x,t)}{\partial\beta} . $$
(3.27)

It is difficult to calculate the robustness parameters as above because we usually cannot get its exact solution \(u_{\alpha,\beta}(x,t)\). As an alternative, we explore the effects of \(d_{\omega}\) and \(d_{s}\) on the maximum absolute error \(E_{\infty}\), through the robustness parameters \(\tilde{\Re}_{d_{s}}\) and \(\tilde{\Re}_{d_{\omega}}\), which are defined as follows:

$$\begin{aligned}& \tilde{\Re}_{d_{s}}(\tau,h)=\frac{\partial E_{\infty}}{\partial d_{s}}, \end{aligned}$$
(3.28)
$$\begin{aligned}& \tilde{\Re}_{d_{\omega}}(\tau,h)=\frac{\partial E_{\infty}}{\partial d_{\omega}}. \end{aligned}$$
(3.29)

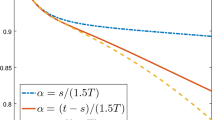
As shown in Figure 3, it is observed that the maximum absolute error increases drastically as the spectral dimension \(d_{s}\) increases. However, in Figure 4, with a change in the anomalous diffusion exponent \(d_{\omega}\), the maximum absolute error is almost constant. It shows that the influence of the spectral dimension \(d_{s}\) on the maximum absolute error \(E_{\infty}\) is larger than that of the anomalous diffusion exponent \(d_{\omega}\). Moreover, it is interesting to see that \(\tilde{\Re}_{d_{s}}(\tau,h)\) decreases as the parameter \(d_{s}\) increases for fixed τ and h, and that \(\tilde{\Re}_{d_{s}}(\tau ,h)\) decreases as the parameters τ and h decrease for fixed \(d_{s}\). In strong contrast to this case, \(\tilde{\Re}_{d_{\omega}}(\tau ,h)\) is almost constant, namely zero. Figure 5 shows the numerical solution of the time fractional diffusion equation. In Figure 6 the absolute error between the exact solution and numerical solution is presented. All of our tests are performed with MATLAB.

Figure 1
figure 1

Numerical results for time fractional diffusion equation at time \(\pmb{t=1.0}\) , \(\pmb{\alpha=0.5, \beta\in[0,1]}\) , from top to bottom: \(\pmb{\tau =h=0.1, 0.05, 0.025, 0.0125 }\) .

Full size image
Figure 2
figure 2

Numerical results for time fractional diffusion equation at time \(\pmb{t=1.0}\) , \(\pmb{\beta=0.5, \alpha\in[0,1]}\) , from top to bottom: \(\pmb{\tau =h=0.1, 0.05, 0.025, 0.0125 }\) .

Full size image
Figure 3
figure 3

The effect of spectral dimension \(\pmb{d_{s}}\) on the maximum absolute error, from top to bottom: \(\pmb{\tau=h=0.1, 0.05, 0.025, 0.0125}\) .

Full size image
Figure 4
figure 4

The effect of anomalous diffusion exponent \(\pmb{d_{\omega}}\) on the maximum absolute error, from top to bottom: \(\pmb{\tau=h=0.1, 0.05, 0.025, 0.0125 }\) .

Full size image
Figure 5
figure 5

Numerical solution of time fractional diffusion equation at time \(\pmb{t=1.0}\) , \(\pmb{\alpha=0.5, \beta=0.4, h=\tau=0.0125}\) .

Full size image
Figure 6
figure 6

The absolute error between the exact solution and numerical solution at time \(\pmb{t=1.0, \alpha=0.5, \beta=0.4, h=\tau=0.0125}\) .

Full size image
Table 1 The maximum absolute error \(\pmb{E_{\infty}}\) between the numerical solution and the exact solution, at time \(\pmb{t=1.0}\) , \(\pmb{\alpha=0.5}\)
Full size table
Table 2 The maximum absolute error \(\pmb{E_{\infty}}\) between the numerical solution and the exact solution, at time \(\pmb{t=1.0}\) , \(\pmb{\beta=0.5}\)
Full size table

4 Conclusion

In summary, we have presented the Sturm-Liouville problem and the series solution of the fractional sub-diffusion equation on fractals, and an implicit numerical scheme is also given. Furthermore, we have proved that the implicit numerical scheme is unconditionally stable and convergent. The computational examples show that the results from the numerical method agree quite well with the analytical solution. Previous research focuses only on analytical methods and numerical methods for fractional differential equation. However, the robustness analysis of the parameters, which is concerned with the fractional derivative order, is not considered. Through the numerical analysis, we found that the maximum error for the numerical solution is more sensitive to the spectral dimension in comparison with the anomalous diffusion exponent. The physical meaning is that the diffusion processes on fractals depend more on the value of the ratio of the fractal Hausdorff dimension to the anomalous diffusion exponent than on the anomalous diffusion exponent. This work is helpful for researchers dealing with similar fractional differential equations in physics and engineering.