1 Introduction

Mathematical models plays an important role in the study of epidemiology, which provides understanding of the underlying mechanisms that influence the spread of disease, and in the process, it suggests control strategies. Various epidemic models have been proposed and explored extensively, and great progress has been achieved in the studies of disease control and prevention (see, e.g., [1–4]).

For establishing a mathematical model of disease transmission with the population under study being divided into compartments and with assumptions about the nature and time rate of transfer from one compartment to another, we can formulate our descriptions as compartmental models. One of the most fundamental compartment models is the SIR model [5]. This model classifies individuals to be susceptible, infectious, or removed and permanently immune. Let \(S(t)\) be the number of susceptible individuals, \(I(t)\) the number of infective individuals, and \(R(t)\) the number of removed individuals at time t, respectively. A general SIR epidemic model can be formulated as

$$ \left \{ \textstyle\begin{array}{l} \frac{dS}{dt} = \Lambda-g(I)S-\mu S, \\ \frac{dI}{dt} = g(I)S-(\mu+\gamma)I, \\ \frac{dR}{dt} = \gamma I-\mu R, \end{array}\displaystyle \right . $$
(1.1)

where \(\Lambda>0\) is the recruitment rate of the population, \(\mu>0\) is the natural death rate of the population, and \(\gamma>0\) is the natural recovery rate of the infective individuals. The transmission of the infection is governed by the incidence rate \(g(I)S\), and \(g(I)\) is called the infection force.

In real life, the incidence rate \(g(I)S\) may be affected by many factors, such as media coverage, density of population, and life style. Especially, media coverage plays an important role in helping both the government authority make interventions to contain the disease and people response to the disease [6, 7]. Recently, many mathematical models have been proposed to investigate the impact of media coverage on the transmission dynamics of infectious diseases. Especially, Cui et al. [8], Tchuenche et al. [9], and Sun et al. [10] incorporated a nonlinear function of the number of infective individuals in their transmission term to investigate the effects of media coverage on the transmission dynamics:

$$ g(I)= \biggl( \beta_{1}-\frac{\beta_{2}I}{m+I} \biggr)I, $$
(1.2)

where \(\beta_{1}>0\) is the contact rate before media alert; the terms \(\beta_{2}I/(m+I)\) measure the effect of reduction of the contact rate when infectious individuals are reported in the media. Because the coverage report cannot prevent disease from spreading completely, we have \(\beta_{1}\geqslant\beta_{2}>0\). The half-saturation constant \(m>0\) reflects the impact of media coverage on the contact transmission. The function \(I/(m+I)\) is a continuous bounded function that takes into account disease saturation or psychological effects [10]. Hence, considering the effects of media coverage on the transmission dynamics, model (1.1) can be modified as follows:

$$ \left \{ \textstyle\begin{array}{l} \frac{dS}{dt} = \Lambda- ( \beta_{1}-\frac{\beta_{2}I }{m+I } )S I -\mu S , \\ \frac{dI }{dt} = (\beta_{1}-\frac{\beta_{2}I }{m+I } )S I -(\mu+\gamma)I , \\ \frac{dR }{dt} = \gamma I -\mu R . \end{array}\displaystyle \right . $$
(1.3)

As is known to us, real life is full of randomness and stochasticity, so it is important whether or not the long-time behavior of the solution for deterministic dynamics system can be changed by stochastic perturbations. In this paper, following the idea of [11–13], we introduce a random noise to model (1.3). Following the approach used in [14, 15], for Δt small, it is appropriate to model \(X(t)= (S(t), I(t), R(t))^{T}\) as a Markov process with the following specifications:

$$\begin{aligned}& \mathbb{E}\bigl[S(t+\Delta t)-S(t)|X(t)=x\bigr] \approx \biggl[ \Lambda- \biggl( \beta_{1}-\frac{\beta_{2}I }{m+I } \biggr)S I -\mu S \biggr]\Delta t, \\& \mathbb{E}\bigl[I(t+\Delta t)-I(t)|X(t)=x\bigr] \approx \biggl[ \biggl(\beta _{1}-\frac{\beta_{2}I }{m+I } \biggr)S I -(\mu+\gamma)I \biggr]\Delta t, \\& \mathbb{E}\bigl[R(t+\Delta t)-R(t)|X(t)=x\bigr] \approx [ \gamma I -\mu R ] \Delta t, \end{aligned}$$

and

$$\begin{aligned}& \operatorname{Var}\bigl[S(t+\Delta t)-S(t)|X(t)=x\bigr] \approx\sigma _{1}^{2}S^{2}\Delta t, \\& \operatorname{Var}\bigl[I(t+\Delta t)-I(t)|X(t)=x\bigr] \approx\sigma _{2}^{2}I^{2}\Delta t, \\& \operatorname{Var}\bigl[R(t+\Delta t)-R(t)|X(t)=x\bigr] \approx\sigma _{3}^{2}R^{2}\Delta t. \end{aligned}$$

More formally, we consider the following stochastic system:

$$ \left \{ \textstyle\begin{array}{l} dS(t) = [ \Lambda- ( \beta_{1}-\frac{\beta_{2}I(t) }{m+I(t)} )S(t) I(t) -\mu S(t) ]\, dt +\sigma_{1}S(t)\, dB_{1}(t), \\ dI(t) = [ (\beta_{1}-\frac{\beta_{2}I(t) }{m+I(t) } )S(t) I(t) -(\mu+\gamma)I(t) ]\, dt + \sigma_{2}I(t)\, dB_{2}(t), \\ dR(t) = [ \gamma I(t) -\mu R(t) ]\, dt +\sigma _{3}R(t)\, dB_{3}(t) . \end{array}\displaystyle \right . $$
(1.4)

Here we assume that \(B_{i}(t)\) (\(i=1,2,3\)) are independent Brownian motions and \(\sigma_{i}\) (\(i=1,2,3\)) are the coefficients of the effects of environmental stochastic perturbations on \(S(t)\), \(I(t)\), and \(R(t)\).

In the following, unless otherwise specified, we assume that \((\Omega, \mathcal{F}, \{\mathcal{F}_{t} \}_{t\geqslant0}, P)\) is a complete probability space with filtration \(\{\mathcal{F}_{t} \}_{t\geqslant0}\) satisfying the usual conditions (i.e., it is increasing and right continuous, and \(\mathcal{F}_{0}\) contains all P-null sets). Let \(B_{i}(t)\), \(i=1,2,3\), be Brownian motions defined on this probability space. Also, let \(\mathbb{R}^{3}_{+}=\{\mathbf{x}\in\mathbb{R}^{3}, x_{i}>0 \mbox{ for all } 1\leqslant i \leqslant3 \}\) and \(\mathbf {x}(t)=(S(t), I(t), R(t))^{T}\).

The rest of the paper is organized as follows. In Section 2, we first show the positivity and boundedness of the deterministic model (1.3); the existence and stability of equilibria of model (1.3) is also investigated in this section. In Section 3, we first study the existence of the global positive solution of the stochastic model (1.4), and then, we investigate the asymptotic behavior around the equilibria of model (1.3). In Section 4, we give some numerical simulations to support the theoretical prediction. In Section 5, a brief discussion is given.

2 Deterministic model

In this section, we first discuss some basic dynamical properties of the deterministic model (1.3), which is subjected to positive initial conditions

$$ S(0)\equiv S_{0}>0, \qquad I(0)\equiv I_{0}>0, \qquad R(0) \equiv R_{0}>0. $$
(2.1)

2.1 Positivity and boundedness

In this subsection, we study the positivity and boundedness of solutions of system (1.3) with initial condition (2.1).

Theorem 2.1

Solutions of system (1.3) with initial condition (2.1) are positive for all \(t \geqslant0\).

Proof

Let \((S(t),I(t),R(t))\) be a solution of system (1.3) with initial condition (2.1). Let us consider \(I(t)\) for \(t \geqslant 0\). It follows from the second equation of system (1.3) that

$$I(t)=I(0)e^{\int_{0}^{t} ( (\beta_{1}-\frac{\beta_{2}I(s)}{m+I(s)} ) S(s) -(\mu+\gamma))\,ds}. $$

From the initial condition (2.1) we have \(I(t)>0\) for \(t \geqslant0\). Then, from the third equation of system (1.3) we have

$$\frac{dR(t)}{dt} = \gamma I(t)-\mu R(t) > -dR(t). $$

A comparison argument shows that

$$R(t)\geqslant R(0)e^{-\mu t}. $$

From the initial condition (2.1) we have \(R(t)>0\) for \(t \geqslant0\).

Next, we prove that \(S(t)\) is positive. Assume the contrary; then let \(t_{1}\) be the first time such that \(S(t_{1})=0\). By the first equation of (1.3) we have

$$\frac{dS(t)}{dt}\bigg|_{t=t_{1}} = \Lambda>0. $$

This means that \(S(t)<0\) for \(t\in(t_{1}-\epsilon, t_{1})\), where ϵ is an arbitrarily small positive constant. This leads to a contradiction. It follows that \(S(t)\) is always positive for \(t \geqslant0\). This ends the proof. □

Theorem 2.2

Solutions of system (1.3) with initial condition (2.1) are ultimately bounded.

Proof

From Theorem 2.1, solutions of system (1.3) with initial condition (2.1) are positive for all \(t \geqslant0\). Let \(N(t)= S(t)+I(t)+R(t)\). From (1.3) we have

$$ \frac{dN(t)}{dt} = \Lambda-\mu N(t). $$
(2.2)

Therefore, \(N(t)<\frac{\Lambda}{\mu} +\epsilon\) for all large t, where ϵ is an arbitrarily small positive constant. Thus, \(S(t),I(t),R(t)\) are ultimately bounded. □

2.2 Equilibria and their existence

By the next generation method in [16] the basic reproduction number for model (1.3) is

$$ R_{0}=\frac{ \beta_{1}\Lambda}{\mu(\mu+\gamma)}. $$
(2.3)

Irrespective of the parameter values, system (1.3) always possesses a disease-free equilibrium \(E_{0}(\frac{\Lambda}{d},0,0)\). We next discuss the existence of endemic equilibrium. Suppose that \(E^{*}(S^{*},I^{*},R^{*})\) is an endemic equilibrium. Then \((S^{*},I^{*},R^{*})\) satisfies

$$ \left \{ \textstyle\begin{array}{l} \Lambda- g(I^{*})S^{*}I^{*}-\mu S^{*}=0, \\ g(I^{*})S^{*}I^{*} -(\mu+\gamma)I^{*} =0, \\ \gamma I^{*} -\mu R^{*}=0. \end{array}\displaystyle \right . $$
(2.4)

It follows that

$$ S^{*}=\frac{\Lambda}{g(I^{*})I^{*}+\mu}, \qquad R^{*}=\frac{\gamma I^{*} }{\mu}, $$
(2.5)

and \(I^{*}\) determined by

$$ \frac{\Lambda}{g(I^{*})I^{*}+\mu} = \frac{\mu+\gamma}{g(I^{*}) }, $$
(2.6)

where \(g(I)=\beta_{1}-\frac{\beta_{2}I}{m+I}\). Equation (2.6) is equivalent to

$$ \Lambda g\bigl(I^{*}\bigr) = ( \mu+\gamma ) \bigl(g\bigl(I^{*}\bigr)I^{*}+\mu\bigr). $$
(2.7)

Denote

$$ \left \{ \textstyle\begin{array}{l} G(I)= \Lambda g(I), \\ H(I)= ( \mu+\gamma ) (g(I)I+ \mu ). \end{array}\displaystyle \right . $$
(2.8)

From Theorem 2.1 and (2.2) we have \(I^{*}\in[0,\frac{\Lambda}{\mu }]\). From (2.8) we have

$$ \begin{aligned} &G(0)=\beta_{1}\Lambda, \qquad H(0)= ( \mu+ \gamma )\mu , \\ &G\biggl(\frac{\Lambda}{\mu}\biggr) = \Lambda g\biggl(\frac{\Lambda}{\mu}\biggr), \qquad H\biggl(\frac{\Lambda}{\mu}\biggr) = ( \mu+\gamma )\mu + ( \mu +\gamma )g \biggl(\frac{\Lambda}{\mu}\biggr)\frac{\Lambda}{\mu}. \end{aligned} $$
(2.9)

Hence, for \(R_{0}>1\), we have

$$ G(0)>H(0)\quad \mbox{and}\quad G \biggl(\frac{\Lambda}{\mu} \biggr)= \Lambda g \biggl(\frac{\Lambda}{\mu} \biggr) < ( \mu+\gamma )g \biggl(\frac{\Lambda}{\mu} \biggr)\frac{\Lambda}{\mu}< H \biggl(\frac{\Lambda}{\mu} \biggr). $$
(2.10)

For \(R_{0}<1\), we have

$$ G(0)< H(0). $$
(2.11)

Moreover, we can compute that

$$ \begin{aligned} &G^{\prime}(I)= -\frac{\Lambda\beta_{2}m}{(m+I)^{2}}, \\ &H^{\prime}(I)=(\mu+\gamma) \biggl( \beta_{1}-\frac{\beta _{2}(2mI+I^{2})}{(m+I)^{2}} \biggr). \end{aligned} $$
(2.12)

Note that \(\beta_{1} \geqslant\beta_{2}>0\). From (2.12) we can easily prove that \(G(I)\) is decreasing and \(H(I)\) is increasing. Hence, from (2.10)-(2.12) we can verify that if \(R_{0}>1\), then the two curves \(G(I)\) and \(H(I)\) have only one positive intersection in \([0,\frac{\Lambda}{\mu}]\), which gives only one endemic equilibrium. However, if \(R_{0}<1\), then it follows that the two curves \(G(I)\) and \(H(I)\) have no intersection in \([0,+\infty)\), which implies that there is no endemic equilibria.

From the discussion above we obtain the following:

Theorem 2.3

If \(R_{0}<1\), then system (1.3) has no endemic equilibria. If \(R_{0}>1\), then system (1.3) has only one endemic equilibrium.

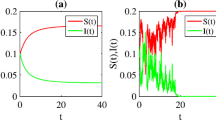
Figure 1 shows two possible cases of the intersection of the curves \(G(I)\) and \(H(I)\). Figure 1(a) shows that the two curves have no intersection with parameter I varying when \(R_{0}<1\). Figure 1(b) shows that the two curves have only one intersection with parameter I varying when \(R_{0}>1\).

Figure 1
figure 1

Two possible cases of the intersection of the curves \(\pmb{G(I)}\) and \(\pmb{H(I)}\) indicating the existence of positive equilibria. (a) \(\Lambda=15\), \(\beta_{1}=0.0008\), \(\beta_{2}=0.0006\), \(m=30\), \(\mu=0.05\), \(\gamma=0.2 \). \(R_{0}=0.96<1\). (b) \(\Lambda=15\), \(\beta_{1}=0.002\), \(\beta_{2}=0.0018\), \(m=30\), \(\mu=0.05\), \(\gamma=0.2 \). \(R_{0}=2.4>1\).

Full size image

2.3 Stability of equilibria

In this subsection, by analyzing the corresponding characteristic equations we discuss the local stability of a disease-free equilibrium and endemic equilibrium of system (1.3), respectively.

The characteristic equation of system (1.3) at \(E_{0}\) is

$$ \det \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \lambda+\mu & \frac{\beta_{1}\Lambda}{\mu} & 0 \\ 0 & \lambda+ \mu+\gamma-\frac{\beta_{1}\Lambda}{\mu} & 0 \\ 0 & -\gamma & \lambda+\mu \end{array}\displaystyle \right ] = 0, $$
(2.13)

which is equivalent to

$$ (\lambda+\mu) (\lambda+\mu) \biggl(\lambda+\mu+\gamma-\frac{\beta _{1}\Lambda}{\mu} \biggr)=0. $$
(2.14)

It is easy to see that, when \(R_{0}<1\), (2.14) has three negative roots and, when \(R_{0}>1\), (2.14) always has one positive root. Thus, we have the following:

Theorem 2.4

  1. (i)

    The disease-free equilibrium \(E_{0}\) of (1.3) is locally asymptotically stable if \(R_{0}<1\).

  2. (ii)

    The disease-free equilibrium \(E_{0}\) of (1.3) is unstable if \(R_{0}>1\).

Next, we discuss the global stability of \(E_{0}\). It is easy to prove the following lemma.

Lemma 2.1

The plane \(S+I+R= \frac{\Lambda}{\mu}\) is an invariant manifold of system (1.3), which is globally attractive in \(\mathbb{R}^{3}_{+}\).

Theorem 2.5

If \(R_{0}<1\), then the disease-free equilibrium \(E_{0}\) is globally asymptotically stable.

Proof

Let \((S(t),I(t),R(t))\) be any positive solution of system (1.3) with initial condition (2.1).

If \(R_{0}<1\), then choose \(\epsilon>0\) sufficiently small to satisfy

$$ \beta_{1} \biggl( \frac{\Lambda}{\mu}+\epsilon \biggr) < \mu+\gamma. $$
(2.15)

It follows from the first equation of system (1.3) that

$$ \frac{dS(t)}{dt} = \Lambda- \biggl( \beta_{1}-\frac{\beta _{2}I(t)}{m+I(t)} \biggr)S(t)I(t)-\mu S(t) \leqslant \mu \biggl( \frac {\Lambda}{\mu}-S(t) \biggr). $$

By comparison we obtain that

$$ \limsup_{t \rightarrow+\infty} S(t)\leqslant\frac{\Lambda }{\mu} . $$
(2.16)

Hence, for \(\epsilon>0\) sufficiently small to satisfy (2.15), there is \(T_{1}>0\) such that if \(t>T_{1}\), then \(S(t)<\frac{\Lambda }{\mu} +\epsilon\).

For \(\epsilon>0\) sufficiently small to satisfy (2.15), it follows from the second equation of system (1.3) that, for \(t>T_{1}\),

$$\begin{aligned} \frac{dI(t)}{dt} =& \biggl(\beta_{1}-\frac{\beta_{2}I(t)}{m+I(t)} \biggr)S(t)I(t) -(\mu+\gamma)I(t) \leqslant\beta_{1} S(t)I(t) -(\mu+ \gamma )I(t) \\ < & \beta_{1} \biggl( \frac{\Lambda}{\mu}+\epsilon \biggr)I(t)-(\mu + \gamma)I(t). \end{aligned}$$

From (2.15) a comparison argument shows that

$$ \lim_{t\rightarrow+\infty} I(t)=0. $$

Hence, for \(\epsilon>0\) sufficiently small to satisfy (2.15), there is \(T_{2}>T_{1}\) such that if \(t>T_{2}\), then \(I(t)<\epsilon\).

From the first equation of system (1.3), for \(t>T_{2}\), we have

$$ \frac{dS(t)}{dt} = \Lambda- \biggl( \beta_{1}-\frac{\beta _{2}I(t)}{m+I(t)} \biggr)S(t)I(t)-\mu S(t) \geqslant\Lambda- \beta _{1}\epsilon \biggl( \frac{\Lambda}{\mu}+\epsilon \biggr)-\mu S(t) . $$

By comparison it follows that

$$ \liminf_{t\rightarrow+\infty} S(t) \geqslant\frac{1}{\mu} \biggl( \Lambda- \beta_{1}\epsilon \biggl(\frac{\Lambda}{\mu}+\epsilon \biggr) \biggr). $$

Letting \(\epsilon\rightarrow0\), we derive that

$$ \liminf_{t\rightarrow+\infty} S(t) \geqslant\frac{\Lambda }{\mu} . $$
(2.17)

Thus, by (2.16) and (2.17),

$$ \lim_{t\rightarrow+\infty} S(t) = \frac{\Lambda}{\mu} . $$

Note that if \(R_{0}<1\), then the disease-free equilibrium \(E_{0}\) is locally asymptotically stable. Then, combining this with Lemma 2.1, we conclude that if \(R_{0}<1\), then the disease-free equilibrium \(E_{0}(\Lambda/\mu, 0, 0)\) is globally asymptotically stable. □

In the following, we suppose that \(R_{0}>1\) and \(E^{*}\) is an endemic equilibrium satisfying Eqs. (2.4)-(2.6).

Theorem 2.6

If \(R_{0}>1\), then the endemic equilibrium \(E^{*}\) is globally stable in \(\mathbb{R}^{3}_{+}\).

Proof

Noting that the variable R only occurs in the third equation of system (1.3), by Lemma 2.1 it suffices to investigate the subsystem

$$ \left \{ \textstyle\begin{array}{l} \frac{dS(t)}{dt} = \Lambda- ( \beta_{1}-\frac{\beta _{2}I(t)}{m+I(t)} )S(t)I(t)-\mu S(t), \\ \frac{dI(t)}{dt} = (\beta_{1}-\frac{\beta_{2}I(t)}{m+I(t)} )S(t)I(t) -(\mu+\gamma)I(t). \end{array}\displaystyle \right . $$
(2.18)

Taking the Dulac function \(D=\frac{1}{S(t)I(t)}\), we have

$$ \frac{\partial(Df_{1})}{\partial S}+\frac{\partial(Df_{2})}{\partial S}=- \biggl( \frac{1}{S^{2} I} + \frac{\beta_{2}m}{(m+I)^{2}} \biggr) < 0. $$

From the Bendixson-Dulac theorem [17] we know that system (2.18) has no limit cycle in \(\mathbb{R}^{2}_{+}\). Hence, system (1.3) has no limit cycle in \(\mathbb{R}^{3}_{+}\).

When \(R_{0}>1\), by Theorem 2.1, \(E_{0}\) is a hyperbolic unstable saddle point and repels solutions in its neighborhood. Due to the hyperbolicity of \(E_{0}\), it is not part of any cycle chain in \(\mathbb {R}^{3}_{+}\). Thus, every bounded forward orbit of (1.3) in \(\mathbb{R}^{3}_{+}\) converges to the unique endemic equilibrium \(E^{*}\). Therefore, \(E^{*}\) is globally asymptotically stable. The proof is complete. □

3 Stochastic model

In this section, we first show that the solution of system (1.4) is global and nonnegative. As we know, in order for a stochastic differential equation to have a unique global (i.e., without explosion in finite time) solution for any given initial value, the coefficients of the equation are generally required to satisfy the linear growth condition and local Lipschitz condition [18]. However, the coefficients of Eq. (1.4) do not satisfy the linear growth condition, though they are locally Lipschitz continuous, so the solution of Eq. (1.4) may explode in finite time [18]. Using the Lyapunov analysis method (mentioned in [18]), it is easy to show that the solution of Eq. (1.4) is positive and global.

Theorem 3.1

For any given initial value \((S(0),I(0),R(0))\in\mathbb {R}^{3}_{+}\), there is a unique positive solution \((S(t),I(t),R(t))\) of model (1.4) on \(t\geqslant0\), and the solution remains in \(\mathbb{R}^{3}_{+}\) with probability 1, namely \((S(t),I(t),R(t)) \in \mathbb{R}^{3}_{+}\) for all \(t\geqslant0\) almost surely.

From the discussion of Section 2, for the deterministic model (1.3), there is a disease-free equilibrium \(E_{0}=(\frac{\Lambda }{d},0,0)\), which is globally stable if \(R_{0}=\frac{ \beta_{1}\Lambda }{\mu(\mu+\gamma)}<1\). However, for the stochastic model (1.4), \(E_{0}=(\frac{\Lambda}{d},0,0)\) is no longer a disease-free equilibrium. In this subsection, we investigate the asymptotic behavior around \(E_{0}\).

Theorem 3.2

Suppose that \(R_{0}=\frac{ \beta_{1}\Lambda}{\mu(\mu+\gamma)}<1\) and

$$ \sigma_{1}^{2}< \mu,\qquad \sigma_{2}^{2}< 2( \mu+\gamma). $$
(3.1)

Then, for any given initial value \((S(0),I(0),R(0))\in\mathbb {R}^{3}_{+}\), the solution of model (1.4) has the property

$$ \limsup_{t\rightarrow\infty} \frac{1}{t} E \int_{0}^{t} \biggl[ \biggl( S(r)-\frac{\Lambda}{\mu} \biggr)^{2} +I^{2}(r) + R(r) \biggr] \, dr \leqslant \frac{2\sigma_{1}^{2}\Lambda^{2}}{\mu^{2}K_{1}}, $$

where

$$ K_{1}= \min \biggl\{ 2\bigl(\mu-\sigma_{1}^{2} \bigr), 2(\mu+\gamma)-\sigma _{2}^{2}, \frac{2(2\mu+\gamma)[\mu(\mu+\gamma)-\beta_{1}\Lambda ]}{\beta_{1}\mu\gamma} \biggr\} . $$

Proof

Let \(x=S-\frac{\Lambda}{\mu}\), \(y=I\), \(z=R\). Then system (1.4) can be rewritten as

$$ \left \{ \textstyle\begin{array}{l} dx= [- ( \beta_{1}-\frac{\beta_{2}y }{m+y} ) ( x+\frac{\Lambda}{\mu} )y -\mu x ] \,dt + \sigma_{1} ( x+\frac{\Lambda}{\mu} )\,dB_{1}(t), \\ dy= [ ( \beta_{1}-\frac{\beta_{2}y }{m+y} ) ( x+\frac{\Lambda}{\mu} )y -(\mu+\gamma)y ] \,dt + \sigma_{2} y\,dB_{2}(t), \\ dz= [\gamma y- \mu z ] \,dt + \sigma_{3} z\,dB_{3}(t). \end{array}\displaystyle \right . $$
(3.2)

By Theorem 3.1 we have \(x=S-\frac{\Lambda}{\mu}> -\frac{\Lambda}{\mu}\), \(y>0\), \(z>0\). Define the function

$$ V(x,y,z)=(x+y)^{2}+c_{1}y+c_{2}z, $$

where \(c_{1}\) and \(c_{2}\) are positive constants to be determined later. Then the function V is positive definite. Applying Itô’s formula, we obtain

$$ dV= LV\, dt + 2\sigma_{1} \biggl( x+\frac{\Lambda}{\mu} \biggr) (x+y) \,dB_{1}(t) + \sigma_{2}(2x+2y+c_{1})y \,dB_{2}(t)+c_{2}\sigma_{3}z\,dB_{3}(t), $$

where

$$\begin{aligned} LV =& -\bigl(2\mu-\sigma_{1}^{2}\bigr)x^{2} - \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2} -c_{2}\mu z +2\sigma _{1}^{2}\frac{\Lambda}{\mu}x + \sigma_{1}^{2}\frac{\Lambda^{2}}{\mu ^{2}} \\ &{} + \bigl[c_{1}\beta_{1}-2(2\mu+\gamma) \bigr]xy + \biggl[ c_{2}\gamma-c_{1}\beta_{1} \frac{\Lambda}{\mu} \biggl( \frac {1}{R_{0}}-1 \biggr) \biggr]y - \frac{\beta_{2}y}{m+y} \biggl(x+\frac {\Lambda}{\mu} \biggr)y. \end{aligned}$$

We can choose \(c_{1}=\frac{2(2\mu+\gamma)}{\beta_{1}}>0\) such that \(c_{1}\beta_{1}-2(2\mu+\gamma)=0\), and noting that \(R_{0}<1\), we can choose \(c_{2}>0\) such that \(c_{2}\gamma-c_{1}\beta_{1}\frac{\Lambda }{\mu} ( \frac{1}{R_{0}}-1 )=0\); then \(c_{2}=\frac{2\Lambda (2\mu+\gamma)(1-R_{0})}{\gamma\mu R_{0}} \). Thus, we obtain

$$\begin{aligned} LV =& -\bigl(2\mu-\sigma_{1}^{2}\bigr)x^{2} - \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2} -c_{2}\mu z +2\sigma _{1}^{2}\frac{\Lambda}{\mu}x + \sigma_{1}^{2}\frac{\Lambda^{2}}{\mu ^{2}} \\ &{} -\frac{\beta_{2}y}{m+y} \biggl(x+\frac{\Lambda}{\mu} \biggr)y \\ \leqslant& -\bigl(2\mu-\sigma_{1}^{2}\bigr)x^{2} - \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2} -c_{2}\mu z +2\sigma _{1}^{2}\frac{\Lambda}{\mu}x + \sigma_{1}^{2}\frac{\Lambda^{2}}{\mu ^{2}} \\ \leqslant& -\bigl(2\mu-\sigma_{1}^{2}\bigr)x^{2} - \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2} -c_{2}\mu z +\sigma _{1}^{2}x^{2} + 2 \sigma_{1}^{2}\frac{\Lambda^{2}}{\mu^{2}} \\ =& -2\bigl(\mu-\sigma_{1}^{2}\bigr)x^{2} - \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2} -c_{2}\mu z + 2\sigma _{1}^{2}\frac{\Lambda^{2}}{\mu^{2}} . \end{aligned}$$
(3.3)

Therefore,

$$\begin{aligned} dV =& LV\, dt + 2\sigma_{1} \biggl( x+\frac{\Lambda}{\mu} \biggr) (x+y)\,dB_{1}(t) + \sigma_{2}(2x+2y+c_{1})y \,dB_{2}(t) \\ &{} +c_{2}\sigma_{3}z\,dB_{3}(t) \\ \leqslant& \biggl[ -2\bigl(\mu-\sigma_{1}^{2} \bigr)x^{2} - \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2} -c_{2}\mu z + 2\sigma _{1}^{2} \frac{\Lambda^{2}}{\mu^{2}} \biggr] \,dt \\ &{} + 2\sigma_{1} \biggl( x+\frac{\Lambda}{\mu} \biggr) (x+y) \,dB_{1}(t) + \sigma_{2}(2x+2y+c_{1})y \,dB_{2}(t) \\ &{} +c_{2}\sigma_{3}z\,dB_{3}(t) . \end{aligned}$$
(3.4)

Integrating both sides of (3.4) from 0 to t and then taking expectation yield

$$\begin{aligned} 0 \leqslant& E\bigl[V\bigl(x(t),y(t),z(t)\bigr)\bigr] \\ \leqslant& E\bigl[V\bigl(x(0),y(0),z(0)\bigr)\bigr] \\ &{} + E \int_{0}^{t} \biggl[ -2\bigl(\mu- \sigma_{1}^{2}\bigr)x^{2}(r) - \bigl[2(\mu+\gamma)- \sigma_{2}^{2} \bigr]y^{2}(r) -c_{2}\mu z(r) + 2\sigma_{1}^{2}\frac{\Lambda^{2}}{\mu^{2}} \biggr] \,dr, \end{aligned}$$

which implies

$$\begin{aligned}& E \int_{0}^{t} \bigl[ 2\bigl(\mu-\sigma_{1}^{2} \bigr)x^{2}(r) + \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2}(r) + c_{2}\mu z(r) \bigr] \,dr \\& \quad \leqslant E\bigl[V\bigl(x(0),y(0),z(0)\bigr)\bigr] + 2\sigma_{1}^{2} \frac{\Lambda^{2}}{\mu ^{2}} t . \end{aligned}$$

Therefore,

$$\begin{aligned}& \limsup_{t\rightarrow\infty} \frac{1}{t} E \int_{0}^{t} \bigl[ 2\bigl(\mu-\sigma_{1}^{2} \bigr)x^{2}(r) + \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]y^{2}(r) + c_{2}\mu z(r) \bigr] \,dr \\& \quad \leqslant 2 \sigma_{1}^{2}\frac{\Lambda^{2}}{\mu^{2}}, \end{aligned}$$

from which it follows that

$$\begin{aligned}& \limsup_{t\rightarrow\infty} \frac{1}{t} E \int_{0}^{t} \biggl[ 2\bigl(\mu- \sigma_{1}^{2}\bigr) \biggl( S(r)-\frac{\Lambda}{\mu} \biggr)^{2} + \bigl[2(\mu+\gamma)-\sigma_{2}^{2} \bigr]I^{2}(r) + c_{2}\mu R(r) \biggr] \,dr \\& \quad \leqslant 2\sigma_{1}^{2}\frac{\Lambda^{2}}{\mu^{2}}. \end{aligned}$$
(3.5)

Letting

$$ K_{1}= \min \biggl\{ 2\bigl(\mu-\sigma_{1}^{2} \bigr), 2(\mu+\gamma)-\sigma _{2}^{2}, \frac{2(2\mu+\gamma)[\mu(\mu+\gamma)-\beta_{1}\Lambda ]}{\beta_{1}\mu\gamma} \biggr\} , $$

we have

$$ \limsup_{t\rightarrow\infty} \frac{1}{t} E \int_{0}^{t} \biggl[ \biggl( S(r)-\frac{\Lambda}{\mu} \biggr)^{2} + I^{2}(r) + R(r) \biggr] \,dr \leqslant 2 \sigma_{1}^{2}\frac{\Lambda^{2}}{\mu^{2}K_{1}}. $$

This ends the proof. □

Remark 3.1

From Theorem 3.2 we can conclude that if \(R_{0}<1\) and condition (3.1) holds, then the solution of Eq. (1.4) will fluctuate around the disease-free equilibrium of Eq. (1.3).

3.1 Asymptotic behavior around the endemic equilibrium of the deterministic model

In this subsection, we assume that \(R_{0} >1\). Then model (1.3) has a single endemic equilibrium \(E^{*}\), but for model (1.4), \(E^{*}\) is not an endemic equilibrium. Similarly, we also expect to find out whether or not the solution goes around \(E^{*}\). The following result gives a positive answer.

Theorem 3.3

If \(R_{0}=\frac{ \beta_{1}\Lambda}{\mu(\mu+\gamma )}>1\) and

$$ \sigma_{1}^{2}< 2\mu, \qquad \sigma_{2}^{2}< 2( \mu+\gamma),\qquad \sigma _{3}^{2}< \mu, $$
(3.6)

then for any given initial value \((S(0),I(0),R(0))\in\mathbb {R}^{3}_{+}\), the solution of model (1.4) has the property

$$\begin{aligned}& \limsup_{t\rightarrow\infty} \frac{1}{t} E \int_{0}^{t} \biggl\{ \biggl(S(r)- \frac{2\mu}{2\mu-\sigma_{1}^{2}}S^{*} \biggr)^{2} + \biggl[I(r)- \frac{2\mu(\mu+\gamma-p\gamma^{2})}{2\mu(\mu+\gamma) -p\gamma^{2}-\mu\sigma_{2}^{2}} I^{*} \biggr]^{2} \\& \quad {}+ \biggl(R(r)- \frac{\mu}{\mu-\sigma_{3}^{2}} R^{*} \biggr)^{2} \biggr\} \,dr \leqslant \frac{M}{K_{2}} , \end{aligned}$$

where

$$\begin{aligned}& 0< p< \frac{2\mu(\mu+\gamma)-\mu\sigma_{2}^{2}}{\gamma^{2}}, \\& M = \frac{\mu\sigma_{1}^{2}}{2\mu-\sigma_{1}^{2}}S^{*2} +\frac{[2\mu(\mu+\gamma)-p\gamma^{2}]\sigma_{2}^{2}}{4\mu(\mu+\gamma) -2p\gamma^{2}-2\mu\sigma_{2}^{2}}I^{*2} + \frac{p\mu\sigma _{3}^{2}}{2(\mu-\sigma_{3}^{2})}R^{*2} +\frac{2\mu+\gamma}{2\beta}I^{*} \sigma_{2}^{2}, \\& K_{2}=\min \biggl\{ \mu-\frac{1}{2}\sigma_{1}^{2}, \mu+\gamma-\frac {1}{2}\sigma_{2}^{2} - \frac{p\gamma^{2}}{2\mu}, \frac{p}{2}\bigl(\mu -\sigma_{3}^{2} \bigr) \biggr\} . \end{aligned}$$

Proof

Define the \(\mathcal{C}^{2}\)-function \(V: \mathbb{R}^{2}_{+}\rightarrow\bar{\mathbb {R}}_{+}\) by

$$ V(x)= \frac{1}{2} \bigl(S-S^{*}+I-I^{*} \bigr)^{2} + a \biggl( I-I^{*}-I^{*}\ln \frac{I}{I^{*}} \biggr) + \frac{1}{2}p \bigl( R-R^{*} \bigr)^{2}, $$
(3.7)

where \(a>0\) and \(p>0\) are constants to be determined later. For simplicity, we divide (3.7) into two functions: \(V(x)=V_{1}(x) +V_{2}(x)\), where

$$\begin{aligned}& V_{1}(x)= \frac{1}{2} \bigl(S-S^{*}+I-I^{*} \bigr)^{2} + a \biggl( I-I^{*}-I^{*}\ln \frac{I}{I^{*}} \biggr), \\& V_{2}(x)= \frac{1}{2}p \bigl( R-R^{*} \bigr)^{2}. \end{aligned}$$

Applying Itô’s formula, we obtain

$$ dV_{1}(x)= LV_{1}\,dt + \bigl(S-S^{*}+I-I^{*} \bigr) \bigl(\sigma _{1}S\,dB_{1}(t) + \sigma_{2}I\,dB_{2}(t)\bigr) + a \biggl( 1-\frac{I}{I^{*}} \biggr) \sigma_{2}I\,dB_{2}(t) $$

and

$$ dV_{2}(x)= LV_{2}\,dt + p \bigl(R-R^{*} \bigr) \sigma_{3}R\,dB_{3}(t), $$

where

$$\begin{aligned} LV_{1}(x) =& \bigl(S-S^{*}+I-I^{*} \bigr) \bigl[\Lambda-\mu S -(\mu+\gamma)I\bigr] +\frac{1}{2}\bigl( \sigma_{1}^{2}S^{2}+ \sigma _{2}^{2}I^{2} \bigr) \\ &+ a \biggl(1-\frac{I}{I^{*}} \biggr) \biggl[ \biggl(\beta_{1} - \frac{\beta_{2}I(t) }{m+I(t) } \biggr)S(t) I(t) -(\mu+\gamma)I(t) \biggr] + \frac{1}{2}aI^{*}\sigma_{2}^{2} \\ =& \bigl(S-S^{*}+I-I^{*} \bigr)\bigl[\mu S^{*}+(\mu+\gamma)I^{*} -\mu S -(\mu+\gamma)I\bigr] + \frac{1}{2}\bigl(\sigma_{1}^{2}S^{2}+ \sigma _{2}^{2}I^{2}\bigr) \\ &{} +\frac{1}{2}aI^{*}\sigma_{2}^{2}+ a \bigl(I-I^{*} \bigr) \biggl(\beta_{1} -\frac{\beta_{2}I^{*} }{m+I^{*} } \biggr) \bigl(S-S^{*}\bigr) -a \bigl(I-I^{*} \bigr) \biggl[ \frac{\beta_{2}I }{m+I }- \frac{\beta _{2}I^{*} }{m+I^{*} } \biggr] \\ =& -\mu\bigl(S-S^{*}\bigr)^{2} - (\mu+\gamma) \bigl(I-I^{*}\bigr)^{2} +\frac{1}{2}\bigl( \sigma_{1}^{2}S^{2}+ \sigma_{2}^{2}I^{2} \bigr)+\frac {1}{2}aI^{*}\sigma_{2}^{2} \\ &{}+ \biggl[a \biggl(\beta_{1} -\frac{\beta_{2}I^{*} }{m+I^{*} } \biggr)-(2\mu+ \gamma) \biggr]\bigl(S-S^{*}\bigr) \bigl(I-I^{*}\bigr) \\ &{}-a \bigl(I-I^{*} \bigr) \biggl[ \frac{\beta_{2}I }{m+I }- \frac{\beta_{2}I^{*} }{m+I^{*} } \biggr] \end{aligned}$$
(3.8)

and

$$\begin{aligned} LV_{2}(x) =& p\bigl(R-R^{*}\bigr) (\gamma I-\mu R) + \frac{1}{2}p\sigma_{3}^{2}R^{2} \\ =& p\bigl(R-R^{*}\bigr)\bigl[\gamma\bigl(I-I^{*}\bigr) - \mu\bigl(R-R^{*}\bigr)\bigr]+ \frac{1}{2}p\sigma_{3}^{2}R^{2} \\ =& p\gamma\bigl(I-I^{*}\bigr) \bigl(R-R^{*}\bigr)- p\mu \bigl(R-R^{*}\bigr)^{2}+ \frac{1}{2}p \sigma_{3}^{2}R^{2} \\ \leqslant& \frac{p\gamma^{2}}{2\mu}\bigl(I-I^{*}\bigr)^{2} - \frac{p\mu}{2}\bigl(R-R^{*}\bigr)^{2}+ \frac{1}{2}p\sigma_{3}^{2}R^{2}. \end{aligned}$$
(3.9)

Choose \(a=\frac{2\mu+\gamma}{\beta}>0\) such that \(a\beta-(2\mu+\gamma )=0\), where \(\beta=\beta_{1}-\frac{\beta_{2}I^{*} }{m+I^{*} }\). Noticing that \((I-I^{*})\) and \([ \frac{\beta_{2}I }{m+I }- \frac {\beta_{2}I^{*} }{m+I^{*} } ]\) have the same sign, it follows from (3.8) that

$$\begin{aligned} LV_{1}(x) =& -\mu\bigl(S-S^{*}\bigr)^{2} - ( \mu+\gamma) \bigl(I-I^{*}\bigr)^{2} +\frac{1}{2} \bigl(\sigma_{1}^{2}S^{2}+ \sigma_{2}^{2}I^{2} \bigr)+\frac {1}{2}aI^{*}\sigma_{2}^{2} \\ &{}+ \biggl[a \biggl(\beta_{1} -\frac{\beta_{2}I^{*} }{m+I^{*} } \biggr)-(2\mu+ \gamma) \biggr]\bigl(S-S^{*}\bigr) \bigl(I-I^{*}\bigr) \\ &{}-a \bigl(I-I^{*} \bigr) \biggl[ \frac{\beta_{2}I }{m+I }- \frac{\beta_{2}I^{*} }{m+I^{*} } \biggr] \\ \leqslant& -\mu\bigl(S-S^{*}\bigr)^{2} - (\mu+\gamma) \bigl(I-I^{*}\bigr)^{2} +\frac{1}{2}\bigl( \sigma_{1}^{2}S^{2}+ \sigma_{2}^{2}I^{2} \bigr)+\frac {1}{2}aI^{*}\sigma_{2}^{2}. \end{aligned}$$
(3.10)

Taking (3.9) and (3.10) together, we have

$$\begin{aligned} LV(x) =& LV_{1}(x) + LV_{2}(x) \\ \leqslant& -\mu\bigl(S-S^{*}\bigr)^{2} - (\mu+\gamma) \bigl(I-I^{*}\bigr)^{2} +\frac{1}{2}\bigl( \sigma_{1}^{2}S^{2}+ \sigma_{2}^{2}I^{2} \bigr)+\frac{2\mu +\gamma}{2\beta}I^{*}\sigma_{2}^{2} \\ &{}+ \frac{p\gamma^{2}}{2\mu}\bigl(I-I^{*}\bigr)^{2} - \frac{p\mu}{2}\bigl(R-R^{*}\bigr)^{2}+ \frac{1}{2}p\sigma_{3}^{2}R^{2} \\ =& -\mu\bigl(S-S^{*}\bigr)^{2} -\biggl(\mu+\gamma- \frac{p\gamma^{2}}{2\mu}\biggr) \bigl(I-I^{*}\bigr)^{2}- \frac{p\mu }{2}\bigl(R-R^{*}\bigr)^{2} \\ &{} +\frac{1}{2}\bigl(\sigma_{1}^{2}S^{2}+ \sigma_{2}^{2}I^{2}\bigr)+\frac{2\mu +\gamma}{2\beta}I^{*} \sigma_{2}^{2}+ \frac{1}{2}p\sigma_{3}^{2}R^{2} \\ =& - \biggl(\mu-\frac{1}{2}\sigma_{1}^{2} \biggr)S^{2} +2\mu SS^{*}-\mu S^{*2} - \biggl(\mu+ \gamma-\frac{1}{2}\sigma_{2}^{2} -\frac{p\gamma^{2}}{2\mu} \biggr)I^{2} \\ &{} +2 \biggl(\mu+\gamma-\frac{p\gamma^{2}}{2\mu} \biggr)II^{*} - \biggl( \mu+\gamma-\frac{p\gamma^{2}}{2\mu} \biggr)I^{*2} -\frac{p}{2}\bigl( \mu-\sigma_{3}^{2}\bigr)R^{2} \\ &{} + p\mu RR^{*} -\frac{p}{2}\mu R^{*2}+ \frac{2\mu+\gamma}{2\beta}I^{*}\sigma_{2}^{2} \\ =& - \biggl(\mu-\frac{1}{2}\sigma_{1}^{2} \biggr) \biggl(S-\frac{2\mu}{2\mu-\sigma_{1}^{2}}S^{*} \biggr)^{2} \\ &{} - \biggl(\mu+\gamma-\frac{1}{2}\sigma_{2}^{2} - \frac{p\gamma^{2}}{2\mu} \biggr) \biggl[I- \frac{2\mu(\mu+\gamma-p\gamma ^{2})}{2\mu(\mu+\gamma) -p\gamma^{2}-\mu\sigma_{2}^{2}} I^{*} \biggr]^{2} \\ &{}-\frac{p}{2}\bigl(\mu-\sigma_{3}^{2}\bigr) \biggl(R- \frac{\mu}{\mu-\sigma_{3}^{2}} R^{*} \biggr)^{2} + \frac{\mu\sigma_{1}^{2}}{2\mu-\sigma_{1}^{2}}S^{*2} \\ &{}+\frac{[2\mu(\mu+\gamma)-p\gamma^{2}]\sigma_{2}^{2}}{4\mu(\mu+\gamma) -2p\gamma^{2}-2\mu\sigma_{2}^{2}}I^{*2} +\frac{p\mu\sigma_{3}^{2}}{2(\mu-\sigma_{3}^{2})}R^{*2} +\frac{2\mu+\gamma}{2\beta}I^{*} \sigma_{2}^{2}. \end{aligned}$$
(3.11)

Note that \(\sigma_{2}^{2}<2(\mu+\gamma)\). Then we can choose \(0< p<\frac {2\mu(\mu+\gamma)-\mu\sigma_{2}^{2}}{\gamma^{2}}\), and the condition (3.6) implies that

$$ \mu-\frac{1}{2}\sigma_{1}^{2}>0, \qquad \mu+\gamma- \frac{1}{2}\sigma _{2}^{2} -\frac{p\gamma^{2}}{2\mu}>0,\qquad \frac{p}{2}\bigl(\mu-\sigma_{3}^{2}\bigr)>0. $$

Thus,

$$\begin{aligned} dV(x) =& LV(x)\,dt+ \bigl(S(t)-S^{*}+I(t)-I^{*} \bigr) \bigl( \sigma_{1}S(t)\,dB_{1}(t) + \sigma_{2}I(t) \,dB_{2}(t) \bigr) \\ &{}+ \frac{2\mu+\gamma}{\beta} \bigl( I(t)-I^{*} \bigr) \sigma _{2}\,dB_{2}(t) + p \bigl(R(t)-R^{*} \bigr) \sigma_{3}R(t)\,dB_{3}(t). \end{aligned}$$
(3.12)

Integrating both sides of (3.12) from 0 to t, taking expectations, and considering inequality (3.11), we obtain

$$\begin{aligned} 0 \leqslant& EV\bigl(x(t)\bigr) \\ \leqslant& V\bigl(x(0)\bigr) - E \int_{0}^{t} \biggl\{ \biggl(\mu-\frac{1}{2} \sigma_{1}^{2} \biggr) \biggl(S(r)-\frac{2\mu}{2\mu-\sigma_{1}^{2}}S^{*} \biggr)^{2} \\ &{} + \biggl(\mu+\gamma-\frac{1}{2}\sigma_{2}^{2} - \frac{p\gamma^{2}}{2\mu} \biggr) \biggl[I(r)- \frac{2\mu(\mu+\gamma -p\gamma^{2})}{2\mu(\mu+\gamma) -p\gamma^{2}-\mu\sigma_{2}^{2}} I^{*} \biggr]^{2} \\ &{} +\frac{p}{2}\bigl(\mu-\sigma_{3}^{2}\bigr) \biggl(R(r)- \frac{\mu}{\mu-\sigma_{3}^{2}} R^{*} \biggr)^{2} \biggr\} \,dr +Mt, \end{aligned}$$
(3.13)

where

$$ M = \frac{\mu\sigma_{1}^{2}}{2\mu-\sigma_{1}^{2}}S^{*2} +\frac{[2\mu(\mu+\gamma)-p\gamma^{2}]\sigma_{2}^{2}}{4\mu(\mu+\gamma) -2p\gamma^{2}-2\mu\sigma_{2}^{2}}I^{*2} + \frac{p\mu\sigma _{3}^{2}}{2(\mu-\sigma_{3}^{2})}R^{*2} +\frac{2\mu+\gamma}{2\beta}I^{*} \sigma_{2}^{2}. $$

Thus, we have

$$\begin{aligned}& E \int_{0}^{t}\biggl\{ \biggl(\mu-\frac{1}{2} \sigma_{1}^{2} \biggr) \biggl(S(r)-\frac{2\mu}{2\mu-\sigma_{1}^{2}}S^{*} \biggr)^{2} \\& \quad {}+ \biggl(\mu+\gamma-\frac{1}{2}\sigma_{2}^{2} -\frac{p\gamma^{2}}{2\mu} \biggr) \biggl[I(r)- \frac{2\mu(\mu+\gamma -p\gamma^{2})}{2\mu(\mu+\gamma) -p\gamma^{2}-\mu\sigma_{2}^{2}} I^{*} \biggr]^{2} \\& \quad {}+\frac{p}{2}\bigl(\mu-\sigma_{3}^{2}\bigr) \biggl(R(r)- \frac{\mu}{\mu-\sigma_{3}^{2}} R^{*} \biggr)^{2}\biggr\} \,dr \leqslant V\bigl(x(0)\bigr) +Mt . \end{aligned}$$
(3.14)

Dividing both sides of (3.14) by t and letting \(t\rightarrow \infty\), we have

$$\begin{aligned}& \limsup_{t\rightarrow\infty} \frac{1}{t} E \int_{0}^{t} \biggl\{ \biggl(\mu-\frac{1}{2} \sigma_{1}^{2} \biggr) \biggl(S(r)-\frac{2\mu}{2\mu-\sigma_{1}^{2}}S^{*} \biggr)^{2} \\& \quad{} + \biggl(\mu+\gamma-\frac{1}{2}\sigma_{2}^{2} -\frac{p\gamma^{2}}{2\mu} \biggr) \biggl[I(r)- \frac{2\mu(\mu+\gamma -p\gamma^{2})}{2\mu(\mu+\gamma) -p\gamma^{2}-\mu\sigma_{2}^{2}} I^{*} \biggr]^{2} \\& \quad{} +\frac{p}{2}\bigl(\mu-\sigma_{3}^{2}\bigr) \biggl(R(r)- \frac{\mu}{\mu-\sigma_{3}^{2}} R^{*} \biggr)^{2} \biggr\} \,dr \leqslant M . \end{aligned}$$
(3.15)

Let \(K_{2}=\min \{ \mu-\frac{1}{2}\sigma_{1}^{2}, \mu+\gamma -\frac{1}{2}\sigma_{2}^{2} -\frac{p\gamma^{2}}{2\mu}, \frac{p}{2}(\mu -\sigma_{3}^{2}) \} \). Then from (3.15) we have

$$\begin{aligned}& \limsup_{t\rightarrow\infty} \frac{1}{t} E \int_{0}^{t}\biggl\{ \biggl(S(r)- \frac{2\mu}{2\mu-\sigma_{1}^{2}}S^{*} \biggr)^{2} + \biggl[I(r)- \frac{2\mu(\mu+\gamma-p\gamma^{2})}{2\mu(\mu+\gamma) -p\gamma^{2}-\mu\sigma_{2}^{2}} I^{*} \biggr]^{2} \\& \quad {} + \biggl(R(r)- \frac{\mu}{\mu-\sigma_{3}^{2}} R^{*} \biggr)^{2} \biggr\} \,dr \leqslant \frac{M}{K_{2}} . \end{aligned}$$

This ends the proof. □

Remark 3.2

From Theorem 3.3 we can conclude that if \(R_{0}>1\) and condition (3.6) holds, then the solution of Eq. (1.4) fluctuates around the endemic equilibrium of Eq. (1.3).

4 Numerical simulations

In this section, we provide numerical simulation results to substantiate the analytical findings for the stochastic model system reported in the previous sections. Using Milstein’s higher-order method [19], we get the discretization equation

$$ \left \{ \textstyle\begin{array}{l} S_{k+1} = S_{k} + [ \Lambda- ( \beta_{1}-\frac{\beta _{2}I_{k} }{m+I_{k}} )S_{k}I_{k} -\mu S_{k} ]\Delta t + \sigma_{1}S_{k}\sqrt{\Delta t} \varepsilon_{1,k} +\frac{\sigma _{1}^{2}}{2}S_{k}\Delta t (\varepsilon_{1,k}^{2} -1), \\ I_{k+1} = I_{k} + [ (\beta_{1}-\frac{\beta_{2}I_{k}}{m+I_{k} } )S_{k}I_{k} -(\mu+\gamma)I_{k} ]\Delta t + \sigma _{2}I_{k}\sqrt{\Delta t} \varepsilon_{2,k} +\frac{\sigma _{2}^{2}}{2}I_{k}\Delta t (\varepsilon_{2,k}^{2} -1), \\ R_{k+1} = R_{k} + [ \gamma I_{k} -\mu R_{k} ]\Delta t +\sigma_{3}R_{k}\sqrt{\Delta t} \varepsilon_{3,k} +\frac{\sigma _{3}^{2}}{2}R_{k}\Delta t (\varepsilon_{3,k}^{2} -1), \end{array}\displaystyle \right . $$
(4.1)

where the time increment \(\Delta t>0\), and \(\varepsilon_{1k,i}\), \(\varepsilon_{2k,i}\), \(\varepsilon_{3k,i}\), \(k=1,2,3\), are \(N(0,1)\)-distributed independent random variables.

Example 4.1

In this case, we set \(\Lambda=15\), \(\beta_{1}=0.0008\), \(\beta_{2}=0.0006\), \(m=30\), \(\mu=0.05\), \(\gamma=0.2 \), where ‘year’ is used as the unit of time [20].

From Eq. (2.3) we compute \(R_{0}=0.96<1\). From the discussion of Section 2 we know that system (1.3) has only one disease-free equilibrium \(E_{0}(300,0,0)\), which is globally asymptotically stable.

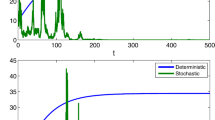
We now consider the environment noise in (1.3) and study the dynamics of the resulting system (1.4). By Theorem 3.2 the expectations of \(S(t)\), \(I(t)\), \(R(t)\) are bounded in time average when condition (3.1) is also satisfied. Obviously, the boundedness is proportional to \(\sigma_{1}\); moreover, the smaller \(\sigma_{1}\), the less the boundedness. The following numerical simulations of the strong solution of (1.4) confirm the results we have shown. Figure 2(a), (b) shows that the curves of system (1.4) always fluctuate around the curves of system (1.3) with different intensities of white noise. Moreover, comparison of Figure 2(a) and Figure 2(b) suggest that the fluctuations reduce as the noise level decreases.

Figure 2
figure 2

Solutions of deterministic model ( 1.3 ) (blue) and stochastic model ( 1.4 ) (red) with \(\pmb{\Lambda=15}\) , \(\pmb{\beta _{1}=0.0008}\) , \(\pmb{\beta_{2}=0.0006}\) , \(\pmb{m=30}\) , \(\pmb{\mu=0.05}\) , \(\pmb{\gamma=0.2 }\) . (a) \(\sigma_{1}=0.1\), \(\sigma_{2}=0.05\), \(\sigma_{3}=0.05\). (b) \(\sigma_{1}=0.05\), \(\sigma_{2}=0.02\), \(\sigma_{3}=0.02\).

Full size image

Example 4.2

In this case, we set \(\Lambda=15\), \(\beta_{1}=0.002\), \(\beta_{2}=0.0018\), \(m=30\), \(\mu=0.05\), \(\gamma=0.2 \), where ‘year’ is used as the unit of time [20].

From Eq. (2.3) we compute \(R_{0}=2.4>1\). From the discussion of Section 2 we know that system (1.3) has an unstable disease-free equilibrium \(E_{0}(300,0,0)\) and a globally asymptotically stable endemic equilibrium \(E^{*}=(197.1728, 20.5654, 82.2617)\).

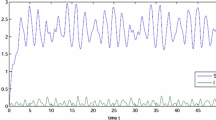
We next consider the environment noise in (1.3) and study the dynamics of the resulting system (1.4). By Theorem 3.3 the expectations of \(S(t)\), \(I(t)\), \(R(t)\) are bounded in time average when condition (3.6) is also satisfied. Similarly as before, the solution of (1.4) also fluctuates around the solution of (1.3), which supports the results of Theorem 3.3. In detail, in Figure 3(a) and Figure 3(b), the parameters are the same except for the decreasing intensities. From Figure 3(a), (b) we can also see that the fluctuation is weaker with intensities decreasing.

Figure 3
figure 3

Solutions of deterministic model ( 1.3 ) (blue) and stochastic model ( 1.4 ) (red) with \(\pmb{\Lambda=15}\) , \(\pmb{\beta _{1}=0.002}\) , \(\pmb{\beta_{2}=0.0018}\) , \(\pmb{m=30}\) , \(\pmb{\mu=0.05}\) , \(\pmb{\gamma=0.2 }\) . (a) \(\sigma_{1}=0.1\), \(\sigma_{2}=0.05\), \(\sigma_{3}=0.05\). (b) \(\sigma_{1}=0.02\), \(\sigma_{2}=0.02\), \(\sigma_{3}=0.01\).

Full size image

5 Discussion

In this paper, we proposed a stochastic SIR epidemic model incorporating media coverage. We first investigated the positivity and boundedness of the solution of model (1.3). We showed that the solution of model (1.3) with the initial condition (2.1) is positive and bounded. Our results also show that, when \(R_{0}<1\), model (1.3) has only one disease-free equilibrium and, when \(R_{0}>1\), model (1.3) has a disease-free equilibrium and an endemic equilibrium. Then, we studied the stability of the disease-free and endemic equilibria. Our results show that the disease-free equilibrium is globally stable when the basic reproduction number \(R_{0}<1\) and is unstable when \(R_{0}>1\). This result shows that media coverage cannot change the basic feature of the SIR epidemic model (1.1) [21]. That is to say, disease eventually disappears when the basic reproduction number \(R_{0}<1\); however, the epidemic eventually becomes an endemic disease when \(R_{0}>1\).

Section 3 deals with the stochastic differential equations; by using suitable Lyapunov functions we show that the solution of the stochastic model is positive and global, and this solution oscillates around the equilibria of the deterministic model under certain conditions. That is to say, if the effects of environmental stochastic perturbations are smaller enough than the natural death rate, then the solution of the stochastic model (1.4) oscillates around the disease-free equilibrium when \(R_{0}<1\); however, the solution of the stochastic model (1.4) oscillates around the endemic equilibrium when \(R_{0}>1\). Moreover, the numerical results also suggest that the fluctuations reduce as the noise level decreases.