1 Introduction

Fluid convection at vertical plates, resulting from buoyancy forces, has found applications in several industrial and technological fields such as heat exchangers, electronic cooling equipments, aeronautics, and nuclear reactors. Free convection flow occurs not only due to temperature difference, but also due to concentration difference or combination of these two. Many transport processes exist in nature and in industrial applications, in which the simultaneous heat and mass transfer occur as a result of combined buoyancy effects and diffusion of chemical species.

The flows of free convection are common in environmental heat transfer processes. As a result, many investigations have been made by considering a wide range of mechanical and thermal boundary conditions [1]. Using the Laplace transform technique, Soundalgekar [2] has obtained an exact solution to the flow of a viscous fluid past an impulsively started semiinfinite isothermal vertical plate. Effects of heating or cooling of the plate on the flow field were analyzed through Grashof number. Transient free convection flow past an infinite vertical plate has been studied by Ingham [3]. Merkin [4] gave the similarity solutions for the same problem. Seth and Ansari [5] analyzed the natural convection flows past an impulsively moving vertical plate with ramped wall temperature in the presence of thermal diffusion with heat absorption. Narahari and Nayan [6] studied the free convection flow past an impulsively started vertical plate with Newtonian heating in the presence of thermal radiation and mass diffusion. The problem of free convection under the influence of a magnetic field has attracted the interest of researchers in view of its applications in geophysics, astrophysics, petroleum industries, and cooling of nuclear reactors. Georgantopoulos et al. [7] studied the magnetohydrodynamic free convection flow past an impulsively started vertical plate with constant temperature. Raptis and Singh [8] have studied the effect of a uniform transverse magnetic field on the free convection flow of an electrically conducting fluid past an accelerated vertical plate. Tokis [9] have obtained a class of exact solutions of the unsteady free convection flow of an electrically conducting fluid near a moving infinite vertical plate in the presence of uniform transverse magnetic field fixed to the fluid or to the plate. Narahari and Debnath [10] studied the unsteady magnetohydrodynamic free convection flow past an accelerated vertical plate with constant heat flux and heat generation or absorption. Toki and Tokis [11] obtained an elegant exact solution for the unsteady free convection flows on a porous plate with time-dependent heating. In last time, the fractional calculus has become an interesting mathematical method for solution of diverse problems in mathematics, science, and engineering [12–14]. Fractional calculus involves the computation of integrals or derivatives of any real order. This calculus has applications in study of the heat flux, temperature and entropy generation, diffusion phenomena, modeling control systems, viscoelasticity, biology, etc. The advantage of the fractional derivatives in theory of viscoelasticity is that it affords possibilities for obtaining constitutive equations for elastic complex modulus of viscoelastic materials with only few experimentally determined parameters [15]. Debnath [16] obtained solutions for the Stokes and Rayleigh problems for a viscous fluid with time-fractional derivatives. For the same model of fluid, the unsteady Couette flow was analyzed. The well-known time-fractional diffusion equations have been treated in different contexts by many authors [17–20]. Other studies regarding the flow of complex fluids whose governing equations contain time-fractional derivatives can be found in [21–26].

In this paper we investigate the unsteady free convection flow of a Newtonian fluid near a vertical heated plate in the case of the time-fractional derivatives models. Solutions of the temperature and velocity fields are obtained, in the case of the oscillating motion of the vertical plate, by means of the Laplace transform technique. By using the Wright functions and the generalized G-Lorenzo-Hartley functions elegant closed forms for temperature and fluid velocity were obtained. The fundamental solution corresponding to the temperature is also obtained. This allows obtaining the temperature field for different conditions on the wall temperature. Some numerical examples were analyzed. To check the accuracy of the obtained results, we have used the Stehfest algorithm to the inverse Laplace transform [27]. The values found with the analytical solutions and with the Stehfest algorithm are in good agreement. Also, the influence of the fractional parameters on the temperature and velocity is studied.

2 Statement of the problem

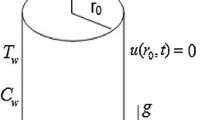
Let us consider the unsteady free convection flow of an incompressible viscous fluid with time-fractional derivatives, in the vicinity of an infinite vertical wall with time-dependent temperature. Initially, the wall and the fluid are at rest at the constant temperature \(T_{\infty}\). The wall is situated in the \((x,z)\)-plane of a Cartesian coordinate system \(Oxyz\), the x-axis being the ascendant vertical. After time \(t = 0^{ +}\), the plate has a translational motion along the vertical axis with the velocity \(u_{w}(t) = U_{0}\sin(wt)\), and the plate temperature changes according with the ramp-type function \(T_{w}(t) = T_{\infty} + T_{0}(t/t_{0})\). The flow is considered to be laminar without any pressure gradient in the flow direction. Because the plate is infinite in x- and z-directions, all physical quantities, except possibly the pressure, are functions of y and t only. Assuming that the convective effects and viscous dissipation are negligible and using the boundary layer and Bussinesq approximations, the governing equations for such flows are [4, 16, 17]

$$\begin{aligned}& {}^{c}D_{t}^{\alpha} u(y,t) = \nu_{\alpha} \frac{\partial^{2}u(y,t)}{\partial y^{2}} + g\beta {}_{\alpha} \bigl[T(y,t) - T_{\infty} \bigr],\quad y, t > 0, \alpha \in (0,1], \end{aligned}$$
(1)
$$\begin{aligned}& {}^{c}D_{t}^{\gamma} T(y,t) = k_{\gamma} \frac{\partial^{2}T(y,t)}{\partial y^{2}}, \quad y, t > 0, \gamma \in (0,1], \end{aligned}$$
(2)

where

$$ {}^{c}D_{t}^{\alpha} f(y,t) = \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \frac{1}{\Gamma (1 - \alpha )}\int_{0}^{t} (t - \tau )^{ - \alpha} \frac{\partial f(y,\tau )}{\partial \tau}\,d\tau,& \alpha \in (0,1), \\ \frac{\partial f(y,t)}{\partial t},& \alpha = 1, \end{array}\displaystyle \right . $$
(3)

is the time-fractional derivative in the Caputo sense [12, 28]. In the above equations, \(u(y,t)\) is the fluid velocity along the x-axis, \(T(y,t)\) is the temperature field, g is the acceleration due to gravity, and \(\nu_{\alpha} [m^{2} / s^{\alpha} ]\), \(\beta_{\alpha} [s^{1 - \alpha} / K]\), and \(k_{\gamma} [m^{2} / s^{\gamma} ]\) are the coefficients of the material. Obviously, for \(\alpha = \gamma = 1\), these coefficients become the kinematic viscosity \(\nu_{1} = \nu\), the volumetric coefficient of thermal expansion \(\beta_{1} = \beta\), and \(k_{1} = k / \rho c_{p}\) (k is the thermal conductivity, ρ is the density, and \(c_{p}\) is the specific heat), corresponding to an ordinary viscous fluid.

We consider the following initial and boundary conditions:

$$\begin{aligned}& u(y,0) = 0,\qquad T(y,0) = T_{\infty}, \quad y \ge 0, \end{aligned}$$
(4)
$$\begin{aligned}& u(0,t) = u_{w}(t) = U_{0}\sin (\omega t),\quad t \ge 0, U_{0} > 0, \end{aligned}$$
(5)
$$\begin{aligned}& T(0,t) = T_{\infty} + T_{0}(t/t_{0}),\quad t \ge 0, T_{0} \ne 0, \end{aligned}$$
(6)
$$\begin{aligned}& u(y,t) \to 0,\qquad T(y,t) \to T_{\infty}\quad \mbox{as }y \to \infty \end{aligned}$$
(7)

and the nondimensional

$$ t^{*} = \frac{t}{t_{0}},\qquad y^{*} = \frac{y}{\sqrt{\nu_{\alpha} t_{0}^{\alpha}}}, \qquad u^{*} = \frac{u}{U_{0}},\qquad T^{*} = \frac{T - T_{\infty}}{ T_{0}},\qquad\omega^{*} = \omega t_{0}, $$
(8)

with a characteristic time \(t_{0} > 0\). Dropping the star notation, we obtain the next dimensionless initial-boundary-value problem:

$$\begin{aligned}& {}^{c}D_{t}^{\alpha} u(y,t) = \frac{\partial^{2}u(y,t)}{\partial y^{2}} + G_{\alpha} T(y,t),\quad y,t > 0, \alpha \in (0,1], \end{aligned}$$
(9)
$$\begin{aligned}& {}^{c}D_{t}^{\gamma} T(y,t) = \frac{1}{P_{\alpha \gamma}} \frac{\partial^{2}T(y,t)}{\partial y^{2}},\quad y,t > 0, \gamma \in (0,1], \end{aligned}$$
(10)
$$\begin{aligned}& u(y,0) = 0,\qquad T(y,0) = 0,\quad y \ge 0, \end{aligned}$$
(11)
$$\begin{aligned}& u(0,t) = f(t) = \sin (\omega t),\qquad T(0,t) = h(t) = t,\quad t \ge 0, \end{aligned}$$
(12)
$$\begin{aligned}& u(y,t) \to 0,\qquad T(y,t) \to 0\quad \mbox{as }y \to \infty, \end{aligned}$$
(13)

where \(G_{\alpha} = \frac{1}{U_{0}}\beta_{\alpha} gt_{0}^{\alpha}\), and \(P_{\alpha \gamma} = \frac{\nu_{\alpha} t_{0}^{\alpha}}{k_{\gamma} t_{0}^{\gamma}}\) are the dimensionless constants.

For \(\alpha = \gamma = 1\), these coefficients are the Grashof and Prandtl numbers, respectively.

3 Solution of the problem

In order to determine solutions of the initial-boundary-value problem (9)-(13), we use the Laplace transform with respect to variable t [29]. The transform domain problem is given by

$$\begin{aligned}& s^{\alpha} \bar{u}(y,s) = \frac{\partial^{2}\bar{u}(y,s)}{\partial y^{2}} + G_{\alpha} \bar{T}(y,s), \end{aligned}$$
(14)
$$\begin{aligned}& P_{\alpha \gamma} s^{\gamma} \bar{T}(y,s) = \frac{\partial^{2}\bar{T}(y,s)}{\partial y^{2}}, \end{aligned}$$
(15)
$$\begin{aligned}& \bar{u}(0,s) = \bar{f}(s) = \frac{\omega}{s^{2} + \omega^{2}},\qquad \bar{T}(0,s) = \bar{h}(s) = \frac{1}{s^{2}}, \end{aligned}$$
(16)
$$\begin{aligned}& \bar{u}(y,s) \to 0,\qquad \bar{T}(y,s) \to 0\quad \mbox{as }y \to \infty, \end{aligned}$$
(17)

where \(\bar{u}(y,s)\), \(\bar{T}(y,s)\), \(\bar{f}(s)\), and \(\bar{h}(s)\) are the Laplace transforms of the functions \(u(y,t)\), \(T(y,t)\), \(f(t)\), and \(h(t)\), respectively.

3.1 Temperature field

The solution of problem (15), (16)2, and (17)2 is given by

$$ \bar{T}(y,s) = s^{ - 2}\exp \bigl( - y\sqrt{P_{\alpha \gamma}} s^{\gamma /2}\bigr). $$
(18)

Using the formula [30]

$$ L^{ - 1} \bigl\{ s^{ - \beta} \exp \bigl( - as^{\sigma} \bigr) \bigr\} = t^{\beta - 1}\Phi \bigl(\beta, - \sigma; - at^{ - \sigma} \bigr), \quad a,\beta \ge 0, 0 < \sigma < 1, $$
(19)

we obtain the next \((y,t)\)-solution for the temperature:

$$ T(y,t) = t\Phi \biggl(2, - \frac{\gamma}{2}; - y\sqrt{P_{\alpha \gamma}} t^{ - \gamma /2}\biggr), $$
(20)

where

$$ \Phi (a, - b;z) = \sum_{n = 0}^{\infty} \frac{z^{n}}{n!\Gamma (a - bn)},\quad 0 < b < 1, $$
(21)

is the Whright function [30, 31].

Function (20) satisfies the initial condition (11) and the natural condition (13) at infinity. Also, the boundary condition (12) is satisfied. Indeed, we have

$$\lim_{y \to 0^{ +}} t \Phi \biggl(2, - \frac{\gamma}{2}; - y \sqrt{P_{\alpha \gamma}} t^{ - \gamma /2}\biggr) = L^{ - 1} \Bigl\{ \lim _{y \to 0^{ +}} s^{ - 2}\exp \bigl( - y\sqrt{P_{\alpha \gamma}} s^{\gamma /2}\bigr) \Bigr\} = L^{ - 1}\bigl\{ s^{ - 2}\bigr\} = h(t). $$

3.1.1 Fundamental solution

The expression of the temperature field was determined by the Laplace transform technique. It is useful, however, to determine the fundamental solution \(G_{T}(y,t)\) for the temperature field, namely, solution corresponding to the problem (10), the second condition (11), and the second condition (13), with the Dirichlet boundary condition \(T(0,t) = \delta (t)\), \(\delta (t)\) being the Dirac distribution.

Using the Laplace transform with respect to time t and the Fourier sine transform with respect to the space coordinate x, we obtained the following equivalent forms of the fundamental solution \(G_{T}(y,t)\) for the temperature field:

$$\begin{aligned} G_{T}(y,t) &= t^{ - 1}\Phi \bigl(0, - \gamma /2; - y\sqrt{P_{\alpha \gamma}} t^{ - \gamma /2}\bigr) \\ &= \frac{1}{2}\gamma y\sqrt{P_{\alpha \gamma}} t^{ - 1 - \gamma /2}M_{\gamma /2}\bigl(y \sqrt{P_{\alpha \gamma}} t^{ - \gamma /2}\bigr) \\ & = \frac{2t^{\gamma - 1}}{\pi P_{\alpha \gamma}} \int_{0}^{\infty} \xi \sin (y\xi )E_{\gamma,\gamma} \bigl( - P_{\alpha \gamma}^{ - 1}\xi^{2}t^{\gamma} \bigr)\,d\xi, \quad y,t > 0, G_{T}(0,t) = \delta (t), \end{aligned}$$
(22)

where \(M_{\alpha} (z)\) is the auxiliary Wright-type function, introduced by Mainardi et al. [32] and \(E_{\alpha,\beta} (z)\), defined as \(t^{\beta - 1}E_{\alpha,\beta} ( - bt^{\alpha} ) = L^{ - 1} ( \frac{s^{\alpha - \beta}}{s^{\alpha} + b} )\), is the generalized Mittag-Leffler function [33]. Now, by means of the fundamental solution, we find the temperature field corresponding to several boundary condition \(T(0,t) = h(t)\). Indeed, it is easy to see that the function \(T(y,t) = h(t) * G_{T}(y,t) = \int_{0}^{t} h(\tau )G_{T}(y,t - \tau )\,d\tau\) is a solution of problem (10), and the second condition from equations (11), (12), (13). In the problem studied in this work, we have

$$\begin{aligned} T(y,t) &= h(t) * G_{T}(y,t) \\ & = L^{ - 1} \bigl[ \bar{h}(s)G_{T}(y,s) \bigr] \\ &= L^{ - 1} \bigl[ s^{ - 2}\exp \bigl( - y\sqrt{P_{\alpha \gamma}} s^{\gamma /2}\bigr) \bigr] \\ &= t\Phi \bigl(2, - \gamma /2; - y \sqrt{P_{\alpha \gamma}} s^{\gamma /2}\bigr), \end{aligned}$$
(23)

and we recover Eq. (20).

3.1.2 The Nusselt number

As a measure of the heat transfer rate at the plate, the Nuselt number is given by

$$\begin{aligned} Nu &= - \frac{\partial T(y,t)}{\partial y} \bigg| _{y = 0} = \lim _{y \to 0^{ +}} \sqrt{P_{\alpha \gamma}} t^{(2 - \gamma /2) - 1}\Phi \bigl(2 - \gamma /2, - \gamma /2; - y\sqrt{P_{\alpha \gamma}} t^{ - \gamma /2}\bigr) \\ &= \sqrt{P_{\alpha \gamma}} L^{ - 1} \Bigl\{ \lim_{y \to 0^{ +}} s^{ - (2 - \gamma /2)}\exp \bigl( - y\sqrt{P_{\alpha \gamma}} s^{\gamma /2}\bigr) \Bigr\} \\ &= \sqrt{P_{\alpha \gamma}} L^{ - 1} \bigl\{ s^{ - (2 - \gamma /2)} \bigr\} \\ &= \frac{\sqrt{P_{\alpha \gamma}} t^{1 - \gamma /2}}{\Gamma (2 - \gamma /2)}. \end{aligned}$$
(24)

3.1.3 Particular case \(\gamma = 1\)

For comparison between ordinary model and the fractional models, it is important to present solutions corresponding to the case \(\gamma = 1\). In this particular case, the fundamental solution becomes

$$ G_{T}(y,t) = \frac{y\sqrt{P_{\alpha 1}}}{2t\sqrt{t}} M_{1/2}\bigl(y \sqrt{P_{\alpha 1}} t^{ - 1/2}\bigr). $$
(25)

By using the formula \(M_{1/2}(z) = \frac{1}{\sqrt{\pi}} \exp ( \frac{ - z^{2}}{4} )\) [34] we obtain the known expression of the fundamental solution

$$ G_{T}(y,t) = \frac{y\sqrt{P_{\alpha 1}}}{2t\sqrt{\pi t}} \exp \biggl( \frac{ - y^{2}P_{\alpha 1}}{4t} \biggr). $$
(26)

The temperature field is given by the convolution

$$ T(y,t) = \frac{y\sqrt{P_{\alpha 1}}}{2\sqrt{\pi}} \int_{0}^{t} \frac{t - \tau}{\tau \sqrt{\tau}} \exp \biggl( \frac{ - y^{2}P_{\alpha 1}}{4\tau} \biggr)\,d\tau, $$
(27)

which can be written in the elegant form (see [11], Appendix B)

$$ T(y,t) = \biggl( t + \frac{y^{2}P_{\alpha 1}}{2} \biggr)\operatorname{erfc} \biggl( \frac{y\sqrt{P_{\alpha 1}}}{2\sqrt{t}} \biggr) - \frac{y\sqrt{P_{\alpha 1}}}{2\sqrt{\pi}} \exp \biggl( \frac{ - y^{2}P_{\alpha 1}}{4\tau} \biggr), $$
(28)

where \(\operatorname{erfc}(\cdot)\) is the complementary error function.

The Nusselt number is obtained from Eq. (24) making \(\gamma = 1\):

$$ Nu = \frac{\sqrt{P_{\alpha 1}t}}{\Gamma (3/2)} = \frac{2\sqrt{P_{\alpha 1}t}}{\sqrt{\pi}}. $$
(29)

3.2 Velocity field

Using the expression of Laplace transform of the temperature, given by Eq. (18), we obtain a solution of the set of Eqs. (14), (16), and (17) in the form

$$\begin{aligned} \bar{u}(y,s) &= \bar{f}(s)\exp \bigl( - ys^{\alpha /2} \bigr) - \frac{G_{\alpha} [ \exp ( - ys^{\alpha /2} ) - \exp ( - y\sqrt{P_{\alpha \gamma}} s^{\gamma /2} ) ]}{s^{2}(s^{\alpha} - P_{\alpha \gamma} s^{\gamma} )} \\ &= \bar{f}(s)\exp \bigl( - ys^{\alpha /2} \bigr) + \frac{G_{\alpha} s^{ - \gamma - 1}}{s^{\alpha - \gamma} - P_{\alpha \gamma}} \frac{\exp ( - y\sqrt{P_{\alpha \gamma}} s^{\gamma /2} ) - \exp ( - ys^{\alpha /2} )}{s}. \end{aligned}$$
(30)

Applying the inverse Laplace transform, the \((y,t)\)-domain velocity is given by

$$\begin{aligned} u(y,t) ={}& f(t) * \bigl[t^{ - 1}\Phi \bigl(0, - \alpha /2; - yt^{ - \alpha /2}\bigr)\bigr] \\ &{}+ G_{\alpha} G_{\alpha - \gamma, - \gamma - 1,1}(P_{\alpha \gamma},t) * \bigl[ \Phi \bigl(1, - \gamma /2; - y\sqrt{P_{\alpha \gamma}} t^{ - \gamma /2}\bigr) \\ &{}- \Phi \bigl(1, - \alpha /2; - yt^{ - \alpha /2}\bigr) \bigr], \end{aligned}$$
(31)

where

$$\begin{aligned} &G_{a,b,c}(d,t) = L^{ - 1} \biggl\{ \frac{s^{b}}{(s^{a} - d)^{c}} \biggr\} = \sum_{j = 0}^{\infty} \frac{d^{j}\Gamma (c + j)}{\Gamma (c)\Gamma (j + 1)}\frac{t^{(c + j)a - b - 1}}{\Gamma [(c + j)a - b]}, \\ &\operatorname{Re} (ac - b) > 0, \operatorname{Re}(s) > 0, \bigl\vert s^{a} \bigr\vert > \vert d \vert , \end{aligned}$$
(32)

is the generalized G-function introduced by Lorenzo and Hartley [34], and the symbol ‘∗’ represents the convolution product.

In the particular case \(\alpha = \gamma = 1\), Eq. (31) becomes

$$\begin{aligned} u(y,t) ={}& \frac{2}{\sqrt{\pi}} \int_{y/(2\sqrt{t} )}^{\infty} f \biggl( t - \frac{y^{2}}{4x^{2}} \biggr) \exp \bigl( - x^{2}\bigr)\,dx \\ &{}+ \frac{G_{1}}{1 - P_{11}} \biggl[ \frac{12t^{2} - 5P_{11}^{2}y^{4}}{24}\operatorname{erfc} \biggl( \frac{y\sqrt{P_{11}}}{2\sqrt{t}} \biggr) + \frac{5y\sqrt{P_{11}t} (y^{2}P_{11} - 2t)}{12\sqrt{\pi}} \exp \biggl( \frac{ - y^{2}P_{11}}{4t} \biggr) \biggr] \\ &{}- \frac{G_{1}}{1 - P_{11}} \biggl[ \frac{12t^{2} - 5y^{4}}{24}\operatorname{erfc} \biggl( \frac{y}{2\sqrt{t}} \biggr) + \frac{5y\sqrt{t} (y^{2} - 2t)}{12\sqrt{\pi}} \exp \biggl( \frac{ - y^{2}}{4t} \biggr) \biggr], \\ &{} P_{11} \ne 1. \end{aligned}$$
(33)

3.2.1 Skin friction on the wall

Expression of the skin friction on the vertical plate in the x-direction is given by

$$\begin{aligned} C_{fx} ={}& \frac{\partial u(y,t)}{\partial y} \bigg| _{{y = 0}} = L^{ - 1} \biggl\{ \lim_{y \to 0^{ +}} \frac{\partial \bar{u}(y,s)}{\partial y} \biggr\} = L^{ - 1} \biggl\{ \frac{ - \omega s^{\alpha /2}}{s^{2} + \omega^{2}} \biggr\} \\ &{} + G_{\alpha} L^{ - 1} \biggl\{ \frac{s^{ - 2 - \gamma + \alpha /2}}{s^{\alpha - \gamma} - P_{\alpha \gamma}} - \sqrt{P_{\alpha \gamma}} \frac{s^{ - 2 - \gamma /2}}{s^{\alpha - \gamma} - P_{\alpha \gamma}} \biggr\} \\ ={}& {-} \omega G_{2,\alpha /2,1}\bigl( - \omega^{2},t\bigr) + G_{\alpha} \bigl[ G_{\alpha - \gamma,\alpha /2 - \gamma - 2,1}(P_{\alpha \gamma},t) - G_{\alpha - \gamma, - \gamma /2.1}(P_{\alpha \gamma},t) \bigr]. \end{aligned}$$
(34)

Inthecase\(\alpha = \gamma\) and \(P_{\alpha \gamma} \ne 1\),

$$\begin{aligned} C_{fx} &= L^{ - 1} \biggl\{ \frac{ - \omega s^{\alpha /2}}{s^{2} + \omega^{2}} + \frac{G_{\alpha}}{(1 + \sqrt{P_{\alpha \alpha}} )s^{2 + \alpha /2}} \biggr\} \\ &= - \omega G_{2,\alpha /2,1}\bigl( - \omega^{2},t\bigr) + \frac{G_{\alpha}}{ 1 + \sqrt{P_{\alpha \alpha}}} \frac{t^{1 + \alpha /2}}{\Gamma (2 + \alpha /2)}. \end{aligned}$$
(35)

4 Numerical results

To obtain some information on the fluids behavior, the authors analyzed some numerical examples using the coefficient values \(t_{0} = 10\), \(U_{0} = 0.1\), \(\beta_{\alpha} = 21 \times 10^{ - 5}\), \(k_{\gamma} = 0.613\), and \(\nu_{\alpha} = 1.792 \times 10^{ - 6}\). The numerical simulations were done using the subroutines of the software package Mathcad. For the temperature field, we have used the expressions given by the Eqs. (20) and (28), and for the velocity, expressions given by Eqs. (31) and (33). To check the accuracy of the obtained results, we have used the Stehfest algorithm [27] for calculating the inverse Laplace transform, namely:

$$ \begin{aligned} &T(y,t) = \frac{\ln 2}{t}\sum _{j = 1}^{2p} d_{j}\bar{T} \biggl( y,j \frac{\ln 2}{t} \biggr),\qquad u(y,t) = \frac{\ln 2}{t}\sum _{j = 1}^{2p} d_{j}\bar{u} \biggl( y,j \frac{\ln 2}{t} \biggr), \\ &d_{j} = ( - 1)^{j + p}\sum_{i = [ \frac{j + 1}{2} ]}^{\min (j,p)} \frac{i^{p}(2i)!}{(p - i)!i!(i - 1)!(j - i)!(2i - j)!}. \end{aligned} $$
(36)

Here \([r]\) denotes the integer part of a real number r, and p is a positive integer.

Tables 1 and 2 show that the numerical values obtained by the Eqs. (20) and the first formula (36) and by Eqs. (31) and the second formula (36), respectively, are in good agreement.

Table 1 Comparison of the temperature values at the time \(\pmb{t = 15}\) for \(\pmb{\alpha = 0.75}\)
Full size table
Table 2 Comparison of the velocity values at the time \(\pmb{t = 2}\) , for \(\pmb{\alpha = 0.873}\) and \(\pmb{\gamma = 0.628}\)
Full size table

In Figure 1 we plotted the curves corresponding to the temperature field \(T(y,t)\) versus the spatial coordinate y for \(t = 15\) and for various values of the fractional coefficients α and γ. It is important to point out that, in comparison with the ordinary case \(\alpha = \gamma =1\), the thermal boundary layer thickness is smaller for \(\alpha,\gamma \in (0,1)\). Also, for a fixed value of the fractional parameter α, the thickness of the thermal boundary layer is decreasing according to the fractional parameter γ. An opposite effect is observed if values of the parameter α are decreasing. In this case, the thermal boundary layer thickness is greater for lower values of the fractional parameter α. In Figures 2 and 3 we sketched the graphs of velocity \(u(y,t)\) versus y for two values of time t and for several values of the fractional parameters α and γ. From these figures we see that, for \(\alpha = \gamma =1\) (the ordinary case), the fluid flows are faster than in the cases modeled by the time-fractional derivatives. The velocity boundary layer thickness decreases for small values of fractional coefficient α. On the other hand, the thickness of the velocity boundary layer increases depending on the fractional parameter γ.

Figure 1
figure 1

Variations in temperature field. (a), (b), (c) represent the variation of the temperature \(T(y,t)\) for \(t = 15\) and various values of the fractional coefficients α and γ.

Full size image
Figure 2
figure 2

Variations in velocity field for time \(\pmb{t=5}\) . (a), (b), (c) represents the variation of velocity \(u(y,t)\) for \(t = 5\), \(\omega = \pi/6\), and various values of the fractional parameters α and γ.

Full size image
Figure 3
figure 3

Variations in velocity field for time \(\pmb{t=15}\) . (a), (b), (c) represents the variation of velocity \(u(y,t)\) for \(t = 15\), \(\omega = \pi/6\), and various values of the fractional coefficients α and γ.

Full size image

5 Concluding remarks

In this paper we studied the unsteady free convection flow of a viscous fluid near a heated vertical plate. Both governing equations, the momentum equation and energy equation, are considered as time-fractional differential equations of order \(\alpha \in (0,1]\) and \(\gamma \in (0,1]\), respectively. Based on the Laplace transform technique and using the Wright functions and G-Lorenzo-Hartley functions, the closed forms of the temperature and velocity fields were determined. The fundamental solution corresponding to the temperature, the Nusselt number, and the friction coefficient on the wall are obtained. Some physical aspects of the fluid behavior were studied by numerical simulation and graphical illustrations. As a general result, it should be noted that for decreasing values of the fractional coefficient α, the fluid velocity and boundary layer thickness are decreasing. The fluid temperature decreases if the values of the fractional coefficient γ decreases and increases for decreasing values of α.