1 Introduction

Over the past decade, for better modeling and describing the large-scale physical systems consisting of interactive individuals, many kinds of dynamical networks coupled with continuous- or discrete-time dynamical systems have been introduced [1–26]. For example, discrete-time networks are used to model digitally transmitted signals in a dynamical way [1]. Synchronization, as one of the most important and interesting collective behaviors, has been widely studied, and many valuable results have been obtained. In fact, dynamical networks usually cannot synchronize themselves or synchronize with given orbits without external control. Therefore, many control schemes are proposed to design effective controllers for achieving network synchronization, such as feedback control, intermittent control, impulsive control, pinning control, and so on.

In real world, many complex systems contain large numbers of interactive individuals, that is, the corresponding networks consisting of large numbers of nodes. For this case, applying controllers to all nodes is expensive and even impracticable. Pinning control, as an effective control scheme for reducing the number of controlled nodes, has been extensively used to investigate network synchronization, and many valuable results have been obtained [5–17]. Chen et al. [8] investigated pinning synchronization of complex network using only one controller. Liu et al. [10] studied cluster synchronization in directed networks through combining intermittent with pinning control schemes. Zhang et al. [11] studied pinning control of some typical discrete-time dynamical networks. Mwaffo et al. [12] studied stochastic pinning control of networks of chaotic maps. In [15–17], authors studied synchronization of continuous-time networks through combining impulsive with pinning control schemes. Wherein, the impulsively controlled nodes are chosen according to the norm of the synchronization errors at distinct control instants. As we know, research on synchronization of continuous- and discrete-time dynamical networks has significant differences. Therefore, extension of the results obtained in [15–17] for continuous-time networks to discrete-time networks is an important issue and deserves further study.

Motivated by the above discussions, in this paper, we investigate the impulsive pinning synchronization of discrete-time dynamical network. At different impulsive instants, the pinned nodes are chosen according to the norm of synchronization errors. Since the synchronization errors are time-varying, the pinned nodes become nonidentical at different impulsive instants. Based on the Lyapunov function method and mathematical analysis approach, we analytically derive two synchronization criteria with respect to the impulsive intervals and gains. The obtained results are verified to be effective and correct by two numerical examples.

The rest of this paper is organized as follows. Section 2 introduces the network model and some preliminaries. Section 3 studies the synchronization of discrete-time network via impulsive pinning control. Section 4 provides two numerical examples to verify the effectiveness of the derived results. Section 5 concludes the paper.

2 Model and preliminaries

Consider a discrete-time dynamical network consisting of N nodes described by

$$ x_{i}(k+1)= f\bigl(x_{i}(k)\bigr)+\sum _{j=1}^{N}c_{ij} \Gamma x_{j}(k), $$
(1)

where \(i=1,2,\ldots,N\), \(x_{i}(k)=(x_{i1}(k),\ldots,x_{in}(k))^{T}\in R^{n}\) is the state variable of node i, \(f:R^{n}\to R^{n}\) denotes the node dynamics, and \(\Gamma=\operatorname {diag}\{\gamma_{1},\gamma_{2},\ldots,\gamma_{n}\}\in R^{n\times n}\) is an inner coupling matrix. The matrix \(C=(c_{ij})_{N\times N}\) is a zero-row-sum outer coupling matrix, which denotes the network topology and coupling strength and is defined as follows: if there is a connection from node j to node i (\(i\neq j\)), then \(c_{ij}\neq0\); otherwise, \(c_{ij}=0\).

The objective here is to synchronize network (1) to a given orbit \(s(k)\) through designing proper impulsive pinning controllers, where \(s(k)\) is a solution of an isolated node satisfying \(s(k+1)=f(s(k))\). The controlled network can be written as

$$ \begin{aligned} &x_{i}(k+1)= f \bigl(x_{i}(k)\bigr)+\sum_{j=1}^{N}c_{ij} \Gamma x_{j}(k), \quad k=\mathcal{I}_{l-1}+1,\mathcal{I}_{l-1}+2,\ldots,\mathcal {I}_{l}-1, \\ &x_{i}(k+1)= x_{i}(k)+U_{i}\bigl(k,x_{i}(k),s(k) \bigr),\quad k=\mathcal{I}_{l}, \end{aligned} $$
(2)

where \(l=1,2,\ldots \) , the discrete instant set \(\{\mathcal{I}_{l}\}\) satisfies \(\mathcal{I}_{l}\in Z^{+}\), \(0=\mathcal{I}_{0}<\mathcal {I}_{1}<\mathcal{I}_{2}<\cdots<\mathcal{I}_{l}<\cdots\) , and \(\lim_{l\to +\infty}\mathcal{I}_{l}=+\infty\), and \(U_{i}(k,x_{i}(k),s(k))\) are impulsive controllers to be designed.

Let \(e_{i}(k)=x_{i}(k)-s(k)\) be the synchronization errors. Choosing the impulsive controllers in (2) as \(U_{i}(k,x_{i}(k),s(k))=f(s(k))-s(k)+B_{i}(k)(x_{i}(k)-s(k))\), we have the following error dynamical system:

$$ \begin{aligned} &e_{i}(k+1)= f \bigl(x_{i}(k)\bigr)-f\bigl(s(k)\bigr)+\sum _{j=1}^{N}c_{ij} \Gamma e_{j}(k), \quad k=\mathcal{I}_{l-1}+1,\mathcal{I}_{l-1}+2,\ldots,\mathcal {I}_{l}-1, \\ &e_{i}(k+1)=e_{i}(k)+B_{i}(k)e_{i}(k),\quad k=\mathcal{I}_{l}, \end{aligned} $$
(3)

where \(B_{i}(\mathcal{I}_{l})\in R\) are impulsive gains at \(k=\mathcal {I}_{l}\), and \(B_{i}(k)=0\) for \(k\neq\mathcal{I}_{l}\), \(i=1,2,\ldots,N\), \({l=1,2,3,\ldots} \) .

When \(k=\mathcal{I}_{l}\), arrange the synchronization errors \(e_{i}(k)\) as follows:

$$\begin{aligned} \bigl\| e_{i_{1}(k)}(k)\bigr\| \geq& \bigl\| e_{i_{2}(k)}(k)\bigr\| \geq\cdots\geq\bigl\| e_{i_{p}(k)}(k)\bigr\| \\ \geq&\bigl\| e_{i_{p+1}(k)}(k)\bigr\| \geq\cdots\geq\bigl\| e_{i_{N}(k)}(k)\bigr\| , \end{aligned}$$
(4)

where \(i_{p}(k)\in\{1,2,\ldots,N\}\), \(p=1,2,\ldots,N\), \(i_{p}(k)\neq i_{q}(k)\) for \(p\neq q\). Further, if \(\|e_{i_{p}(k)}(k)\|=\|e_{i_{p+1}(k)}(k)\|\), then let \(i_{p}(k)< i_{p+1}(k)\). Let \(P(\mathcal{I}_{l})=\{i_{1}(\mathcal {I}_{l}),\ldots,i_{p}(\mathcal{I}_{l})\}\) be a set of p nodes. Choose \(B_{i}(\mathcal{I}_{l})=b_{l}\in(-2,-1)\cup(-1,0)\) for \(i\in P(\mathcal {I}_{l})\) and \(B_{i}(\mathcal{I}_{l})=0\) for \(i\notin P(\mathcal{I}_{l})\), which means that \(P(\mathcal{I}_{l})\) is the set of pinned nodes at \(k=\mathcal{I}_{l}\).

Assumption 1

The function \(f(x)\) satisfies the Lipschitz condition, that is, there exists a positive constant L such that

$$\bigl\| f(y)-f(x)\bigr\| \leq L\|y-x\| $$

for any vectors \(x,y\in R^{n}\), where \(\|x\|\) denotes the Euclidean vector norm, that is, \(\|x\|=\sqrt{x^{T}x}\).

3 Main result

In what follows, let \(e(k)=(e_{1}^{T}(k),e_{2}^{T}(k),\ldots,e_{N}^{T}(k))^{T}\), \(F(e(k))=((f(x_{1})-f(s))^{T},\ldots, (f(x_{N})-f(s))^{T})^{T}\), \(\mathcal {T}_{l}=\mathcal{I}_{l}-1-\mathcal{I}_{l-1}\) be the impulsive intervals, \(\lambda^{2}\) be the largest eigenvalue of the matrix \((C^{T}\otimes\Gamma )(C\otimes\Gamma)\) with \(\lambda>0\), \(\beta_{l}=(1+b_{l})^{2}\), and \(\rho _{l}=1-(1-\beta_{l})p/N\).

Theorem 1

Suppose that Assumption  1 holds and that there exists a positive constant \(\alpha>0\) such that

$$ \ln\rho_{l}+\alpha+2\mathcal{T}_{l}\ln(L+ \lambda)< 0,\quad l=1,2,\ldots. $$
(5)

Then the synchronization of the discrete-time network (2) with impulsive pinning controllers is achieved.

Proof

Consider the following Lyapunov function candidate

$$ V\bigl(e(k)\bigr)=\sum_{i=1}^{N} \bigl\| e_{i}(k)\bigr\| ^{2}. $$

When \(k=\mathcal{I}_{l-1}+1,\mathcal{I}_{l-1}+2,\ldots,\mathcal {I}_{l}-1\), we have

$$\begin{aligned} V\bigl(e(k+1)\bigr) =&\sum_{i=1}^{N} \bigl\| e_{i}(k+1)\bigr\| ^{2} \\ =&\bigl\| e(k+1)\bigr\| ^{2} \\ =&\bigl\| F\bigl(e(k)\bigr)+C\otimes\Gamma e(k)\bigr\| ^{2} \\ \leq&\bigl(\bigl\| F\bigl(e(k)\bigr)\bigr\| +\Bigl\| C\otimes\Gamma e(k)\Bigr\| \bigr)^{2} \\ \leq&\bigl(L\bigl\| e(k)\bigr\| +\lambda\bigl\| e(k)\bigr\| \bigr)^{2} \\ \leq&(L+\lambda)^{2}V\bigl(e(k)\bigr), \end{aligned}$$

which gives

$$ V\bigl(e(k+1)\bigr)\leq(L+\lambda)^{2(k-\mathcal{I}_{l-1})}V\bigl(e( \mathcal{I}_{l-1}+1)\bigr). $$
(6)

When \(k=\mathcal{I}_{l}\), we have

$$\begin{aligned} V\bigl(e(\mathcal{I}_{l}+1) \bigr) = &\sum_{i=1}^{N}\bigl\| e_{i}( \mathcal{I}_{l}+1)\bigr\| ^{2} \\ =& \sum_{i\in P(\mathcal{I}_{l})}\bigl\| e_{i}(\mathcal{I}_{l}+1) \bigr\| ^{2}+\sum_{i\notin P(\mathcal{I}_{l})}\bigl\| e_{i}( \mathcal{I}_{l}+1)\bigr\| ^{2} \\ = &\sum_{i\in P(\mathcal{I}_{l})}(1+b_{l})^{2}\cdot \bigl\| e_{i}(\mathcal{I}_{l})\bigr\| ^{2}+\sum _{i\notin P(\mathcal{I}_{l})}\bigl\| e_{i}(\mathcal{I}_{l}) \bigr\| ^{2} \\ =& \beta_{l}\sum_{i=1}^{N} \bigl\| e_{i}\bigl(\mathcal{I}_{l}^{-}\bigr)\bigr\| ^{2}+(1- \beta_{l})\sum_{i\notin P(\mathcal{I}_{l})}\bigl\| e_{i}\bigl( \mathcal{I}_{l}^{-}\bigr)\bigr\| ^{2}. \end{aligned}$$
(7)

According to the definition of \(P(\mathcal{I}_{l})\), we have

$$ \frac{1}{N-p}\sum_{i\notin P(\mathcal{I}_{l})} \bigl\| e_{i}(\mathcal{I}_{l})\bigr\| ^{2}\leq \frac{1}{N}\sum_{i=1}^{N} \bigl\| e_{i}(\mathcal{I}_{l})\bigr\| ^{2}. $$
(8)

Combining (7) and (8), we have

$$\begin{aligned} V\bigl(e(\mathcal{I}_{l}+1) \bigr) \leq& \biggl(\beta_{l}+\frac{(1-\beta_{l})(N-p)}{N} \biggr)\sum _{i=1}^{N}\bigl\| e_{i}(\mathcal{I}_{l}) \bigr\| ^{2} \\ =&\rho_{l} V\bigl(e(\mathcal{I}_{l})\bigr). \end{aligned}$$
(9)

For \(l=1\), from inequalities (6) and (9) we have

$$ \begin{aligned} &V\bigl(e(\mathcal{I}_{1}) \bigr)\leq (L+\lambda)^{2(\mathcal{I}_{1}-1-\mathcal {I}_{0})}V\bigl(e(\mathcal{I}_{0}+1)\bigr) \\ &\hphantom{V\bigl(e(\mathcal{I}_{1}) \bigr)}= (L+\lambda)^{2\mathcal{T}_{1}}V\bigl(e(1)\bigr), \\ &V\bigl(e(\mathcal{I}_{1}+1)\bigr)\leq \rho_{1}(L+ \lambda)^{2\mathcal{T}_{1}}V\bigl(e(1)\bigr). \end{aligned} $$
(10)

For \(l=2\), from inequalities (6), (9), and (10) we have

$$ \begin{aligned} &V\bigl(e(\mathcal{I}_{2}) \bigr)\leq (L+\lambda)^{2(\mathcal{I}_{2}-1-\mathcal {I}_{1})}V\bigl(e(\mathcal{I}_{1}+1)\bigr) \\ &\hphantom{V\bigl(e(\mathcal{I}_{2}) \bigr)}= \rho_{1}(L+\lambda)^{2(\mathcal{T}_{1}+\mathcal{T}_{2})}V\bigl(e(1)\bigr), \\ &V\bigl(e(\mathcal{I}_{2}+1)\bigr)\leq \rho_{1} \rho_{2}(L+\lambda)^{2(\mathcal {T}_{1}+\mathcal{T}_{2})}V\bigl(e(1)\bigr). \end{aligned} $$
(11)

According to mathematical induction, for any positive integer l, we can prove the following inequalities:

$$ \begin{aligned} &V\bigl(e(\mathcal{I}_{l}) \bigr)\leq\prod_{\sigma=1}^{l-1}\rho_{\sigma}\prod_{\kappa =1}^{l}(L+\lambda)^{2\mathcal{T}_{\kappa}}V \bigl(e(1)\bigr), \\ &V\bigl(e(\mathcal{I}_{l}+1)\bigr)\leq\prod _{\kappa=1}^{l}\bigl(\rho_{\kappa}(L+\lambda )^{2\mathcal{T}_{\kappa}}\bigr)V\bigl(e(1)\bigr). \end{aligned} $$
(12)

Assume that inequalities (12) hold for \(l\leq m\), Then we have

$$ \begin{aligned} &V\bigl(e(\mathcal{I}_{m}) \bigr)\leq\prod_{\sigma=1}^{m-1}\rho_{\sigma}\prod_{\kappa=1}^{m}(L+\lambda)^{2\mathcal{T}_{\kappa}}V \bigl(e(1)\bigr), \\ &V\bigl(e(\mathcal{I}_{m}+1)\bigr)\leq\prod _{\kappa=1}^{m}\bigl(\rho_{\kappa}(L+\lambda )^{2\mathcal{T}_{\kappa}}\bigr)V\bigl(e(1)\bigr). \end{aligned} $$
(13)

From inequalities (6), (9), and (13) we have

$$ \begin{aligned}& V\bigl(e(\mathcal{I}_{m+1}) \bigr) \leq(L+\lambda)^{2(\mathcal {I}_{m+1}-1-\mathcal{I}_{m})} V\bigl(e(\mathcal{I}_{m}+1)\bigr) \\ & \hphantom{ V\bigl(e(\mathcal{I}_{m+1}) \bigr)}\leq\prod_{\sigma=1}^{m}\rho_{\sigma}\prod_{\kappa=1}^{m+1}(L+\lambda )^{2\mathcal{T}_{\kappa}}V \bigl(e(1)\bigr), \\ &V\bigl(e(\mathcal{I}_{m+1}+1)\bigr) \leq\prod _{\kappa=1}^{m+1}\bigl(\rho_{\kappa}(L+ \lambda)^{2\mathcal{T}_{\kappa}}\bigr)V\bigl(e(1)\bigr). \end{aligned} $$
(14)

That is to say, inequalities (12) hold for \(l=m+1\).

From conditions (5) we have

$$ \rho_{l}(L+\lambda)^{2\mathcal{T}_{l}}< e^{-\alpha},\quad l=1,2,\ldots, $$

and

$$ V\bigl(e(\mathcal{I}_{l}+1)\bigr)\leq e^{-l\alpha}V\bigl(e(1) \bigr), $$

which implies that \(V(e(\mathcal{I}_{l}+1))\to0\) as \(l\to\infty\). Then, for \(k=\mathcal{I}_{l}+1,\mathcal{I}_{l}+2,\ldots,\mathcal {I}_{l+1}-1\), we have

$$ V\bigl(e(k+1)\bigr)\leq (L+\lambda)^{2(k-\mathcal{I}_{l})}V\bigl(e(\mathcal {I}_{l}+1)\bigr)\to0 \quad\mbox{as } l\to\infty, $$

which implies that \(\|e_{i}(k)\|\to0\) as \(k\to\infty\), that is, the error system (3) is globally asymptotically stable about zero. Therefore, the synchronization of discrete-time network (2) with impulsive pinning controllers is achieved, and the proof is completed. □

If the impulsive gains \(b_{l}\) and the impulsive intervals \(\mathcal {T}_{l}\) are chosen as a constant \(b_{0}\) and a positive constant \(\mathcal {T}_{0}\), the following corollary can be easily derived.

Corollary 1

Suppose that Assumption  1 holds and that there exists a positive constant \(\alpha>0\) such that

$$ \ln\rho_{0}+\alpha+2\mathcal{T}_{0}\ln(L+ \lambda)< 0, $$
(15)

where \(\beta_{0}=(1+b_{0})^{2}\) and \(\rho_{0}=1-(1-\beta_{0})p/N\). Then the synchronization of discrete-time network (2) with impulsive pinning controllers can be achieved.

Remark 1

In many existing results about pinning control, the outer coupling matrix is assumed to be irreducible, that is, the network is connected. From the proof of Theorem 1 it is clear that the outer coupling matrix C need not be symmetrical or irreducible. That is, the obtained results can be applied to more general networks and even to disconnected networks.

Remark 2

For any given network, fixing the impulsive gains \(b_{l}\) and the number of pinned nodes p, we can easily estimate the largest impulsive interval for achieving synchronization from condition (5) or (15).

4 Numerical simulations

Consider a discrete-time dynamical network consisting of six nodes and choose the node dynamics as the following Chirikov standard map [12, 27]:

$$ \begin{aligned} &x_{i1}(k+1)= x_{i1}(k)+ \eta\sin\bigl(x_{i2}(k)\bigr), \\ &x_{i2}(k+1)= x_{i1}(k)+x_{i2}(k)+\eta\sin \bigl(x_{i2}(k)\bigr), \end{aligned} $$
(16)

where \(x_{i1}(k)\) and \(x_{i2}(k)\) are taken modulo 2π for \(i=1,2,\ldots,6\). This map exhibits chaotic behavior when \(\eta>0\). By simple calculations we can choose \(L=1+2\eta\) such that Assumption 1 holds.

Example 1

Consider an undirected discrete-time dynamical network. Choose the inner coupling matrix Γ as the identity matrix and the outer coupling matrix as

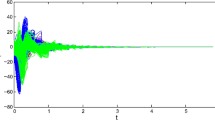
$$ C=0.005\times \begin{pmatrix} -5 & 1 & 2 & 1 & 0 & 1 \\ 1 &-3 & 0 & 1 & 1 & 0 \\ 2 & 0 &-4 & 1 & 0 & 1 \\ 1 & 1 & 1 &-5 & 1 & 1 \\ 0 & 1 & 0 & 1 &-4 & 2 \\ 1 & 0 & 1 & 1 & 2 & -5 \end{pmatrix}. $$

In numerical simulations, choose the number of pinned nodes \(p=2\), the impulsive gain \(b_{0}=-0.9\), \(\alpha=0.001\), \(\eta=0.01\), \(\mathcal {T}_{0}=3\), and the initial values of \(x_{i}(k)\) and \(s(k)\) randomly. By simple calculations we have \(\lambda=0.0361\), \(\beta_{0}=0.01\), \(\rho _{0}=0.67\), and \(\ln0.67+0.001+ 6\ln1.0561 =-0.072<0\), that is, condition (15) in Corollary 1 holds, and the synchronization can be achieved. Figure 1 shows the orbits of the norm of synchronization errors.

Figure 1
figure 1

The orbits of the norm of synchronization errors, \(\pmb{E_{i}(t)=\sqrt{e_{i}^{T}(t)e_{i}(t)}}\) , \(\pmb{i=1,2,\ldots,6}\) .

Full size image

Example 2

Consider a directed discrete-time dynamical network. Choose the inner coupling matrix Γ as identity matrix and the outer coupling matrix as

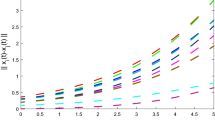
$$ C=0.005\times \begin{pmatrix} -5 & 1 & 2 & 1 & 0 & 1 \\ 2 &-4 & 0 & 1 & 1 & 0 \\ 1 & 1 &-6 & 3 & 0 & 1 \\ 0 & 2 & 1 &-5 & 1 & 1 \\ 0 & 0 & 2 & 2 &-6 & 2 \\ 1 & 1 & 0 & 1 & 1 & -4 \end{pmatrix}. $$

In numerical simulations, choose the number of pinned nodes \(p=2\), the impulsive gain \(b_{0}=-0.9\), \(\alpha=0.001\), \(\eta=0.01\), \(\mathcal{T}_{0}=3\), and the initial values of \(x_{i}(k)\) and \(s(k)\) randomly. By simple calculations we have \(\lambda=0.0412\), \(\beta_{0}=0.01\), \(\rho_{0}=0.67\), and \(\ln0.67+0.001+ 6\ln 1.0612 =-0.0431<0\), that is, condition (15) in Corollary 1 holds, and the synchronization can be achieved. Figure 2 shows the orbits of the norm of synchronization errors.

Figure 2
figure 2

The orbits of the norm of synchronization errors, \(\pmb{E_{i}(t)=\sqrt{e_{i}^{T}(t)e_{i}(t)}}\) , \(\pmb{i=1,2,\ldots,6}\) .

Full size image

5 Conclusions

In this paper, we studied the synchronization problem of discrete-time network via impulsive pinning control. In the proposed control scheme, the impulsive controllers are applied to only a fraction of nodes, and the pinned nodes are chosen according to the norm of the synchronization errors at different control instants. Two sufficient conditions for achieving synchronization are derived based on Lyapunov function method and mathematical analysis technique. From the conditions, for any given networks, we can easily estimate the largest impulsive interval by fixing the impulsive gains and the number of pinned nodes p. Finally, two numerical examples are performed to illustrate the obtained results.