1 Introduction

Switched systems are a class of important hybrid systems which consist of a finite number of subsystems that are governed by differential or difference equations and a switching law which defines a specific subsystem being activated during a certain interval of time. Due to the physical properties or various environmental factors, many real-world systems can be modeled as switched systems such as computer science, autonomous transmission systems, computer disc drivers, control systems, electrical engineering and technology, automotive industry, air traffic management, chemical systems, power systems and communication networks, and other applications [1–9]. On the other hand, considerable efforts have been made as regards the analysis and the design of switched systems. There are still many open and challenging issues remaining to be tackled, despite great successes reported during the past several decades. Among those research topics, stability analysis and stabilization have attracted most attention [1–4, 10–41]. Hence, several methods have been proposed for these matters. It is commonly recognized that there are mainly three basic types of problems considering the stability and the stabilization issues of switched systems [10–12]: (i) guaranteeing of asymptotical stability of the switched system with arbitrary switching; (ii) identification of the limited but useful class of stabilizing switching laws; and (iii) construction of asymptotically stabilizing switching signals. Specifically, the stability analysis under arbitrary switching problem (i) which will be focused on in this work deals with the case that all subsystems are stable. This problem seems trivial, but it is fundamental and important [10, 13–17], since we can find many examples where all subsystems are stable but inappropriate switching rules can make the whole system unstable. In addition, stability under arbitrary switching is a desirable property of switched systems due to its practical importance and also it allows us to consider higher control specifications for the system. For this problem, it is well known that the existence of a common Lyapunov function for individual systems guarantees stability of the switched system under arbitrary switching [16, 19]. Therefore, this method is usually very difficult to apply even for continuous-time switched linear systems [18, 19]; however, it becomes more complicated for switched nonlinear systems. Yet, some attempts are presented to construct a common Lyapunov function for nonlinear switched systems [20, 21].

On the other hand, time delay is a common phenomenon encountered in various practical and engineering systems [42, 43] such as chemical processes, nuclear reactors, models of lasers, electrical systems, aircraft stabilization, biological systems, and systems with lossless transmission lines; and most of them appear in the form of time-varying delay. It is a well-known fact that the presence of delays is an inherent feature of many physical processes, the big sources of instability and poor performances in switched systems. Thus, it is important to investigate the stability analysis problem for switched delay systems [22–24, 27, 28, 30–41]. It is noted that current methods of the analysis and design for time-delay systems can be classified into two categories: delay-independent criteria and delay-dependent ones. In this work, in view of a delay-independent analysis, we expect to aid in studying stability analysis of switched systems under an arbitrary switching law.

Presently, the most important consideration in the analysis of switched systems is their stability. Recently, many researchers focused on switched time-delay systems. Indeed, the stability analysis problem of switched time-delay systems has attracted a lot of attention from many researchers [32, 35–40]. However, the presence of delays makes this problem much more complicated. Thus, the main approach for stability analysis under arbitrary switching relies on the use of a Lyapunov-Krasovskii functional and the LMI approach for constructing a common Lyapunov function [40]. In fact, getting such a function becomes more complicated even for switched linear systems. Consequently, few results have been obtained for continuous-time switched nonlinear time-delay systems [40].

Motivated by these mentioned shortcomings for the existing results in this framework as well in the sense of various methods that can be employed in this paper, we address this challenging problem. Indeed, based on the construction of a common Lyapunov function as well as the use of the Borne-Gentina practical stability criterion [22–26, 44–57] associated with the M-matrix properties [58, 59], new delay-independent sufficient stability conditions for continuous-time switched nonlinear time-delay systems under arbitrary switching are established. Subsequently, these obtained results are extended to be generalized for continuous-time switched nonlinear systems with multiple delays. Note that these proposed results can guarantee stability under arbitrary switching and allow us to avoid searching of a common Lyapunov function, which is very difficult in this case.

Within the frame of studying the stability analysis, this approach was introduced in [44, 45] for continuous-time-delay systems and in our previous work [22, 24] for discrete-time switched time-delay systems.

This paper is organized as follows. Section 2 formulates the problem and presents some definitions. The main results of this paper are given in Section 3. Section 4 is devoted to the derivation of new delay-independent conditions for the asymptotic stability of a class of switched nonlinear systems defined by differential equations. Then this result is extended for switched systems with multiple delays in Section 5. A numerical example is provided to illustrate the design results in Section 6. Finally, concluding remarks are given in Section 7.

Notations

The notations in this paper are fairly standard. If not explicitly stated, matrices are assumed to have compatible dimensions. I is an identity matrix with appropriate dimension. Let \(\Re^{n}\) denote an n dimensional linear vector space over the reals; \(\Vert \cdot \Vert \) stands for the Euclidean norm of vectors. For any \(u = ( u_{i} )_{1 \le i \le n}, v = ( v_{i} )_{1 \le i \le n} \in \Re^{n}\) we define the scalar product of the vector u and v as \(\langle u,v \rangle = \sum_{i = 1}^{n} u_{i}v_{i}\). Denote by \(\lambda ( M )\) the set of eigenvalues of the matrix \(M = ( m_{i,j} )_{1 \le i,j \le n}\), \(M^{T}\) is its transpose and \(M^{ - 1}\) its inverse and we denote \(M^{*} = ( m_{{i,j}}^{*} )_{1 \le i,j \le n}\) with \(m_{{i,j}}^{*} = m_{i,j}\) if \(i = j\) and \(m_{{i,j}}^{*} = \vert m_{i,j} \vert \) if \(i \ne j\) and \(\vert M \vert = \vert m_{i,j} \vert \), \(\forall i,j\).

In the sequel, we denote \(( x ( t ),t ) = (\cdot )\).

2 Preliminaries and problem formulation

Consider the following continuous-time switched time-varying delay system:

$$ \left \{ \textstyle\begin{array}{l} \dot{x} ( t ) = A_{\sigma ( t )} (\cdot )x ( t ) + D_{\sigma ( t )} (\cdot )x ( t - h ), \\ x ( t ) = \phi ( t ),\quad t \in [ - h, 0 ], \end{array}\displaystyle \right . $$
(1)

where \(\sigma ( t ): \Re^{ +} \to \underline{N} = \{ 1, 2,\ldots, N \}\) is a right continuous piecewise constant mapping, called the switching signal, N is the number of subsystems, \(x ( t ) \in \Re^{n}\) is the state, \(A_{\sigma ( t )} (\cdot )\) and \(D_{\sigma ( t )} (\cdot )\) are matrices with nonlinear elements of appropriate dimensions. \(\varphi ( t )\) is the continuous vector valued function specifying the initial state of the system. \(h > 0\) is the time delay.

Before addressing the main results, some definitions are first introduced.

Definition 1

The equilibrium point of system (1) is said to be uniformly asymptotically stable if for any \(\varepsilon > 0\), there is a \(\delta ( \varepsilon ) > 0\) such that \(\max_{ - h \le t \le 0}\Vert \phi ( t ) \Vert < \delta\) implies \(\Vert x ( t,\phi ) \Vert \le \varepsilon\), \(t \ge 0\). For arbitrary switching \(\sigma ( t )\), there is also a \(\delta '\) such that \(\max_{ - h \le t \le 0}\Vert \phi ( t ) \Vert < \delta '\) implies \(\Vert x ( t,\phi ) \Vert \to 0\) as \(t \to \infty\).

Now, the following lemma and criterion are preliminarily presented, which will play important roles in our further derivation.

Kotelyanski lemma

[58]

The real parts of the eigenvalues of the matrix A, with non-negative off-diagonal elements, are less than a real number μ if and only if all those of the matrix M; \(M = \mu I_{n} - A\) are positive, with \(I_{n}\) the n identity matrix.

Borne-Gentina practical stability criterion

[30]

Let consider the autonomous nonlinear continuous process described in state space by \(\dot{x} = A (\cdot )x\); \(A (\cdot )\) is an \(n \times n\) matrix, \(A (\cdot ) = \{ a_{ij} \}_{1 \le i,j \le n}\). If the overvaluing matrix \(M ( A (\cdot ) )\) has its non-constant elements isolated in only one row, the verification of the Kotelyanski condition enables one to conclude to the stability of the initial system.

As an example, if the non-constant elements are isolated in only one row of \(A (\cdot )\), the Kotelyanski lemma applied to the overvaluing matrix obtained by the use of the n regular vector norm \(p ( x )\) with \(x = [ x_{1},x_{2},\ldots,x_{n} ]^{T}\), such that \(p ( x ) = [ \vert x_{1} \vert ,\vert x_{2} \vert ,\ldots, \vert x_{n} \vert ]^{T}\), leads to the following stability conditions of the initial system:

$$\begin{aligned}& a_{11} < 0, \\& \left \vert \textstyle\begin{array}{@{}c@{\quad}c@{}} a_{11} & \vert a_{12} \vert \\ \vert a_{21} \vert & a_{22} \end{array}\displaystyle \displaystyle \right \vert > 0,\qquad \ldots,\qquad ( - 1 )^{n} \left \vert \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{11} & \vert a_{12} \vert & \cdots & \vert a_{1n} \vert \\ \vert a_{21} \vert & a_{22} & \cdots & \vert a_{2n} \vert \\ \vdots & \vdots & \cdots & \vdots \\ \vert a_{n1} (\cdot ) \vert & \vert a_{n2} (\cdot ) \vert & \cdots & a_{nn} (\cdot ) \end{array}\displaystyle \displaystyle \right \vert > 0. \end{aligned}$$

The Borne-Gentina practical criterion applied to continuous systems generalizes the Kotelyanski lemma for nonlinear systems and defines large classes of systems for which the linearity assumption can be applied, either for the initial system or for its comparison system.

The following theorem of the M-matrix properties is required.

Theorem 1

[44]

The matrix \(A = \{ a_{ij} \}_{1 \le i,j \le n}\) is an M-matrix if the properties below are satisfied:

  • The principal minors of A are positive:

    $$ ( A )\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 1& 2&\cdots& j \\ 1& 2&\cdots& j \end{array}\displaystyle \right ) > 0, \quad \forall j = 1,\ldots,n. $$
    (2)

  • For any positive real numbers \(\eta = ( \eta_{1},\ldots,\eta_{n} )^{T}\) the algebraic equations \(Ax = \eta\) have a positive solution \(w = ( w_{1},\ldots,w_{n} )\).

Remark 1

A continuous-time system characterized by a matrix A is stable if the matrix A is the opposite of an M-matrix.

Here the definition of a pseudo-overvaluing matrix is given, which will be used in the subsequent analysis.

Definition 2

[49, 60]

The matrix \(T_{c} (\cdot )\) is said to be a pseudo-overvaluing matrix of the system given by \(\dot{x} = A (\cdot )x\) with respect to the vector norm p, when the following inequality is verified:

$$ \dot{p} ( x ) \le T_{c} (\cdot )p ( x ), $$
(3)

\(\forall x \in E\) and \(t > 0\) is verified for each corresponding component. Thus, the stability of the comparison system: \(\dot{z} ( t ) = T_{c} (\cdot )z ( t )\) with the initial conditions such as \(z_{0} = p ( x_{0} )\), implies the same property for the initial system.

When the pseudo-overvaluing matrix \(T_{c} (\cdot )\) is defined with respect to regular vector norms, the following properties can be considered:

  • The off-diagonal elements of the matrix \(T_{c} (\cdot )\) are non-negative.

  • When all the real parts of the eigenvalues of \(T_{c} (\cdot )\) are negative, this matrix is the opposite of an M-matrix. It allows an inverse whose elements are all non-positive.

  • When we denote by \(\lambda_{M} < 0\) the real part of the eigenvalue of maximum real part of \(T_{c} (\cdot )\), it comes the inequalities: \(\operatorname{Re} ( \lambda_{M_{C} (\cdot )} ) \le \lambda_{M}\).

  • When its inverse is an irreducible matrix, then \(T_{c} (\cdot )\) admits an eigenvector \(u ( x,t )\) relative to the eigenvalues \(\lambda_{M}\) and whose components are strictly positive.

  • In addition, if we suppose now that the non-constant elements are isolated in only one row of \(T_{c} (\cdot )\). Then the main eigenvector u related to the main eigenvalue \(\lambda_{M}\) is a constant vector.

Remark 2

In the case that the nonlinear elements of the matrix \(A (\cdot )\) are isolated in only one row, the conditions of Theorem 1, Definition 2 and Remark 1 still valid.

Assumption 1

We suppose that the nonlinear elements of the pseudo-overvaluing matrix \(T_{c} (\cdot )\) are isolated in only the last row.

3 Main results

Theorem 2

System (1) is asymptotically globally stable under arbitrary switching rule (1) \(\sigma ( t ) = i \in \underline{N}\), if the matrix \(T_{c} (\cdot )\) is the opposite of an M-matrix, with

$$ T_{c} (\cdot ) = \max_{1 \le i \le N} \Bigl( \bigl( A_{i} (\cdot ) \bigr)^{*} + \sup_{ [\cdot ]} \bigl( \bigl\vert D_{i} (\cdot ) \bigr\vert \bigr) \Bigr). $$
(4)

Proof

Let \(w \in \Re^{n}\) with components (\(w_{m} > 0\), \(\forall m = 1,\ldots,n \)) and \(x ( t ) \in \Re^{n}\) is the state vector.

Choose a radially unbound common Lyapunov function as follows:

$$ V \bigl( x ( t ),t \bigr) = V_{1} \bigl( x ( t ),t \bigr) + V_{2} \bigl( x ( t ),t \bigr) $$
(5)

with

$$ V_{1} \bigl( x ( t ),t \bigr) = \bigl\langle \bigl\vert x ( t ) \bigr\vert ,w \bigr\rangle $$
(6)

and

$$ V_{2} \bigl( x ( t ),t \bigr) = \biggl\langle \vert D_{c} \vert \int_{t - h}^{t} \bigl\vert x ( \theta ) \bigr\vert \, d\theta,w \biggr\rangle , $$
(7)

where

$$ D_{c} (\cdot ) = \max_{1 \le i \le N} \bigl( \bigl\vert D_{i} (\cdot ) \bigr\vert \bigr) $$
(8)

and \(D_{c} = \max_{1 \le i \le N} ( \sup_{ [\cdot ]} ( \vert D_{i} (\cdot ) \vert ) )\).

It is clear that \(V ( t = 0 ) \ge 0\).

Taking the right derivative of \(V ( x ( t ),t )\) along the trajectory of system (1) yields

$$ \frac{d^{+} V ( x ( t ),t )}{dt^{ +}} = \frac{d^{ +} V_{1} ( x ( t ),t )}{dt^{+}} + \frac{d^{ +} V_{2} ( x ( t ),t )}{dt^{+}}, $$
(9)

where

$$ \frac{d^{ +} V_{1} ( x ( t ),t )}{dt^{ +}} = \biggl\langle \frac{d^{ +} \vert x ( t ) \vert }{dt^{ +}},w \biggr\rangle = \biggl\langle \operatorname{sgn} \bigl( x ( t ) \bigr)\frac{d^{ +} x ( t )}{dt^{ +}},w \biggr\rangle $$
(10)

and

$$ \operatorname{sgn} \bigl( x ( t ) \bigr) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \operatorname{sgn} ( x_{1} ( t ) )&& \\ &\ddots& \\ &&\operatorname{sgn} ( x_{n} ( t ) ) \end{array}\displaystyle \right ). $$
(11)

Then

$$\begin{aligned} \frac{d^{ +} V_{1} ( t )}{dt^{ +}} =& \bigl\langle \operatorname{sgn} \bigl( x ( t ) \bigr) \bigl( A_{\sigma ( t )} (\cdot )x ( t ) + D_{\sigma ( t )} (\cdot )x ( t - h ) \bigr),w \bigr\rangle \\ \le& \bigl\langle \bigl( \bigl( A_{\sigma ( t )} (\cdot ) \bigr)^{*} \bigl\vert x ( t ) \bigr\vert + \bigl\vert D_{\sigma ( t )} (\cdot ) \bigr\vert \bigl\vert x \bigl( t - h ( t ) \bigr) \bigr\vert \bigr),w \bigr\rangle \\ \le& \bigl\langle \bigl( \bigl( A_{c} (\cdot ) \bigr)^{*}\bigl\vert x ( t ) \bigr\vert + \bigl\vert D_{c} (\cdot ) \bigr\vert \bigl\vert x ( t - h ) \bigr\vert \bigr),w \bigr\rangle \end{aligned}$$
(12)

with \(A_{c} (\cdot ) = \max_{1 \le i \le N} ( \vert A_{i} (\cdot ) \vert )\).

Also we have

$$ \frac{d^{ +} V_{2} ( x ( t ),t )}{dt^{ +}} = \bigl\langle \bigl\vert D_{c} (\cdot ) \bigr\vert \bigl( \bigl\vert x ( t ) \bigr\vert - \bigl\vert x ( t - h ) \bigr\vert \bigr),w \bigr\rangle . $$
(13)

From (12) and (13), we obtain the following inequality:

$$\begin{aligned} \frac{d^{ +} V ( t )}{dt^{ +}} < & \bigl\langle \bigl( \bigl( A_{c} (\cdot ) \bigr)^{*}\bigl\vert x ( t ) \bigr\vert + \bigl\vert D_{c} (\cdot ) \bigr\vert \bigl\vert x ( t - h ) \bigr\vert \bigr) + \bigl\vert D_{c} (\cdot ) \bigr\vert \bigl\vert x ( t ) \bigr\vert - \bigl\vert D_{c} (\cdot ) \bigr\vert \bigl\vert x ( t - h ) \bigr\vert ,w \bigr\rangle \\ =& \bigl\langle \bigl( \bigl( A_{c} (\cdot ) \bigr)^{*} \bigl\vert x ( t ) \bigr\vert \bigr) + \bigl\vert D_{c} (\cdot ) \bigr\vert \bigl\vert x ( t ) \bigr\vert ,w \bigr\rangle = \bigl\langle \bigl\vert T_{c} (\cdot ) \bigr\vert \bigl\vert x ( t ) \bigr\vert ,w \bigr\rangle , \end{aligned}$$
(14)

where \(T_{c} (\cdot )\) is given in (5).

We know that

$$ \bigl\langle T_{c} (\cdot )\bigl\vert x ( t ) \bigr\vert ,w \bigr\rangle = \bigl\langle T_{c} (\cdot )^{T}w,\bigl\vert x ( t ) \bigr\vert \bigr\rangle . $$
(15)

In the case that the nonlinear elements of \(T_{c} (\cdot )\) are isolated in the last row (Assumption 1 is satisfied) the eigenvector \(v ( t,x ( t ) )\) relative to the eigenvalue \(\lambda_{m}\) is constant [44] where \(\lambda_{m}\) is such that \(\operatorname{Re} ( \lambda_{m} ) = \max \{ \operatorname{Re} ( \lambda_{m} ), \lambda \in \lambda T_{c} (\cdot ) \}\). Then, to complete this proof, we assume that \(T_{c} (\cdot )\) is the opposite of an M-matrix. Indeed, according to the M-matrix properties, we can find a vector \(\rho \in \Re_{ +}^{*n}\) (\(\rho_{l} \in \Re_{ +}^{*}\), \(l = 1,\ldots,n \)) satisfying the relation \(( T_{c} (\cdot ) )^{T}w = - \rho\), \(\forall w \in \Re_{ +}^{*n}\).

We have

$$ \bigl\langle \bigl( T_{c} (\cdot ) \bigr)\bigl\vert x ( t ) \bigr\vert ,w \bigr\rangle = \bigl\langle \bigl( T_{c} (\cdot ) \bigr)^{T}w ,\bigl\vert x ( t ) \bigr\vert \bigr\rangle = \bigl\langle - \rho ,\bigl\vert x ( t ) \bigr\vert \bigr\rangle . $$
(16)

Substituting (16) into (15) gives rise to

$$ \frac{dV ( t,x ( t ) )}{dt} < \bigl\langle - \rho ,\bigl\vert x ( t ) \bigr\vert \bigr\rangle = - \sum_{l = 1}^{n} \rho_{l}\bigl\vert x ( t ) \bigr\vert < 0. $$
(17)

Thus, the proof is completed. □

4 Stability of switched nonlinear systems modeled by delay differential equations

This section discusses the stability property of a class of switched nonlinear delay systems described by a set of delay differential equations described as follows:

$$ \left \{ \textstyle\begin{array}{l} y^{n} ( t ) + ( \sum_{j = 0}^{n - 1} a_{i}^{j} (\cdot )y^{ ( j )} ( t ) ) + ( \sum_{p = 0}^{n - 1} d_{i}^{j} (\cdot )y^{ ( j )} ( t - h ) ) = 0,\quad h > 0, \\ y^{ ( j )} ( \theta ) = \phi_{j} ( \theta ),\quad \theta \in [ - h, 0 ], j = 1,\ldots,n - 1, \end{array}\displaystyle \right . $$
(18)

where \(y ( t ) \in \Re^{n}\), \(a_{i}^{j} (\cdot )\) and \(d_{i}^{j} (\cdot )\) are nonlinear coefficients for each \(i \in \underline{N}\) and \(j = 1,\ldots, n - 1\). \(u ( t ) \in \Re\) is the control input. \(h > 0\) denotes the delay. \(\phi_{j} ( \theta )\) (\(j = 1,\ldots, n - 1 \)) are the initial conditions on \([ - h, 0 ]\).

The following changes:

$$ x_{j + 1} ( t ) = y^{ ( j )} ( t ),\quad j = 0,\ldots, n - 1, $$
(19)

imply the state variables

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{j} ( t ) = x_{j + 1} ( t ), \quad j = 0,\ldots, n - 1, \\ \dot{x}_{n} ( t ) = - ( \sum_{j = 0}^{n - 1} a_{i}^{j} (\cdot )x_{j + 1} ( t ) + \sum_{j = 0}^{n - 1} d_{i}^{j} (\cdot )x_{j + 1} ( t - h ) ). \end{array}\displaystyle \right . $$
(20)

Therefore, all the studied subsystems are described by the following state space representation:

$$ \left \{ \textstyle\begin{array}{l} \dot{x} ( t ) = ( A_{i} (\cdot )x ( t ) + D_{i} (\cdot )x ( t - h ) + B_{i} (\cdot )u ( t ) ), \\ x ( \theta ) = \phi ( \theta ),\quad \theta \in [ - \tau,0 ], \end{array}\displaystyle \right . \quad i \in \underline{N}, $$
(21)

where \(x ( t )\) is the state vector, whose components are \(x_{j} ( t )\), \(j = 1,\ldots,n\), and the matrices \(A_{i} (\cdot )\) and \(D_{i} (\cdot )\) are given by

$$\begin{aligned}& A_{i} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 1 & \cdots & 0 \\ 0 & 0 & \ddots & \vdots \\ \vdots & \vdots & \ddots & 1 \\ - a_{i}^{0} (\cdot ) & - a_{i}^{1} (\cdot ) & \cdots & - a_{i}^{n - 1} (\cdot ) \end{array}\displaystyle \right ], \quad i \in \underline{N}, \end{aligned}$$
(22)
$$\begin{aligned}& D_{i} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & \cdots & 0 \\ 0 & 0 & \ddots & \vdots \\ \vdots & \vdots & \ddots & 0 \\ - d_{i}^{0} (\cdot ) & - d_{i}^{1} (\cdot ) & \cdots & - d_{i}^{n - 1} (\cdot ) \end{array}\displaystyle \right ], \quad i \in \underline{N}, \end{aligned}$$
(23)

where \(a_{i}^{j} (\cdot )\) is a coefficient of the instantaneous characteristic polynomial \(P_{A_{i} (\cdot )} ( \lambda )\) of the matrix \(A_{i} (\cdot )\) given as follows:

$$ P_{A_{i} (\cdot )} ( \lambda ) = \lambda^{n} + \sum _{q = 0}^{n - 1} a_{i}^{q} (\cdot ) \lambda^{q} $$
(24)

and \(d_{i}^{j} (\cdot )\) is a coefficient of the instantaneous characteristic polynomial \(Q_{D_{i} (\cdot )} ( \lambda )\) of the matrix \(D_{i} (\cdot )\) defined by

$$ Q_{D_{i} (\cdot )} ( \lambda ) = \sum_{q = 0}^{n - 1} d_{i}^{q} (\cdot ) \lambda^{q}. $$
(25)

By considering the switching rule (1), the switched nonlinear time-delay system is deduced as below:

$$ \left \{ \textstyle\begin{array}{l} \dot{x} ( t ) = A_{\sigma ( t )} (\cdot )x ( t ) + D_{\sigma ( t )} (\cdot )x ( t - h ), \\ x ( \theta ) = \phi ( \theta ), \quad \theta \in [ - h, 0 ]. \end{array}\displaystyle \right . $$
(26)

Therefore, to complete this development a change to base of system (26) into the arrow matrix form is performed. Indeed, apply the following transformation:

$$ z ( t ) = Px ( t ), $$
(27)

where P is the corresponding passage matrix given as follows:

$$ P = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1 & 1 & \cdots & 1 & 0 \\ \alpha_{1} & \alpha_{2} & \cdots & \alpha_{n - 1} & 0 \\ ( \alpha_{1} )^{2} & ( \alpha_{2} )^{2} & \cdots & ( \alpha_{n - 1} )^{2} & \vdots \\ \vdots & \vdots & \cdots & \vdots & 0 \\ ( \alpha_{1} )^{n - 1} & ( \alpha_{2} )^{n - 1} & \ldots & ( \alpha_{n - 1} )^{n - 1} & 1 \end{array}\displaystyle \right ] $$
(28)

with \(\alpha_{j}\), \(j = 1,\ldots,n - 1\) are distinct arbitrary constant parameters.

This leads to the new following state representation:

$$ \dot{z} ( t ) = F_{i} (\cdot )z ( t ) + E_{i} (\cdot )z ( t - h ), \quad i \in \underline{N}. $$
(29)

The matrix \(F_{i} (\cdot )\), \(i \in \underline{N}\) is given by

$$ F_{i} (\cdot ) = P^{ - 1}A_{i} (\cdot )P = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots & 0 & \beta_{1} \\ 0 & \ddots & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & \alpha_{n - 1} & \beta_{n - 1} \\ \gamma_{i}^{1} (\cdot ) & \cdots & \cdots & \gamma_{i}^{n - 1} (\cdot ) & \gamma_{i}^{n} (\cdot ) \end{array}\displaystyle \right ]. $$
(30)

The elements of the matrix \(F_{i} (\cdot )\), \(i \in \underline{N}\) are defined by

$$ \left \{ \textstyle\begin{array}{l} \gamma_{i}^{j} (\cdot ) = - P_{A_{i} (\cdot )} ( \alpha _{j} ),\quad \forall j = 1,\ldots,n - 1, \\ \gamma_{i}^{n} (\cdot ) = - a_{i}^{n - 1} (\cdot ) - \sum_{j = 1}^{n - 1} \alpha_{j} \end{array}\displaystyle \right . $$
(31)

with

$$ \beta_{j} = \prod_{\substack{q = 1\\q \ne j}}^{n - 1} ( \alpha_{j} - \alpha_{q} )^{ - 1},\quad \forall j = 1, \ldots,n - 1. $$
(32)

The matrix \(E_{i} (\cdot )\), \(i \in \underline{N}\) is given by

$$ E_{i} (\cdot ) = P^{ - 1}D_{i} (\cdot )P = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0_{n - 1,n - 1}&\cdots & 0_{n - 1,1}& \\ \delta_{i}^{1} (\cdot )& \cdots &\delta_{i}^{n - 1} (\cdot ) & \delta_{i}^{n} (\cdot ) \end{array}\displaystyle \right ] $$
(33)

with

$$ \left \{ \textstyle\begin{array}{l} \delta_{i}^{j} (\cdot ) = - Q_{D_{i} (\cdot )} ( \alpha_{j} ), \quad \forall j = 1,\ldots,n - 1, \\ \delta_{i}^{n} (\cdot ) = - d_{i}^{n - 1} (\cdot ). \end{array}\displaystyle \right . $$
(34)

According to the previous relations, the matrices \(T_{i} (\cdot )\), \(i \in \underline{N}\) are defined by

$$ T_{i} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots & 0 & \vert \beta_{1} \vert \\ 0 & \ddots & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & \alpha_{n - 1} & \vert \beta_{n - 1} \vert \\ t_{i}^{1} (\cdot ) & \cdots & \cdots & t_{i}^{n - 1} (\cdot ) & t_{i}^{n} (\cdot ) \end{array}\displaystyle \right ] $$
(35)

with

$$ \left \{ \textstyle\begin{array}{l} t_{i}^{j} (\cdot ) = \vert \gamma_{i}^{j} (\cdot ) \vert + \sup_{ [\cdot ]} ( \vert \delta_{i}^{j} (\cdot ) \vert ),\quad j = 1,\ldots,n - 1, \\ t_{i}^{n} (\cdot ) = \gamma_{i}^{n} (\cdot ) + \sup_{ [\cdot ]} ( \vert \delta_{i}^{n} (\cdot ) \vert ). \end{array}\displaystyle \right . $$
(36)

Next, by considering the switched rule given in (1) the comparison system corresponding to system (26) is defined by

$$ \dot{z} ( t ) = T_{c} (\cdot )z ( t ), $$
(37)

where \(T_{c} (\cdot )\) is the comparison matrix relative to system (26), given by

$$ T_{c} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots & 0 & \vert \beta_{1} \vert \\ 0 & \ddots & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & \alpha_{n - 1} & \vert \beta_{n - 1} \vert \\ \bar{t}_{i}^{1} (\cdot ) & \cdots & \cdots & \bar{t}_{i}^{n - 1} (\cdot ) & \bar{t}_{i}^{n} (\cdot ) \end{array}\displaystyle \right ] $$
(38)

with

$$ \bar{t}^{j} (\cdot ) = \max_{1 \le i \le N} \bigl( t_{i}^{j} (\cdot ) \bigr), \quad j = 1,\ldots,n. $$
(39)

Now we are in a position to provide the following theorem which presents a new delay-independent stability conditions for system (26).

Theorem 3

System (26) is globally asymptotically stable under the arbitrary switching rule (1), if there exist \(\alpha_{j} < 0 \) (\(j = 1,\ldots,n - 1 \)), \(\alpha_{j} \ne \alpha_{q}\), \(\forall j \ne q\), satisfying the following condition:

$$ - \bar{t}^{n} (\cdot ) + \sum_{j = 1}^{n - 1} \bar{t}^{j} (\cdot )\vert \beta_{j} \vert \alpha_{j}^{ - 1} > 0. $$
(40)

Proof

According to the Borne-Gentina criterion [34] we have

$$ ( - 1 )^{j}\Delta_{j} > 0,\quad j = 1, \ldots,n, $$
(41)

where \(\Delta_{j}\) is the jth principal minor of the matrix \(T_{c} (\cdot )\).

It is clear that, for \(j = 1,\ldots, n - 1\), the condition (41) is verified for \(\alpha_{j} \in \Re_{ -}^{*}\). Therefore, the last condition, \(j = n\), yields

$$ ( - 1 )^{n}\det \bigl( T_{c} (\cdot ) \bigr) = ( - 1 )^{n}\left \vert \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots & 0 & \vert \beta_{1} \vert \\ 0 & \ddots & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & \alpha_{n - 1} & \vert \beta_{n - 1} \vert \\ \vert \bar{t}^{1} (\cdot ) \vert & \cdots & \cdots & \vert \bar{t}^{n - 1} (\cdot ) \vert & \bar{t}^{n} (\cdot ) \end{array}\displaystyle \right \vert . $$
(42)

That is,

$$= ( - 1 )^{n} \Biggl[ \bar{t}^{n} (\cdot )\prod _{q = 1}^{n - 1} \alpha_{q} - \sum _{{j} = 1}^{n - 1} \Biggl( \bigl\vert \bar{t}^{j} (\cdot ) \bigr\vert \vert \beta_{j} \vert \prod _{\substack{ j = 1 \\ j \ne q}}^{n - 1} \alpha_{j} \Biggr) \Biggr] > 0. $$

The last condition in Theorem 3 is obtained by dividing this previous condition by \(( ( - 1 )^{n - 1}\prod_{q = 1}^{n - 1} \alpha_{q} )\).

This gives rise to

$$- \bar{t}^{n} (\cdot ) + \sum_{j = 1}^{n - 1} \bar{t}^{j} (\cdot )\vert \beta_{j} \vert \alpha_{j}^{ - 1} > 0. $$

This completes the proof of the theorem. □

Thus, if there exist \(\alpha_{j}\) (\(j = 1,\ldots, n - 1 \)) such that

$$ \beta_{j} \Bigl( P_{A_{i} (\cdot )} ( \alpha _{j} ) + \sup _{ [\cdot ]} \bigl( Q_{D_{i} (\cdot )} ( \alpha_{j} ) \bigr) \Bigr) = - \beta_{j} \Bigl( \gamma_{i}^{n} (\cdot ) + \sup_{ [\cdot ]} \bigl( \delta_{i}^{n} ( \cdot ) \bigr) \Bigr) < 0 $$
(43)

we obtain the following result.

Corollary 1

System (26) is globally asymptotically stable under arbitrary switching rule (1), if there exist \(\alpha_{j} \in \Re_{-}\) (\(j = 1,\ldots, n - 1 \)), \(\alpha_{j} \ne \alpha_{q}\), \(\forall j \ne q\) for each \(i \in \underline{N}\) such that

$$\begin{aligned} (\mathrm{i})&\quad \beta_{j} \Bigl( P_{A_{i} (\cdot )} ( \alpha _{j} ) + \sup_{ [\cdot ]} \bigl( Q_{D_{i} (\cdot )} ( \alpha_{j} ) \bigr) \Bigr) < 0, \end{aligned}$$
(44)
$$\begin{aligned} (\mathrm{ii})&\quad \Bigl( P_{A_{i} (\cdot )} ( 0 ) + \sup_{ [\cdot ]} \bigl( Q_{D_{i} (\cdot )} ( 0 ) \bigr) \Bigr) > 0. \end{aligned}$$
(45)

Proof

[61] If there exist \(\alpha_{j} < 0\), \(j = 1,\ldots, n - 1\), such that

$$\beta_{j} \Bigl( P_{A_{i} (\cdot )} ( \alpha _{j} ) + \sup _{ [\cdot ]} \bigl( Q_{D_{i} (\cdot )} ( \alpha_{j} ) \bigr) \Bigr) = - \beta_{j} \Bigl( \gamma_{i}^{n} (\cdot ) + \sup_{ [\cdot ]} \bigl( \delta_{i}^{n} ( \cdot ) \bigr) \Bigr) < 0 $$

and the comparison matrix \(T (\cdot )\) can be chosen identically to

$$\begin{aligned} T (\cdot ) =& \left[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots \\ 0 & \ddots & \ddots \\ \vdots & \ddots & \ddots \\ 0 & \cdots & 0 \\ \max_{1 \le i \le N} ( \gamma_{i}^{1} (\cdot ) + \sup_{ [\cdot]} ( \delta_{i}^{1} (\cdot ) ) ) & \cdots & \cdots \end{array}\displaystyle \right. \\ &\left. \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & \beta_{1} \\ \vdots & \vdots \\ 0 & \vdots \\ \alpha_{n - 1} & \beta_{n - 1} \\ \max_{1 \le i \le N} ( \gamma_{i}^{n - 1} (\cdot ) + \sup_{ [\cdot ]} ( \delta_{i}^{n - 1} (\cdot ) )) & \max_{1 \le i \le N} ( \gamma_{i}^{n} (\cdot ) + \sup_{ [\cdot ]} ( \delta_{i}^{n} (\cdot ) ) ) \end{array}\displaystyle \right]. \end{aligned}$$

Then, the nth principal minor of \(T (\cdot )\) is deduced as follows:

$$\begin{aligned} \Delta_{n} =& - \Bigl( \sup_{ [\cdot ]} \bigl( \delta_{i}^{n} (\cdot ) \bigr) + \gamma_{i}^{n} (\cdot ) \Bigr) + \sum_{j = 1}^{n - 1} ( \alpha_{j} )^{ - 1} \Bigl( \sup_{ [\cdot ]} \bigl( \delta_{i}^{j} (\cdot ) \bigr) + \gamma_{i}^{j} (\cdot ) \Bigr) \beta_{j} \\ =& \prod_{j = 1}^{n - 1} ( \alpha_{j} )^{ - 1} \Bigl( P_{A_{i} (\cdot )} ( 0 ) + \sup _{ [\cdot ]} \bigl( Q_{D_{i} (\cdot )} ( 0 ) \bigr) \Bigr). \end{aligned}$$

This implies that \(P_{A_{i} (\cdot )} ( 0 ) + \sup_{ [\cdot ]} ( Q_{D_{i} (\cdot )} ( 0 ) ) > 0\).

The proof is completed. □

5 Stability analysis of switched systems with multiple delays

In this part, a generalization of the previous results will be given to a class of switched nonlinear systems with multiple delays.

Consider a class of switched nonlinear systems with multiple delays formed by N subsystems given by

$$ \left \{ \textstyle\begin{array}{l} \dot{x} ( t ) = A_{\sigma ( t )}x ( t ) + \sum_{l = 1}^{m} D_{\sigma ( t ),l} x ( t - h_{l} ), \\ x ( t ) = \phi ( t ),\quad t \in [ - \max_{1 \le l \le m} ( h_{l} ), 0 ], \end{array}\displaystyle \right . $$
(46)

where \(\sigma ( t )\) is the switching signal given in (1), \(A_{i} (\cdot ) \in \Re^{n \times n}\) and \(D_{l,i} (\cdot ) \in \Re^{n \times n}\) (\(l = 1,\ldots, m \)) are matrices of appropriate dimensions with nonlinear elements. \(\varphi ( t )\) is the continuous vector valued function specifying the initial state of the system. \(h_{l} > 0\) denotes the delays.

Generalizing the Lyapunov function introduced in (5), it is easy to obtain the following sufficient stability conditions for system (46).

Theorem 4

System (46) is globally asymptotically stable under arbitrary switching (1) if matrix \(T_{m,c} (\cdot )\) is the opposite of an M-matrix, with

$$ T_{m,c} (\cdot ) = \max_{1 \le i \le N} \Biggl( \bigl( A_{i} (\cdot ) \bigr)^{*} + \sup_{ [\cdot ]} \Biggl( \Biggl\vert \sum_{l = 1}^{m} D_{l,i} (\cdot ) \Biggr\vert \Biggr) \Biggr). $$
(47)

Proof

It suffices to choose the Lyapunov function \(V ( t )\) given as below and to follow the same steps as described in the proof of Theorem 2:

$$ V \bigl( x ( t ),t \bigr) = V_{1} \bigl( x ( t ),t \bigr) + V_{2} \bigl( x ( t ),t \bigr) $$
(48)

with

$$ V_{1} \bigl( x ( t ),t \bigr) = \bigl\langle \bigl\vert x ( t ) \bigr\vert ,w \bigr\rangle $$
(49)

and

$$ V_{2} \bigl( x ( t ),t \bigr) = \sum_{l = 1}^{m} \biggl\langle D_{l,c}\int_{t - h_{l}}^{t} \bigl\vert x ( \theta ) \bigr\vert \, d\theta,w \biggr\rangle , $$
(50)

where

$$ D_{l,c} = \max_{1 \le i \le N} \Biggl( \sup _{ [\cdot ]} \Biggl( \Biggl\vert \sum_{l = 1}^{m} D_{l,i} (\cdot ) \Biggr\vert \Biggr) \Biggr). $$
(51)

 □

Now, the conditions of Theorem 4 will be applied to switched systems with multiple delays given by N subsystems which are modeled by the following differential equation:

$$ \left \{ \textstyle\begin{array}{l} y^{n} ( t ) + ( \sum_{j = 0}^{n - 1} a_{i}^{j} (\cdot )y^{ ( j )} ( t ) ) + \sum_{l = 1}^{m} ( \sum_{j = 0}^{n - 1} d_{l,i}^{j} (\cdot )y^{ ( j )} ( t - h_{l} ) ) \\ \quad = 0, \quad h_{l} > 0, l \in \{ 1,\ldots, m \}, \\ y^{ ( j )} ( t ) = \varphi_{j} ( t ),\quad j \in \{ 0,\ldots, n - 1 \}, t \in [ - \max_{1 \le l \le m} ( h_{l} ), 0 ]. \end{array}\displaystyle \right . $$
(52)

Now, the same idea performed for the system given by the subsystems defined in (18) will be applied in order to obtain stability conditions for the studied system. Then, to this aim, the following change of variables is performed: \(x_{j + 1} ( t ) = y^{ ( j )} ( t )\), \(j = 0,\ldots, n - 1\), and taking into consideration the switched rule signal \(\sigma ( t )\) given in (1), the resulting switched nonlinear system is given by the following state representation:

$$ \left \{ \textstyle\begin{array}{l} \dot{x} ( t ) = A_{\sigma ( t )} (\cdot )x ( t ) + \sum_{l = 1}^{m} D_{l,\sigma ( t )} (\cdot ) x ( t - h_{l} ), \\ x ( t ) = \phi ( t ),\quad t \in [ - \max_{1 \le l \le m} ( h_{l} ), 0 ], \end{array}\displaystyle \right . $$
(53)

where \(x ( t )\) is the state vector, the matrices \(A_{i} (\cdot )\), \(i \in \underline{N}\) are given in (22), and \(D_{l,i} (\cdot )\) for each \(l = 1,\ldots,m\) and \(i \in \underline{N}\) are given as follows:

$$ D_{l,i} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & \cdots & 0 \\ 0 & 0 & \ddots & \vdots \\ \vdots & \vdots & \ddots & 0 \\ - d_{l,i}^{0} (\cdot ) & - d_{l,i}^{1} (\cdot ) & \cdots & - d_{l,i}^{n - 1} (\cdot ) \end{array}\displaystyle \right ]. $$
(54)

The characteristic polynomial \(P_{A_{i} (\cdot )} ( \lambda )\) of the matrix \(A_{i} (\cdot )\), \(i \in \underline{N}\) is given in (24) and for each \(l = 1,\ldots,m\) and \(i \in \underline{N}\) the new polynomial \(Q_{D_{l,i} (\cdot )} ( \lambda )\) is defined by

$$ Q_{D_{l,i} (\cdot )} ( \lambda ) = \sum_{q = 0}^{n - 1} d_{l,i}^{q} (\cdot ) \lambda^{q}. $$
(55)

By introducing the same variable change given in (28), system (47) will be represented in the arrow form as follows:

$$ \left \{ \textstyle\begin{array}{l} \dot{z} ( t ) = F_{\sigma ( t )} (\cdot )z ( t ) + \sum_{l = 1}^{m} E_{l,\sigma ( t )} (\cdot )z ( t - h_{l} ), \\ z ( t ) = P\phi ( t ),\quad t \in [ - \max_{1 \le l \le m} ( h_{l} ), 0 ], \end{array}\displaystyle \right . $$
(56)

where the matrices \(F_{i} (\cdot )\), \(i \in \underline{N}\) are introduced in (30) and \(E_{l,i} (\cdot )\) (\(l = 1,\ldots,m \)), \(i \in \underline{N}\) are given as follows:

$$ E_{l,i} (\cdot ) = P^{ - 1}D_{l,i} (\cdot )P = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0_{n - 1,n - 1}&\cdots & 0_{n - 1,1}& \\ \delta_{l,i}^{1} (\cdot )& \cdots &\delta_{l,i}^{n - 1} (\cdot ) & \delta_{l,i}^{n} (\cdot ) \end{array}\displaystyle \right ] $$
(57)

with

$$ \left \{ \textstyle\begin{array}{l} \delta_{l,i}^{j} (\cdot ) = - Q_{D_{l,i} (\cdot )} ( \alpha_{j} ), \quad \forall j = 1,\ldots,n - 1, l = 1,\ldots,m, \\ \delta_{l,i}^{n} (\cdot ) = - d_{l,i}^{n - 1} (\cdot ). \end{array}\displaystyle \right . $$
(58)

Finally, the matrices \(T_{l,i} (\cdot )\) (\(l = 1,\ldots,m \)), \(i \in \underline{N}\) are given by

$$ T_{l,i} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots & 0 & \vert \beta_{1} \vert \\ 0 & \ddots & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & \alpha_{n - 1} & \vert \beta_{n - 1} \vert \\ t_{l,i}^{1} (\cdot ) & \cdots & \cdots & t_{l,i}^{n - 1} (\cdot ) & t_{l,i}^{n} (\cdot ) \end{array}\displaystyle \right ], $$
(59)

where

$$ \left \{ \textstyle\begin{array}{l} t_{l,i}^{j} (\cdot ) = \vert \gamma_{i}^{j} (\cdot ) \vert + \sup_{ [\cdot ]}\vert \sum_{l = 1}^{m} \delta_{l,i}^{j} (\cdot ) \vert ,\quad j = 1,\ldots,n - 1, \\ t_{l,i}^{n} (\cdot ) = \gamma_{i}^{n} (\cdot ) + \sup_{ [\cdot ]}\vert \sum_{l = 1}^{m} \delta_{l,i}^{n} (\cdot ) \vert . \end{array}\displaystyle \right . $$
(60)

Therefore, the comparison system corresponding to system (53) is given as follows:

$$ \dot{z} ( t ) = T_{l,c} (\cdot )z ( t ), $$
(61)

where the comparison matrix relative to system (50) \(T_{l,c} (\cdot )\) is deduced thus:

$$ T_{l,c} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots & 0 & \vert \beta_{1} \vert \\ 0 & \ddots & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & \alpha_{n - 1} & \vert \beta_{n - 1} \vert \\ \bar{t}_{l}^{1} (\cdot ) & \cdots & \cdots & \bar{t}_{l}^{n - 1} (\cdot ) & \bar{t}_{l}^{n} (\cdot ) \end{array}\displaystyle \right ] $$
(62)

with

$$ \bar{t}_{l}^{j} (\cdot ) = \max_{1 \le i \le N} \bigl( t_{l,i}^{j} (\cdot ) \bigr),\quad j = 1,\ldots,n. $$
(63)

Next, using the special form of system (53) we can announce the following theorem.

Theorem 5

System (53) is globally asymptotically stable under the arbitrary switching rule (1), if there exist \(\alpha_{j} < 0\) (\(j = 1,\ldots,n - 1\)), \(\alpha_{j} \ne \alpha_{q}\), \(\forall j \ne q\) (\(l = 1,\ldots,m\)) satisfying the following condition:

$$ - \bar{t}_{l}^{n} (\cdot ) + \sum _{j = 1}^{n - 1} \bar{t}_{l}^{j} ( \cdot )\vert \beta_{j} \vert \alpha_{j}^{ - 1} > 0. $$
(64)

Next, Theorem 5 can be simplified to the following delay-dependent stability conditions.

Corollary 2

System (53) is globally asymptotically stable under the arbitrary switching rule (1), if there exist \(\alpha_{j} \in \Re_{ -}\) (\(j = 1,\ldots, n - 1\)), \(\alpha_{j} \ne \alpha_{q}\), \(\forall j \ne q\) for each \(i \in \underline{N}\) and \(l = 1,\ldots,m\) such that

$$\begin{aligned} (\mathrm{iii})&\quad \beta_{j} \Biggl( P_{A_{i} (\cdot )} ( \alpha _{j} ) + \sup_{ [\cdot ]} \Biggl( \sum _{l = 1}^{m} Q_{D_{l,i} (\cdot )} ( \alpha_{j} ) \Biggr) \Biggr) < 0 , \end{aligned}$$
(65)
$$\begin{aligned} (\mathrm{iv})&\quad \Biggl( P_{A_{i} (\cdot )} ( 0 ) + \sup_{ [\cdot ]} \Biggl( \sum_{l = 1}^{m} Q_{D_{l,i} (\cdot )} ( 0 ) \Biggr) \Biggr) > 0. \end{aligned}$$
(66)

Proof

[60] Consider the comparison matrix \(T_{l} (\cdot )\) chosen as follows:

$$\begin{aligned} T_{l} (\cdot ) =& \left[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \alpha_{1} & 0 & \cdots \\ 0 & \ddots & \ddots \\ \vdots & \ddots & \ddots \\ 0 & \cdots & 0 \\ \max_{1 \le i \le N} ( \sup_{ [\cdot ]} ( \sum_{l = 1}^{m} \delta_{l,i}^{1} (\cdot ) ) + \gamma_{i}^{1} (\cdot ) ) & \cdots & \cdots \end{array}\displaystyle \right. \\ &\left.\textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & \beta_{1} \\ \vdots & \vdots \\ 0 & \vdots \\ \alpha_{n - 1} & \beta_{n - 1} \\ \max_{1 \le i \le N} ( \sup_{ [\cdot ]} ( \sum_{l = 1}^{m} \delta_{l,i}^{n - 1} (\cdot ) ) + \gamma_{i}^{n - 1} (\cdot ) ) & \max_{1 \le i \le N} ( \sup_{ [\cdot ]} ( \sum_{l = 1}^{m} \delta_{l,i}^{n} (\cdot ) ) + \gamma_{i}^{n} (\cdot ) ) \end{array}\displaystyle \right]. \end{aligned}$$

If there exist \(\alpha_{j} < 0\), \(j = 1,\ldots, n - 1\) such that

$$\beta_{j} \Biggl( P_{A_{i} (\cdot )} ( \alpha _{j} ) + \sup _{ [\cdot ]} \Biggl( \sum_{l = 1}^{m} Q_{D_{l,i} (\cdot )} ( \alpha_{j} ) \Biggr) \Biggr) = - \beta_{j} \Biggl( \gamma_{i}^{n} (\cdot ) + \sup _{ [\cdot ]} \Biggl( \sum_{l = 1}^{m} \delta_{l,i}^{n - 1} (\cdot ) \Biggr) \Biggr) < 0, $$

then the nth principal minor of \(T_{l} (\cdot )\) is deduced as follows:

$$\begin{aligned} \Delta_{n} =& - \Biggl( \sup_{ [\cdot ]} \Biggl( \sum _{l = 1}^{m} \delta_{l,i}^{n - 1} (\cdot ) \Biggr) + \gamma_{i}^{n} (\cdot ) \Biggr) \\ &{}+ \sum _{j = 1}^{n - 1} ( \alpha_{j} )^{ - 1} \Biggl( \sup_{ [\cdot ]} \Biggl( \sum _{l = 1}^{m} \delta_{l,i}^{n - 1} ( \cdot ) \Biggr) + \gamma_{i}^{j} (\cdot ) \Biggr) \beta_{j} \\ =& \prod_{j = 1}^{n - 1} ( \alpha_{j} )^{ - 1} \Biggl( P_{A_{i} (\cdot )} ( 0 ) + \sup _{ [\cdot ]} \Biggl( \sum_{l = 1}^{m} Q_{D_{l,i} (\cdot )} ( 0 ) \Biggr) \Biggr). \end{aligned}$$

This implies that

$$P_{A_{i} (\cdot )} ( 0 ) + \sup_{ [\cdot ]} \Biggl( \sum _{l = 1}^{m} Q_{D_{l,i} (\cdot )} ( 0 ) \Biggr) > 0. $$

This completes the proof of the corollary. □

6 Simulation results

In this section, we provide a numerical example to demonstrate the proposed results. In what follows, we consider the continuous-time switched nonlinear time-delay system (53) given by three subsystems which are modeled by the following differential equation:

$$\left \{ \textstyle\begin{array}{l} y^{2} ( t ) + ( \sum_{j = 0}^{1} a_{i}^{j} (\cdot )y^{ ( j )} ( t ) ) + \sum_{l = 1}^{2} ( \sum_{j = 0}^{1} d_{l,i}^{j} (\cdot )y^{ ( j )} ( t - h_{l} ) ) = 0,\quad h_{l} > 0, l \in \{ 1, 2 \}, \\ y^{ ( j )} ( t ) = \varphi_{j} ( t ),\quad j \in \{ 0, 1 \}, t \in [ - \max_{1 \le l \le 2} ( h_{l} ), 0 ]. \end{array}\displaystyle \right . $$

All the subsystems \(i = \{ 1, 2, 3 \}\) are given in the state form by

$$\left \{ \textstyle\begin{array}{l} \dot{x} ( t ) = ( A_{i} (\cdot )x ( t ) + \sum_{l = 1}^{2} D_{l,i} (\cdot )x ( t - h_{l} ) ), \\ x ( t ) = \phi ( t ),\quad t \in [ - \max_{1 \le l \le 2} ( h_{l} ),0 ], \end{array}\displaystyle \right . $$

where

$$\begin{aligned}& A_{1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 1 \\ - 4f (\cdot ) + 1 & - 3\varphi (\cdot ) \end{array}\displaystyle \right ],\qquad A_{2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 1 \\ - 3f (\cdot ) + 2 & - 3\varphi (\cdot ) \end{array}\displaystyle \right ], \\& A_{3} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 1 \\ - 2f (\cdot ) + 1 & - 2\varphi (\cdot ) - 1 \end{array}\displaystyle \right ], \qquad D_{1,1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ - \psi (\cdot ) + 1 & - 1 \end{array}\displaystyle \right ], \\& D_{1,2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ - \psi (\cdot ) + 2 & - 2\psi (\cdot ) \end{array}\displaystyle \right ],\qquad D_{2,1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ - 2\psi (\cdot ) & - 1 \end{array}\displaystyle \right ], \\& D_{2,2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ - 0.2\psi (\cdot ) + 0.5 & - 1 \end{array}\displaystyle \right ], \qquad D_{3,1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ - \psi (\cdot ) + 1 & - 1 \end{array}\displaystyle \right ], \\& D_{3,2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ - \psi (\cdot ) + 1 & - 2 \end{array}\displaystyle \right ], \end{aligned}$$

where \(f (\cdot )\), \(\Phi (\cdot )\) and \(\psi (\cdot )\) are unknown nonlinear functions.

The two delays are \(h_{1} > 0\) and \(h_{2} > 0\).

Note that, due to the complexity and the important number of the subsystems, it is difficult to find a common Lyapunov function for all the subsystems. Then we cannot guarantee stability of this switched system under the arbitrary switching sequence (1).

Now, due to (28), (30), (31), (57), and (58), the matrices in arrow form are the following:

$$\begin{aligned}& F_{1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \alpha & 1 \\ \gamma_{1}^{1} (\cdot ) & \gamma_{1}^{2} (\cdot ) \end{array}\displaystyle \right ],\qquad F_{2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \alpha & 1 \\ \gamma_{2}^{1} (\cdot ) & \gamma_{2}^{2} (\cdot ) \end{array}\displaystyle \right ], \\& F_{3} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \alpha & 1 \\ \gamma_{3}^{1} (\cdot ) & \gamma_{3}^{2} (\cdot ) \end{array}\displaystyle \right ],\qquad E_{1,1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ \delta_{1,1}^{1} (\cdot ) & \delta_{1,1}^{2} (\cdot ) \end{array}\displaystyle \right ], \\& E_{1,2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ \delta_{1,2}^{1} (\cdot ) & \delta_{1,2}^{2} (\cdot ) \end{array}\displaystyle \right ], \qquad E_{2,1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ \delta_{2,1}^{1} (\cdot ) & \delta_{2,1}^{2} (\cdot ) \end{array}\displaystyle \right ], \\& E_{2,2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ \delta_{2,2}^{1} (\cdot ) & \delta_{2,2}^{2} (\cdot ) \end{array}\displaystyle \right ], \qquad E_{3,1} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ \delta_{3,1}^{1} (\cdot ) & \delta_{3,1}^{2} (\cdot ) \end{array}\displaystyle \right ], \\& E_{3,2} (\cdot ) = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & 0 \\ \delta_{3,2}^{1} (\cdot ) & \delta_{3,2}^{2} (\cdot ) \end{array}\displaystyle \right ] \end{aligned}$$

with

$$\begin{aligned}& \left \{ \textstyle\begin{array}{l} \gamma_{1}^{1} (\cdot ) = - P_{A_{1} (\cdot )} ( \alpha ) = - [ \alpha^{2} + 3\varphi (\cdot )\alpha + 4f (\cdot ) - 1 ], \\ \gamma_{1}^{2} (\cdot ) = - ( 3\varphi (\cdot ) + \alpha ), \end{array}\displaystyle \right . \\& \left \{ \textstyle\begin{array}{l} \gamma_{2}^{1} (\cdot ) = - P_{A_{2} (\cdot )} ( \alpha ) = - [ \alpha^{2} + 3\varphi (\cdot )\alpha + 3f (\cdot ) - 2 ], \\ \gamma_{2}^{2} (\cdot ) = - ( 3\varphi (\cdot ) + \alpha ), \end{array}\displaystyle \right . \\& \left \{ \textstyle\begin{array}{l} \gamma_{3}^{1} (\cdot ) = - P_{A_{3} (\cdot )} ( \alpha ) = - [ \alpha^{2} + ( 2\varphi (\cdot ) + 1 )\alpha + 2f (\cdot ) - 1 ], \\ \gamma_{3}^{2} (\cdot ) = - ( 2\varphi (\cdot ) + 1 + \alpha ) \end{array}\displaystyle \right . \end{aligned}$$

and

$$\begin{aligned}& \left \{ \textstyle\begin{array}{l} \delta_{1,1}^{1} (\cdot ) = - Q_{D_{1,1} (\cdot )} ( \alpha ) = - [ \alpha + \Phi (\cdot ) - 1 ], \\ \delta_{1,1}^{2} (\cdot ) = - 1, \end{array}\displaystyle \right . \\& \left \{ \textstyle\begin{array}{l} \delta_{2,1}^{1} (\cdot ) = - Q_{D_{2,1} (\cdot )} ( \alpha ) = - [ 2\psi (\cdot )\alpha + \Phi (\cdot ) - 2 ], \\ \delta_{2,1}^{2} (\cdot ) = - 2\psi (\cdot ), \end{array}\displaystyle \right . \\& \left \{ \textstyle\begin{array}{l} \delta_{1,2}^{1} (\cdot ) = - Q_{D_{1,2} (\cdot )} ( \alpha ) = - [ \alpha + 2\psi (\cdot ) ], \\ \delta_{1,2}^{2} (\cdot ) = - 1, \end{array}\displaystyle \right . \\& \left \{ \textstyle\begin{array}{l} \delta_{2,2}^{1} (\cdot ) = - Q_{D_{2,2} (\cdot )} ( \alpha ) = - [ \alpha + 0.2\Phi (\cdot ) - 0.5 ], \\ \delta_{2,2}^{2} (\cdot ) = - 1, \end{array}\displaystyle \right . \\& \left \{ \textstyle\begin{array}{l} \delta_{1,3}^{1} (\cdot ) = - Q_{D_{1,3} (\cdot )} ( \alpha ) = - [ \alpha + \psi (\cdot ) - 1 ], \\ \delta_{1,3}^{2} (\cdot ) = - 1, \end{array}\displaystyle \right . \\& \left \{ \textstyle\begin{array}{l} \delta_{2,3}^{1} (\cdot ) = - Q_{D_{2,3} (\cdot )} ( \alpha ) = - [ 2\alpha + \psi (\cdot ) - 1 ], \\ \delta_{2,3}^{2} (\cdot ) = - 2. \end{array}\displaystyle \right . \end{aligned}$$

In the case \(\alpha = - 1\), \(\beta = 1\), the stability conditions for the example given by Corollary 2 are the following:

$$\begin{aligned} (\mathrm{i})&\quad \bigl( P_{A_{1} (\cdot )} ( \alpha ) + Q_{D_{1,1} (\cdot )} ( \alpha ) + Q_{D_{2,1} (\cdot )} ( \alpha ) \bigr) < 0, \\ (\mathrm{ii})&\quad \bigl( P_{A_{2} (\cdot )} ( \alpha ) + Q_{D_{1,2} (\cdot )} ( \alpha ) + Q_{D_{2,2} (\cdot )} ( \alpha ) \bigr) < 0, \\ (\mathrm{iii})&\quad \bigl( P_{A_{3} (\cdot )} ( \alpha ) + Q_{D_{1,3} (\cdot )} ( \alpha ) + Q_{D_{2,3} (\cdot )} ( \alpha ) \bigr) < 0, \\ (\mathrm{iv})&\quad \bigl( P_{A_{1} (\cdot )} ( 0 ) + Q_{D_{1,1} (\cdot )} ( 0 ) + Q_{D_{2,1} (\cdot )} ( 0 ) \bigr) > 0, \\ (\mathrm{v})&\quad \bigl( P_{A_{2} (\cdot )} ( 0 ) + Q_{D_{1,2} (\cdot )} ( 0 ) + Q_{D_{2,2} (\cdot )} ( 0 ) \bigr) > 0, \\ (\mathrm{vi})&\quad \bigl( P_{A_{3} (\cdot )} ( 0 ) + Q_{D_{1,3} (\cdot )} ( 0 ) + Q_{D_{2,3} (\cdot )} ( 0 ) \bigr) > 0. \end{aligned}$$

Then, in the case that we assume that \(\psi (\cdot ) \in E ( [ 0.5, 1.2, 1.8 ] )\) conditions (ii), (iii), (iv), (v), and (vi) allow for deducing the following stability conditions:

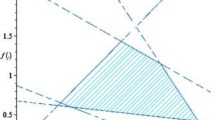
$$\begin{aligned} (\mathrm{i})&\quad f (\cdot ) < \frac{3}{4}\Phi (\cdot ) + 1 , \\ (\mathrm{ii})&\quad f (\cdot ) < \Phi (\cdot ) + 0.51 , \\ (\mathrm{iii})&\quad f (\cdot ) < \Phi (\cdot ) + 1.2 , \\ (\mathrm{iv})&\quad f (\cdot ) > 0.1 . \end{aligned}$$

Due to these inequalities, we determine the stability domain for the chosen α. Figure 1 illustrates the stability domain given by the nonlinear \(f (\cdot )\) relative to the nonlinear \(\Phi (\cdot )\).

Figure 1
figure 1

Stability domain given of the switched system illustrate in example obtained from Corollary 2 .

Full size image

According to the stability domain given in Figure 1 and for particular values chosen for the nonlinearity functions \(f (\cdot ) = 4.7\) and \(\Phi (\cdot ) = 3.5\). The simulation results are on the assumption that the vector valued initial function \(\phi ( t ) = [ - 1\ 1 ] ^{T}\). According to the switched law given in Figure 2 and from the particular values of the delay functions \(h_{1} = h_{2} = 1.2~\mbox{s}\), a typical result is plotted in Figure 3, Figure 4, and Figure 5, which show the norm of the state, the system state, and state space converge to zero.

Figure 2
figure 2

Switching function \(\pmb{\sigma ( t )}\) between subsystems.

Full size image
Figure 3
figure 3

The state’s norm of the switched system in the example.

Full size image
Figure 4
figure 4

State response of the switched system in the example.

Full size image
Figure 5
figure 5

The state of the switched system in the example.

Full size image

Therefore, Figure 3, Figure 4, and Figure 5 allow one to conclude that the switched system converges to zero. This implies that the system given in this example is globally asymptotically stable, which demonstrates the effectiveness of the proposed method.

This example shows that the obtained stability conditions are sufficient and very close to be necessary; on the other hand, the proposed results make it possible to avoid searching a common Lyapunov function, which is a very difficult matter in this case.

7 Conclusion

In this paper, a new approach for the stability analysis problem of a class of continuous-time switched nonlinear time-delay systems under arbitrary switched rules has been developed. By introducing a new constructed common Lyapunov function, the application of the Borne-Gentina criterion, the M-matrix properties, the aggregation techniques, and the vector norms notion. New delay-independent stability conditions under arbitrary switching are deduced. In addition, these obtained conditions are extended to be generalized for switched nonlinear systems with multiple delays. Compared with the existing results, the benefit of this method is that it can avoid the research of a common Lyapunov function which is usually very difficult, or even not possible. A numerical example is given to demonstrate the applicability of the proposed approach.

Note that these proposed results could be further used as a constructive solution to the problems of state and static output feedback stabilization.

The limit of this paper is that it has been confined to the boundaries of numerical examples. It would be beneficial to extend the research further so as to include real systems.