1 Introduction

Closely related with people’s life, network ranges from the Internet, the communication network to the biological networks, neural networks in nature, etc. It can be manifested in the form of complex networks. Generally speaking, it exists in nature and society. The studies on complex networks have become one of the hottest topics in the scientific research, and they have attracted wide attention of researchers working in the fields of information science, mathematics, physics, biology, system control, engineering, economics, society, military and so on [1–5]. In the studies on a variety of dynamical behaviors of complex networks, synchronization, as a typical form of describing collective motion of networks is one of the most important group dynamic behaviors of the network. Because of scientific importance and universality of real networks as well as a wealth of theoretical basis and challenge, it occupies a very important position in the studies of complex networks, and fruitful research results are achieved. In the literature, there are many widely studied synchronization patterns, for example, complete synchronization [6–8], lag synchronization [9–11], anti-synchronization [12–14], phase synchronization [15, 16], projective synchronization [17–29], and so on. Projective synchronization refers to the state variable response network gradually tending to a percentage value of the drive network state variables under some control. Due to the flexibility of the synchronization state scaling factor in projective synchronization, it is popular in the field of security digital communication.

Recently, projective synchronization under various cases of complex dynamical networks has been studied [17–29]. In Ref. [25], Li studied the generalized projective synchronization between two different chaotic systems: Lorenz system and Chen’s system. The proposed method combines backstepping methods and active control without having to calculate the Lyapunov exponents and the eigenvalues of the Jacobian matrix, which makes it simple and convenient. In Ref. [26], Lü et al. proposed a method of the lag projective synchronization of a class of complex networks containing nodes with chaotic behavior. Discrete chaotic systems are taken as nodes to constitute a complex network, and the topological structure of the network can be arbitrary. Considering the lag effect between a network node and a chaos signal of the target system, the control input of the network and the identification law of adjustment parameters are designed based on the Lyapunov theorem. In Ref. [27], Zhu et al. explored the mode-dependent projective synchronization problem of a couple of stochastic neutral-type neural networks with distributed time-delays. By using the Lyapunov stability theory and the adaptive control method, a sufficient projective synchronization criterion for this neutral-type neural network model is derived.

In the existing research, the most complex networks are usually described by the real variable differential system. The two complex networks (the so-called drive-response networks) based on real number, real matrix, or even real function evolve along the same or inverse directions [17–27]. However, the drive-response networks based on complex number can often evolve in different directions with a constant intersection angle, for example, \(y=\rho e^{j\theta}x\), where x denotes the drive system, y denotes the response system, \(\rho>0\) denotes the zoom rate, \(\theta\in [0,2\pi)\) denotes the rotation angle and \(j=\sqrt{-1}\). The state variables of the system defined in the complex field can describe a lot of practical problems. For example, in Ref. [30], authors use the state variables of a complex Lorenz system to describe the physical properties of parameters of atom polarization amplitude in the laser harmonic, electric field and population inversion, has realized the synchronization between two chaotic attractors, which fully illustrates that the complex system has the important application in the engineering. At the same time, if the projective synchronization methods combined with complex system are applied in the field of secure communications, this will further enhance the security of secret communication. Recently, some related works have come out, such as [28, 29]. In Refs. [28, 29], Wu and Fu introduced the concept of complex projective synchronization based on Lyapunov stability theory, several typical chaotic complex dynamical systems are considered and the corresponding controllers are designed to achieve the complex projective synchronization. This synchronization scheme has a large number of real-life examples. For instance, in a social network or games of economic activities, behaviors of individuals (response systems) will be affected not only by powerful one (drive system), but also by those with a similar role as themselves [28]. Another example, in a distributed computers collaboration, each distributed computer (response system) not only receives unified command from a server (drive system), but they also share resources between each other for collaboration [31].

Besides, in a lot of real network systems, nodes coupling way (the so-called topology) is not fixed but changing over time. For example, in the urban traffic network, the city partial obstruction caused by a traffic accident in the main street can result in the change of urban traffic network structure; in an interpersonal network, along with the development of society, economy etc., the relationships between different people are also changing. These factors also lead to changes in the whole network topology, they all belong to the structure of switch network topology, and the existing research on the static dynamic network synchronization methods is no longer suitable for this switch topology with time-varying dynamic network, which requires us to design a new network synchronization method [32–35].

Furthermore, a signal transmitted between the network nodes usually is affected by the network bandwidth, transmission medium and measuring noise factors, which result in time delays [21, 23, 25, 36], randomly missing or incomplete information [14–18]. Therefore, it is important to study the effect of time delay and stochastic noise in complex projective synchronization of drive-response networks.

Based on the above, the complex projective synchronization in drive-response stochastic switching networks with complex-variable systems is considered in this paper. The complex projective synchronization is achieved via a pinning control scheme and an adaptive coupling strength method. Several simple and practical criteria for complex projective synchronization are obtained by using the Lyapunov functional method, stochastic differential theory and linear matrix inequality (LMI) approaches.

Notation: Throughout this paper, \(\mathbb{C}^{n}\) and \(\mathbb {C}^{m\times n}\) denote n-dimensional complex vectors and the set of \(m\times n\) complex matrices, respectively. For the Hermite matrix H, the notation \(H > 0\) (\(H<0\)) means that the matrix H is positive definite (negative definite). For any complex (real) matrix M, \(M^{s}=M^{T}+\overline{M}\). For any complex number (or complex vector) x, the notations \(x^{r}\) and \(x^{i}\) denote its real and imaginary parts, respectively, and \(\bar{x}\) denotes the complex conjugate of x. \(\lambda_{\mathrm{min}}(A)\) (\(\lambda_{\mathrm{max}}(A)\)) represents the smallest (largest) eigenvalue of a symmetric matrix A. ⊗ is the Kronecker product. The superscript T of \(x^{T}\) or \(A^{T}\) denotes the transpose of the vector \(x\in\mathbb{R}^{n}\) or the matrix \(A\in\mathbb{C}^{m\times n}\). \(I_{n}\) is an identity matrix with n nodes.

2 Model description and preliminaries

Consider a drive-response network coupled with \(1+N\) identical partially linear stochastic complex network with coupling time delay, which is described as follows:

$$\begin{aligned}& \left \{ \begin{array}{l} \dot{x}(t)=M(z(t))x(t), \\ \dot{z}(t)=f(x(t),z(t)), \end{array} \right . \end{aligned}$$
(1)
$$\begin{aligned}& d{y}_{i}(t)= \Biggl\{ M\bigl(z(t)\bigr)y_{i}(t)+ \varepsilon_{1}\sum_{k=1}^{N}a_{ik} \bigl(r(t)\bigr)\Gamma y_{k}(t)+\varepsilon_{2}\sum _{k=1}^{N}b_{ik}\bigl(r(t)\bigr)\Gamma y_{k}(t-\tau) \Biggr\} \, dt \\& \hphantom{d{y}_{i}(t)=}{}+\sigma_{i}\bigl(y(t),y(t-\tau)\bigr)\, dw_{i}(t), \quad i=1,2,\ldots,N, \end{aligned}$$
(2)

where \(x(t)=(x_{1},x_{2},\ldots,x_{m})^{T}\in\mathbb{C}^{m}\), and \(z(t)\in \mathbb{R}\) is the drive system variable, \(y_{i}(t)=(y_{i1},y_{i2},\ldots ,y_{im})^{T}\in\mathbb{C}^{m}\) is the state variable of a node i in the response network. \(M(z(t))\in\mathbb{R}^{m\times m}\) is a complex matrix function, \(\varepsilon_{1}>0\), \(\varepsilon_{2}>0\) is the coupling strength and \(\Gamma\in\mathbb{R}^{m\times m}\) is the inner coupling matrix. τ is the coupling time delay; \(r(t) = r: [0,+\infty) \rightarrow(1, 2, \ldots, M)\) is a switching signal. Matrices \(A(r(t))=(a_{ij}(r(t)))_{N\times N}\) and \(B(r(t))=(b_{ij}(r(t)))_{N\times N}\) are the zero-row-sum outer coupling matrices, which denote the network switching topology and are defined as follows: if there is a connection (information transmission) from node j to node i (\(i\neq j\)), then \(a_{ij}(r(t))\neq0\) and \(b_{ij}(r(t))\neq0\); otherwise, \(a_{ij}(r(t))=0\) and \(b_{ij}(r(t))=0\); and \(w_{i}(t)=(w_{i1}(t), w_{i2}(t), \ldots, w_{in}(t))^{T} \in\mathbb{R}^{n}\) is a bounded vector-form Weiner process satisfying

$$\mathbb{E}w_{ij}(t)=0, \qquad \mathbb{E}w_{ij}^{2}(t)=1, \qquad \mathbb{E}w_{ij}(t)w_{ij}(s)=0\quad (s \neq t). $$

Now, two mathematical definitions for the generalized projective synchronization are introduced as follows.

Definition 1

If there is a complex α such that

$$\sum_{i=1}^{N}\mathbb{E}\bigl\Vert y_{i}(t)-\alpha x(t)\bigr\Vert ^{2} \leq K e^{-\kappa t} $$

for some \(K >0\) and some \(\kappa>0\), then the drive-response network (1) and (2) is said to achieve complex projective synchronization in the mean-square, and the parameter α is called a scaling factor.

Without loss of generality, let \(\alpha=\rho(\cos\theta+j\sin\theta)\), where \(\rho=|\alpha|\) is the module of α and \(\theta\in[0,2\pi )\) is the phase of α. Therefore, the projective synchronization is achieved when \(\theta=0\) or π. Furthermore, the complete synchronization is achieved when \(\rho=1\) and \(\theta=0\), the anti-synchronization is achieved when \(\rho=1\) and \(\theta=\pi\) [28].

Definition 2

[28]

Matrix \(A=(a_{ik})^{N}_{i,k}\) is said to belong to class \(A_{1}\), denoted as \(A\in A_{1}\), if

  1. (1)

    \(a_{ik}\geq0\), \(i\neq k\), \(a_{ii}=-\sum^{N}_{k=1,k\neq i}a_{ik}=-\sum^{N}_{k=1,k\neq i}a_{ki}\), \(i=1,2,\ldots,N\);

  2. (2)

    A is irreducible.

The following lemmas and assumption are used throughout the paper.

Lemma 1

[28]

Let \(m\times m\) be a complex matrix, H be Hermitian, then

  1. (1)

    \(x^{T}H\bar{x}\) is real for all \(x\in C^{m}\);

  2. (2)

    all the eigenvalues of H are real.

Lemma 2

[36]

If \(A=(a_{ij})_{m\times m}\) is irreducible, \(a_{ij}=a_{ji}\geq0\) for \(i\neq j\), and \(\sum_{j=1}^{m}a_{ij}=0\) for all \(i=1,2,\ldots,m\), then all eigenvalues of the matrix

$$\left ( \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{11}-\varepsilon& a_{12} & \cdots& a_{1m}\\ a_{21} & a_{22} & \cdots& a_{2m}\\ \vdots& \vdots& \ddots& \vdots\\ a_{m1} & a_{m2} & \cdots& a_{mm} \end{array} \right ) $$

are negative for any positive constant ε.

Lemma 3

[31, 37]

Consider an n-dimensional stochastic differential equation

$$ dx(t)=f\bigl(t,x(t),x(t-\tau)\bigr)\, dt+\sigma\bigl(t,x(t),x(t- \tau)\bigr)\, d\omega(t). $$
(3)

Let \(C^{2,1}(\mathbb{C}_{+}\times\mathbb{C}^{n};\mathbb{R}_{+})\) denote the family of all nonnegative functions \(V(t,x)\) on \(\mathbb{R}_{+}\times\mathbb{C}^{n}\), which are twice continuously differentiable in x and once differentiable in t. If \(V\in C^{2,1}(\mathbb{R}_{+}\times\mathbb{C}^{n};\mathbb{R}_{+})\), define an operator \(\mathcal{L}V\) from \(\mathbb{R}_{+}\times\mathbb {C}^{n}\) to \(\mathbb{R}\) by

$$ \mathcal{L}V(t,x)=V_{t}(t,x)+V_{x}(t,x)f(t,x,y)+ \frac{1}{2}\operatorname{Tr}\bigl[\sigma (t,x,y)^{T}V_{xx} \sigma(t,x,y)\bigr], $$

where \(V_{t}(t,x)=\partial V(t,x)/\partial t\), \(V_{x}(t,x)=(\partial V(t,x)/\partial x_{1},\ldots,\partial V(t,x)/\partial x_{n})\), \(V_{xx}(t,x)= (\frac{\partial^{2}V(t,x)}{\partial x_{i} x_{j}})_{n\times n}\). If \(V\in C^{2,1}(\mathbb{R}_{+}\times\mathbb{C}^{n};\mathbb{R}_{+})\), then for any \(\infty>t>t_{0} \geq0\),

$$\mathbb{E}V\bigl(t,x(t)\bigr)=\mathbb{E}V\bigl(t_{0},x(t_{0}) \bigr)+\mathbb{E}\int_{t_{0}}^{t}\mathcal{L}V \bigl(s,x(s)\bigr)\, ds $$

as long as the expectations of the integrals exist.

Assumption 1

[28]

Suppose that there exists a constant L such that the largest eigenvalue of \(M^{s}(z(t))\) satisfies

$$\lambda_{\mathrm{max}}\bigl(M^{s}\bigl(z(t)\bigr)\bigr)\leq L. $$

Remark 1

All the chaotic systems satisfy Assumption 1 due to \(z(t)\) is bounded [28].

Assumption 2

Denote \(e_{i}(t)=y_{i}(t)-\alpha x(t)\), suppose \(\sigma_{i}(e(t),e(t-\tau ))=\sigma_{i}(y(t),y(t-\tau))\). Then there exist positive definite constant matrices \(\Upsilon_{i1}\), \(\Upsilon_{i2}\) for \(i=1,2,\ldots,N\) such that

$$\begin{aligned}& \operatorname{Tr} \bigl[\sigma_{i}^{T}\bigl(e(t),e(t-\tau) \bigr)\overline{\sigma _{i}\bigl(e(t),e(t-\tau)\bigr)} \bigr] \\& \quad \leq \sum_{j=1}^{N} e_{j}^{T}(t)\Upsilon_{i1}\overline{e_{j}(t)}+ \sum_{j=1}^{N} e_{j}^{T}(t- \tau) \Upsilon_{i2}\overline{e_{j}(t-\tau)}. \end{aligned}$$

Remark 2

Assumption 2 is easily satisfied, for instance, because of existing noise in the process of information transmission, the noise strength \(\sigma_{i}(y(t),y(t-\tau)) =|\bar{\sigma}_{i}\times \sum_{k=1}^{N}a_{ik}(r(t)) (y_{k}(t)-y_{i}(t)) +\tilde{\sigma}_{i}\sum_{k=1}^{N}b_{ik}(r(t))(y_{k}(t-\tau)-y_{i}(t-\tau))|\), which depends on the states of the nodes, where \(\bar{\sigma}_{i}\) and \(\tilde{\sigma}_{i}\) are constants, \(i=1,2,\ldots,N\), so that \(\Upsilon_{i1}=\bar{\sigma}_{i}N \operatorname{diag}\{ a^{2}_{i1},a^{2}_{i2},\ldots,a^{2}_{iN}\}\), \(\Upsilon_{i2}=\tilde{\sigma}_{i}N \operatorname{diag}\{b^{2}_{i1},b^{2}_{i2},\ldots,b^{2}_{iN}\}\).

3 Main results

Our objective here is to achieve complex projective synchronization in the drive-response network (1) and (2) by adopting different control schemes. Firstly, several sufficient conditions for achieving complex projective synchronization in the drive-response network (1) and (2) by applying proper controllers \(u_{i}(t)\) on the response network are obtained. Then the controlled response network is

$$\begin{aligned} d{y}_{i}(t) =& \Biggl\{ M\bigl(z(t)\bigr)y_{i}(t)+ \varepsilon_{1}\sum_{k=1}^{N}a_{ik} \bigl(r(t)\bigr)\Gamma y_{k}(t)+\varepsilon_{2}\sum _{k=1}^{N}b_{ik}\bigl(r(t)\bigr)\Gamma y_{k}(t-\tau)+u_{i}(t) \Biggr\} \, dt \\ &{}+\sigma_{i}\bigl(y(t),y(t-\tau)\bigr)\, dw_{i}(t), \quad i=1,2,\ldots,N. \end{aligned}$$
(4)

Define the synchronization errors between the drive network (1) and the response network (2) as \(e_{i}(t)=y_{i}(t)-\alpha x(t)\) because of \(\sigma _{i}(e(t),e(t-\tau))=\sigma_{i}(y(t),y(t-\tau))\), then we have the following error system:

$$\begin{aligned} de_{i}(t) =& \Biggl\{ M\bigl(z(t)\bigr)e_{i}(t)+ \varepsilon_{1}\sum_{k=1}^{N}a_{ik} \bigl(r(t)\bigr)\Gamma e_{k}(t)+\varepsilon_{2}\sum _{k=1}^{N}b_{ik}\bigl(r(t)\bigr)\Gamma e_{k}(t-\tau)+u_{i}(t) \Biggr\} \, dt \\ &{}+\sigma_{i}\bigl(e(t),e(t-\tau)\bigr)\, dw_{i}(t),\quad i=1,2,\ldots,N. \end{aligned}$$
(5)

Next, we consider complex projective synchronization between (1) and (3) via pinning control under the assumption \(A\in A_{1}\), \(B\in A_{1}\) and \(\Gamma>0\). Especially, only one node is pinning for achieving complex projective synchronization.

Theorem 1

Suppose that Assumption  1 holds, \(A (r) \in A_{1}\), \(B (r) \in A_{1}\) for \(r=1,2,\ldots,M\) and \(\Gamma>0\). The complex projective synchronization in the drive-response network (1) and (3) with the following single controller

$$ \begin{aligned} &u_{1}(t)=-\varepsilon_{1} d_{1}\Gamma e_{1}(t), \\ &u_{i}(t)=0, \quad i=2,\ldots,N, \end{aligned} $$
(6)

can be achieved if the following condition is satisfied:

$$ \gamma+a+be^{\gamma\tau}< 0, $$
(7)

where \(\gamma>0\), \(a=\min_{r} \lambda_{\mathrm{min}}((L+\alpha) I_{Nm}+\varepsilon _{1}((A(r))^{s}-D_{1})\otimes\Gamma)+\Upsilon_{i1}\), \(b=\max_{r} \lambda_{\mathrm{max} }(\frac{1}{\alpha}\varepsilon_{2}^{2}((B(r))\otimes\Gamma )^{sT}((B(r))\otimes\Gamma)+\Upsilon_{i2})\), \(d_{1}>0\) and \(D_{1}=\operatorname{diag}(2d_{1},0,\ldots,0)\).

Proof

Consider the Lyapunov functional candidate

$$ V(t)=\sum_{i=1}^{N}e_{i}^{T}(t) \overline{e_{i}(t)}. $$

Calculating \(\mathcal{L}V(t)\) with respect to t along the solution of (4) and noticing the adaptive feedback controllers (5), for \(r(t) = r\), one has

$$\begin{aligned} \mathcal{L}V(t) =&\sum_{i=1}^{N} \Biggl\{ \Biggl[e^{T}_{i}(t)M^{T}\bigl(z(t)\bigr)+ \varepsilon_{1}\sum_{k=1}^{N}a_{ik}(r)e^{T}_{k}(t) \Gamma^{T} +\varepsilon_{2}\sum_{k=1}^{N}b_{ik}(r)e^{T}_{k}(t- \tau)\Gamma^{T}\Biggr]\overline {e_{i}(t)} \\ &{} +e^{T}_{i}(t)\Biggl[\overline{M\bigl(z(t) \bigr)e_{i}(t)}+\varepsilon_{1}\sum _{k=1}^{N}a_{ik}(r)\Gamma \overline{e_{k}(t)}+\varepsilon_{2}\sum _{k=1}^{N}b_{ik}(r)\Gamma \overline{e_{k}(t-\tau)}\Biggr] \Biggr\} \\ &{}-2\varepsilon_{1} d_{1}e_{1}^{T}(t) \Gamma\overline{e_{1}(t)} +\frac{1}{2}\sum _{i=1}^{N}\operatorname{Tr}\bigl[\sigma_{i} \bigl(e(t),e(t-\tau)\bigr)^{T}\overline {\sigma_{i} \bigl(e(t),e(t-\tau)\bigr)}\bigr] \\ =&\sum_{i=1}^{N}\bigl[e_{i}^{T}(t)M^{T} \bigl(z(t)\bigr)\overline{e_{i}(t)}+e_{i}^{T}(t) \overline {M\bigl(z(t)\bigr)}\overline{e_{i}(t)}\bigr] \\ &{}+ \varepsilon_{1}\sum_{i=1}^{N}\sum _{k=1}^{N}a_{ik}(r) \bigl[e_{k}^{T}(t)\Gamma ^{T}+e_{i}^{T}(t) \Gamma\bigr]\overline{e_{k}(t)} \\ &{} +\varepsilon_{2}\sum_{i=1}^{N} \sum_{k=1}^{N}b_{ik}(r) \bigl[e_{k}^{T}(t-\tau)\Gamma ^{T} \overline{e_{k}(t)}+e_{i}^{T}(t)\Gamma \overline{e_{k}(t-\tau)}\bigr] -2\varepsilon_{1} d_{1}e_{1}^{T}(t)\Gamma\overline{e_{1}(t)} \\ &{} +\frac{1}{2}\sum_{i=1}^{N} \operatorname{Tr}\bigl[\sigma_{i}\bigl(e(t),e(t-\tau) \bigr)^{T}\overline {\sigma_{i}\bigl(e(t),e(t-\tau)\bigr)} \bigr] \\ \leq&\sum_{i=1}^{N}Le_{i}^{T}(t) \overline{e_{i}(t)} +\varepsilon_{1}\sum _{i=1}^{N}\sum_{k=1}^{N}a_{ik}(r) \bigl[e_{k}^{T}(t)\Gamma ^{T}+e_{i}^{T}(t) \Gamma\bigr]\overline{e_{k}(t)} -2\varepsilon_{1} d_{1}e_{1}^{T}(t)\Gamma\overline{e_{1}(t)} \\ &{} +\varepsilon_{2}\sum_{i=1}^{N} \sum_{k=1}^{N}b_{ik}(r) \bigl[e_{k}^{T}(t)\Gamma ^{T}+e_{i}^{T}(t) \Gamma\bigr]\overline{e_{k}(t-\tau)} \\ &{}+\sum _{i=1}^{N}e_{i}^{T}(t) \Upsilon_{i1}\overline{e_{i}(t)} +\sum _{i=1}^{N}e_{i}^{T}(t-\tau) \Upsilon_{i2}\overline{e_{i}(t-\tau)} . \end{aligned}$$

Let \(e(t)=(e_{1}^{T}(t),e_{2}^{T}(t),\ldots,e_{N}^{T}(t))^{T}\), then one has

$$\begin{aligned} \mathcal{L}V(t) \leq&e^{T}(t) \bigl(\bigl((L+\alpha)I_{Nm}+ \varepsilon _{1}\bigl(\bigl(A(r)\bigr)^{s}-D_{1} \bigr)\otimes\Gamma\bigr)+\Upsilon_{i1}\bigr)\overline{e(t)} \\ &{}+e^{T}(t-\tau) \biggl(\frac{1}{\alpha}\varepsilon_{2}^{2} \bigl(B(r)\otimes\Gamma \bigr)^{sT}\bigl(B(r)\otimes\Gamma\bigr)+ \Upsilon_{i2}\biggr)\overline{e(t-\tau)}. \end{aligned}$$

In view of condition (6), we have

$$ \mathcal{L}V(t)\leq aV(t)+bV(t-\tau). $$
(8)

Define

$$W(t)=e^{\gamma t}V(t) $$

and use equation (6) to compute the operator

$$\begin{aligned} \mathcal{L}W(t)&=e^{\gamma t}\bigl[\gamma V(t)+\mathcal{L}V(t)\bigr] \\ &\leq e^{\gamma t}\bigl[\gamma V(t)+aV(t)+bV(t-\tau)\bigr], \end{aligned}$$

which, after applying the generalized Itô formula, gives

$$ e^{\gamma t}\mathbb{E}V(t)=\mathbb{E}V(0)+\mathbb{E}\int ^{t}_{0} \mathcal{L}W(s)\, ds $$
(9)

for any \(t\geq0\). Hence we have

$$\begin{aligned} e^{\gamma t}\mathbb{E}V(t)&\leq\mathbb{E}V(0)+\mathbb{E}\int _{0}^{t}e^{\gamma s}\bigl[\gamma V(s) +aV(s)+bV(s-\tau)\bigr]\, ds \\ &\leq\mathbb{E}V(0)+(\gamma+a)\int_{0}^{t} e^{\gamma s}\mathbb{E}V(s)\, ds +be^{\gamma\tau}\int_{0}^{t}e^{\gamma(s-\tau)} \mathbb{E}V(s-\tau)\, ds. \end{aligned}$$
(10)

By changing variable \(s-\tau=u\), we have

$$ \int_{0}^{t}e^{\gamma(s-\tau)} \mathbb{E}V(s-\tau)\, ds =\int_{-\tau}^{t-\tau}e^{\gamma u} \mathbb{E}V(u)\, du \leq \int_{-\tau}^{t}e^{\gamma u}\mathbb{E}V(u) \, du. $$
(11)

Substituting equation (11) into equation (10), we get

$$ e^{\gamma t}\mathbb{E}V(t)\leq\mathbb{E}V(0)+\bigl(\gamma+a+be^{\gamma\tau } \bigr)\int_{- \tau}^{t}e^{\gamma u}\mathbb{E}V(u)\, du. $$

By using Gronwall’s inequality, we get

$$ e^{\gamma t}\mathbb{E}V(t)\leq K e^{-\kappa t}, $$

where \(K=\mathbb{E}V(0)e^{(\gamma+a+be^{\gamma\tau})\tau}\) and \(\kappa =-(\gamma+a+be^{\gamma\tau})\). In light of condition (7), the proof is completed. □

Remark 3

In Theorem 1, the coupling matrix A must be strongly connected and the coupling matrix B is not necessarily a symmetrical or irreducible matrix. From condition (7) of Theorem 1, we can determine the control strength \(\varepsilon_{1}\) and \(\varepsilon_{2}\) to reach complex project synchronization.

If considering the system without delay, that is, \(\tau=0\), we can derive the following controlled response network and the error system:

$$\begin{aligned} d{y}_{i}(t) =& \Biggl\{ M\bigl(z(t)\bigr)y_{i}(t)+ \varepsilon_{1}\sum_{k=1}^{N}a_{ik} \bigl(r(t)\bigr)\Gamma y_{k}(t)+u_{i}(t) \Biggr\} \, dt \\ &{}+\sigma _{i}\bigl(y(t)\bigr)\, dw_{i}(t),\quad i=1,2,\ldots,N \end{aligned}$$
(12)

and

$$\begin{aligned} de_{i}(t) =& \Biggl\{ M\bigl(z(t)\bigr)e_{i}(t)+ \varepsilon_{1}\sum_{k=1}^{N}a_{ik} \bigl(r(t)\bigr)\Gamma e_{k}(t)+u_{i}(t) \Biggr\} \, dt \\ &{}+\sigma _{i}\bigl(e(t)\bigr)\, dw_{i}(t),\quad i=1,2,\ldots,N, \end{aligned}$$
(13)

then, without loss of generality, one has the following corollary.

Corollary 1

Suppose that Assumption  1 holds, \(A(r)\in A_{1}\), \(\Gamma>0\) for \(r=1,2,\ldots,M\). The complex projective synchronization in the drive-response network (1) and (3) with the following single controller:

$$ \left \{ \begin{array}{l} u_{1}(t)=-\varepsilon_{1} d_{1}\Gamma e_{1}(t), \\ u_{i}(t)=0,\quad i=2,\ldots,N, \end{array} \right . $$

can be achieved if \(a<0\) is satisfied where \(a=\min_{r}\lambda_{\mathrm{min}}(LI_{Nm}+\varepsilon_{1}((A(r))^{s}-D_{1})\otimes \Gamma)+\Upsilon_{i1}\), \(d_{1}>0\) and \(D_{1}=\operatorname{diag}(2d_{1},0,\ldots,0)\).

Theorem 1 and Corollary 1 state that a drive-response stochastic coupled networks can achieve complex projective synchronization by controlling only a fraction of the nodes, provided that its control strength is sufficiently large. It is usually much larger than the value needed. Clearly it is a natural idea to make the control strength as small as possible. Next, we will realize complex projective synchronization for relatively small control strengths by using adaptive adjustments. Let

$$ \left \{ \textstyle\begin{array}{l} u_{1}(t)=-\varepsilon_{1} d(t)\Gamma e_{1}(t), \\ u_{i}(t)=0,\quad i=2,\ldots,N, \\ \dot{d}(t)=\delta\sum^{N}_{i=1}e_{i}^{T}(t)\overline{e_{i}(t)}, \end{array} \right . $$

where \(\delta>0\) is the adaptive gain.

Theorem 2

Suppose that Assumption  1 holds, P is a positive definite matrix, the complex projective synchronization in the drive-response network (1) and (3) with controllers (12) can be achieved if the following conditions are satisfied:

$$ \begin{aligned} &I_{N}\otimes\bigl((L+ \alpha)I_{m}+P+\Upsilon_{i1}\bigr)+\varepsilon_{1} \bigl(\bigl(A(r)\bigr)^{s} - D^{\ast}\bigr)\otimes\Gamma< 0 \quad \textit{for } r=1,2,\ldots,M, \\ &\frac{1}{\alpha}\varepsilon_{2}^{2}\bigl(\bigl(B(r)\bigr) \otimes\Gamma\bigr)^{sT}\bigl(\bigl(B(r)\bigr)\otimes \Gamma \bigr)-I_{N}\otimes(P-\Upsilon_{i2})<0\quad \textit{for } r=1,2,\ldots,M \end{aligned} $$
(14)

for a small positive constant δ and \(D^{\ast}_{1}=\operatorname {diag}(2d^{\ast}_{1},0,\ldots,0)\).

Proof

Consider the Lyapunov functional candidate

$$ V(t)=\sum_{i=1}^{N}e_{i}^{T}(t) \overline{e_{i}(t)}+\frac{1}{\delta }\bigl(d(t)-d^{*}\bigr)^{2}+ \sum_{i=1}^{N}\int_{t-\tau}^{t}e_{i}^{T}(s)P \overline {e_{i}(s)}\, ds. $$

Calculating \(\mathcal{L}V(t)\) with respect to t along the solution of (4) and noticing the adaptive feedback controllers (5), for \(r(t)=r\), one has

$$\begin{aligned} \mathcal{L}V(t) =&\sum_{i=1}^{N} \Biggl\{ \Biggl[e^{T}_{i}(t)M^{T}\bigl(z(t)\bigr)+ \varepsilon_{1}\sum_{k=1}^{N}a_{ik}(r)e^{T}_{k}(t) \Gamma^{T} \\ &{}+\varepsilon_{2}\sum_{k=1}^{N}b_{ik}(r)e^{T}_{k}(t- \tau)\Gamma ^{T}-e^{T}_{i}(t)d(t)\Biggr] \overline{e_{i}(t)} \\ &{} +e^{T}_{i}(t)\Biggl[\overline{M\bigl(z(t) \bigr)e_{i}(t)}+\varepsilon_{1}\sum _{k=1}^{N}a_{ik}(r)\Gamma \overline{e_{k}(t)} \\ &{}+\varepsilon_{2}\sum_{k=1}^{N}b_{ik}(r) \Gamma\overline{e_{k}(t-\tau )}-d(t)\overline{e_{i}(t)} \Biggr] +e_{i}^{T}(t)P\overline{e_{i}(t)}-e_{i}^{T}(t- \tau)P\overline{e_{i}(t-\tau)} \Biggr\} \\ &{} +\frac{2}{\delta}\bigl(d(t)-d^{\ast}\bigr)\delta e_{1}^{T}(t)\Gamma\overline{e_{1}(t)} + \frac{1}{2}\sum_{i=1}^{N} \operatorname{Tr}\bigl[\sigma_{i}\bigl(e(t),e(t-\tau) \bigr)^{T}\overline {\sigma_{i}\bigl(e(t),e(t-\tau)\bigr)} \bigr] \\ =&\sum_{i=1}^{N}\bigl[e_{i}^{T}(t)M^{T} \bigl(z(t)\bigr)\overline{e_{i}(t)}+e_{i}^{T}(t) \overline {M\bigl(z(t)\bigr)}\overline{e_{i}(t)}+e_{i}^{T}(t)P \overline{e_{i}(t)}\bigr] \\ &{} +\varepsilon_{1}\sum_{i=1}^{N} \sum_{k=1}^{N}a_{ik}(r) \bigl[e_{k}^{T}(t)\Gamma^{T}+e_{i}^{T}(t) \Gamma\overline {e_{k}(t)}\bigr] \\ &{} +\varepsilon_{2}\sum_{i=1}^{N} \sum_{k=1}^{N}b_{ik}(r) \bigl[e_{k}^{T}(t-\tau)\Gamma ^{T}+e_{i}^{T}(t) \Gamma\overline{e_{k}(t-\tau)}\bigr] \\ &{} -2d^{\ast}e_{1}^{T}(t) \Gamma\overline{e_{1}(t)}-e_{i}^{T}(t-\tau)P \overline {e_{i}(t-\tau)} \\ &{} +\frac{1}{2}\sum_{i=1}^{N} \operatorname{Tr}\bigl[\sigma_{i}\bigl(e(t),e(t-\tau) \bigr)^{T}\overline {\sigma_{i}\bigl(e(t),e(t-\tau)\bigr)} \bigr] \\ \leq&\sum_{i=1}^{N}e_{i}^{T}(t) (LI_{m}+P)\overline{e_{i}(t)} +\varepsilon_{1}\sum _{i=1}^{N}\sum_{k=1}^{N}a_{ik}(r) \bigl[e_{k}^{T}(t)\Gamma ^{T}+e_{i}^{T}(t) \Gamma\overline{e_{k}(t)}\bigr] \\ &{}-\sum_{i=1}^{N} e_{i}^{T}(t- \tau)P\overline{e_{i}(t-\tau)}-2d^{\ast }e_{1}^{T}(t) \Gamma\overline{e_{1}(t)} \\ &{} +\varepsilon_{2}\sum_{i=1}^{N} \sum_{k=1}^{N}b_{ik}(r) \bigl[e_{k}^{T}(t-\tau)\Gamma ^{T}+e_{i}^{T}(t) \Gamma\overline{e_{k}(t-\tau)}\bigr] \\ &{}+\sum _{i=1}^{N}e_{i}^{T}(t) \Upsilon_{i1}\overline{e_{i}(t)} +\sum _{i=1}^{N}e_{i}^{T}(t-\tau) \Upsilon_{i2}\overline{e_{i}(t-\tau)}. \end{aligned}$$

Let \(e(t)=(e_{1}^{T},e_{2}^{T},\ldots,e_{N}^{T})\), then one has

$$\begin{aligned} \mathcal{L}V(t) \leq&e^{T}(t) \bigl(I_{N}\otimes\bigl((L+ \alpha)I_{m}+P+\Upsilon _{i1}\bigr)+\varepsilon_{1} \bigl(\bigl(A(r)\bigr)^{s} - D^{\ast}\bigr)\otimes\Gamma\bigr) \overline {e(t)} \\ &{}+e^{T}(t-\tau) \biggl(\frac{1}{\alpha}\varepsilon_{2}^{2} \bigl(B(r)\otimes\Gamma \bigr)^{sT}\bigl(B(r)\otimes\Gamma \bigr)-I_{N}\otimes(P-\Upsilon_{i2})\biggr)\overline{e(t-\tau )}. \end{aligned}$$

In light of condition (14) of Theorem 2, we can get \(\mathcal{L}V(t) < 0\). In view of the LaSalle invariance principle of stochastic differential equation, which was developed in [38], we have \(\lim_{t\rightarrow\infty}V(t)=0\), which in turn illustrates that \(\lim_{t\rightarrow\infty}e_{i}(t)=0\) and, at the same time, \(\lim_{t\rightarrow\infty}d(t)=d^{\ast}\). The proof is completed. □

4 Numerical simulations

In this section, we conduct some numerical simulations to illustrate the effectiveness of the theorems of the previous section.

Consider a drive-response network coupled with the following complex Lorenz systems:

$$ \left \{ \begin{array}{l} \dot{x}=M(z)x, \\ \dot{z}=-bz+\frac{1}{2}(\bar{x}_{1}x_{2}+x_{1}\bar{x}_{2}), \end{array} \\ \right . $$
(15)

where

$$M(z)=\left ( \begin{array}{@{}c@{\quad}c@{}} -\sigma& \sigma \\ r-z & -a \end{array} \right ), $$

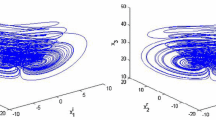
which exhibit chaotic behavior when \(\sigma=2\), \(b=0.8\), \(r=60+0.02j\) and \(a=1-0.06j\). Figure 1 shows a chaotic attractor of the complex Lorenz system with initial values \(x_{1}(0)=2.040 + 2.020j\), \(x_{2}(0)=5.062 + 4.067j\), \(z=5.1\), which is the synchronization orbit in the following simulations; and the noise strength \(\sigma_{i}(y(t),y(t-\tau)) =0.001\sum_{k=1}^{N}a_{ik}(r) (y_{k}(t)-y_{i}(t)) +0.001\sum_{k=1}^{N}b_{ik}(r)(y_{k}(t-\tau)-y_{i}(t-\tau))\), so we have \(\Upsilon_{i1} < 0.05I_{10}\), \(\Upsilon_{i2} < 0.02I_{10}\).

Figure 1
figure 1

A chaotic attractor of the complex Lorenz system with initial values \(\pmb{x_{1}(0) = 2.040 + 2.020j}\) , \(\pmb{x_{2}(0) = 5.062 + 4.067j}\) , \(\pmb{z = 5.1}\) .

Full size image

According to (9), one can easily calculate the eigenvalues of \(M^{s}(z(t))\): \(\lambda_{1,2}=-(\sigma+1)\pm\sqrt{(\sigma-1)^{2}+|\sigma -z+r|^{2}}\). From Figure 1, it is found that \(20\leq z\leq100\), and then one can choose \(L=40\) such that Assumption 1 holds.

Firstly, consider complex projective synchronization in a drive-response network coupled with \(1+10\) identical complex Lorenz systems with switching topology via adaptive feedback control, where the outer coupling matrices \(A(r)\) and \(B(r)\) for \(r=(1,2)\) are

$$\begin{aligned}& A(1)=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} -6& 0& 1& 1& 0& 1& 1& 1& 1& 0 \\ 1&-6& 0& 1& 1& 1& 0& 1& 1& 0 \\ 0& 1&-6& 1& 1& 1& 0& 1& 1& 0 \\ 1& 1& 1&-6& 1& 0& 0& 1& 1& 0 \\ 1& 1& 1& 1&-6& 1& 0& 0& 1& 0 \\ 0& 1& 1& 1& 1&-6& 1& 0& 1& 0 \\ 1& 1& 1& 1& 1& 0&-6& 0& 1& 0 \\ 1& 1& 0& 1& 1& 0& 1&-6& 1& 0 \\ 1& 1& 1& 0& 1& 1& 1& 0&-6& 0 \\ 0& 1& 1& 1& 1& 1& 0& 0& 1&-6 \end{array} \right ], \\& A(2)=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} -7& 1& 1& 1& 1& 1& 1& 1& 0& 0 \\ 1&-7& 1& 1& 1& 1& 1& 1& 0& 0 \\ 0& 1&-7& 1& 1& 1& 1& 1& 1& 0 \\ 1& 1& 1&-7& 1& 0& 1& 1& 1& 0 \\ 1& 1& 1& 1&-7& 1& 1& 0& 1& 0 \\ 1& 1& 1& 1& 0&-7& 1& 1& 1& 0 \\ 0& 1& 1& 1& 1& 1&-7& 1& 1& 0 \\ 1& 1& 1& 1& 1& 1& 1&-7& 0& 0 \\ 0& 1& 1& 1& 1& 1& 1& 1&-7& 0 \\ 1& 1& 1& 1& 1& 1& 0& 1& 0&-7 \end{array} \right ], \\& B(1)=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} -2& 0& 0& 0& 1& 0& 0& 0& 1& 0 \\ 0&-2& 1& 0& 0& 0& 1& 0& 0& 0 \\ 0& 0&-2& 1& 0& 0& 1& 0& 0& 0 \\ 0& 0& 1&-2& 1& 0& 0& 0& 0& 0 \\ 0& 1& 0& 1&-2& 0& 0& 0& 0& 0 \\ 0& 0& 0& 0& 0&-2& 1& 1& 0& 0 \\ 0& 1& 0& 0& 1& 0&-2& 0& 0& 0 \\ 0& 1& 0& 0& 0& 0& 1&-2& 0& 0 \\ 0& 1& 0& 0& 0& 0& 1& 0&-2& 0 \\ 0& 1& 1& 0& 0& 0& 0& 0& 0&-2 \end{array} \right ], \\& B(2)=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} -3& 0& 1& 1& 0& 1& 0& 0& 0& 0 \\ 1&-3& 1& 0& 1& 0& 0& 0& 0& 0 \\ 0& 0&-3& 1& 0& 0& 1& 1& 0& 0 \\ 0& 1& 1&-3& 0& 0& 1& 0& 0& 0 \\ 0& 1& 0& 0&-3& 0& 0& 1& 1& 0 \\ 0& 0& 1& 1& 0&-3& 0& 0& 1& 0 \\ 1& 1& 1& 0& 0& 0&-3& 0& 0& 0 \\ 1& 0& 0& 1& 0& 0& 1&-3& 0& 0 \\ 1& 0& 0& 1& 0& 1& 0& 0&-3& 0 \\ 0& 1& 0& 1& 1& 0& 0& 0& 0&-3 \end{array} \right ], \end{aligned}$$

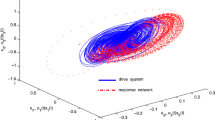
respectively. Choosing \(\alpha=1+0.1j\), \(\Gamma=\operatorname{diag}(1,1)\), \(d_{1}=150\). By a simple calculation, one has that the largest eigenvalue of \(A^{s}-D\) is −0.2605, and then one can choose \(\alpha= 1\), \(\varepsilon_{1}=100\) and \(\varepsilon_{2}=1\) such that \(a=-5.8225\) and \(b=0.0264\). Let \(\tau=0.1\), we can get \(\gamma=0.5 \) such that condition (7) holds. The initial values of complex state variables \(y_{i}(t)\) (\(i=1,2,\ldots,10\)) are chosen as \(y_{i1}(0)=2+2i+j(3+i)\) and \(y_{i2}(0)=(3+2i)+j(4+2i)\). Figures 2 and 3 show the evolution of synchronization trajectory and errors by pinning control, respectively.

Figure 2
figure 2

The evolution of the synchronization trajectory \(\pmb{y_{i}}\) ( \(\pmb{i=1,2,\ldots,10}\) ) by pinning control.

Full size image
Figure 3
figure 3

The evolution of the synchronization errors \(\pmb{y_{i}}\) ( \(\pmb{i=1,2,\ldots,10}\) ) by pinning control.

Full size image

Finally, consider complex projective synchronization in a drive-response network coupled with \(1+10\) identical complex Lorenz systems via a single controller and adaptive coupling strength. In numerical simulations, we choose \(P=I_{m}\sigma=0.001\) and the initial values of \(\varepsilon (t)\) as \(\varepsilon(0)=2.3\). The other parameters are chosen the same as those in the above example such that condition (14) holds. Figures 4 and 5 show the evolution of synchronization trajectory and errors by adaptive control, respectively. From Figure 6, one can see that the needed control strength value is much less than that calculated by inequality (7) in the above example.

Figure 4
figure 4

The evolution of the synchronization trajectory \(\pmb{y_{i}}\) ( \(\pmb{i=1,2,\ldots,10}\) ) by adaptive control.

Full size image
Figure 5
figure 5

The evolution of the synchronization errors \(\pmb{y_{i}}\) ( \(\pmb{i=1,2,\ldots,10}\) ) by adaptive control.

Full size image
Figure 6
figure 6

The evolution of adaptive control strength \(\pmb{d(t)}\) .

Full size image

5 Conclusion

The complex projective synchronization in drive-response stochastic coupled networks with complex-variable systems and linear coupling time delays are considered in this paper. Since drive-response systems may evolve in different directions with a constant intersection angle in many real situations, and they not simultaneously evolve along the same or inverse direction based on real number, real matrix, or even real function in a complex plane, we focus on the projective synchronization of this situation considering the time delay and stochastic disturbance for response systems through two theorems and one corollary. Eventually, several numerical simulations have verified the validity of those results.