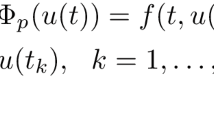1 Introduction

In this paper, we discuss the following Neumann boundary value problem:

$$ \left \{ \begin{array}{l} -(\Phi_{p}(u'(t)))'+\Phi_{p}(u(t))=\lambda f(t,u(t)), \quad t \neq t_{j}, t\in [0, T], T>0, \\ \Delta\Phi_{p}(u'(t_{j}))=I_{j}(u(t_{j})),\quad j=1,2,\ldots,m, \\ u'(0)=u'(T)=0, \end{array} \right . $$
(1.1)

where \(f\in C(J\times R,R)\), \(I_{j}\in C(R,R)\), \(0=t_{0}< t_{1}<t_{2}<\cdots <t_{m}<t_{m+1}=T\), \(\Phi_{p}(s)\) is a p-Laplacian operator with \(\Phi_{p}(s)=|s|^{p-2}s\), \(1< p<+\infty\), \(\Delta\Phi_{p}(u'(t_{j}))= \Phi_{p}(u'(t^{+}_{j}))-\Phi_{p}(u'(t^{-}_{j}))\), where \(u'(t^{+}_{j})\), \(u'(t^{-}_{j})\) denote the right and left limits, respectively, of \(u'(t)\) at \(t=t_{j}\), \(j=1,2,\ldots,m\). \(\lambda\in[0,+\infty)\) is a real parameter.

In recent years, there seems to be increasing interest in the existence of multiple solutions for boundary value problems, we refer the reader to [1–5]. Results on this topic are usually achieved by using various fixed point theorems and degree theory. It is well known that variational methods and critical point theorem are very important tools for dealing with the problems for differential equations and in the last few years, some researchers have gradually paid more attention to applying variational methods to dealing with the existence of solutions for impulsive differential equation boundary value problems [6–11]. But few researches have paid more attention to the existence of three solutions for the system (1.1).

Xie and Luo in [12] have investigated the existence of three solutions to the boundary value problem

$$ \left \{ \begin{array}{l} -(\Phi_{p}(u'(t)))'+\Phi_{p}(u(t))=\lambda f(t,u(t)), \quad t\in[0, T], T>0, \\ u'(0)=u'(T)=0. \end{array} \right . $$
(1.2)

Obviously, system (1.2) is a special case of system (1.1) with \(I_{j}=0\). So, the results which are obtained in this paper generalize their results.

The rest of this paper is organized as follows. In Section 2 we present some important lemmas. In Section 3, under suitable hypotheses, we establish that the problem (1.1) possesses at least three solutions, moreover, we present an example to illustrate our results.

2 Preliminaries

In the following, we first introduce some notation.

Put \(H=W^{1,P}([0,T])\) and define

$$ \|u\|= \biggl(\int_{0}^{T}\bigl\vert u'(t)\bigr\vert ^{p}\, dt+\int_{0}^{T} \bigl\vert u(t)\bigr\vert ^{p}\, dt \biggr)^{\frac{1}{p}}, \quad u\in H. $$

Note that H is a separable and reflexive Banach space.

Definition 2.1

The function \(u:[0,T]\rightarrow\mathbb {R}\) is called a weak solution of problem (1.1) if \(u \in H\) and

$$ \int_{0}^{T}\bigl(\Phi_{p} \bigl(u'(t)\bigr)v'(t)+\Phi_{p}\bigl(u(t) \bigr)v(t)\bigr)\, dt +\sum_{j=1}^{m}I_{j} \bigl(u(t_{j})\bigr)v(t_{j})=\lambda\int _{0}^{T}f\bigl(t,u(t)\bigr)v(t)\, dt $$

for all \(v\in H\).

The following three functions will be used later.

Define \(\Phi:H\rightarrow R\), \(J :H\rightarrow R \) by

$$ \Phi(u)= \frac{1}{p}\|u\|^{p}+\sum _{j=1}^{m}\int_{0}^{u(t_{j})}I_{j}(s) \, ds,\qquad J(\xi)= \int_{0}^{T}F(t,\xi)\, dt, $$
(2.1)

where \(F(t,\xi)= \int_{0}^{\xi}f(t,s)\, ds\).

Define \(\varphi:H\rightarrow R\), by

$$ \varphi(u)=\Phi(u)-\lambda J(u). $$
(2.2)

Note that Φ, J, φ are Fréchet differentiable at any \(u\in H\) and

$$\begin{aligned} \varphi'(u)v =& \int_{0}^{T} \bigl(\Phi _{p}\bigl(u'(t)\bigr)v'(t)+ \Phi_{p}\bigl(u(t)\bigr)v(t)\bigr)\, dt \\ &{}+\sum_{j=1}^{m}I_{j} \bigl(u(t_{j})\bigr)v(t_{j})-\lambda\int _{0}^{T}f\bigl(t,u(t)\bigr)v(t)\, dt \end{aligned}$$
(2.3)

for any \(v\in H\). Further, a critical point of φ by (2.2), gives us a weak solution of the system (1.1).

Lemma 2.2

If function \(u(t)\in H\) is a critical point of the functional φ, then \(u(t)\), \(t\in[0,T]\) is a solution of the system (1.1).

Proof

Let \(u(t)\in H\) be a critical point of functional φ. Then

$$ \varphi'(u)v(t)=0,\quad \forall v(t)\in H. $$
(2.4)

By integrating (2.3), we have

$$\begin{aligned}& \int_{0}^{T}\bigl( \Phi_{p}\bigl(u'(t)\bigr)v'(t) + \Phi_{p}\bigl(u(t)\bigr)v(t)\bigr)\, dt \\& \qquad {}+\sum _{j=1}^{m}I_{j}\bigl(u(t_{j}) \bigr)v(t_{j})-\lambda\int_{0}^{T}f \bigl(t,u(t)\bigr)v(t)\, dt \\& \quad = \int_{0}^{T}\bigl(-\bigl( \Phi_{p}\bigl(u'(t)\bigr)\bigr)'+ \Phi_{p}\bigl(u(t)\bigr)\bigr)v(t)\, dt \\& \qquad {} + \sum_{j=1}^{m}\bigl(-\Delta \Phi _{p}\bigl(u'(t_{j})\bigr)+I_{j} \bigl(u(t_{j})\bigr)\bigr)v(t_{j})-\lambda\int _{0}^{T}f\bigl(t,u(t)\bigr)v(t)\, dt, \end{aligned}$$
(2.5)

which holds for all \(v(t)\in H\). For \(j\in\{1,2,\ldots,m\}\), we choose \(v(t)\in H\), with \(v(t)=0\) for every \(t\in[0,t_{j}]\cup[t_{j+1},T]\), then

$$ \int_{t_{j}}^{t_{j+1}}\bigl(\bigl(-\Phi_{p} \bigl(u'(t)\bigr)\bigr)'+\Phi _{p}\bigl(u(t) \bigr)-\lambda f\bigl(t,u(t)\bigr)\bigr)v(t)\, dt=0. $$

Therefore,

$$ -\bigl(\Phi_{p}\bigl(u'(t)\bigr) \bigr)'+\Phi_{p}\bigl(u(t)\bigr)=\lambda f\bigl(t,u(t) \bigr) \quad \mbox{a.e. }t\in(t_{j},t_{j+1}). $$
(2.6)

Thus, u satisfies (1.1).

Combining (2.4), (2.5), and (2.6) we have

$$\sum_{j=1}^{m}\bigl(-\Delta \Phi_{p}\bigl(u'(t_{j})\bigr)+I_{j} \bigl(u(t_{j})\bigr)\bigr)v(t_{j})=0. $$

If the impulsive condition in (1.1) does not hold, then there exist some \(j\in\{1,2,\ldots,m\}\) such that

$$-\Delta\Phi_{p}\bigl(u'(t_{j}) \bigr)+I_{j}\bigl(u(t_{j})\bigr)\neq0. $$

Pick \(v(t)= \prod_{i=0,i\neq j}^{m+1}(t-t_{i})\). We have

$$\begin{aligned}& \sum_{j=1}^{m}\bigl(-\Delta\Phi _{p}\bigl(u'(t_{j})\bigr)+I_{j} \bigl(u(t_{j})\bigr)\bigr)v(t_{j}) \\& \quad = \bigl(-\Delta\Phi_{p}\bigl(u'(t_{j}) \bigr)+I_{j}\bigl(u(t_{j})\bigr)\bigr)\prod _{i=0,i\neq j}^{m+1}(t_{j}-t_{i})\neq0. \end{aligned}$$

This is a contradiction. So u satisfies the impulsive condition in (1.1). Therefore, u is a solution of the system (1.1). □

Lemma 2.3

For any \(u(t)\in H\), there exists \(c= 2^{\frac{1}{q}} \max\{ T^{-\frac{1}{p}}, T^{\frac {1}{q}}\}\), \(\frac{1}{p}+\frac{1}{q}=1 \) such that

$$ \|u\|_{\infty}\leq c\|u\|, $$
(2.7)

where \(\|u\|_{\infty}=\max_{t\in[0,T]}|u(t)|\).

Proof

For any \(u(t)\in H\), it follows from the mean value theorem that

$$\biggl(\frac{1}{T}\biggr)\int_{0}^{T}u(s)\, ds=u(\tau) $$

for some \(\tau\in[0,T]\). Hence, for \(t \in[0,T]\), using the Hölder inequality,

$$\begin{aligned} \bigl\vert u(t)\bigr\vert =& \biggl\vert u(\tau)+\int _{\tau}^{t}u'(s)\, ds\biggr\vert \leq \bigl\vert u(\tau )\bigr\vert +\int_{0}^{T} \bigl\vert u'(s)\bigr\vert \, ds \\ \leq& \biggl(\frac{1}{T}\biggr)\biggl\vert \int_{0}^{T}u(s) \, ds\biggr\vert +T^{\frac {1}{q}}\biggl(\int_{0}^{T} \bigl\vert u'(s)\bigr\vert ^{p}\, ds \biggr)^{\frac{1}{p}} \\ \leq& T^{-{\frac{1}{p}}}\biggl(\int_{0}^{T}\bigl\vert u(s)\bigr\vert ^{p}\, ds\biggr)^{\frac {1}{p}}+T^{\frac{1}{q}} \biggl(\int_{0}^{T}\bigl\vert u'(s) \bigr\vert ^{p}\, ds\biggr)^{\frac{1}{p}} \\ \leq& 2^{\frac{1}{q}}\max \bigl\{ T^{-\frac {1}{p}},T^{\frac{1}{q}}\bigr\} \|u \|, \end{aligned}$$

and we obtain (2.7). □

To verify our main results, we need the following three critical points theorem. For the reader’s convenience we recall here the definition of the weak closure.

Suppose that \(E\subset X\). We denote \(\bar{E}^{w}\) as the weak closure of E, that is, \(x\in\bar{E}^{w}\), if there exists a sequence \(\{x_{n}\}\subset E \) such that \(f(x_{n})\rightarrow f(x) \) for every \(f\in X^{*}\).

Lemma 2.4

([13], Theorem 2.1)

Let X be a separable and reflexive real Banach space. \(\Phi:X\rightarrow R\) is a nonnegative continuously Gâteaux differentiable and sequentially weakly lower semicontinuous functional whose Gâteaux derivative admits a continuous inverse on  \(X^{*}\). \(J : X\rightarrow R \) is a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact. Assume that there exists \(x_{0}\in X\) such that \(\Phi(x_{0})=J(x_{0})=0\) and that:

  1. (i)

    \(\lim_{\|x\|\rightarrow+\infty}(\Phi(x)-\lambda J(x))=+\infty\) for all \(\lambda\in[0,+\infty)\).

Further, assume that there are \(r > 0\), \(x_{1} \in X \) such that:

  1. (ii)

    \(r<\Phi(x_{1})\).

  2. (iii)

    \(\sup_{x\in\overline{{\Phi^{-1}((-\infty,r))}}^{w}}J(x)<\frac {r}{r+\Phi(x_{1})}J(x_{1})\).

Then, for each

$$\lambda\in\Lambda_{1}=\biggl(\frac{\Phi(x_{1})}{J(x_{1})-\sup_{x\in\overline {{\Phi^{-1}((-\infty,r))}}^{w}}J(x)},\frac{r}{\sup_{x\in\overline {{\Phi^{-1}((-\infty,r))}}^{w}}J(x)} \biggr), $$

the equation

$$ \Phi'(x)-\lambda J'(x)=0 $$
(2.8)

has at least three solutions in X, and, moreover, for each \(h>1\), there exists an open interval

$$\Lambda_{2}\subseteq\biggl[0,\frac{hr}{r(J(x_{1})/\Phi(x_{1}))-\sup_{x\in \overline{{\Phi^{-1}((-\infty,r))}}^{w}}J(x)}\biggr) $$

and a positive real number σ such that, for each \(\lambda\in \Lambda_{2}\), (2.8) has at least three solutions in X whose norms are less than σ.

3 Main results

In this section, we state our main results and proofs.

Theorem 3.1

Assume that the following conditions hold:

(H1):

There exist two positive constants α, β with \(\alpha< c\beta T^{\frac{1}{p}}\), where c is a constant in (2.7), such that

$$\max_{(t,u)\in[0,T]\times[-\alpha,\alpha]}F(t,u)< \frac{\alpha ^{p}}{T(\alpha^{p}+T(c\beta)^{p}+c^{p}p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds)}\int_{0}^{T}F(t, \beta)\, dt. $$
(H2):

There exist constants \(a_{i}>0\) (\(i=1,2\)), \(M>0\), and \(0<\mu<p\) such that

$$F(t,u)\leq a_{1}|u|^{\mu}+a_{2} \quad \textit{for all } |u|\geq M. $$
(H3):

\(\int_{0}^{u}I_{j}(s)\, ds\geq0\), \(s=1,2,\ldots,m\), \(u>0\).

Moreover, put

$$\begin{aligned}& \varphi_{1} = \frac{c^{p}pT\max_{(t,u)\in[0,T]\times[-\alpha,\alpha ]}F(t,u)}{\alpha^{p}}, \\& \varphi_{2} = \frac{p(\int_{0}^{T}F(t,\beta)\, dt-T\max_{(t,u)\in [0,T]\times[-\alpha,\alpha]}F(t,u))}{T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds} \end{aligned}$$

and for each \(h>1\),

$$b= \frac{hT(\alpha\beta)^{p}+h\alpha^{p}p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}{p\alpha^{p}\int_{0}^{T}F(t,\beta)\, dt-c^{p}pT(T\beta ^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds)\max_{(t,u)\in [0,T]\times[-\alpha,\alpha]}F(t,u)}. $$

Then, for each

$$\lambda\in\Lambda_{3}=\biggl(\frac{1}{\varphi_{2}},\frac{1}{\varphi_{1}} \biggr), $$

the system (1.1) admits at least three solutions in H and, moreover, for each \(h>1\), there exist an open interval \(\Lambda_{4} \subseteq[0,b]\) and a positive real number σ such that, for each \(\lambda\in\Lambda_{4}\), the system (1.1) admits at least three solutions in H whose norms in H are less than σ.

Proof

Let the space X be the Sobolev space H. By the definitions in (2.1), it is very clear that Φ is a nonnegative Gâteaux differentiable and sequentially weakly lower semicontinuous functional whose Gâteaux derivative admits a continuous inverse on \(X^{*}\), and J is a continuously Gâteaux differentiable functional whose Gâteaux derivative is compact. It is clear that \(\Phi(0)=J(0)=0\).

Secondly, in view of the assumption (H2) and by computing, we have for any \(u\in H\), \(|u|\geq M\) and \(\lambda\geq0\),

$$\begin{aligned} \Phi(u)-\lambda J(u) =& \frac{1}{p}\|u\|^{p}+\sum _{j=1}^{m}\int_{0}^{u(t_{j})}I_{j}(s) \, ds-\lambda\int_{0}^{T}F\bigl(t,u(t)\bigr)\, dt \\ \geq& \frac{1}{p}\|u\|^{p}-\lambda a_{1}T\|u \|^{\mu}-\lambda a_{2}T. \end{aligned}$$

From \(0<\mu<p\), we obtain \(\lim_{\|u\|\rightarrow+\infty} \Phi (u)-\lambda J(u)=+\infty\), for all \(\lambda\in[0,+\infty)\). The condition (i) of Lemma 2.4 is satisfied.

Now, we choose

$$ u_{1}(t)=\beta>0,\quad t\in[0,T], r=\frac{\alpha^{p}}{c^{p}p}. $$

It is clear that \(u_{1}(t)\in H\), and

$$\begin{aligned}& \Phi(u_{1}) = \frac{1}{p}\|u_{1}\|^{p}+ \sum_{j=1}^{m}\int_{0}^{u_{1}(t_{j})}I_{j}(s) \, ds=\frac{T\beta^{p}}{p}+\sum_{j=1}^{m}\int _{0}^{\beta}I_{j}(s)\, ds, \\& J(u_{1}) = \int_{0}^{T}F \bigl(t,u_{1}(t)\bigr)\, dt=\int_{0}^{T} F(t,\beta)\, dt. \end{aligned}$$

In view of \(\alpha< c\beta T^{\frac{1}{p}}\), we have

$$\Phi(u_{1})\geq\frac{T\beta^{p}}{p}> \frac{\alpha^{p}}{c^{p}p}=r, $$

from which the assumption (ii) of Lemma 2.4 is obtained.

Thirdly, we verify that the assumption (iii) of Lemma 2.4 holds.

From Lemma 2.3, the estimate \(\Phi(u)\leq r\) implies that

$$ \bigl\vert u(t)\bigr\vert ^{p}\leq c^{p} \|u\|^{p}\leq c^{p} p\Phi (u)\leq c^{p} pr $$
(3.1)

for all \(t\in[0,T]\). By the definition of r and (3.1), we get

$$\begin{aligned} \bigl\vert u(t)\bigr\vert ^{p}\leq\alpha^{p} \end{aligned}$$

for all \(t\in[0,T]\). This implies

$$\Phi^{-1}(-\infty,r)\subseteq\bigl\{ u\in H,|u(t)|\leq\alpha,t\in[0,T] \bigr\} . $$

Thus for all \(u\in H\), we have

$$ \sup_{u\in\overline{{\Phi^{-1}((-\infty ,r))}}^{w}}J(u) =\sup_{u\in{\Phi^{-1}((-\infty,r))}}J(u)\leq T \max_{(t,u)\in [0,T]\times[-\alpha,\alpha]}F(t,u). $$
(3.2)

On the other hand, we have

$$ \frac{r}{r+\Phi(u_{1})}J(u_{1})=\frac {\alpha^{p}}{\alpha^{p}+T(c\beta)^{p}+c^{p}p \sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds }\int _{0}^{T}F(t,\beta)\, dt. $$
(3.3)

Therefore, by the assumption (H1), (3.2), and (3.3) we have

$$\sup_{u\in\overline{{\Phi^{-1}((-\infty,r))}}^{w}}J(u)< \frac {r}{r+\Phi(u_{1})}J(u_{1}) , $$

which shows the condition (iii) of Lemma 2.4 is satisfied.

Note that

$$ \frac{\Phi(u_{1})}{J(u_{1})-\sup_{u\in\overline {{\Phi^{-1}((-\infty,r))}}^{w}}J(u)}\leq\frac{T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}{p(\int_{0}^{T}F(t,\beta)\, dt-T\max_{(t,u)\in[0,T]\times[-\alpha,\alpha]}F(t,u))} $$
(3.4)

and

$$ \frac{r}{\sup_{u\in\overline {{\Phi^{-1}((-\infty,r))}}^{w}}J(u)}\geq\frac{\alpha^{p}}{c^{p}pT\max_{(t,u)\in[0,T]\times[-\alpha,\alpha]}F(t,u)}. $$
(3.5)

By the assumption (H1) we have

$$ T\max_{(t,u)\in[0,T]\times[-\alpha,\alpha]}F(t,u)< \frac {\alpha^{p}}{\alpha^{p}+T(c\beta)^{p}+c^{p}p\sum_{j=0}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}\int _{0}^{T}F(t,\beta)\, dt. $$
(3.6)

This implies

$$ \frac{c^{p}pT\max_{(t,u)\in[0,T]\times[-\alpha ,\alpha]}F(t,u)}{\alpha^{p}}< \frac{p(\int_{0}^{T}F(t,\beta)\, dt-T\max_{(t,u)\in[0,T]\times[-\alpha,\alpha]}F(t,u))}{T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}. $$
(3.7)

We set

$$\begin{aligned}& \varphi_{1} = \frac{c^{p}pT\max_{(t,u)\in[0,T]\times [-\alpha,\alpha]}F(t,u)}{\alpha^{p}}, \\& \varphi_{2} = \frac{p(\int_{0}^{T}F(t,\beta)\, dt-T\max_{(t,u)\in [0,T]\times[-\alpha,\alpha]}F(t,u))}{T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}. \end{aligned}$$

By (3.7), we have \(\varphi_{2}>\varphi_{1}\). By (3.4), (3.5), we apply Lemma 2.4 and find that, for each \(\lambda\in\Lambda_{3}=(\frac{1}{\varphi_{2}},\frac{1}{\varphi_{1}})\), the system (1.1) admits at least three solutions in H.

For each \(h>1\), we take into account that

$$\begin{aligned}& \frac{hr}{r(J(u_{1})/\Phi(u_{1}))-\sup_{u\in\overline{{\Phi ^{-1}((-\infty,r))}}^{w}}J(u)} \\& \quad \leq\frac{hT(\alpha\beta)^{p}+h\alpha^{p}p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}{p\alpha^{p}\int_{0}^{T}F(t,\beta )\, dt-c^{p}pT(T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds)\max_{(t,u)\in[0,T]\times[-\alpha,\alpha]}F(t,u)}=b. \end{aligned}$$

Taking the condition (H1) into account, it implies that \(b>0\). Then from Lemma 2.4 it follows that, for each \(h>1\), there exist an open interval \(\Lambda_{4}\subseteq[0,b]\) and a real number \(\sigma>0\), such that, for \(\lambda\in\Lambda_{4}\), the system (1.1) admits at least three solutions in H whose norms in H are less than σ. □

We conclude this section with considering the following problem, which is a particular case of the problem (1.1), i.e. the equation is an autonomous system. We have

$$ \left \{ \begin{array}{l} -(\Phi_{p}(u'(t)))'+\Phi_{p}(u(t))=\lambda f(u(t)), \quad t\neq t_{j},t\in[0, T], T>0, \\ \Delta\Phi_{p}(u'(t_{j}))=I_{j}(u(t_{j})),\quad j=1,2,\ldots,m, \\ u'(0)=u'(T)=0. \end{array} \right . $$
(3.8)

Corollary 3.2

Assume that the following conditions hold:

(H′1):

There exist two positive constants α, β with \(\alpha< c\beta T^{\frac{1}{p}}\), such that

$$\max_{u\in[-\alpha,\alpha]}F(u)< \frac{\alpha^{p}}{\alpha ^{p}+T(c\beta)^{p}+c^{p}p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}F(\beta). $$
(H′2):

There exist constants \(a'_{i}>0\) (\(i=1, 2\)), \(M>0\), and \(0<\mu <p\) such that

$$F(u)\leq a'_{1}|u|^{\mu}+a'_{2} \quad \textit{for all } |u|\geq M. $$

Moreover, put

$$\begin{aligned}& \widetilde{\varphi}_{1} = \frac{c^{p}pT\max_{u\in[-\alpha,\alpha ]}F(u)}{\alpha^{p}}, \\& \widetilde{\varphi}_{2} = \frac{p T(F(\beta)-\max_{u\in[-\alpha ,\alpha]}F(u))}{T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}, \end{aligned}$$

and for each \(h>1\),

$$b=\frac{hT(\alpha\beta)^{p}+h\alpha^{p}p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}{pT(\alpha^{p}F(\beta)-c^{p}(T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds)\max_{(u)\in[-\alpha,\alpha]}F(u))}. $$

Then, for each

$$\lambda\in\Lambda_{5}=\biggl(\frac{1}{\widetilde{\varphi}_{2}}, \frac {1}{\widetilde{\varphi}_{1}} \biggr), $$

the system (3.8) admits at least three solutions in H and, moreover, for each \(h>1\), there exist an open interval \(\Lambda_{6} \subseteq[0,b]\) and a positive real number σ such that, for each \(\lambda\in\Lambda_{6}\), the system (3.8) admits at least three solutions in H whose norms in H are less than σ.

Example 3.1

Consider the Neumann boundary value problem

$$ \left \{ \begin{array}{l} -u''(t)+u(t)=\lambda f(u(t)), \quad t\neq t_{1},t \in[0, 1], \\ \Delta u'(t_{1})=\frac{1}{10}u(t_{1}),\quad t_{1}=\frac{1}{2}, \\ u'(0)=u'(1)=0, \end{array} \right . $$
(3.9)

where

$$ f\bigl(u(t)\bigr)=\left \{ \begin{array}{l@{\quad}l} e^{u},& u\leq4, \\ u^{\frac{1}{2}}+e^{4}-2,&u>4. \end{array} \right . $$

It is clear that

$$ F\bigl(u(t)\bigr)=\left \{ \begin{array}{l@{\quad}l} e^{u}-1, &u\leq4, \\ \frac{2}{3}u^{\frac{3}{2}}+(e^{4}-2)u+\frac{5}{3}-3e^{4},&u>4, \end{array} \right . $$

and \(c=\sqrt{2}\), \(p=2\), \(T=1\). Let \(\alpha=1\), \(\beta=8\). Direct calculations give

$$\begin{aligned}& \max_{u\in[-1,1]}F(u)=e-1\approx1.718, \\& \frac{\alpha^{p}}{\alpha^{p}+T(c\beta)^{p}+c^{p}p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}F(\beta)>\frac {1}{129+12.8}\times266.47\approx1.88, \\& \widetilde{\varphi}_{1} = \frac{c^{p}pT\max_{u\in[-\alpha,\alpha ]}F(u)}{\alpha^{p}}\approx6.872, \\& \widetilde{\varphi}_{2} = \frac{p T(F(\beta)-\max_{u\in[-\alpha ,\alpha]}F(u))}{T\beta^{p}+p\sum_{j=1}^{m}\int_{0}^{\beta}I_{j}(s)\, ds}\approx7.375. \end{aligned}$$

All conditions of Corollary 3.2 are satisfied. So the problem (3.9) admits at least three solutions provided that \(\lambda\in (0.136,0.146)\).