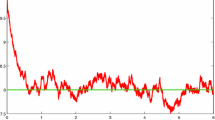
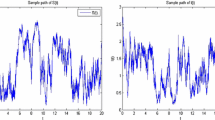
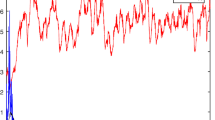
Abstract
In this paper, we introduce stochasticity into a multigroup SIS model. We present the sufficient condition for the exponential extinction of the disease and prove that the noises significantly raise the threshold of a deterministic system. In the case of persistence, we prove that there exists an invariant distribution which is ergodic.
Similar content being viewed by others
1 Introduction
Mathematical models have become important tools in analyzing the spread and control of infectious diseases. In many epidemiological models it is assumed that the population being considered is uniform and homogeneously mixing. However, when dealing with a heterogeneous population, it is appropriate to divide the whole population into subpopulations, each of which is homogeneous. So far a lot of research has been done on various forms of multigroup models, see, e.g., [1–11].
Lajmanovich and Yorke [12] proposed a deterministic model for the spread of gonorrhea. Since the spread of gonorrhea in a population is highly nonuniform, they developed a deterministic SIS (susceptible-infective-susceptible) model with n groups. Because of there being no immunes and negligibly few incubating the disease, they assume the population of every subpopulation is constant in size, i.e. \(S_{k}+I_{k}=N_{k}\), where \(S_{k}\), \(I_{k}\) denote the susceptible and infective population at time t in the kth group, respectively, and \(N_{k}\) the total size of the population of kth group. Then the multigroup SIS model takes the form of
where \(\alpha_{k}\) is the recovery rate, \(\beta_{kj}\) the contact rate of the kth group’s susceptibles with the jth group’s infectives. Here \(\alpha_{k}\), \(\beta_{kj}\), and \(N_{k}\) are positive constants.
Since gonorrhea is in essence a nonseasonal disease with less than a 10 percent seasonal component in the variation [13], the authors [12] give the model (1.1) time-independent coefficients. However, also according to [13], the probability of one susceptible contacting one infective does vary with the time of year, although this does not significantly fluctuate. For more reality, we introduce randomness into the model (1.1) by replacing the parameters \(\beta_{kk}\) by \(\beta_{kk}\rightarrow\beta_{kk}+\sigma_{k}\, dB_{k}(t)\), where \(B_{k}(t)\), \(k=1,2,\ldots,n\) are standard Brownian motions with \(B_{k}(0)=0\), and the intensities of white noises \(\sigma^{2}_{k}>0\). Then the stochastic version of the model (1.1) takes the following form:
Ideally, all of the transmission coefficients \(\beta_{kj}\) should suffer from white noise. If we really do that, the solution will be very sensitive to white noise. The solution may be negative or explosive. But for a population system, we always expect there is a positive solution. This is the main reason why we only introduce white noise into \(\beta_{kk}\), \(k=1,2,\ldots,n\).
Recently, Gray et al. [14] discussed a stochastic SIS model (1.2) with one group. They proved that this SIS model has a unique global positive solution and establish conditions for the extinction and persistence of the disease. In the case of persistence they showed the existence of a stationary distribution and derived expressions for its mean and variance.
The aim of this paper is to study the asymptotical behavior of the solutions of system (1.2). The rest of this paper is organized as follows. In Section 2, we show that system (1.2) has a unique nonnegative solution. In Section 3, we present the sufficient condition for the exponential extinction of the disease. Section 4 focuses on the persistence of the disease. We show there is a stationary distribution for system (1.2) and it is ergodic.
Throughout this paper, let be a complete probability space with a filtration satisfying the usual conditions (i.e. it is right continuous and contains all P-null sets).
In general, consider the d-dimensional stochastic differential equation,
with initial value \(x(t_{0})=x_{0}\in\mathbb{R}^{d}\). Define the differential operator L associated with (1.3) by
By Itô’s formula, if \(x(t)\in R^{d}\), then \(dV(x(t),t)=LV(x(t),t)\, dt+V_{x}(x(t),t)g(x(t),t)\, dB(t)\).
2 Existence and uniqueness of positive solution
To investigate the dynamical behavior, the first concern is whether the solution has a global existence. Moreover, for an epidemics model, whether the solution is nonnegative is also considered, that is, we need to show the solution is global and nonnegative. In this section, we show global existence and uniqueness of a positive solution of system (1.2). From now on, we denote the solution \((I_{1}(t), I_{2}(t),\ldots, I_{n}(t))\) of system (1.2) as \(Y(t)\). Denote
Theorem 2.1
If \((\beta_{kj})_{n\times n}\) is irreducible, then for any initial value \(Y(0)\in\Gamma\), there is a unique solution \(Y(t)\) of system (1.2) on \(t\geq0\), and the solution will remain in Γ with probability 1.
Proof
Since the coefficients of system (1.2) satisfy the local Lipschitz condition, there is a unique local solution \(Y(t)\in\Gamma\) on \(t\in[0, \tau _{e})\), where \(\tau_{e}\) is the explosion time. To show this solution is global, we need to show that \(\tau_{e}=+\infty\) a.s. Define \(C^{2}\)-function \(V(Y):\Gamma\to R_{+}\) by
By direct calculation, we get
By using similar arguments to Theorem 3.1 of Gray et al. [14], we get \(\tau_{e}=+\infty\) a.s. This completes the proof. □
Remark 2.1
An \(n\times n\) matrix \((a_{ij})\) is irreducible if for any nonempty subset S of \(\{1,\ldots,n\}\) with a nonempty complement \(S'\), there exist i in S and j in \(S'\) such that \(a_{ij}\neq0\).
Remark 2.2
From the proof of Theorem 2.1, we obtain \(LV\leq M\). Let \(\tilde {V}=V+M\). Then \(L\tilde{V}\leq\tilde{V}\) and it is clear that \(\inf_{Y\in\Gamma\setminus D_{k}}\tilde{V}(Y)\to\infty\) as \(k\to\infty \), where \(D_{k}=(\frac{1}{k},N_{1}-\frac{1}{k})\times(\frac {1}{k},N_{2}-\frac{1}{k})\times\cdots\times(\frac{1}{k},N_{n}-\frac {1}{k})\). Hence, by Remark 2 of Theorem 4.1 of Hasminskii [15], p.86, we find that the solution \(Y(t)\) is a homogeneous Markov process in Γ.
3 Exponential extinction of infectious disease
It is clear that \(P_{0}= (0,0,\ldots,0 )\) is the disease-free equilibrium of system (1.2). For system (1.1), \(P_{0}\) is globally stable if \({\mathcal{R}}_{0}\leq1\). Hence, it is interesting to study the disease-free equilibrium for controlling the infectious disease. In this section, we present sufficient conditions for the disease to extinct exponentially for system (1.2).
Theorem 3.1
Assume \((\beta_{kj})_{n\times n}\) is irreducible. If \(\beta _{kk}/N_{k}\geq\sigma_{k}^{2}\), \(k=1,2,\ldots,n\) and
then the solution \(Y(t)\) of system (1.2) with initial value \(Y(0)\in\Gamma\) will exponentially tend to \(P_{0}\) almost surely. Here \({\mathcal{R}}_{0}=\rho(M_{0})\) (the spectral radius of \(M_{0}\)), \(M_{0}= ( \beta_{kj}N_{k}/\alpha_{k} )_{n\times n}\).
Proof
Since \((\beta_{kj})_{n\times n}\) is irreducible, \(\beta_{kj}\geq 0\), and \(\sigma_{k}>0\), \(k,j=1,2,\ldots,n\), \(M_{0}\) is also nonnegative and irreducible. By Theorem 1.4 of [16], p.27, there is a left eigenvector of \(M_{0}\) corresponding to \(\rho(M_{0})\), which is denoted as \((\omega_{1},\omega_{2},\ldots,\omega_{n})\) and \(\omega_{k}>0\), \(k=1,2,\ldots,n\), i.e.
Define the \(C^{2}\)-function \(V:\Gamma\to R_{+}\) by \(V(Y)=\sum_{k=1}^{n}a_{k}I_{k}\), \(a_{k}=\omega_{k}/\alpha_{k}\). By Itô’s formula, we compute
where
Here \(H_{1}:=\frac{1}{V}\sum_{k=1}^{n} a_{k} [\sum_{j=1}^{n} \beta_{kj} N_{k} I_{j}-\alpha_{k}I_{k} ] \), \(H_{2}:=-\frac{1}{V}\sum_{k=1}^{n} a_{k}\beta_{kk} I_{k}^{2} -\frac{\sum_{k=1}^{n} a_{k}^{2}\sigma_{k}^{2}(N_{k}-I_{k})^{2}I_{k}^{2}}{2V^{2}}\).
In view of the definition of \(a_{k}\) and (3.2), we have
By the condition \(\beta_{kk}\geq\sigma_{k}^{2}N_{k}\), \(k=1,2,\ldots,n\), we have
Then \(L(\log V)\leq m_{1}+m_{2}\), which combined with (3.3) yields
By the strong law of large numbers (Lemma 2.6 in [17]), we get
Hence, \(\lim_{t\to\infty}\frac{\log V}{t}\leq m_{1}+m_{2}\) a.s. Besides, (3.1) implies \(m_{1}+m_{2}<0\). Thus, the proof of Theorem 3.1 is complete. □
Remark 3.1
Theorem 3.1 tells us the disease will die out if
and the noise intensity is not large. In [12], the disease will extinct when \({\mathcal{R}}_{0}\leq1\). Therefore, the conditions for the disease to become extinct in system (1.2) are weaker than the corresponding deterministic model.
4 Ergodicity of system (1.2)
For a deterministic system, we always discuss the global attractivity of the positive equilibrium of the system. However, there is no positive equilibrium for system (1.2). In this section, we show there is a stationary distribution for system (1.2) when the white noise is small, which in turn implies the stability in stochastic sense. To begin with, we present a well-known result, due to Hasminskii [15].
Let \(X(t)\) be a homogeneous Markov process in \(E_{l}\) (\(E_{l}\) denotes the Euclidean l-space) described by the stochastic equation
The diffusion matrix is
Assumption B
There exists a bounded domain \(U\subset E_{l}\) with regular boundary, having the following properties:
-
(B.1)
In the domain U and some neighborhood thereof, the smallest eigenvalue of the diffusion matrix \(A(x)\) is bounded away from zero.
-
(B.2)
If \(x\in E_{l}\setminus U\), the mean time τ at which a path issuing from x reaches the set U is finite, and \(\sup_{x\in K}E_{x}\tau<\infty\) for every compact subset \(K\subset E_{l}\).
Lemma 4.1
If (B) holds, then the Markov process \(X(t)\) has a stationary distribution \(\mu(\cdot)\). Let \(f(\cdot)\) be a function integrable with respect to the measure μ. Then
Theorem 4.1
Assume \((\beta_{kj})_{n\times n}\) is irreducible and \({\mathcal{R}}_{0}=\rho(M_{0})>1\). If
then, for any initial value \(Y(0)\in\Gamma\), there is a stationary distribution \(\mu(\cdot)\) for system (1.2) and it has the ergodic property, where \(M_{0}= ( \beta_{kj}N_{k}/\alpha_{k} )_{n\times n}\), \(P^{*}=(I_{1}^{*},I_{2}^{*}\cdots,I_{n}^{*})\in\operatorname{int}\Gamma\) is the endemic equilibrium of system (1.1), and the \(\bar {c}_{k}\), \(k=1,2,\ldots, n\) denote the cofactor of the kth diagonal element of \(L_{B}\), \(B=(\bar{\beta}_{kj})_{n\times n}=(I_{j}^{*}(N_{k}-I_{k}^{*})\beta_{kj})_{n\times n}\); \(L_{B}\) is defined as
Proof
Since \({\mathcal{R}}_{0}>1\), from Theorem 3.1 of [12], system (1.1) has a unique endemic equilibrium \(P^{*}\in\operatorname{int}\Gamma\). Then
Let
where
By direct calculation, we get
Obviously,
Hence,
where \(\bar{\beta}_{kj}:=I_{j}^{*}(N_{k}-I_{k}^{*})\beta_{kj}\). Consequently,
By Theorem 2.3 of Li and Shuai [8], we know
Besides, note that \(a-1-\log a\geq0\) for \(a>0\), then
Successively substituting (4.4) and (4.3) into (4.2) yields
The condition (4.1) implies that the ellipsoid
lies entirely in Γ. We can take U to be a neighborhood of the ellipsoid with \(\bar{U}\subseteq\Gamma\), so for \(Y\in\Gamma\setminus U\), \(LV\leq-K\) (K is a positive constant), which implies that the condition (B.2) in Lemma 4.1 is satisfied (see Chapter 3, p.103 of [18]).
The diffusion matrix of system (1.2) is written
For any bounded domain D with \(\bar{D}\subset\Gamma\) there is \(M=\min\{\sigma_{i}^{2}(N_{i}-I_{i})^{2}I_{i}^{2}, i=1,2,\ldots,n, Y\in\bar{D}\}>0 \) such that \(\sum_{i,j=1}^{n}a_{ij}\xi_{i}\xi_{j} =\sum_{i=1}^{n}\sigma_{i}^{2}(N_{i}-I_{i})^{2}I_{i}^{2}\xi_{i}^{2}\geq M\|\xi^{2}\| \) for all \(Y\in\bar{D}\), \(\xi\in R^{n}\), which implies that the condition (B.1) is also satisfied (refer to [19], p.1163 for details). Therefore, by Lemma 4.1, system (1.2) has a stationary distribution \(\mu(\cdot)\) and it is ergodic. □
Remark 4.1
Theorem 4.1 shows that, under some conditions imposed on the parameters, if the noise intensity is small, there exists a stationary distribution for system (1.2), which reveals that the disease will prevail.
5 Conclusions
In this paper, we investigate a multigroup SIS model with the effect of environmental white noise. We obtain the sufficient condition for the extinction of the disease, and we obtain the criteria for the existence of the invariant distribution of system (1.2). Some interesting topics deserve further investigation. For instance, the coefficients of stochastic differential equations can be modeled by fuzzy sets, and this leads to stochastic differential equations with fuzziness [20, 21]. We leave it for future investigation.
References
Beretta, E, Capasso, V: Global stability results for a multigroup SIR epidemic model. In: Hallam, TG, Gross, LJ, Levin, SA (eds.) Mathematical Ecology, pp. 317-342. World Scientific, Singapore (1986)
Feng, Z, Huang, W, Castillo-Chavez, C: Global behavior of a multi-group SIS epidemic model with age structure. J. Differ. Equ. 218, 292-324 (2005)
Guo, H, Li, MY, Shuai, Z: Global stability of the endemic equilibrium of multigroup SIR epidemic models. Can. Appl. Math. Q. 14, 259-284 (2006)
Guo, H, Li, MY, Shuai, Z: A graph-theoretic approach to the method of global Lyapunov functions. Proc. Am. Math. Soc. 136, 2793-2802 (2008)
Hethcote, HW: An immunization model for a heterogeneous population. Theor. Popul. Biol. 14, 338-349 (1978)
Huang, W, Cooke, KL, Castillo-Chavez, C: Stability and bifurcation for a multiple-group model for the dynamics of HIV/AIDS transmission. SIAM J. Appl. Math. 52, 835-854 (1992)
Koide, C, Seno, H: Sex ratio features of two-group SIR model for asymmetric transmission of heterosexual disease. Math. Comput. Model. 23, 67-91 (1996)
Li, MY, Shuai, Z: Global-stability problem for coupled systems of differential equations on networks. J. Differ. Equ. 248, 1-20 (2010)
Sun, R: Global stability of the endemic equilibrium of multigroup SIR models with nonlinear incidence. Comput. Math. Appl. 60, 2286-2291 (2010)
Yuan, Z, Wang, L: Global stability of epidemiological models with group mixing and nonlinear incidence rates. Nonlinear Anal., Real World Appl. 11, 995-1004 (2010)
Yuan, Z, Zou, X: Global threshold property in an epidemic model for disease with latency spreading in a heterogeneous host population. Nonlinear Anal., Real World Appl. 11, 3479-3490 (2010)
Lajmanovich, A, Yorke, JA: A deterministic model for gonorrhea in a nonhomogeneous population. Math. Biosci. 28, 221-236 (1976)
Cornelius, CE III: Seasonality of gonorrhea in the United States. H.S.M.H.A. Health Rep. 86, 157-160 (1971)
Gray, A, Greenhalgh, D, Hu, L, Mao, X, Pan, J: A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 71, 876-902 (2011)
Hasminskii, RZ: Stochastic Stability of Differential Equations. Monographs and Textbooks on Mechanics of Solids and Fluids: Mechanics and Analysis, vol. 7. Sijthoff & Noordhoff, Alphen aan den Rijn (1980)
Berman, A, Plemmons, RJ: Nonnegative Matrices in the Mathematical Sciences. Academic Press, New York (1979)
Mao, X: Stochastic Differential Equations and Applications. Horwood, Chichester (1997)
Gard, TC: Introduction to Stochastic Differential Equations. Dekker, New York (1988)
Zhu, C, Yin, G: Asymptotic properties of hybrid diffusion systems. SIAM J. Control Optim. 46, 1155-1179 (2007)
Malinowski, M: Some properties of strong solutions to stochastic fuzzy differential equations. Inf. Sci. 252, 62-80 (2013)
Malinowski, M, Agarwal, R: On solutions to set-valued and fuzzy stochastic differential equations. J. Franklin Inst. (2014). doi:10.1016/j.jfranklin.2014.11.010
Acknowledgements
The work was supported by NSFC of China (No. 11371085), the PhD Programs Foundation of Ministry of China (No. 200918) and Nature Science Foundation of Changchun Normal University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors have contributed to the manuscript on an equal basis. All authors read and approved the final manuscript.
Rights and permissions
Open Access This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.
About this article
Cite this article
Fu, J., Han, Q., Lin, Y. et al. Asymptotic behavior of a multigroup SIS epidemic model with stochastic perturbation. Adv Differ Equ 2015, 84 (2015). https://doi.org/10.1186/s13662-015-0406-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0406-x