Abstract
In this paper, we study a discrete plant virus disease model with roguing and replanting which is derived from the continuous case by using the well-known backward Euler method. The positivity of solutions with positive initial conditions is obtained. By applying analytic techniques and constructing a discrete Lyapunov function, we obtain the result that the disease-free equilibrium is globally attractive if \(R_{0}\leq1\), and the disease is permanent if \(R_{0}>1\). Numerical simulations show that the main theoretical results are true.
Similar content being viewed by others
1 Introduction
Plants not only provide people with essential means of subsistence, but also they offer other creatures food and shelter. However, plants often suffer from multiple adverse factors in the process of growth, especially viruses, which causes the decline of plants yield and quality, even famine and social unrest.
It is well known that many serious diseases of crop plants are caused by viruses. For severe cases, plant diseases have caused large-scale damage to various crops, which resulted in a diminished output in whole regions; for instance, cocoa swollen shoot in Ghana [1, 2] and banana bunchy top in Australia [3–5]. When a crop is widely planted in a new area, plant disease prevention usually becomes important. In most cases, we rogue (remove) infected plants as a control strategy when disease breaks out. Since 1946, 190 million infected trees have been removed in Ghana [6]. In addition, we can also rogue not only visibly infected plants but also other neighboring plants which do not yet show symptoms [2, 7], but this measure may be unpopular with farmers since it involves removal of apparently healthy plants which may still be highly productive [8].
Recently, more and more attention has been paid to the discrete-time epidemic models. In [9], the authors pointed out that it is more direct, more convenient, and more accurate to describe a disease by using the discrete-time models than the continuous-time models since the statistic data about the disease situation is collected by day, week, month or year. Furthermore the discrete-time models have more wealthy dynamical behaviors, such as the discrete-time epidemic models, which have bifurcations, chaos, and other more complex dynamical behaviors. Many important and interesting results can be found in [10–22] and the references cited therein.
We know that there are usually two methods to construct discrete-time epidemic models: (i) by making use of the compartment model theory and the property of the epidemic disease, (ii) by using techniques (the backward Euler scheme, the forward Euler scheme, and Mickens’ nonstandard discretization) to discretize a continuous-time epidemic model. Until now, some studies have been done on discrete-time epidemic models by using the two methods mentioned above (see [9–33]). For example, by applying Mickens’ nonstandard discretization, Wang et al. [9] discussed dynamical behaviors for a class of discrete SIRS models with disease courses. Muroya et al. [22] proposed a discrete epidemic model for a disease with immunity and latency spreading in a heterogeneous host population, which was derived from the continuous case by using the well-known backward Euler method, and they obtained the result of the global stability of the disease-free equilibrium and the endemic equilibrium. According to the first method, Teng et al. [25] constructed a discrete SIS epidemic model with stage structure and standard incident rate and established sufficient conditions for the permanence and extinction of the disease of the model. Moreover, using the method of linearization, the local asymptotic stability of the endemic equilibrium was studied. Applying the forward Euler scheme, Hu et al. [30] constructed a discrete SIR epidemic model, and they studied the local stability of the disease-free equilibrium and the endemic equilibrium. In addition, numerical simulations showed plentiful and complex dynamical behaviors including bifurcations.
In this paper, we use the well-known backward Euler method to discretize a continuous-time plant virus disease model with roguing and replanting which is investigated in [8]. Our main purpose is to study dynamical behaviors of the model.
The organization of this paper is as follows. In Section 2, the model description and some preliminaries are given. Section 3 deals with the global attractivity of disease-free equilibrium of the model. In Section 4, the criterion on the permanence of the disease of the model is stated and proved. In Section 5, the numerical simulations are provided to illustrate the validity of our theoretical results. Lastly, a brief discussion is given in Section 6.
2 Model formulation and preliminaries
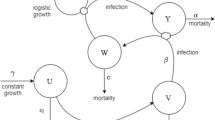
In 1994, Chan and Jeger [8] studied the following continuous-time plant virus disease model with roguing and replanting.
where \(S(t)\), \(E(t)\), \(I(t)\), and \(R(t)\) denote the numbers of susceptible, latently infected, infectious, and post-infectious individuals at time t, respectively. μ is the natural mortality, which is not attributed to disease and is common to each category. α is an additional mortality in the post-infectious category owing to the cumulative effect of the disease. \(k_{i}\) (\(i=1,2,3\)) are the conversion rates of the disease’s progression from susceptible to latent, from latent to infectious, and from infectious to post-infectious, respectively. K is the maximum plant population size, defined in terms of agronomic considerations. It is assumed that the actual total population size is presented by N (\(N=S+E+I+R\)), recruitment to the population is by replanting at a rate proportional r to the difference between the actual number of plants present, N, and the maximum population size, K. A qualitative analysis of this model presents the stable dynamics and threshold conditions for distinguishing the disease’s extinction or permanence.
By applying a variation of backward Euler scheme discretetization, we propose the following discrete plant virus disease model, which is derived from system (2.1).
Considering the biological background of model (2.2), therefore, any solution of model (2.2) satisfies the following initial condition:
Lemma 2.1
Any solution \((S(n),E(n),I(n),R(n))\) of model (2.2) with initial condition (2.3), is positive for any \(n>0\) and ultimately bounded.
Proof
Suppose that \((S(n),E(n),I(n),R(n))\) is any solution of model (2.2) with initial condition (2.3); apparently model (2.2) is equivalent to the following iteration system:
Next, we will prove the positivity of solution by using the inductive method. When \(n=0\), we have
and
From (2.5)-(2.8) we see that if only \(E(1)\) is confirmed, then \(I(1)\), \(R(1)\), \(N(1)\), and \(S(1)\) will be afterwards confirmed.
Firstly, we prove that if \(E(1)>0\) and then \(I(1)>0\), \(R(1)>0\), and \(S(1)>0\). From (2.6), we directly obtain \(I(1)>0\) when \(E(1)>0\). Secondly, from \(I(1)>0\) we further obtain the result that \(R(1)>0\).
Let \(x=S(1)\), from (2.6) and (2.8) we obtain
where \(N(1)=x+E(1)+I(1)+R(1)\). It is obvious that \(\Phi(x)\) is monotonically increasing for \(x\geq0\) when \(E(1)>0\). Because \(\Phi(0)=-S(0)-r(K-I(1)-E(1)-R(1))<0\) and \(\lim_{x\rightarrow+ \infty}\Phi(x)=+\infty\), we obtain the result that \(\Phi(x)=0\) has a unique positive solution \(\bar{x}\). Hence, we finally have \(S(1)=\bar{x}>0\). Moreover, we also have \(N(1)=S(1)+E(1)+I(1)+R(1)>0\).
Let \(y=E(1)\), then from (2.5)-(2.7), we see that y satisfies the following equation:
where
and
where
\(\Psi(y)\) is a quadratic equation in y. Let us rewrite it in the form
with
Here,
Obviously, \(A>0\), \(B>0\), \(C>0\), \(D>0\), \(F>0\), \(a>0\).
By the characteristic of a quadratic equation, we know that if \(c<0\), then \(\Psi(y)=0\) has a unique positive solution \(\overline{y}\in(0,+\infty)\).
Now, we prove that \(c<0\). By calculating, we obtain the result that \(c<0\).
From the above discussions we see that \(\Psi(y)=0\) has a unique positive solution \(\overline{y}\in(0,+\infty)\). Let \(E(1)=\overline {y}\). We also have \(I(1)>0\), \(R(1)>0\), and \(S(1)>0\). Therefore, the positivity of \(S(1)>0\), \(I(1)>0\), and \(R(1)>0\) is finally obtained.
When \(n=1\), we obtain
and
Besides, by arguments similar to the above, we also can obtain the result that \(E(2)>0\), \(I(2)>0\), \(R(2)>0\), and \(S(2)>0\). Finally, by using induction, we can prove that \(S(n)>0\), \(E(n)>0\), \(I(n)>0\), and \(R(n)>0\) for all \(n>0\).
In the following we will prove that the solution of model (2.2) is ultimately bounded. From the fourth equation of model (2.4), we have
It is well known that the auxiliary equation
has a globally asymptotically stable equilibrium \(U^{*}=\frac{rK}{r+\mu }\), since by the comparison principle of the difference equations, we have \(\limsup_{n\rightarrow \infty}N(n)\leq\frac{rK}{r+\mu}\). In other words, \((S(n),E(n),I(n),R(n))\) is ultimately bounded. This completes the proof. □
Define \(\phi(p,n)=pE(n)-I(n)\) and \(\varphi(p)=\frac{pk_{1}r}{r+\mu }+k_{3}- (1+\frac{1}{p} )k_{2}\), where \(p>0\) is a constant and \(n>0\) is an integer.
Lemma 2.2
If there exists a constant \(p>0\) such that \(\varphi(p)\leq0\), then there exists an integer \(N_{1}>0\) such that either \(\phi(p,n)\geq0\) for all \(n\geq N_{1}\) or \(\phi(p,n)\leq 0\) for all \(n\geq N_{1}\).
Proof
Actually, we assume that the conclusion does not hold, then we find that \(\phi(p,n)\) oscillates about 0. Hence, for any \(N_{1}>0\), there exists an integer \(q\geq N_{1}\) such that \(\phi(p,q)<0\) and \(\phi(p,q+1)\geq0\). Thus we have
and
Substituting (2.9) into the above inequality, we further have
that is, \(pE(q+1)\varphi(p)>0\). From Lemma 2.1, we have \(E(q+1)>0\), and hence \(\varphi(p)>0\), which leads to a contradiction. This completes the proof. □
3 Global attractivity of disease-free equilibrium
In this section, we are going to discuss the global attractivity of the disease-free equilibrium of model (2.2). In order to obtain the existence of a disease-free equilibrium and an endemic equilibrium of model (2.2), we introduce a constant
It is easy to verify that model (2.2) has only a disease-free equilibrium \(P_{0}(\frac{rK}{\mu+r},0,0,0)\) when \(R_{0}\leq1\), and it has a unique endemic equilibrium \(P_{*}(S_{*},E_{*},I_{*},R_{*})\) when \(R_{0}>1\), except for \(P_{0}\), where
Therefore, we can claim that \(R_{0}\) is the basic reproduction number of model (2.2).
Theorem 3.1
Disease-free equilibrium \(P_{0}\) of model (2.2) is globally attractive iff \(R_{0}\leq1\).
Proof
The proof of necessity is simple, we hence omit it here. Now, we prove the sufficiency. When \(R_{0}<1\), we have
and
Therefore, there exists a constant \(p>\frac{k_{2}}{\mu+k_{3}}\) with p sufficiently close to \(\frac{k_{2}}{\mu+k_{3}}\) such that \(\varphi(p)<0\) and
When \(R_{0}=0\), we have
and
Hence, for the constant \(p=\frac{k_{2}}{\mu+k_{3}}\), we have \(\varphi (p)=0\), \(\frac{k_{2}}{p}-(\mu+k_{3})=0\), and \(\frac{rk_{1}p}{\mu+r}-(\mu+k_{2})=0\). To sum up, we see that, if \(R_{0}\leq 1\), there always exists a constant \(p>0\) such that
and \(\varphi(p)\leq0\). Therefore, from the point of view of Lemma 2.2, for \(R_{0}\leq1\), we only need to consider the following two cases.
Case 1. \(pE(n)\leq I(n)\) for \(n\geq N_{1}\).
Case 2. \(pE(n)\geq I(n)\) for \(n\geq N_{1}\).
First of all, we consider Case 1. From the third equation of model (2.2), for all \(n\geq N_{1}\), we have
Then (3.3) implies that \(I(n)\) is decreasing for \(n\geq N_{1}\). Therefore, \(\lim_{n\rightarrow\infty}I(n)=:I^{*}\) exists and \(I^{*}\geq0\). Further the second equation of model (2.4) shows that \(\lim_{n\rightarrow\infty}E(n)=:E^{*}\) exists and \(E^{*}=\frac{\mu+k_{3}}{k_{2}}I^{*}\).
For any constant \(\varepsilon>0\) there exists an integer \(N_{\varepsilon}>0\) such that \(I^{*}-\varepsilon\leq I(n)\leq I^{*}+\varepsilon\) for all \(n\geq N_{\varepsilon}\). Then, from the third equation of model (2.4) we obtain for any \(n\geq N_{\varepsilon}\)
Considering the following auxiliary equations:
and
the comparison theorem of difference equations implies that
where \(U(n)\) and \(V(n)\) are the solutions of (3.6) and (3.7) with initial conditions \(U(N_{\varepsilon})=R(N_{\varepsilon})\) and \(V(N_{\varepsilon})=R(N_{\varepsilon})\), respectively. Since
we obtain
This shows that \(\lim_{n\rightarrow\infty}R(n)=:R^{*}\) exists and \(R^{*}=\frac{k_{3}}{\mu+\alpha}I^{*}\). By a similar argument, we obtain the result that \(\lim_{n\rightarrow\infty }N(n)=:N^{*}\) exists and \(N^{*}=\frac{rK(\mu+\alpha)-\alpha k_{3}I^{*}}{(\mu+\alpha)(r+\mu)}\).
From (3.5) we directly obtain \((\frac{k_{2}}{p}-(\mu +k_{3}))I^{*}\geq0\). When \(R_{0}<1\), by (3.1) it follows that \(I^{*}=0\). Consequently, \(E^{*}=0\), \(R^{*}=0\) and \(N^{*}=\frac{rK}{\mu +r}\). Therefore, we finally have
When \(R_{0}=1\), if \(I^{*}>0\), then from the first equation of model (2.4) and \(E^{*}=\frac{\mu+k_{3}}{k_{2}}I^{*}\) we obtain
that is,
Consequently,
which leads to a contradiction. Hence, \(I^{*}=0\). Furthermore, \(E^{*}=0\), \(R^{*}=0\), and \(N^{*}=\frac{rK}{\mu+r}\). Therefore, (3.8) holds.
Next, we consider Case 2. From the second equation of model (2.2), and according to Lemma 2.1 we have \(S(n)\leq\frac{rK}{\mu+r}\). So for \(n\geq N_{1}\), we have
Then (3.4) implies that \(E(n)\) is decreasing for \(n\geq N_{1}\). Therefore, \(\lim_{n\rightarrow\infty}E(n)=:E^{*}\) exists and \(E^{*}\geq0\). By a similar argument to the above, we obtain the result that \(\lim_{n\rightarrow \infty}I(n)=:I^{*}\), \(\lim_{n\rightarrow\infty}R(n)=:R^{*}\) and \(\lim_{n\rightarrow\infty}N(n)=:N^{*}\) exists, respectively. Obviously,
From (3.9) we directly obtain \((\frac{rk_{1}p}{\mu+r}-(\mu +k_{2}))E^{*}\geq0\). When \(R_{0}<1\), by (3.2) it follows \(E^{*}=0\). Furthermore, \(I^{*}=0\), \(R^{*}=0\) and \(N^{*}=\frac{rK}{r+\mu}\). This shows that (3.8) holds.
When \(R_{0}=1\), if \(E^{*}>0\), then from the first equation of model (2.4), as in the above, we also obtain
that is,
From \(E^{*}=\frac{\mu+k_{3}}{k_{2}}I^{*}\), we have
that is,
By a similar argument to the above, we also can obtain
which leads to a contradiction. Hence, \(E^{*}=0\). Furthermore, \(I^{*}=0\), \(R^{*}=0\), and \(N^{*}=\frac{rK}{\mu+r}\). Therefore, (3.8) is true.
From the above discussions, we obtain the result that the disease-free equilibrium \(P_{0}\) is globally attractive. This completes the proof of Theorem 3.1. □
4 Permanence of disease
In this section, we mainly prove the permanence of model (2.2) when \(R_{0}>1\). The disease \(I(n)\) in model (2.2) is to be said permanent, if there exist constants \(M>m>0\) such that for any solution \((S(n),E(n),I(n),R(n))\) of model (2.2) with initial condition (2.3) one has
We have the following result.
Theorem 4.1
The disease \(I(n)\) in model (2.2) is permanent iff \(R_{0}>1\).
Proof
The necessity is obvious. In fact, if \(R_{0}\leq1\), then from Theorem 3.1 the disease-free equilibrium is globally attractive.
Now, we prove the sufficiency. When \(R_{0}>1\), we have
Hence, there exists a constant \(p>0\) with p sufficiently close to \(\frac{(\mu+k_{2})(\mu+r)}{rk_{1}}\) such that \(\varphi(p)<0\) and
Therefore,
and
Let \((S(n),E(n),I(n),R(n))\) be any solution of model (2.2) with initial condition (2.3). From \(\limsup_{n\rightarrow \infty}N(n)\leq\frac{rK}{r+\mu}\), we see that there exists an integer \(T_{0}>0\) such that
for all \(n\geq T_{0}\). By Lemma 2.2 and \(\varphi(p)<0\), we obtain the result that there exists an integer \(T_{1}\geq T_{0}\) such that \(\phi(p,n)\leq0\) for all \(n\geq T_{1}\) or \(\phi(p,n)\geq0\) for all \(n\geq T_{1}\). Suppose that \(\phi(p,n)\geq0\) for all \(n\geq T_{1}\). Then \(E(n)\geq\frac {1}{p}I(n)\) for all \(n\geq T_{1}\). From the third equation of model (2.2), we have
Hence, by (4.1) and (4.4), \(I(n)\) is increasing for all \(n\geq T_{1}\). Consequently, \(\lim_{n\rightarrow\infty}I(n)=:I^{*}\) exists and \(I^{*}>0\). Further, it follows from (4.4)
which leads to a contradiction. Therefore, we only need to consider \(\phi(p,n)\leq0\) for all \(n\geq T_{1}\). That is,
By (4.2), choosing a sufficiently small constant \(0<\varepsilon_{0}<1\) such that
Considering the following auxiliary equation:
where the parameter \(0\leq\rho\leq1\). Equation (4.7) has a positive equilibrium \(W_{\rho}^{*}=\frac{1}{\mu+\frac{k_{1}\rho}{K}}\frac{rK\mu }{r+\mu}\) which is globally asymptotically stable. Obviously, \(\lim_{\rho\rightarrow0}W_{\rho}^{*}=\frac{rK}{r+\mu}\). Hence, for above \(\varepsilon_{0}\), there is a constant \(\rho_{0}\in (0,\varepsilon_{0})\), such that \(W_{\rho_{0}}^{*}>\frac{rK}{r+\mu}-\frac {\varepsilon_{0}K}{2}\).
By the global asymptotic stability of equilibrium \(W_{\rho _{0}}^{*}\) of (4.7), for the above \(\varepsilon_{0}\), there exists an integer \(T_{2}>0\) such that for any initial integer \(n_{0}>0\) and initial value \(W_{0}\) satisfying \(0\leq W_{0}\leq\frac{rK}{r+\mu}\),
where \(W_{\rho_{0}}(n)\) is the solution of (4.7) with \(\rho=\rho_{0}\) and initial condition \(W_{\rho_{0}}(n_{0})=W_{0}\).
Hence,
Furthermore, we consider the following auxiliary equation:
where \(0<\eta<1\). Obviously, (4.9) has the globally asymptotically stable equilibrium \(U_{\eta}^{*}=\frac{rk_{1}\eta}{\mu+k_{2}}\). Thus, for the above \(\rho_{0}\), there is a constant \(\eta_{0}\in(0,\frac {\rho_{0}}{2})\) such that \(U_{\eta_{0}}^{*}<\frac{\rho_{0}}{8}\). By the global uniform asymptotic stability of equilibrium \(U_{\eta_{0}}^{*}\) of (4.9), for \(\frac{\rho_{0}}{8}>0\), there is an integer \(T_{3}>0\) such that for any initial time \(n_{0}\) and initial value \(U_{0}\) for which \(0\leq U_{0}\leq M_{0}\), where \(M_{0}\) is given above, we have
where \(U_{\eta_{0}}(n)\) is the solution of (4.9) with \(\eta=\eta_{0}\) and initial condition \(U_{\eta_{0}}(n_{0})=U_{0}\). Hence,
In order to obtain the permanence of disease \(I(n)\) of model (2.2), we discuss the following three cases.
Case 1. \(I(n)\geq\eta_{0}\) for all \(n\geq T_{1}\). For this case, obviously, \(I(n)\) is permanent.
Case 2. \(I(n)<\eta_{0}\) for all \(n\geq T_{1}\). From the first equation of model (2.2) and Lemma 2.1, we have
that is,
for all \(n\geq T_{1}\). By the comparison theorem of difference equations, we have \(S(n)\geq W_{\rho_{0}}(n)\) for all \(n\geq T_{1}\), where \(W_{\rho_{0}}(n)\) is the solution of (4.7) with \(\rho=\rho_{0}\) and initial condition \(W_{\rho_{0}}(T_{1})=S(T_{1})\). Since \(0\leq W_{\rho_{0}}(T_{1})\leq\frac{rK}{r+\mu}\), by (4.8), \(W_{\rho _{0}}(n)\geq\frac{rK}{r+\mu}-\varepsilon_{0}K\) for all \(n\geq T_{1}+T_{2}\). We have
Considering the second equation of model (2.2), by (4.5), (4.6), and (4.11), for all \(n\geq T_{1}+T_{2}\)
Hence, \(E(n)\) is increasing for all \(n\geq T_{1}+T_{2}\). Consequently, \(\lim_{n\rightarrow\infty}E(n)=:E^{*}\) exists and \(E^{*}>0\). Further, from above inequality we have
which leads to a contradiction.
Case 3. There exist two integer sequences \(\{m_{k}\} _{k=1}^{\infty}\) and \(\{n_{k}\}_{k=1}^{\infty}\) satisfying
and \(\lim_{k\rightarrow\infty}n_{k}=\infty\) such that
Obviously, we have \(n_{k+1}-m_{k}\geq2\) for all \(k=1,2,\ldots\) .
Since \(R_{0}=\frac{rk_{1}k_{2}}{(\mu+r)(\mu+k_{2})(\mu+k_{3})}>1\), we obtain
Thus we can choose constants \(r_{1}>0\), \(r_{2}>0\), and \(0<\theta<1\) such that
Let \(T^{*}=\max\{T_{2},T_{3}\}\). We can choose a positive integer \(K_{0}\) such that
where
In the following, we will prove \(I(n)\geq\xi\) for all \(n\in\bigcup_{k=1}^{\infty}[n_{k},m_{k}]\). Let \(n\in\bigcup_{k=1}^{\infty}[n_{k},m_{k}]\). If \(m_{k}-n_{k}\leq (K_{0}+1)T^{*}\), from the third equation of model (2.2) we have
Hence,
for all \(n\in[n_{k},m_{k}]\). Thus, we finally obtain \(I(n)\geq\xi\) for all \(n\in[n_{k},m_{k}]\).
If \(m_{k}-n_{k}>(K_{0}+1)T^{*}\), then similar to the discussion, we also have
Particularly, we obtain from (4.13) \(I(n)\geq\xi\) for all \(n\in [n_{k},n_{k}+(K_{0}+1)T^{*}]\) and
By the second equation of model (2.2), we obtain for all \(n\geq T_{1}\) and \(n\in\bigcup_{k=1}^{\infty}[n_{k},m_{k}]\),
that is,
By the comparison theorem of difference equations, we have \(E(n)\leq U_{\eta_{0}}\) for all \(n>T_{1}\), where \(U_{\eta_{0}}\) is the solution of (4.9) with \(\eta=\eta_{0}\) and initial condition \(U_{\eta_{0}}(T_{1})=E(T_{1})\). Since \(0\leq U_{\eta_{0}}(T_{1})\leq M_{0}\), by (4.10), \(U_{\eta_{0}}(n)\leq \frac{\rho_{0}}{4}\) for all \(n\geq T_{1}+T_{3}\). Hence, \(E(n)\leq\frac{\rho_{0}}{4}\) for all \(n\geq T_{1}+T_{3}\). So,
for all \(n\in[n_{k}+T_{2},m_{k}]\), where \(k=1,2,\ldots\) .
We claim that \(I(n)\geq\xi\) for all \(n\in[n_{k}+(K_{0}+1)T^{*},m_{k}]\). If it is not true, then there is an integer \(q_{0}\) such that \(I(n_{k}+(K_{0}+1)T^{*}+q_{0})<\xi\) and \(I(n)\geq\xi\) for all \(n\in [n_{k}+(K_{0}+1)T^{*},n_{k}+(K_{0}+1)T^{*}+q_{0}-1]\). Denote \(t_{0}=n_{k}+(K_{0}+1)T^{*}+q_{0}\). Let
where \(r_{1}\) and \(r_{2}\) are constants in (4.12). Hence, as \(n\in [n_{k}+T^{*},m_{k}]\), from (4.12) and (4.15) we have
Then
Consequently,
that is,
By (4.14), we further have
which leads to a contradiction with (4.15). Therefore,
When \(n\notin\bigcup_{k=1}^{\infty}[n_{k},m_{k}]\), we directly have \(I(n)\geq\eta_{0}>\xi\). Therefore, we finally obtain the result that \(I(n)\) is permanent. This completes the proof. □
5 Numerical simulations
In this section, we carry out numerical simulations on model (2.2) to demonstrate the results in Sections 3 and 4.
Example 5.1
The parameters of model (2.2) are chosen as follows:
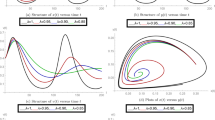
By calculating, we have the endemic equilibrium \(P_{*}=(750.5882,25.2861,6.5446, 72.2460)\) and the basic reproduction number \(R_{0}=1.0188>1\). Therefore, the disease is permanent from Theorem 4.1. The numerical simulations are given in Figure 1. From Figure 1, we can see that \(P_{*}\) is globally attractive.
Example 5.2
The parameters are chosen as follows:
By calculating, we obtain \(R_{0}=0.9770<1\). Thus, the disease-free equilibrium of model (2.2) is globally attractive from Theorem 3.1. The numerical simulations are given in Figure 2.
6 Conclusion
In this paper, we study the dynamic behaviors of a discrete plant virus disease model with roguing and replanting which is derived from the continuous case. By calculating, we obtain the basic reproduction number \(R_{0}\). We also prove that the disease-free equilibrium of model (2.2) is globally attractive when \(R_{0}<1\), in other words, the disease goes extinct. On the contrary, if \(R_{0}>1\), the endemic equilibrium of model (2.2) exists and the disease will be endemic.
In Theorem 4.1, we only discuss the permanence of the disease of model (2.2). However, the numerical simulations in Figure 1 show that the endemic equilibrium of model (2.2) may be globally attractive when \(R_{0}>1\).
In the real world, some plants at the beginning may show no infection, for example Calletotrichum musae. We usually use the time delay to describe this phenomenon in a mathematical model. However, the dynamic behaviors of discrete plant virus disease models with time delay are rarely considered. Therefore, an important and interesting open problem is whether we can obtain similar results on the permanence and extinction of the disease for the discrete plant virus disease models with time delay. We will discuss these problems in our future work.
References
Owusu, GK: The cocoa swollen shoot disease problem in Ghana. In: Plumb, RT, Thresh, JM (eds.): Plant Virus Epidemiology: The Spread and Control of Insect-Borne Viruses. Blackwell Sci., Oxford (1983)
Thresh, JM, Owusu, GK: The control of cocoa swollen shoot disease in Ghana: an evaluation of eradication procedures. Crop Prot. 5, 41-52 (1986)
Allen, RN: The spread of bunchy top disease within a banana plantation subject to roguing. In: Plant Disease Survey, pp. 25-26. New South Wales Department of Agriculture, Biology Branch (1975/1976)
Allen, RN: Epidemiological factors influencing the success of roguing for the control of bunchy top disease of bananas in New South Wales. Aust. J. Agric. Res. 29, 535-544 (1978)
Thresh, JM: Eradication as a virus disease control measure. In: Clifford, BC, Lester, E (eds.): Control of Plant Disease: Costs and Benefits. Blackwell Sci., Oxford (1983)
Ollennu, LAA, Owusu, GK, Thresh, JM: The control of cocoa swollen shoot disease in Ghana. Cocoa Grow. Bull. 42, 25-35 (1989)
Allen, RN: Further studies on epidemiological factors influencing control of banana bunchy top disease and evaluation of control measures by computer simulation. Aust. J. Agric. Res. 38, 373-382 (1987)
Chan, MS, Jeger, MJ: An analytical model of plant virus disease dynamics with roguing and replanting. J. Appl. Ecol. 31, 413-427 (1994)
Wang, L, Cui, Q, Teng, Z: Global dynamics in a class of discrete-time epidemic models with disease courses. Adv. Differ. Equ. 2013, 57 (2013)
Agarwal, RP, O’Regan, O, Wong, PJY: Dynamics of epidemics in homogeneous/heterogeneous populations and the spreading of multiple inter-related infectious diseases: constant-sign periodic solutions for the discrete model. Nonlinear Anal., Real World Appl. 8, 1040-1061 (2007)
Allen, LJS: Some discrete-time SI, SIR and SIS epidemic models. Math. Biosci. 124, 83-105 (1994)
Allen, LJS, Burgin, AM: Comparison of deterministic and stochastic SIS and SIR model in discrete time. Math. Biosci. 163, 1-33 (2000)
Allen, LJS, Driessche, P: The basic reproduction number in some discrete-time epidemic models. J. Differ. Equ. Appl. 14, 1127-1147 (2008)
Allen, LJS, Lou, Y, Nevai, A: Spatial patterns in a discrete-time SIS patch model. J. Math. Biol. 58, 339-375 (2009)
Li, J, Ma, Z, Brauer, F: Global analysis of discrete-time SI and SIS epidemic models. Math. Biosci. Eng. 4, 699-710 (2007)
Li, X, Wang, W: A discrete epidemic model with stage structure. Chaos Solitons Fractals 26, 947-958 (2005)
Franke, L, Yakubu, AA: Discrete-time SIS epidemic model in a seasonal environment. SIAM J. Appl. Math. 66, 1563-1587 (2006)
Franke, L, Yakubu, AA: Disease-induced mortality in density-dependent dicrete-time SIS epidemic models. J. Math. Biol. 57, 755-790 (2008)
Iaao, G, Muroya, Y, Vecchio, A: A general discrete time model of population dynamics in the presence of an infection. Discrete Dyn. Nat. Soc. 2009, Article ID 143019 (2009). doi:10.1155/2009/143019
Izzo, G, Vecchio, A: A discrete time version for models of population dynamics in the presence of an infection. J. Comput. Appl. Math. 201, 201-221 (2007)
Li, J, Lou, J, Luo, M: Some discrete SI and SIS epidemic models. Appl. Math. Mech. 29, 113-119 (2008)
Muroya, Y, Bellen, A, Enatsu, Y, Nakata, Y: Global stability for a discrete epidemic model for disease with immunity and latency spreading in a heterogeneous host population. Nonlinear Anal., Real World Appl. 13, 258-274 (2012)
Franke, JE, Yakubu, AA: Disease-induced mortality in density-dependent discrete-time S-I-S epidemic models. J. Math. Biol. 57, 755-790 (2008)
Castillo-Chavez, C, Yakubu, AA: Discrete-time SIS models with complex dynamics. Nonlinear Anal. 47, 4753-4762 (2001)
Teng, Z, Nie, L, Xu, J: Dynamical behaviors of a discrete SIS epidemic model with standard incidence and stage structure. Adv. Differ. Equ. 2013, Article ID 87 (2013). doi:10.1186/1687-1847-2013-87
Franke, JE, Yakubu, AA: Periodically forced discrete-time SIS epidemic model with disease induced mortality. Math. Biosci. Eng. 8, 385-408 (2011)
Wang, L, Teng, Z, Zhang, L: Global behaviors of a class of discrete SIRS epidemic models with nonlinear incidence rate. Abstr. Appl. Anal. 2014, Article ID 249623 (2014). doi:10.1155/2014/249623
Enatsu, Y, Nakata, Y: Global stability for a class of discrete SIR epidemic models. Math. Biosci. Eng. 7, 347-361 (2010)
Enatsu, Y, Nakata, Y, Muroya, Y, Izzo, G, Vecchio, A: Global dynamics of difference equations for SIR epidemic models with a class of nonlinear incidence rates. J. Differ. Equ. Appl. 18, 1163-1181 (2012)
Hu, Z, Teng, Z, Zhang, L: Stability and bifurcation analysis in a discrete SIR epidemic model. Math. Comput. Simul. 97, 80-93 (2014)
Sekiguchi, M, Ishiwata, E: Global dynamics of a discretized SIRS epidemic model with time delay. J. Math. Anal. Appl. 371, 195-202 (2010)
Sekiguchi, M: Permanence of a discrete SIRS epidemic model with time delays. Appl. Math. Lett. 23, 1280-1285 (2010)
Muroya, Y, Nakata, Y, Izzo, G, Vecchio, A: Permanence and global stability of a class of discrete epidemic models. Nonlinear Anal., Real World Appl. 12, 2015-2117 (2011)
Acknowledgements
Special thanks to the anonymous referees who have given us very useful suggestions. The research has been supported by the Natural Science Foundation of China (11261004), the Science and Technology Plan Projects of Jiangxi Provincial Education Department (GJJ14665, GJJ14673), and the Postgraduate Innovation Fund of Gannan Normal University (YCZ13B002).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors are read and approved the final manuscript.
Rights and permissions
Open Access This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.
About this article
Cite this article
Luo, Y., Gao, S., Xie, D. et al. A discrete plant disease model with roguing and replanting. Adv Differ Equ 2015, 12 (2015). https://doi.org/10.1186/s13662-014-0332-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-014-0332-3