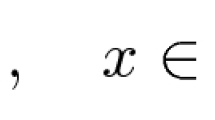Uniqueness and concentration for a fractional Kirchhoff problem with strong singularity

Abstract

In this paper, we consider the following fractional Kirchhoff problem with strong singularity:

$$ \textstyle\begin{cases} (1+ b\int _{\mathbb{R}^{3}}\int _{\mathbb{R}^{3}} \frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}}\,\mathrm{d}x \,\mathrm{d}y )(-\Delta )^{s} u+V(x)u = f(x)u^{-\gamma }, & x \in \mathbb{R}^{3}, \\ u>0,& x\in \mathbb{R}^{3}, \end{cases} $$

where $(-\Delta )^{s}$ is the fractional Laplacian with $0< s<1$, $b>0$ is a constant, and $\gamma >1$. Since $\gamma >1$, the energy functional is not well defined on the work space, which is quite different with the situation of $0<\gamma <1$ and can lead to some new difficulties. Under certain assumptions on V and f, we show the existence and uniqueness of a positive solution $u_{b}$ by using variational methods and the Nehari manifold method. We also give a convergence property of $u_{b}$ as $b\rightarrow 0$, where b is regarded as a positive parameter.

1 Introduction

Nonlinear equations involving fractional powers of the Laplacian have attracted increasing attention in recent years. The fractional Laplacian is the infinitesimal generator of Lévy stable diffusion process and arises in anomalous diffusion in plasma, population dynamics, geophysical fluid dynamics, flames propagation, chemical reactions in liquids, and American options in finance, see [1] for instance. There are a lot of applications for nonlocal fractional problems, see for example [3, 6, 26, 33] and the references therein. In this paper, we consider the following fractional Kirchhoff problem:

where $b>0$ is a constant and $\gamma >1$. The fractional Laplacian operator $(-\Delta )^{s}$ in $\mathbb{R}^{3}$ is defined by

$$ (-\Delta )^{s} u(x)=C(s) \textit{ P.V. } \int _{\mathbb{R}^{3}} \frac{u(x)-u(y)}{ \vert x-y \vert ^{3+2s}}\,\mathrm{d}y,\quad u\in \mathbb{S}\bigl( \mathbb{R}^{3}\bigr), $$

where $P.V$. stands for the Cauchy principal value, $C(s)$ is a normalized constant, $\mathbb{S}(\mathbb{R}^{3})$ is the Schwartz space of rapidly decaying function. Throughout the paper, we suppose that V and f satisfy:

$(V_{1})$:

$V\in C(\mathbb{R}^{3})$ satisfies $\inf_{x\in \mathbb{R}^{3}}V(x)>V_{0}>0$, where $V_{0}$ is a constant;

$(V_{2})$:

$\text{meas}\{x\in R^{3} : -\infty < V(x)\le h\}<+\infty$ for all $h\in \mathbb{R}$;

$(f_{1})$:

$f\in L^{\frac{2}{1+\gamma }}(\mathbb{R}^{3})$ is a nonnegative function.

The motivation for studying problem ($P_{b}$) comes from Kirchhoff equation of the form

$$ - \biggl(a+b \int _{\Omega } \vert \nabla u \vert ^{2}\, \mathrm{d}x \biggr) \Delta u=f(x,u),\quad x\in \Omega , $$

(1.1)

where $\Omega \subset \mathbb{R}^{n}$ is a bounded domain, $a>0$, $b \ge 0$, and u satisfies some boundary conditions. Problem (1.1) is related to the stationary analogue of the equation

$$ \rho \frac{\partial ^{2}u}{\partial ^{2}t}- \biggl( \frac{P_{0}}{h}+ \frac{F}{2L} \int _{0}^{L} \biggl\vert \frac{\partial u}{\partial x} \biggr\vert ^{2} \,\mathrm{d}x \biggr) \frac{\partial ^{2}u}{\partial ^{2}x}=f(x,u), $$

(1.2)

which was introduced by Kirchhoff [12] in 1883. This equation is an extension of the classical d’Alembert wave equation by considering the effects of changes in the length of the string during vibrations. The parameters in (1.2) have the following meanings: L is the length of the string, h is the area of the cross-section, F is the Young modulus of the material, ρ is the mass density, and $P_{0}$ is the initial tension. Problem (1.2) was proposed and studied as the fundamental equation for understanding several physical systems, where u describes a process which depends on its average. After the pioneering work of Lions [22], the Kirchhoff type equation began to receive the attention of many researchers.

Recently, many scholars have paid attention to fractional Kirchhoff problem, which was first studied by Fiscella and Valdinoci [10], where they proposed the following stationary Kirchhoff variational model in bounded regular domains of $\mathbb{R}^{n}$ ($n>2s$):

$$ \textstyle\begin{cases} M (\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}} \frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{n+2s}}\,\mathrm{d}x \,\mathrm{d}y )(-\Delta )^{s} u=\lambda f(x,u)+ \vert u \vert ^{2_{s}^{*}-2}u, & x \in \Omega , \\ u=0,& x\in \mathbb{R}^{n}\setminus \Omega , \end{cases} $$

(1.3)

with $2_{s}^{*}=\frac{2n}{n-2s}$. Under some suitable conditions on f, Fiscella and Valdinoci [10] proved that the existence of nonnegative solutions of problem (1.3) with the Kirchhoff function M satisfies $M(t)\ge m_{0} = M(0)$ for all $t\in \mathbb{R}^{+}$, i.e., problem (1.3) is a nondegenerate case, see also [5, 9, 11, 27, 30, 36]. In particular, Fiscella [8, 9] provided the existence of two solutions for a fractional Kirchhoff problem involving weak singularity (i.e., $0<\gamma <1$) and a critical nonlinearity on a bounded domain.

In the local setting ($s=1$), problem ($P_{b}$) is related to the following singular Kirchhoff problem which was first considered by Liu and Sun [25]:

$$ \textstyle\begin{cases} - (a+b\int _{\Omega } \vert \nabla u \vert ^{2}\,\mathrm{d}x ) \Delta u=\lambda g(x) \frac{u^{p}}{ \vert u \vert ^{\delta }}+h(x)u^{- \gamma }, & x\in \Omega , \\ u>0,& x\in \Omega , \\ u=0,& x\in \partial \Omega , \end{cases} $$

(1.4)

where Ω is a smooth bounded domain in $\mathbb{R}^{3}$. Considering the weak singular case, when $\lambda >0$ is small, Liu and Sun [25] obtained two positive solutions for problem (1.4) with $3< p<5-2\delta$ and $g,h\in C(\overline{\Omega })$ are nontrivial nonnegative functions. Later, by the variational method and perturbation method, Lei et al. [14] obtained two positive solutions for problem (1.4) with $\delta =0$, $p=5$, i.e., singular Kirchhoff type equation with critical exponent. Liao et al. [21] investigated the existence and multiplicity of positive solutions for problem (1.4) with $\delta =0$, $p=3$. Liu et al. [24] studied the existence and multiplicity of positive solutions for the Kirchhoff type problem with singular and critical nonlinearities in dimension four. Liao et al. [20] obtained the unique result of a class of singular Kirchhoff type problems. When $p=3$, $\lambda =1$, and $g\ge 0$ or g changes sign in Ω, Li et al. [16] showed the existence and multiplicity of positive solutions for problem (1.4). By the perturbation method, variational method, and some analysis techniques, Liu et al. [23], Tang et al. [32], Lei and Liao [13] established a multiplicity theorem for a singular Kirchhoff type problem with critical Sobolev exponent, Hardy–Sobolev critical exponent, and asymptotically linear nonlinearities, respectively. Mu and Lu [28], Li et al. [15], and Zhang [40] studied the existence, uniqueness, and multiple results to a singular Schrödinger–Kirchhoff–Poisson system. Li et al. [17], Tan and Sun [31], Zhang [41], and we [37] established a necessary and sufficient condition on the existence of positive solutions for a Kirchhoff problem, a Kirchhoff–Schrödinger–Poisson system, and a Schrödinger–Poisson system with strong singularity (i.e., $\gamma >1$), respectively. Wang et al. [35] further obtained a uniqueness result for a Kirchhoff type fractional Laplacian problem with strong singularity. However, results on the strong singular problem are dependent on a bounded smooth domain, and there are few studies on the whole space. For more works on Kirchhoff and singular problems, one could refer to [2, 4, 19, 34, 38, 39] and the references cited therein.

Motivated by the above results, we are concerned with the existence and convergence property of positive solutions for problem ($P_{b}$) in this paper. Before stating our main results, we first collect some basic results of fractional Sobolev spaces. In view of the presence of the potential function $V(x)$, we will work in the space

$$ E= \bigl\{ u\in \mathcal{D}^{s,2}\bigl(\mathbb{R}^{3} \bigr) : \Vert u \Vert _{E}< + \infty \bigr\} $$

equipped with inner product and the norm

$$\begin{aligned}& (u,v)_{E}= \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}} \frac{(u(x)-u(y))(v(x)-v(y))}{ \vert x-y \vert ^{3+2s}}\,\mathrm{d}x \,\mathrm{d}y + \int _{\mathbb{R}^{3}} V(x)u(x)v(x)\,\mathrm{d}x, \\& \Vert u \Vert _{E}=(u,u)_{E}^{1/2}. \end{aligned}$$

Here, $\mathcal{D}^{s,2}(\mathbb{R}^{3})$ is the homogeneous fractional Sobolev space as the completion of $C_{0}^{\infty }(\mathbb{R}^{3})$ under the norm

$$ \Vert u \Vert _{\mathcal{D}^{s,2}(\mathbb{R}^{3})}= \biggl( \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}}\frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y \biggr)^{1/2}\doteq [u]_{s}. $$

Moreover, by virtue of Proposition 3.4 and Proposition 3.6 in [7], we also have

$$ \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,\mathrm{d}x= \frac{C(s)}{2} \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}} \frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y. $$

Without loss of generality, we assume that $C(s)=2$.

The energy functional corresponding to problem ($P_{b}$) is given by

$$ I_{b}(u)= \frac{1}{2} \Vert u \Vert _{E}^{2}+ \frac{b}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2}- \frac{1}{1-\gamma } \int _{ \mathbb{R}^{3}}f(x) \vert u \vert ^{1-\gamma }\, \mathrm{d}x, $$

(1.5)

and a function $u\in E$ is called a solution of problem $(P_{\lambda })$ if $u>0$ in $\mathbb{R}^{3}$, and for every $v\in E$,

$$ (u,v)_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u(-\Delta )^{ \frac{s}{2}}v \,\mathrm{d}x - \int _{\mathbb{R}^{3}}f(x)u^{-\gamma }v \,\mathrm{d}x=0. $$

(1.6)

To the best of our knowledge, there are no results on the existence of positive solutions for the fractional Kirchhoff problem with singularity on unbounded domains. Here we need to overcome the lack of compactness as well as the non-differentiability of the functional $I_{b}$ on E and indirect availability of critical point theory due to the presence of singular term. By the variational method and the Nehari method, we obtain the following existence and uniqueness of positive solution and the asymptotic behavior of solutions with respect to the parameter b.

Theorem 1.1

Let $b\ge 0$ and $\gamma >1$. Assume $(V_{1})$, $(V_{2})$, and $(f_{1})$. Then problem ($P_{b}$) admits a unique positive solution $u_{b}$ if and only if there exists $u_{0}\in E$ such that

$$ \int _{\mathbb{R}^{3}}f(x) \vert u_{0} \vert ^{1-\gamma }\,\mathrm{d}x< + \infty . $$

(1.7)

Theorem 1.2

Let $\gamma >1$. Assume $(V_{1})$, $(V_{2})$, and $(f_{1})$. For every vanishing sequence $\{b_{n}\}\subset (0,1)$, let $u_{b_{n}}$ be the unique positive solution to problem ($P_{b}$) provided by Theorem 1.1. Then $u_{b_{n}}$ converge to $w_{0}$ in E, where $w_{0}$ is the unique positive solution to problem

2 Preliminaries and proofs of the main results

Throughout the paper, we use the following notations:

• $L^{p}(\mathbb{R}^{3})$ is a Lebesgue space whose norm is denoted by $\|u\|_{p}=(\int _{\mathbb{R}^{3}}|u|^{p}\,\mathrm{d}x)^{\frac{1}{p}}$.

• For any $\alpha \in (0,1)$, $2_{\alpha }^{*}=\frac{6}{3-2\alpha }$ is the fractional critical exponent in dimension three.

• → denotes the strong convergence and ⇀ denotes the weak convergence.

• $u^{+}=\max \{u,0\}$ and $u^{-}=\max \{-u,0\}$ for any function u.

• C and $C_{i}$ ($i=1,2,\ldots$) denote various positive constants which may vary from line to line.

Using conditions $(V_{1})$ and $(V_{2})$, we can obtain the following continuous or compact embedding theorem (see [18], Lemma 2.2).

Lemma 2.1

Let $0 < s < 1$ and suppose that $(V_{1})$ and $(V_{2})$ hold. If $p\in [2,2_{s}^{*}]$, then the embedding $E\hookrightarrow L^{p}(\mathbb{R}^{3})$ is continuous, and so there exists a constant $C_{p}>0$ such that $\|u\|_{p}\le C_{p}\|u\|_{E}$ for all $u\in E$. If $p\in [2,2_{s}^{*})$, then the embedding $E\hookrightarrow L^{p}(\mathbb{R}^{3})$ is compact.

In order to prove our main results, we consider the following two constrained sets:

$$ \mathcal{N}_{1}^{(b)}= \biggl\{ u\in E : \Vert u \Vert _{E}^{2}+b \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}- \int _{\mathbb{R}^{3}}f(x) \vert u \vert ^{1-\gamma }\, \mathrm{d}x\ge 0 \biggr\} $$

and

$$ \mathcal{N}_{2}^{(b)}= \biggl\{ u\in E : \Vert u \Vert _{E}^{2}+b \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}- \int _{\mathbb{R}^{3}}f(x) \vert u \vert ^{1-\gamma }\, \mathrm{d}x=0 \biggr\} $$

for any $b\ge 0$. We now come to prove our main results.

Proof of Theorem 1.1

(Necessity) Suppose that $u\in E$ is a solution of problem ($P_{b}$), then $u>0$ and satisfies (1.6). Choosing $v=u$ in (1.6), we can get

$$ \int _{\mathbb{R}^{3}}f(x)u^{1-\gamma }\,\mathrm{d}x= \Vert u \Vert _{E}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}< +\infty , $$

and the necessity is proved.

(Sufficiency) The proof will be complete in five steps under assumption (1.7) and $b>0$ always hold.

Step 1. We prove that $\mathcal{N}_{i}^{(b)}\neq \emptyset$, $i=1,2$.

Fix $u\in E$ with $\int _{\mathbb{R}^{3}}f(x)|u|^{1-\gamma }\,\mathrm{d}x<+ \infty$. For any $\eta >0$, we have

$$ I_{b}(\eta u)= \frac{\eta ^{2}}{2} \Vert u \Vert _{E}^{2}+ \frac{b \eta ^{4}}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}- \frac{\eta ^{1-\gamma }}{1-\gamma } \int _{\mathbb{R}^{3}}f(x) \vert u \vert ^{1- \gamma }\, \mathrm{d}x. $$

Set $g(\eta )=\eta \frac{\text{d}I_{b}(\eta u)}{\text{d}\eta }$, then

$$ g(\eta )=\eta ^{2} \Vert u \Vert _{E}^{2}+b \eta ^{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}-\eta ^{1-\gamma } \int _{\mathbb{R}^{3}}f(x) \vert u \vert ^{1-\gamma }\, \mathrm{d}x. $$

By $\gamma >1$, one can easily obtain that $g(\eta )$ is increasing on $(0,+\infty )$, with $\lim_{\eta \rightarrow 0^{+}}g(\eta )=-\infty$ and $\lim_{\eta \rightarrow +\infty }g(\eta )=+\infty$. Thus, there exists unique $\eta (u)>0$ such that $I_{b}(\eta (u)u)=\min_{\eta >0}I_{b}(\eta u)$ and $g(\eta (u))=0$, i.e.,

$$ \eta ^{2}(u) \Vert u \Vert _{E}^{2}+b \eta ^{4}(u) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}-\eta ^{1-\gamma }(u) \int _{\mathbb{R}^{3}}f(x) \vert u \vert ^{1-\gamma }\, \mathrm{d}x=0, $$

that is, $\eta (u)u\in \mathcal{N}_{2}^{(b)}$. Specially, assumption (1.7) implies that there exists $\eta (u_{0})> 0$ such that $\eta (u_{0})u_{0}\in \mathcal{N}_{2}^{(b)}\subset \mathcal{N}_{1}^{(b)}$, and so $\mathcal{N}_{i}^{(b)}\neq \emptyset$, $i=1,2$, for any $b\ge 0$.

Step 2. We prove that $\mathcal{N}_{1}^{(b)}$ is an unbounded closed set, and there exists a positive constant $C_{1}$ such that $\|u\|\ge C_{1}$ for all $u\in \mathcal{N}_{1}^{(b)}$.

According to Step 1, $\eta u\in \mathcal{N}_{1}^{(b)}$ for any $\eta \ge \eta (u_{0})$, so $\mathcal{N}_{1}^{(b)}$ is unbounded. The closeness of $\mathcal{N}_{1}^{(b)}$ follows from Fatou’s lemma. We claim that there exists a positive constant $C_{1}$ such that $\|u\|_{E}\ge C_{1}$ for all $u\in \mathcal{N}_{1}^{(b)}$. Arguing by contradiction, there exists a sequence $\{u_{n}\}\subset \mathcal{N}_{1}^{(b)}$ satisfying $u_{n}\rightarrow 0$ in E. Since $\gamma >1$ and $u_{n}\in \mathcal{N}_{1}^{(b)}$, by the reverse form of Hölder’s inequality, one can get (note that $u_{n}\not \equiv 0$ as $\gamma >1$)

$$\begin{aligned} \biggl( \int _{\mathbb{R}^{3}}f^{\frac{2}{1+\gamma }}(x) \,\mathrm{d}x \biggr)^{\frac{1+\gamma }{2}} \biggl( \int _{ \mathbb{R}^{3}} \vert u_{n} \vert ^{2} \,\mathrm{d}x \biggr)^{\frac{1-\gamma }{2}}& \le \int _{\mathbb{R}^{3}}f(x) \vert u_{n} \vert ^{1-\gamma }\,dx \\ &\le \Vert u_{n} \Vert _{E}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}\rightarrow 0. \end{aligned}$$

Since $f\in L^{\frac{2}{1+\gamma }}(\mathbb{R}^{3})$ is nonnegative and then $(\int _{\mathbb{R}^{3}}f^{\frac{2}{1+\gamma }}(x) \,\mathrm{d}x )^{\frac{1+\gamma }{2}}>0$, we have $\int _{\mathbb{R}^{3}}|u_{n}|^{2}\,\mathrm{d}x \rightarrow \infty$, which is impossible. So there exists a positive constant $C_{1}$ such that $\|u\|_{E}\ge C_{1}$ for all $u\in \mathcal{N}_{1}^{(b)}$.

Step 3. We show the properties of the minimizing sequence $\{u_{n}\}$.

For any $u\in \mathcal{N}_{1}^{(b)}$, according to Step 2, there exists a positive constant $C_{1}$ such that $\|u\|_{E}\ge C_{1}$, then by (1.5) and $\gamma >1$ one has

$$ I_{b}(u)= \frac{1}{2} \Vert u \Vert _{E}^{2}+ \frac{b}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2}- \frac{1}{1-\gamma } \int _{ \mathbb{R}^{3}}f(x) \vert u \vert ^{1-\gamma }\, \mathrm{d}x\ge \frac{1}{2} \Vert u \Vert _{E}^{2}. $$

(2.1)

Therefore, $I_{b}(u)$ is coercive and bounded from below on $\mathcal{N}_{1}^{(b)}$, and so $\inf_{\mathcal{N}_{1}^{(b)}}I_{b}$ is well defined. Since $\mathcal{N}_{1}^{(b)}$ is closed, we apply the Ekeland variational principle to construct a minimizing sequence $\{u_{n}\}\subset \mathcal{N}_{1}^{(b)}$ satisfying

• (1) $I_{b}(u_{n})<\inf_{\mathcal{N}_{1}^{(b)}}I_{b}+\frac{1}{n}$;

• (2) $I_{b}(z)\ge I_{b}(u_{n})-\frac{1}{n}\|u_{n}-z\|_{E}$, $\forall z\in \mathcal{N}_{1}^{(b)}$.

The coerciveness of $I_{b}$ on $\mathcal{N}_{1}^{(b)}$ shows that $\|u_{n}\|_{E}\le C_{2}$ uniformly for some suitable positive constant $C_{2}$. Hence, $C_{1}\le \|u_{n}\|_{E}\le C_{2}$ and then there exist a subsequence of $\{u_{n}\}$ (still denoted by $\{u_{n}\}$) and a function $u_{b}\in E$ such that

$$\begin{aligned} &u_{n}\rightharpoonup u_{b},\quad \text{in } E \text{ and } \mathcal{D}^{s,2}\bigl( \mathbb{R}^{3}\bigr), \\ &u_{n}\rightarrow u_{b}, \quad \text{in } L^{p}\bigl(\mathbb{R}^{3}\bigr), p \in [2,2_{s}^{*}), \\ &u_{n}\rightarrow u_{b}, \quad \text{a.e. in } \mathbb{R}^{3}. \end{aligned}$$

Since $I_{b}(|u|)\le I_{b}(u)$, we could assume $u_{n}\ge 0$, then $u_{b}(x)\ge 0$. By $\{u_{n}\}\subset \mathcal{N}_{1}^{(b)}$ and Fatou’s lemma, we further get $\int _{\mathbb{R}^{3}}f(x)u_{b}^{1-\gamma }\,dx<+\infty$, which implies $u_{b}(x)>0$ a.e. in $\mathbb{R}^{3}$.

Step 4. We prove that $u_{b}\in \mathcal{N}_{2}^{(b)}$, $\inf_{\mathcal{N}_{1}^{(b)}}I_{b}=I_{b}(u_{b})$, and for any $0\le \psi \in E$,

$$ (u_{b},\psi )_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x - \int _{\mathbb{R}^{3}}f(x)u_{b}^{- \gamma }\psi \, \mathrm{d}x\ge 0. $$

To prove the above statements, we consider the following two cases regarding whether $\{u_{n}\}$ belongs to ${\mathcal{N}_{1}^{(b)}}\setminus {\mathcal{N}_{2}^{(b)}}$ or $\mathcal{N}_{2}^{(b)}$.

Case 1. Suppose that $\{u_{n}\}\subset {\mathcal{N}_{1}^{(b)}}\setminus {\mathcal{N}_{2}^{(b)}}$ for all n large.

For any $0\le \psi \in E$, since $\{u_{n}\}\subset {\mathcal{N}_{1}^{(b)}}\setminus {\mathcal{N}_{2}^{(b)}}$, $f(x)$ is nonnegative and $\gamma >1$, we can derive

$$\begin{aligned} \int _{\mathbb{R}^{3}}f(x) (u_{n}+\eta \psi )^{1-\gamma }\,\mathrm{d}x &\le \int _{\mathbb{R}^{3}}f(x)u_{n}^{1-\gamma }\,\mathrm{d}x \\ &< \Vert u_{n} \Vert _{E}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2},\quad \forall \eta \ge 0. \end{aligned}$$

Therefore, we could choose $\eta >0$ small enough such that

$$ \int _{\mathbb{R}^{3}}f(x) (u_{n}+\eta \psi )^{1-\gamma }\,\mathrm{d}x< \Vert u_{n}+ \eta \psi \Vert _{E}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}(u_{n}+ \eta \psi ) \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}, $$

that is, $u_{n}+\eta \psi \in \mathcal{N}_{1}^{(b)}$. Applying condition (2) with $z=u_{n}+\eta \psi$ leads to

$$\begin{aligned} \frac{ \Vert \eta \psi \Vert _{E}}{n}\ge {}&I_{b}(u_{n})-I_{b}(u_{n}+ \eta \psi ) \\ ={}& \frac{1}{2}\bigl( \Vert u_{n} \Vert _{E}^{2}- \Vert u_{n}+\eta \psi \Vert _{E}^{2}\bigr)+ \frac{1}{1-\gamma } \int _{\mathbb{R}^{3}}f(x) \bigl[(u_{n}+ \eta \psi )^{1-\gamma }-u_{n}^{1-\gamma } \bigr]\,\mathrm{d}x \\ &{}+ \frac{b}{4} \biggl[ \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}- \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}(u_{n}+ \eta \psi ) \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2} \biggr]. \end{aligned}$$

Dividing by $\eta >0$ and passing to the liminf as $\eta \rightarrow 0^{+}$, according to Fatou’s lemma, we obtain

$$\begin{aligned} \begin{aligned}& \frac{ \Vert \psi \Vert _{E}}{n}+(u_{n},\psi )_{E} +b \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{ \mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}} \psi \,\mathrm{d}x \\ &\quad \ge \liminf_{\eta \rightarrow 0^{+}} \frac{1}{1-\gamma } \int _{\mathbb{R}^{3}}f(x) \frac{(u_{n}+\eta \psi )^{1-\gamma }-u_{n}^{1-\gamma }}{\eta }\,dx \\ &\quad \ge \int _{\mathbb{R}^{3}}\liminf_{\eta \rightarrow 0^{+}} \frac{f(x)}{1-\gamma } \frac{(u_{n}+\eta \psi )^{1-\gamma }-u_{n}^{1-\gamma }}{\eta }\,\mathrm{d}x \\ &\quad = \int _{\mathbb{R}^{3}}f(x)u_{n}^{-\gamma }\psi \, \mathrm{d}x. \end{aligned} \end{aligned}$$

(2.2)

Letting $n\rightarrow \infty$ and using Fatou’s lemma again, one can get

$$ \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }\psi \, \mathrm{d}x< +\infty $$

(2.3)

for any $0\le \psi \in E$. Choose $\psi =u_{b}$ in (2.3), we get $\int _{\mathbb{R}^{3}}f(x)u_{b}^{1-\gamma }\,\mathrm{d}x<+ \infty$ and then Step 1 shows the existence of unique $\eta (u_{b})>0$ satisfying $\eta (u_{b})u_{b}\in \mathcal{N}_{2}^{(b)}$ and $I_{b}(\eta (u_{b})u_{b})=\min_{\eta >0}I_{b}(\eta u_{b})$. Hence, according to the weak lower semi-continuity of the norm and Fatou’s lemma, one has

$$\begin{aligned} \inf_{\mathcal{N}_{1}^{(b)}}I_{b} =&\lim _{n\rightarrow \infty }I_{b}(u_{n}) \\ =&\liminf_{n\rightarrow \infty } \biggl[ \frac{1}{2} \Vert u_{n} \Vert _{E}^{2}+ \frac{b}{4}[u_{n}]_{s}^{4}- \frac{1}{1-\gamma } \int _{\mathbb{R}^{3}}f(x)u_{n}^{1- \gamma }\,\mathrm{d}x \biggr] \\ \ge &\liminf_{n\rightarrow \infty } \biggl[ \frac{1}{2} \Vert u_{n} \Vert _{E}^{2} \biggr]+\liminf _{n\rightarrow \infty } \biggl[ \frac{b}{4}[u_{n}]_{s}^{4} \biggr]+ \liminf_{n\rightarrow \infty } \biggl[ \frac{1}{\gamma -1} \int _{\mathbb{R}^{3}}f(x)u_{n}^{1-\gamma } \, \mathrm{d}x \biggr] \\ \ge & \frac{1}{2} \Vert u_{b} \Vert _{E}^{2}+ \frac{b}{4}[u_{b}]_{s}^{4}+ \frac{1}{\gamma -1} \int _{ \mathbb{R}^{3}}f(x)u_{b}^{1-\gamma }\, \mathrm{d}x \\ =&I_{b}(u_{b})\ge I_{b}\bigl(\eta (u_{b})u_{b}\bigr) \\ \ge& \inf_{\mathcal{N}_{2}^{(b)}}I_{b} \ge \inf_{\mathcal{N}_{1}^{(b)}}I_{b}. \end{aligned}$$

Thus, the above inequalities are actually equalities. By the uniqueness of $\eta (u_{b})$, we have $\eta (u_{b})=1$, that is,

$$ u_{b}\in \mathcal{N}_{2}^{(b)}, \quad \inf _{\mathcal{N}_{1}^{(b)}}I_{b}=I_{b}(u_{b}). $$

(2.4)

Moreover, we can also obtain that $\liminf_{n\rightarrow \infty }\|u_{n}\|_{E}^{2}=\|u_{b}\|_{E}^{2}$ with $\liminf_{n\rightarrow \infty }[u_{n}]_{s}=[u_{b}]_{s}$ and a subsequence of $\{u_{n}\}$ (still denoted by $\{u_{n}\}$) such that $\lim_{n\rightarrow \infty }\|u_{n}\|_{E}^{2}=\|u_{b}\|_{E}^{2}$ and $\lim_{n\rightarrow \infty }[u_{n}]_{s}=[u_{b}]_{s}$ This together with the weak convergence of $\{u_{n}\}$ in E and $\mathcal{D}^{s,2}(\mathbb{R}^{3})$ implies $u_{n}\rightarrow u_{b}$ strongly in E and $\mathcal{D}^{s,2}(\mathbb{R}^{3})$. Hence, using Fatou’s lemma again, it follows from (2.2) that, for any $0\le \psi \in E$,

$$\begin{aligned}& (u_{b},\psi )_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\& \quad \ge \int _{\mathbb{R}^{3}}f(x)u_{b}^{- \gamma }\psi \, \mathrm{d}x. \end{aligned}$$

(2.5)

Case 2. There exists a subsequence of $\{u_{n}\}$ (still denoted by $\{u_{n}\}$)which belongs to $\mathcal{N}_{2}^{(b)}$.

For any $0\le \psi \in E$, using $\gamma >1$ and the boundedness of $\{u_{n}\}$, we have

$$\begin{aligned} \int _{\mathbb{R}^{3}}f(x) (u_{n}+\eta \psi )^{1-\gamma }\,\mathrm{d}x \le& \int _{\mathbb{R}^{3}}f(x)u_{n}^{1-\gamma }\,\mathrm{d}x \\ =& \Vert u_{n} \Vert _{E}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2}< +\infty , \quad \forall \eta \ge 0, \end{aligned}$$

then Step 1 shows the existence of some functions $h_{n,\psi }(\eta ):[0,+\infty )\rightarrow (0,+\infty )$ corresponding to $u_{n}+\eta \psi$ such that

$$ h_{n,\psi }(0)=1,\qquad h_{n,\psi }(\eta ) (u_{n}+\eta \psi )\in \mathcal{N}_{2}^{(b)},\quad \forall \eta \ge 0. $$

The continuity of $h_{n,\psi }(\eta )$ with respect to $\eta \ge 0$ follows from the dominated convergence theorem since $\gamma >1$ and $\int _{\mathbb{R}^{3}}f(x)u_{n}^{1-\gamma }\,\mathrm{d}x<+\infty$. However, we have no idea whether or not $h_{n,\psi }(\eta )$ is differentiable. For the sake of proof, we set

$$ h'_{n,\psi }(0)=\lim_{\eta \rightarrow 0^{+}} \frac{h_{n,\psi }(\eta )-1}{\eta }\in [-\infty ,+\infty ]. $$

If the above limit does not exist, we choose $\eta _{k}\rightarrow 0$ (instead of $\eta \rightarrow 0$) with $\eta _{k}>0$ such that $h'_{n,\psi }(0)=\lim_{k\rightarrow \infty }\frac{h_{n,\psi }(\eta _{k})-1}{\eta _{k}}\in [-\infty ,+\infty ]$. According to $u_{n}\in \mathcal{N}_{2}^{(b)}$ and $h_{n,\psi }(\eta )(u_{n}+\eta \psi )\in \mathcal{N}_{2}^{(b)}$, we have

$$\begin{aligned}& \Vert u_{n} \Vert _{E}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}= \int _{\mathbb{R}^{3}}f(x)u_{n}^{1- \gamma }\, \mathrm{d}x, \\& h_{n,\psi }^{2}(\eta ) \Vert u_{n}+\eta \psi \Vert _{E}^{2}+b h_{n,\psi }^{4}( \eta ) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}(u_{n}+ \eta \psi ) \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \\& \quad =h_{n,\psi }^{1-\gamma }(\eta ) \int _{\mathbb{R}^{3}}f(x) (u_{n}+\eta \psi )^{1-\gamma }\,\mathrm{d}x. \end{aligned}$$

Since $\gamma >1$, the above two equalities yield

$$\begin{aligned} 0 \ge & \bigl[h_{n,\psi }(\eta )-1 \bigr] \biggl\{ \bigl[h_{n,\psi }( \eta )+1 \bigr] \Vert u_{n}+\eta \psi \Vert _{E}^{2} \\ &{}- \frac{h_{n,\psi }^{1-\gamma }(\eta )-1}{h_{n,\psi }(\eta )-1} \int _{\mathbb{R}^{3}}f(x) (u_{n}+\eta \psi )^{1-\gamma } \,\mathrm{d}x \\ &{}+b \bigl[h_{n,\psi }^{2}(\eta )+1 \bigr] \bigl[h_{n, \psi }(\eta )+1 \bigr] \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}(u_{n}+ \eta \psi ) \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \biggr\} \\ &{}+ \bigl[ \Vert u_{n}+\eta \psi \Vert _{E}^{2}- \Vert u_{n} \Vert _{E}^{2} \bigr] \\ &{}+b \biggl[ \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}(u_{n}+ \eta \psi ) \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}- \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \biggr]. \end{aligned}$$

Dividing by $\eta >0$ and passing to the limit as $\eta \rightarrow 0^{+}$, using the continuity of $h_{n,\psi }(\eta )$ and $u_{n}\in \mathcal{N}_{2}^{(b)}$, we obtain

$$\begin{aligned} 0 \ge &h'_{n,\psi }(0) \biggl\{ 2 \Vert u_{n} \Vert _{E}^{2}+(\gamma -1) \int _{\mathbb{R}^{3}}f(x)u_{n}^{1-\gamma }\, \mathrm{d}x+4b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2} \biggr\} \\ &{}+2(u_{n},\psi )_{E}+4b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(- \Delta )^{\frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\ =&h'_{n,\psi }(0) \biggl\{ (\gamma +1) \Vert u_{n} \Vert _{E}^{2}+b(\gamma +3) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2} \biggr\} \\ &{}+2(u_{n},\psi )_{E}+4b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(- \Delta )^{\frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x, \end{aligned}$$

which implies that $h'_{n,\psi }(0)\neq +\infty$. Since $C_{1}\le \|u_{n}\|_{E}\le C_{2}$ by Step 3, we can further conclude from the above inequality that

$$ h'_{n,\psi }(0)\le C_{3} \quad \text{uniformly in } n $$

(2.6)

for some suitable constant $C_{3}>0$ and

$$ \frac{ \Vert u_{n} \Vert _{E}}{n}- \frac{(\gamma +1)C_{1}^{2}}{\gamma -1}< 0 $$

for n large enough. We claim that there exists a constant $C_{4}$ such that $h'_{n,\psi }(0)\ge C_{4}$ uniformly in all n large. Fix n, without loss of generality, we can assume $h'_{n,\psi }(0)<0$, and so $h_{n,\psi }(\eta )<1$ for $\eta >0$ small. Applying condition (2) with $z=h_{n,\psi }(\eta )(u_{n}+\eta \psi )$ leads to

$$\begin{aligned} \frac{1}{n}\bigl[1-h_{n,\psi }(\eta )\bigr] \Vert u_{n} \Vert _{E}+ \frac{\eta }{n}h_{n,\psi }( \eta ) \Vert \psi \Vert _{E} \ge & \frac{1}{n} \bigl\Vert u_{n}-h_{n,\psi }(\eta ) (u_{n}+\eta \psi ) \bigr\Vert _{E} \\ \ge &I_{b}(u_{n})-I_{b} \bigl[h_{n,\psi }(\eta ) (u_{n}+\eta \psi )\bigr]. \end{aligned}$$

(2.7)

Since $u_{n}\in \mathcal{N}_{2}^{(b)}$, we can further get

$$\begin{aligned} \frac{ \Vert \psi \Vert _{E}}{n}h_{n,\psi }(\eta ) \ge & \frac{h_{n,\psi }(\eta )-1}{\eta } \biggl\{ \frac{ \Vert u_{n} \Vert _{E}}{n}- \biggl( \frac{1}{2}+ \frac{1}{\gamma -1} \biggr)\bigl[h_{n,\psi }(\eta )+1\bigr] \Vert u_{n}+ \eta \psi \Vert _{E}^{2} \\ &{}-b \biggl( \frac{1}{4}+ \frac{1}{\gamma -1} \biggr) \bigl[h_{n,\psi }^{2}(\eta )+1 \bigr] \bigl[h_{n,\psi }( \eta )+1 \bigr] \\ &{}\times \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}(u_{n}+ \eta \psi ) \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2} \biggr\} \\ &{}- \biggl( \frac{1}{2}+ \frac{1}{\gamma -1} \biggr) \frac{ \Vert u_{n}+\eta \psi \Vert _{E}^{2}- \Vert u_{n} \Vert _{E}^{2}}{\eta } \\ &{}-b \biggl( \frac{1}{4}+ \frac{1}{\gamma -1} \biggr) \\ &{} \times \frac{ [ (\int _{\mathbb{R}^{3}} \vert (-\Delta )^{\frac{s}{2}}(u_{n}+\eta \psi ) \vert ^{2}\,\mathrm{d}x )^{2}- (\int _{\mathbb{R}^{3}} \vert (-\Delta )^{\frac{s}{2}}u_{n} \vert ^{2}\,\mathrm{d}x )^{2} ]}{\eta }. \end{aligned}$$

Letting $\eta \rightarrow 0^{+}$, using the continuity of $h_{n,\psi }(\eta )$ and $C_{1}\le \|u_{n}\|_{E}\le C_{2}$, we obtain

$$\begin{aligned} \frac{ \Vert \psi \Vert _{E}}{n} \ge &h'_{n,\psi }(0) \biggl\{ \frac{ \Vert u_{n} \Vert _{E}}{n}- \biggl( \frac{\gamma +1}{\gamma -1} \biggr) \Vert u_{n} \Vert _{E}^{2}-b \biggl( \frac{\gamma +3}{\gamma -1} \biggr) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \biggr\} \\ &{}- \biggl( \frac{\gamma +1}{\gamma -1} \biggr) (u_{n}, \psi )_{E}-b \biggl( \frac{\gamma +3}{\gamma -1} \biggr) \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\ =&h'_{n,\psi }(0) \biggl\{ \frac{ \Vert u_{n} \Vert _{E}}{n}- \frac{1}{\gamma -1} \biggl[(\gamma +1) \Vert u_{n} \Vert _{E}^{2}+b( \gamma +3) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \biggr] \biggr\} \\ &{}- \biggl( \frac{\gamma +1}{\gamma -1} \biggr) (u_{n}, \psi )_{E}-b \biggl( \frac{\gamma +3}{\gamma -1} \biggr) \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\ \ge &h'_{n,\psi }(0) \biggl\{ \frac{ \Vert u_{n} \Vert _{E}}{n}- \frac{(\gamma +1)C_{1}^{2}}{\gamma -1} \biggr\} - \biggl( \frac{\gamma +1}{\gamma -1} \biggr) (u_{n},\psi )_{E} \\ &{}-b \biggl( \frac{\gamma +3}{\gamma -1} \biggr) \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \end{aligned}$$

since $\gamma >1$ and $h'_{n,\psi }(0)<0$. Then, from the construction of coefficient, we see that $h'_{n,\psi }(0)\neq -\infty$ and cannot diverge to −∞ as $n\rightarrow \infty$, that is,

$$ h'_{n,\psi }(0)\neq -\infty , \quad \text{and}\quad h'_{n,\psi }(0)\ge C_{4} \quad \text{uniformly in } n \text{ large} $$

(2.8)

for some suitable constant $C_{4}$. So, it follows from (2.6) and (2.8) that

$$ h'_{n,\psi }(0)\in (-\infty ,+\infty ), \quad \text{and} \quad \bigl\vert h'_{n,\psi }(0) \bigr\vert \le C \quad \text{uniformly in } n \text{ large}, $$

where $C=\max \{C_{3},|C_{4}|\}$ is independent of n. Furthermore, applying condition (2) with $z=h_{n,\psi }(\eta )(u_{n}+\eta \psi )$ again leads to

$$\begin{aligned}& \frac{ \vert 1-h_{n,\psi }(\eta ) \vert }{\eta } \frac{ \Vert u_{n} \Vert _{E}}{n}+ \frac{ \Vert \psi \Vert _{E}}{n}h_{n, \psi }( \eta ) \\& \quad \ge \frac{1}{n\eta } \bigl\Vert u_{n}-h_{n,\psi }( \eta ) (u_{n}+ \eta \psi ) \bigr\Vert _{E} \\& \quad \ge \frac{1}{\eta } \bigl[I_{b}(u_{n})-I_{b} \bigl[h_{n, \psi }(\eta ) (u_{n}+\eta \psi )\bigr] \bigr] \\& \quad \ge \frac{h_{n,\psi }(\eta )-1}{\eta } \biggl\{ - \frac{h_{n,\psi }(\eta )+1}{2} \Vert u_{n}+\eta \psi \Vert _{E}^{2} \\& \qquad {}+ \frac{h_{n,\psi }^{1-\gamma }(\eta )-1}{(1-\gamma )[h_{n,\psi }(\eta )-1]} \int _{\mathbb{R}^{3}}f(x) (u_{n}+\eta \psi )^{1-\gamma } \,\mathrm{d}x \\& \qquad {}- \frac{b}{4} \bigl[h_{n,\varphi }^{2}(\eta )+1 \bigr] \bigl[h_{n,\varphi }(\eta )+1 \bigr] \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}(u_{n}+ \eta \psi ) \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2} \biggr\} \\& \qquad {}- \frac{b}{4} \frac{ [ (\int _{\mathbb{R}^{3}} \vert (-\Delta )^{\frac{s}{2}}(u_{n}+\eta \psi ) \vert ^{2}\,\mathrm{d}x )^{2}- (\int _{\mathbb{R}^{3}} \vert (-\Delta )^{\frac{s}{2}}u_{n} \vert ^{2}\,\mathrm{d}x )^{2} ]}{\eta } \\& \qquad {}- \frac{1}{2} \frac{ \Vert u_{n}+\eta \psi \Vert _{E}^{2}- \Vert u_{n} \Vert _{E}^{2}}{\eta }+ \frac{1}{1-\gamma } \int _{\mathbb{R}^{3}}f(x) \frac{(u_{n}+\eta \psi )^{1-\gamma }-u_{n}^{1-\gamma }}{\eta }\,\mathrm{d}x. \end{aligned}$$

Passing to the liminf as $\eta \rightarrow 0^{+}$, since $u_{n}\in \mathcal{N}_{2}^{(b)}$, by the continuity of $h_{n,\psi }(\eta )$ and Fatou’s lemma, we have

$$\begin{aligned}& \frac{ \vert h'_{n,\psi }(0) \vert \cdot \Vert u_{n} \Vert _{E}}{n}+ \frac{ \Vert \psi \Vert _{E}}{n} \\& \quad \ge h'_{n,\psi }(0) \biggl\{ - \Vert u_{n} \Vert _{E}^{2}+ \int _{ \mathbb{R}^{3}}f(x)u_{n}^{1-\gamma }\, \mathrm{d}x-b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \biggr\} \\& \qquad {}-b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\& \qquad {}-(u_{n},\psi )_{E}+\liminf _{\eta \rightarrow 0^{+}} \frac{1}{1-\gamma } \int _{\mathbb{R}^{3}}f(x) \frac{(u_{n}+\eta \psi )^{1-\gamma }-u_{n}^{1-\gamma }}{\eta }\,\mathrm{d}x \\& \quad \ge-(u_{n},\psi )_{E}-b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(- \Delta )^{\frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\& \qquad {}+ \int _{\mathbb{R}^{3}} \frac{f(x)}{1-\gamma }\liminf_{\eta \rightarrow 0^{+}} \frac{(u_{n}+\eta \psi )^{1-\gamma }-u_{n}^{1-\gamma }}{\eta }\,\mathrm{d}x \\& \quad =-(u_{n},\psi )_{E}-b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x+ \int _{ \mathbb{R}^{3}}f(x)u_{n}^{-\gamma }\psi \, \mathrm{d}x. \end{aligned}$$

Furthermore, for n large, we have

$$\begin{aligned}& \int _{\mathbb{R}^{3}}f(x)u_{n}^{-\gamma }\psi \, \mathrm{d}x \\& \quad \le \frac{ \vert h'_{n,\psi }(0) \vert \cdot \Vert u_{n} \Vert _{E}+ \Vert \psi \Vert _{E}}{n}+(u_{n}, \psi )_{E} \\& \qquad {}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{n} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\& \quad \le \frac{C\cdot C_{2}+ \Vert \psi \Vert _{E}}{n}+(u_{n},\psi )_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{n}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x, \end{aligned}$$

thanks to $C_{1}\le \|u_{n}\|_{E}\le C_{2}$ and $|h'_{n,\varphi }(0)|\le C$ uniformly in n large. Passing to the limit as $n\rightarrow \infty$ with using Hölder’s inequality and Fatou’s lemma again leads to

$$ \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }\psi \, \mathrm{d}x< +\infty $$

for any $0\le \psi \in E$. By the same argument as in Case 1, we can also obtain that

$$ u_{b}\in \mathcal{N}_{2}^{(b)}, \quad \inf _{\mathcal{N}_{1}^{(b)}}I_{b}=I_{b}(u_{b}), $$

(2.9)

and for any $0\le \psi \in E$,

$$\begin{aligned}& (u_{b},\psi )_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \\& \quad \ge \int _{\mathbb{R}^{3}}f(x)u_{b}^{- \gamma }\psi \, \mathrm{d}x \end{aligned}$$

(2.10)

in Case 2. Therefore, combining (2.4), (2.5), (2.9), and (2.10), we could conclude that in either case, up to a subsequence, $u_{n}\rightarrow u_{b}$ strongly in E, $u_{b}\in \mathcal{N}_{2}^{(b)}$, $\inf_{\mathcal{N}_{1}^{(b)}}I_{b}=I_{b}(u_{b})$, and

$$ (u_{b},\psi )_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}\psi \,\mathrm{d}x \ge \int _{\mathbb{R}^{3}}f(x)u_{b}^{- \gamma }\psi \, \mathrm{d}x $$

(2.11)

for any $0\le \psi \in E$.

Step 5. We prove that $u_{b}>0$ in $\mathbb{R}^{3}$ and $u_{b}$ is a solution of problem ($P_{b}$).

According to Step 4, $u_{b}\in \mathcal{N}_{2}^{(b)}$, that is,

$$ \Vert u_{b} \Vert _{E}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}- \int _{ \mathbb{R}^{3}}f(x)u_{b}^{1-\gamma }=0. $$

(2.12)

For any $v\in E$ and $\varepsilon >0$, set $v_{\varepsilon }=u_{b}+\varepsilon v$, then

$$\begin{aligned}& \bigl(u_{b}(x)-u_{b}(y)\bigr) \bigl(v_{\varepsilon }^{+}(x)-v_{\varepsilon }^{+}(y) \bigr) \\& \quad =\bigl(u_{b}(x)-u_{b}(y)\bigr) \bigl(v_{\varepsilon }(x)+v_{\varepsilon }^{-}(x)-v_{\varepsilon }(y)-v_{\varepsilon }^{-}(y) \bigr) \\& \quad = \bigl\vert u_{b}(x)-u_{b}(y) \bigr\vert ^{2}+\varepsilon \bigl(u_{b}(x)-u_{b}(y) \bigr) \bigl(v(x)-v(y)\bigr) \\& \quad \quad {}+\bigl(u_{b}(x)-u_{b}(y)\bigr) \bigl(v_{\varepsilon }^{-}(x)-v_{\varepsilon }^{-}(y) \bigr). \end{aligned}$$

(2.13)

Using the proof of Theorem 3.2 in [8], we can obtain

$$ \liminf_{\varepsilon \rightarrow 0^{+}} \frac{1}{\varepsilon } \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}} \frac{(u_{b}(x)-u_{b}(y)) [v_{\varepsilon }^{-}(x)-v_{\varepsilon }^{-}(y) ]}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y \le 0. $$

(2.14)

Set $\Omega _{\varepsilon }=\{x\in \mathbb{R}^{3}:v_{\varepsilon }\le 0\}$, then using (2.12)–(2.13) and applying inequality (2.11) with $\psi =v_{\varepsilon }^{+}$ lead to

$$\begin{aligned} 0 \le & \frac{1}{\varepsilon } \biggl\{ \int _{ \mathbb{R}^{3}} \int _{\mathbb{R}^{3}} \frac{(u_{b}(x)-u_{b}(y))(v_{\varepsilon }^{+}(x)-v_{\varepsilon }^{+}(y))}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y+ \int _{\mathbb{R}^{3}} V(x)u_{b}v_{\varepsilon }^{+} \,\mathrm{d}x \\ &{} +b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v_{\varepsilon }^{+} \,\mathrm{d}x- \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }v_{\varepsilon }^{+} \,\mathrm{d}x \biggr\} \\ =& \frac{1}{\varepsilon } \int _{\mathbb{R}^{3}} \int _{ \mathbb{R}^{3}}\frac{ \vert u_{b}(x)-u_{b}(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x\,\mathrm{d}y + \int _{\mathbb{R}^{3}} \int _{ \mathbb{R}^{3}}\frac{(u_{b}(x)-u_{b}(y))(v(x)-v(y))}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y \\ &{}+ \frac{1}{\varepsilon } \int _{\mathbb{R}^{3}} \int _{ \mathbb{R}^{3}} \frac{(u_{b}(x)-u_{b}(y))(v_{\varepsilon }^{-}(x)-v_{\varepsilon }^{-}(y))}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y \\ &{}+ \frac{1}{\varepsilon } \biggl( \int _{\mathbb{R}^{3}}- \int _{\Omega _{\varepsilon }} \biggr) \biggl\{ V(x)u_{b}(u_{b}+ \varepsilon v) \\ &{} +b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \,\mathrm{d}x \biggr) (-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}(u_{b}+ \varepsilon v)-f(x)u_{b}^{-\gamma }(u_{b}+ \varepsilon v) \biggr\} \,\mathrm{d}x \\ =& \frac{1}{\varepsilon } \biggl\{ \Vert u_{b} \Vert _{E}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}- \int _{\mathbb{R}^{3}}f(x)u_{b}^{1-\gamma }\, \mathrm{d}x \biggr\} \\ &{}+ \biggl\{ (u_{b},v)_{E}+ b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(- \Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v \,\mathrm{d}x- \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }v \, \mathrm{d}x \biggr\} \\ &{}- \frac{1}{\varepsilon } \int _{\Omega _{\varepsilon }} \biggl\{ V(x)u_{b}(u_{b}+ \varepsilon v)+b \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \biggr) (- \Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}(u_{b}+ \varepsilon v) \\ &{}-f(x)u_{b}^{-\gamma }(u_{b}+\varepsilon v) \biggr\} \,\mathrm{d}x+ \frac{1}{\varepsilon } \int _{\mathbb{R}^{3}} \int _{ \mathbb{R}^{3}} \frac{(u_{b}(x)-u_{b}(y))(v_{\varepsilon }^{-}(x)-v_{\varepsilon }^{-}(y))}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y \\ \le & \biggl\{ (u_{b},v)_{E}+ b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(- \Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v \,\mathrm{d}x- \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }v \, \mathrm{d}x \biggr\} \\ &{}- \frac{1}{\varepsilon } \int _{\Omega _{\varepsilon }} \biggl[V(x)u_{b}^{2}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \biggr) \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \biggr] \, \mathrm{d}x \\ &{}- \int _{\Omega _{\varepsilon }} \biggl[V(x)u_{b} v+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \biggr) (-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v \biggr] \,\mathrm{d}x \\ &{}+ \frac{1}{\varepsilon } \int _{\mathbb{R}^{3}} \int _{ \mathbb{R}^{3}} \frac{(u_{b}(x)-u_{b}(y))(v_{\varepsilon }^{-}(x)-v_{\varepsilon }^{-}(y))}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y \\ \le & \biggl\{ (u_{b},v)_{E}+ b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(- \Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v \,\mathrm{d}x- \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }v \, \mathrm{d}x \biggr\} \\ &{}- \int _{\Omega _{\varepsilon }} \biggl[V(x)u_{b} v+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \biggr) (-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v \biggr] \,\mathrm{d}x \\ &{}+ \frac{1}{\varepsilon } \int _{\mathbb{R}^{3}} \int _{ \mathbb{R}^{3}} \frac{(u_{b}(x)-u_{b}(y))(v_{\varepsilon }^{-}(x)-v_{\varepsilon }^{-}(y))}{ \vert x-y \vert ^{3+2s}} \,\mathrm{d}x \,\mathrm{d}y. \end{aligned}$$

Passing to the liminf as $\varepsilon \rightarrow 0^{+}$ to the above inequality and using (2.14) and the fact that $|\Omega _{\varepsilon }|\rightarrow 0$ as $\varepsilon \rightarrow 0^{+}$, we have

$$ (u_{b},v)_{E}+ b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v \,\mathrm{d}x- \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }v \, \mathrm{d}x \ge 0, \quad \forall v\in E. $$

This inequality also holds for −v, hence we obtain

$$\begin{aligned}& (u_{b},v)_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u_{b}(- \Delta )^{\frac{s}{2}}v \,\mathrm{d}x \\& \quad - \int _{\mathbb{R}^{3}}f(x)u_{b}^{-\gamma }v \, \mathrm{d}x=0, \quad \forall v\in E. \end{aligned}$$

(2.15)

From an argument similar to [29, Theorem 6.3], we know that $u_{b}\in C^{\alpha }_{\mathrm{loc}}(\mathbb{R}^{3})$ for some $\alpha \in (0, s)$. On the other hand, (2.15) implies that

$$ \biggl[1+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2} \,\mathrm{d}x \biggr](-\Delta )^{s}u_{b}+V(x)u_{b} \ge 0. $$

(2.16)

Assume that there exists $x_{0}\in \mathbb{R}^{3}$ such that $u_{b}(x_{0}) = 0$, then from (2.16) we have $(-\Delta )^{s}u_{b}(x_{0})\ge 0$. On the other hand, since $u_{b}\ge 0$ and $u_{b}\not \equiv 0$, we can get from Lemma 3.2 in [7] that

$$\begin{aligned} (-\Delta )^{s}u_{b}(x_{0}) =&- \int _{\mathbb{R}^{3}} \frac{u_{b}(x_{0}+y)+u_{b}(x_{0}-y)-2u_{b}(x_{0})}{ \vert y \vert ^{3+2s}} \,\mathrm{d}y \\ =&- \int _{\mathbb{R}^{3}} \frac{u_{b}(x_{0}+y)+u_{b}(x_{0}-y)}{ \vert y \vert ^{3+2s}}\,\mathrm{d}y< 0, \end{aligned}$$

a contradiction. Therefore, $u_{b}>0$ in $\mathbb{R}^{3}$ and $u_{b}\in E$ is a solution of problem ($P_{b}$).

Step 6. We show that $u_{b}$ is a unique solution of problem ($P_{b}$).

Suppose that $u_{*}\in E$ is also a solution of problem ($P_{b}$), then we have

$$\begin{aligned}& (u_{*},v)_{E}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{*} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{*}(- \Delta )^{\frac{s}{2}}v \,\mathrm{d}x \\& \quad {} - \int _{\mathbb{R}^{3}}f(x)u_{*}^{- \gamma }v \, \mathrm{d}x=0, \quad \forall v\in E. \end{aligned}$$

(2.17)

Taking $v=u_{b}-u_{*}$ in both equations (2.15)–(2.17) and subtracting term by term, we obtain

$$\begin{aligned} 0 \ge & \int _{\mathbb{R}^{3}}f(x) \bigl(u_{b}^{-\gamma }-u_{*}^{- \gamma } \bigr) (u_{b}-u_{*})\,\mathrm{d}x \\ =& \Vert u_{b}-u_{*} \Vert _{E}^{2}+b \biggl[ \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \\ &{}- \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b} \bigr\vert ^{2}\,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{b}(- \Delta )^{ \frac{s}{2}}u_{*} \,\mathrm{d}x \\ &- \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{*} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{*}(- \Delta )^{\frac{s}{2}}u_{b} \,\mathrm{d}x+ \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u_{*} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \biggr] \\ \ge & \Vert u_{b}-u_{*} \Vert _{E}^{2}+b \bigl([u_{b}]_{s}^{4}-[u_{b}]_{s}^{3}[u_{*}]_{s}-[u_{*}]_{s}^{3}[u_{b}]_{s}+[u_{*}]_{s}^{4} \bigr) \\ =& \Vert u_{b}-u_{*} \Vert _{E}^{2}+b \bigl([u_{b}]_{s}-[u_{*}]_{s} \bigr)^{2}\bigl([u_{b}]_{s}^{2}+[u_{b}]_{s}[u_{*}]_{s}+[u_{*}]_{s}^{2} \bigr) \\ \ge & \Vert u_{b}-u_{*} \Vert _{E}^{2}\ge 0, \end{aligned}$$

where we use Hölder’s inequality. So $\|u_{b}-u_{*}\|_{E}^{2}=0$, then $u_{b}=u_{*}$ and $u_{b}$ is the unique solution of problem ($P_{b}$). This ends the proof of Theorem 1.1. □

Proof of Theorem 1.2

In the proof of Theorem 1.1, $b=0$ and $b=1$ are allowed. Hence, under the assumptions of Theorem 1.2, there exist a unique positive solution $w_{0}\in E$ to problem ($P_{0}$) and a unique positive solution $w_{1}\in E$ to problem $(P_{1})$, that is, for any $v\in E$, one has

$$\begin{aligned}& \textstyle\begin{cases} (w_{0},v)_{E}= \int _{\mathbb{R}^{3}}f(x)w_{0}^{-\gamma }v \,\mathrm{d}x, \\ w_{0}\in \mathcal{N}_{2}^{(0)}, \qquad \inf_{\mathcal{N}_{1}^{(0)}}I_{0}=I_{0}(w_{0}), \end{cases}\displaystyle \end{aligned}$$

(2.18)

$$\begin{aligned}& \textstyle\begin{cases} (w_{1},v)_{E}+\int _{\mathbb{R}^{3}} \vert (-\Delta )^{ \frac{s}{2}}w_{1} \vert ^{2}\,\mathrm{d}x\int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}w_{1}(-\Delta )^{\frac{s}{2}}v \,\mathrm{d}x =\int _{ \mathbb{R}^{3}}f(x)w_{1}^{-\gamma }v \,\mathrm{d}x, \\ w_{1}\in \mathcal{N}_{2}^{(1)},\quad \inf_{\mathcal{N}_{1}^{(1)}}I_{1}=I_{1}(w_{1}). \end{cases}\displaystyle \end{aligned}$$

(2.19)

Step 1. We prove that $c_{b}\le c_{1}$ for $b\in [0,1]$ where $c_{b}=\inf_{\mathcal{N}_{1}^{(b)}}I_{b}$.

By the proof of the necessity of Theorem 1.1, we have $\int _{\mathbb{R}^{3}}f(x)w_{1}^{1-\gamma }\,\mathrm{d}x<+ \infty$. According to Step 1 in the proof of Theorem 1.1 and (2.19), there exists unique $\eta (w_{1})>0$ such that $\eta (w_{1})w_{1}\in \mathcal{N}_{2}^{(b)}$, $I_{b}(\eta (w_{1})w_{1})=\min_{\eta >0}I_{b}(\eta w_{1})$, and $c_{1}=I_{1}(w_{1})=\min_{\eta >0}I_{1}(\eta w_{1})$. Since $\mathcal{N}_{2}^{(b)}\subset \mathcal{N}_{1}^{(b)}$ and $b\in [0,1]$, we then have

$$ c_{b}=\inf_{\mathcal{N}_{1}^{(b)}}I_{b}\le \inf _{\mathcal{N}_{2}^{(b)}}I_{b} \le I_{b}\bigl(\eta (w_{1})w_{1}\bigr)=\min_{\eta >0}I_{b}( \eta w_{1}) \le \min_{\eta >0}I_{1}(\eta w_{1})=c_{1}. $$

For every vanishing sequence $\{b_{n}\}\subset (0,1)$, since $\{u_{b_{n}}\}$ is a positive solution sequence to problem ($P_{b}$) provided by Theorem 1.1, then $c_{b_{n}}\le c_{1}$ and for every $v\in E$,

$$ (u_{b_{n}},v)_{E}+b_{n} \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b_{n}} \bigr\vert ^{2} \,\mathrm{d}x \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{b_{n}}(- \Delta )^{\frac{s}{2}}v \,\mathrm{d}x = \int _{\mathbb{R}^{3}}f(x)u_{b_{n}}^{- \gamma }v \, \mathrm{d}x. $$

(2.20)

Using (2.1), we can further get

$$ \frac{1}{2} \Vert u_{b_{n}} \Vert _{E}^{2} \le I_{b_{n}}(u_{b_{n}})=c_{b_{n}} \le c_{1}, $$

which implies that $\{u_{b_{n}}\}$ is bounded in E, and so there exist a subsequence of $\{u_{b_{n}}\}$ (still denoted by $\{u_{b_{n}}\}$) and a nonnegative function $u_{0}\in E$ such that

$$\begin{aligned}& u_{b_{n}}\rightharpoonup u_{0},\quad \text{in } E, \\& u_{b_{n}}\rightarrow u_{0}, \quad \text{in } L^{p}\bigl(\mathbb{R}^{3}\bigr), p\in [2,2_{s}^{*}), \\& u_{b_{n}}\rightarrow u_{0}, \quad \text{a.e. in } \mathbb{R}^{3}. \end{aligned}$$

(2.21)

Step 2. We prove that $u_{0}\in \mathcal{N}_{2}^{(0)}$, $\inf_{\mathcal{N}_{1}^{(0)}}I_{0}=I_{0}(u_{0})$, $u_{b_{n}}\rightarrow u_{0}$ in E, and for any $0\le v\in E$,

$$ (u_{0},v)_{E}\ge \int _{\mathbb{R}^{3}}f(x)u_{0}^{-\gamma }v \, \mathrm{d}x. $$

Passing to the liminf as $n\rightarrow \infty$ in (2.20) and using Fatou’s lemma, for any $0 \le v \in E$, we have

$$ (u_{0},v)_{E}- \int _{\mathbb{R}^{3}}f(x)u_{0}^{-\gamma }v \, \mathrm{d}x \ge 0. $$

(2.22)

Similar to Step 4 in the proof of Theorem 1.1, we have $u_{0}> 0$ in $\mathbb{R}^{3}$. Choosing $v=u_{0}$ in (2.22) leads to $\|u_{0}\|_{E}^{2}-\int _{\mathbb{R}^{3}}f(x)u_{0}^{1- \gamma }\,\mathrm{d}x\ge 0$, i.e., $u_{0}\in \mathcal{N}_{1}^{(0)}$, so $I_{0}(u_{0})\ge c_{0}$. Similar to Step 1, for any $n\in \mathbb{N}$, there exists unique $\eta _{n}(w_{0})>0$ such that $\eta _{n}(w_{0})w_{0}\in \mathcal{N}_{2}^{(b_{n})}$, $I_{b_{n}}(\eta _{n}(w_{0})w_{0})=\min_{\eta >0}I_{b_{n}}( \eta w_{0})$. Thus

$$\begin{aligned} c_{0} =&I_{0}(w_{0}) \\ =&I_{b_{n}}(w_{0})- \frac{b_{n}}{4} \biggl( \int _{ \mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}w_{0} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2} \\ \ge &I_{b_{n}}\bigl(\eta _{n}(w_{0})w_{0} \bigr)- \frac{b_{n}}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}w_{0} \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2} \\ \ge &c_{b_{n}}- \frac{b_{n}}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}w_{0} \bigr\vert ^{2}\,\mathrm{d}x \biggr)^{2}, \end{aligned}$$

which yields

$$ \limsup_{n\rightarrow +\infty }c_{b_{n}}\le c_{0}. $$

(2.23)

On the other hand,

$$\begin{aligned} c_{b_{n}} =&I_{b_{n}}(u_{b_{n}}) \\ =& \frac{1}{2} \Vert u_{b_{n}} \Vert _{E}^{2}+ \frac{b_{n}}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{b_{n}} \bigr\vert ^{2} \,\mathrm{d}x \biggr)^{2}- \frac{1}{1-\gamma } \int _{ \mathbb{R}^{3}}f(x)u_{b_{n}}^{1-\gamma }\, \mathrm{d}x \\ \ge & \frac{1}{2} \Vert u_{b_{n}} \Vert _{E}^{2}- \frac{1}{1-\gamma } \int _{\mathbb{R}^{3}}f(x)u_{b_{n}}^{1-\gamma } \, \mathrm{d}x. \end{aligned}$$

By the weak lower semi-continuity of the norm, (2.21), Fatou’s lemma, and $I_{0}(u_{0})\ge c_{0}$, we have

$$\begin{aligned} \liminf_{n\rightarrow \infty }c_{b_{n}} \ge &\liminf _{n \rightarrow \infty } \biggl[ \frac{1}{2} \Vert u_{b_{n}} \Vert _{E}^{2} \biggr]+\liminf _{n\rightarrow \infty } \biggl[ \frac{1}{\gamma -1} \int _{\mathbb{R}^{3}}f(x)u_{b_{n}}^{1-\gamma } \, \mathrm{d}x \biggr] \\ \ge & \frac{1}{2} \Vert u_{0} \Vert _{E}^{2}+ \frac{1}{\gamma -1} \int _{\mathbb{R}^{3}}f(x)u_{0}^{1-\gamma } \, \mathrm{d}x=I_{0}(u_{0})\ge c_{0}. \end{aligned}$$

(2.24)

This combined with (2.23) leads to $\lim_{n\rightarrow +\infty }c_{b_{n}}=c_{0}$. Thus, the above inequalities are actually equalities, so $u_{b_{n}}\rightarrow u_{0}$ in E and $I_{0}(u_{0})=c_{0}=\inf_{\mathcal{N}_{1}^{(0)}}I_{0}$. Choosing $v = u_{b_{n}}$ in (2.20) and passing to the liminf as $n\rightarrow +\infty$, one can get

$$ \Vert u_{0} \Vert _{E}^{2}= \int _{\mathbb{R}^{3}}f(x)u_{0}^{1-\gamma } \, \mathrm{d}x. $$

That is to say, $u_{0}\in \mathcal{N}_{2}^{(0)}$.

Step 3. We prove that $u_{0}=w_{0}$ and then $u_{b_{n}}\rightarrow w_{0}$ in E.

By (2.22) and $u_{0}\in \mathcal{N}_{2}^{(0)}$, similar to Step 5 in the proof of Theorem 1.1, we can further that $0< u_{0}\in E$ is also a solution of problem ($P_{0}$). By the uniqueness of solution to problem ($P_{0}$), $u_{0}=w_{0}$. Hence $u_{b_{n}}\rightarrow w_{0}$ in E and $w_{0}$ is the unique positive solution to problem ($P_{0}$). This completed the proof of Theorem 1.2. □