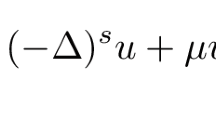Multiple sign-changing solutions for nonlinear fractional Kirchhoff equations

Abstract

This paper is concerned with the following nonlinear fractional Kirchhoff equation:

$$\biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) (- \Delta )^{s}u+V(x)u=f(u), \quad x\in \mathbb{R}^{3}, $$

where $s\in (\frac{3}{4}, 1)$, $a>0$, $b\geq 0$, $(-\Delta )^{s}$ denotes the fractional Laplacian operator. Based on the methods of mountain pass theorem and invariant sets of descending flow, the existence of a positive solution, a negative solution, and multiple sign-changing solutions is obtained.

1 Introduction

Consider the following nonlinear fractional Kirchhoff equation:

$$ \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx\biggr) (-\Delta )^{s}u+V(x)u=f(u), \quad x\in \mathbb{R}^{3}, $$

(1.1)

where $a>0$ and $b\geq 0$ are parameters, V and f are continuous. $(-\Delta )^{s}$ denotes the fractional Laplacian operator of order $s\in (\frac{3}{4}, 1)$ which is defined as

$$(-\Delta )^{s}u(x)=C_{3,s}\mathit{P.V.} \int _{\mathbb{R}^{3}} \frac{u(x)-u(y)}{ \vert x-y \vert ^{3+2s}}\,dy, \quad x\in \mathbb{R}^{3}, $$

where $u\in \mathcal{S}$, $\mathit{P.V.}$ denotes the Cauchy principle value and $C_{3,s}$ denotes a normalization constant. For simplicity, we omit the constant $C_{3,s}$ hereafter. Here, $\mathcal{S}$ stands for the Schwartz space of rapidly decaying $C^{\infty }$ functions in $\mathbb{R}^{3}$. It can be viewed as the infinitesimal generator of Lévy stable diffusion process [1,2,3]. Obviously, $(-\Delta )^{s}$ is a nonlocal operator. In the last few years, the research of nonlocal operators has appeared in various areas such as phase transitions, chemical reaction in liquids, optimization and finance, population dynamics, crystal dislocation, flames propagation, and so on. One can see [4,5,6] and the references therein. That is one of the reasons why the fractional problems have been widely investigated by more and more mathematical scholars.

When $s=1$, Eq. (1.1) reduces to the following Kirchhoff equation:

$$ \biggl(a+b \int _{\mathbb{R}^{3}} \vert \nabla u \vert ^{2}\,dx\biggr) \Delta u+V(x)u=f(u), \quad x\in \mathbb{R}^{3}, $$

(1.2)

which is related to the stationary version of the Kirchhoff equation

$$ u_{tt}-\biggl(a+b \int _{\varOmega } \vert \nabla u \vert ^{2}\,dx\biggr) \Delta u=f(x,u). $$

(1.3)

Equation (1.3) was first presented by Kirchhoff [7] as a generalization of the classical D’Alembert wave equation

$$\rho \frac{\partial ^{2}u}{\partial t^{2}}-\biggl(\frac{P_{0}}{h}+ \frac{E}{2L} \int _{0}^{L}\biggl(\frac{\partial u}{\partial x} \biggr)^{2}\,dx\biggr)\frac{ \partial ^{2}u}{\partial x^{2}}=f(x,u) $$

for free vibrations of elastic string in order to describe the changes in the length of the string during the vibrations. Here, ρ, $p _{0}$, h, E, L are constants which represent some physical meanings respectively. For more details in physical background, we refer to [8, 9]. In particular, after an abstract framework to (1.2) was proposed by Lions [10], Eq. (1.2) received more and more attention. For different nonlinearities, many important results have been obtained for Eq. (1.2), especially on the existence and nonexistence of solutions, ground state solutions, semiclassical state solutions, positive and negative solutions, high energy and least energy solutions, and sign-changing solutions. Those results can be found in [11,12,13,14,15,16,17] and the references therein.

When $a=1$ and $b=0$, Eq. (1.1) reduces to the following fractional Schrödinger equation:

$$ (-\Delta )^{s}u+V(x)u= f(u), \quad x\in \mathbb{R}^{3}. $$

(1.4)

In the last decade, many results have appeared for Eq. (1.4). For example, see [18,19,20,21] and the references therein.

Recently, Fiscella and Valdinoci [22] first proposed a stationary Kirchhoff model involving the fractional Laplacian, see [22, Appendix A] for more details in physical background. Then, many papers have been devoted to studying the existence of solutions for fractional Kirchhoff equation like (1.1). For instance, Peng, Tang, and Chen [23] investigated the existence of ground state solutions for Eq. (1.1) by using the method of Nehari manifold. Liu et al. [24] proved the existence of ground state solutions by using the monotonicity trick and the profile decomposition. Zhang et al. [25] studied the critical case of (1.1) and obtained the existence of ground state solutions by establishing Pohozave type identity when $s\in (\frac{3}{4}, 1)$. They also obtained the non-existence result when $s\in (0,\frac{3}{4})$.

To our best knowledge, there is no result on the existence of positive, negative, and sign-changing solutions for Eq. (1.1). The main reason is that the operator $(-\Delta )^{s}$ is nonlocal and very few things are known about it. The purpose of this paper is to fill this gap. In this paper, we are interested in the existence of one positive solution, one negative solution, and infinitely many sign-changing solutions for Eq. (1.1). Firstly, one positive solution and one negative solution are obtained by using the mountain pass theorem. Then we apply the method of invariant sets of descending flow to the situation of fractional Kirchhoff equation to prove the existence of infinitely many sign-changing solutions for Eq. (1.1). It is worth mentioning that our method does not depend on the existence of Nehari manifold, and the sign-changing solutions are obtained without any symmetry.

For convenience, we state our assumptions on potential V and nonlinear term f.

$(V)$ :

$V\in C(\mathbb{R}^{3}, \mathbb{R})$, $\inf_{x\in \mathbb{R}^{3}}V(x)>0$, and $\lim_{ \vert x \vert \rightarrow \infty } V(x)=\infty$.

$(f_{1})$ :

$f\in C(\mathbb{R}, \mathbb{R})$ and $\lim_{\tau \rightarrow 0}\frac{f(\tau )}{\tau }=0$.

$(f_{2})$ :

$\lim \sup_{ \vert \tau \vert \rightarrow +\infty }\frac{ \vert f(\tau ) \vert }{ \vert \tau \vert ^{p-1}}<\infty$ for some $p\in (4, 2_{s}^{\star })$, where $2_{s}^{\star }=\frac{6}{3-2s}$.

$(f_{3})$ :

There exists $\mu >4$ such that $\tau f(\tau )\geq \mu F( \tau )>0$ for all $\tau \neq 0$, where $F(\tau )=\int _{0}^{\tau }f(u)\,du$.

As a consequence of $(f_{2})$ and $(f_{3})$, one has $4<\mu \leq p < 2_{s}^{\star }$. Here are the main results.

Theorem 1.1

Assume that $(V)$ and $(f_{1})$–$(f_{3})$ hold. Then Eq. (1.1) has at least a positive solution, a negative solution, and a sign-changing solution.

Theorem 1.2

Assume that $(V)$ and $(f_{1})$–$(f_{3})$ hold. If, in addition, f is odd, then Eq. (1.1) has infinitely many sign-changing solutions.

The rest of this paper is organized as follows. Section 2 contains preliminary results. In Sect. 3, we apply the methods of mountain pass theorem and invariant sets of descending flow to prove Theorem 1.1 and Theorem 1.2.

Throughout this paper, $\Vert \cdot \Vert _{p}$ denotes the norm in $L^{p}( \mathbb{R}^{3})$ for $p\in [2,\infty )$. C, $C_{j}$ denote the different positive constants.

2 Preliminaries

In this section, we offer some preliminary lemmas and definitions which will be used later. Let us list some facts of the fractional order Sobolev space as follows.

For $0< s<1$, the fractional Sobolev space $H^{s}(\mathbb{R}^{3})$ can be defined as follows:

$$H^{s}\bigl(\mathbb{R}^{3}\bigr)=\biggl\{ u\in L^{2} \bigl(\mathbb{R}^{3}\bigr):\frac{ \vert u(x)-u(y) \vert }{ \vert x-y \vert ^{ \frac{3+2s}{2}}}\in L^{2}\bigl( \mathbb{R}^{3}\times \mathbb{R}^{3}\bigr)\biggr\} , $$

endowed with the natural norm

$$\Vert u \Vert _{H^{s}(\mathbb{R}^{3})}= \biggl( \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}}\frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}}\,dx\,dy+ \int _{\mathbb{R}^{3}} \vert u \vert ^{2}\,dx \biggr)^{\frac{1}{2}}, $$

and the inner product is

$$(u,v)_{H^{s}(\mathbb{R}^{3})}= \int _{\mathbb{R}^{3}} \int _{\mathbb{R} ^{3}}\frac{ (u(x)-u(y) ) (v(x)-v(y) )}{ \vert x-y \vert ^{3+2s}}\,dx\,dy+ \int _{\mathbb{R}^{3}}uv\,dx. $$

Furthermore, according to [21], we know that the norms on $H^{s}(\mathbb{R}^{3})$,

$$u \mapsto \biggl( \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}} \frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}}\,dx\,dy+ \int _{\mathbb{R}^{3}} \vert u \vert ^{2}\,dx \biggr)^{\frac{1}{2}} $$

and

$$u \mapsto \biggl( \int _{\mathbb{R}^{3}}\bigl( \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}+ \vert u \vert ^{2}\bigr)\,dx \biggr)^{\frac{1}{2}} $$

are equivalent.

In this paper, because of the presence of potential $V(x)$, we consider its subspace

$$E=\biggl\{ u\in H^{s}\bigl(\mathbb{R}^{3}\bigr): \int _{\mathbb{R}^{3}}V(x)u^{2} \,dx< \infty \biggr\} . $$

Define the norm in E by

$$\Vert u \Vert _{E}= \biggl( \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}} \frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}}\,dx\,dy+ \int _{\mathbb{R}^{3}}V(x)u ^{2}\,dx \biggr)^{\frac{1}{2}}. $$

Obviously, E is a Hilbert space with the inner product

$$(u,v)_{E}= \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}}\frac{ (u(x)-u(y) ) (v(x)-v(y) )}{ \vert x-y \vert ^{3+2s}}\,dx\,dy+ \int _{\mathbb{R}^{3}}V(x)uv\,dx. $$

Moreover, $\Vert \cdot \Vert _{E}$ is equivalent to the norm

$$\Vert u \Vert = \biggl( \int _{\mathbb{R}^{3}} \bigl( \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}+V(x) \vert u \vert ^{2} \bigr)\,dx \biggr)^{\frac{1}{2}}. $$

The corresponding inner product is

$$(u,v)= \int _{\mathbb{R}^{3}} \bigl((-\Delta )^{\frac{s}{2}}u(-\Delta )^{ \frac{s}{2}}v+V(x)uv \bigr)\,dx. $$

Throughout this paper, we will use the norm $\Vert \cdot \Vert$ in E.

Lemma 2.1

([26])

Under assumption $(V)$, E is continuously embedded into $L^{p}(\mathbb{R}^{3})$ for $p\in [2, 2_{s} ^{\star }]$ and compactly embedded into $L^{p}(\mathbb{R}^{3})$ for $p\in [2, 2_{s}^{\star })$.

The energy functional $I: E\rightarrow \mathbb{R}$ for (1.1) is defined by

$$ I(u)=\frac{1}{2} \int _{\mathbb{R}^{3}} \bigl(a \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}+V(x)u ^{2} \bigr)\,dx+\frac{b}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr)^{2} - \int _{\mathbb{R}^{3}}F(u)\,dx. $$

(2.1)

It is standard to show that $I\in C^{1}(E,\mathbb{R})$ and

$$\begin{aligned} \bigl(I'(u),\phi \bigr) =& \int _{\mathbb{R}^{3}} \bigl(a(-\Delta )^{\frac{s}{2}}u(- \Delta )^{\frac{s}{2}}\phi +V(x)u\phi \bigr)\,dx \\ & {}+b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u(-\Delta )^{\frac{s}{2}} \phi \,dx \\ & {} - \int _{\mathbb{R}^{3}}f(u)\phi \,dx, \quad u, \phi \in E. \end{aligned}$$

(2.2)

Recall that $I\in C^{1}(E,\mathbb{R})$ is said to satisfy the (PS) condition if any sequence $\{u_{n}\}\subset E$ such that $\{I(u_{n})\}$ is bounded and $I'(u_{n})\rightarrow 0$ as $n\rightarrow \infty$ admits a convergent subsequence.

Lemma 2.2

Assume that $(V)$ and $(f_{1})$–$(f_{3})$ hold. Then the functional I satisfies the (PS) condition.

Proof

Assume $\{u_{n}\}$ is a (PS) sequence of I. Then $\vert I(u_{n}) \vert \leq C$ and $I'(u_{n})\rightarrow 0$ as $n\rightarrow \infty$. By $(f_{3})$, Hölder’s inequality, and Lemma 2.1, we have

$$\begin{aligned} C+o(1) \Vert u_{n} \Vert \geq & I(u_{n})- \frac{1}{\mu }\bigl(I'(u_{n}), u_{n}\bigr) \\ =& \biggl(\frac{1}{2}-\frac{1}{\mu }\biggr) \int _{\mathbb{R}^{3}} \bigl(a \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}+V(x)u_{n}^{2} \bigr)\,dx \\ & {}+b \biggl(\frac{1}{4}-\frac{1}{ \mu }\biggr) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,dx \biggr)^{2} \\ & {} + \int _{\mathbb{R}^{3}} \biggl(\frac{1}{\mu }f(u_{n})u_{n}-F(u_{n}) \biggr)\,dx \\ \geq & \biggl(\frac{1}{2}-\frac{1}{\mu }\biggr)\min \{a,1\} \Vert u_{n} \Vert ^{2}, \end{aligned}$$

which implies that $\{u_{n}\}$ is bounded in E. Then there exists $u\in E$ such that $u_{n}\rightharpoonup u$ in E. By Lemma 2.1, $u_{n}\rightarrow u$ in $L^{p}(\mathbb{R}^{3})$ for $p\in [2, 2_{s} ^{\star })$ and $u_{n}(x)\rightarrow u(x)$, a.e. $x\in \mathbb{R}^{3}$. From $I'(u_{n})\rightarrow 0$, we know that

$$\bigl(I'(u_{n}), u_{n}-u \bigr)\rightarrow 0, \quad n\rightarrow \infty . $$

Also from $u_{n}\rightharpoonup u$ in E, we have

$$\bigl(I'(u), u_{n}-u \bigr)\rightarrow 0, \quad n \rightarrow \infty . $$

So,

$$\bigl(I'(u_{n})-I'(u), u_{n}-u \bigr)\rightarrow 0, \quad n\rightarrow \infty . $$

By $(f_{1})$–$(f_{2})$, for any fixed $\delta >0$, there exists $C_{\delta }>0$ such that

$$ \bigl\vert f(u) \bigr\vert \leq \delta \vert u \vert + C_{\delta } \vert u \vert ^{p-1}. $$

(2.3)

According to (2.3) and Hölder’s inequality, we have

$$\begin{aligned}& \biggl\vert \int _{\mathbb{R}^{3}}\bigl(f(u_{n})-f(u)\bigr) (u_{n}-u)\,dx \biggr\vert \\& \quad \leq \int _{\mathbb{R}^{3}} \bigl(\delta \vert u_{n} \vert +C_{\delta } \vert u_{n} \vert ^{p-1}+ \delta \vert u \vert +C_{\delta } \vert u \vert ^{p-1} \bigr) \vert u_{n}-u \vert \,dx \\& \quad \leq \delta _{1} \bigl( \Vert u_{n} \Vert _{2}+ \Vert u \Vert _{2} \bigr) \Vert u_{n}-u \Vert _{2}+C _{\delta _{1}} \bigl( \Vert u_{n} \Vert _{p}^{p-1}+ \Vert u \Vert _{p}^{p-1} \bigr) \Vert u_{n}-u \Vert _{p} \\& \quad \rightarrow 0, \quad n\rightarrow \infty . \end{aligned}$$

Set

$$\bar{E}=\biggl\{ u\in L^{2}\bigl(\mathbb{R}^{3}\bigr): \frac{ \vert u(x)-u(y) \vert }{ \vert x-y \vert ^{ \frac{3+2s}{2}}}\in L^{2}\bigl(\mathbb{R}^{3}\times \mathbb{R}^{3}\bigr)\biggr\} $$

endowed with the norm

$$\Vert u \Vert _{\bar{E}}= \biggl( \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}} \frac{ \vert u(x)-u(y) \vert ^{2}}{ \vert x-y \vert ^{3+2s}}\,dx\,dy \biggr)^{\frac{1}{2}} = \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr)^{ \frac{1}{2}}. $$

Then $E\hookrightarrow \bar{E}$. So, $u_{n}\rightharpoonup u$ in Ē. Thus

$$\int _{\mathbb{R}^{3}} \bigl( \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}- \bigl\vert (- \Delta )^{\frac{s}{2}}u \bigr\vert ^{2} \bigr)\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u (-\Delta )^{\frac{s}{2}}(u_{n}-u)\,dx\rightarrow 0, \quad n\rightarrow \infty . $$

Then

$$\begin{aligned} o(1) =& \bigl(I'(u_{n})-I'(u), u_{n}-u \bigr) \\ =& \int _{\mathbb{R}^{3}} \bigl(a \bigl\vert (-\Delta )^{\frac{s}{2}}(u_{n}-u) \bigr\vert ^{2}+V(x) (u _{n}-u)^{2} \bigr)\,dx \\ & {}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{n} \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u _{n} \\ &{}\times(-\Delta )^{\frac{s}{2}}(u_{n}-u)\,dx- \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u(- \Delta )^{\frac{s}{2}}(u_{n}-u)\,dx \biggr) \\ & {} + \int _{\mathbb{R}^{3}}\bigl(f(u)-f(u_{n})\bigr) (u_{n}-u)\,dx \\ \geq & \min \{a, 1\} \Vert u_{n}-u \Vert ^{2} \\ & {}+ b \int _{\mathbb{R}^{3}}\bigl( \bigl\vert (- \Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}- \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\bigr)\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u (-\Delta )^{ \frac{s}{2}}(u_{n}-u)\,dx \\ & {} + \int _{\mathbb{R}^{3}}\bigl(f(u)-f(u_{n})\bigr) (u_{n}-u)\,dx \\ \geq & \min \{a, 1\} \Vert u_{n}-u \Vert ^{2}+o(1). \end{aligned}$$

That means $u_{n}\rightarrow u$ in E. Then I satisfies the (PS) condition. □

Lemma 2.3

(Mountain pass geometry)

Assume that $(V)$ and $(f_{1})$–$(f_{3})$ hold. Then the functional I satisfies the following conditions:

• (1) There exist $\beta , \rho >0$ such that $I(u)\geq \beta$ for $\Vert u \Vert =\rho$.

• (2) There exists $e\in E$ with $\Vert e \Vert >\rho$ such that $I(e)<0$.

Proof

(1) According to (2.3), Hölder’s inequality, and Lemma 2.1, for $\Vert u \Vert =\rho$, we have

$$\begin{aligned} I(u) \geq & \frac{1}{2}\min \{a, 1\} \Vert u \Vert ^{2}- \frac{\delta }{2} \Vert u \Vert ^{2}-\frac{\delta }{p}C_{p} \Vert u \Vert ^{p} \\ =& \biggl(\frac{1}{2}\min \{a, 1\}-\frac{\delta }{2} \biggr) \Vert u \Vert ^{2}-\frac{ \delta }{p}C_{p} \Vert u \Vert ^{p}. \end{aligned}$$

Then there exists $\beta >0$ such that $I(u)\geq \beta$ for $\Vert u \Vert =\rho$.

(2) By $(f_{3})$, we have

$$F(u)\geq C_{3} \vert u \vert ^{\mu }-C_{4}. $$

Thus, taking $v\in E$ and $v>0$, we have

$$I(tv)\leq \frac{(a+1)t^{2}}{2} \Vert v \Vert ^{2}+\frac{bt^{4}}{4} \Vert v \Vert ^{4}-C _{5}t^{\mu }\Vert v \Vert ^{\mu}+C_{6}< 0 $$

for large t. Consequently, we can take $e=t^{\star }v$ for some large $t^{\star }$ such that (2) holds. □

Set $u^{+}(x)=\max \{u(x),0\}$, $u^{-}(x)=\min \{u(x),0\}$. Then $u(x)=u^{+}(x)+u^{-}(x)$.

Note that $(-\Delta )^{s}$ is a nonlocal operator. Generally speaking, for $u\in E$, $(u^{+},u^{-}) \equiv 0$ is not true.

Lemma 2.4

$(u^{+},u^{-})\geq 0$ for $u\in E$.

Proof

For $u\in E$, it is well known that $u^{+},u^{-} \in E$. So

$$\begin{aligned} \bigl(u^{+},u^{-}\bigr) =& \int _{\mathbb{R}^{3}} \bigl((-\Delta )^{\frac{s}{2}}u ^{+}(- \Delta )^{\frac{s}{2}}u^{-}+V(x)u^{+}u^{-} \bigr) \,dx \\ =& \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u^{+}(-\Delta )^{ \frac{s}{2}}u^{-}\,dx \\ =& \int _{\mathbb{R}^{3}} \int _{\mathbb{R}^{3}}\frac{ (u^{+}(x)-u ^{+}(y) ) (u^{-}(x)-u^{-}(y) )}{ \vert x-y \vert ^{3+2s}}\,dx\,dy \\ =& \int _{\{u(x)\geq 0\}\times \{u(y)\geq 0\}}\frac{ (u^{+}(x)-u ^{+}(y) ) (u^{-}(x)-u^{-}(y) )}{ \vert x-y \vert ^{3+2s}}\,dx\,dy \\ & {} + \int _{\{u(x)\geq 0\}\times \{u(y)\leq 0\}}\frac{ (u^{+}(x)-u ^{+}(y) ) (u^{-}(x)-u^{-}(y) )}{ \vert x-y \vert ^{3+2s}}\,dx\,dy \\ & {} + \int _{\{u(x)\leq 0\}\times \{u(y)\geq 0\}}\frac{ (u^{+}(x)-u ^{+}(y) ) (u^{-}(x)-u^{-}(y) )}{ \vert x-y \vert ^{3+2s}}\,dx\,dy \\ & {} + \int _{\{u(x)\leq 0\}\times \{u(y)\leq 0\}}\frac{ (u^{+}(x)-u ^{+}(y) ) (u^{-}(x)-u^{-}(y) )}{ \vert x-y \vert ^{3+2s}}\,dx\,dy \\ =& \int _{\{u(x)\geq 0\}\times \{u(y)\leq 0\}} \frac{-u(x)u(y)}{ \vert x-y \vert ^{3+2s}}\,dx\,dy+ \int _{\{u(x)\leq 0\}\times \{u(y)\geq 0\}} \frac{-u(x)u(y)}{ \vert x-y \vert ^{3+2s}}\,dx\,dy \\ \geq & 0. \end{aligned}$$

Then $(u^{+},u^{-})\geq 0$. □

Remark 2.5

Lemma 2.4 implies that

• (i) $(u,u^{+})\geq (u^{+},u^{+})$, $u\in E$;

• (ii) $(u,u^{-})\geq (u^{-},u^{-})$, $u\in E$.

In the end of this section, let us list the following two critical point theorems which will be used to prove the existence of sign-changing solutions.

Let X be a Banach space, $P, Q\subset X$ be open sets, $W=P \cup Q$, $M= P\cap Q$, $\varSigma =\partial P \cap \partial Q$ and $J\in C^{1}(X, \mathbb{R})$. For $c\in \mathbb{R}$, $J_{c}=\{x\in X: J(x) \leq c\}$ and $K_{c}=\{x\in X: J(x)=c, J'(x)=0\}$.

Definition 2.6

([27])

$\{P, Q\}$ is called an admissible family of invariant sets with respect to J at level c provided that the following deformation property holds: if $K_{c}\setminus W =\emptyset$, then there exists $\varepsilon _{0}>0$ such that, for $\varepsilon \in (0,\varepsilon _{0})$, there exists $\eta \in C(X, X)$ satisfying

• (1) $\eta (\bar{P})\subset \bar{P}$, $\eta (\bar{Q})\subset \bar{Q}$;

• (2) $\eta| _{J^{c-2\varepsilon }}=\mathit{id}$;

• (3) $\eta (J^{c+\varepsilon }\setminus W)\subset J^{c-\varepsilon }$.

Lemma 2.7

([27])

Assume that $\{P, Q\}$ is an admissible family of invariant sets with respect to J at level $c\geq c_{\star }:= \inf_{u\in \varSigma }J(u)$ and there exists a map $\varphi _{0}:\Delta \rightarrow X$ satisfying

• (1) $\varphi _{0}(\partial _{1}\Delta )\subset P$, $\varphi _{0}( \partial _{2}\Delta )\subset Q$,

• (2) $\varphi _{0}(\partial _{0}\Delta )\cap M= \emptyset$,

• (3) $\sup_{u\in \varphi _{0}(\partial _{0}\Delta )}J(u)< c_{\star }$,

where $\Delta =\{(t_{1}, t_{2})\in \mathbb{R}^{2}: t_{1}, t_{2} \geq 0, t_{1}+ t_{2}\leq 1\}$, $\partial _{1}\Delta =\{0\}\times [0,1]$, $\partial _{2}\Delta =[0,1]\times \{0\}$, $\partial _{0}\Delta =\{(t _{1}, t_{2})\in \mathbb{R}^{2}: t_{1}, t_{2}\geq 0, t_{1}+ t_{2}=1 \}$. Define

$$c=\inf_{\varphi \in \varGamma }\sup_{u\in \varphi (\Delta )\setminus W}J(u), $$

where $\varGamma :=\{\varphi \in C(\Delta , X): \varphi (\partial _{1} \Delta )\subset P, \varphi (\partial _{2}\Delta )\subset Q, \varphi| _{\partial _{0}\Delta }=\varphi _{0}| _{\partial _{0}\Delta }\}$. Then c is a critical value of J and $K_{c}\setminus W\neq \emptyset$.

Assume that $G: X\rightarrow X$ is an isometric involution, that is, $G^{2}=\mathit{id}$, $d(Gx,Gy)=d(x,y)$ for any $x, y\in X$. Also assume that J is G-invariant on X in the sense that $J(Gx)=J(x)$ for any $x\in X$. Assume $Q=GP$. A subset $F\subset X$ is said to be symmetric if $Gx\in F$ for any $x\in F$. The genus of a closed symmetric subset F of $X\setminus \{0\}$ is denoted by $\gamma (F)$.

Definition 2.8

([27])

P is called a G-admissible invariant set with respect to J at level c if the following deformation property holds: There exist $\varepsilon _{0}>0$ and a symmetric open neighborhood N of $K_{c}\setminus W$ with $\gamma (\overline{N})<\infty$ such that, for $\varepsilon \in (0, \varepsilon _{0})$, there exists $\eta \in C(X, X)$ satisfying

• (1) $\eta (\bar{P})\subset \bar{P}$, $\eta (\bar{Q})\subset \bar{Q}$;

• (2) $\eta \circ G= G\circ \eta$;

• (3) $\eta| _{J^{c-2\varepsilon }}=\mathit{id}$;

• (4) $\eta (J^{c+\varepsilon }\setminus (N\cup W))\subset J^{c-\varepsilon }$.

Lemma 2.9

([27])

Assume that P is a G-admissible invariant set with respect to J at any level $c\geq c^{\ast }:= \inf_{u\in \varSigma }J(u)$, and for any $n\in \mathbb{N}$, there exists a continuous map $\varphi _{n}: B_{n}=\{x \in \mathbb{R}^{n}: \vert x \vert \leq 1\}\rightarrow X$ satisfying

• (1) $\varphi _{n}(0)\in M:=P\cap Q$, $\varphi _{n}(-t)=G\varphi _{n}(t)$ for $t\in B_{n}$,

• (2) $\varphi _{n}(\partial B_{n})\cap M=\emptyset$,

• (3) $\sup_{u\in \mathit{Fix}_{G}\cup \varphi _{n}(\partial B_{n})}J(u)< c^{ \ast }$, where $\mathit{Fix}_{G}:=\{u\in X:Gu=u\}$.

For $j\in \mathbb{N}$, define

$$c_{j}=\inf_{B\in \varGamma _{j}}\sup_{u\in B\setminus W}J(u), $$

where

$$\varGamma _{j}:= \left \{B \left\vert \textstyle\begin{array}{l} B=\varphi (B_{n}\setminus Y)\textit{ for some }\varphi \in G_{n}, n\geq j, \textit{and open }Y \subset B _{n}, \\ \textit{such that }-Y=Y\textit{ and }\gamma (\overline{Y})\leq n-j, \end{array}\displaystyle \right. \right \} $$

and

$$G_{n}:= \left \{\varphi \left\vert \textstyle\begin{array}{l} \varphi \in C(B_{n},X), \varphi (-t)= G\varphi (t) \textit{ for }t\in B_{n}, \\ \varphi (0)\in M\textit{ and }\varphi| _{\partial B_{n}}=\varphi _{n}| _{\partial B_{n}}. \end{array}\displaystyle \right. \right \}. $$

Then, for $j\geq 2$, $c_{j}$ are critical values of J with $c_{j}\rightarrow \infty$ as $j\rightarrow \infty$ and $K_{c_{j}} \setminus W\neq \emptyset$.

3 Proof of the main results

First, we introduce some notations. Let $D^{\pm }$ be the positive and negative cones. Precisely, define

$$D^{+}=\{u\in E: u\geq 0\}, \quad\quad D^{-}=\{u\in E: u \leq 0\}. $$

For $\varepsilon >0$, set

$$D^{+}_{\varepsilon }=\bigl\{ u\in E: \operatorname{dist} \bigl(u,D^{+}\bigr)< \varepsilon \bigr\} , \quad\quad D^{-}_{\varepsilon }=\bigl\{ u\in E, \operatorname{dist} \bigl(u,D^{-}\bigr)< \varepsilon \bigr\} , $$

where $\operatorname{dist}(u,D^{\pm }) =\inf_{v\in D^{\pm }} \Vert u-v \Vert$. Obviously, $D^{+}_{\varepsilon } = -D^{-}_{\varepsilon }$. Set $W=D^{+}_{\varepsilon }\cup D^{-}_{\varepsilon }$. Then W is a symmetric and open subset of E and $E\setminus W$ contains only sign-changing functions.

Next, define an operator $A: E\rightarrow E$, which is used to construct a descending flow for functional I. For $u\in E$, let $v=A(u)\in E$ be the unique solution of the following equation:

$$ \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) (- \Delta )^{s}v+V(x)v= f(u). $$

(3.1)

Clearly, the three statements are equivalent: u is a solution of (1.1), u is a critical point of I, and u is a fixed point of A.

Moreover, the operator A has the following properties.

Lemma 3.1

• (1) A is well defined and continuous.

• (2) For any $u\in E$, we have

  $$\begin{aligned}& \bigl(I'(u), u-A(u) \bigr)\geq \min \{a, 1\} \bigl\Vert u-A(u) \bigr\Vert ^{2}, \end{aligned}$$

  (3.2)
  $$\begin{aligned}& \Vert I'(u) \Vert \leq (a+1+b\int _{\mathbb{R}^{3}} \vert (-\Delta )^{\frac{s}{2}}u \vert ^{2}\,dx ) \Vert u-A(u) \Vert . \end{aligned}$$

  (3.3)

• (3) There exists $\varepsilon _{0} > 0$ such that

  $$A\bigl(\partial D_{\varepsilon }^{\pm }\bigr) \subset D_{\varepsilon }^{\pm }, \quad \forall \varepsilon \in (0, \varepsilon _{0}). $$

Moreover, every nontrivial solution $u\in D_{\varepsilon }^{+}$ is positive and every nontrivial solution $u\in D_{\varepsilon }^{-}$ is negative.

Proof

(1) Define

$$\begin{aligned} J_{u}(v)&=\frac{1}{2} \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}v \bigr\vert ^{2}\,dx\\&\quad{} +\frac{1}{2} \int _{\mathbb{R}^{3}}V(x)v^{2}\,dx - \int _{\mathbb{R}^{3}}f(u)v\,dx, \quad v\in E. \end{aligned} $$

By $(f_{1})$, $(f_{2})$, and Lemma 2.1, it is easy to see that $J_{u}\in C^{1}$ and is coercive, weakly lower semicontinuous, bounded below, strictly convex. Therefore, $J_{u}$ admits a unique minimizer $v=A(u)\in E$, which is the unique solution to (3.1). Thus, A is well defined.

In the following, we show that A is continuous. Let $\{u_{n}\} \subset E$ with $u_{n} \rightarrow u$ in E. Set $v_{n}=A(u_{n})$ and $v=A(u)$. We need to show that $\Vert v_{n}-v \Vert \rightarrow 0$. By the definition of A, for any $w\in E$, we have

$$ \begin{aligned}[b] &\biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v(-\Delta )^{ \frac{s}{2}}w \,dx+ \int _{\mathbb{R}^{3}}V(x)vw \,dx\\&\quad = \int _{\mathbb{R}^{3}}f(u)w\,dx \end{aligned} $$

(3.4)

and

$$ \begin{aligned}[b] & \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v_{n}(- \Delta )^{\frac{s}{2}}w \,dx+ \int _{\mathbb{R}^{3}} V(x)v_{n}w\,dx\\&\quad = \int _{\mathbb{R}^{3}}f(u_{n})w\,dx. \end{aligned} $$

(3.5)

Choosing $w=v_{n}-v$ in (3.4), (3.5) and subtracting, we get

$$\begin{aligned} \min \{a, 1\} \Vert v_{n}-v \Vert ^{2} \leq & \int _{\mathbb{R}^{3}} \bigl(f(u _{n})-f(u) \bigr) (v_{n}-v) \\ & {}+b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2} \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v (- \Delta )^{\frac{s}{2}}(v_{n}-v) \\ & {} - \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v_{n} (-\Delta )^{ \frac{s}{2}}(v_{n}-v) \biggr) \\ =&\varLambda _{1}+\varLambda _{2}. \end{aligned}$$

Let $\varphi \in C_{0}^{\infty }(\mathbb{R})$ be such that

$$\varphi (t)= \textstyle\begin{cases} 1, & \vert t \vert \leq 1, \\ 0, & \vert t \vert \geq 2. \end{cases} $$

Let

$$h_{1}(t)=\varphi (t)f(t), \quad\quad h_{2}(t)=f(t)-h_{1}(t). $$

According to $(f_{1})$ and $(f_{2})$, there exists $C>0$ such that

$$h_{1}(t)\leq C \vert t \vert , \quad\quad h_{2}(t)\leq C \vert t \vert ^{p-1}, \quad t\in \mathbb{R}. $$

Therefore, by Hölder’s inequality and Lemma 2.2, we get

$$\begin{aligned} \varLambda _{1} =& \int _{\mathbb{R}^{3}} \bigl(h_{1}(u)-h_{1}(u_{n}) \bigr) (v-v_{n} )+ \int _{\mathbb{R}^{3}} \bigl(h_{2}(u)-h_{2}(u_{n}) \bigr) (v-v_{n} ) \\ \leq & \biggl( \int _{\mathbb{R}^{3}} \bigl\vert h_{1}(u)-h_{1}(u_{n}) \bigr\vert ^{2} \biggr)^{ \frac{1}{2}} \biggl( \int _{\mathbb{R}^{3}} \vert v-v_{n} \vert ^{2} \biggr)^{ \frac{1}{2}} \\ & {}+ \biggl( \int _{\mathbb{R}^{3}} \bigl\vert h_{2}(u)-h_{2}(u_{n}) \bigr\vert ^{ \frac{p}{p-1}} \biggr)^{\frac{p-1}{p}} \biggl( \int _{\mathbb{R}^{3}} \vert v-v _{n} \vert ^{p} \biggr)^{\frac{1}{p}} \\ \leq & C_{1} \Vert v-v_{n} \Vert \biggl[ \biggl( \int _{\mathbb{R}^{3}} \bigl\vert h_{1}(u)-h _{1}(u_{n}) \bigr\vert ^{2} \biggr)^{\frac{1}{2}}+ \biggl( \int _{\mathbb{R}^{3}} \bigl\vert h_{2}(u)-h _{2}(u_{n}) \bigr\vert ^{\frac{p}{p-1}} \biggr)^{\frac{p-1}{p}} \biggr] \end{aligned}$$

and

$$\begin{aligned} \varLambda _{2} \leq &b \biggl[ \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2} \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v(-\Delta )^{\frac{s}{2}}(v _{n}-v) \\ & {} - \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v(-\Delta )^{\frac{s}{2}}(v _{n}-v) \\ & {} + \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v(-\Delta )^{\frac{s}{2}}(v _{n}-v) \\ & {} - \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v_{n}(-\Delta )^{ \frac{s}{2}}(v_{n}-v) \biggr] \\ \leq &b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}- \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v(-\Delta )^{\frac{s}{2}}(v _{n}-v) \\ \leq &b \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}- \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \biggr) \Vert v \Vert \Vert v-v _{n} \Vert . \end{aligned}$$

Then

$$\begin{aligned} \min \{a, 1\} \Vert v-v_{n} \Vert \leq & C_{1} \biggl[ \biggl( \int _{\mathbb{R}^{3}} \bigl\vert h _{1}(u)-h_{1}(u_{n}) \bigr\vert ^{2} \biggr)^{\frac{1}{2}}+ \biggl( \int _{\mathbb{R} ^{3}} \bigl\vert h_{2}(u)-h_{2}(u_{n}) \bigr\vert ^{\frac{p}{p-1}} \biggr)^{\frac{p-1}{p}} \biggr] \\ & {} +C_{2} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}- \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2} \biggr). \end{aligned}$$

By virtue of $u_{n}\rightarrow u$, we have $\Vert u_{n} \Vert \rightarrow \Vert u \Vert$. Together with

$$\lim_{n\rightarrow \infty } \int _{\mathbb{R}^{3}}V(x)u_{n}^{2}= \int _{\mathbb{R}^{3}}V(x)u^{2}, $$

we get

$$ \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}- \int _{\mathbb{R} ^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{n} \bigr\vert ^{2}\rightarrow 0. $$

(3.6)

Thus, by (3.6) and the dominated convergence theorem, we obtain that $\Vert v-v_{n} \Vert \rightarrow 0$ as $n\rightarrow \infty$.

(2) Since $A(u)$ is the solution of Eq. (3.1), we have

$$ \begin{aligned}[b] &\biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}A(u) (-\Delta )^{ \frac{s}{2}}\phi \,dx+ \int _{\mathbb{R}^{3}}V(x)A(u)\phi \,dx \\ &\quad = \int _{\mathbb{R}^{3}}f(u)\phi \,dx, \quad \forall \phi \in E.\end{aligned} $$

(3.7)

Taking $\phi =u-A(u)$ in (3.7) and (2.2), we get

$$\begin{aligned}& \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}A(u) (-\Delta )^{ \frac{s}{2}} \bigl(u-A(u) \bigr)\,dx \\& \quad\quad {}+ \int _{\mathbb{R}^{3}}V(x)A(u) \bigl(u-A(u) \bigr)\,dx \\& \quad = \int _{\mathbb{R}^{3}}f(u) \bigl(u-A(u) \bigr)\,dx \end{aligned}$$

(3.8)

and

$$\begin{aligned} \bigl(I'(u),u-A(u) \bigr) =& \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u(-\Delta )^{\frac{s}{2}} \bigl(u-A(u) \bigr)\,dx \\ & {} + \int _{\mathbb{R}^{3}}V(x)u \bigl(u-A(u) \bigr)\,dx- \int _{\mathbb{R}^{3}}f(u) \bigl(u-A(u) \bigr)\,dx. \end{aligned}$$

(3.9)

Combining (3.8) and (3.9), it follows that

$$\begin{aligned}& \bigl(I'(u),u-A(u)\bigr) \\& \quad = \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}} \bigl(u-A(u) \bigr) \bigr\vert ^{2}\,dx+ \int _{\mathbb{R}^{3}}V(x) \bigl(u-A(u) \bigr)^{2}\,dx \\& \quad \geq a \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}} \bigl(u-A(u) \bigr) \bigr\vert ^{2}\,dx+ \int _{\mathbb{R}^{3}}V(x) \bigl(u-A(u) \bigr)^{2}\,dx \\& \quad \geq \min \{a, 1\} \bigl\Vert u-A(u) \bigr\Vert ^{2}. \end{aligned}$$

In the same way as above, for any $w\in E$, we have

$$\begin{aligned} \bigl(I'(u),w \bigr)&= \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}} \bigl(u-A(u) \bigr) (-\Delta )^{\frac{s}{2}}w\,dx \\ & \quad {}+ \int _{\mathbb{R}^{3}}V(x) \bigl(u-A(u) \bigr)w\,dx. \end{aligned} $$

By Hölder’s inequality, we get

$$\begin{aligned} \bigl(I'(u),w \bigr) \leq & \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}} \bigl(u-A(u) \bigr) \bigr\vert ^{2}\,dx \biggr)^{\frac{1}{2}} \\ & {}\times\biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}w \bigr\vert ^{2}\,dx \biggr)^{ \frac{1}{2}} \\ & {} + \biggl( \int _{\mathbb{R}^{3}}V(x) \bigl(u-A(u) \bigr)^{2}\,dx \biggr)^{ \frac{1}{2}} \biggl( \int _{\mathbb{R}^{3}}V(x)w^{2}\,dx \biggr)^{\frac{1}{2}} \\ \leq & \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \bigl\Vert u-A(u) \bigr\Vert \Vert w \Vert + \bigl\Vert u-A(u) \bigr\Vert \Vert w \Vert \\ =& \biggl(a+1+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \bigl\Vert u-A(u) \bigr\Vert \Vert w \Vert . \end{aligned}$$

Thus,

$$\bigl\Vert I'(u) \bigr\Vert \leq \biggl(a+1+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \bigl\Vert u-A(u) \bigr\Vert . $$

(3) We need only to show that $A(\partial D_{\varepsilon }^{+}) \subset D_{\varepsilon }^{+}$. The other case can be shown similarly. According to $(f_{1})$ and $(f_{2})$, for any $\xi >0$, there exists $C_{\xi }>0$ such that

$$ \bigl\vert f(\tau ) \bigr\vert \leq \xi \vert \tau \vert +C_{\xi } \vert \tau \vert ^{p-1}. $$

(3.10)

Let $u\in \partial D_{\varepsilon }^{+}$ and $v=A(u)$. Then

$$ \operatorname{dist}\bigl(v, D^{+}\bigr)=\inf_{w\in D^{+}} \Vert v-w \Vert \leq \bigl\Vert v^{-} \bigr\Vert . $$

(3.11)

By Lemma 2.1, for any $q\in [2,2_{s}^{\star }]$, there exists $C_{q}>0$ such that

$$ \bigl\Vert u^{\pm } \bigr\Vert _{q}=\inf _{w\in D^{\mp }} \Vert u-w \Vert _{q}\leq C_{q} \inf_{w\in D^{\mp }} \Vert u-w \Vert =C_{q} \operatorname{dist}\bigl(u, D^{\mp }\bigr). $$

(3.12)

Choosing $w=v^{-}$ in (3.4), we get

$$ \begin{aligned}[b] & \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v(-\Delta )^{\frac{s}{2}}v ^{-}+ \int _{\mathbb{R}^{3}}V(x)vv^{-}\,dx\\&\quad = \int _{\mathbb{R}^{3}}f(u)v^{-}\,dx. \end{aligned} $$

(3.13)

By (3.13), we obtain

$$ \min \{a, 1\}\bigl(v, v^{-}\bigr)\leq \int _{\mathbb{R}^{3}}f(u)v ^{-}\,dx-b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}v(-\Delta )^{\frac{s}{2}} v^{-}\,dx. $$

(3.14)

Together with (3.10)–(3.12), (3.14), (ii) of Remark 2.5, and $(f_{3})$, we obtain

$$\begin{aligned} \operatorname{dist}\bigl(v, D^{+}\bigr) \bigl\Vert v^{-} \bigr\Vert \leq & \bigl\Vert v^{-} \bigr\Vert ^{2} \\ \leq & \bigl(v,v^{-}\bigr) \\ \leq & C \biggl[ \int _{\mathbb{R}^{3}}f(u)v^{-}\,dx-b \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}v(-\Delta )^{\frac{s}{2}} v^{-}\,dx \biggr] \\ \leq &C \int _{\mathbb{R}^{3}}f\bigl(u^{-}\bigr)v^{-}\,dx \\ \leq &C \int _{\mathbb{R}^{3}}\bigl(\xi \bigl\vert u^{-} \bigr\vert +C_{\xi } \bigl\vert u^{-} \bigr\vert ^{p-1}\bigr) \bigl\vert v ^{-} \bigr\vert \,dx \\ \leq &C\xi \bigl\Vert u^{-} \bigr\Vert _{2} \bigl\Vert v^{-} \bigr\Vert _{2}+C_{\xi } \bigl\Vert u^{-} \bigr\Vert ^{p-1}_{p} \bigl\Vert v ^{-} \bigr\Vert _{p} \\ \leq &C_{4}\bigl(\xi \operatorname{dist}\bigl(u, D^{+} \bigr)+C_{\xi } \bigl(\operatorname{dist}\bigl(u, D^{+}\bigr) \bigr)^{p-1}\bigr) \bigl\Vert v ^{-} \bigr\Vert . \end{aligned}$$

It follows that

$$\operatorname{dist}\bigl(A(u), D^{+}\bigr)\leq C_{4}\bigl( \xi \operatorname{dist}\bigl(u, D^{+}\bigr)+C_{\xi } \bigl( \operatorname{dist}\bigl(u, D ^{+}\bigr)\bigr)^{p-1}\bigr). $$

Therefore, taking ξ small enough, there exists $\varepsilon _{0} > 0$ such that, for $\varepsilon \in (0, \varepsilon _{0})$,

$$ \operatorname{dist}\bigl(A(u), D^{+}\bigr)\leq \frac{1}{2} \operatorname{dist}\bigl(u, D^{+}\bigr). $$

(3.15)

This means that $A(\partial D_{\varepsilon }^{+}) \subset D_{\varepsilon }^{+}$. If there exists $u\in D_{\varepsilon }^{+}$ such that $A(u)=u$, it follows from (3.15) that $\operatorname{dist}(u, D^{+})=0$. Then $u\in D^{+}$. If $u \not \equiv 0$, by the maximum principle (see [28]), we have $u>0$. □

Lemma 3.2

Let $a_{1}< b_{1}$ and $\beta _{1}>0$. Then there exists $\beta _{2}>0$ such that $\Vert u-A(u) \Vert \geq \beta _{2}$ if $u\in E$, $I(u)\in [a_{1},b_{1}]$, and $\Vert I'(u) \Vert \geq \beta _{1}$.

Proof

Taking $\phi =u$ in (3.7), we obtain

$$ \begin{aligned}[b] & \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}A(u) (-\Delta )^{ \frac{s}{2}}u\,dx \\ &\quad{} + \int _{\mathbb{R}^{3}}V(x)A(u)u\,dx= \int _{\mathbb{R}^{3}}f(u)u \,dx. \end{aligned} $$

(3.16)

By virtue of (3.16), (2.1), and $(f_{3})$, we get

$$\begin{aligned}& I(u)-\frac{1}{\mu } \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u(- \Delta )^{\frac{s}{2}} \bigl(u-A(u)\bigr)\,dx \\& \quad\quad{} -\frac{1}{\mu } \int _{\mathbb{R}^{3}}V(x)u\bigl(u-A(u)\bigr)\,dx \\& \quad = I(u)-\frac{1}{\mu } \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u(- \Delta )^{\frac{s}{2}}u \,dx -\frac{1}{\mu } \int _{\mathbb{R}^{3}}V(x)u ^{2}\,dx \\& \quad \quad {} +\frac{1}{\mu } \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u(- \Delta )^{\frac{s}{2}}A(u)\,dx +\frac{1}{\mu } \int _{\mathbb{R}^{3}}V(x)u A(u)\,dx \\& \quad = I(u)-\frac{1}{\mu } \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx -\frac{1}{\mu } \int _{\mathbb{R}^{3}}V(x)u^{2}\,dx \\& \quad\quad{} +\frac{1}{ \mu } \int _{\mathbb{R}^{3}}f(u)u\,dx \\& \quad = a\biggl(\frac{1}{2}-\frac{1}{\mu }\biggr) \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx +\biggl(\frac{1}{2}-\frac{1}{\mu }\biggr) \int _{\mathbb{R} ^{3}}V(x)u^{2}\,dx \\& \quad\quad{} +b\biggl(\frac{1}{4}- \frac{1}{\mu }\biggr) \biggl( \int _{\mathbb{R} ^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr)^{2} \\& \quad \quad {} + \int _{\mathbb{R}^{3}} \biggl(\frac{1}{\mu }f(u)u-F(u) \biggr)\,dx \\& \quad \geq \biggl(\frac{1}{2}-\frac{1}{\mu }\biggr)\min \{a, 1\} \Vert u \Vert ^{2}+b\biggl( \frac{1}{4}-\frac{1}{\mu }\biggr) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr)^{2}. \end{aligned}$$

Thus,

$$\begin{aligned}& \biggl(\frac{1}{2}-\frac{1}{\mu }\biggr)\min \{a, 1\} \Vert u \Vert ^{2} \\& \quad \leq \bigl\vert I(u) \bigr\vert +\frac{1}{\mu } \biggl(a+1+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr) \bigl(u, u-A(u) \bigr) \\& \quad\quad{} -b\biggl(\frac{1}{4}- \frac{1}{ \mu }\biggr) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr)^{2} \\& \quad \leq \bigl\vert I(u) \bigr\vert +\frac{1}{\mu }(a+1) \Vert u \Vert \bigl\Vert u-A(u) \bigr\Vert +\frac{1}{\mu }b \Vert u \Vert \bigl\Vert u-A(u) \bigr\Vert \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \\& \quad\quad {} -b\biggl(\frac{1}{4}-\frac{1}{\mu }\biggr) \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr)^{2} \\& \quad \leq \bigl\vert I(u) \bigr\vert +\frac{1}{\mu }(a+1) \Vert u \Vert \bigl\Vert u-A(u) \bigr\Vert +\frac{b}{\mu ( \mu -4)} \Vert u \Vert ^{2} \bigl\Vert u-A(u) \bigr\Vert ^{2}. \end{aligned}$$

(3.17)

If there exists $\{u_{n}\}\subset E$ with $I(u_{n}) \in [a_{1},b_{1}]$ and $\Vert I'(u_{n}) \Vert \geq \beta _{1}$ such that $\Vert u_{n}-A(u_{n}) \Vert \rightarrow 0$ as $n\rightarrow \infty$, it follows from (3.17) that $\{ \Vert u_{n} \Vert \}$ is bounded. According to (3.3), it is easy to see that $\Vert I'(u_{n}) \Vert \rightarrow 0$ as $n\rightarrow \infty$, which is a contradiction with $\Vert I'(u_{n}) \Vert \geq \beta _{1}$. Thus, the proof is completed. □

Denote $K=\{u\in E, I'(u)=0\}$, $E_{0}=E\setminus K$. Observe that A is merely continuous and cannot be used to construct a descending flow. So, constructing a locally Lipschitz continuous operator B which inherits the main properties of A is necessary. Similar to ([29], Lemma 4.4), we give the following lemma.

Lemma 3.3

There exists a locally Lipschitz continuous operator $B: E\rightarrow E_{0}$ such that

• (1) $B(\partial D_{\varepsilon }^{\pm }) \subset D_{\varepsilon } ^{\pm }$, $\forall \varepsilon \in (0, \varepsilon _{0})$;

• (2) $(I'(u), u-B(u))\geq \frac{1}{2} \Vert u-A(u) \Vert ^{2}$, $u\in E$;

• (3) $\frac{1}{2} \Vert u-B(u) \Vert \leq \Vert u-A(u) \Vert \leq 2 \Vert u-B(u) \Vert$, $u \in E$;

• (4) If A is odd, so is B.

To apply Lemma 2.7 to prove Theorem 1.1, we take $X=E$, $P=D_{ \varepsilon }^{+}$, $Q=D_{\varepsilon }^{-}$, and $J=I$. Then $M=D_{\varepsilon }^{+}\cap D_{\varepsilon }^{-}$, $\varSigma =\partial D _{\varepsilon }^{+}\cap \partial D_{\varepsilon }^{-}$, and $W=D_{\varepsilon }^{+}\cup D_{\varepsilon }^{-}$. In the following, a deformation lemma is given in order to prove that $\{D_{\varepsilon }^{+}, D_{\varepsilon }^{-}\}$ is an admissible family of invariant sets with respect to J at level $c\in \mathbb{R}$.

Lemma 3.4

If $K_{c}\setminus W =\emptyset$, then there exists $\varepsilon _{0}>0$ such that, for $0<\varepsilon <\varepsilon '< \varepsilon _{0}$, there exists a continuous map $\sigma : [0,1] \times E\rightarrow E$ satisfying

• (1) $\sigma (0,u)=u$ for $u\in E$;

• (2) $\sigma (t,u)=u$ for $t\in [0,1]$ and $u\notin I^{-1}[c- \varepsilon ', c+\varepsilon ']$;

• (3) $\sigma (1,I^{c+\varepsilon }\setminus W)\subset I^{c-\varepsilon }$;

• (4) $\sigma (t, \overline{D_{\varepsilon }^{\pm }})\subset \overline{D _{\varepsilon }^{\pm }}$, $t\in [0,1]$.

Proof

For $\delta >0$, let $N(\delta )=\{ u\in E: \operatorname{dist}(u, K_{c})<\delta \}$. If δ is small enough, then $N(\delta ) \subset W$. By Lemma 2.2, I satisfies the (PS) condition. So, there exist $\varepsilon _{0}, \beta _{1} >0$ such that

$$\bigl\Vert I'(u) \bigr\Vert \geq \beta _{1}, \quad \text{for } u\in I^{-1}\bigl([c-\varepsilon _{0}, c+ \varepsilon _{0}]\bigr)\setminus N\biggl(\frac{\delta }{2}\biggr). $$

According to Lemma 3.2 and Lemma 3.3, there exists $\beta _{2} >0$ such that

$$\bigl\Vert u-B(u) \bigr\Vert \geq \beta _{2}, \quad \text{for } u\in I^{-1}\bigl([c-\varepsilon _{0}, c+\varepsilon _{0}]\bigr)\setminus N\biggl(\frac{\delta }{2}\biggr). $$

Without loss of generality, assume that $\varepsilon _{0}\leq \frac{ \beta _{2}\delta }{32}$. Let

$$V(u)=\frac{u-B(u)}{ \Vert u-B(u) \Vert }, \quad \text{for } u\in E_{0}= E\setminus K. $$

Define two locally Lipschitz continuous functions $h, p: E\rightarrow [0,1]$ such that

$$h(u)= \textstyle\begin{cases} 0, & u\in N(\frac{\delta }{4}), \\ 1, & u\notin N(\frac{\delta }{2}), \end{cases} $$

and

$$p(u)= \textstyle\begin{cases} 0, & u\notin I^{-1}([c-\varepsilon ', c+\varepsilon ']), \\ 1, & u\in I^{-1}([c-\varepsilon , c+\varepsilon ]). \end{cases} $$

Consider the initial value problem

$$\textstyle\begin{cases} \frac{d\tau }{dt}=-h(\tau )p(\tau )V(\tau ), \\ \tau (0,u)=u. \end{cases} $$

For $u\in E$, this problem admits a unique continuous solution $\tau (t,u)$. Define $\sigma (t,u)=\tau (\frac{16\varepsilon }{\beta _{2}}t,u)$. Now we shall prove (3) and (4) since (1) and (2) are obvious.

To prove (3), we need only to show that

$$I\bigl(\sigma (1,u)\bigr)=I\biggl(\tau \biggl(\frac{16\varepsilon }{\beta _{2}},u\biggr)\biggr) \leq c- \varepsilon \quad\text{for } u\in I^{c+\varepsilon }\setminus W. $$

In fact, from Lemma 3.3, we know $I(\tau (t,u))$ is decreasing for $t\in [0,\frac{16\varepsilon }{\beta _{2}}]$. If there exists $t_{0}\in [0,\frac{16\varepsilon }{\beta _{2}}]$ such that $I(\tau (t _{0},u))\leq c-\varepsilon$, then

$$I\bigl(\sigma (1,u)\bigr)=I\biggl(\tau \biggl(\frac{16\varepsilon }{\beta _{2}},u\biggr)\biggr) \leq I\bigl( \tau (t_{0},u)\bigr)\leq c-\varepsilon . $$

Otherwise, if $I(\tau (t, u))\geq c-\varepsilon$ for all $t\in [0,\frac{16 \varepsilon }{\beta _{2}}]$, then $p(\tau (t, u))=1$ for $t\in [0,\frac{16 \varepsilon }{\beta _{2}}]$.

On the other hand, if there exists $t_{1}\in [0,\frac{16\varepsilon }{\beta _{2}}]$ such that $\tau (t_{1},u)\in N(\frac{\delta }{2})$, noting that $u\notin N(\delta )$, then we have

$$\frac{\delta }{2}\leq \bigl\Vert \tau (t_{1},u)-u \bigr\Vert \leq \int _{0}^{t_{1}} \bigl\Vert \tau '(s,u) \bigr\Vert \,ds\leq t_{1}\leq \frac{16\varepsilon }{\beta _{2}}, $$

which contradicts the fact that $\varepsilon <\varepsilon _{0}<\frac{ \beta _{2}\delta }{32}$. So, $\tau (t,u)\notin N(\frac{\delta }{2})$ for all $t\in [0,\frac{16\varepsilon }{\beta _{2}}]$. Therefore, $h(\tau (t,u))=1$ for $t\in [0,\frac{16\varepsilon }{\beta _{2}}]$. Immediately, it follows from (2) and (3) of Lemma 3.3 that

$$\begin{aligned} I\bigl(\sigma (1,u)\bigr) =&I\biggl(\tau \biggl(\frac{16\varepsilon }{\beta _{2}},u\biggr) \biggr) \\ =& I(u)- \int _{0}^{\frac{16\varepsilon }{\beta _{2}}}\bigl(I'\bigl(\tau (s,u) \bigr), V\bigl( \tau (s,u)\bigr)\bigr) \\ \leq & I(u)- \int _{0}^{\frac{16\varepsilon }{\beta _{2}}}\frac{1}{8} \bigl\Vert \tau (s,u), B\bigl(\tau (s,u)\bigr) \bigr\Vert \\ \leq & c+\varepsilon -\frac{16\varepsilon }{\beta _{2}}\frac{\beta _{2}}{8} \\ =& c-\varepsilon , \end{aligned}$$

which implies that (3) holds.

Finally, similar to [29], (4) is a consequence of (1) of Lemma 3.3 (see [30] for detailed proof). □

Proof of Theorem 1.1

In order to prove the existence of positive and negative solutions for Eq. (1.1), it is necessary to introduce the following functions:

$$f^{+}(t)= \textstyle\begin{cases} f(t), &t\geq 0, \\ 0, & t< 0, \end{cases} $$

and

$$f^{-}(t)= \textstyle\begin{cases} 0, &t> 0, \\ f(t), &t\leq 0. \end{cases} $$

Then

$$F^{\pm }(t)= \int _{0}^{t} f^{\pm }(u)\,du. $$

Observe that $f^{\pm }(t)$ satisfy assumptions $(f_{1})$–$(f_{2})$, while assumption $(f_{3})$ is verified by $f^{+}$ and $F^{+}$ for any $t>0$ and by $f^{-}$ and $F^{-}$ for any $t<0$.

Define functional $I^{\pm }: E\rightarrow \mathbb{R}$ as follows:

$$ \begin{aligned}[b] I^{\pm }(u)&=\frac{1}{2} \int _{\mathbb{R}^{3}}(a\bigl( \bigl\vert (-\Delta )^{ \frac{s}{2}}u \bigr\vert ^{2}+V(x)u^{2}\bigr)\,dx+\frac{b}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (- \Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx\biggr)^{2} \\ &\quad{} - \int _{\mathbb{R}^{3}}F^{\pm }(u)\,dx. \end{aligned} $$

(3.18)

It is easy to show that $I^{\pm }\in C^{1}(E,\mathbb{R})$ and

$$\begin{aligned} \bigl(\bigl(I^{\pm }\bigr)'(u),v \bigr) =& \int _{\mathbb{R}^{3}}\bigl(a(-\Delta )^{ \frac{s}{2}}u(-\Delta )^{\frac{s}{2}}v+V(x)uv\bigr)\,dx \\ & {}+b \int _{\mathbb{R} ^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u(-\Delta )^{\frac{s}{2}}v \,dx \\ & {} - \int _{\mathbb{R}^{3}}f^{\pm }(u)v\,dx,\quad u, v \in E. \end{aligned}$$

(3.19)

Moreover, by the same arguments as Lemma 2.2 and Lemma 2.3, we may show that $I^{\pm }$ satisfy the (PS) condition and mountain pass geometry. Then, according to the mountain pass theorem, $I^{+}$ has a critical point $u_{1}$ and $I^{-}$ has a critical point $u_{2}$.

Let $u_{1}^{-}$ be a test function. By (3.19) and Lemma 2.4, we get

$$\begin{aligned} 0 =& \bigl(\bigl(I^{+}\bigr)'(u_{1}), u_{1}^{-} \bigr) \\ =& \int _{\mathbb{R}^{3}} \bigl(a(-\Delta )^{\frac{s}{2}}u_{1}(- \Delta )^{ \frac{s}{2}}u_{1}^{-}+V(x)u_{1}u_{1}^{-} \bigr)\,dx \\ & {}+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{1} \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{ \frac{s}{2}}u_{1}(-\Delta )^{\frac{s}{2}}u_{1}^{-}\,dx \\ & {} - \int _{\mathbb{R}^{3}}f^{+}(u_{1})u_{1}^{-} \,dx \\ =& \int _{\mathbb{R}^{3}}a(-\Delta )^{\frac{s}{2}}u_{1}(-\Delta )^{ \frac{s}{2}}u_{1}^{-}\,dx+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{ \frac{s}{2}}u_{1} \bigr\vert ^{2}\,dx \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u _{1}(-\Delta )^{\frac{s}{2}}u_{1}^{-}\,dx \\ & {}+ \int _{\mathbb{R}^{3}}V(x) \bigl(u _{1}^{-} \bigr)^{2}\,dx \\ \geq & \biggl(a+b \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u_{1} \bigr\vert ^{2}\,dx\biggr) \int _{\mathbb{R}^{3}}(-\Delta )^{\frac{s}{2}}u_{1}^{-}(- \Delta )^{ \frac{s}{2}}u_{1}^{-}\,dx + \int _{\mathbb{R}^{3}}V(x) \bigl(u_{1}^{-} \bigr)^{2}\,dx \\ \geq &\min \{a,1\} \bigl\Vert u_{1}^{-} \bigr\Vert ^{2}. \end{aligned}$$

Thus, we have $u_{1}^{-}=0$, which means $u_{1}\geq 0$. Notice that $u _{1}\not \equiv 0$, by the maximum principle (see [28]), we have $u_{1}>0$. With the same arguments it is easy to show that $u_{2}<0$.

In what follows, we claim the existence of a sign-changing solution.

According to Lemma 3.4, if we set $\varepsilon '=2\varepsilon$ and $\eta (u)=\sigma (1,u)$, it is easy to see that $\{D_{\varepsilon } ^{+}, D_{\varepsilon }^{-}\}$ is an admissible family of invariant sets with respect to J at level $c\in \mathbb{R}$. Suppose $v _{1}, v_{2} \in C_{0}^{\infty } (\mathbb{R}^{3})\setminus \{0\}$ satisfying

$$\operatorname{supp}(v_{1})\cap \operatorname{supp}(v_{2})= \emptyset , \quad v_{1}< 0, v_{2}> 0. $$

Let $\varphi _{0}:\Delta \rightarrow X$ be such that

$$\varphi _{0}(t,s)= R(tv_{1}+sv_{2}), \quad \forall (t,s)\in \Delta , $$

where R is a positive number to be determined later.

Obviously,

$$\varphi _{0}(0,s)= Rsv_{2}\in D^{+}_{\varepsilon }, \quad\quad \varphi _{0}(t,0)= Rtv_{1}\in D^{-}_{\varepsilon }, $$

which guarantees that

$$\varphi _{0}(\partial _{1}\Delta )\subset D^{+}_{\varepsilon }, \quad\quad \varphi _{0}(\partial _{2}\Delta )\subset D^{-}_{\varepsilon }. $$

Therefore, assumption (1) of Lemma 2.7 holds.

Next, we verify assumption (2) of Lemma 2.7. By a direct calculation, we have

$$\rho =\min \bigl\{ \bigl\Vert tv_{1}+(1-t)v_{2} \bigr\Vert _{2}: 0\leq t\leq 1\bigr\} >0. $$

Then

$$ \Vert u \Vert _{2}\geq \rho R, \quad u\in \varphi _{0}( \partial _{0}\Delta ). $$

(3.20)

By (3.12), for $q\in [2,2_{s}^{\star })$, there exists $m_{q}>0$ such that

$$ \Vert u \Vert _{q}\leq m_{q}\varepsilon , \quad u\in M. $$

(3.21)

Immediately, $\varphi _{0}(\partial _{0}\Delta )\cap M= \emptyset$ if R is large enough.

Finally, it remains to verify assumption (3) of Lemma 2.7.

In fact, for $u\in \partial D_{\varepsilon }^{+}\cap \partial D_{ \varepsilon }^{-}$, we have

$$\bigl\Vert u^{\pm } \bigr\Vert \geq \operatorname{dist}\bigl(u, D^{\mp }\bigr)=\varepsilon . $$

This together with Lemma 2.4 guarantees that

$$ \Vert u \Vert ^{2}=\bigl(u^{+}+u^{-}, u^{+}+u^{-}\bigr)\geq \bigl(u^{+}, u^{+}\bigr)+ \bigl(u^{-}, u ^{-}\bigr)\geq 2 \varepsilon ^{2}. $$

(3.22)

Notice from $(f_{1})$–$(f_{2})$ that

$$ F(\tau )\leq \frac{\min \{a, 1\}}{2m_{2}^{2}} \vert \tau \vert ^{2}+ C_{2} \vert \tau \vert ^{p}, \quad \forall \tau \in \mathbb{R}. $$

(3.23)

Therefore, by virtue of (3.21)–(3.23), for $\varepsilon >0$ small enough, we have

$$\begin{aligned} I(u) \geq & \frac{1}{2}\min \{a, 1\} \Vert u \Vert ^{2}+ \frac{b}{4} \biggl( \int _{\mathbb{R}^{3}} \bigl\vert (-\Delta )^{\frac{s}{2}}u \bigr\vert ^{2}\,dx \biggr)^{2}- \int _{\mathbb{R}^{3}}F(u)\,dx \\ \geq &\frac{1}{2} \min \{a, 1\} \Vert u \Vert ^{2}- \frac{\min \{a, 1\}}{2m _{2}^{2}} \Vert u \Vert ^{2}_{2}-C_{2} \Vert u \Vert ^{p}_{p} \\ \geq & \min \{a, 1\}\varepsilon ^{2}-\frac{1}{2}\min \{a, 1\} \varepsilon ^{2}-C_{2}m_{p}^{p} \varepsilon ^{p} \\ \geq & \frac{1}{4}\min \{a, 1\} \varepsilon ^{2}, \quad u\in \varSigma . \end{aligned}$$

Then

$$ c_{\star }=\inf_{u\in \varSigma }I(u)\geq \frac{1}{4}\min \{a, 1\} \varepsilon ^{2}>0. $$

(3.24)

On the other hand, by $(f_{3})$, we have

$$ F(\tau )\geq C_{3} \vert \tau \vert ^{\mu }-C_{4}. $$

(3.25)

For $u\in \varphi _{0}(\partial _{0}\Delta )$, it follows from (3.25) that

$$\begin{aligned} I(u) \leq & \frac{a+1}{2} \Vert u \Vert ^{2}+ \frac{b}{4} \Vert u \Vert ^{4}- \int _{\operatorname{supp}(v_{1})\cup \operatorname{supp}(v_{2})}F(u) \\ \leq & \frac{a+1}{2} \Vert u \Vert ^{2}+\frac{b}{4} \Vert u \Vert ^{4}-C_{3} \Vert u \Vert ^{ \mu }_{\mu }+C_{6}. \end{aligned}$$

This together with (3.20) guarantees that

$$ \sup_{u\in \varphi _{0}(\partial _{0}\Delta )}I(u)< 0. $$

(3.26)

Then, by virtue of (3.24) and (3.26), we know

$$\sup_{u\in \varphi _{0}(\partial _{0}\Delta )}I(u)< c_{\star } $$

for R large enough, which means that assumption (3) of Lemma 2.7 holds.

Then, by Lemma 2.7, I has a critical point $u\in E\setminus (D _{\varepsilon }^{+}\cup D_{\varepsilon }^{-})$, which is a sign-changing solution of Eq. (1.1).

In summary, there exist a positive solution, a negative solution, and a sign-changing solution for Eq. (1.1). □

Now we are in a position to prove Theorem 1.2. For this sake, take $X=E$, $G=-\mathit{id}$, $P=D_{\varepsilon }^{+}$, $Q=D_{\varepsilon }^{-}$, and $J=I$. Then $M=D_{\varepsilon }^{+}\cap D_{\varepsilon }^{-}$, $\varSigma =\partial D_{\varepsilon }^{+}\cap \partial D_{\varepsilon }^{-}$, and $W=D_{\varepsilon }^{+}\cup D_{\varepsilon }^{-}$. I is even since f is assumed to be odd. In the following, a deformation lemma is given in order to prove $D_{\varepsilon }^{+}$ is a G-admissible invariant set with respect to J at level c. Owing to the proof being similar to that of Lemma 3.4, the details are omitted.

Lemma 3.5

There exists $\varepsilon _{0}>0$ such that, for $0<\varepsilon <\varepsilon '<\varepsilon _{0}$, there exists a continuous map $\sigma : [0,1]\times E\rightarrow E$ satisfying

• (1) $\sigma (0,u)=u$ for $u\in E$;

• (2) $\sigma (t,-u)=-\sigma (t,u)$ for $(t,u)\in [0,1]\times E$;

• (3) $\sigma (t,u)=u$, for $t\in [0,1]$ and $u\notin I^{-1}[c- \varepsilon ', c+\varepsilon ']$;

• (4) $\sigma (1,I^{c+\varepsilon }\setminus W)\subset I^{c-\varepsilon }$;

• (5) $\sigma (t, \overline{D_{\varepsilon }^{\pm }})\subset \overline{D _{\varepsilon }^{\pm }}$ for $t\in [0,1]$.

Proof of Theorem 1.2

According to Lemma 3.5 and Definition 2.8, it is easy to see that $D_{\varepsilon }^{+}$ is a G-admissible invariant set with respect to J at level c. For any $n\in \mathbb{N}$, suppose $\{v_{i}\}_{1} ^{n}\subset C_{0}^{\infty }(\mathbb{R}^{3})\setminus \{0\}$ such that

$$\operatorname{supp}(v_{i})\cap \operatorname{supp}(v_{j})= \emptyset , \quad i \neq j. $$

Let $B_{n}$ be the same as in Lemma 2.9. Define $\varphi _{n}\in C( B _{n}, E)$ as

$$\varphi _{n}(t)= R_{n}\sum_{i=1}^{n}t_{i}v_{i}, \quad t=(t_{1}, t_{2},\ldots, t_{n})\in B_{n}, $$

where $R_{n}>0$. Similar to the proof of Theorem 1.1, it is easy to verify that all the assumptions of Lemma 2.9 are satisfied.

Consequently, by Lemma 2.9, I has infinitely many critical points in $E\setminus (D_{\varepsilon }^{+}\cup D_{\varepsilon }^{-})$, which are sign-changing solutions of Eq. (1.1). □