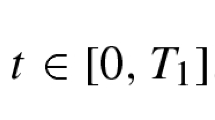The existence of affine-periodic solutions for nonlinear impulsive differential equations

Abstract

In this paper, we study the existence of affine-periodic solutions of nonlinear impulsive differential equations. The affine-periodic solutions have the form $x(t+T)=Qx(t)$ with some nonsingular matrix Q. We give a theorem on the existence of the affine-periodic solutions, respectively, depending on wether $\operatorname{det}(I-Q)$ (I= identity matrix) is equal to 0 or not.

1 Introduction

The periodicity is a very important property in the study of the impulsive differential equations [1, 2]. However, not all natural phenomena can be described alone by periodicity. Some differential equations often exhibit certain symmetries rather than periodicity. For example, consider the system

$$ \dot{x}=f(t,x), $$

(1)

where $f:R^{1}\times R^{n}\rightarrow R^{n}$ is continuous, and for some $Q\in GL_{n}(R)$ (general linear group), satisfies the following affine symmetry:

$$ f(t+T,x)=Qf \bigl(t,Q^{-1}x \bigr). $$

We call it a $(Q,T)$-affine-periodic system. For this $(Q,T)$-affine-periodic system, we are concerned with the existence of $(Q,T)$-affine-periodic solutions $x(t)$ with

$$ x(t+T)=Qx(t), \quad \forall t. $$

It should be pointed out that when $Q=I$ (identity matrix) or $Q=-I$, the solutions are just the pure periodic solutions or antiperiodic ones; when $Q\in SO_{n}$ (special orthogonal group), the solutions correspond to the solutions with Q-rotating symmetry, particularly to some special quasi-periodic solutions. So the interest to particular kinds of periodic solutions that we are going to study is not purely theoretical. The antiperiodicity property or some quasi-periodicity property, which is obviously a particular case of affine-periodic solutions, has drawn wide attention from physicists and astronomers [3, 4].

Recently, these conceptions and existence results of the solutions have been introduced and proved by Li and his coauthors; see [5] for Levinson’s problem, [6] for Lyapunov function type theorems, [7] for averaging methods of affine-periodic solutions, and [8] for some dissipative dynamical systems. The aim of this paper is to touch such a topic for affine-periodic solutions of nonlinear impulsive differential equations.

The paper is organized as follows. We first change the affine-periodic solutions problem to the boundary value problem in Sect. 2. In Sect. 3, when $\operatorname{det}(I-Q)\neq0$, we give an unique affine-periodic solution by using the Banach contraction mapping principle. Furthermore, via the topological degree theory, we prove the existence of affine-periodic solutions for nonlinear impulsive system when $\operatorname{det}(I-Q)=0$ in Sect. 4. We give two examples by numerical simulation in Sect. 5.

2 Nonlinear impulsive differential system

In this paper, we investigate the following system:

$$ \begin{aligned} &\dot{x}=f(t,x), \quad t\neq t_{k} , t\in R, \\ &\Delta x=I_{k}(x), \quad t=t _{k},k \in Z. \end{aligned}$$

(2)

The system satisfies the following hypotheses H:

• (1) $f(\cdot)\in C(R\times R^{n},R^{n})$ and $f(t+T,x)= Qf(t,Q^{-1}x)$ for some $G\in SO_{n}(R)$.

• (2) $I_{k}(\cdot)\in C(R^{n},R^{n})$, $t_{k}< t_{k+1}$ ($k \in Z$).

• (3) There exists $q\in N$ such that $I_{k+q}(x)=Q I_{k}(Q^{-1}x)$ and $t_{k+q}=t_{k}+T$ ($k \in Z$).

In system (2), the continuous part corresponds to a nonlinear $(Q,T)$-affine-periodic system. The discrete component models the affine-periodic impulsive change of $x(t)$.

Lemma 2.1

The existence of Q-affine-periodic solutions of equation (2) is equivalent to the existence of the boundary value problem (2) with $x(T)=Qx(0)$.

Proof

Let $x(t)$ be a solution of equation (2) defined on $t\in[0,T]$. Then

$$ u(t)= \textstyle\begin{cases} x(t),& t\in(0,T], \\ Q^{j}x(t-jT),& t\in(jT,jT+T], \end{cases} $$

(3)

is a Q-affine-periodic solution of (2). Indeed, if $t\in(jT,jT+T]$ and $t\neq t_{k}$, then $t-jT \in(0,T]$, and

$$ \begin{aligned}[b] \frac{d u(t)}{dt} &=Q^{j} \frac{dx(t-jT)}{dt} \\ &=Q^{j}f \bigl(t-jT,x(t-jT) \bigr) \\ &=Q^{j}\cdot Q^{-j}f \bigl(t,Q^{j}x(t-jT) \bigr) \\ &=f \bigl(t,u(t) \bigr), \end{aligned} $$

(4)

and if $t_{k}\in(jT,jT+T]$, then $t_{k-jq}=t_{k}-jT\in(0,T]$ and

$$ \begin{aligned}[b] \Delta u(t_{k})&=Q^{j}\Delta x(t_{k}-jT) \\ &=Q^{j}I_{k-jq} \bigl(x(t_{k}-jT) \bigr) \\ &=Q^{j}\cdot Q^{-j}I_{k} \bigl(Q^{j}x(t_{k}-jT) \bigr) \\ & =I_{k} \bigl(u(t_{k}) \bigr). \end{aligned} $$

(5)

Let $x(t)$ be any solution of (2) with $x(T)=Qx(0)$. Then $x(t)$ has the form

$$ x(t)=x(0)+ \int_{0}^{t}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< t}I_{k} \bigl(x(t_{k}) \bigr). $$

Denote $x(0)$ by $x_{0}$. Then we have

$$ (I-Q)x_{0}=- \biggl[ \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}I_{k} \bigl(x(t _{k}) \bigr) \biggr]. $$

(6)

 □

3 Noncritial case

$$ \operatorname{det}(I-Q)\neq0. $$

In this case, $(I-Q)^{-1}$ exists. Then

$$ x_{0}=-(I-Q)^{-1} \biggl[ \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}I_{k} \bigl(x(t _{k}) \bigr) \biggr]. $$

(7)

So, the existence of Q-affine-periodic solutions of equation (2) is equivalent to the existence of solutions of the following impulsive integral equation:

$$\begin{aligned} x(t) =&-(I-Q)^{-1} \biggl[ \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}I_{k} \bigl(x(t _{k}) \bigr) \biggr] \\ &{}+ \int_{0}^{t}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< t}I_{k} \bigl(x(t_{k}) \bigr). \end{aligned}$$

(8)

Let

$$ \textrm{X}= \bigl\{ x:[0,T]\rightarrow R^{n}: x(t) \text{ is continuous on } [0,T] \bigr\} , $$

and define the norm $\|x\|=\sup_{t\in[0,T]}|x(t)|$. It is easy to see that X is a Banach space with norm $\|x\|$. We also define the norm of the matrix $\|X(t)\|=\|(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))\|= \max_{i=1,2,\ldots,n}\|x_{i}\|$. Then we have the following theorem.

Theorem 3.1

Let a function $p\in L([0,T],R^{+})$ and nonnegative constants $\alpha_{k}$ ($k=1,2,\ldots,q$) be such that

$$\begin{aligned}& \bigl\vert f(t,y)-f(t,x) \bigr\vert \leq p(t) \vert y-x \vert , \quad \forall t\in[0,T], x,y\in R^{n}, \\& \bigl\vert I_{k}(y)-I_{k}(x) \bigr\vert \leq a_{k} \vert y-x \vert ,\quad \alpha_{k}\in R(k=1,2, \ldots,q), x,y \in R^{n}, \end{aligned}$$

and

$$ \Biggl( \int_{0}^{T}p(s)\,ds+\sum _{k=1}^{q}a_{k} \Biggr)< \frac{1}{ \Vert (I-Q)^{-1} \Vert +1}. $$

Then system (2) has an unique Q-affine-periodic solution.

Proof

Define

$$\begin{aligned} A \bigl(x(t) \bigr) =&-(I-Q)^{-1} \biggl[ \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}I_{k} \bigl(x(t _{k}) \bigr) \biggr] \\ &{}+ \int_{0}^{t}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< t}I_{k} \bigl(x(t_{k}) \bigr). \end{aligned}$$

Then

$$\begin{aligned}& \bigl\vert A \bigl(y(t) \bigr)-A \bigl(x(t) \bigr) \bigr\vert \\& \quad = \biggl\vert -(I-Q)^{-1} \biggl[ \int_{0}^{T} \bigl(f \bigl(s,y(s) \bigr)-f \bigl(s,x(s) \bigr) \bigr)\,ds+ \sum_{0\leq t_{k}< T}(I_{k} \bigl(y(t_{k})-I_{k} \bigl(x(t_{k}) \bigr) \bigr) \biggr] \\& \qquad {}+ \int_{0} ^{t} \bigl(f \bigl(s,y(s) \bigr)-f \bigl(s,x(s) \bigr) \bigr)\,ds+\sum_{0\leq t_{k}< t} \bigl(I_{k} \bigl(y(t_{k}) \bigr)-I _{k} \bigl(x(t_{k}) \bigr) \bigr) \biggr\vert \\& \quad \leq \bigl\Vert (I-Q)^{-1} \bigr\Vert \Biggl( \int_{0}^{T}p(s)\,ds+\sum _{k=1} ^{q}a_{k} \Biggr) \vert y-x \vert \\& \qquad {}+ \Biggl( \int_{0}^{t}p(s)\,ds+\sum _{k=1}^{q^{,}}a_{k} \Biggr) \vert y-x \vert \\& \quad \leq \bigl( \bigl\Vert (I-Q)^{-1} \bigr\Vert +1 \bigr) \Biggl( \int_{0}^{T}p(s)\,ds+\sum _{k=1}^{q}a_{k} \Biggr) \vert y-x \vert . \end{aligned}$$

(9)

So, if $(\int_{0}^{T}p(s)\,ds+\sum_{k=1}^{q}a_{k})<\frac{1}{\|(I-Q)^{-1} \|+1}$, then by the Banach contraction mapping principle system (2) has a unique Q-affine-periodic solution. □

4 Critial case

$$ \operatorname{det}(I-Q)=0. $$

To investigate the existence of solutions of system (2), the following auxiliary equation is often considered:

$$\begin{aligned}& \begin{aligned} &\dot{x}=\lambda f(t,x), \quad t\neq t_{k} , t\in R, \\ &\Delta x=\lambda I _{k}(x), \quad t=t_{k},k \in Z. \end{aligned} \end{aligned}$$

(10)

Then we give the following existence theorem for (Q,T)-affine-periodic solutions by using the topological degree theory [6, 7, 9–11].

Theorem 4.1

Let $D\subset R^{n}$ be a bounded open set. Assume that the following hypotheses hold for system (10):

• (H1) For each $\lambda\in(0,1]$, every Q-affine-periodic solution $x(t)$ of system (10) satisfies

  $$ x(t)\notin\partial D \quad \textit{for all }t; $$

• (H2) the Brouwer degree,

  $$ \operatorname{deg}\bigl(g,D\cap \operatorname{Ker}(I-Q),0 \bigr)\neq0 \quad \textit{if } \operatorname{Ker}(I-Q) \neq{0}, $$

where

$$ g(a)=\frac{1}{T} \biggl[ \int_{0}^{T}Pf(s,a)\,ds+\sum _{0\leq t_{k}< T}PI_{k} \bigl(x(t _{k}) \bigr) \biggr], $$

with an orthogonal projection $P:R^{n}\rightarrow \operatorname{Ker}(I-Q)$.

Then system (2) has at least one Q-affine-periodic solution $x_{*}(t)\in D$ for all t.

Proof

Consider the auxiliary equation (10) with the boundary value condition $x(T)=Qx(t)$, where $\lambda\in(0,1]$. Let $x(t)$ be any solution of (10) with $x(T)=Qx(0)$. Then

$$\begin{aligned}& (I-Q)x_{0} \\& \quad =-\lambda \biggl[ \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}I _{k} \bigl(x(t_{k}) \bigr) \biggr]. \end{aligned}$$

(11)

In this case, $(I-Q)^{-1}$ does not exist. By coordinate transformation, without loss of generality, we can just let

$$ Q= \left ( \begin{matrix} I & 0 \\ 0 & Q_{1} \end{matrix} \right ) , $$

(12)

where $(I-Q_{1})^{-1}$ exists. Here $Q=Q_{1}\oplus I$.

Let $P:R^{n}\rightarrow{ \operatorname{Ker}(I-Q)}$ be the orthogonal projection. Then

$$ \begin{aligned}[b] (I-Q)x_{0}={} &(I-Q) \bigl(x^{0}_{\ker }+x^{0}_{\bot} \bigr) \\ ={}&{-}\lambda \biggl[ \int _{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\ ={}&{-}\lambda \biggl[ \int_{0}^{T}Pf \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}PI_{k} \bigl(x(t_{k}) \bigr) \biggr] \\ &{}- \lambda \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t _{k}) \bigr) \biggr], \end{aligned} $$

(13)

where $x^{0}_{\ker }\in \operatorname{Ker}(I-Q)$, $x^{0}_{\bot}\in \operatorname{Im}(I-Q)$ and $x_{0}=x^{0}_{\ker }+x^{0}_{\bot}$.

Let $L_{p}=(I-Q)|_{\operatorname{Im}(I-Q)}$. It is easy to see that $L^{-1}_{p}$ exists. Thus equation (13) is equivalent to

$$\begin{aligned}& (I-Q)x^{0}_{\ker }=-\lambda \biggl[ \int_{0}^{T}Pf \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}PI_{k} \bigl(x(t_{k}) \bigr) \biggr]=0, \\& (I-Q)x^{0}_{\bot}=-\lambda \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr]. \end{aligned}$$

Thus we have

$$ x^{0}_{\bot}=\lambda L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr]. $$

For $x\in\textrm{X}$ such that $x(t)\in\overline{D}$ for all $t\in[0,T]$, we define the operator $\mathtt{T}(x^{0}_{\ker },x, \lambda)$ by

$$ \mathtt{T} \bigl(x^{0}_{\ker },x,\lambda \bigr) = \left ( \begin{matrix} {x^{0}_{\ker }+ \frac{1}{T} [ \int_{0}^{T}Pf (s,x(s) )\,ds+\sum_{0\leq t _{k}< T}PI_{k} (x(t_{k}) ) ]} \\ {x^{0}_{\ker }-\lambda L^{-1}_{p} [ \int_{0}^{T}(I-P)f (s,x(s) )\,ds+\sum_{0\leq t_{k}< T}(I-P)I_{k} (x(t_{k}) ) ]} \\ {{}+\lambda [ \int_{0}^{t}f (s,x(s) )\,ds+\sum_{0\leq t_{k}< t}I_{k} (x(t _{k}) ) ]} \end{matrix} \right ), $$

(14)

where $\lambda\in[0,1]$. We claim that each fixed point x of T in X is a solution of (10) with $x(T)=Qx(0)$.

In fact, if x is a fixed point of T, we have

$$ \left ( \begin{matrix} {x^{0}_{\ker}} \\ {x(t)} \end{matrix} \right ) = \left ( \begin{matrix} {x^{0}_{\ker}+\frac{1}{T} [ \int_{0}^{T}Pf (s,x(s) )\,ds+\sum_{0\leq t_{k}< T}PI _{k} (x(t_{k}) ) ]} \\ {x^{0}_{\ker}-\lambda L^{-1}_{p} [ \int_{0}^{T}(I-P)f (s,x(s) )\,ds+ \sum_{0\leq t_{k}< T}(I-P)I_{k} (x(t_{k}) ) ]} \\ {{}+\lambda [ \int_{0}^{t}f (s,x(s) )\,ds+ \sum_{0\leq t_{k}< t}I_{k} (x(t_{k}) ) ]} \end{matrix} \right ) . $$

Thus

$$\begin{aligned}& \frac{1}{T} \biggl[ \int_{0}^{T}Pf \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}PI_{k} \bigl(x(t _{k}) \bigr) \biggr]=0, \end{aligned}$$

(15)

$$\begin{aligned}& x(t)= x^{0}_{\ker } -\lambda L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\& \hphantom{x(t)=}{}+\lambda \biggl[ \int_{0}^{t}f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< t}I_{k} \bigl(x(t_{k}) \bigr) \biggr]. \end{aligned}$$

(16)

By equation (16) we know that

$$ x_{0}=x^{0}_{\ker }-\lambda L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr]. $$

According to $(I-Q)x^{0}_{\ker }=0$, we have

$$ \begin{aligned} Qx_{0} &=Qx^{0}_{\ker }- \lambda QL^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\ &=x^{0}_{\ker }-\lambda QL^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I _{k} \bigl(x(t_{k}) \bigr) \biggr]. \end{aligned} $$

Since equation (15) holds, we have

$$\begin{aligned}& (I-Q)L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I _{k} \bigl(x(t_{k}) \bigr) \biggr] \\& \quad = \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I _{k} \bigl(x(t_{k}) \bigr) \biggr] \\& \quad = \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I _{k} \bigl(x(t_{k}) \bigr) \biggr] \\& \qquad {} + \biggl[ \int_{0}^{T}Pf \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}PI_{k} \bigl(x(t_{k}) \bigr) \biggr] \\& \quad = \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}I_{k} \bigl(x(t_{k}) \bigr). \end{aligned}$$

Thus

$$\begin{aligned}& \lambda QL^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I _{k} \bigl(x(t_{k}) \bigr) \biggr] \\& \quad =\lambda L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\& \qquad {}-\lambda \biggl[ \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}I_{k} \bigl(x(t_{k}) \bigr) \biggr]. \end{aligned}$$

Then

$$\begin{aligned} Qx_{0} = &x^{0}_{\ker }- \lambda QL^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\ =&x^{0}_{\ker }-\lambda L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I _{k} \bigl(x(t_{k}) \bigr) \biggr] \\ &{}+\lambda \biggl[ \int_{0}^{T}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t _{k}< T}I_{k} \bigl(x(t_{k}) \bigr) \biggr] =x(T). \end{aligned}$$

(17)

By equations (16) and (17), equation (11) holds. Thus,

$$ x^{0}_{\bot}=-\lambda L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr]. $$

Then,

$$\begin{aligned} x(t) = &x^{0}_{\ker }-\lambda L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\ &{}+\lambda \biggl[ \int_{0}^{t}f \bigl(s,x(s) \bigr)\,ds+ \sum _{0\leq t_{k}< t}I \bigl(x(t_{k}) \bigr) \biggr] \\ =&x^{0}_{\ker }+x^{0}_{\bot}+ \lambda \biggl[ \int_{0}^{t}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< t}I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\ =&x_{0}+\lambda \biggl[ \int_{0}^{t}f \bigl(s,x(s) \bigr)\,ds+\sum _{0\leq t_{k}< t}I_{k} \bigl(x(t _{k}) \bigr) \biggr]. \end{aligned}$$

This means that the fixed point x is a solution of (10) with $x(T)=Qx(0)$.

Now, we need to prove the existence of the fixed point of T. Take a constant M such that $M> \sup_{t\in[0,T],x\in\overline{D}}|f(t,x)|$, and let

$$ \textrm{X}_{\lambda}= \biggl\{ x\in\textrm{X}: \biggl\vert \frac{x(t)-x(r)}{t-r} \biggr\vert \leq \lambda M \text{ for all } t,r \in(t_{k},t_{k+1}],t\neq r \biggr\} . $$

Then, it is easy to make a retraction $\alpha_{\lambda}:\textrm{X} \rightarrow\textrm{X}_{\lambda}$.

Define an operator $\widehat{\mathtt{T}}(x^{0}_{\ker },x,\lambda)$ by

$$ \begin{aligned} &\widehat{\mathtt{T}} \bigl(x^{0}_{\ker },x, \lambda \bigr) \\ &\quad = \left ( \begin{matrix} {x^{0}_{\ker} +\frac{1}{T} [ \int_{0}^{T}Pf (s,\alpha_{\lambda}\circ x(s) )\,ds+ \sum_{0\leq t_{k}< T}PI_{k} ( \alpha_{\lambda}\circ x(t_{k}) ) ]} \\ {\alpha_{\lambda}\circ x^{0}_{\ker }-\lambda L^{-1}_{p} [ \int_{0} ^{T}(I-P)f (s,\alpha_{\lambda} \circ x(s) )\,ds+\sum_{0\leq t_{k}< T}(I-P)I _{k} (\alpha_{\lambda}\circ x(t_{k}) ) ]} \\ {{}+\lambda [ \int_{0}^{t}f (s, \alpha_{\lambda}\circ x(s) )\,ds+\sum_{0\leq t_{k}< t}I_{k} ( \alpha_{ \lambda}\circ x(t_{k}) ) ]} \end{matrix} \right ). \end{aligned} $$

(18)

Since $P:R^{n}\rightarrow \operatorname{Ker}(I-Q)$, it is easy to see that

$$ \frac{1}{T} \biggl[ \int_{0}^{T}Pf \bigl(s, x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}PI_{k} \bigl(x(t _{k}) \bigr) \biggr] \in \operatorname{Ker}(I-Q). $$

Also,

$$ \frac{1}{T} \biggl[ \int_{0}^{T}Pf \bigl(s,\alpha_{\lambda}\circ x(s) \bigr)\,ds+ \sum_{0\leq t_{k}< T}PI_{k} \bigl( \alpha_{\lambda}\circ x(t_{k}) \bigr) \biggr]\in \operatorname{Ker}(I-Q). $$

Let us consider the homotopy

$$\begin{aligned}& H \bigl(x^{0}_{\ker },x,\lambda \bigr)= \widehat{ \mathtt{T}} \bigl(x^{0}_{\ker },x, \lambda \bigr), \end{aligned}$$

(19)

$$\begin{aligned}& \bigl(x^{0}_{\ker },x,\lambda \bigr)\in \bigl(D \cap \operatorname{Ker}(I-Q)\times\widetilde{D} \times[0,1] \bigr), \end{aligned}$$

(20)

where $\widetilde{D}=\{x\in X:x(t)\in D \text{ for all } t \in[0,T]\}$.

We claim that

$$ 0\notin(id-H) (\partial \bigl( \bigl(D\cap \operatorname{Ker}(I-Q)\times \widetilde{D} \bigr)\times[0,1] \bigr). $$

(21)

Suppose, on the contrary, that there exists $(\widehat{x}^{0}_{\ker }, \widehat{x},\widehat{\lambda})\in\partial((D\cap \operatorname{Ker}(I-Q)\times \widetilde{D})\times[0,1]$ such that $(id-H)(\widehat{x}^{0}_{\ker }, \widehat{x},\widehat{\lambda})=0$. Since $\widehat{x}^{0}_{\ker } \in\partial D$ is contradictory to ($H_{1}$) and since $\partial(D \cap \operatorname{Ker}(I-Q))\subset\partial D$, we have that $\widehat{x}^{0}_{ \ker }\notin\partial(D\cap \operatorname{Ker}(I-Q))$. In other words, $\widehat{x}\in\partial D$. Then (21) can be proved as follows.

(i) When $\widehat{\lambda}=0$, by the definition of the set $\textrm{X}_{\lambda}$ we have

$$ \textrm{X}_{0}= \biggl\{ x\in X: \biggl\vert \frac{x(t)-x(r)}{t-r} \biggr\vert \leq0 \text{ for all } t,r\in(t_{k},t_{k+1}],t \neq r \biggr\} . $$

Hence $\alpha_{0}\circ x(t)\equiv\alpha_{0}\circ x(t_{k+1})$ for all $t\in(t_{k},t_{k+1}]$. Since $(id-H)(\widehat{x}^{0}_{\ker}, \widehat{x},0)=0$, we have

$$ \left ( \begin{matrix} {\widehat{x}^{0}_{\ker }} \\ {\widehat{x}(t)} \end{matrix} \right ) = \left ( \begin{matrix} { \widehat{x}^{0}_{\ker } +\frac{1}{T} [ \int_{0}^{T}Pf (s,\alpha_{ \lambda}\circ x(s) )\,ds+\sum_{0\leq t_{k}< T}PI_{k} ( \alpha_{\lambda} \circ x(t_{k}) ) ]} \\ {\alpha_{0} \circ\widehat{x}^{0}_{\ker }} \end{matrix} \right ) . $$

(22)

This means that $\widehat{x}(t)\equiv\widehat{x}(0)$ for all $t\in[0,T]$. Taking $\widehat{x}(t)=p$, we have $\alpha_{0}\circ \widehat{x}^{0}_{\ker }=\widehat{x}(t)=p$. Consequently,

$$ \frac{1}{T} \biggl[ \int_{0}^{T}Pf \bigl(s,\alpha_{\lambda}\circ x(s) \bigr)\,ds+ \sum_{0\leq t_{k}< T}PI_{k} \bigl( \alpha_{\lambda}\circ x(t_{k}) \bigr) \biggr]=0, $$

and this is equivalent to $g(p)=0$ by the definition of $g(a)$. Notice that $\widehat{x}\in\partial\widetilde{D}$ and $\widetilde{D}=\{x \in D \text{ for all } t\in[0,T]\}$. Then there exists $t_{0}\in[0,T]$ such that $\widehat{x(t)}_{0}\in\partial D$. Since $\widehat{x}(t)\equiv p$ for all $t\in[0,T]$, we obtain that $p\in\partial D$. Thus, we have $p\in\partial D$ and $g(p)=0$. It is contradictory to ($H_{2}$) because the Brouwer degree $\operatorname{deg}(g,D,0) \neq0$.

(ii) When $\widehat{\lambda}\in(0,1]$, as $0=(id-H)(\widehat{x}^{0} _{\ker },\widehat{x},\widehat{\lambda})$, we have

$$\begin{aligned}& \left ( \begin{matrix} {\widehat{x}^{0}_{\ker }} \\ {\widehat{x}(t)} \end{matrix} \right ) \\& \quad = \left ( \begin{matrix} {\widehat{x}^{0}_{\ker } +\frac{1}{T} [ \int_{0}^{T}Pf (s, \alpha_{\widehat{\lambda}}\circ x(s) )\,ds+\sum_{0\leq t_{k}< T}PI_{k} ( \alpha_{\widehat{\lambda}}\circ x(t_{k}) ) ]} \\ {\alpha_{\widehat{\lambda}}\circ x^{0}_{\ker }-\widehat{\lambda} L ^{-1}_{p} [ \int_{0}^{T}(I-P)f (s,\alpha_{\widehat{\lambda}} \circ x(s) )\,ds+ \sum_{0\leq t_{k}< T}(I-P)I_{k} ( \alpha_{\widehat{\lambda}}\circ x(t _{k}) ) ]} \\ {{}+\widehat{\lambda} [ \int_{0}^{t}f (s,\alpha_{ \widehat{\lambda}}\circ x(s) )\,ds+\sum_{0\leq t_{k}< t}I_{k} ( \alpha_{\widehat{\lambda}}\circ x(t_{k}) ) ]} \end{matrix} \right ) . \end{aligned}$$

Thus

$$ \frac{1}{T} \biggl[ \int_{0}^{T}Pf \bigl(s,\alpha_{\widehat{\lambda}}\circ x(s) \bigr)\,ds+ \sum_{0\leq t_{k}< T}PI_{k} \bigl( \alpha_{\widehat{\lambda}}\circ x(t_{k}) \bigr) \biggr]=0 $$

and

$$ \begin{aligned}[b] \widehat{x}(t)={} & \alpha_{\widehat{\lambda}} \circ x^{0}_{\ker }- \widehat{\lambda} L^{-1}_{p} \biggl[ \int_{0}^{T}(I-P)f \bigl(s, \alpha_{\widehat{\lambda}} \circ x(s) \bigr)\,ds+\sum_{0\leq t_{k}< T}(I-P)I _{k} \bigl(\alpha_{\widehat{\lambda}}\circ x(t_{k}) \bigr) \biggr] \\ &{}+ \widehat{\lambda} \biggl[ \int_{0}^{t}f \bigl(s,\alpha_{\widehat{\lambda}}\circ x(s) \bigr)\,ds+ \sum_{0\leq t_{k}< t}I_{k} \bigl( \alpha_{\widehat{\lambda}}\circ x(t_{k}) \bigr) \biggr]. \end{aligned} $$

(23)

Note that

$$\begin{aligned}& \biggl\vert \frac{x(t)-x(r)}{t-r} \biggr\vert \\& \quad = \frac{1}{ \vert t-r \vert } \biggl\vert \widehat{\lambda} \int _{0}^{t}f \bigl(s,\alpha_{\widehat{\lambda}}\circ \widehat{x}(s) \bigr)\,ds- \widehat{\lambda} \int_{0}^{r}f \bigl(s,\alpha_{\widehat{\lambda}}\circ \widehat{x}(s) \bigr)\,ds \biggr\vert \\& \quad =\frac{1}{ \vert t-r \vert } \biggl\vert \widehat{\lambda} \int _{r}^{t}f \bigl(s,\alpha_{\widehat{\lambda}}\circ \widehat{x}(s) \bigr)\,ds \biggr\vert \\& \quad \leq \lambda M. \end{aligned}$$

By the definition of $\textrm{X}_{\lambda}$ we obtain $\widehat{x} \in\textrm{X}_{\widehat{\lambda}}$, which means that $\alpha_{\widehat{\lambda}}\circ\widehat{x}=\widehat{x}$. Now we can rewrite equation (23) as

$$\begin{aligned} \widehat{x}(t) =& x^{0}_{\ker } - \widehat{ \lambda} L^{-1}_{p} \biggl[ \int _{0}^{T}(I-P)f \bigl(s, x(s) \bigr)\,ds+\sum _{0\leq t_{k}< T}(I-P)I_{k} \bigl(x(t_{k}) \bigr) \biggr] \\ &{}+\widehat{\lambda} \biggl[ \int_{0}^{t}f \bigl(s, x(s) \bigr)\,ds+\sum _{0\leq t_{k}< t}I _{k} \bigl(x(t_{k}) \bigr) \biggr]. \end{aligned}$$

By a similar discussion of equation (16) we can prove that $\widehat{x}(t)$ is a solution of equation (10). By hypothesis ($H_{1}$) we know that $\widehat{x}(t)\notin\partial\widetilde{D}$ for any $t\in[0,T]$. This is a contradiction to $\widehat{x}\in\partial \widetilde{D}$.

By (i) and (ii) we obtain that

$$ 0\notin(id-H) \bigl(\partial \bigl( \bigl(D\cap \operatorname{Ker}(I-Q) \bigr)\times \widetilde{D} \bigr)\times [0,1] \bigr). $$

Therefore, by the homotopy invariance and the theory of Brouwer degree we have

$$ \begin{aligned} &\operatorname{deg}\bigl(id-H \bigl(x^{0}_{\ker}, \cdot,1 \bigr), \bigl(D\cap \operatorname{Ker}(I-Q) \bigr)\times\widetilde{D},0 \bigr) \\ &\quad =\operatorname{deg}\bigl(id-H \bigl(x^{0}_{\ker},\cdot,0 \bigr), \bigl(D \cap \operatorname{Ker}(I-Q) \bigr)\times \widetilde{D},0 \bigr) \\ &\quad =\operatorname{deg}\bigl(g,D\cap \operatorname{Ker}(I-Q),0 \bigr)\neq0. \end{aligned} $$

This means that there exists $\widehat{x}_{*}\in\widetilde{D}$ such that

$$ \left ( \begin{matrix} {\widehat{x}^{0}_{*\ker }} \\ {\widehat{x}_{*}(t)} \end{matrix} \right ) =\widehat{ T} \bigl(\widehat{x}^{0}_{*\ker }, \widehat{x} _{*}(t),1 \bigr). $$

(24)

Similarly to the proof in (ii), we get $\widehat{x}_{*}\in\textrm{X} _{\lambda}$. Then

$$ { } \widehat{T} \bigl(\widehat{x}^{0}_{*\ker }, \widehat{x}_{*}(t),1 \bigr)= T \bigl(\widehat{x}^{0}_{*\ker }, \widehat{x}_{*}(t),1 \bigr). $$

(25)

By equations (24) and (25) we obtain that $\widehat{x}_{*}$ is a fixed point of T in X. Thus, $\widehat{x}_{*}$ is a solution of system (2) with boundary value condition $x(T)=Qx(0)$. □

5 Numerical simulation

Example 1

Consider the system

$$ \begin{aligned} &\dot{x}=- \vert x \vert ^{2}x+(\sin\pi t,\cos\pi t)^{T}, \quad t\neq N, \\ &\Delta x= \biggl(\frac{1}{e}-1 \biggr)x,\quad t=N. \end{aligned} $$

(26)

Set

$$ Q= \left ( \begin{matrix} -1& 0 \\ 0& -1 \end{matrix} \right ) . $$

In this example, $Q=-I$. System (26) has an antiperiodic solution (see Fig. 1).

Figure 1

The antiperiodic solution of system (26). The green line is the trajectory of $x(t)$ for $t\in(0,1]$, the red line corresponds to the trajectory of $Qx(t)$ for $t\in(0,1]$

Example 2

Consider the system

$$ \begin{aligned} &\dot{x}=- \vert x \vert ^{2}x+(\sin t,\cos t,1)^{T},\quad t\neq N, \\ &\Delta x= \biggl(\frac{1}{e}-1 \biggr)x, \quad t=N. \end{aligned} $$

(27)

Set

$$ Q= \left ( \begin{matrix} {\cos(2\pi-1)}& {-\sin(2\pi-1)} &0 \\ {\sin(2\pi-1)}& {\cos(2\pi-1)} &0 \\ 0 &0 &1 \end{matrix} \right ) . $$

Similarly to Example 1, system (26) has a $(Q,1)$-affine-periodic solution., which is a quasi-periodic solution (see Fig. 2).

Figure 2

The $(Q,T)$-affine-periodic solution of system (27). The black line is the trajectory of $x(t)$ for $t\in(0,1]$, the red line corresponds to the trajectory of $Qx(t)$ for $t\in(0,1]$, and the green line corresponds to the trajectory of $Q^{2}x(t)$ for $t\in(0,1]$. It is easy to see that $x(t)$ is a quasi-periodic solution of system (27)