Existence of positive solutions for a third-order multipoint boundary value problem and extension to fractional case

Abstract

In this paper, we study a nonlinear third-order multipoint boundary value problem by the monotone iterative method. We then obtain the existence of monotone positive solutions and establish iterative schemes for approximating the solutions. In addition, we extend the considered problem to the Riemann-Liouville-type fractional analogue. Finally, we give a numerical example for demonstrating the efficiency of the theoretical results.

1 Introduction

In this article, we are concerned with the existence of monotone positive solutions to the third-order and fractional-order multipoint boundary value problems. In the first part, we consider the following third-order multipoint boundary value problem:

$$ \begin{aligned} &u'''(t)+q(t)f \bigl(t,u(t),u'(t)\bigr)=0,\quad 0< t < 1, \\ &u(0)=u'(0)=0,\qquad u'(1)=\sum _{i=1}^{m}\alpha_{i} u'( \eta_{i}), \end{aligned} $$

(1)

where $0<\eta_{1}<\eta_{2}<\cdots<\eta_{m}<1$ ($m\geqslant1$), $\alpha _{i}\geqslant0$ ($i=1,2,\ldots,m$), and $\sum_{i=1}^{m}\alpha_{i}\eta_{i}<1$.

Presently, the study of existence of positive solutions of third-order boundary value problems has gained much attention [1–12]. For example, Zhang et al. [1] obtained the existence of single and multiple monotone positive solutions for problem (1) by replacing $q(t)f(t,u(t),u'(t))$ with $\lambda a(t)f(t,u(t))$, where λ is a positive parameter. By the Guo-Krasnoselskii fixed point theorem, the authors established the intervals of the parameter, which yields the existence of one, two, or infinitely many monotone positive solutions under some suitable conditions. Zhang and Sun [2] established a generalization of the Leggett-Williams fixed point theorem and studied the existence of multiple nondecreasing positive solutions for problem (1) by replacing $q(t)f(t,u(t),u'(t))$ with $f(t,u(t),u'(t),u''(t))$. Recently, by using the Leray-Schauder nonlinear alternative, the Banach contraction theorem, and the Guo-Krasnoselskii theorem, Guezane-Lakoud and Zenkoufi [3] discussed the existence, uniqueness, and positivity of a solution in (1) with $q(t)\equiv1$.

In the second part, we extend our discussion to the fractional case by considering the boundary value problems with Riemann-Liouville fractional derivative given by

$$ \begin{aligned} &D^{\alpha}_{0^{+}}u(t)+q(t)f \bigl(t,u(t),u'(t)\bigr)=0,\quad 0< t < 1, \\ &u(0)=u'(0)=0,\qquad u'(1)=\sum _{i=1}^{m}\alpha_{i} u'( \eta_{i}), \end{aligned} $$

(2)

where $0<\eta_{1}<\eta_{2}<\cdots<\eta_{m}<1$ ($m\geqslant1$), $2 <\alpha< 3$, $\alpha_{i}\geqslant0$ ($i=1,2,\ldots,m$), and $\sum_{i=1}^{m}\alpha_{i}\times \eta_{i}^{\alpha-2}<1$. Presently, fractional differential equations have attracted increasing interest in the research community [13–31], for example, specially introducing the fractional dynamics into the synchronization of complex networks [32, 33]. Problem (2) with $q(t)f(t,u(t),u'(t))=\tilde{f}(t,u(t))$ has been studied in [34–36]. Zhong [34] studied the existence and multiplicity of positive solutions by the Krasnoselskii and Leggett-Williams fixed point theorems. Liang and Zhang [35] investigated the existence and uniqueness of positive and nondecreasing solutions by using a fixed point theorem in partially ordered sets and the lower and upper solution method. Cabrera et al. [36] focused themselves on the existence and uniqueness of a positive and nondecreasing solution based on a fixed point theorem in partially ordered sets, which is different from that used in [35].

2 Preliminaries

In this section, we assume that the following conditions hold:

• (H1) $0<\eta_{1}<\eta_{2}<\cdots<\eta_{m}<1$ ($m\geqslant1$), $\alpha _{i}\geqslant0$ ($i=1,2,\ldots,m$), $\rho:=\sum_{i=1}^{m}\alpha_{i}\eta_{i}<1$;

• (H2) $q\in L^{1}[0,1]$ is nonnegative, and $0<\int _{0}^{1}(1-s)q(s)\,ds<\infty$;

• (H3) $f\in C([0,1]\times[0,\infty)\times[0, \infty),[0,\infty))$, and $f(t,0,0)\not\equiv0$ for $t\in(0,1)$.

Lemma 1

see [3]

Let $h\in C(0,1)\cap L[0,1]$. Then the boundary value problem

$$\begin{aligned}& u'''(t)+h(t)=0, \quad 0< t < 1, \\& u(0)=u'(0)=0, \qquad u'(1)=\sum _{i=1}^{m}\alpha_{i}u'( \eta_{i}), \end{aligned}$$

has a unique solution

$$ u(t)= \int_{0}^{1}G(t,s)h(s)\,ds,\quad t\in[0,1], $$

where

$$ \begin{aligned} &G(t,s)=H(t,s)+\frac{t^{2}}{2(1-\rho)}\sum _{i=1}^{m}\alpha_{i}H_{1}( \eta_{i},s),\quad t, s\in[0,1], \\ &H(t,s)=\frac{1}{2}\left \{ \textstyle\begin{array}{l@{\quad}l} (1-s)t^{2}-(t-s)^{2},& 0\leqslant s\leqslant t\leqslant1, \\ (1-s)t^{2}, &0\leqslant t\leqslant s\leqslant1, \end{array}\displaystyle \right . \end{aligned} $$

(3)

and

$$ H_{1}(t,s):=\frac{\partial G(t,s)}{\partial t}=\left \{ \textstyle\begin{array}{l@{\quad}l} (1-t)s,& 0\leqslant s\leqslant t\leqslant1, \\ (1-s)t,& 0\leqslant t\leqslant s\leqslant1. \end{array}\displaystyle \right . $$

In the following, we provide some properties of the functions $H(t,s)$, $H_{1}(t,s)$, and $G(t,s)$.

Lemma 2

For all $(t, s)\in[0,1]\times[0,1]$, we have:

• (a) $t^{2}H(1,s)\leqslant H(t,s)\leqslant H(1,s)$;

• (b) $0\leqslant H(t,s)\leqslant\frac{1}{2}t^{2}(1-s)$, $0\leqslant H_{1}(t,s)\leqslant t(1-s)$;

• (c) $t^{2}G(1,s)\leqslant G(t,s)\leqslant G(1,s)$;

• (d) $G(t,s)\leqslant\frac{(1-s)t^{2}}{2(1-\rho)}$, $\frac {\partial G(t,s)}{\partial t}\leqslant\frac{(1-s)t}{1-\rho}$.

Proof

For a proof of (a), see [3]. It is easy to check that (b) holds. Next, we prove (c). By Lemma 2(a) and (3),

$$\begin{aligned} G(t,s)&=H(t,s)+\frac{t^{2}}{2(1-\rho)}\sum_{i=1}^{m} \alpha_{i}H_{1}(\eta _{i},s) \\ &\leqslant H(1,s)+\frac{1}{2(1-\rho)}\sum_{i=1}^{m} \alpha_{i}H_{1}(\eta _{i},s) \\ &=G(1,s). \end{aligned}$$

On the other hand,

$$\begin{aligned} G(t,s)&=H(t,s)+\frac{t^{2}}{2(1-\rho)}\sum_{i=1}^{m} \alpha_{i}H_{1}(\eta _{i},s) \\ &\geqslant t^{2}H(1,s)+\frac{t^{2}}{2(1-\rho)}\sum _{i=1}^{m}\alpha_{i}H_{1}(\eta _{i},s) \\ &=t^{2}G(1,s). \end{aligned}$$

This means that (c) holds.

Finally, we prove (d). By Lemma 2(b) and (3) we have

$$\begin{aligned} G(t,s)&=H(t,s)+\frac{t^{2}}{2(1-\rho)}\sum_{i=1}^{m} \alpha_{i}H_{1}(\eta _{i},s) \\ &\leqslant\frac{1}{2}(1-s)t^{2}+\frac{t^{2}}{2(1-\rho)}\sum _{i=1}^{m}\alpha _{i}\eta_{i}(1-s) \\ &=\frac{1}{2}(1-s)t^{2}+\frac{\rho(1-s)t^{2}}{2(1-\rho)} \\ &=\frac{(1-s)t^{2}}{2(1-\rho)}. \end{aligned}$$

For s fixed, this gives

$$\begin{aligned} \frac{\partial G(t,s)}{\partial t}&=H_{1}(t,s)+\frac{t}{1-\rho}\sum _{i=1}^{m}\alpha_{i}H_{1}( \eta_{i},s) \\ &\leqslant(1-s)t+\frac{t}{1-\rho}\sum_{i=1}^{m} \alpha_{i}\eta_{i}(1-s) \\ &=(1-s)t+\frac{\rho(1-s)t}{1-\rho} \\ &=\frac{\rho(1-s)t}{1-\rho}. \end{aligned}$$

This completes the proof. □

In this paper, to study (1), we will use the space $E=C^{1}[0,1]$ equipped with the norm

$$\|u\|:= \Bigl\{ \max_{0\leqslant t\leqslant1}\bigl\vert u(t)\bigr\vert , \max _{0\leqslant t\leqslant1}\bigl\vert u'(t)\bigr\vert \Bigr\} . $$

Define the cone $K\subset E$ by

$$K= \Bigl\{ u\in C^{1}[0,1]: u(t)\geqslant0, u'(t) \geqslant0, \mbox{and } u(t)\geqslant t^{2}\max_{0\leqslant t\leqslant1} \bigl\vert u(t)\bigr\vert , t\in [0,1] \Bigr\} . $$

Introduce the integral operator $T: K\to E$ by

$$ (Tu) (t) = \int_{0}^{1}G(t,s)q(s)f\bigl(s,u(s),u'(s) \bigr)\,ds, $$

(4)

where $G (t, s)$ is defined by (3). By Lemma 1, the problem (1) has a solution $u\in K$ if u is a fixed point of T defined by (4).

Lemma 3

Let (H1)-(H3) hold. Then $T:K\to K$ is completely continuous.

Proof

Suppose that $u\in K$. In view of Lemma 2(a),

$$\begin{aligned} 0&\leqslant(Tu) (t)= \int_{0}^{1}G(t,s)q(s)f\bigl(s,u(s),u'(s) \bigr)\,ds \\ &\leqslant \int_{0}^{1}G(1,s)q(s)f\bigl(s,u(s),u'(s) \bigr)\,ds, \quad t \in[0, 1], \end{aligned}$$

which implies that

$$ \max_{t\in[0,1]}\bigl\vert Tu(t)\bigr\vert \leqslant \int _{0}^{1}G(1,s)q(s)f\bigl(s,u(s),u'(s) \bigr)\,ds. $$

(5)

On the other hand, we have

$$\begin{aligned} \begin{aligned}[b] (Tu) (t)&= \int_{0}^{1}G(t,s)q(s)f\bigl(s,u(s),u'(s) \bigr)\,ds \\ &\geqslant t^{2} \int_{0}^{1}G(1,s)q(s)f\bigl(s,u(s),u'(s) \bigr)\,ds, \quad t \in[0, 1]. \end{aligned} \end{aligned}$$

(6)

Using inequalities (5) and (6) yields

$$(Tu) (t)\geqslant t^{2}\max_{0\leqslant t\leqslant1}\bigl\vert (Tu) (t)\bigr\vert , \quad t\in[0,1]. $$

It is easy to see that $(Tu)'(t)\geqslant0$ for $t\in[0,1]$. Hence, the operator T maps K into itself. In addition, a standard argument shows that $T:K\to K$ is completely continuous. This completes the proof. □

3 Main results

The main results of this section are given as follows. For notational convenience, denote

$$\varLambda _{1}= \biggl(\frac{1}{1-\rho} \int_{0}^{1}(1-s)q(s)\,ds \biggr)^{-1}. $$

Theorem 1

Suppose that conditions (H1)-(H3) hold. Let $a>0$ and suppose that f satisfies the following condition:

$$ f(t,u_{1},v_{1})\leqslant f(t,u_{2},v_{2}) \leqslant \varLambda _{1} a \quad \textit{for } 0\leqslant t\leqslant1, 0 \leqslant u_{1}\leqslant u_{2}\leqslant a , 0\leqslant v_{1}\leqslant v_{2}\leqslant a. $$

(7)

Then problem (1) has two monotone positive solutions v and w, which satisfy

• $0<\|v\|\leqslant a$ and $\lim_{n\to\infty}v_{n}=v$, where $v_{n}=Tv_{n-1}$, $n=1,2,\ldots$ , $v_{0}(t)=0$, $t\in[0,1]$;

• $0<\|w\|\leqslant a$ and $\lim_{n\to\infty}w_{n}=w$, where $w_{n}=Tw_{n-1}$, $n=1,2,\ldots$ , $w_{0}(t)=\frac{1}{2}at^{2}$, $t\in[0,1]$.

Proof

Firstly, we check that $T:K_{a}\to K_{a}$, where $K_{a}=\{u\in K:\|u\|\leqslant a\}$. In fact, if $u\in K_{a}$, then

$$ 0\leqslant u(s)\leqslant\max_{0\leqslant s\leqslant1} u(s)\leqslant\| u\| \leqslant a,\qquad 0\leqslant u'(s)\leqslant\max _{0\leqslant s\leqslant1} u'(s)\leqslant \|u\|\leqslant a, \quad t \in[0,1], $$

which, together with condition (7) and Lemma (2)(d), implies that

$$0\leqslant f\bigl(s,u(s),u'(s)\bigr)\leqslant f(s,a,a)\leqslant \varLambda _{1} a,\quad s\in[0,1]. $$

Thus, by Lemma 2 we have

$$\begin{aligned} (T u) (t)&= \int_{0}^{1}G(t,s)q(s)f\bigl(s,u(s),u'(s) \bigr)\,ds \\ &\leqslant\frac{t^{2}}{2(1-\rho)} \int_{0}^{1}(1-s)q(s)f(s,a,a)\,ds \\ &\leqslant\frac{\varLambda _{1} a }{2(1-\rho)} \int_{0}^{1}(1-s)q(s)\,ds \\ &=\frac{a}{2}< a,\quad t \in[0, 1], \end{aligned}$$

(8)

and

$$\begin{aligned} (T u)'(t)&= \int_{0}^{1} G_{1}(t,s)q(s)f \bigl(s,u(s),u'(s)\bigr)\,ds \\ &\leqslant\frac{t}{1-\rho} \int_{0}^{1}(1-s)q(s)f(s,a,a)\,ds \\ &\leqslant\frac{\varLambda _{1} a}{1-\rho} \int_{0}^{1}(1-s)q(s)\,ds \\ &= a,\quad t \in[0, 1]. \end{aligned}$$

(9)

Inequalities (8) and (9) give $\|T\|\leqslant a$. Thus, $T:K_{a}\to K_{a}$.

Now, we prove that there exist $w, v\in K_{a}$ such that $\lim_{n\to \infty}w_{n}=w$, $\lim_{n\to \infty}v_{n}=v$, and w, v are monotone positive solutions of problem (1).

Indeed, in view of $w_{0}, v_{0}\in K_{a}$ and $T:K_{a}\to K_{a}$, we have $w_{n}, v_{n}\in K_{a}$, $n=0,1,2,\ldots$ . Since $\{w_{n}\}_{n=1}^{\infty}$ and $\{v_{n}\}_{n=1}^{\infty}$ are bounded and T is completely continuous, we know that the sets $\{w_{n}\}_{n=1}^{\infty}$ and $\{v_{n}\}_{n=1}^{\infty}$ are sequentially compact sets. Since $w_{1}=Tw_{0}=T(\frac{1}{2}at^{2})\in K_{a}$, by (7) and (4) we have

$$\begin{aligned} w_{1}(t)&=(T w_{0}) (t) \\ &= \int_{0}^{1}G(t,s)q(s)f\bigl(s,w_{0}(s),w'_{0}(s) \bigr)\,ds \\ &= \int_{0}^{1}G(t,s)q(s)f\biggl(s, \frac{1}{2}as^{2},as\biggr)\,ds \\ &\leqslant\frac{t^{2}}{2(1-\rho)} \int_{0}^{1}(1-s)q(s)f(s,a,a)\,ds \\ &\leqslant\frac{1}{2}at^{2}=w_{0}(t),\quad t \in[0, 1], \end{aligned}$$

and

$$\begin{aligned} w'_{1}(t)&= \int_{0}^{1} \frac{\partial G(t,s)}{\partial t}q(s)f \bigl(s,w_{0}(s),w'_{0}(s)\bigr)\,ds \\ &\leqslant\frac{t}{1-\rho} \int_{0}^{1}(1-s)q(s)f\biggl(s,\frac{1}{2}as^{2},as \biggr)\,ds \\ &\leqslant\frac{t}{1-\rho} \int_{0}^{1}(1-s)q(s)f(s,a,a)\,ds \\ &\leqslant at=w'_{0}(t),\quad t \in[0, 1]. \end{aligned}$$

Thus,

$$ w_{1}(t)\leqslant w_{0}(t),\qquad w'_{1}(t) \leqslant w'_{0}(t), \quad t \in[0, 1]. $$

Further,

$$\begin{aligned}& w_{2}(t)=(Tw_{1}) (t)\leqslant(Tw_{0}) (t)=w_{1}(t),\quad t\in[0,1], \\& w'_{2}(t)=(Tw_{1})'(t) \leqslant(Tw_{0})'(t)=w'_{1}(t), \quad t\in[0,1]. \end{aligned}$$

Finally, this gives

$$w_{n+1}(t)\leqslant w_{n}(t),\qquad w'_{n+1}(t) \leqslant w'_{n}(t),\quad t\in[0,1], n=0,1,2,\ldots. $$

Hence, there exists $w\in K_{a}$ such that $\lim_{n\to\infty}w_{n}=w$. This, together with the continuity of T and $w_{n+1}= Tw_{n}$, implies that $Tw=w$. By a similar argument there exists $v\in K_{a}$ such that $\lim_{n\to\infty}v_{n}=v$ and $v=Tv$.

Thus, w and v are two nonnegative solutions of problem (1). Because the zero function is not a solution of problem (1), we have $\max_{0\leqslant t\leqslant1}|w(t)|>0$ and $\max_{0\leqslant t\leqslant1}|v(t)|>0$, and from the definition of the cone K it follows that $w(t)\geqslant t^{2}\max_{0\leqslant t\leqslant1}|w(t)|>0$, $v(t)\geqslant t^{2}\max_{0\leqslant t\leqslant1}|v(t)|>0$, $t\in(0,1]$, that is, w and v are positive solutions of problem (1). The proof is completed. □

4 An example

We consider the following four-point boundary value problem:

$$ \begin{aligned} &u'''(t)+ \frac{1}{4} \bigl[2t+u^{2}(t)+u'(t) \bigr]=0, \quad 0< t < 1, \\ &u(0)=u'(0)=0, \qquad u'(1)=u'\biggl( \frac{1}{4}\biggr)+\frac{1}{2}u'\biggl( \frac{1}{2}\biggr). \end{aligned} $$

(10)

In this case,

$$\begin{aligned}& m=4,\qquad q(t)=1, \qquad \alpha_{1}=1, \qquad \alpha_{2}= \frac{1}{2}, \\& \eta_{1}=\frac{1}{4}, \qquad \eta _{2}=\frac{1}{2},\qquad f(t,u,v)=\frac{1}{2}t+ \frac{1}{4}u^{2}+\frac{1}{4}v. \end{aligned}$$

It is obvious that (H1)-(H3) hold. By simple calculations we obtain $\varLambda _{1}=1$. Let $a=2$. Then

$$\begin{aligned} f(t,u_{1},v_{1})&\leqslant f(t,u_{2},v_{2}) \leqslant f(1,2,2)=2 \\ &= \varLambda _{1} a,\quad 0\leqslant t\leqslant1, 0 \leqslant u_{1}\leqslant u_{2}\leqslant2 , 0\leqslant v_{1}\leqslant v_{2}\leqslant2. \end{aligned}$$

Then all hypotheses of Theorem 1 hold. Hence, problem (10) has two positive and nondecreasing solutions v and w such that $0<\|v\|\leqslant2$, $\lim_{n\to\infty}v_{n}=v$, where $v_{0}(t)=0$, $t\in[0,1]$, and $0<\|w\|\leqslant2$, $\lim_{n\to\infty}w_{n}=w$, where $w_{0}(t)=t^{2}$, $t\in[0,1]$.

For $n=0,1,2,\ldots$ , the two iterative schemes are

$$\begin{aligned}& w_{0}(t) =t^{2},\quad t\in[0,1], \\& w_{n+1}(t) =-\frac{1}{8} \int_{0}^{t}(t-s)^{2}\bigl[2s+w_{n}^{2}(s)+w_{n}'(s) \bigr]\,ds+\frac {t^{2}}{4}\biggl( \int_{0}^{1}(1-s)\bigl[2s+w_{n}^{2}(s)+w_{n}'(s) \bigr]\,ds \\& \hphantom{w_{n+1}(t) ={}}{}- \int_{0}^{\frac{1}{4}}\biggl(\frac{1}{4}-s \biggr)\bigl[2s+w_{n}^{2}(s)+w_{n}'(s) \bigr]\,ds \\& \hphantom{w_{n+1}(t) ={}}{}-\frac {1}{2} \int_{0}^{\frac{1}{2}}\biggl(\frac{1}{2}-s \biggr)\bigl[2s+w_{n}^{2}(s)+w_{n}'(s) \bigr]\,ds\biggr),\quad t\in[0,1], \end{aligned}$$

and

$$\begin{aligned}& v_{0}(t) =0,\quad t\in[0,1], \\& v_{n+1}(t) =-\frac{1}{8} \int_{0}^{t}(t-s)^{2}\bigl[2s+v_{n}^{2}(s)+v_{n}'(s) \bigr]\,ds++\frac {t^{2}}{4}\biggl( \int_{0}^{1}(1-s)\bigl[2s+v_{n}^{2}(s)+v_{n}'(s) \bigr]\,ds \\& \hphantom{v_{n+1}(t) ={}}{}- \int_{0}^{\frac{1}{4}}\biggl(\frac{1}{4}-s \biggr)\bigl[2s+v_{n}^{2}(s)+v_{n}'(s) \bigr]\,ds \\& \hphantom{v_{n+1}(t) ={}}{}-\frac {1}{2} \int_{0}^{\frac{1}{2}}\biggl(\frac{1}{2}-s \biggr)\bigl[2s+v_{n}^{2}(s)+v_{n}'(s) \bigr]\,ds\biggr),\quad t\in[0,1]. \end{aligned}$$

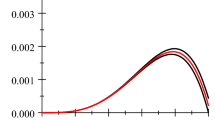
The first, second, and third terms of these two schemes are as follows:

$$\begin{aligned}& w_{0}(t) =t^{2}, \\& w_{1}(t) =\frac{79\text{,}583}{491\text{,}520}t^{2}-\frac{1}{24}t^{4}- \frac{1}{840}t^{7}, \\& w_{2}(t) =\frac{59}{786}t^{2}-\frac{1}{48}t^{4}+ \frac {82\text{,}334\text{,}900\text{,}557}{30\text{,}923\text{,}764\text{,}531\text{,}200}t^{6}-\frac {6\text{,}333\text{,}453\text{,}889}{5\text{,}798\text{,}205\text{,}849\text{,}600}t^{7} \\& \hphantom{w_{2}(t) ={}}{}- \frac{1\text{,}034\text{,}579}{754\text{,}974\text{,}720}t^{8}+ \frac {79\text{,}583}{141\text{,}557\text{,}760}t^{9}-\frac{1\text{,}262\text{,}591}{11\text{,}324\text{,}620\text{,}800}t^{11}+\frac{11\text{,}369}{707\text{,}788\text{,}800}t^{12} \\& \hphantom{w_{2}(t) ={}}{}+ \frac {13}{1\text{,}290\text{,}240}t^{13}- \frac{1}{241\text{,}920} t^{14}+ \frac {13}{90\text{,}316\text{,}800}t^{16}-\frac{1}{16\text{,}934\text{,}400} t^{17}, \end{aligned}$$

and

$$\begin{aligned}& v_{0}(t) =0, \\& v_{1}(t) =\frac{59}{768}t^{2}-\frac{1}{48}t^{4}, \\& v_{2}(t) =\frac{59}{768}t^{2}-\frac{1}{48}t^{4}+ \frac {45\text{,}253}{75\text{,}497\text{,}472}t^{6}-\frac{3\text{,}481}{14\text{,}155\text{,}776}t^{7} \\& \hphantom{v_{2}(t) ={}}{} - \frac{767}{2\text{,}359\text{,}296}t^{8}+\frac{59}{442\text{,}368}t^{9}+ \frac {13}{294\text{,}912}t^{10}-\frac{1}{55\text{,}296}t^{11}. \end{aligned}$$

5 Fractional case

In this section, we consider the boundary value problems with Riemann-Liouville fractional derivative (2). Before proceeding further, we recall some basic definitions of fractional calculus [37].

Definition 1

The Riemann-Liouville fractional derivative of order $\alpha> 0$ of a continuous function $h:[0,\infty)\to\mathbb{R}$ is defined to be

$$ D_{0^{+}}^{\alpha}h(t)=\frac{1}{\varGamma (n-\alpha)} \biggl(\frac {d}{dt} \biggr)^{n} \int_{0}^{t}(t-s)^{n-\alpha-1} h(s)\,ds ,\quad n=[ \alpha]+1, $$

where Γ denotes the Euler gamma function, and $[\alpha]$ denotes the integer part of a number α, provided that the right side is pointwise defined on $(0,\infty)$.

Definition 2

The Riemann-Liouville fractional integral of order α is defined as

$$I_{0^{+}}^{\alpha}h(t)= \frac {1}{\varGamma (\alpha)} \int_{0}^{t}(t-s)^{\alpha-1}h(s)\,ds,\quad t>0, \alpha>0, $$

provided that the integral exists.

In this section, we assume that the following conditions hold:

• (A1) $0<\eta_{1}<\eta_{2}<\cdots<\eta_{m}<1$, $\alpha_{i}\geqslant0$ ($i=1,2,\ldots,m$), and $\rho=\sum_{i=1}^{m}\alpha_{i}\eta_{i}^{\alpha-2}$ with $\rho<1$,

• (A2) $q\in L^{1}[0,1]$ is nonnegative, and $0<\int _{0}^{1}(1-s)^{\alpha-2}q(s)\,ds<\infty$,

• (A3) $f\in C([0,1]\times[0,\infty)\times[0, \infty),[0,\infty))$, and $f(t,0,0)\not\equiv0$ for $t\in(0,1)$.

Lemma 4

[34]

Let $h\in C(0,1)\cap L[0,1]$. Then the boundary value problem

$$\begin{aligned}& D^{\alpha}_{0^{+}}u(t)+h(t)=0,\quad 0< t < 1, \\& u(0)=u'(0)=0,\qquad u'(1)=\sum _{i=1}^{m}\alpha_{i}u'( \eta_{i}), \end{aligned}$$

has a unique solution

$$ u(t)= \int_{0}^{1}G(t,s)h(s)\,ds,\quad t\in[0,1], $$

where

$$\begin{aligned}& G(t,s)=H(t,s)+\frac{t^{\alpha-1}}{(\alpha-1)(1-\rho)}\sum_{i=1}^{m} \alpha_{i}H_{1}(\eta_{i},s),\quad t, s\in[0,1], \\& H(t,s)=\frac{1}{\varGamma (\alpha)}\left \{ \textstyle\begin{array}{l@{\quad}l} (1-s)^{\alpha-2}t^{\alpha-1}-(t-s)^{\alpha-1},& 0\leqslant s\leqslant t\leqslant1, \\ (1-s)^{\alpha-2}t^{\alpha-1},& 0\leqslant t\leqslant s\leqslant1, \end{array}\displaystyle \right . \end{aligned}$$

and

$$ H_{1}(t,s):=\frac{\partial H(t,s)}{\partial t}=\frac{1}{\varGamma (\alpha -1)}\left \{ \textstyle\begin{array}{l@{\quad}l} (1-s)^{\alpha-2}t^{\alpha-2}-(t-s)^{\alpha-2},& 0\leqslant s\leqslant t\leqslant1, \\ (1-s)^{\alpha-2}t^{\alpha-2},& 0\leqslant t\leqslant s\leqslant1. \end{array}\displaystyle \right . $$

Lemma 5

For all $(t, s)\in[0,1]\times[0,1]$, we have:

• (a) $t^{\alpha-1}H(1,s)\leqslant H(t,s)\leqslant H(1,s)$;

• (b) $0\leqslant H(t,s)\leqslant\frac{t^{\alpha -1}(1-s)^{\alpha-2}}{\varGamma (\alpha)}$, $0\leqslant H_{1}(t,s)\leqslant\frac{t^{\alpha-2}(1-s)^{\alpha-2}}{\varGamma (\alpha-1)}$;

• (c) $t^{\alpha-1}G(1,s)\leqslant G(t,s)\leqslant G(1,s)$;

• (d) $0\leqslant G(t,s)\leqslant\frac{t^{\alpha -1}(1-s)^{\alpha-2}}{\varGamma (\alpha)(1-\rho)}$, $0\leqslant\frac{\partial G(t,s)}{\partial t}\leqslant\frac{t^{\alpha -2}(1-s)^{\alpha-2}}{\varGamma (\alpha-1)(1-\rho)}$.

Let

$$\varLambda _{2}= \biggl(\frac{1}{1-\rho} \int_{0}^{1}(1-s)^{\alpha-2}q(s)\,ds \biggr)^{-1}. $$

Theorem 2

Suppose that (A1)-(A3) hold. Let $a>0$ and suppose that f satisfies the following condition:

$$ f(t,u_{1},v_{1})\leqslant f(t,u_{2},v_{2}) \leqslant \varLambda _{2} a \quad \textit{for } 0\leqslant t\leqslant1, 0 \leqslant u_{1}\leqslant u_{2}\leqslant a , 0\leqslant v_{1}\leqslant v_{2}\leqslant a. $$

Then problem (2) has two monotone positive solutions v and w such that

• $0<\|v\|\leqslant a$ and $\lim_{n\to\infty}v_{n}=v$, where $v_{n}=Tv_{n-1}$, $n=1,2,\ldots$ , $v_{0}(t)=0$, $t\in[0,1]$;

• $0<\|w\|\leqslant a$ and $\lim_{n\to\infty}w_{n}=w$, where $w_{n}=Tw_{n-1}$, $n=1,2,\ldots$ , $w_{0}(t)=\frac{a}{\varGamma (\alpha)}t^{\alpha -1}$, $t\in[0,1]$.

The proof is similar to that of Theorem 1, so we omit it.