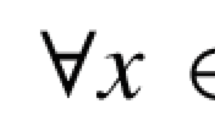1 Introduction and main results

Let \(\mathbf{R}^{n}\) be the n-dimensional Euclidean space, where \(n\geq2\). Let E be an open set in \(\mathbf{R}^{n}\), the boundary and the closure of it are denoted by ∂E and E̅, respectively. A point P is denoted by \((X,x_{n})\), where \(X=(x_{1},x_{2},\ldots,x_{n-1})\). For \(P\in\mathbf{R}^{n}\) and \(r>0\), let \(B(P,r)\) denote the open ball with center at P and radius r in \(\mathbf{R}^{n}\).

We introduce a system of spherical coordinates \((r,\Theta)\), \(\Theta=(\theta_{1},\theta_{2},\ldots,\theta_{n-1})\), in \(\mathbf{R}^{n}\) which are related to the cartesian coordinates \((X,x_{n})=(x_{1},x_{2},\ldots,x_{n-1},x_{n})\) by \(x_{n}=r\cos\theta_{1}\).

Let \(\mathbf{S}^{n-1}\) and \(\mathbf{S}_{+}^{n-1}\) denote the unit sphere and the upper half unit sphere, respectively. For \(\Omega\subset\mathbf{S}^{n-1}\), a point \((1,\Theta)\) on \(\mathbf{S}^{n-1}\), and the set \(\{\Theta; (1,\Theta)\in\Omega\}\) are simply denoted by Θ and Ω respectively. The set \(\{(r,\Theta)\in\mathbf{R}^{n}; r\in\Xi,(1,\Theta)\in\Omega\}\) in \(\mathbf{R}^{n}\) is simply denoted by \(\Xi\times\Omega\), where \(\Xi\subset\mathbf{R}_{+}\) and \(\Omega\subset \mathbf{S}^{n-1}\). Especially, the set \(\mathbf{R}_{+}\times\Omega\) by \(C_{n}(\Omega)\), where \(\mathbf{R}_{+}\) is the set of positive real number and \(\Omega\subset \mathbf{S}^{n-1}\).

Let \(C_{n}(\Omega;I)\) and \(S_{n}(\Omega;I)\) denote the sets \(I\times\Omega\) and \(I\times\partial{\Omega}\), respectively, where I is an interval on R and R is the set of real numbers. Especially, the set \(S_{n}(\Omega)\) denotes \(S_{n}(\Omega; (0,+\infty))\), which is \(\partial{C_{n}(\Omega)}-\{O\}\).

Let \(\Delta^{\ast}\) be the spherical part of the Laplace operator Δ (see [1]),

$$\Delta=\frac{n-1}{r}\frac{\partial}{\partial r}+\frac{\partial^{2}}{\partial r^{2}}+\frac{\Delta^{\ast}}{r^{2}}, $$

and Ω be a domain on \(\mathbf{S}^{n-1}\) with smooth boundary. We consider the Dirichlet problem (see [2], p.41)

$$\begin{aligned}& \bigl(\Delta^{\ast}+\lambda\bigr)\varphi(\Theta)=0 \quad\mbox{on } \Omega, \\& \varphi(\Theta)=0 \quad\mbox{on } \partial{\Omega}. \end{aligned}$$

The least positive eigenvalue of the above boundary value problem is denoted by λ and the normalized positive eigenfunction corresponding to λ by \(\varphi(\Theta)\), \(\int_{\Omega}\varphi^{2}(\Theta)\,d\Omega=1\), where dΩ denotes the \((n-1)\)-dimensional volume element.

We put a rather strong assumption on Ω: if \(n\geq3\), then Ω is a \(C^{2,\alpha}\)-domain (\(0<\alpha<1\)) on \(\mathbf{S}^{n-1}\) surrounded by a finite number of mutually disjoint closed hypersurfaces (e.g. see [3], pp.88-89, for the definition of the \(C^{2,\alpha}\)-domain).

Let \(\mathscr{A}_{a}\) denote the class of nonnegative radial potentials \(a(P)\), i.e. \(0\leq a(P)=a(r)\), \(P=(r,\Theta)\in C_{n}(\Omega)\), such that \(a\in L_{\mathrm{loc}}^{b}(C_{n}(\Omega))\) with some \(b> {n}/{2}\) if \(n\geq4\) and with \(b=2\) if \(n=2\) or \(n=3\).

Let I be the identical operator. If \(a\in\mathscr{A}_{a}\), then the stationary Schrödinger operator

$$SSE_{a}=-\Delta+a(P)I $$

can be extended in the usual way from the space \(C_{0}^{\infty}(C_{n}(\Omega))\) to an essentially self-adjoint operator on \(L^{2}(C_{n}(\Omega))\) (see [4], Chapter 13). We will denote it \(SSE_{a}\) as well. This last one has a Green-Sch function \(G_{\Omega}^{a}(P,Q)\) which is positive on \(C_{n}(\Omega)\) and its inner normal derivative \(\partial G_{\Omega}^{a}(P,Q)/{\partial n_{Q}}\geq0\), where \({\partial}/{\partial n_{Q}}\) denotes the differentiation at Q along the inward normal into \(C_{n}(\Omega)\).

In this paper, we are concerned with the weak solutions of the inequality

$$ SSE_{a}u(P)\leq0, $$
(1.1)

where \(P=(r,\Theta)\in C_{n}(\Omega)\).

We will also consider the class \(\mathscr{B}_{a}\), consisting of the potentials \(a\in\mathscr{A}_{a}\) such that there exists the finite limit \(\lim _{r\rightarrow\infty}r^{2} a(r)=k\in[0,\infty)\), moreover, \(r^{-1}|r^{2} a(r)-k|\in L(1,\infty)\).

We denote by \(SbH_{a}(\Omega)\) the class of all weak solutions of the inequality (1.1) for any \(P=(r,\Theta)\in C_{n}(\Omega)\), which are continuous when \(a\in\mathscr{B}_{a}\) (see [5]). We denote by \(SpH_{a}(\Omega)\) the class of \(u(P)\) satisfying \(-u(P)\in SbH_{a}(\Omega )\). If \(u(P)\in SbH_{a}(\Omega)\) and \(u(P)\in SpH_{a}(\Omega)\), then \(u(P)\) is the solution of \(SSE_{a}u(P)=0\) for any \(P=(r,\Theta)\in C_{n}(\Omega)\). In our terminology we follow Nirenberg [6]. Other authors have under similar circumstances used various terms such as subfunctions, subsolutions, submetaharmonic function, subelliptic functions, panharmonic functions, etc.; see, for example, Duffin, Littman, Qiao et al., Topolyansky, Vekua (see [7–11]).

Solutions of the ordinary differential equation

$$ -\Pi''(r)-\frac{n-1}{r} \Pi'(r)+ \biggl( \frac{\lambda}{r^{2}}+a(r) \biggr)\Pi(r)=0,\quad 0< r< \infty, $$
(1.2)

play an essential role in this paper. It is well known (see, for example, [12]) that if the potential \(a\in\mathscr{A}_{a}\), then equation (1.2) has a fundamental system of positive solutions \(\{V,W\}\) such that V is non-decreasing with

$$0\leq V(0+)\leq V(r)\nearrow\infty \quad\mbox{as } r\rightarrow+\infty, $$

and W is monotonically decreasing with

$$+\infty=W(0+)>W(r)\searrow0 \quad\mbox{as } r\rightarrow+\infty. $$

Denote

$$\iota_{k}^{\pm}=\frac{2-n\pm\sqrt{(n-2)^{2}+4(k+\lambda)}}{2}, $$

then the solutions to equation (1.2) have the following asymptotic (see [3]):

$$ V(r)\approx r^{\iota_{k}^{+}},\qquad W(r)\approx r^{\iota _{k}^{-}}, \quad\mbox{as } r \rightarrow\infty. $$

Let \(u(P) \) (\(P=(r,\Theta)\in C_{n}(\Omega)\)) be a function. We introduce the following notations: \(u^{+}=\max\{u,0\}\), \(u^{-}=-\min\{u,0\}\), \(M_{u}(r)=\sup_{\Theta\in \Omega}u(P)\), \(l=\max_{\Theta\in\Omega}\varphi(\Theta)\),

$$S_{u}(r)=\sup_{\Theta\in\Omega}\frac{u(P)}{\varphi(\Theta )}, \qquad L_{u}=\limsup_{r\rightarrow0}\frac{S_{u}(r)}{W(r)}, \qquad J_{u}=\sup_{P\in C_{n}(\Omega)}\frac{u(P)}{W(r)\varphi(\Theta)}. $$

For any two positive numbers δ an r, we put

$$E_{0}^{u}(r;\delta)=\bigl\{ \Theta\in\Omega:u(P)\leq-\delta W(r)\bigr\} $$

and

$$\xi_{u}(\delta)=\limsup_{r\rightarrow0} \int_{E_{0}^{u}(r;\delta)}\varphi (\Theta)\,d\Omega. $$

The integral

$$\int_{\Omega}u(r,\Theta)\varphi(\Theta)\,d\Omega, $$

is denoted by \(N_{u}(r)\), when it exists. The finite or infinite limits

$$\lim_{r\rightarrow\infty}\frac{N_{u}(r)}{V(r)} \quad \mbox{and} \quad \lim _{r\rightarrow0}\frac{N_{u}(r)}{W(r)} $$

are denoted by \(\mu_{u}\) and \(\eta_{u}\), respectively, when they exist.

We shall say that \(u(P)\) (\(P=(r,\Theta)\in C_{n}(\Omega)\)) satisfies the Phragmén-Lindelöf boundary condition on \(S_{n}(\Omega)\), if

$$\limsup_{P\rightarrow Q, Q \in S_{n}(\Omega)} u(P)\leq0 $$

for every \(Q\in S_{n}(\Omega)\).

Throughout this paper, unless otherwise specified, we will always assume that \(u(P)\in SbH_{a}(\Omega)\) and satisfy the Phragmén-Lindelöf boundary condition on \(S_{n}(\Omega)\). Recently, about the Phragmén-Lindelöf theorems for subfunctions in a cone, Qiao and Deng (see [9], Theorem 3) proved the following result.

Theorem A

If

$$\mu_{u^{+}}=\eta_{u^{+}}=0, $$

then

$$u(P)\leq0 $$

for any \(P=(r,\Theta)\in C_{n}(\Omega)\).

A stronger version of a Phragmén-Lindelöf type theorem is also due to Qiao and Deng (see [9], Theorem 3).

Theorem B

If

$$ \liminf_{r\rightarrow\infty}\frac{M_{u}(r)}{V(r)}< +\infty $$
(1.3)

and

$$ \liminf_{r\rightarrow 0}\frac{M_{u}(r)}{W(r)}< +\infty, $$
(1.4)

then

$$ u(P)\leq \bigl(\mu_{u}V(r)+\eta_{u}W(r)\bigr) \varphi(\Theta) $$
(1.5)

for any \(P=(r,\Theta)\in C_{n}(\Omega)\).

However, they do not tell us in [9] whether or not the limit

$$B_{u}=\lim_{r\rightarrow0}\frac{M_{u}(r)}{W(r)} $$

exists. In this paper, we first of all answer this question positively and prove the following result.

Theorem 1

If (1.3) is satisfied, then the limit \(B_{u} \) (\(0\leq B_{u}\leq+\infty\)) exists and

$$ B_{u}=(L_{u})^{+}l, $$
(1.6)

where

$$ (L_{u})^{+}=\eta_{u^{+}}. $$
(1.7)

Remark

It is obvious that \(\eta_{u}\leq L_{u}\). On the other hand, we have \(\eta_{u}\geq L_{u}\) from (1.5). Thus, if (1.3) and (1.4) are satisfied, then we have \(\eta_{u}=L_{u}\).

As an application of Theorem 1 we immediately have the following result by using Lemma 3 in Section 2.

Corollary

If

$$ \liminf_{r\rightarrow \infty}\frac{M_{u}(r)}{V(r)}\leq0, $$
(1.8)

then

$$ B_{u}=(J_{u})^{+}l. $$
(1.9)

In [9], the authors gave the properties of the positive part of weak solutions satisfying the Phragmén-Lindelöf boundary condition on \(S_{n}(\Omega)\). Finally, we shall show one of the properties of its negative part.

From the remark, we have

$$ \eta_{u^{+}}=L_{u^{+}}=(L_{u})^{+}=(\eta_{u})^{+}. $$

Since

$$ N_{u}(r)=N_{u^{+}}(r)-N_{u^{-}}(r), $$

Theorem 2 follows immediately.

Theorem 2

Under the conditions of Theorem  B, if \(\eta_{u}\geq0\), then

$$ \lim_{r\rightarrow0}\frac{N_{u^{-}}(r)}{W(r)}=0. $$

2 Some lemmas

Lemma 1

(see [9], Lemma 8)

  1. (1)

    Both of the limits \(\mu_{u}\) and \(\eta_{u}\) (\(-\infty<\mu_{u},\eta_{u}\leq+\infty\)) exist.

  2. (2)

    If \(\eta_{u}\leq0\), then \(V^{-1}(r)N_{u}(r)\) is non-decreasing on \((0,+\infty)\).

  3. (3)

    If \(\mu_{u}\leq0\), then \(W^{-1}(r)N_{u}(r)\) is non-increasing on \((0,+\infty)\).

Lemma 2

If (1.3) is satisfied and there exists a positive number R such that \(u(P)\leq0\) for any \(P=(r,\Theta)\in C_{n}(\Omega;(0,R))\), then for any positive number δ, we have

$$ u(P)\leq\bigl(\mu_{u}V(r)-\delta\xi_{u}( \delta)W(r)\bigr)\varphi(\Theta) $$
(2.1)

for any \(P=(r,\Theta)\in C_{n}(\Omega)\).

Proof

Let δ be any given positive number and \(\{r_{k}\}\) be a sequence such that

$$ \lim_{k\rightarrow\infty}r_{k}=0 \quad \mbox{and}\quad \lim _{k\rightarrow\infty} \int_{E_{0}^{u}(r_{k};\delta)}\varphi (\Theta)\,d\Omega=\xi_{u}(\delta). $$

Then we have

$$ N_{u}(r_{k})\leq \int_{E_{0}^{u}(r_{k};\delta)} u(r_{k},\Theta)\varphi(\Theta )\,d\Omega \leq-\delta W(r_{k}) \int_{E_{0}^{u}(r_{k};\delta)} \varphi (\Theta)\,d\Omega $$

for any \(0< r_{k}< R\) and hence

$$ \eta_{u} \leq-\delta\xi_{u}(\delta). $$

Thus we obtain (2.1) from Theorem B. □

Lemma 3

Under the conditions of the corollary, \(L_{u}>-\infty\) and \(J_{u}=L_{u}\).

Proof

It is evident that

$$ J_{u}\geq L_{u}. $$
(2.2)

Hence, we shall prove that \(J_{u}=L_{u}\) under the assumption that \(L_{u}<+\infty\). Since (1.3) and (1.4) are satisfied and (1.8) gives \(\mu_{u}\leq0\), we have

$$ u(P)\leq\eta_{u}W(r)\varphi(\Theta) $$

for any \(P=(r,\Theta)\in C_{n}(\Omega)\) from Theorem B, which gives

$$ \eta_{u}\geq J_{u}. $$
(2.3)

Since Lemma 1 and the remark give \(\eta_{u}> -\infty\) and \(\eta_{u}= L_{u}\), respectively, we have the conclusion from (2.2) and (2.3).

Given a continuous function ψ defined on the truncated cone \(\partial C_{n}(\Omega;(R_{1},R_{2}))\), where \(R_{1}\) and \(R_{2}\) are two positive real numbers satisfying \(R_{1}< R_{2}\), then the solution of the Dirichlet-Sch problem on \(C_{n}(\Omega;(R_{1},R_{2}))\) with ψ is denoted by \(H_{\psi}(P; C_{n}(\Omega;(R_{1},R_{2})))\). □

Lemma 4

If

$$ \mu_{u^{+}}< +\infty \quad\textit{and} \quad \eta_{u^{+}}< +\infty, $$
(2.4)

are satisfied, then

$$ B_{u}\leq\eta_{u^{+}}. $$

Proof

Take any \(P=(r,\Theta)\in C_{n}(\Omega)\) and any pair of numbers \(R_{1}\), \(R_{2}\) satisfying \(0<2R_{1}<r<\frac {1}{2}R_{2}<\infty\). If \(\psi(P)\) is a boundary function on \(\partial {C_{n}(\Omega;(R_{1},R_{2}))}\) satisfying

$$\psi(P)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} u(R_{i},\Phi) & \mbox{on } \{R_{i}\} \times\Omega\ (i=1,2), \\ 0& \mbox{on } S_{n}(\Omega;(R_{1},R_{2})), \end{array}\displaystyle \right . $$

then we have

$$\begin{aligned} u(P) \lesssim &H_{\psi}\bigl(P;C_{n}\bigl( \Omega;(R_{1},R_{2})\bigr)\bigr) \\ =& \int_{\Omega}u^{+}(R_{1},\Phi) \frac{G_{C_{n}(\Omega ;(R_{1},R_{2}))}^{a}(P,(R_{1},\Phi))}{\partial y}R_{1}^{n-1}\,d\Omega \\ &{}- \int_{\Omega}u^{+}(R_{2},\Phi) \frac{G_{C_{n}(\Omega ;(R_{1},R_{2}))}^{a}(P,(R_{2},\Phi))}{\partial y}R_{2}^{n-1}\,d\Omega, \end{aligned}$$

where \(G_{C_{n}(\Omega;(R_{1},R_{2}))}^{a}(\cdot,\cdot)\) is the Green-Sch function on \(C_{n}(\Omega;(R_{1},R_{2}))\) with the pole at P.

Here we use the following inequalities (see [1], p.124):

$$\begin{aligned} \frac{\partial(G_{C_{n}(\Omega;(R_{1},R_{2}))}^{a}(P, (R_{1},\Phi)))}{\partial R}\lesssim c_{1}\frac{W(r)}{W(R_{1})}\frac{\varphi(\Theta)\varphi(\Phi)}{R_{1}^{n-1}} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial(G_{C_{n}(\Omega;(R_{1},R_{2}))}^{a}(P,(R_{2},\Phi)))}{\partial R}\gtrsim-c_{2}\frac{V(r)}{V(R_{2})}\frac{\varphi(\Theta)\varphi(\Phi)}{R_{2}^{n-1}}, \end{aligned}$$

where \(c_{1}\) and \(c_{2}\) are two positive constants.

Then we have

$$\begin{aligned} u(P)\leq c_{3} W^{-1}(R_{1})N_{u^{+}}(R_{1})W(r) \varphi(\Theta)+c_{4} V^{-1}(R_{2})N_{u^{+}}(R_{2})V(r) \varphi(\Theta), \end{aligned}$$
(2.5)

where \(c_{3}\) and \(c_{4}\) are two positive constants.

As \(R_{1}\rightarrow0\) and \(R_{2}\rightarrow\infty\) in (2.5), we obtain

$$\begin{aligned} M_{u}(r)\leq \bigl(c_{3} \eta_{u^{+}}W(r)+c_{4} \mu_{u^{+}}V(r) \bigr)\max_{\Theta\in\Omega}\varphi(\Theta) \end{aligned}$$

from Lemma 1, which gives the conclusion of Lemma 4 from (2.4). □

3 Proof of Theorem 1

Put

$$ \tau= \liminf_{r\rightarrow0}\frac{M_{u}(r)}{W(r)}. $$

Since

$$ N_{u}(r)\leq M_{u}(r) \int_{\Omega}\varphi(\Theta)\,d\Omega, $$

and Lemma 1 gives

$$ \eta_{u}>-\infty, $$
(3.1)

we immediately see that \(\tau>-\infty\).

Now we distinguish two cases.

Case 1 \(\tau=+\infty\).

In this case \(B_{u}\) exists and is equal to +∞. It is obvious that for any positive number r

$$ \frac{M_{u^{+}}(r)}{W(r)}\leq l\frac{S_{u^{+}}(r)}{W(r)}, $$
(3.2)

which gives \(L_{u}=+\infty\).

These results show that (1.7) holds in this case.

Case 2 \(\tau<+\infty\).

From Theorem B, we see that \(L_{u}<+\infty\). On the other hand, we have \(L_{u}>-\infty\) from (3.1).

Subcase 2.1 \(0\leq L_{u}<+\infty\).

There exists a positive number \(R_{\epsilon}\) such that

$$ u(P)\leq(L_{u}+\epsilon)W(r)\varphi(\Theta) $$

for any \(\epsilon>0\), where \(P=(r,\Theta)\in C_{n}(\Omega;(0,R_{\epsilon}))\).

This gives

$$ \limsup_{r\rightarrow0}\frac{M_{u}(r)}{W(r)}\leq L_{u}l. $$
(3.3)

Now, assume that \(\tau< L_{u}l\). There exist a positive number \(\delta_{1}\) and a set \(E_{u}\subset\Omega\) such that

$$ \int_{E_{u}}\varphi(\Theta)\,d\Omega>0 $$

and

$$ L_{u} \varphi(\Theta)-\tau\geq2\delta_{1} $$
(3.4)

for \(\Theta\in E_{u}\).

We define \(v_{1}(P) \) (\(P=(r,\Theta)\in C_{n}(\Omega)\)) by

$$ v_{1}(P)=u(P)-(L_{u}+\epsilon)W(r)\varphi( \Theta) $$
(3.5)

and apply Lemma 2 to \(v_{1}(P)\). It gives

$$ u(P)\leq\bigl[\bigl\{ L_{u}+\epsilon-\delta_{1} \xi_{v_{1}}(\delta_{1})\bigr\} W(r)+\mu _{v_{1}}V(r)\bigr] \varphi(\Theta) $$

for any \(P=(r,\Theta)\in C_{n}(\Omega)\).

So we have

$$ L_{u}\leq L_{u}-\delta_{1}\xi_{v_{1}}( \delta_{1}). $$

If we can show that

$$ \xi_{v_{1}}(\delta_{1})>0, $$
(3.6)

then we have a contradiction.

To prove (3.6), take a sequence \(\{r_{k}\}\), with \(\lim_{k\rightarrow\infty}r_{k}=0\), such that

$$ \frac{M_{u}(r_{k})}{W(r_{k})}\leq\tau+\delta_{1} \quad(k=1,2,3,\ldots). $$

From (3.4) and (3.5) we have

$$ \frac{v_{1}(r_{k},\Theta)}{W(r_{k})}\leq\frac{u(r_{k},\Theta )}{W(r_{k})}-L_{u}\varphi(\Theta)\leq- \delta_{1} $$

for any \(\Theta\in E_{u}\), which gives

$$ E_{u}\subset E_{0}^{v_{1}}(r_{k}; \delta_{1})\quad (k=1,2,3,\ldots). $$

Hence

$$ \xi_{v_{1}}(\delta_{1})\geq \int_{E_{u}}\varphi(\Theta)\,d\Omega>0. $$

Thus from (3.3) we can simultaneously prove the existence of \(B_{u}\) and (1.6).

Subcase 2.2 \(-\infty\leq L_{u}<0\).

Take any small number \(\epsilon>0\) satisfying \(L_{u}+\epsilon<0\). There exists a positive number \(R_{\epsilon}\) such that

$$ u(P)\leq(L_{u}+\epsilon)W(r)\varphi(\Theta) $$

for any \(P=(r,\Theta)\in C_{n}(\Omega;(0,R_{\epsilon}))\).

This gives

$$ \limsup_{r\rightarrow0}\frac{M_{u}(r)}{W(r)}\leq0. $$
(3.7)

Now suppose that \(\tau<0\). There are a sequence \(\{r_{k}\}\) tending to 0 and a positive number \(\delta_{2}\) such that

$$ \frac{M_{u}(r_{k})}{W(r_{k})}\leq-2\delta_{2} \quad(k=1,2,3,\ldots). $$

Define \(v_{2}(P) \) (\(P=(r,\Theta)\in C_{n}(\Omega)\)) by

$$ v_{2}(P)=u(P)-(L_{u}+\epsilon)W(r)\varphi(\Theta) $$

and apply Lemma 2 to \(v_{2}(P)\). Then we obtain

$$ u(P)\leq\bigl[\bigl\{ L_{u}+\epsilon-\delta_{2} \xi_{v_{2}}(\delta_{2})\bigr\} W(r)+\mu _{v_{2}}V(r)\bigr] \varphi(\Theta) $$

for any \(P=(r,\Theta)\in C_{n}(\Omega)\), which gives

$$ L_{u}\leq L_{u}-\delta_{2}\xi_{v_{2}}( \delta_{2}). $$

If we can show that

$$ \xi_{v_{2}}(\delta_{2})>0, $$
(3.8)

then we have a contradiction.

To prove (3.8), write

$$ F_{u}=\bigl\{ \Theta\in\Omega; -L_{u}\varphi(\Theta)\leq \delta_{2}\bigr\} . $$

It is evident that

$$ \int_{F_{u}}\varphi(\Theta)\,d\Omega>0. $$

For every \(\Theta\in F_{u}\), we have

$$ \frac{v_{1}(r_{k},\Theta)}{W(r_{k})}\leq\frac{u(r_{k},\Theta )}{W(r_{k})}-L_{u}\varphi(\Theta)\leq- \delta_{2}, $$

which shows that

$$ F_{u}\subset E_{0}^{v_{2}}(r_{k}; \delta_{2}) \quad(k=1,2,3,\ldots). $$

Hence we have

$$ \xi_{v_{2}}(\delta_{2})\geq \int_{F_{u}}\varphi(\Theta)\,d\Omega>0. $$

Thus we can prove that \(\tau\geq0\). With (3.7), this also gives the existence of \(B_{u}\) and

$$ B_{u}=0=(L_{u})^{+}l. $$

Lastly, we shall show that (1.7) holds.

If \(\eta_{u^{+}}=+\infty\), then it is evident that \(B_{u^{+}}=+\infty\). This together with (3.2) gives \(L_{u^{+}}=+\infty\). Since

$$ L_{u^{+}}=(L_{u})^{+}, $$
(3.9)

we know that (1.7) holds.

Next suppose that \(\eta_{u^{+}}<+\infty\). We have \(B_{u}<+\infty\) by Lemma 4 and hence \(L_{u^{+}}=\eta_{u^{+}}\) by the remark. With (3.9), this gives (1.7).