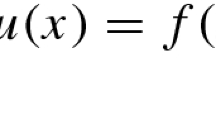1 Introduction

Fractional differential equations both ordinary and partial ones are applied in mathematical modeling of process in physics, mechanics, control theory, biochemistry, bioengineering and economics. Therefore, the theory of fractional differential equations is an area intensively developed during the last decades [1, 2]. The monographs [3–5] enclose a review of methods of solving fractional differential equations, which are an extension of procedures from differential equations theory.

Recently, also equations including both left and right fractional derivatives are discussed. Apart from their possible applications, equations with left and right derivatives is an interesting and new field in fractional differential equations theory. In this topic, many results are obtained dealing with the existence and multiplicity of solutions of nonlinear fractional differential equations by using techniques of nonlinear analysis, such as fixed point theory (including the Leray-Schauder nonlinear alternative) [6], topological degree theory (including co-incidence degree theory) [7] and comparison method (including upper and lower solutions and monotone iterative method) [8] and so on.

It should be noted that critical point theory and variational methods have also turned out to be very effective tools in determining the existence of solutions for integer order differential equations. The idea behind them is to try to find solutions of a given boundary value problem by looking for critical points of a suitable energy functional defined on an appropriate function space. In the last 30 years, critical point theory has become a wonderful tool in studying the existence of solutions to differential equations with variational structures; we refer the reader to Mawhin and Willem [9], Rabinowitz [10], Schechter [11], and the references listed therein.

Recently, in [12] the author was first to discuss the following perturbed fractional Hamiltonian systems:

$$ \textstyle\begin{cases} - {}_{t}D^{\alpha}_{\infty}({}_{-\infty}D^{\alpha }_{t}u(t))-L(t)u(t)+\nabla W(t,u(t))=f(t), \\ u\in H^{\alpha}(\mathbb {R},\mathbb {R}^{n}), \end{cases} $$
(PFHS)

where \(\alpha\in(1/2,1)\), \(t\in \mathbb {R}\), \(u\in \mathbb {R}^{n}\), \(L\in C(\mathbb {R},\mathbb {R}^{n^{2}})\) is a symmetric and positive definite matrix for all \(t\in \mathbb {R}\), \(W\in C^{1}(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R})\), and \(\nabla W(t,u)\) is the gradient of \(W(t,u)\) at u, \(f\in C(\mathbb {R},\mathbb {R}^{n})\) and belongs to \(L^{2}(\mathbb {R},\mathbb {R}^{n})\). Under the conditions of (L), (W1)-(W3) (see below) and assuming that the \(L^{2}\) norm of f is sufficiently small, he showed that (PFHS) has at least two nontrivial solutions.

Equation (PFHS), if \(\alpha=1\) and \(f(t)\equiv0\), reduces to the following second order Hamiltonian systems:

$$ \ddot{u}-L(t) u+\nabla W(t,u)=0. $$
(HS)

It is well known that the existence of homoclinic solutions for Hamiltonian systems and their importance in the study of the behavior of dynamical systems have been recognized from Poincaré [13]. They may be ‘organizing centers’ for the dynamics in their neighborhood. From their existence one may, under certain conditions, infer the existence of chaos nearby or the bifurcation behavior of periodic orbits. During the past two decades, with the works of [14] and [15] variational methods and critical point theory have been successfully applied for the search of the existence and multiplicity of homoclinic solutions of (HS).

Assuming that \(L(t)\) and \(W(t,u)\) are independent of t or periodic in t, many authors have studied the existence of homoclinic solutions for (HS); see for instance [15–17] and the references therein and some more general Hamiltonian systems are considered in [18, 19]. In this case, the existence of homoclinic solutions can be obtained by going to the limit of periodic solutions of approximating problems. If \(L(t)\) and \(W(t,u)\) are neither autonomous nor periodic in t, the existence of homoclinic solutions of (HS) is quite different from the periodic systems, because of the lack of compactness of the Sobolev embedding, such as in [14, 17, 20] and the references mentioned there.

Motivated by the above classical works, in [21] the author considered the following fractional Hamiltonian systems:

$$ \textstyle\begin{cases} {}_{t}D^{\alpha}_{\infty}({}_{-\infty}D^{\alpha}_{t}u(t))+L(t)u(t)=\nabla W(t,u(t)), \\ u\in H^{\alpha}(\mathbb {R},\mathbb {R}^{n}), \end{cases} $$
(FHS)

where \(\alpha\in(1/2,1)\), \(t\in \mathbb {R}\), \(u\in \mathbb {R}^{n}\), \(L\in C(\mathbb {R},\mathbb {R}^{n^{2}})\) is a symmetric and positive definite matrix for all \(t\in \mathbb {R}\), \(W\in C^{1}(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R})\), and \(\nabla W(t,u)\) is the gradient of \(W(t,u)\) at u. Assuming that \(L(t)\) and \(W(t,u)\) satisfy the following hypotheses, the author showed that (FHS) possesses at least one nontrivial solution via the mountain pass theorem. Explicitly,

(L):

\(L(t)\) is a positive definite symmetric matrix for all \(t\in \mathbb {R}\) and there exists an \(l\in C(\mathbb {R},(0,\infty))\) such that \(l(t)\rightarrow\infty\) as \(|t|\rightarrow\infty\) and

$$ \bigl(L(t)u,u\bigr)\geq l(t)|u|^{2} \quad\mbox{for all } t\in \mathbb {R}\mbox{ and } u\in \mathbb {R}^{n}. $$
(1.1)
(W1):

\(W\in C^{1}(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R})\) and there is a constant \(\theta>2\) such that

$$0< \theta W(t,u)\leq\bigl(\nabla W(t,u),u\bigr) \quad\mbox{for all } t\in \mathbb {R}\mbox{ and } u\in \mathbb {R}^{n}\backslash\{0\}. $$
(W2):

\(|\nabla W(t,u)|=o(|u|)\) as \(|u|\rightarrow0\) uniformly with respect to \(t\in \mathbb {R}\).

(W3):

There exists \(\overline{W}\in C(\mathbb {R}^{n},\mathbb {R})\) such that

$$\bigl|W(t,u)\bigr|+\bigl|\nabla W(t,u)\bigr|\leq\bigl|\overline{W}(u)\bigr| \quad\mbox{for every } t\in \mathbb {R}\mbox{ and } u\in \mathbb {R}^{n}. $$

(W1) is the so-called global Ambrosetti-Rabinowitz condition, which implies that \(W(t,u)\) is of superquadratic growth as \(|u|\rightarrow \infty\). Inspired by this work, using the genus properties of critical point theory, in [22] the authors established some new criterion to guarantee the existence of infinitely many solutions of (FHS) for the case that \(W(t,u)\) is subquadratic as \(|u|\rightarrow\infty\), where the condition (L) is also needed to guarantee that the functional corresponding to (FHS) satisfies the (PS) condition.

As is well known, the condition (L) is the so-called coercive condition and is very restrictive. In fact, for a simple choice like \(L(t)=\tau \mathrm{Id}_{n}\), the condition (1.1) is not satisfied, where \(\tau>0\) and \(\mathrm{Id}_{n}\) is the \(n\times n\) identity matrix. Therefore, in [23] the authors focused their attention on the case that \(L(t)\) is bounded in the sense that

(L)′:

\(L\in C(\mathbb {R},\mathbb {R}^{n^{2}})\) is a symmetric and positive definite matrix for all \(t\in \mathbb {R}\) and there are constants \(0<\tau _{1}<\tau_{2}<\infty\) such that

$$\tau_{1}|u|^{2}\leq\bigl(L(t)u,u\bigr)\leq \tau_{2}|u|^{2} \quad\mbox{for all } (t,u)\in \mathbb {R}\times \mathbb {R}^{n}. $$

If the potential \(W(t,u)\) is supposed to be subquadratic as \(|u|\rightarrow\infty\), then, as they also showed, (FHS) possesses infinitely many solutions.

Inspired by [12, 23], in the present paper we deal with (PFHS) for the case that \(L(t)\) is bounded, i.e., (L)′ holds and \(W(t,u)\) is superquadratic as \(|u|\rightarrow\infty\). Explicitly, we assume that the potential \(W(t,u)\) satisfies (W1) and the following condition:

(W2)′:

there exists some positive continuous function \(a:\mathbb {R}\rightarrow \mathbb {R}\) with

$$ \lim_{|t|\rightarrow\infty}a(t)=0 $$
(1.2)

such that

$$\bigl|\nabla W(t,u)\bigr|\leq a(t)|u|^{\theta-1} \quad\mbox{for all } (t,u)\in \mathbb {R}\times \mathbb {R}^{n}. $$

Let \(\varrho=\sup\{W(t,u):t\in \mathbb {R}, |u|=1\}\) and assume that

(W f ):

\(\varrho<\frac{1}{2C_{2}}\) and \(f:\mathbb {R}\rightarrow \mathbb {R}^{n}\) is a continuous square integrable function such that

$$ \|f\|_{L^{2}}< \frac{1}{C_{\infty}} \biggl(\frac{1}{2C_{2}}- \varrho C_{2} \biggr), $$
(1.3)

where \(C_{2}\) and \(C_{\infty}\) are defined in Section 2.

Now, we are in the position to state our main result.

Theorem 1.1

Suppose that (L)′, (W1), (W2)′ and (W f ) are satisfied, then (PFHS) possesses at least two nontrivial solutions.

Remark 1.2

Note that in (L)′, we assume that \(L(t)\) is bounded. Therefore, the coercive condition (L) is not satisfied. Thus the results in [12] are generalized and improved significantly.

Moreover, as mentioned above, the coercive condition (L) is used to establish some compact embedding theorems to guarantee that the (PS) condition (or the other weak compactness conditions) holds, which is the essential step to obtain the existence of homoclinic solutions of (PFHS) via critical point theory and variational methods. In the present paper, we assume that \(L(t)\) satisfies (L)′ and could not obtain some compact embedding theorem. Therefore, the main difficulty is to adapt some new technique to overcome this difficulty and test that the (PS) condition is verified; see Lemmas 3.1 and 3.2 below.

The remaining part of this paper is organized as follows. Some preliminary results are presented in Section 2. Section 3 is devoted to accomplishing the proof of Theorem 1.1.

2 Preliminary results

In this section, for the reader’s convenience, first we introduce some basic definitions of fractional calculus. The Liouville-Weyl fractional integrals of order \(0<\alpha<1\) are defined as

$${}_{-\infty}I^{\alpha}_{x} u(x)=\frac{1}{\Gamma(\alpha)}\int ^{x}_{-\infty} (x-\xi)^{\alpha-1}u(\xi)\,d\xi $$

and

$${}_{x}I^{\alpha}_{\infty} u(x)=\frac{1}{\Gamma(\alpha)}\int ^{\infty }_{x}(\xi-x)^{\alpha-1}u(\xi)\,d\xi. $$

The Liouville-Weyl fractional derivative of order \(0<\alpha<1\) are defined as the left-inverse operators of the corresponding Liouville-Weyl fractional integrals

$$ {}_{-\infty}D^{\alpha}_{x} u(x)=\frac{d}{dx} {{}_{-\infty}I^{1-\alpha}_{x} u(x)} $$
(2.1)

and

$$ {}_{x}D^{\alpha}_{\infty} u(x)=- \frac{d}{dx} {{}_{x}I^{1-\alpha }_{\infty} u(x)}. $$
(2.2)

The definitions of (2.1) and (2.2) may be written in an alternative form as follows:

$${}_{-\infty}D^{\alpha}_{x} u(x)=\frac{\alpha}{\Gamma(1-\alpha)}\int ^{\infty}_{0} \frac{u(x)-u(x-\xi)}{\xi^{\alpha+1}}\,d\xi $$

and

$${}_{x}D^{\alpha}_{\infty} u(x)=\frac{\alpha}{\Gamma(1-\alpha)}\int ^{\infty}_{0} \frac{u(x)-u(x+\xi)}{\xi^{\alpha+1}}\,d\xi. $$

Moreover, recall that the Fourier transform \(\widehat{u}(w)\) of \(u(x)\) is defined by

$$\widehat{u}(w)=\int_{-\infty}^{\infty}e^{-iwx}u(x) \,dx. $$

In order to establish the variational structure which enables us to reduce the existence of solutions of (PFHS) to find critical points of the corresponding functional, it is necessary to construct the appropriate functional spaces. In what follows, we introduce some fractional spaces; for more details see [24]. To this end, denote by \(L^{p}(\mathbb {R},\mathbb {R}^{n})\) (\(2\leq p <\infty\)) the Banach spaces of functions on \(\mathbb {R}\) with values in \(\mathbb {R}^{n}\) under the norms

$$\|u\|_{L^{p}}= \biggl(\int_{\mathbb {R}}\bigl|u(t)\bigr|^{p} \,dt \biggr)^{1/p}, $$

and \(L^{\infty}(\mathbb {R},\mathbb {R}^{n})\) is the Banach space of essentially bounded functions from \(\mathbb {R}\) into \(\mathbb {R}^{n}\) equipped with the norm

$$\|u\|_{\infty}=\operatorname{ess} \sup \bigl\{ \bigl|u(t)\bigr|: t\in \mathbb {R}\bigr\} . $$

For \(\alpha>0\), define the semi-norm

$$|u|_{I^{\alpha}_{-\infty}}=\bigl\| {}_{-\infty}D^{\alpha}_{x} u \bigr\| _{L^{2}} $$

and the norm

$$ \|u\|_{I^{\alpha}_{-\infty}}= \bigl(\|u\|^{2}_{L^{2}}+|u|^{2}_{I^{\alpha }_{-\infty}} \bigr)^{1/2} $$
(2.3)

and let

$$I^{\alpha}_{-\infty}=\overline{C^{\infty}_{0}\bigl( \mathbb {R},\mathbb {R}^{n}\bigr)}^{\|\cdot\| _{I^{\alpha}_{-\infty}}}, $$

where \(C_{0}^{\infty}(\mathbb {R},\mathbb {R}^{n})\) denotes the space of infinitely differentiable functions from \(\mathbb {R}\) into \(\mathbb {R}^{n}\) with vanishing property at infinity.

Now we can define the fractional Sobolev space \(H^{\alpha}(\mathbb {R},\mathbb {R}^{n})\) in terms of the Fourier transform. Choose \(0<\alpha<1\), define the semi-norm

$$|u|_{\alpha}=\bigl\| |w|^{\alpha}\widehat{u}\bigr\| _{L^{2}} $$

and the norm

$$\|u\|_{\alpha}= \bigl(\|u\|^{2}_{L^{2}}+|u|^{2}_{\alpha} \bigr)^{1/2} $$

and let

$$H^{\alpha}=\overline{C^{\infty}_{0}\bigl(\mathbb {R}, \mathbb {R}^{n}\bigr)}^{\|\cdot\|_{\alpha}}. $$

Moreover, we note that a function \(u\in L^{2}(\mathbb {R},\mathbb {R}^{n})\) belongs to \(I^{\alpha}_{-\infty}\) if and only if

$$|w|^{\alpha}\widehat{u}\in L^{2}\bigl(\mathbb {R},\mathbb {R}^{n}\bigr). $$

Especially, we have

$$|u|_{I^{\alpha}_{-\infty}}=\bigl\| |w|\widehat{u}\bigr\| _{L^{2}}. $$

Therefore, \(I^{\alpha}_{-\infty}\) and \(H^{\alpha}\) are equivalent with equivalent semi-norm and norm. Analogous to \(I^{\alpha}_{-\infty}\), we introduce \(I^{\alpha}_{\infty}\). Define the semi-norm

$$|u|_{I^{\alpha}_{\infty}}=\bigl\| {}_{x}D^{\alpha}_{\infty} u \bigr\| _{L^{2}} $$

and the norm

$$ \|u\|_{I^{\alpha}_{\infty}}= \bigl(\|u\|^{2}_{L^{2}}+|u|^{2}_{I^{\alpha }_{\infty}} \bigr)^{1/2} $$
(2.4)

and let

$$I^{\alpha}_{\infty}=\overline{C^{\infty}_{0}\bigl( \mathbb {R},\mathbb {R}^{n}\bigr)}^{\|\cdot\| _{I^{\alpha}_{\infty}}}. $$

Then \(I^{\alpha}_{-\infty}\) and \(I^{\alpha}_{\infty}\) are equivalent with equivalent semi-norm and norm; see [24].

Let \(C(\mathbb {R},\mathbb {R}^{n})\) denote the space of continuous functions from \(\mathbb {R}\) into \(\mathbb {R}^{n}\). Then we obtain the following lemma.

Lemma 2.1

([21], Theorem 2.1)

If \(\alpha>1/2\), then \(H^{\alpha}\subset C(\mathbb {R},\mathbb {R}^{n})\) and there is a constant \(C=C_{\alpha}\) such that

$$\|u\|_{\infty}=\sup_{x\in \mathbb {R}}\bigl|u(x)\bigr|\leq C\|u \|_{\alpha}. $$

Remark 2.2

From Lemma 2.1, we know that if \(u\in H^{\alpha}\) with \(1/2<\alpha<1\), then \(u\in L^{p}(\mathbb {R},\mathbb {R}^{n})\) for all \(p\in [2,\infty)\), since

$$\int_{\mathbb {R}}\bigl|u(x)\bigr|^{p} \,dx \leq\|u \|^{p-2}_{\infty}\|u\|^{2}_{L^{2}}. $$

In what follows, we introduce the fractional space in which we will construct the variational framework of (PFHS). Let

$$X^{\alpha}= \biggl\{ u\in H^{\alpha}: \int_{\mathbb {R}} \bigl[\bigl|{}_{-\infty}D^{\alpha }_{t}u(t)\bigr|^{2}+ \bigl(L(t)u(t),u(t)\bigr)\bigr]\,dt< \infty \biggr\} , $$

then \(X^{\alpha}\) is a reflexive and separable Hilbert space with the inner product

$$\langle u,v \rangle_{X^{\alpha}}=\int_{\mathbb {R}}\bigl[ \bigl({}_{-\infty}D^{\alpha }_{t}u(t),{}_{-\infty}D^{\alpha}_{t}v(t) \bigr)+\bigl(L(t)u(t),v(t)\bigr)\bigr]\,dt $$

and the corresponding norm is

$$\|u\|^{2}_{X^{\alpha}}=\langle u,u \rangle_{X^{\alpha}}. $$

Similar to Lemma 2.1 in [21], we have the following conclusion. Its proof is just the repetition of Lemma 2.1 of [21], so we omit the details.

Lemma 2.3

Suppose \(L(t)\) satisfies (L)′, then \(X^{\alpha}\) is continuously embedded in \(H^{\alpha}\).

Remark 2.4

From Remark 2.1 and Lemma 2.3, the embedding of \(X^{\alpha}\) into \(L^{\infty}(\mathbb {R},\mathbb {R}^{n})\) is continuous. On the other hand, it is obvious that the embedding \(X^{\alpha}\hookrightarrow L^{2}(\mathbb {R},\mathbb {R}^{n})\) is also continuous. Therefore, combining this with Remark 2.2, for any \(p\in[2,\infty]\), there exists \(C_{p}>0\) such that

$$ \|u\|_{L^{p}}\leq C_{p}\|u\|_{X^{\alpha}}. $$
(2.5)

Proposition 2.5

([18], Fact 2.1)

Under the assumption of (W1), we have

  1. (i)

    \(W(t,u)\leq W(t,\frac{u}{|u|})|u|^{\theta}\) for \(t\in \mathbb {R}\) and \(0<|u|\leq1\);

  2. (ii)

    \(W(t,u)\geq W(t,\frac{u}{|u|})|u|^{\theta}\) for \(t\in \mathbb {R}\) and \(|u|\geq1\).

Now we introduce some more notations and necessary definitions. Let \(\mathcal{B}\) be a real Banach space, \(I\in C^{1}(\mathcal{B},\mathbb {R})\) means that I is a continuously Fréchet-differentiable functional defined on \(\mathcal{B}\). Recall that \(I\in C^{1}(\mathcal{B},\mathbb {R})\) is said to satisfy the (PS) condition if any sequence \(\{u_{n} \}_{n\in \mathbb {N}}\subset \mathcal{B}\), for which \(\{I(u_{n}) \}_{n\in \mathbb {N}}\) is bounded and \(I'(u_{n})\rightarrow0\) as \(n\rightarrow\infty\), possesses a convergent subsequence in \(\mathcal{B}\).

Moreover, let \(B_{r}\) be the open ball in \(\mathcal{B}\) with the radius r and centered at 0 and \(\partial B_{r}\) denotes its boundary. Under the conditions of Theorem 1.1, we obtain the existence of the first solution of (PFHS) by using the following well-known mountain pass theorem; see [10].

Lemma 2.6

([10], Theorem 2.2)

Let \(\mathcal{B}\) be a real Banach space and \(I\in C^{1}(\mathcal{B},\mathbb {R})\) satisfying the (PS) condition. Suppose that \(I(0)=0\) and

  1. (A1)

    there are constants ρ, \(\alpha>0\) such that \(I|_{\partial B_{\rho}}\geq\alpha\), and

  2. (A2)

    there is an \(e\in\mathcal{B}\setminus\overline {B}_{\rho}\) such that \(I(e)\leq0\).

Then I possesses a critical value \(c\geq\alpha\). Moreover, c can be characterized as

$$c=\inf_{g\in\Gamma}\max_{s\in[0,1]}I\bigl(g(s)\bigr), $$

where

$$\Gamma= \bigl\{ g\in C\bigl([0,1], \mathcal{B}\bigr): g(0)=0,g(1)=e \bigr\} . $$

As far as the second one is concerned, we obtain it by a minimizing method, which is concerned with a small ball centered at 0; see Step 4 in proof of Theorem 1.1.

3 Proof of Theorem 1.1

The aim of section is to establish the proof of Theorem 1.1. For this purpose, we are going to establish the corresponding variational framework to obtain solutions of (PFHS). To this end, define the functional \(I:\mathcal{B}=X^{\alpha}\rightarrow \mathbb {R}\) by

$$ \begin{aligned}[b] I(u)&=\int_{\mathbb {R}} \biggl[\frac{1}{2}\bigl|{}_{-\infty}D_{t}^{\alpha }u(t)\bigr|^{2}+ \frac{1}{2}\bigl(L(t)u(t),u(t)\bigr)-W\bigl(t,u(t)\bigr)+\bigl(f(t),u(t) \bigr) \biggr]\,dt \\ &=\frac{1}{2}\|u\|^{2}_{X^{\alpha}}-\int_{\mathbb {R}} \bigl[W\bigl(t,u(t)\bigr)-\bigl(f(t),u(t)\bigr) \bigr]\,dt. \end{aligned} $$
(3.1)

Under the conditions of Theorem 1.1, as usual, we see that \(I\in C^{1}(X^{\alpha}, \mathbb {R})\), i.e., I is a continuously Fréchet-differentiable functional defined on \(X^{\alpha}\). Moreover, we have

$$\begin{aligned} I'(u)v={}&\int_{\mathbb {R}} \bigl[\bigl({}_{-\infty}D_{t}^{\alpha}u(t), {}_{-\infty }D_{t}^{\alpha}v(t)\bigr)+\bigl(L(t)u(t),v(t) \bigr) \\ &{}-\bigl(\nabla W\bigl(t,u(t)\bigr),v(t)\bigr)+\bigl(f(t),u(t)\bigr) \bigr] \,dt \end{aligned} $$

for all u, \(v\in X^{\alpha}\), which yields

$$ I'(u)u =\|u\|^{2}_{X^{\alpha}}-\int _{\mathbb {R}} \bigl[\bigl(\nabla W\bigl(t,u(t)\bigr),u(t)\bigr)- \bigl(f(t),u(t)\bigr) \bigr]\,dt. $$
(3.2)

Lemma 3.1

Under the conditions of Theorem  1.1, \(\Phi'\) is compact, i.e., \(\Phi'(u_{n})\rightarrow\Phi'(u)\) if \(u_{n}\rightharpoonup u\) in \(X^{\alpha}\), where \(\Phi:X^{\alpha}\rightarrow \mathbb {R}\) is defined by

$$ \Phi(u)=\int_{\mathbb {R}}W(t,u)\,dt. $$
(3.3)

Proof

Assume that \(u_{n}\rightharpoonup u\) in \(X^{\alpha}\), then there is some constant \(M>0\) such that

$$\|u_{n}\|_{X^{\alpha}}\leq M \quad\mbox{and}\quad \|u \|_{X^{\alpha}}\leq M $$

for \(n\in \mathbb {N}\). In addition, from (W2)′, for any \(\epsilon>0\) there exists \(R>0\) such that

$$ \bigl|\nabla W(t,u)\bigr|\leq\epsilon|u|^{\theta-1} \quad\mbox{and}\quad \bigl|\nabla W(t,u_{n})\bigr|\leq\epsilon|u_{n}|^{\theta-1} $$
(3.4)

for \(|t|>R\).

Consequently, for n large enough, we have

$$\begin{aligned} \bigl|\bigl(\Phi'(u_{n})- \Phi'(u)\bigr) v\bigr|\leq{}&\int_{\mathbb {R}}\bigl|\nabla W(t,u_{n})-\nabla W(t,u)\bigr||v|\,dt \\ \leq{}&\int_{-R}^{R}\bigl|\nabla W(t,u_{n})- \nabla W(t,u)\bigr||v|\,dt \\ &{}+\int_{|t|>R}\bigl|\nabla W(t,u_{n})\bigr||v|\,dt+\int _{|t|>R}\bigl|\nabla W(t,u)\bigr||v|\,dt \\ \leq{}& \epsilon\|v\|_{\infty}+\epsilon\int_{|t|>R}|u_{n}|^{\theta -1}|v| \,dt+\epsilon\int_{|t|>R}|u|^{\theta-1}|v|\,dt \\ \leq{}& \epsilon C_{\infty} \|v\|_{X^{\alpha}}+\epsilon\int _{|t|>R} \biggl(\frac{\theta-1}{\theta}|u_{n}|^{\theta}+ \frac {1}{\theta}|v|^{\theta} \biggr)\,dt \\ &{}+ \epsilon\int_{|t|>R} \biggl(\frac{\theta-1}{\theta}|u|^{\theta }+ \frac{1}{\theta}|v|^{\theta} \biggr)\,dt \\ \leq{}& \epsilon C_{\infty} \|v\|_{X^{\alpha}}+\epsilon \frac{\theta -1}{\theta} \int_{|t|>R}\bigl(|u_{n}|^{\theta}+|u|^{\theta} \bigr)\,dt \\ &{}+\epsilon\frac{2}{\theta} \int_{|t|>R}|v|^{\theta} \,dt. \end{aligned}$$
(3.5)

Here we apply the Young inequality:

$$ab\leq\frac{a^{p}}{p}+\frac{b^{q}}{q},\quad a, b>0, p,q>1 \mbox{ and } \frac {1}{p}+\frac{1}{q}=1. $$

In view of (3.5) and (2.5), we obtain

$$\begin{aligned} \bigl\| \Phi'(u_{n})- \Phi'(u)\bigr\| &=\sup_{\|v\|_{X^{\alpha}}=1} \biggl|\int_{\mathbb {R}} \bigl(\nabla W(t,u_{n})- \nabla W(t,u), v\bigr)\,dt \biggr| \\ &\leq\epsilon C_{\infty} + \epsilon2(C_{\theta}M)^{\theta} \frac {\theta-1}{\theta} + \epsilon C_{\theta}^{\theta}\frac{2}{\theta}, \end{aligned} $$

which yields \(\Phi'(u_{n})\rightarrow\Phi'(u)\) as \(u_{n}\rightharpoonup u\), that is, \(\Phi'\) is compact. □

Lemma 3.2

Under the conditions of Theorem  1.1, I satisfies the (PS) condition.

Proof

Assume that \(\{u_{k} \}_{k\in \mathbb {N}} \subset X^{\alpha}\) is a sequence such that \(\{I(u_{k}) \}_{k\in \mathbb {N}}\) is bounded and \(I'(u_{k})\rightarrow0\) as \(k\rightarrow\infty\). Then there exists a constant \(M>0\) such that

$$ \bigl|I(u_{k})\bigr|\leq M \quad\mbox{and}\quad \bigl\| I'(u_{k})\bigr\| _{(X^{\alpha})^{*}}\leq M $$
(3.6)

for every \(k\in \mathbb {N}\), where \((X^{\alpha})^{*}\) is the dual space of \(X^{\alpha}\).

First, we show that \(\{u_{n}\}_{k\in \mathbb {N}}\) is bounded. In fact, in view of (W1), (3.1), (3.2), and (3.6), we obtain

$$\begin{aligned} M+\frac{M}{\theta} \|u_{k} \|_{X^{\alpha}}\geq{}& I(u_{k})-\frac{1}{\theta }I'(u_{k})u_{k} \\ ={}& \biggl(\frac{1}{2}-\frac{1}{\theta} \biggr)\|u_{k} \|_{X^{\alpha} }^{2}-\int_{\mathbb {R}} \biggl[W \bigl(t,u_{k}(t)\bigr)-\frac{1}{\theta}\bigl(\nabla W \bigl(t,u_{k}(t)\bigr),u_{k}(t)\bigr) \biggr]\,dt \\ &{}+ \biggl(1-\frac{1}{\theta} \biggr)\int_{\mathbb {R}} \bigl(f(t),u_{k}(t)\bigr)\,dt \\ \geq{}& \biggl(\frac{1}{2}-\frac{1}{\theta} \biggr)\|u_{k} \|_{X^{\alpha} }^{2}- \biggl(1-\frac{1}{\theta} \biggr)C_{2} \|f\|_{L^{2}}\|u_{k}\|_{X^{\alpha}}. \end{aligned} $$

Since \(\theta>2\), the boundedness of \(\{u_{k}\}_{k\in \mathbb {N}}\) follows directly. Then the sequence \(\{u_{k}\}_{k\in \mathbb {N}}\) has a subsequence, again denoted by \(\{u_{k}\}_{k\in \mathbb {N}}\), and there exists \(u\in E\) such that

$$u_{k}\rightharpoonup u \quad\mbox{weakly in } E, $$

which yields

$$\bigl(I'(u_{k})-I'(u)\bigr) (u_{k}-u)\rightarrow0 \quad\mbox{as } k\rightarrow\infty. $$

Note that, according to (3.2), we have

$$\bigl(I'(u_{k})-I'(u)\bigr) (u_{k}-u)=\|u_{k}-u\|_{X^{\alpha}}^{2}-\bigl( \Phi'(u_{k})-\Phi '(u)\bigr) \bigl(u_{k}(t)-u(t)\bigr). $$

On the other hand, in view of Lemma 3.1, \(\Phi '(u_{k})\rightarrow\Phi'(u)\) as \(k\rightarrow\infty\). Consequently, we deduce that \(\|u_{k}-u\|_{X^{\alpha}}\rightarrow0\) as \(k\rightarrow\infty\) and prove that the (PS) condition holds. □

Now we are in the position to give the proof of Theorem 1.1. We divide its proof into four steps.

Proof

Step 1. It is clear that \(I(0)=0\) and \(I\in C^{1}(X^{\alpha}, \mathbb {R})\) satisfies the (PS) condition by Lemma 3.2.

Step 2. We now show that there exist constants \(\rho>0\) and \(\alpha>0\) such that I satisfies condition (A1) of Lemma 2.6. Let \(\rho=\frac{1}{C_{\infty}}\), where \(C_{\infty}\) is defined in (2.5). Assume that \(u\in E\) with \(\|u\|_{X^{\alpha} }\leq\rho\), then \(\|u\|_{\infty}\leq1\).

In consequence, combining this with (i) of Proposition 2.5, we obtain

$$ \begin{aligned}[b] I(u)&\geq\frac{1}{2}\|u \|_{X^{\alpha}}^{2}-\int_{\mathbb {R}}W \biggl(t, \frac {u(t)}{|u(t)|} \biggr)\bigl|u(t)\bigr|^{\theta}\,dt-\int_{\infty} \bigl(f(t),u(t)\bigr)\,dt \\ &\geq\frac{1}{2}\|u\|_{X^{\alpha}}^{2}-\varrho\int _{\mathbb {R}}\bigl|u(t)\bigr|^{2}\,dt-C_{2}\|f \|_{L^{2}}\|u\|_{X^{\alpha}} \\ &= \biggl(\frac{1}{2}-\varrho C_{2}^{2} \biggr)\|u \|_{X^{\alpha}}^{2}-C_{2}\|f\| _{L^{2}}\|u \|_{X^{\alpha}},\quad \|u\|_{X^{\alpha}}=\rho, \end{aligned} $$
(3.7)

where ϱ is defined in (W f ). The inequalities (1.3) and (3.7) imply that

$$I|_{\partial B_{\rho}}\geq\frac{1}{2C_{\infty}^{2}}-\varrho\frac {C_{2}^{2}}{C_{\infty}^{2}}-\|f \|_{L^{2}}\frac{C_{2}}{C_{\infty}}=\alpha>0. $$

Step 3. It remains to prove that there exists an \(e\in X^{\alpha}\) such that \(I(e)\leq0\) with \(\|e\|_{X^{\alpha}}>\rho\), where ρ is defined in Step 2. Choose \(\varphi\in X^{\alpha}\) such that \(|\varphi(t)|=1\) for all \(t\in[0,1]\). In view of (3.1) and (ii) of Proposition 2.5, we have, for every \(s\in[1,\infty)\),

$$ \begin{aligned}[b] I(s\varphi)&=\frac{s^{2}}{2}\| \varphi\|_{X^{\alpha}}^{2} -\int_{\mathbb {R}}W\bigl(t,s \varphi(t)\bigr)\,dt+s\int_{\mathbb {R}}\bigl(f(t),\varphi(t)\bigr)\,dt \\ &\leq\frac{s^{2}}{2}\|\varphi\|_{X^{\alpha}}^{2}-s^{\theta} \int_{0}^{1} W \biggl(t,\frac{\varphi(t)}{|\varphi(t)|} \biggr)\bigl| \varphi(t)\bigr|^{\theta} \,dt+s C_{2}\|f\|_{L^{2}}\|\varphi \|_{X^{\alpha}} \\ &\leq\frac{s^{2}}{2}\|\varphi\|_{X^{\alpha}}^{2}-m s^{\theta}\int_{0}^{1} \bigl| \varphi(t)\bigr|^{\theta} \,dt+ s C_{2} \|f\|_{L^{2}}\|\varphi \|_{X^{\alpha}}, \end{aligned} $$
(3.8)

where \(m=\min\{W(t,u):t\in[0,1], |u|=1\}\). Since \(\theta>2\), (3.8) implies that \(I(s\varphi)=I(e)<0\) for some \(s\gg1\) with \(\|s\varphi\|_{X^{\alpha}}>\rho\), where ρ is defined in Step 2. By Lemma 2.6, I possesses a critical value \(c_{1}\geq\alpha >0\) given by

$$c_{1}=\inf_{g\in\Gamma}\max_{s\in[0,1]}I \bigl(g(s)\bigr), $$

where

$$\Gamma= \bigl\{ g\in C\bigl([0,1], X^{\alpha}\bigr): g(0)=0, g(1)=e \bigr\} . $$

Hence there is \(0\neq u_{1}\in X^{\alpha}\) such that

$$I(u_{1})=c_{1} \quad\mbox{and}\quad I'(u_{1})=0. $$

That is, the first nontrivial solution of (PFHS) exists.

Step 4. From (3.7), we see that I is bounded from below on ̅. Therefore, we can denote

$$c_{2}=\inf_{\|u\|_{X^{\alpha}}\leq\rho} I(u), $$

where ρ is defined in Step 1. Due to the fact that \(I(0)=0\), \(c_{2}< c_{1}\). Then there is a minimizing sequence \(\{v_{k}\}_{k\in \mathbb {N}}\subset\overline{B_{\rho}(0)}\) such that

$$I(v_{k})\rightarrow c_{2} \quad\mbox{and}\quad I'(v_{k})\rightarrow0 $$

as \(k\rightarrow\infty\). That is, \(\{v_{k}\}_{k\in \mathbb {N}}\) is a (PS) sequence. Furthermore, from Lemma 3.2 I satisfies the (PS) condition. Therefore, \(c_{2}\) is one nontrivial critical value of I (note that in our case \(u(t)\equiv0\) is not a solution of (PFHS)). Consequently, there is \(0\neq u_{2}\in X^{\alpha}\) such that

$$I(u_{2})=c_{2} \quad\mbox{and}\quad I'(u_{2})=0. $$

That is, I has another nontrivial solution. □