Heat transfer in an unsteady MHD flow through an infinite annulus with radiation

Abstract

An analytical study of a laminar unsteady magnetohydrodynamic flow of a viscous incompressible and electrically conducting Newtonian non-Gray optically thin fluid between two infinite concentric vertical cylinders influenced by time dependent periodic pressure gradient subjected to a magnetic field applied in azimuthal direction and in the presence of appreciable thermal radiation and periodic wall temperature is presented. The governing equations of motion and energy are transformed into ordinary differential equations which are solved in closed form in terms of the modified Bessel functions (of first and second kind) of order zero. The induced magnetic field is neglected, assuming the magnetic Reynolds number to be considerably small. A parametric study accounting for the effects of various physical parameters on the velocity and temperature fields and on the coefficient of skin friction, the rate of heat transfer at the surface of the cylinders, and mass flux across a normal section of the annulus is conducted and the results are discussed graphically.

1 Introduction

The magnetohydrodynamic flow and heat transfer problems in an annular region have assumed considerable industrial significance in the light of advancements in hydraulics and nuclear technology. Several authors have studied the magnetohydrodynamic (MHD) flows and heat transfer in channels and circular pipes. Chamkha [1] studied the unsteady laminar MHD flow and heat transfer in channels and circular pipes under the influence of two different applied pressure gradients (oscillating and ramp). Singh [2] analyzed the problem of MHD mixed convection periodic flow in a rotating vertical channel with heat radiation and presented an exact solution. MHD heat transfer problems with periodic wall temperature are also frequently encountered. Israel-Cookey et al. [3] investigated the problem of MHD free convection and oscillating flow of an optically thin fluid bounded by two horizontal porous parallel walls with a periodic wall temperature. Reddy et al. [4] also introduced a periodic wall temperature into their study. Marin and Marinescu [5] proceeded with an analysis of thermoelasticity of initially stressed bodies with asymptotic equipartition of energies. Marin et al. [6] also carried out a theoretical investigation of thermoelasticity taking into account the heat conduction in deformable bodies depending on two different temperatures viz. a conductive temperature and a thermodynamic temperature. Othman and Zaki [7] studied the effect of a vertical magnetic field on the onset of a convective instability in a conducting micropolar fluid layer heated from below and confined between two horizontal planes under the coupled action of the rotation of the system and a vertical temperature gradient.

In this study, the problem of an unsteady MHD flow of a Newtonian non-Gray optically thin fluid within the annulus of two infinite concentric vertical cylinders is analyzed. The current is set up within the annulus due to the application of a time dependent periodic pressure gradient and this is subjected to a magnetic field applied in the azimuthally direction. Heat is simultaneously applied to both walls of the annulus in the form of periodic wall temperature whence the thermal radiation too is considered. The magnetic Reynolds number is considered to be small enough, as a result of which the induced magnetic field can be neglected. The introduction of a cylindrical polar coordinate system renders the resulting governing equations of motion and energy to a form which can be solved exactly, thus obtaining the expressions for velocity and temperature fields. Subsequently, the mass flux coefficient, the skin friction coefficient, and the coefficient of heat transfer (Nusselt number) are derived and are depicted graphically.

2 Basic equations

The fundamental equations governing the motion of an incompressible, viscous, radiating, and electrically conducting fluid are:

• Equation of continuity:

  $$ \vec{\nabla} \cdot \vec{q} = 0. $$

  (1)

• MHD momentum equation:

  $$ \rho \biggl[ \frac{\partial \vec{q}}{\partial t} + ( \vec{q} \cdot \vec{\nabla} )\vec{q} \biggr] = - \vec{\nabla} p + \mu \nabla^{2}\vec{q} + \vec{J} \times \vec{B} + \rho \vec{g}. $$

  (2)

• Energy equation:

  $$ \rho C_{p} \biggl[ \frac{\partial T}{\partial t} + ( \vec{q} \cdot \vec{\nabla} )T \biggr] = K_{T}\nabla^{2}T + \varphi - \vec{\nabla} \cdot \vec{q}_{r}. $$

  (3)

• Ohm’s law for an electrically conducting fluid:

  $$ \vec{J} = \sigma ( \vec{q} \times \vec{B} ). $$

  (4)

All the physical quantities are described in the list of abbreviations.

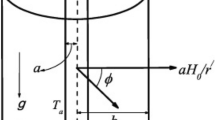
Consider a laminar, radiative flow of an incompressible, Newtonian, electrically conducting, non-Gray and optically thin fluid within an annulus, influenced by a time dependent periodic pressure gradient and a periodic temperature applied to the walls of the annulus. The annulus is assumed to be bounded by two cylinders of radii a and b, where $a < b$.

A cylindrical polar coordinate system $( r,\theta,z )$ is introduced with the axis of the coaxial cylinders as the z-axis. A magnetic field of intensity $H_{0}$ (constant) is applied in the azimuthal direction. In order to make the physical model idealized, the present investigation is restricted to the following assumptions:

• (I) All the fluid properties are considered constants except the influence of the variation in density in the buoyancy force term.

• (II) The viscous dissipation of energy is negligible.

• (III) The radiation heat flux ($q_{r}$) in the vertical direction is considered to be negligible in comparison to that in the normal direction.

We recall that the fluid moves parallel to the z-axis, suggesting us to take $\vec{q}$ as $( 0,0,V_{z} )$. Equation (1) in $( r,\theta,z )$ system becomes $\frac{1}{r}\frac{\partial}{\partial z} ( rV_{z} ) = 0$ which yields $V_{z} = V_{z} ( r,t )$, due to symmetry of the model. Proceeding with the analysis, the momentum equation takes the form

$$ \rho \frac{\partial V_{z}}{\partial t} = - \frac{\partial p}{\partial z} + \mu \biggl( \frac{\partial^{2}V_{z}}{\partial r^{2}} + \frac{1}{r}\frac{\partial V_{z}}{\partial r} \biggr) - \sigma \mu_{e}^{2}H_{0}^{2}V_{z} - \rho g. $$

(5)

The equation of state on the basis of classical Boussinesq approximation (Bergman et al. [8]) is

$$ \rho_{s} \simeq \rho \bigl[ 1 + \beta ( T - T_{s} ) \bigr]. $$

(6)

In the static condition, (5) renders $0 = - \frac{\partial p_{s}}{\partial z} - \rho_{s}g$, where $p_{s}$ is the static fluid pressure. Utilization of this in (5) produces

$$ \rho \frac{\partial V_{z}}{\partial t} = - \frac{\partial ( p - p_{s} )}{\partial z} + \mu \biggl( \frac{\partial^{2}V_{z}}{\partial r^{2}} + \frac{1}{r}\frac{\partial V_{z}}{\partial r} \biggr) - \sigma \mu_{e}^{2}H_{0}^{2}V_{z} - g ( \rho - \rho_{s} ). $$

(7)

With $p^{*} = p - p_{s}$, the application of (6) leads to the following equation of motion:

$$ \frac{\partial V_{z}}{\partial t} = - \frac{1}{\rho} \frac{\partial p^{*}}{\partial z} + \frac{\mu}{\rho} \biggl( \frac{\partial^{2}V_{z}}{\partial r^{2}} + \frac{1}{r}\frac{\partial V_{z}}{\partial r} \biggr) - \frac{\sigma \mu_{e}^{2}H_{0}^{2}}{\rho} V_{z} + g\beta ( T - T_{s} ). $$

(8)

In lieu of the assumptions (II) and (III), the energy equation takes the form

$$ \rho C_{p}\frac{\partial T}{\partial t} = K_{T} \biggl[ \frac{\partial^{2}T}{\partial r^{2}} + \frac{1}{r}\frac{\partial T}{\partial r} \biggr] - 4I ( T - T_{s} ). $$

(9)

On account of the axial symmetry and the annulus being infinite in the z-direction, the temperature field is independent of θ and z. In (9), the rate of radiative heat flux in the optically thin limit for a non-Gray gas near equilibrium is due to the following formula attributed to Cogley et al. [9]:

$$ \frac{\partial q_{r}}{\partial r} = 4I ( T - T_{s} ), $$

(10)

where $I = \int_{0}^{\infty} ( K_{\lambda '} )_{w} ( \frac{\partial e_{\lambda 'h}}{\partial T} )_{w}\, d\lambda '$.

The boundary conditions to be satisfied by (8) and (9) are

$$ \left . \begin{array}{l} V_{z} = 0 \quad \mbox{at } r = a, \\ V_{z} = 0 \quad \mbox{at } r = b, \\ T = T_{s} + T_{s}n_{1}e^{i\alpha_{1}t}\quad \mbox{at } r = a, \\ T = T_{s} + T_{s}n_{2}e^{i\alpha_{1}t}\quad \mbox{at } r = b. \end{array} \right \} $$

(11)

The following non-dimensional quantities are introduced in order to normalize the model:

$$ \left . \begin{array}{l} V_{z}^{\prime} = \frac{V_{z}a}{\nu},\qquad r' = \frac{r}{a},\qquad z' = \frac{z}{a}, \qquad p^{*\prime} = \frac{p^{*}a^{2}}{\mu \nu}, \\ t' = \frac{t\nu}{a^{2}},\qquad \lambda = \frac{b}{a},\qquad \alpha = \frac{\alpha_{1}a^{2}}{\nu},\qquad \psi ' = \frac{T - T_{s}}{T_{s}}, \\ \mathit{Gr} = \frac{g\beta a^{3}}{\nu^{2}}T_{s},\qquad \mathit{Pr} = \frac{\mu C_{p}}{K_{T}}, \qquad Q = \frac{4Ia^{2}}{\mu C_{p}}. \end{array} \right \} $$

(12)

The dimensionless forms of (8), (9), and (11) are (removing the primes):

$$\begin{aligned}& \frac{\partial V_{z}}{\partial t} = - \frac{\partial p^{*}}{\partial z} + \biggl( \frac{\partial^{2}V_{z}}{\partial r^{2}} + \frac{1}{r}\frac{\partial V_{z}}{\partial r} \biggr) - M^{2}V_{z} - \mathit{Gr}\psi, \end{aligned}$$

(13)

$$\begin{aligned}& \mathit{Pr}\frac{\partial \psi}{\partial t} = \frac{\partial^{2}\psi}{\partial r^{2}} + \frac{1}{r} \frac{\partial \psi}{\partial r} - Q\mathit{Pr}\psi, \end{aligned}$$

(14)

$$\begin{aligned}& \left . \begin{array}{l} V_{z} = 0 \quad \mbox{at } r = 1, \\ V_{z} = 0\quad \mbox{at } r = \lambda, \\ \psi = n_{1}e^{i\alpha t} \quad \mbox{at } r = 1, \\ \psi = n_{2}e^{i\alpha t} \quad \mbox{at } r = \lambda, \end{array} \right \} \end{aligned}$$

(15)

where $M = \mu_{e}H_{0}a\sqrt{\frac{\sigma}{\mu}}$ is the Hartmann number and $1 \le r \le \lambda$.

3 Exact solution

We consider the temperature as $\psi ( r,t ) = f(r)e^{i\alpha t}$. With this form of ψ, (14) reduces to the ordinary differential equation $r^{2}\frac{d^{2}f(r)}{dr^{2}} + r\frac{df(r)}{dr} - \eta^{2}r^{2}f(r) = 0$ where $\eta^{2} = \mathit{Pr} ( i\alpha + Q )$. The substitution $z = ir\eta$, $f ( \frac{z}{i\eta} ) = f_{1}(z)$ leads us to Bessel’s differential equation of order 0:

$$ z^{2}\frac{d^{2}f_{1}(z)}{dz^{2}} + z\frac{df_{1}(z)}{dz} + z^{2}f_{1}(z) = 0. $$

(16)

The general solution to (16) is $f(r) = A_{1}J_{0}(ir\eta ) + B_{1}Y_{0}(ir\eta )$, in which $J_{0}$ and $Y_{0}$ are Bessel’s function of order 0 of the first kind and of the second kind, respectively, and $A_{1}$ and $B_{1}$ are constants to be determined subject to (15). Utilizing the established identities $J_{0}(ix) = I_{0}(x)$ and $Y_{0}(ix) = - \frac{2}{\pi} K_{0}(x) - \frac{1}{i}I_{0}(x)$, and the boundary conditions (15) we are able to arrive at

$$ \psi ( r,t ) = \biggl[ A_{1}I_{0}(r\eta ) + B_{1} \biggl\{ - \frac{2}{\pi} K_{0}(r\eta ) - \frac{1}{i}I_{0}(r\eta ) \biggr\} \biggr] \times e^{i\alpha t}, $$

(17)

where $A_{1}$ and $B_{1}$ are defined as

$$\begin{aligned}& A_{1} = \frac{\frac{2}{\pi} \{ n_{2}K_{0}(\eta ) - n_{1}K_{0}(\lambda \eta ) \} + \frac{1}{i} \{ n_{2}I_{0}(\eta ) - n_{1}I_{0}(\lambda \eta ) \}}{\frac{2}{\pi} \{ I_{0}(\lambda \eta )K_{0}(\eta ) - I_{0}(\eta )K_{0}(\lambda \eta ) \}}, \\& B_{1} = \frac{n_{2}I_{0}(\eta ) - n_{1}I_{0}(\lambda \eta )}{\frac{2}{\pi} \{ I_{0}(\lambda \eta )K_{0}(\eta ) - I_{0}(\eta )K_{0}(\lambda \eta ) \}}. \end{aligned}$$

We now employ the complex variable technique used by Messiha [10] and also by Vajravelu and Sastri [11] to solve the boundary value problem in closed form. Assuming that the pressure gradient is a periodic function of t, we formulate

$$ - \frac{\partial p^{*}}{\partial z} = P_{0}e^{i\alpha t}, $$

(18)

where α is the frequency parameter and $P_{0}$ is a constant which equals the pressure gradient at time $t = 0$.

Due to the assumptions made previously, we consider the velocity to be interpreted as $V_{z} ( r,t ) = g(r)e^{i\alpha t}$. All these considerations in (13) finally present us with the following expression for the velocity field:

$$\begin{aligned} V_{z} ( r,t ) =& \biggl[ \frac{P_{0}}{\delta^{2}} + A_{2}I_{0}(r \delta ) + B_{2} \biggl\{ - \frac{2}{\pi} K_{0}(r\delta ) - \frac{1}{i}I_{0}(r\delta ) \biggr\} + \frac{1}{\delta^{2} - \eta^{2}} \\ &{}\times \biggl\{ \biggl( \mathit{Gr}A_{1} + \mathit{Gr}B_{1} \frac{1}{i} \biggr)I_{0}(r\eta ) + \frac{2\mathit{Gr}B_{1}}{\pi} K_{0}(r\eta ) \biggr\} \biggr]e^{i\alpha t} \end{aligned}$$

(19)

with $A_{2}$ and $B_{2}$ in the form

$$\begin{aligned}& A_{2} = \frac{1}{\frac{2}{\pi} [ I_{0}(\lambda \delta )K_{0}(\delta ) - I_{0}(\delta )K_{0}(\lambda \delta ) ]} \\& \hphantom{A_{2} =}{}\times \biggl[ \frac{P_{0}}{\delta^{2}} \frac{2}{\pi} \bigl\{ K_{0}(\lambda \delta ) - K_{0}( \delta ) \bigr\} + \frac{P_{0}}{\delta^{2}}\frac{1}{i} \bigl\{ I_{0}( \lambda \delta ) - I_{0}(\delta ) \bigr\} \\& \hphantom{A_{2} =}{}+ \frac{1}{\delta^{2} - \eta^{2}} \biggl( \mathit{Gr}A_{1} + \mathit{Gr}B_{1}\frac{1}{i} \biggr) \biggl\{ \frac{2}{\pi} \biggr\} \times \bigl\{ I_{0}(\eta )K_{0}(\lambda \delta ) - I_{0}(\lambda \eta )K_{0}(\delta ) \bigr\} \\& \hphantom{A_{2} =}{}+ \frac{1}{\delta^{2} - \eta^{2}}\biggl( \mathit{Gr}A_{1}+\mathit{Gr}B_{1}\frac{1}{i} \biggr) \frac{1}{i} \bigl\{ I_{0}(\eta )I_{0}(\lambda \delta ) - I_{0}(\lambda \eta )I_{0}(\delta ) \bigr\} \\& \hphantom{A_{2} =}{} + \frac{4\mathit{Gr}B_{1}}{\delta^{2} - \eta^{2}}\frac{1}{\pi^{2}} \bigl\{ K_{0}(\eta )K_{0}(\lambda \delta ) - K_{0}(\lambda \eta )K_{0}(\delta ) \bigr\} \\& \hphantom{A_{2} =}{} + \frac{2\mathit{Gr}B_{1}}{\delta^{2} - \eta^{2}}\frac{1}{\pi i} \bigl\{ K_{0}(\eta )I_{0}(\lambda \delta ) - K_{0}( \lambda \eta )I_{0}(\delta ) \bigr\} \biggr], \\& B_{2} = \frac{1}{\frac{2}{\pi} [ I_{0}(\lambda \delta )K_{0}(\delta ) - I_{0}(\delta )K_{0}(\lambda \delta ) ]} \\& \hphantom{B_{2} =}{}\times \biggl[ \frac{P_{0}}{\delta^{2}} \bigl\{ I_{0}(\lambda \delta ) - I_{0}(\delta ) \bigr\} + \frac{1}{\delta^{2} - \eta^{2}} \biggl( \mathit{Gr}A_{1} + \mathit{Gr}B_{1} \frac{1}{i} \biggr) \\& \hphantom{B_{2} =}{}\times \bigl\{ I_{0}(\eta )I_{0}(\lambda \delta ) - I_{0}(\lambda \eta )I_{0}(\delta ) \bigr\} + \frac{2\mathit{Gr}B_{1}}{\delta^{2} - \eta^{2}}\frac{1}{\pi} \bigl\{ K_{0}(\eta )I_{0}(\lambda \delta ) - K_{0}(\lambda \eta )I_{0}(\delta ) \bigr\} \biggr], \end{aligned}$$

where $\delta^{2} = M^{2} + i\alpha$.

It may be noted that only the real part of $V_{z}$ contributes to the fluid velocity, so far as the numerical calculations are concerned.

4 Mass flux

The total discharge of flux per unit time is given by

$$\begin{aligned} M_{f} =& \int_{0}^{2\pi} \int _{1}^{\lambda} V_{z}r\, dr\, d\theta \\ =& 2\pi e^{i\alpha t}\biggl[ \biggl( A_{2} - \frac{B_{2}}{i} \biggr) \frac{1}{\delta} \bigl\{ \lambda I_{1}(\lambda \delta ) - I_{1}(\delta ) \bigr\} - \frac{2B_{2}}{\pi \delta} \bigl\{ K_{1}( \delta ) - \lambda K_{1}(\lambda \delta ) \bigr\} \\ &{}+ \frac{P_{0}}{\delta^{2}}\frac{1}{2} \bigl( \lambda^{2} - 1 \bigr) + \frac{1}{\delta^{2} - \eta^{2}}\frac{1}{\eta} \biggl\{ \biggl( \mathit{Gr}A_{1} + \mathit{Gr}B_{1}\frac{1}{i} \biggr) \bigl\{ \lambda I_{1}(\lambda \eta ) - I_{1}(\eta ) \bigr\} \\ &{}+ \frac{2\mathit{Gr}B_{1}}{\pi} \bigl\{ K_{1}(\eta ) - \lambda K_{1}(\lambda \eta ) \bigr\} \biggr\} \biggr]. \end{aligned}$$

(20)

5 Skin friction

The viscous drags per unit area on the surface of the inner cylinder and outer cylinder, respectively, are specified by Newton’s law of viscosity as mentioned below:

$$\begin{aligned}& \tau_{1} = \biggl.{- \mu \frac{\partial V_{z}}{\partial r} }\biggr|_{r = a}, \end{aligned}$$

(21)

$$\begin{aligned}& \tau_{2} = \biggl.{- \mu \frac{\partial V_{z}}{\partial r} }\biggr|_{r = b}. \end{aligned}$$

(22)

The non-dimensional form of (21) and (22) are

$$\tau_{1} = \biggl.{- \frac{\mu \nu}{a^{2}} \frac{\partial V_{z}^{\prime}}{ \partial r'} }\biggr|_{r' = 1} \quad \mbox{and} \quad \tau_{2} = \biggl.{- \frac{\mu \nu}{ a^{2}} \frac{\partial V_{z}^{\prime}}{\partial r'} }\biggr|_{r' = \lambda}. $$

The coefficients of the skin friction on the surface of the inner and outer cylinders are, respectively, specified by

$$\begin{aligned}& C_{f1} = \frac{\tau_{1}}{\frac{\mu \nu}{a^{2}}} = \biggl.{- \frac{\partial V_{z}}{\partial r} }\biggr|_{r = 1} \\& \hphantom{C_{f1}}= - \biggl[ \delta \biggl\{ A_{2}I_{ - 1}( \delta ) + \frac{2B_{2}}{\pi} K_{ - 1}(\delta ) - \frac{B_{2}}{i}I_{ - 1}( \delta ) \biggr\} + \frac{1}{\delta^{2} - \eta^{2}} \biggl( \mathit{Gr}A_{1} + \mathit{Gr}B_{1}\frac{1}{i} \biggr)\eta I_{ - 1}(\eta ) \\& \hphantom{C_{f1} = }{} - \frac{1}{\delta^{2} - \eta^{2}}\frac{2\eta \mathit{Gr}B_{1}}{\pi} K_{ - 1}(\eta ) \biggr]e^{i\alpha t}, \end{aligned}$$

(23)

$$\begin{aligned}& C_{f2} = \frac{\tau_{2}}{\frac{\mu \nu}{a^{2}}} = \biggl.{- \frac{\partial V_{z}}{\partial r} }\biggr|_{r = \lambda} \\& \hphantom{C_{f2}}= - \biggl[ \delta \biggl\{ A_{2}I_{ - 1}( \lambda \delta ) + \frac{2B_{2}}{\pi} K_{ - 1}(\lambda \delta ) - \frac{B_{2}}{i}I_{ - 1}(\lambda \delta ) \biggr\} + \frac{1}{\delta^{2} - \eta^{2}} \biggl( \mathit{Gr}A_{1} + \mathit{Gr}B_{1} \frac{1}{i} \biggr) \\& \hphantom{C_{f2}=}{}\times\eta I_{ - 1}(\lambda \eta ) - \frac{1}{\delta^{2} - \eta^{2}} \frac{2\eta \mathit{Gr}B_{1}}{\pi} K_{ - 1}(\lambda \eta ) \biggr]e^{i\alpha t}. \end{aligned}$$

(24)

6 Nusselt number

The heat fluxes $q^{*}$ from the surface of the inner and outer cylinders into the fluid region are given by the Fourier law of conduction as stated below:

$$\begin{aligned}& q_{1}^{*} = \biggl.{- K_{T}\frac{\partial T}{\partial r} }\biggr|_{r = a}, \end{aligned}$$

(25)

$$\begin{aligned}& q_{2}^{*} = \biggl.{- K_{T} \frac{\partial T}{\partial r} }\biggr|_{r = b}. \end{aligned}$$

(26)

Using non-dimensional quantities defined, as in (12), we deduce $q_{1}^{*} = - \frac{K_{T}T_{s}}{a}\frac{\partial \psi '}{\partial r'} |_{r' = 1}$ and $q_{2}^{*} = - \frac{K_{T}T_{s}}{a} \frac{\partial \psi '}{\partial r'} |_{r' = \lambda}$.

The coefficients of heat transfer (Nusselt number) on the surface of the inner and outer cylinder are, respectively,

$$\begin{aligned}& Nu_{1} = \frac{q_{1}^{*}a}{K_{T}T_{s}} = \biggl.{- \frac{\partial \psi}{ \partial r} }\biggr|_{r = 1} = - \biggl[ A_{1}\eta I_{ - 1}(\eta ) - B_{1}\eta \biggl\{ \frac{2}{\pi} K_{ - 1}(\eta ) - \frac{1}{i}I_{ - 1}( \eta ) \biggr\} \biggr]e^{i\alpha t}, \end{aligned}$$

(27)

$$\begin{aligned}& Nu_{2} = \frac{q_{2}^{*}a}{K_{T}T_{s}} = \biggl.{- \frac{\partial \psi}{ \partial r} }\biggr|_{r = \lambda} = - \biggl[ A_{1}\eta I_{ - 1}(\lambda \eta ) - B_{1} \eta \biggl\{ \frac{2}{\pi} K_{ - 1}(\lambda \eta ) - \frac{1}{i}I_{ - 1}(\lambda \eta ) \biggr\} \biggr]e^{i\alpha t}. \end{aligned}$$

(28)

7 Results and discussion

In order to have a clear insight of the physical problem, it is imperative to carry out numerical computations from the analytical solutions for the velocity field, temperature field, the mass flux coefficient, the coefficient of skin friction, and the Nusselt number by assigning some arbitrarily chosen specific values to the physical parameters like the Hartmann number M, Prandtl number Pr, radiation parameter Q, Grashof number Gr, the frequency parameter α and time t, and the results are presented in Figures 1 to 22. In most of the cases of our investigation, the value of the Prandtl number Pr is chosen to be 0.025 which corresponds to mercury at 20^∘ C and at 1 atmospheric pressure. In Figures 21 and 22, Pr is specified to be 0.71, which represents air at 20^∘ C and at 1 atmospheric pressure.

Figure 1

Velocity versus r for $\pmb{\mathit{Gr} = 10}$ , $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{\alpha=0.01}$ , $\pmb{Q = 5}$ , $\pmb{t = 0.5}$ , $\pmb{\lambda=2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figures 1 to 4 demonstrate the velocity profiles under the influence of M, Pr, Q and Gr, respectively. The Hartmann number M is associated with the ratio of the magnetic body force (Lorentz force) to viscous force. Figure 1 shows that an increase in the values of the Hartmann number M causes retardation to the fluid flow indicating the fact that the imposition of the azimuthal magnetic field decelerates the flow and consequently the thickness of the velocity boundary layer gets diminished. This observation is consistent with the physical fact that the Lorentz force that appears due to the interaction of the magnetic field and the fluid velocity resists the corresponding fluid flow, resulting in the velocity to decrease gradually. Pr (Prandtl number) is the ratio of the momentum diffusivity (kinematic viscosity) to thermal diffusivity. Figure 2 indicates how the velocity field is affected corresponding to an increase in the values of Pr. We recall that an increase in Pr means a fall in thermal diffusivity for the model under consideration. It is learnt from this figure that when the thermal diffusivity of the fluid is reduced, the flow gets decelerated substantially which may be linked to the fact that a low thermal diffusivity leads to a corresponding decrease in the kinetic energy of the molecules of the fluid, which in turn affects the fluid velocity adversely. The radiation parameter Q registers the effect of thermal radiation. Retardation in fluid flow under the effect of thermal radiation is also observed and this is visualized in Figure 3. Thermal radiation results in a fall in thermal energy and the physics of this situation indicate a loss in kinetic energy of the fluid; as a consequence the fluid velocity is inhibited substantially. Gr (Grashof number) is the ratio of the buoyancy force to viscous force. Figure 4 uniquely indicates that buoyancy force causes the fluid flow to accelerate and this is in good agreement to the observations of known theory. We may conclude that the behavior of the velocity profile is fairly consistent with the known laws of physics.

Figure 2

Velocity versus r for $\pmb{\mathit{Gr} = 10}$ , $\pmb{M = 0.4}$ , $\pmb{\alpha=0.01}$ , $\pmb{Q = 5}$ , $\pmb{t = 0.5}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 3

Velocity versus r for $\pmb{\mathit{Gr} = 10}$ , $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{\alpha=0.01}$ , $\pmb{M = 0.4}$ , $\pmb{t = 0.5}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 4

Velocity versus r for $\pmb{M = 0.4}$ , $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{\alpha=0.01}$ , $\pmb{Q = 5}$ , $\pmb{t = 0.5}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figures 5 to 7 outline the influence of Pr, Q and α on the temperature profile of the fluid. It is inferred from Figure 5 that the reduction in fluid temperature is directly proportional to the diminution in thermal diffusivity. Further, Figure 6 registers the fact that the fluid temperature gets lowered with an increasing dissipation of thermal energy caused due to thermal radiation. An interesting observation is made from Figure 7 which suggest that the fluid temperature can be diminished comprehensively by raising the magnitude of the frequency parameter associated with the fluid flow. This presents us with an innovative mechanism for controlling and regularizing the fluid temperature on enhancement of the frequency parameter.

Figure 5

Temperature versus r for $\pmb{Q = 5}$ , $\pmb{\alpha=0.01}$ , $\pmb{t = 0.5}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

Figure 6

Temperature versus r for $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{\alpha=0.01}$ , $\pmb{t = 0.5}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

Figure 7

Temperature versus r for $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{Q = 5}$ , $\pmb{t = 0.5}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

The effects of Gr, Pr, and Q on the mass flux with increasing time are presented in Figures 8, 9, and 10, respectively. These figures demonstrate that the mass flux changes its direction periodically which may be accredited to the pressure gradient being periodic in nature. Figure 8 depicts that an increase in Gr results in the mass flux to increase in the direction of the fluid flow and this may be attributed to the buoyancy force acting on the fluid. However, Figures 9 and 10 show a reverse trend in mass flux direction with an increase in Pr as well as Q. The observations in Figures 9 and 10 are consistent with those made in the case of Figures 2 and 3, respectively. All three figures lead us to conclude that the parameters Gr, Pr, and Q have significant contributions in regulating the amount of total discharge of fluid through the annulus and they may be adjusted conveniently to control the mass flux.

Figure 8

Mass flux versus time t for $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{Q = 5}$ , $\pmb{\alpha=0.01}$ , $\pmb{M = 0.4}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 9

Mass flux versus time t for $\pmb{\mathit{Gr} = 10}$ , $\pmb{Q = 5}$ , $\pmb{\alpha=0.01}$ , $\pmb{M = 0.4}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 10

Mass flux versus time t for $\pmb{\mathit{Gr} = 10}$ , $\pmb{\mathit{Pr} =0.025}$ , $\pmb{\alpha=0.01}$ , $\pmb{M = 0.4}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

The variations in skin friction with respect to the frequency parameter α under the influence of Gr, Pr and Q, in both the inner and the outer walls of the annulus are presented in Figures 11 to 16. From Figures 11 and 12 it may be concluded that for a particular frequency α and a fixed time, the friction at the inner and outer wall have a similar magnitude but acting in opposite directions (a similar observation is made in the case of Figures 13 and 14 as well as Figures 15 and 16, respectively); and as the buoyancy force gets magnified, the fluid velocity is uplifted, resulting in the friction at the walls also to increase substantially. On the other hand an opposite trend of behavior is evident in Figures 13 and 14 when Pr is increased and in the case of Figures 15 and 16 when Q is raised. This reverse trend may be linked to a decline of thermal transport in the fluid in both cases. This suggests that if one considers to reduce the friction at the walls, fluids with higher Prandtl numbers like water ($\mathit{Pr} = 7$) or various refrigerants (Pr between 4 and 5) need be used. We note that the effect of thermal radiation parameter is highly unpronounced on the friction at both walls of the annulus (Figure 15 and 16). This phenomenon is rooted in the fact that mercury is a good carrier of heat and dissipates very little energy in the form of thermal radiation. Fluids other than mercury will have different radiation properties and this needs further investigation in this connection.

Figure 11

Skin friction (inner wall) versus α for $\pmb{M = 0.4}$ , $\pmb{Q = 5}$ , $\pmb{\mathit{Pr} =0.025}$ , $\pmb{t = 2}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 12

Skin friction (outer wall) versus α for $\pmb{M = 0.4}$ , $\pmb{Q = 5}$ , $\pmb{\mathit{Pr} =0.025}$ , $\pmb{t = 2}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 13

Skin friction (inner wall) versus α for $\pmb{M = 0.4}$ , $\pmb{Q = 5}$ , $\pmb{\mathit{Gr} =10}$ , $\pmb{t = 2}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 14

Skin friction (outer wall) versus α for $\pmb{M = 0.4}$ , $\pmb{Q = 5}$ , $\pmb{\mathit{Gr} =10}$ , $\pmb{t = 2}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 15

Skin friction (inner wall) versus α for $\pmb{M = 0.4}$ , $\pmb{\mathit{Gr} =10}$ , $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{t = 2}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figure 16

Skin friction (outer wall) versus α for $\pmb{M = 0.4}$ , $\pmb{\mathit{Gr} =10}$ , $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{t = 2}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ , $\pmb{P_{0}= 1}$ .

Figures 17 to 22 illustrate how the rate of heat transfer from the walls to the fluid is influenced by Pr and α with an increase in radiation parameter Q. Figures 17 and 18 indicate that at a given time t, while the rate of heat transfer increases in one of the walls (say inner wall), a reverse behavior gets played on the other wall. This is attributed to the periodic nature of the wall temperature. From Figures 17 and 18 it is observed that as thermal diffusivity of the fluid gets reduced, increased rate of heat transfer from one of the walls is evident, provided that the thermal radiation is assumed to be constant. Figures 19 and 20 suggest that an enhancement of the frequency parameter leads to a comprehensive growth in the rate of heat transfer at the walls. This property is, in fact, dependent on the Prandtl number of the fluid. When air is used (Figures 21 and 22), a completely different behavior is marked for Nusselt number at the walls of the annulus. This motivates us to comment that the fluid must be carefully selected if different rates of heat transfer are desired at the inner and the outer walls of the annulus.

Figure 17

Nusselt number (inner wall) versus Q for $\pmb{t = 0.5}$ , $\pmb{\alpha= 0.01}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

Figure 18

Nusselt number (outer wall) versus Q for $\pmb{t = 0.5}$ , $\pmb{\alpha= 0.01}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

Figure 19

Nusselt number (inner wall) versus Q for $\pmb{t = 0.5}$ , $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

Figure 20

Nusselt number (outer wall) versus Q for $\pmb{t = 0.5}$ , $\pmb{\mathit{Pr} = 0.025}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

Figure 21

Nusselt number (inner wall) versus Q for $\pmb{t = 0.5}$ , $\pmb{\mathit{Pr} = 0.71}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

Figure 22

Nusselt number (outer wall) versus Q for $\pmb{t = 0.5}$ , $\pmb{\mathit{Pr} = 0.71}$ , $\pmb{\lambda= 2}$ , $\pmb{n_{1}= 1}$ , $\pmb{n_{2}= 2}$ .

8 Conclusions

The following are the significant outcomes of the preceding analysis:

• An increase in the Hartmann number M causes the fluid flow to be retarded.

• The flow gets decelerated and therefore mass flux gets reduced corresponding to a reduction in the thermal diffusivity of the fluid.

• Retardation in the fluid flow and a decrease in mass flux are observed with an increase in thermal radiation.

• The buoyancy force causes the fluid flow to accelerate, thereby causing the mass flux to increase proportionately.

• A reduction in fluid temperature is directly proportional to the diminution in thermal diffusivity.

• Fluid temperature can be reduced by increasing the frequency parameter associated with the fluid flow.

• Viscous drags at the inner and outer walls have identical magnitude but they act in opposite directions.

• Friction at the walls increases with an increase in thermal Grashof number, but it diminishes with an increase in Prandtl number and radiation parameter, respectively.

• The rate of heat transfer at either walls of the annulus with increasing frequency parameter depends on the Prandtl number of the fluid.