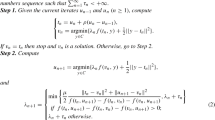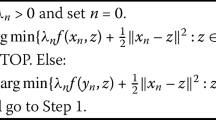Convergence analysis of a general inertial projection-type method for solving pseudomonotone equilibrium problems with applications

Abstract

In this paper, we introduce a new algorithm by incorporating an inertial term with a subgradient extragradient algorithm to solve the equilibrium problems involving a pseudomonotone and Lipschitz-type continuous bifunction in real Hilbert spaces. A weak convergence theorem is well established under certain mild conditions for the bifunction and the control parameters involved. Some of the applications to solve variational inequalities and fixed point problems are considered. Finally, several numerical experiments are performed to demonstrate the numerical efficacy and superiority of the proposed algorithm over other well-known existing algorithms.

1 Introduction

Let C be a closed and convex subset of a real Hilbert space $\mathbb{H}$. The inner product and the induced norm on $\mathbb{H}$ are denoted by $\langle \cdot , \cdot \rangle$ and $\|\cdot \|$, respectively. Assume that $f : \mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ is a bifunction with $f (y, y) = 0$ for all $y \in C$. The equilibrium problem (EP) for a bifunction f on C is defined in the following way [10, 17]:

$$ \text{Find } \xi ^{*} \in C \text{ such that } f\bigl( \xi ^{*}, y\bigr) \geq 0, \quad \forall y \in C. $$

(EP)

Moreover, $S_{\operatorname{EP}(f, C)}$ stands for the solution set of an equilibrium problem over the set C and $\xi ^{*}$ is an arbitrary element of $S_{\operatorname{EP}(f, C)}$. A bifunction $f : \mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ is said to be (see for more details [8, 10]):

• (1) strongly monotone on C if there exists $\gamma > 0$ such that

  $$ f(x_{1}, x_{2}) + f(x_{2}, x_{1}) \leq -\gamma \Vert x_{1} - x_{2} \Vert ^{2}, \quad \forall x_{1}, x_{2} \in C; $$

• (2) monotone on C if

  $$ f(x_{1}, x_{2}) + f(x_{2}, x_{1}) \leq 0,\quad \forall x_{1}, x_{2} \in C; $$

• (3) strongly pseudomonotone on C if there exists $\gamma > 0$ such that

  $$ f (x_{1}, x_{2}) \geq 0 \quad \Longrightarrow\quad f(x_{2}, x_{1}) \leq -\gamma \Vert x_{1} - x_{2} \Vert ^{2}, \quad \forall x_{1}, x_{2} \in C; $$

• (4) pseudomonotone on C if

  $$ f (x_{1}, x_{2}) \geq 0\quad \Longrightarrow\quad f(x_{2}, x_{1}) \leq 0, \quad \forall x_{1}, x_{2} \in C. $$

It is clear from the above definitions that the following implications hold:

$$ {(1)} \quad \Longrightarrow\quad {{(2)}}\quad \Longrightarrow \quad {{(4)}} \quad \text{and} \quad {(1)}\quad \Longrightarrow \quad {{(3)}}\quad \Longrightarrow\quad { {(4)}}. $$

In general, the reverse implications do not hold. A bifunction $f : \mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ is said to be Lipschitz-type continuous [28] on C if there exist two constants $c_{1}, c_{2} > 0$ such that

$$ f(x_{1}, x_{3}) \leq f(x_{1}, x_{2}) + f(x_{2}, x_{3}) + c_{1} \Vert x_{1} - x_{2} \Vert ^{2} + c_{2} \Vert x_{2} - x_{3} \Vert ^{2}, \quad \forall x_{1}, x_{2}, x_{3} \in C. $$

The above-defined problem (EP) is a general mathematical problem in the sense that it unifies a number of mathematical problems, i.e., the fixed point problems, the vector and scalar minimization problems, the variational inequality problems (VIP), the complementarity problems, the saddle point problems, the Nash equilibrium problems in non-cooperative games, and the inverse optimization problems [9, 10, 30]. The problem (EP) is also known as the well-known Ky Fan inequality [17]. Many authors have established and generalized several results on the existence and nature of the solution of an equilibrium problem (see for more details [5, 9, 17]).

A number of effective algorithmic schemes have been well established along their convergence analysis to solve the equilibrium problems in finite and in-finite dimensional spaces. The regularization method is one of the most important approaches to solving various ill-posed problems in different fields of pure and applied mathematics. A significant feature of the regularization methodology is that it has been applied to solve monotone equilibrium problems, and the original problem is transformed into strongly monotone sub-problems. Thus, each sub-problem is strongly monotone and guarantees the existence of a unique solution. In particular, the formalized sub-problem can be resolved more effectively than the original monotone problem, and the sequence of regularization solutions converges to one solution of the initial problem once the regularization variables appear to have an appropriate limit. The proximal point method and Tikhonov’s regularized method are two famous regularization approaches. Recently, these approaches have been extended in the case of equilibrium problems (see [20, 25, 29, 31] for more details) and others types on the method in [1–3, 13, 21–24, 34, 35, 39–41].

The proximal point method is used to solve the problem (EP) and is also known as the two-step extragradient method in [37] due to the previous contribution of Korpelevich [26] to solve the saddle point problems. Tran et al. [37] established a weakly convergent iterative sequence $\{x_{n}\}$ to solve the monotone equilibrium problem in a real Hilbert space. The method has the following form:

$$ \textstyle\begin{cases} x_{0} \in C, \\ y_{n} = \arg \min_{y \in C} \{ \lambda f(x_{n}, y) + \frac{1}{2} \Vert x_{n} - y \Vert ^{2} \}, \\ x_{n+1} = \arg \min _{y \in C} \{ \lambda f(y_{n}, y) + \frac{1}{2} \Vert x_{n} - y \Vert ^{2} \}, \end{cases} $$

(1)

where $0 < \lambda < \min \{\frac{1}{2 c_{1}}, \frac{1}{2 c_{2}} \}$. On the other hand, inertial-like methods are two-step iterative methods, and the next iteration is obtained from the previous two iterations (see [33] for more details). An inertial extrapolation term is used to enhance the iterative sequence performance in order to improve its rate of convergence. Numerical results suggest that inertial effects improve algorithmic efficiency during running time and the number of iterations. Recently, several inertial methods have been developed to solve different classes of equilibrium problems [14–16, 19, 38, 42].

In this paper, we first introduce a new inertial subgradient algorithm to solve a pseudomonotone equilibrium problem involving the Lipschitz-type condition in a real Hilbert space. This algorithm is designed around three methods: the extragradient method [37], the subgradient extragradient method [12], and the inertial method [33]. The weak convergence of the resulting algorithm is well established under mild conditions. Some of the applications to resolve variational inequalities and fixed point problems are considered. Numerical results are provided to show the computational effectiveness of our algorithm. Finally, the numerical evaluation demonstrates that the new method is more effective than the family of existing methods [19, 37, 38, 42].

The rest of the article has been arranged as follows: Sect. 2 includes some preliminary and basic results. Section 3 includes our proposed method and its convergence analysis. In Sect. 4 we present two mathematical applications of our proposed scheme, variational inequalities, and fixed points. Finally, in Sect. 5 we provide numerical examples with comparison with other related results in the literature in order to illustrate the validity and practical advantages of our method.

2 Preliminaries

The normal cone of C at $x \in C$ is defined by

$$ N_{C}(x) = \bigl\{ z \in \mathbb{H} : \langle z, y - x \rangle \leq 0, \forall y \in C \bigr\} . $$

Let $h : C \rightarrow \mathbb{R}$ be a convex function. The subdifferential of h at $x \in C$ is defined by

$$ \partial h(x) = \bigl\{ z \in \mathbb{H} : h(y) - h(x) \geq \langle z, y - x \rangle , \forall y \in C \bigr\} . $$

The metric projection $P_{C}(x)$ of $x \in \mathbb{H}$ onto a closed and convex subset C of $\mathbb{H}$ is defined by

$$ P_{C}(x) = \mathop{\arg \min }_{y \in C} \Vert y - x \Vert . $$

Lemma 2.1

([7])

For any $x, y \in \mathbb{H}$ and $\kappa \in \mathbb{R}$, the following relationship is true:

$$ \bigl\Vert \kappa x + (1 - \kappa ) y \bigr\Vert ^{2} = \kappa \Vert x \Vert ^{2} + (1 - \kappa ) \Vert y \Vert ^{2} - \kappa (1 - \kappa ) \Vert x - y \Vert ^{2}. $$

Lemma 2.2

([36])

Let $h: C \rightarrow \mathbb{R}$ be a subdifferentiable, convex, and lower semi-continuous function on C. An element $x \in C$ is said to be a minimizer of a function h iff

$$ 0 \in \partial h(x) + N_{C}(x). $$

Lemma 2.3

([6])

Let $\{\vartheta _{n}\}$, $\{\theta _{n}\}$, and $\{\gamma _{n}\}$ be nonnegative sequences that satisfy the following condition:

$$ \vartheta _{n+1} \leq \vartheta _{n} + \theta _{n} (\vartheta _{n} - \vartheta _{n-1}) + \gamma _{n},\quad \forall n \geq 1, $$

where $\sum_{n=1}^{+\infty } \gamma _{n} < +\infty$, and let $\theta >0$ be such that $0 \leq \theta _{n} \leq \theta < 1$ for each $n \in \mathbb{N}$. Then we have

• (i) $\sum_{n=1}^{+\infty } [\vartheta _{n} - \vartheta _{n-1}]_{+} < +\infty$ with $[a]_{+} := \max \{a, 0\}$ for any $a \in \mathbb{R}$;

• (ii) $\lim_{n \rightarrow +\infty } \vartheta _{n} = \vartheta ^{*} \in [0, \infty )$.

Lemma 2.4

([32])

Let $\{\eta _{n}\}$ be a sequence in $\mathbb{H}$ and $C \subset \mathbb{H}$ such that

• (i) for every $\eta \in C$, $\lim_{n\rightarrow \infty } \|\eta _{n} - \eta \|$ exists;

• (ii) each weak sequentially cluster point of the sequence $\{\eta _{n}\}$ belongs to C.

Then $\{\eta _{n}\}$ converges weakly to an element of C.

In order to study convergence analysis, we assume that $f: \mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ satisfies the following conditions:

• (A1) $f (y, y) = 0$ for all $y \in C$ and f is pseudomonotone on a feasible set C.

• (A2) f satisfies the Lipschitz-type condition on $\mathbb{H}$ with $c_{1}>0$ and $c_{2}>0$.

• (A3) $\limsup_{n\rightarrow \infty } f(x_{n}, y) \leq f(p^{*}, y)$ for all $y \in C$ and $\{x_{n}\} \subset C$ satisfy $x_{n} \rightharpoonup p^{*}$.

• (A4) $f (x,\cdot )$ is subdifferentiable and convex on $\mathbb{H}$ for every fixed $x \in \mathbb{H}$.

3 Main result

In this section, we introduce the main method and prove a weak convergence result. The main algorithm is in the following form:

Algorithm 1

(An inertial subgradient extragradient method for problem (EP))

Lemma 3.1

Let a bifunction $f : \mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ satisfy conditions (A1)–(A4). For each $\xi ^{*} \in S_{\operatorname{EP}(f, C)}$, we have

$$ \bigl\Vert z_{n} - \xi ^{*} \bigr\Vert ^{2} \leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - (1 - 2c_{1} \lambda ) \Vert \varrho _{n} - y_{n} \Vert ^{2} -(1 - 2c_{2} \lambda ) \Vert z_{n} - y_{n} \Vert ^{2}. $$

Proof

By using Lemma 2.2, we have

$$ 0 \in \partial _{2} \biggl(\lambda f(y_{n}, y) + \frac{1}{2} \Vert \varrho _{n} - y \Vert ^{2} \biggr) (z_{n}) + N_{H_{n}}(z_{n}). $$

Thus, there exist $\omega \in \partial f(y_{n}, z_{n})$ and $\overline{\omega } \in N_{H_{n}}(z_{n})$ such that

$$ \lambda \omega + z_{n} - \varrho _{n} + \overline{\omega } = 0. $$

Thus, the above implies that $\langle \varrho _{n} - z_{n}, y - z_{n} \rangle = \lambda \langle \omega , y - z_{n} \rangle + \langle \overline{\omega }, y - z_{n} \rangle$ for all $y \in H_{n}$. Since $\overline{\omega } \in N_{H_{n}}(z_{n})$, it follows that $\langle \overline{\omega }, y - z_{n} \rangle \leq 0$ for all $y \in H_{n}$. Thus, we have

$$ \lambda \langle \omega , y - z_{n} \rangle \geq \langle \varrho _{n} - z_{n}, y - z_{n} \rangle ,\quad \forall y \in H_{n}. $$

(4)

Since $\omega \in \partial f(y_{n}, z_{n})$ and by using the subdifferential definition, we have

$$ f(y_{n}, y) - f(y_{n}, z_{n}) \geq \langle \omega , y - z_{n} \rangle ,\quad \forall y \in \mathbb{H}. $$

(5)

Combining expressions (4) and (5), we obtain

$$ \lambda f(y_{n}, y) - \lambda f(y_{n}, z_{n}) \geq \langle \varrho _{n} - z_{n}, y - z_{n} \rangle , \quad \forall y \in H_{n}. $$

(6)

By substituting $y=\xi ^{*}$ in expression (6), we obtain

$$ \lambda f\bigl(y_{n}, \xi ^{*}\bigr) - \lambda f(y_{n}, z_{n}) \geq \bigl\langle \varrho _{n} - z_{n}, \xi ^{*} - z_{n} \bigr\rangle . $$

(7)

It is given that $\xi ^{*} \in S_{\operatorname{EP}(f, C)}$ implies that $f(\xi ^{*}, y_{n}) \geq 0$ and $f(y_{n}, \xi ^{*}) \leq 0$ due to the pseudomonotonicity of the bifunction f. From expression (7), we have

$$ \bigl\langle \varrho _{n} - z_{n}, z_{n} - \xi ^{*}\bigr\rangle \geq \lambda f(y_{n}, z_{n}). $$

(8)

Due to the Lipschitz-type continuity of a bifunction f, we have

$$ f(\varrho _{n}, z_{n}) \leq f (\varrho _{n}, y_{n}) + f(y_{n}, z_{n}) + c_{1} \Vert \varrho _{n} - y_{n} \Vert ^{2} + c_{2} \Vert y_{n} - z_{n} \Vert ^{2}. $$

(9)

Combining expressions (8) and (9), we have

$$ \bigl\langle \varrho _{n} - z_{n}, z_{n} - \xi ^{*} \bigr\rangle \geq \lambda \bigl\{ f(\varrho _{n}, z_{n}) - f (\varrho _{n}, y_{n}) \bigr\} - c_{1} \lambda \Vert \varrho _{n} - y_{n} \Vert ^{2} - c_{2} \lambda \Vert y_{n} - z_{n} \Vert ^{2}. $$

(10)

Since $z_{n} \in H_{n}$ and by the definition of $H_{n}$, we obtain

$$ \langle \varrho _{n} - \lambda t_{n} - y_{n}, z_{n} - y_{n} \rangle \leq 0, $$

which implies that

$$ \langle \varrho _{n} - y_{n}, z_{n} - y_{n} \rangle \leq \lambda \langle t_{n}, z_{n} - y_{n} \rangle . $$

(11)

Since $t_{n} \in \partial _{2} f(\varrho _{n}, y_{n})$, by using the subdifferential definition, we have

$$ f(\varrho _{n}, y) - f(\varrho _{n}, y_{n}) \geq \langle t_{n}, y - y_{n} \rangle , \quad \forall y \in \mathbb{H}. $$

By substituting $y = z_{n}$ in the above expression, we obtain

$$ f(\varrho _{n}, z_{n}) - f(\varrho _{n}, y_{n}) \geq \langle t_{n}, z_{n} - y_{n} \rangle . $$

(12)

It follows from inequalities (11) and (12) that

$$ \lambda \bigl\{ f(\varrho _{n}, z_{n}) - f(\varrho _{n}, y_{n}) \bigr\} \geq \langle \varrho _{n} - y_{n}, z_{n} - y_{n} \rangle . $$

(13)

From (10) and (13), we have

$$ \bigl\langle \varrho _{n} - z_{n}, z_{n} - \xi ^{*} \bigr\rangle \geq \langle \varrho _{n} - y_{n}, z_{n} - y_{n} \rangle - c_{1} \lambda \Vert \varrho _{n} - y_{n} \Vert ^{2} - c_{2} \lambda \Vert y_{n} - z_{n} \Vert ^{2}. $$

(14)

We have the following equalities:

$$ 2 \bigl\langle \varrho _{n} - z_{n}, z_{n} - \xi ^{*}\bigr\rangle = \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \Vert z_{n} - \varrho _{n} \Vert ^{2} - \bigl\Vert z_{n} - \xi ^{*} \bigr\Vert ^{2} $$

and

$$ 2 \langle y_{n} - \varrho _{n}, y_{n} - z_{n} \rangle = \Vert \varrho _{n} - y_{n} \Vert ^{2} + \Vert z_{n} - y_{n} \Vert ^{2} - \Vert \varrho _{n} - z_{n} \Vert ^{2}. $$

The above facts and (14) complete the proof. □

Now, we are in a position to prove our weak convergence theorem.

Theorem 3.2

The sequences $\{\varrho _{n}\}$, $\{x_{n}\}$, $\{y_{n}\}$, and $\{z_{n}\}$ generated by Algorithm 1 are weakly convergent to an element $\xi ^{*} \in S_{\operatorname{EP}(f, C)}$.

Proof

From the value of $x_{n+1}$ and Lemma 2.1, we have

$$\begin{aligned} \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} &= \bigl\Vert (1- \beta _{n}) \varrho _{n} + \beta _{n} z_{n} - \xi ^{*} \bigr\Vert ^{2} \\ &= \bigl\Vert (1- \beta _{n}) \bigl(\varrho _{n} - \xi ^{*}\bigr) + \beta _{n} \bigl(z_{n} - \xi ^{*}\bigr) \bigr\Vert ^{2} \\ &= (1- \beta _{n}) \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} + \beta _{n} \bigl\Vert z_{n} - \xi ^{*} \bigr\Vert ^{2} - \beta _{n}(1 - \beta _{n}) \Vert \varrho _{n} - z_{n} \Vert ^{2} \\ &\leq (1- \beta _{n}) \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} + \beta _{n} \bigl\Vert z_{n} - \xi ^{*} \bigr\Vert ^{2}. \end{aligned}$$

(15)

By using Lemma 3.1, we have

$$ \bigl\Vert z_{n} - \xi ^{*} \bigr\Vert ^{2} \leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - (1 - 2c_{1} \lambda ) \Vert \varrho _{n} - y_{n} \Vert ^{2} -(1 - 2c_{2} \lambda ) \Vert z_{n} - y_{n} \Vert ^{2}. $$

(16)

Combining expressions (15) and (16), we obtain

$$\begin{aligned} \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} &\leq (1- \beta _{n}) \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} + \beta _{n} \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} \\ &\quad {} - \beta _{n}(1 - 2c_{1}\lambda ) \Vert \varrho _{n} - y_{n} \Vert ^{2} - \beta _{n}(1 - 2c_{2} \lambda ) \Vert z_{n} - y_{n} \Vert ^{2} \\ &\leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \beta _{n} (1 - b\lambda ) \bigl[ \Vert \varrho _{n} - y_{n} \Vert ^{2} + \Vert z_{n} - y_{n} \Vert ^{2} \bigr] \\ &= \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \frac{\beta _{n} (1 - b\lambda )}{2} \bigl[ 2 \Vert \varrho _{n} - y_{n} \Vert ^{2} + 2 \Vert z_{n} - y_{n} \Vert ^{2} \bigr] \\ &\leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \frac{\beta _{n} (1 - b\lambda )}{2} \bigl[ \Vert \varrho _{n} - y_{n} \Vert + \Vert z_{n} - y_{n} \Vert \bigr]^{2} \\ &\leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \frac{\beta _{n} (1 - b\lambda )}{2} \Vert z_{n} - \varrho _{n} \Vert ^{2}, \end{aligned}$$

(17)

where $b=\max \{2c_{1}, 2c_{2}\}$. From the value of $x_{n+1}$, we have

$$ \Vert x_{n+1} - \varrho _{n} \Vert = \bigl\Vert (1- \beta _{n}) \varrho _{n} + \beta _{n} z_{n} - \varrho _{n} \bigr\Vert = \bigl\Vert \beta _{n} (z_{n} - \varrho _{n}) \bigr\Vert . $$

(18)

Combining (17) and (18), we have

$$ \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} \leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \frac{(1 - b\lambda )}{2 \beta _{n}} \Vert x_{n+1} - \varrho _{n} \Vert ^{2}. $$

(19)

Due to the condition on λ, we infer that $\frac{1-b\lambda }{2} \geq \frac{1}{6}$, and expression (19) is converted into

$$ \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} \leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \frac{1}{6 \beta _{n}} \Vert x_{n+1} - \varrho _{n} \Vert ^{2}. $$

(20)

By taking the value of $\varrho _{n}$, we have

$$\begin{aligned} \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} &= \bigl\Vert x_{n} + \vartheta _{n}(x_{n} - x_{n-1}) - \xi ^{*} \bigr\Vert ^{2} \\ &= \bigl\Vert (1 + \vartheta _{n}) \bigl(x_{n} - \xi ^{*}\bigr) - \vartheta _{n}\bigl(x_{n-1} - \xi ^{*}\bigr) \bigr\Vert ^{2} \\ &= (1 + \vartheta _{n}) \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} + \vartheta _{n}(1 + \vartheta _{n}) \Vert x_{n} - x_{n-1} \Vert ^{2}. \end{aligned}$$

(21)

By taking the value of $\varrho _{n}$, we have

$$\begin{aligned} \Vert x_{n+1} - \varrho _{n} \Vert ^{2} &= \bigl\Vert x_{n+1} - x_{n} - \vartheta _{n}(x_{n} - x_{n-1}) \bigr\Vert ^{2} \\ &= \Vert x_{n+1} - x_{n} \Vert ^{2} + \vartheta _{n}^{2} \Vert x_{n} - x_{n-1} \Vert ^{2} + 2 \vartheta _{n} \langle x_{n} - x_{n+1}, x_{n} - x_{n-1} \rangle \end{aligned}$$

(22)

$$\begin{aligned} &\geq \Vert x_{n+1} - x_{n} \Vert ^{2} + \vartheta _{n}^{2} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\quad {} - \rho _{n}\vartheta _{n} \Vert x_{n+1} - x_{n} \Vert ^{2} - \frac{\vartheta _{n}}{\rho _{n}} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\geq (1 - \rho _{n}\vartheta _{n}) \Vert x_{n+1} - x_{n} \Vert ^{2} + \biggl( \vartheta _{n}^{2} - \frac{\vartheta _{n}}{\rho _{n}} \biggr) \Vert x_{n} - x_{n-1} \Vert ^{2}, \end{aligned}$$

(23)

where $\rho _{n}=\frac{1}{\delta \beta _{n}+\vartheta _{n}}$. It follows from (20), (21), and (23) that

$$\begin{aligned} & \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} \\ &\quad \leq (1 + \vartheta _{n}) \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} + \vartheta _{n}(1 + \vartheta _{n}) \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\qquad {} - \frac{1}{6 \beta _{n}} \biggl[(1 - \rho _{n}\vartheta _{n}) \Vert x_{n+1} - x_{n} \Vert ^{2} + \biggl( \vartheta _{n}^{2} - \frac{\vartheta _{n}}{\rho _{n}} \biggr) \Vert x_{n} - x_{n-1} \Vert ^{2} \biggr] \end{aligned}$$

(24)

$$\begin{aligned} &\quad = (1 + \vartheta _{n}) \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} - \frac{1}{6 \beta _{n}} (1 - \rho _{n}\vartheta _{n}) \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\qquad {} + \biggl[\vartheta _{n}(1 + \vartheta _{n}) - \frac{1}{6 \beta _{n}} \biggl( \vartheta _{n}^{2} - \frac{\vartheta _{n}}{\rho _{n}} \biggr) \biggr] \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\quad = (1 + \vartheta _{n}) \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} - \frac{1}{6 \beta _{n}} (1 - \rho _{n}\vartheta _{n}) \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\qquad {} + \gamma _{n} \Vert x_{n} - x_{n-1} \Vert ^{2}, \end{aligned}$$

(25)

where

$$ \gamma _{n} = \vartheta _{n}(1 + \vartheta _{n}) - \frac{1}{6 \beta _{n}} \biggl( \vartheta _{n}^{2} - \frac{\vartheta _{n}}{\rho _{n}} \biggr) = \vartheta _{n}(1 + \vartheta _{n}) + \frac{1}{6 \beta _{n}} \biggl( \frac{\vartheta _{n}}{\rho _{n}} - \vartheta _{n}^{2} \biggr) > 0. $$

(26)

By taking the value $\{\rho _{n}\}$, we have

$$ \gamma _{n} = \vartheta _{n}(1 + \vartheta _{n}) + \frac{1}{6 \beta _{n}} \biggl(\frac{\vartheta _{n}}{\rho _{n}} - \vartheta _{n}^{2} \biggr) \leq \vartheta (1 + \vartheta ) + \frac{1}{6} \vartheta \delta . $$

(27)

Set $\Psi _{n} = \|x_{n} - \xi ^{*} \|^{2} - \vartheta _{n} \|x_{n-1} - \xi ^{*}\|^{2} + \gamma _{n} \|x_{n} - x_{n-1}\|^{2}$. By using (25), we have

$$\begin{aligned} \Psi _{n+1} - \Psi _{n} &= \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n+1} \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} + \gamma _{n+1} \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\quad {} - \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} + \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} - \gamma _{n} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\leq \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} - (1 + \vartheta _{n}) \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} + \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} \\ &\quad {} + \gamma _{n+1} \Vert x_{n+1} - x_{n} \Vert ^{2} - \gamma _{n} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\leq - \biggl( \frac{1}{6 \beta _{n}} (1 - \rho _{n}\vartheta _{n}) - \gamma _{n+1} \biggr) \Vert x_{n+1} - x_{n} \Vert ^{2}. \end{aligned}$$

(28)

Observe that

$$\begin{aligned} \frac{1}{6 \beta _{n}} (1 - \rho _{n}\vartheta _{n}) - \gamma _{n+1} \geq \sigma &\quad \Longleftrightarrow\quad (1 - \rho _{n}\vartheta _{n}) - 6 \beta _{n} \gamma _{n+1} \geq 6 \beta _{n} \sigma \\ &\quad \Longleftrightarrow\quad (1 - \rho _{n}\vartheta _{n}) - 6 \beta _{n} ( \gamma _{n+1} + \sigma ) \geq 0 \\ &\quad \Longleftrightarrow\quad \frac{\delta \beta _{n}}{\delta \beta _{n} + \vartheta _{n}} - 6 \beta _{n} (\gamma _{n+1} + \sigma ) \geq 0 \\ &\quad \Longleftrightarrow\quad - 6 (\gamma _{n+1} + \sigma ) (\delta \beta _{n} + \vartheta _{n}) \geq - \delta . \end{aligned}$$

(29)

From expressions (2), (3), and (27), we have

$$ - 6 (\gamma _{n+1} + \sigma ) (\delta \beta _{n} + \vartheta _{n}) \geq - 6 \biggl[ \vartheta (1 + \vartheta ) + \frac{1}{6} \vartheta \delta + \sigma \biggr] (\delta \beta _{n} + \vartheta _{n}) \geq - \delta . $$

(30)

It follows that

$$ \Psi _{n+1} - \Psi _{n} \leq -\sigma \Vert x_{n+1} - x_{n} \Vert ^{2} \leq 0. $$

(31)

The above implies that the sequence $\{\Psi _{n}\}$ is nonincreasing. From $\Psi _{n+1}$ we have

$$ \begin{aligned}[b] \Psi _{n+1} &= \bigl\Vert x_{n+1} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n+1} \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} + \gamma _{n+1} \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\geq - \vartheta _{n+1} \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2}. \end{aligned} $$

(32)

From the value of $\Psi _{n}$, we have

$$ \begin{aligned}[b] \Psi _{n} &= \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} + \gamma _{n} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\geq \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} - \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2}. \end{aligned} $$

(33)

From expression (33), we obtain

$$\begin{aligned} \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} &\leq \Psi _{n} + \vartheta _{n} \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} \\ &\leq \Psi _{1} + \vartheta \bigl\Vert x_{n-1} - \xi ^{*} \bigr\Vert ^{2} \\ &\leq \cdots \\ & \leq \Psi _{1}\bigl(\vartheta ^{n-1} + \cdots + 1\bigr) + \vartheta ^{n} \bigl\Vert x_{0} - \xi ^{*} \bigr\Vert ^{2} \\ &\leq \frac{\Psi _{1}}{1 - \vartheta } + \vartheta ^{n} \bigl\Vert x_{0} - \xi ^{*} \bigr\Vert ^{2}. \end{aligned}$$

(34)

Combining expressions (33) and (34), we obtain

$$ - \Psi _{n+1} \leq \vartheta _{n+1} \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} \leq \vartheta \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} \leq \vartheta \frac{\Psi _{1}}{1 - \vartheta } + \vartheta ^{n+1} \bigl\Vert x_{0} - \xi ^{*} \bigr\Vert ^{2}. $$

(35)

Following inequalities (31) and (35), we can write

$$\begin{aligned} \sigma \sum_{n=1}^{k} \Vert x_{n+1} - x_{n} \Vert ^{2} &\leq \Psi _{1} - \Psi _{k+1} \\ &\leq \Psi _{1} + \vartheta \frac{\Psi _{1}}{1 - \vartheta } + \vartheta ^{k+1} \bigl\Vert x_{0} - \xi ^{*} \bigr\Vert ^{2} \\ &\leq \frac{\Psi _{1}}{1 - \vartheta } + \bigl\Vert x_{0} - \xi ^{*} \bigr\Vert ^{2}. \end{aligned}$$

(36)

By letting $k \rightarrow +\infty$ in (36), we get

$$ \sum_{n=1}^{+\infty } \Vert x_{n+1} - x_{n} \Vert ^{2} < +\infty , $$

(37)

which implies that

$$ \lim_{n \rightarrow \infty } \Vert x_{n+1} - x_{n} \Vert = 0. $$

(38)

By (22) and (38), we obtain

$$ \lim_{n \rightarrow \infty } \Vert x_{n+1} - \varrho _{n} \Vert = 0. $$

(39)

From the value of $x_{n+1}$, we have

$$ \Vert x_{n+1} - \varrho _{n} \Vert = \bigl\Vert (1- \beta _{n}) \varrho _{n} + \beta _{n} z_{n} - \varrho _{n} \bigr\Vert = \beta _{n} \Vert z_{n} - \varrho _{n} \Vert , $$

(40)

and from (39) and (40), we have

$$ \lim_{n \rightarrow \infty } \Vert z_{n} - \varrho _{n} \Vert = 0. $$

(41)

By using the triangular inequality with expressions (38) and (39), we obtain

$$ \lim_{n \rightarrow \infty } \Vert x_{n} - \varrho _{n} \Vert \leq \lim_{n \rightarrow \infty } \Vert x_{n} - x_{n+1} \Vert + \lim_{n \rightarrow \infty } \Vert x_{n+1} - \varrho _{n} \Vert = 0 $$

(42)

and

$$ \lim_{n \rightarrow \infty } \Vert x_{n} - z_{n} \Vert \leq \lim_{n \rightarrow \infty } \Vert x_{n} - \varrho _{n} \Vert + \lim_{n \rightarrow \infty } \Vert \varrho _{n} - z_{n} \Vert = 0. $$

(43)

From (24), (37), and Lemma 2.3, it follows that

$$ \lim_{n \rightarrow \infty } \bigl\Vert x_{n} - \xi ^{*} \bigr\Vert ^{2} = l \quad \text{for some } l \geq 0. $$

(44)

From expressions (42) and (43), we have

$$ \lim_{n \rightarrow \infty } \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} = \bigl\Vert z_{n} - \xi ^{*} \bigr\Vert ^{2} = l. $$

(45)

Thus, Lemma 3.1 implies that

$$ (1 - 2c_{1} \lambda ) \Vert \varrho _{n} - y_{n} \Vert ^{2} \leq \bigl\Vert \varrho _{n} - \xi ^{*} \bigr\Vert ^{2} - \bigl\Vert z_{n} - \xi ^{*} \bigr\Vert ^{2}, $$

(46)

with expressions (44) and (45), we have

$$ \lim_{n \rightarrow \infty } \Vert \varrho _{n} - y_{n} \Vert = 0, \qquad \lim_{n \rightarrow \infty } \bigl\Vert y_{n} - \xi ^{*} \bigr\Vert ^{2} = l. $$

(47)

The above implies that the sequences $\{x_{n}\}$, $\{\varrho _{n}\}$, $\{y_{n}\}$, and $\{z_{n}\}$ are bounded, and for each $\xi ^{*} \in S_{\operatorname{EP}(f, C)}$, $\lim_{n\rightarrow \infty } \|x_{n} - \xi ^{*}\|^{2}$ exists. Next, our aim is to prove that the solution set $S_{\operatorname{EP}(f, C)}$ contains all sequential weak cluster points of the sequence $\{x_{n}\}$. Let z be an arbitrary weak cluster point of the sequence $\{x_{n}\}$. Then there exists a subsequence $\{x_{n_{k}}\}$ of $\{x_{n}\}$ such that $\{x_{n_{k}}\}$ weakly converges to z. It follows from (42) and (43) that the subsequences $\{y_{n_{k}}\}$ and $\{z_{n_{k}}\}$ are weakly convergent to $z \in C$. Next, we show that $z \in S_{\operatorname{EP}(f, C)}$. Due to inequality (6), the Lipschitz-type continuity of f and (13), we obtain

$$\begin{aligned} \lambda f(y_{n_{k}}, y) &\geq \lambda f(y_{n_{k}}, z_{n_{k}}) + \langle \varrho _{n_{k}} - z_{n_{k}}, y - z_{n_{k}} \rangle \\ &\geq \lambda f(\varrho _{n_{k}}, z_{n_{k}}) - \lambda f( \varrho _{n_{k}}, y_{n_{k}}) - c_{1}\lambda \Vert \varrho _{n_{k}} - y_{n_{k}} \Vert ^{2} \\ &\quad {} - c_{2} \lambda \Vert y_{n_{k}} - z_{n_{k}} \Vert ^{2} + \langle \varrho _{n_{k}} - z_{n_{k}}, y - z_{n_{k}} \rangle \\ &\geq \langle \varrho _{n_{k}} - y_{n_{k}}, z_{n_{k}} - y_{n_{k}} \rangle - c_{1}\lambda \Vert \varrho _{n_{k}} - y_{n_{k}} \Vert ^{2} \\ &\quad {} - c_{2} \lambda \Vert y_{n_{k}} - z_{n_{k}} \Vert ^{2} + \langle \varrho _{n_{k}} - z_{n_{k}}, y - z_{n_{k}} \rangle , \end{aligned}$$

(48)

where y is an arbitrary element in $H_{n}$. It follows from (41), (42), (43), and the boundedness of $\{x_{n}\}$ that the right-hand side goes to zero. From $\lambda > 0$, condition (A3), and $y_{n_{k}} \rightharpoonup z$, we have

$$ 0 \leq \limsup_{k \rightarrow \infty } f(y_{n_{k}}, y) \leq f(z, y), \quad \forall y \in H_{n}. $$

(49)

The above implies that $f(z, y) \geq 0$ for all $y \in C$, and hence $z \in S_{\operatorname{EP}(f, C)}$. This completes the proof. □

Setting $\vartheta _{n}=0$ in Algorithm 1, we have the following variant of Anh et al. [4].

Corollary 3.3

Let $f : \mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ be a bifunction satisfying conditions (A1)–(A4). Then $\{y_{n}\}$, $\{z_{n}\}$, and $\{x_{n}\}$ are the sequences generated in the following manner:

• Initialization: Let $x_{0} \in \mathbb{H}$ arbitrarily and choose $0 < \lambda < \min \{\frac{1}{2c_{1}}, \frac{1}{2c_{2}} \}$, and $\{\beta _{n}\}$ is a control parameter.

• Step 1: Compute $y_{n} = \arg \min _{y \in C} \{ \lambda f(x_{n}, y) + \frac{1}{2} \|x_{n} - y\|^{2} \}$. If $y_{n} = x_{n}$, then stop and $x_{n}$ is the solution of the problem (EP). Otherwise go to the next step.

• Step 2: Next, construct a half-space $H_{n} = \{z \in \mathbb{H} : \langle x_{n} - \lambda t_{n} - y_{n}, z - y_{n} \rangle \leq 0 \}$, where $t_{n} \in \partial _{2} f(x_{n}, y_{n})$, and then compute $z_{n} = \arg \min _{y \in H_{n}} \{ \lambda f(y_{n}, y) + \frac{1}{2} \|x_{n} - y\|^{2} \}$.

• Step 3: Evaluate $x_{n+1} = (1- \beta _{n}) x_{n} + \beta _{n} z_{n}$, where $\{\beta _{n}\}$ is a real sequence and there exist $\beta , \delta , \sigma > 0$ such that $0 < \beta \leq \beta _{n} \leq \frac{1}{6 \sigma }$. Then the sequences $\{x_{n}\}$, $\{y_{n}\}$, and $\{z_{n}\}$ are weakly convergent to $\xi ^{*} \in S_{\operatorname{EP}(f, C)}$.

4 Applications

4.1 Variational inequalities

In this subsection we apply our results for solving variational inequality problems involving a pseudomonotone and Lipschitz-type continuous operator. Let us recall that an operator $G : \mathbb{H} \rightarrow \mathbb{H}$ is said to be

• (1) monotone on C if

  $$ \bigl\langle G(x) - G(y), x - y \bigr\rangle \geq 0,\quad \forall x, y \in C; $$

• (2) L-Lipschitz continuous on C if

  $$ \bigl\Vert G(x) - G(y) \bigr\Vert \leq L \Vert x - y \Vert ,\quad \forall x, y \in C; $$

• (3) pseudomonotone on C if

  $$ \bigl\langle G(x), y - x \bigr\rangle \geq 0 \quad \Longrightarrow \quad \bigl\langle G(y), x - y \bigr\rangle \leq 0, \quad \forall x, y \in C. $$

The variational inequality problem is defined as follows:

$$ \text{Find } \xi ^{*} \in C \text{ such that } \bigl\langle G\bigl(\xi ^{*}\bigr), y - \xi ^{*} \bigr\rangle \geq 0 \quad \text{for all } y \in C. $$

(VIP)

If we define $f(x, y) := \langle G(x), y - x \rangle$ for all $x, y \in C$, then the equilibrium problem becomes the problem of variational inequality described above where $L = 2c_{1} = 2 c_{2}$. From the above value of the bifunction f, we have

$$\begin{aligned} y_{n} &= \mathop{\arg \min }_{y \in C} \biggl\{ \lambda f(\varrho _{n}, y) + \frac{1}{2} \Vert \varrho _{n} - y \Vert ^{2} \biggr\} \\ &= \mathop{\arg \min }_{y \in C} \biggl\{ \lambda \bigl\langle G(\varrho _{n}), y - \varrho _{n} \bigr\rangle + \frac{1}{2} \Vert \varrho _{n} - y \Vert ^{2} + \frac{\lambda ^{2}}{2} \bigl\Vert G(\varrho _{n}) \bigr\Vert ^{2} - \frac{\lambda ^{2}}{2} \bigl\Vert G(\varrho _{n}) \bigr\Vert ^{2} \biggr\} \\ &= P_{C}\bigl(\varrho _{n} - \lambda G(\varrho _{n})\bigr). \end{aligned}$$

(50)

The value $z_{n}$ in Algorithm 1 is converted into

$$ z_{n} = P_{H_{n}}\bigl(\varrho _{n} - \lambda G(y_{n})\bigr). $$

Since $t_{n} \in \partial _{2} f(\varrho _{n}, y_{n})$ and by the subdifferential definition, we obtain

$$\begin{aligned} \langle t_{n}, z - y_{n} \rangle &\leq \bigl\langle G( \varrho _{n}), z - \varrho _{n} \bigr\rangle - \bigl\langle G(\varrho _{n}), y_{n} - \varrho _{n} \bigr\rangle \\ &= \bigl\langle G(\varrho _{n}), z - y_{n} \bigr\rangle ,\quad \forall z \in \mathbb{H}, \end{aligned}$$

(51)

which further implies that $0 \leq \langle G(\varrho _{n}) - t_{n}, z - y_{n} \rangle$ for all $z \in \mathbb{H}$. Thus

$$\begin{aligned} & \bigl\langle \varrho _{n} - \lambda G(\varrho _{n}) - y_{n}, z - y_{n} \bigr\rangle \\ &\quad \leq \bigl\langle \varrho _{n} - \lambda G(\varrho _{n}) - y_{n}, z - y_{n} \bigr\rangle + \lambda \bigl\langle G(\varrho _{n}) - t_{n}, z - y_{n} \bigr\rangle \\ &\quad = \langle \varrho _{n} - \lambda t_{n} - y_{n}, z - y_{n} \rangle . \end{aligned}$$

(52)

Suppose that G satisfies the following conditions:

• (G1) G is pseudomonotone on C and a solution set $\operatorname{VI}(G, C) \neq \emptyset$;

• (G2) G is L-Lipschitz continuous on C through a positive constant $L > 0$;

• (G3) $\limsup_{n\rightarrow \infty } \langle G(x_{n}), y-x_{n} \rangle \leq \langle G(p^{*}), y-p^{*} \rangle$ for all $y \in C$, where $\{x_{n}\} \subset C$ satisfies $x_{n} \rightharpoonup p^{*}$.

As a consequence of the results in Sect. 3, we have the following results.

Corollary 4.1

Let $G : C \rightarrow \mathbb{H}$ be a mapping satisfying conditions (G1)–(G3). Let $\{\varrho _{n}\}$, $\{y_{n}\}$, $\{z_{n}\}$, and $\{x_{n}\}$ be the sequences generated in the following way:

• Initialization: Let $x_{-1}, x_{0} \in \mathbb{H}$, $0 < \lambda < \frac{1}{L}$, $\{\vartheta _{n}\}$ and $\{\beta _{n}\}$ are control parameters.

• Step 1: Compute $y_{n} = P_{C} (\varrho _{n} - \lambda G(\varrho _{n}))$, where $\varrho _{n} = x_{n} + \vartheta _{n}(x_{n} - x_{n-1})$. If $y_{n} = \varrho _{n}$, then $\varrho _{n}$ is a solution of the problem (VIP).

• Step 2: Construct a half-space $H_{n} = \{z \in \mathbb{H} : \langle \varrho _{n} - \lambda G ( \varrho _{n}) - y_{n}, z - y_{n} \rangle \leq 0 \}$ and compute $z_{n} = P_{H_{n}} (\varrho _{n} - \lambda G(y_{n}))$.

• Step 3: Compute $x_{n+1} = (1- \beta _{n}) \varrho _{n} + \beta _{n} z_{n}$, where $\{\vartheta _{n}\}$ and $\{\beta _{n}\}$ are real sequences. Here, we assume that the sequence $\{\vartheta _{n}\}$ is nondecreasing with $0 \leq \vartheta _{n} \leq \vartheta < 1$ for each $n \geq 1$ and that there exist $\beta , \delta , \sigma > 0$ such that

  $$ \delta > \frac{6 \vartheta [ \vartheta (1+\vartheta ) + \sigma ]}{1 - \vartheta ^{2}} $$

  (53)

  and

  $$ 0 < \beta \leq \beta _{n} \leq \frac{\delta - 6 \vartheta [ \vartheta (1+\vartheta ) + \sigma + \frac{1}{6} \vartheta \delta ]}{6 \delta [ \vartheta (1+\vartheta ) + \sigma + \frac{1}{6} \vartheta \delta ]}. $$

  (54)

Then the sequences $\{\varrho _{n}\}$, $\{y_{n}\}$, $\{z_{n}\}$, and $\{x_{n}\}$ converge weakly to $\xi ^{*} \in \operatorname{VI}(G, C)$.

Corollary 4.2

Let $G : C \rightarrow \mathbb{H}$ be a mapping satisfying conditions (G1)–(G3). Then $\{x_{n}\}$ is the sequence generated in the following manner:

• Initialization: Choose $x_{0} \in \mathbb{H}$, $0 < \lambda < \frac{1}{L}$, and $\{\beta _{n}\}$ is a control parameter.

• Step 1: Compute $y_{n} = P_{C} (x_{n} - \lambda G(x_{n}))$. If $y_{n} = x_{n}$, then $x_{n}$ is the solution of the problem.

• Step 2: Next, construct a half-space $H_{n} = \{z \in \mathbb{H} : \langle x_{n} - \lambda G (x_{n}) - y_{n}, z - y_{n} \rangle \leq 0 \}$ and compute $z_{n} = P_{H_{n}} (x_{n} - \lambda G(y_{n}))$.

• Step 3: Evaluate $x_{n+1} = (1- \beta _{n}) x_{n} + \beta _{n} z_{n}$, where $\{\beta _{n}\}$ is a real sequence and there are $\beta , \delta , \sigma > 0$ such that $0 < \beta \leq \beta _{n} \leq \frac{1}{6 \sigma }$. Then the sequences $\{y_{n}\}$, $\{z_{n}\}$, and $\{x_{n}\}$ converge weakly to $\xi ^{*} \in \operatorname{VI}(G, C)$.

Note that condition (G3) could be deleted when G is monotone. Indeed, this condition, which is a particular case of condition (A3), is only used to prove (49). Without condition (G3), inequality (49) can be obtained by imposing the monotonicity of G. In that case, we can write

$$ \bigl\langle G(y), y - y_{n} \bigr\rangle \geq \bigl\langle G(y_{n}), y - y_{n} \bigr\rangle , \quad \forall y \in C. $$

(55)

By the use of $f(x, y) = \langle G(x), y-x \rangle$ in (48), we have

$$ \limsup_{k \rightarrow \infty } \bigl\langle G(y_{n_{k}}), y - y_{n_{k}} \bigr\rangle \geq 0,\quad \forall y \in H_{n}. $$

(56)

Combining (55) and (56), we obtain

$$ \limsup_{k \rightarrow \infty } \bigl\langle G(y), y - y_{n_{k}} \bigr\rangle \geq 0, \quad \forall y \in C. $$

(57)

Let $y_{t} = (1 - t)z + ty$ for all $t \in [0, 1]$. Due to the convexity of the set C, $y_{t} \in C$ for every $t \in (0, 1)$. Since $y_{n_{k}} \rightharpoonup z \in C$ and $\langle G(y), y - z \rangle \geq 0$ for every $y \in C$, we have

$$ 0 \leq \bigl\langle G(y_{t}), y_{t} - z \bigr\rangle = t \bigl\langle G(y_{t}), y - z \bigr\rangle . $$

(58)

Thus, $\langle G(y_{t}), y - z \rangle \geq 0$ for all $t\in (0, 1)$. Since $y_{t} \rightarrow z$ as $t \rightarrow 0$ and due to the continuity of G, we have $\langle G(z), y - z \rangle \geq 0$ for all $y \in C$, which gives that $z \in \operatorname{VI}(G, C)$.

Remark 4.1

From the above discussion, it can be concluded that Corollary 4.1 and Corollary 4.2 still hold, even if we remove condition (G3) in the case of monotone bifunctions.

4.2 Fixed points

Following Sect. 3, we show how our results can be applied for solving fixed point problems involving a κ-strict pseudocontraction mapping. Let us recall that a mapping $T : C \rightarrow C$ is said to be

• (i) κ-strict pseudocontraction [11] on C if

  $$ \Vert Tx - Ty \Vert ^{2} \leq \Vert x - y \Vert ^{2} + \kappa \bigl\Vert (x - Tx) - (y - Ty) \bigr\Vert ^{2}, \quad \forall x, y \in C, $$

  that is equivalent to

  $$ \langle Tx - Ty, x - y \rangle \leq \Vert x - y \Vert ^{2} - \frac{1- \kappa }{2} \bigl\Vert (x - Tx) - (y - Ty) \bigr\Vert ^{2}, \quad \forall x, y \in C; $$

• (ii) sequentially weakly continuous on C if

  $$ T(x_{n}) \rightharpoonup T\bigl(x^{*}\bigr) \quad \text{for any sequence in } C \text{ satisfying } x_{n} \rightharpoonup x^{*}\ ( \text{weakly converges}). $$

If we consider that the mapping T is a κ-strict pseudocontraction and weakly continuous, then $f(x, y) = \langle x - Tx, y - x \rangle$ satisfies conditions (A1)–(A4) (see [43] for details) and $2 c_{1} = 2 c_{2} = \frac{3 - 2 \kappa }{1 - \kappa }$. The values of $y_{n}$ and $z_{n}$ turn into the following:

$$ \textstyle\begin{cases} y_{n} = \arg \min _{y \in C} \{ \lambda f(\varrho _{n}, y) + \frac{1}{2} \Vert \varrho _{n} - y \Vert ^{2} \} = P_{C} [ \varrho _{n} - \lambda (\varrho _{n} - T (\varrho _{n})) ], \\ z_{n} = \arg \min _{y \in H_{n}} \{ \lambda f(y_{n}, y) + \frac{1}{2} \Vert \varrho _{n} - y \Vert ^{2} \} = P_{H_{n}} [ \varrho _{n} - \lambda (y_{n} - T (y_{n})) ]. \end{cases} $$

(59)

As a consequence of the results in Sect. 3, we have the following results.

Corollary 4.3

Let C be a nonempty, convex, and closed subset of a Hilbert space $\mathbb{H}$, and $T : C \rightarrow C$ be a κ-strict pseudocontraction and weakly continuous with a solution set $\operatorname{Fix}(T) \neq \emptyset$. Let $\{x_{n}\}$ be the sequence generated in the following way:

• Initialization: Let $x_{-1}, x_{0} \in \mathbb{H}$, $0 < \lambda < \frac{1 - \kappa }{3 - 2 \kappa }$, $\{\vartheta _{n}\}$ and $\{\beta _{n}\}$ are control parameters.

• Step 1: Compute $y_{n} = P_{C} [ \varrho _{n} - \lambda (\varrho _{n} - T ( \varrho _{n})) ]$, where $\varrho _{n} = x_{n} + \vartheta _{n}(x_{n} - x_{n-1})$. If $y_{n} = \varrho _{n}$, then $\varrho _{n}$ is a solution of the fixed point problem.

• Step 2: Construct a half-space $H_{n} = \{z \in \mathbb{H} : \langle (1 - \lambda ) \varrho _{n} + \lambda T(\varrho _{n}) - y_{n}, z - y_{n} \rangle \leq 0 \}$ and calculate $z_{n} = P_{H_{n}} [ \varrho _{n} - \lambda (y_{n} - T (y_{n})) ]$.

• Step 3: Compute $x_{n+1} = (1- \beta _{n}) \varrho _{n} + \beta _{n} z_{n}$, where $\{\vartheta _{n}\}$ and $\{\beta _{n}\}$ are real sequences. Here, we assume that the sequence $\{\vartheta _{n}\}$ is nondecreasing with $0 \leq \vartheta _{n} \leq \vartheta < 1$ for each $n \geq 1$ and that there exist $\beta , \delta , \sigma > 0$ such that

  $$ \delta > \frac{6 \vartheta [ \vartheta (1+\vartheta ) + \sigma ]}{1 - \vartheta ^{2}} $$

  (60)

  and

  $$ 0 < \beta \leq \beta _{n} \leq \frac{\delta - 6 \vartheta [ \vartheta (1+\vartheta ) + \sigma + \frac{1}{6} \vartheta \delta ]}{6 \delta [ \vartheta (1+\vartheta ) + \sigma + \frac{1}{6} \vartheta \delta ]}. $$

  (61)

Then the sequences $\{\varrho _{n}\}$, $\{y_{n}\}$, $\{z_{n}\}$, and $\{x_{n}\}$ converge weakly to $\xi ^{*} \in \operatorname{Fix}(T)$.

Corollary 4.4

Let C be a nonempty, convex, and closed subset of a Hilbert space $\mathbb{H}$ and $T : C \rightarrow C$ be a κ-strict pseudocontraction and weakly continuous with a solution set $\operatorname{Fix}(T) \neq \emptyset$. Let $\{x_{n}\}$ be the sequences generated in the following way:

• Initialization: Choose $x_{0} \in \mathbb{H}$, $0 < \lambda < \frac{1 - \kappa }{3 - 2 \kappa }$, and $\{\beta _{n}\}$ is a control parameter.

• Step 1: Compute $y_{n} = P_{C} [ x_{n} - \lambda (x_{n} - T (x_{n})) ]$. If $y_{n} = x_{n}$, then $x_{n}$ is a solution of the fixed point problem.

• Step 2: Construct a half-space $H_{n} = \{z \in \mathbb{H} : \langle (1 - \lambda ) x_{n} + \lambda T(x_{n}) - y_{n}, z - y_{n} \rangle \leq 0 \}$ and calculate $z_{n} = P_{H_{n}} [ x_{n} - \lambda (y_{n} - T (y_{n})) ]$.

• Step 3: Evaluate $x_{n+1} = (1- \beta _{n}) x_{n} + \beta _{n} z_{n}$, where $\{\beta _{n}\}$ is a real sequence and there are $\beta , \delta , \sigma > 0$ such that $0 < \beta \leq \beta _{n} \leq \frac{1}{6 \sigma }$. Then the sequences $\{y_{n}\}$, $\{z_{n}\}$, and $\{x_{n}\}$ converge weakly to $\xi ^{*} \in \operatorname{Fix}(T)$.

5 Numerical examples

In this section we present four numerical examples with comparisons to related results in the literature. The examples are both in infinite and infinite dimensional spaces. The MATLAB implementations are done via MATLAB version 9.5 (R2018b) on the Intel(R) Core(TM)i5-6200 CPU PC @ 2.30 GHz 2.40 GHz, RAM 8.00 GB.

• (1) For Tran et al. [37] (egA), we use

  $$ \lambda = \min \biggl\{ \frac{1}{3c_{1}}, \frac{1}{3c_{2}} \biggr\} , \qquad D_{n} = \Vert x_{n} - y_{n} \Vert ^{2}. $$

• (2) For Hieu et al. [19] (iHegA), we use

  $$\begin{aligned}& \theta =0.45,\qquad \lambda = \frac{1}{2c_{2}+8c_{1}}, \\& D_{n} = \max \bigl\{ \Vert x_{n+1} - y_{n} \Vert ^{2}, \Vert x_{n+1} - w_{n} \Vert ^{2} \bigr\} . \end{aligned}$$

• (3) For Rehman et al. [38] (iRegA), we use

  $$\begin{aligned}& \alpha _{n}=0.20,\qquad \beta _{n}=0.80, \\& \lambda = 0.8 \biggl( \frac{\frac{1}{2}-2\alpha -\frac{1}{2}\alpha ^{2}}{(c_{1}+c_{2})(1-\alpha )^{2}} \biggr),\qquad D_{n} = \Vert w_{n} - y_{n} \Vert ^{2}. \end{aligned}$$

• (4) For Vinh et al. [42] (iVegA), we use

  $$\begin{aligned}& \epsilon _{n}=\frac{1}{n^{2}}, \qquad \theta =0.45, \\& \lambda = \min \biggl\{ \frac{1}{3c_{1}}, \frac{1}{3c_{2}} \biggr\} , \qquad D_{n} = \Vert w_{n} - y_{n} \Vert ^{2}. \end{aligned}$$

• (5) For Algorithm 1 (Algo1), we use

  $$\begin{aligned}& \vartheta _{n}=0.50,\qquad \beta _{n}=0.80, \\& \lambda = \min \biggl\{ \frac{1}{3c_{1}}, \frac{1}{3c_{2}} \biggr\} , \qquad D_{n} = \Vert w_{n} - y_{n} \Vert ^{2}. \end{aligned}$$

Example 5.1

Assume that the bifunction $f: C \times C \rightarrow \mathbb{R}$ is defined by

$$ f(x, y) = \langle P x + Q y + c, y - x \rangle , \quad \forall x, y \in C, $$

where $c \in \mathbb{R}^{n}$ and P, Q are matrices of order n. The matrix P is symmetric positive semi-definite and the matrix $Q - P$ is symmetric negative semi-definite with Lipschitz-type constants $c_{1} = c_{2} = \frac{1}{2}\| P - Q\|$ (see [37] for details). The matrices P, Q are taken randomly.¹ The constraint set $C \subset \mathbb{R}^{n}$ is defined by

$$ C := \bigl\{ x \in \mathbb{R}^{n} : -5 \leq x_{i} \leq 5, i = 1, 2, \ldots , n \bigr\} . $$

Numerical results are shown in Figs. 1–5 by assuming $x_{-1}=x_{0}=y_{0}=(1,\ldots , 1)$ and $\mathit{TOL}=10^{-8}$.

Figure 1

Example 5.1 when $n=5$: the number of iterations is 63, 56, 46, 38, 44, respectively

Figure 2

Example 5.1 when $n=50$: the number of iterations is 137, 145, 120, 119, 126, respectively

Figure 3

Example 5.1 when $n=200$: the number of iterations is 154, 150, 135, 129, 113, respectively

Figure 4

Example 5.1 when $n=400$: the number of iterations is 165, 163, 146, 143, 129, respectively

Figure 5

Example 5.1 when $n=600$: the number of iterations is 173, 171, 153, 146, 133, respectively

Example 5.2

Suppose that $\mathbb{H} = L^{2}([0, 1])$ is a Hilbert space with the induced norm

$$ \Vert x \Vert = \sqrt{ \int _{0}^{1} \bigl\vert x(t) \bigr\vert ^{2} \,dt} $$

and the inner product $\langle x, y \rangle = \int _{0}^{1} x(t) y(t) \,dt$ for all $x, y \in \mathbb{H}$. Assume that $C := \{ x \in L^{2}([0, 1]): \|x\| \leq 1 \}$. Let $F : C \rightarrow \mathbb{H}$ be defined by

$$ F(x) (t) = \int _{0}^{1} \bigl( x(t) - H(t, s) f\bigl(x(s) \bigr) \bigr) \,ds + g(t), $$

where $H(t, s) = \frac{2ts e^{(t+s)}}{e \sqrt{e^{2}-1}}$, $f(x) = \cos x$, $g(t) = \frac{2t e^{t}}{e \sqrt{e^{2}-1}}$. As stated in [18], the operator F is monotone and Lipschitz continuous with $L = 2$. Figures 6 and 7 show the numerical results obtained with $x_{-1}=x_{0}=y_{0}$.

Figure 6

Example 5.2 when $x_{0}=1$: the number of iterations is 72, 65, 55, 44, 56, respectively

Figure 7

Example 5.2 when $x_{0}=t$: the number of iterations is 83, 76, 69, 59, 65, respectively

Example 5.3

Let $G : \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ be an operator defined by

$$ G(x) = A x + B(x), \quad \forall x \in \mathbb{R}^{n}, $$

where A is a degree n symmetric semi-definite matrix. The proximal mapping $B(x)$ derives from the function $h(x) = \frac{1}{4} \|x\|^{4}$ such that

$$ B(x) = \mathop{\arg \min }_{y \in \mathbb{R}^{n}} \biggl\{ \frac{ \Vert y \Vert ^{4}}{4} + \frac{1}{2} \Vert y - x \Vert ^{2} \biggr\} . $$

The above description implies that F is monotone on C [27]. The feasible set C is defined by

$$ C := \bigl\{ x \in \mathbb{R}^{n} : -2 \leq x_{i} \leq 5 \bigr\} . $$

Figures 8–11 show the numerical results by assuming $x_{-1}=x_{0}=y_{0}$.

Figure 8

Example 5.3 when $x_{0}=(1,1,1,1,1)^{T}$: the number of iterations is 68, 63, 49, 45, 47, respectively

Figure 9

Example 5.3 when $x_{0}=(1,2,3,4,5)^{T}$: the number of iterations is 88, 81, 61, 56, 50, respectively

Figure 10

Example 5.3 when $x_{0}=(1,2,3,4,0)^{T}$: the number of iterations is 73, 67, 50, 46, 42, respectively

Figure 11

Example 5.3 when $x_{0}=(-1,2,0,3,4)^{T}$: the number of iterations is 87, 80, 60, 56, 53, respectively

Example 5.4

Let $\mathbb{H} = l_{2}$ be a real Hilbert space having sequences of real numbers that are square-summable with $\|x\|= \sqrt{\sum_{i} |x_{i}|^{2}}$ and $C= \{ x \in \mathbb{H} : \|x\| \leq 10 \}$. Let a bifunction f be defined by

$$ f(x, y) = \bigl(13 - \Vert x \Vert \bigr) \langle x, y - x \rangle ,\quad \forall x, y \in \mathbb{H}. $$

It is easy to see that $S_{\operatorname{EP}(f, C)} \neq \emptyset$ and meets condition (A3). Next, we need to prove that f is Lipschitz-type continuous. In fact, we have successively

$$\begin{aligned} & f(x, w) - f(x, y) - f(y, w) \\ &\quad = \bigl(13 - \Vert x \Vert \bigr) \langle x, w-x \rangle - \bigl(13 - \Vert x \Vert \bigr) \langle x, y-x \rangle - \bigl(13 - \Vert y \Vert \bigr) \langle y, w-y \rangle \\ &\quad = \bigl(13 - \Vert x \Vert \bigr) \langle x, w - y \rangle - \bigl(13 - \Vert y \Vert \bigr) \langle y, w-y \rangle \\ &\quad = \bigl\langle \bigl(13 - \Vert x \Vert \bigr) x - \bigl(13 - \Vert y \Vert \bigr) y , w-y \bigr\rangle \\ &\quad \leq \bigl\Vert \bigl(13 - \Vert x \Vert \bigr) x - \bigl(13 - \Vert y \Vert \bigr) y \bigr\Vert \Vert y - w \Vert \\ &\quad = \bigl\Vert 13(x-y) - \bigr\Vert x \bigl\Vert (x-y) - \bigl( \Vert x \Vert - \Vert y \Vert \bigr) y \bigr\Vert \Vert y - w \Vert \\ &\quad \leq \bigl[ 13 \Vert x - y \Vert + \Vert x \Vert \Vert x - y \Vert + \bigl\vert \Vert x \Vert - \Vert y \Vert \bigr\vert \Vert y \Vert \bigr] \Vert y - w \Vert \\ &\quad \leq \bigl[ 13 \Vert x - y \Vert + 10 \Vert x - y \Vert + 10 \Vert x - y \Vert \bigr] \Vert y - w \Vert \\ &\quad = 33 \Vert x - y \Vert \Vert y - w \Vert \\ &\quad \leq \frac{33}{2} \Vert x - y \Vert ^{2} + \frac{33}{2} \Vert y - w \Vert ^{2}, \end{aligned}$$

where $x, y, w \in C$ and $c_{1}=c_{2}=\frac{33}{2}$. We show that the bifunction is pseudomonotone. Let $x, y \in C$ be such that $f(x, y) = (13 - \|x\|) \langle x, y-x \rangle \geq 0$, which means that $\langle x, y-x \rangle \geq 0$. Thus, we have

$$\begin{aligned} f(y, x) &= \bigl(13 - \Vert y \Vert \bigr) \langle y, x - y \rangle \\ &\leq \bigl(13 - \Vert y \Vert \bigr) \langle y, x - y \rangle + \bigl(13 - \Vert y \Vert \bigr) \langle x, y - x \rangle \\ &\leq \bigl(13 - \Vert y \Vert \bigr) \langle y, x - y \rangle - \bigl(13 - \Vert y \Vert \bigr) \langle x, x - y \rangle \\ &\leq \bigl( \Vert y \Vert - 13\bigr) \Vert x - y \Vert ^{2} \leq 0. \end{aligned}$$

Moreover, we prove that f is not monotone. In fact, let $x = (\frac{13}{2}, 0, 0, \ldots , 0, \ldots )$ and $y = (10, 0, 0, \ldots , 0, \ldots )$ such that

$$ f(x, y) + f(y, x) = \frac{13}{2} \langle x, y - x \rangle + 2 \langle y, x - y \rangle > 0. $$

A metric projection $P_{C}$ upon C is defined by

$$ P_{C} (x) = \textstyle\begin{cases} x, &\text{if } \Vert x \Vert \leq 10, \\ \frac{10 x}{ \Vert x \Vert }, &\text{otherwise}. \end{cases} $$

Numerical results regarding Example 5.4 are shown in Figs. 12–14 and Table 1.

Figure 12

Example 5.2 when $x_{-1}=x_{0}=y_{0}=(2,\ldots ,2_{500},0,\ldots )$

Figure 13

Example 5.2 when $x_{-1}=x_{0}=y_{0}=(e^{1},e^{2},\ldots ,e^{500},0,\ldots )$

Figure 14

Example 5.2 when $x_{-1}=x_{0}=y_{0}=(1^{2},2^{2},\ldots ,500^{2},0,\ldots )$

Table 1 Numerical results for Figs. 12–14