Abstract
Some trapezoid and mid-point type inequalities related to the Hermite–Hadamard inequality on the disk of center \(C=(a,b)\) and radius R, \(D(C,R)\subseteq \mathbb{R}^{2}\), are investigated. It is shown that the estimated value obtained in the trapezoid and mid-point type inequalities has a relation with the integral of the partial derivative of the considered function on \(\partial (C,R)\), the boundary of \(D(C,R)\).
Similar content being viewed by others
1 Introduction
Let \(f: I\subseteq \mathbb{R}\to \mathbb{R}\) be a convex mapping defined on the interval I of real numbers and \(a, b\in I\) with \(a < b\). The following double inequality
is known in the literature as Hermite–Hadamard inequality for convex mappings. For more results and generalization about (1), see [1, 5,6,7,8,9,10,11] and the references therein.
An interesting problem in (1) is estimating the difference between the right term and the integral of f on \([a,b]\) and also estimating the difference between the left term and the integral of f on \([a,b]\).
In [3], the authors have obtained an estimation for the difference between the right term of (1) and the integral of f as follows.
Theorem 1.1
Let \(f : I^{\circ }\subseteq \mathbb{R}\to \mathbb{R}\) be a differentiable mapping on \(I^{\circ }, a, b\in I^{\circ }\) with \(a < b\). If \(|f'|\) is convex on \([a, b]\), then the following inequality holds:
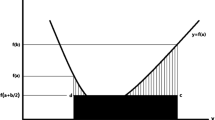
As we can see in Theorem 1.1, the estimation value is in connection with the absolute value of the derivative of the considered function on the boundary points of the corresponding interval \([a,b]\). In fact the striped area shown in Fig. 1, which is equivalent to the difference between the area of trapezoid \(abcd\) and the area under the graph of f, is estimated in (2) as well. Due to this geometric property, we call inequality (2) trapezoid type inequalities related to the Hermite–Hadamard inequality.
Also in [4], the author obtained an estimation for the difference between the left term of (1) and the integral of f:
Theorem 1.2
([4])
Let \(f : I^{\circ }\subseteq \mathbb{R}\to \mathbb{R}\) be a differentiable mapping on \(I^{\circ }\), \(a, b\in I^{ \circ }\) with \(a < b\). If \(|f'|\) is convex on \([a, b]\), then we have
According to (3), the striped area shown in Fig. 2, which is in fact equivalent to the difference between the area under the graph of f and the area of rectangle \(abcd\), is estimated. Due to this geometric property, we call inequality (3) mid-point type inequalities related to the Hermite–Hadamard inequality.
Now let us consider a point \(C=(a, b)\in \mathbb{R}^{2}\) and the disk \(D(C,R)\) centered at the point C and having the radius \(R > 0\). The following inequality has been obtained in [2], which is a Hermite–Hadamard inequality related to convex functions defined on the disk \(D(C,R)\) in \(\mathbb{R}^{2}\).
Theorem 1.3
If the mapping \(f: D(C,R)\to \mathbb{R}\) is convex on \(D(C,R)\), then one has the inequality
where \(\partial (C,R)\) is the circle centered at the point \(C=(a,b)\) with radius R. The above inequalities are sharp.
Motivated by the above-mentioned works, we investigate the trapezoid and mid-point type inequalities related to (4). We show that on a disk \(D(C,R)\), these kinds of estimations have a relation with the integral of \(|\frac{\partial f}{\partial r}|\) (in polar coordinates) on \(\partial (C,R)\), the boundary of the disk \(D(C,R)\), provided that \(|\frac{\partial f}{\partial r}|\) is convex with respect to the variable \(r\in [0,R]\).
2 Main results
The first result of this section is the trapezoid type inequality related to (4).
Theorem 2.1
Consider a set \(I\subset \mathbb{R}^{2}\) with \(D(C,R)\subset I^{ \circ }\). Suppose that the mapping \(f:D(C,R)\to \mathbb{R}\) has continuous partial derivatives in the disk \(D(C,R)\) with respect to the variables r and θ in polar coordinates. If, for any constant \(\theta \in [0,2\pi ]\), the function \(|\frac{\partial f}{\partial r} |\) is convex with respect to the variable r on \([0,R]\), then
Proof
For a constant \(\theta \in [0,2\pi ]\), if we consider
and
then we have \(([\dot{x}(r)]^{2}+[\dot{y}(r)]^{2} )^{ \frac{1}{2}}= (\sin ^{2}(\theta )+\cos ^{2}(\theta ) )^{ \frac{1}{2}}=1\), where ẋ, ẏ are the derivatives of x, y, respectively, with respect to the variable r on \([0,R]\). So, by the use of integration by parts, we have the following equalities:
The integration of (6) with respect to θ on \([0,2\pi ]\) implies that
Since \(|\frac{\partial f}{\partial r}|\) is convex with respect to the variable r on \([0,R]\) for any \(\theta \in [0,2\pi ]\), then
Now, consider the curve \(\gamma : [0, 2\pi ] \to \mathbb{R}^{2}\) given by
Then \(\gamma ([0, 2\pi ] ) =\partial (C,R)\), and we write (integrating with respect to arc length)
Also using the convexity of \(|\frac{\partial f}{\partial r}|\) in (4) we have
So by replacing (10) in (9) we obtain
Finally dividing (11) with \(2\pi R^{2}\) we get
□
Example 2.2
Consider the bifunction \(f(x,y)=R-\sqrt{(x-a)^{2}+(y-b)^{2}}\) defined on the disk \(D(C,R)\). In polar coordinates we have that
for \(0\leq r\leq R\), \(\theta \in [0,2\pi ]\) and specially \(f(a+R\cos \theta ,b+R\sin \theta )=0\) for all \(\theta \in [0,2\pi ]\). So
On the other hand, it is not hard to see that \(|\frac{\partial f}{ \partial r}|(a+R\cos\theta ,b+R\sin\theta )=1\) for all \(\theta \in [0,2 \pi ]\), and so
Then identities (12) and (13) show that inequality (5) is sharp.
The following result is the mid-point type inequality related to (4).
Theorem 2.3
Consider a set \(I\subset \mathbb{R}^{2}\) with \(D(C,R)\subset I^{ \circ }\). Suppose that the mapping \(f:D(C,R)\to \mathbb{R}\) has continuous partial derivatives in the disk \(D(C,R)\) with respect to the variables r and θ in polar coordinates. If, for any constant \(\theta \in [0,2\pi ]\), the function \(|\frac{\partial f}{\partial r} |\) is convex with respect to the variable r on \([0,R]\), then
Proof
As we have seen in the proof of Theorem 2.1, for a constant \(\theta \in [0,2\pi ]\), if we consider \(x(r)=a+r\cos \theta \) and \(y(r)=b+r\sin \theta \), then we have \(([\dot{x}(r)]^{2}+[\dot{y}(r)]^{2} )^{\frac{1}{2}}=1\). So from fundamental theorem of calculus we have
Hence
which implies that
Now from (15) we obtain
Since \(|\frac{\partial f}{\partial r}|\) is convex, then it follows that
From the triangle inequality and (16) we get
Since \(|\frac{\partial f}{\partial r}|\) satisfies the Hermite–Hadamard inequality (4), then
So, by replacing (5) and the inequality in (17) above, we obtain
□
Remark 2.4
If the functions f and \(|\frac{\partial f}{\partial r} |\) are convex on \(D(C,R)\), then by the use of inequalities (5), (14), and (4) we have
and
Example 2.5
There exists a function satisfying all the conditions of Remark 2.4 as well. Consider the function \(f(x,y)=x^{2}+y^{2}\) with \((x,y)\in \mathbb{R}^{2}\) defined on a disk \(D((0,0),R)\). It is clear that \(f(r,\theta )=r^{2}\) and \(|\frac{\partial f}{\partial r} |=2r\), which is equivalent to \(f(x,y)=2\sqrt{x^{2}+y^{2}}\) with \((x,y)\in \mathbb{R}^{2}\) defined on a disk \(D ((0,0),R )\). As we can see in Fig. 3, the functions f and \(|\frac{\partial f}{ \partial r} |\) are convex.
References
Alomari, M., Darus, M., Kirmaci, U.S.: Refinements of Hadamard-type inequalities for quasi-convex functions with applications to trapezoidal formula and to special means. Comput. Math. Appl. 59, 225–232 (2010)
Dragomir, S.S.: On Hadamard’s inequality on a disk. J. Inequal. Pure Appl. Math. 1(1), Article 2 (2000)
Dragomir, S.S., Agarwal, R.P.: Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Appl. Math. Lett. 11, 91–95 (1998)
Kirmaci, U.S.: Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula. Appl. Math. Comput. 147(1), 137–146 (2004)
Pearce, C.E.M., Pecaric, J.E.: Inequalities for differentiable mappings with application to special means and quadrature formula. Appl. Math. Lett. 13, 51–55 (2000)
Rostamian Delavar, M., De La Sen, M.: Some generalizations of Hermite–Hadamard type inequalities. SpringerPlus 5, 1661 (2016)
Rostamian Delavar, M., Dragomir, S.S.: On η-convexity. Math. Inequal. Appl. 20, 203–216 (2017)
Sarikaya, M.Z., Saglam, A., Yildirim, H.: On some Hadamard-type inequalities for h-convex functions. J. Math. Inequal. 2, 335–341 (2008)
Wasowicz, S., Witkowski, A.: On some inequality of Hermite–Hadamard type. Opusc. Math. 32(3), 591–600 (2012)
Yang, G.S.: Inequalities of Hadamard type for Lipschitzian mappings. J. Math. Anal. Appl. 260, 230–238 (2001)
Yang, G.S., Hwang, D.Y., Tseng, K.L.: Some inequalities for differentiable convex and concave mappings. Comput. Math. Appl. 47, 207–216 (2004)
Acknowledgements
Author M. De La Sen is grateful to the Spanish Government for funding received from the European Fund of Regional Development FEDER through Grant DPI2015-64766-R and to UPV/EHU for Grant PGC 17/33.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rostamian Delavar, M., Dragomir, S.S. & De La Sen, M. Hermite–Hadamard’s trapezoid and mid-point type inequalities on a disk. J Inequal Appl 2019, 105 (2019). https://doi.org/10.1186/s13660-019-2061-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-019-2061-3