1 Introduction

The Gaussian hypergeometric function \(_{2}F_{1}(a,b;c;x)\) with real parameters \(a,b\), and c \((c\neq0,-1,-2,\dots)\) is defined by [1, 4, 24, 41]

$$ F(a,b;c;x)=_{2}F_{1}(a,b;c;x)=\sum _{n=0}^{\infty}\frac {(a,n)(b,n)}{(c,n)}\frac{x^{n}}{n!} $$

for \(x\in(-1,1)\), where \((a,n)=a(a+1)(a+2)\cdots(a+n-1)\) for \(n=1,2,\dots\), and \((a,0)=1\) for \(a\neq0\). The function \(F(a,b;c;x)\) is called zero-balanced if \(c=a+b\). The asymptotical behavior for \(F(a,b;c;x)\) as \(x\rightarrow1\) is as follows (see [4, Theorems 1.19 and 1.48])

$$ \textstyle\begin{cases} F(a,b;c;1)=\Gamma(c)\Gamma(c-a-b)/[\Gamma(c-a)\Gamma(c-b)],&a+b< c,\\ B(a,b)F(a,b;c;z)+\log(1-z)=R(a,b)+O((1-z)\log(1-z)),&a+b=c,\\ F(a,b;c;z)=(1-z)^{c-a-b}F(c-a,c-b;c;z),&a+b>c, \end{cases} $$
(1.1)

where \(\Gamma(x)=\int_{0}^{\infty}t^{x-1}e^{-t}\,dt\) [10, 25, 43, 44, 47] and \(B(p,q)=[{\Gamma(p)\Gamma(q)}]/[{\Gamma(p+q)}]\) are the classical gamma and beta functions, respectively, and

$$ R(a,b)=-\psi(a)-\psi(b)-2\gamma,\qquad R \biggl(\frac{1}{4}, \frac{3}{4} \biggr)=\log64, $$
(1.2)

\(\psi(z) =\Gamma'(z)/\Gamma(z)\)), and \(\gamma=\lim_{n\rightarrow \infty} (\sum_{k=1}^{n}{1}/{k}-\log n )=0.577\dots\) is the Euler–Mascheroni constant [21, 50].

As is well known, making use of the hypergeometric function, Branges proved the famous Bieberbach conjecture in 1984. Since then, \(F(a,b;c;x)\) and its special cases and generalizations have attracted attention of many researchers, and was studied deeply in various fields [2, 5, 9, 11–18, 20, 22, 23, 26, 30, 31, 35–37, 40, 45, 46, 48]. A lot of geometrical and analytic properties, and inequalities of the Gaussian hypergeometric function have been obtained [3, 6–8, 19, 29, 32, 34, 38, 49].

Recently, in order to investigate the Ramanujan’s generalized modular equation in number theory, Landen inequalities, Ramanujan cubic transformation inequalities, and several other quadratic transformation inequalities for zero-balanced hypergeometric function have been proved in [27, 28, 32, 39, 42]. For instance, using the quadratic transformation formula [24, (15.8.15), (15.8.21)]

$$ F \biggl(\frac{1}{4},\frac{3}{4};1;\frac{8r(1+r)}{(1+3r)^{2}} \biggr)=\sqrt {1+3r}F \biggl(\frac{1}{4},\frac{3}{4};1;r^{2} \biggr), $$
(1.3)

Wang and Chu [32] found the maximal regions of the \((a,b)\)-plane in the first quadrant such that inequality

$$ F \biggl(a,b;a+b;\frac{8r(1+r)}{(1+3r)^{2}} \biggr)\leq \sqrt{1+3r}F \bigl(a,b;a+b;r^{2}\bigr) $$
(1.4)

or its reversed inequality

$$ F \biggl(a,b;a+b;\frac{8r(1+r)}{(1+3r)^{2}} \biggr)\geq \sqrt{1+3r}F \bigl(a,b;a+b;r^{2}\bigr) $$
(1.5)

holds for each \(r\in(0,1)\). Moreover, very recently in [33], some Landen-type inequalities for a class of Gaussian hypergeometric function \(_{2}F_{1} (a,b;(a+b+1)/2;x )\ (a,b>0)\), which can be viewed as a generalization of Landen identities of the complete elliptic integrals of the first kind

$$ F \biggl(\frac{1}{2},\frac{1}{2};1;\frac{4r}{(1+r)^{2}} \biggr)=(1+r)F \biggl(\frac{1}{2},\frac{1}{2};1;r^{2} \biggr), $$

have also been proved. As an application, the analogs of duplication inequalities for the generalized Grötzsch ring function with two parameters [33]

$$ \mu_{a,b}(r)=\frac{B(a,b)}{2}\frac{ F (a,b;(a+b+1)/2;1-r^{2} )}{F (a,b;(a+b+1)/2;r^{2} )},\quad r \in(0,1), $$
(1.6)

have been derived. In fact, the authors have proved

Theorem 1.1

For \((a,b)\in\{(a,b)|a,b>0,ab\geq a+b-10/9, a+b\geq2\}\), let \(x=x(r)=2\sqrt{r}/(1+r)\), then the Landen-type inequality

$$ \bigl(xx'\bigr)^{(a+b-1)/2} F \biggl(a,b; \frac{a+b+1}{2};x^{2} \biggr)>(1+r) \bigl(rr' \bigr)^{(a+b-1)/2} F \biggl(a,b;\frac{a+b+1}{2};r^{2} \biggr) $$
(1.7)

holds for all \(r\in(0,1)\).

Theorem 1.2

For \((a,b)\in\{(a,b)|a,b>0,ab\geq a+b-10/9, a+b\geq2\}\), define the function g on \((0,1)\) by

$$ g(r)=2\mu_{a,b} \biggl(\frac{2\sqrt{r}}{1+r} \biggr)-\mu_{a,b}(r). $$

Then g is strictly increasing from \((0,1)\) onto \((-\infty,0)\). In particular, the inequality

$$ 2\mu_{a,b} \biggl(\frac{2\sqrt{r}}{1+r} \biggr)< \mu_{a,b}(r) $$

holds for each \(r\in(0,1)\) with \((a,b)\in\{(a,b)|a,b>0,ab\geq a+b-10/9, a+b\geq2\}\).

The purpose of this paper is to establish several quadratic transformation inequalities for Gaussian hypergeometric function \(_{2}F_{1}(a,b;(a+b+1)/2;x)\) \((a,b>0)\), such as inequalities (1.4), (1.5) and (1.7), and thereby prove the analogs of Theorem 1.2.

We recall some basic facts about \(\mu_{a,b}(r)\) (see [33]). The limiting values of \(\mu_{a,b}(r)\) at 0 and 1 are

$$\begin{aligned} \mu_{a,b}\bigl(0^{+}\bigr)={}&\lim_{r\rightarrow0^{+}} \frac{B(a,b)}{2}F \biggl(a,b;\frac {a+b+1}{2};1-r^{2} \biggr) \\ ={}&\textstyle\begin{cases}\frac{B(a,b)}{2}H(a,b), &a+b< 1,\\ +\infty,&a+b\geq1, \end{cases}\displaystyle \end{aligned}$$
(1.8)
$$\begin{aligned} \mu_{a,b}\bigl(1^{-}\bigr)={}&\lim_{r\rightarrow1^{-}} \frac{B(a,b)}{2 F (a,b;\frac {a+b+1}{2};r^{2} )} =\textstyle\begin{cases}\frac{B(a,b)}{2H(a,b)}, &a+b< 1,\\ 0,&a+b\geq1, \end{cases}\displaystyle \end{aligned}$$
(1.9)

and the derivative formula of \(\mu_{a,b}(r)\) is

$$ \frac{d\mu_{a,b}(r)}{dr}=-\frac{{\Gamma(\frac{a+b+1}{2})}^{2}}{\Gamma (a+b)}\frac{1}{r^{a+b}{r'}^{a+b+1}{F (a,b;(a+b+1)/2;r^{2} )}^{2}}. $$
(1.10)

Here and in what follows,

$$H(a,b)=\frac{B(\frac{a+b+1}{2},\frac{1-a-b}{2})}{B(\frac{1+b-a}{2},\frac {1+a-b}{2})}. $$

2 Lemmas

In order to prove our main results, we need several lemmas, which we present in this section. Throughout this section, we denote

$$ F(x)=F \biggl(a,b,\frac{a+b+1}{2};x \biggr),\qquad G(x)=F \biggl(a+1,b+1;\frac {a+b+3}{2};x \biggr) $$
(2.1)

for \((a,b)\in(0,+\infty)\times(0,+\infty)\setminus\{p,q\}\) with \(p=(1/4, 3/4)\) and \(q=(3/4, 1/4)\), and

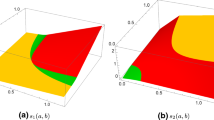
$$ \widehat{F}(x)= \biggl(\frac{1}{4},\frac{3}{4};1;x \biggr),\qquad \widehat {G}(x)=F \biggl(\frac{5}{4},\frac{7}{4};2;x \biggr). $$
(2.2)

For the convenience of readers, we introduce some regions in \(\{(a,b)\in \mathbb{R}^{2}| a>0,b>0\}\) and refer to Fig. 1 for illustration:

Figure 1
figure 1

The regions \(D_{i}\) for \(i=1,2,3,4\), \(E_{1},E_{2}\) and their boundary curves

Full size image
$$\begin{aligned} &D_{1}= \biggl\{ (a,b)\Big| a,b>0, a+b\leq1,ab-\frac{3(a+b+1)}{32}\leq0 \biggr\} , \\ &D_{2}= \biggl\{ (a,b)\Big| a,b>0, a+b\geq1,ab-\frac{3(a+b+1)}{32}\geq0 \biggr\} , \\ &D_{3}= \biggl\{ (a,b)\Big| a,b>0, a+b< 1,ab-\frac{3(a+b+1)}{32}>0 \biggr\} , \\ &D_{4}= \biggl\{ (a,b)\Big| a,b>0, a+b>1,ab-\frac{3(a+b+1)}{32}< 0 \biggr\} , \\ &E_{1}= \biggl\{ (a,b)\Big| a,b>0, a+b\leq1,2ab+\frac{29(a+b)-41}{32}\leq0 \biggr\} , \\ &E_{2}= \biggl\{ (a,b)\Big| a,b>0, a+b\geq1,2ab+\frac{29(a+b)-41}{32}\geq0 \biggr\} . \end{aligned}$$

Obviously, \(\bigcup_{i=1}^{4}D_{i}=(0,+\infty)\times(0,+\infty)\) and \(D_{i}\cap D_{j}=\emptyset\) for \(i\neq j\in\{1,2,3,4\}\) except that \(D_{1}\cap D_{2}=\{p,q\}\). Moreover, \(D_{1}\subset E_{1}\) and \(D_{2}\subset E_{2}\).

Lemma 2.1

([42, Theorem 2.1])

Suppose that the power series \(f(x)=\sum_{n=0}^{\infty}a_{n}x^{n}\) and \(g(x)=\sum_{n=0}^{\infty}b_{n}x^{n}\) have the radius of convergence \(r>0\) with \(b_{n}>0\) for all \(n\in\{0,1,2,\dots\}\). Let \(h(x)=f(x)/g(x)\) and \(H_{f,g}=(f'/g')g-f\), then the following statements hold true:

  1. 1.

    If the non-constant sequence \(\{a_{n}/b_{n}\}_{n=0}^{\infty}\) is increasing (decreasing) for all \(n>0\), then \(h(x)\) is strictly increasing (decreasing) on \((0,r)\);

  2. 2.

    If the non-constant sequence \(\{a_{n}/b_{n}\}_{n=0}^{\infty}\) is increasing (decreasing) for \(0< n\leq n_{0}\) and decreasing (increasing) for \(n>n_{0}\), then \(h(x)\) is strictly increasing (decreasing) on \((0,r)\) if and only if \(H_{f,g}(r^{-})\geq(\leq) 0\). Moreover, if \(H_{f,g}(r^{-})<(>) 0\), then there exists an \(x_{0}\in(0,r)\) such that \(h(x)\) is strictly increasing (decreasing) on \((0,x_{0})\) and strictly decreasing (increasing) on \((x_{0},r)\).

Lemma 2.2

  1. 1.

    The function \(\eta(x)=F(x)/\widehat{F}(x)\) is strictly decreasing on \((0,1)\) if \((a,b)\in D_{1}\setminus\{p,q\}\) and strictly increasing on \((0,1)\) if \((a,b)\in D_{2}\setminus\{p,q\}\). Moreover, if \((a,b)\in D_{3} (\textit{or }D_{4})\), then there exists \(\delta_{0}\in(0,1)\) such that \(\eta(x)\) is strictly increasing (decreasing) on \((0,\delta _{0})\) and strictly decreasing (increasing) on \((\delta_{0},1)\).

  2. 2.

    The function \(\widetilde{\eta}(x)=G(x)/\widehat{G}(x)\) is strictly decreasing on \((0,1)\) if \((a,b)\in E_{1}\setminus\{p,q\}\) and strictly increasing on \((0,1)\) if \((a,b)\in E_{2}\setminus\{p,q\}\). In the remaining case, namely for \(x\in(0,+\infty)\times(0,+\infty )\setminus(E_{1}\cup E_{2})\), \(\widetilde{\eta}(x)\) is piecewise monotone on \((0,1)\).

Proof

Suppose that

$$A_{n}=\frac{(a,n)(b,n)}{ (\frac{a+b+1}{2},n )n!},\qquad A^{*}_{n}=\frac {(\frac{1}{4},n)(\frac{3}{4},n)}{(1,n)n!}, $$

then we have

$$ \eta(x)=\frac{F(x)}{\widehat{F}(x)}=\frac{\sum_{n=0}^{\infty}A_{n}x^{n}}{\sum_{n=0}^{\infty}A^{*}_{n}x^{n}}. $$
(2.3)

It suffices to take into account the monotonicity of \(\{A_{n}/A^{*}_{n}\} _{n=0}^{\infty}\). By simple calculations, one has

$$ \frac{A_{n+1}}{A^{*}_{n+1}}-\frac{A_{n}}{A^{*}_{n}}=\frac{A_{n}\cdot\Delta _{n}}{A^{*}_{n} (\frac{a+b+1}{2} ) (\frac{1}{4}+n ) (\frac{3}{4}+n )}, $$
(2.4)

where

$$ \Delta_{n}= \biggl(\frac{a+b-1}{2} \biggr)n^{2}+ \biggl(ab+\frac{a+b}{2}-\frac {11}{16} \biggr)n+ab-\frac{3(a+b+1)}{32}. $$
(2.5)

We divide the proof into four cases.

Case 1 \((a,b)\in D_{1}\setminus\{p,q\}\). Then it follows easily that \(a+b\leq1\), \(ab-\frac{3(a+b+1)}{32}\leq0\) and \(ab+\frac {a+b}{2}-\frac{11}{16}<0\). This, in conjunction with (2.4) and (2.5), implies that \(\{A_{n}/A^{*}_{n}\}_{n=0}^{\infty}\) is strictly decreasing for all \(n>0\). Therefore, (2.3) and Lemma 2.1(1) lead to the conclusion that \(\eta(x)\) is strictly decreasing on \((0,1)\).

Case 2 \((a,b)\in D_{2}\setminus\{p,q\}\). Then a similar argument as in Case 1 yields \(\Delta_{n}>0\) and this implies that \(\eta(x)\) is strictly increasing on \((0,1)\) from (2.3), (2.4) and Lemma 2.1(1).

Case 3 \((a,b)\in D_{3}\). It follows from (2.4) and (2.5) that the sequence \(\{A_{n}/A^{*}_{n}\}\) is increasing for \(0\leq n\leq n_{0}\) and decreasing for \(n\geq n_{0}\) for some integer \(n_{0}\). Furthermore, making use of the derivative formula for Gaussian hypergeometric function

$$\frac{d F(a,b;c;x)}{dx}=\frac{ab}{c}F(a+1,b+1;c+1;x), $$

and in conjunction with (1.1) and \(a+b<1\), we obtain

$$\begin{aligned} H_{F,\widehat{F}}(x)&=\frac{32ab}{3(a+b+1)} \frac{F (a+1,b+1;\frac {a+b+3}{2};x )}{F (\frac{3}{4},\frac{1}{4};2;x )}(1-x)\widehat{F}(x)-F(x) \\ &\rightarrow-H(a,b)< 0 \end{aligned}$$
(2.6)

as \(x\rightarrow1^{-}\). Combing with (2.3), (2.6) and Lemma 2.1(2), we conclude that there exists an \(x_{1}\in(0,1)\) such that \(\eta(x)\) is strictly increasing on \((0,x_{1})\) and strictly decreasing on \((x_{1},1)\).

Case 4 \((a,b)\in D_{4}\). In this case, we follow a similar argument as in Case 3 and use the fact that

$$\begin{aligned} H_{F,\widehat{F}}(x)={}&\frac{32ab}{3(a+b+1)}(1-x) \frac{F (a+1,b+1;\frac{a+b+3}{2};x )}{F (\frac{3}{4},\frac {1}{4};2;x )}\widehat{F}(x)-F(x) \\ ={}&\frac{32ab}{3(a+b+1)}(1-x)^{\frac{1-a-b}{2}} \biggl[\frac{F (\frac {b-a+1}{2},\frac{a-b+1}{2};\frac{a+b+3}{2};x )}{F (\frac {3}{4},\frac{1}{4};2;x )}F \biggl(\frac{1}{4},\frac{3}{4};1;x \biggr) \\ &{}-F \biggl(\frac{b-a+1}{2},\frac{a-b+1}{2}; \frac{a+b+1}{2};x \biggr) \biggr] \\ \rightarrow{}&+\infty \end{aligned}$$
(2.7)

as \(x\rightarrow1^{-}\) since \(a+b>1\). Therefore, (2.3), (2.7) and Lemma 2.1(2) lead to the conclusion that there exists an \(x_{2}\in(0,1)\) such that \(\eta(x)\) is strictly decreasing on \((0,x_{2})\) and strictly increasing on \((x_{2},1)\).

Let

$$B_{n}=\frac{(a+1,n)(b+1,n)}{ (\frac{a+b+3}{2},n )n!},\qquad B^{*}_{n}=\frac {(\frac{5}{4},n)(\frac{7}{4},n)}{(2,n)n!}, $$

then we can write

$$ \widetilde{\eta}(x)=\frac{G(x)}{\widehat{G}(x)}=\frac{\sum_{n=0}^{\infty}B_{n}x^{n}}{\sum_{n=0}^{\infty}B^{*}_{n}x^{n}}. $$
(2.8)

Easy calculations lead to the conclusion that the monotonicity of \(\{ B_{n}/B^{*}_{n}\}_{n=0}^{\infty}\) depends on the sign of

$$ \widetilde{\Delta}_{n}= \biggl(\frac{a+b-1}{2} \biggr)n^{2}+ \biggl[ab+\frac {3(a+b)}{2}-\frac{27}{16} \biggr]n+2ab+\frac{29(a+b)-41}{32}. $$
(2.9)

Notice that

$$\begin{aligned} H_{G,\widehat{G}}(x)&=\frac{2(a+1)(b+1)}{(a+b+3)}\cdot \frac{32F (a+2,b+2;\frac{a+b+5}{2};x )}{35F (\frac{9}{4},\frac {11}{4};3;x )}\widehat{G}(x)-G(x) \\ &=(1-x)^{-\frac{1+a+b}{2}}\omega(a,b;x), \end{aligned}$$
(2.10)

where

$$\begin{aligned} \omega(a,b;x)={}&\frac{64(a+1)(b+1)}{35(a+b+3)}\frac{F (\frac {b-a+1}{2},\frac{a-b+1}{2};\frac{a+b+5}{2};x )}{F (\frac {3}{4},\frac{1}{4};3;x )}F \biggl(\frac{3}{4},\frac{1}{4};2;x \biggr) \\ &{}-F \biggl(\frac{b-a+1}{2},\frac{a-b+1}{2};\frac{a+b+3}{2};x \biggr). \end{aligned}$$
(2.11)

It follows easily from (1.1) and (2.11) that

$$\begin{aligned} \lim_{x\rightarrow1^{-}}\omega(a,b;x)={}& \frac {64(a+1)(b+1)}{35(a+b+3)}\frac{\Gamma(\frac{a+b+5}{2})\Gamma(\frac {a+b+3}{2})}{\Gamma(a+2)\Gamma(b+2)}\frac{\Gamma(\frac{9}{4})\Gamma (\frac{11}{4})}{\Gamma(3)\Gamma(2)}\frac{\Gamma(2)\Gamma(1)}{\Gamma (\frac{5}{4})\Gamma(\frac{7}{4})} \\ &{}-\frac{\Gamma(\frac{a+b+3}{2})\Gamma(\frac{a+b+1}{2})}{\Gamma (a+1)\Gamma(b+1)} \\ ={}& \biggl(\frac{a+b-1}{2} \biggr)\frac{\Gamma(\frac{a+b+3}{2})\Gamma(\frac {a+b+1}{2})}{\Gamma(a+1)\Gamma(b+1)} \\ ={}&\textstyle\begin{cases}< 0, &a+b< 1,\\ >0, &a+b>1. \end{cases}\displaystyle \end{aligned}$$
(2.12)

Employing similar arguments mentioned in part (1), we obtain the desired assertions easily from (2.8)–(2.12). □

Lemma 2.3

Let \(D_{0}=\{(a,b)| a,b>0,a+b\geq7/4,ab\geq a+b-31/28\}\) and \(x'=\sqrt {1-x^{2}}\) for \(0< x<1\), then the function

$$ f(x)=\frac{(xx')^{\frac{a+b-1}{2}}F(a,b;\frac{a+b+1}{2};x^{2})}{F(\frac {1}{4},\frac{3}{4};1;x^{2})} $$
(2.13)

is strictly increasing on \((0,1)\) if \((a,b)\in D_{0}\).

Proof

Taking the derivative of \(f(x)\) yields

$$ f'(x)=\frac{(xx')^{\frac{a+b-3}{2}}}{x'F(\frac{1}{4},\frac {3}{4};1;x^{2})^{2}}f_{1}(x), $$
(2.14)

where

$$\begin{aligned} f_{1}(x)={}& \biggl[\frac{a+b-1}{2} \bigl(1-2x^{2}\bigr)F \biggl(a,b;\frac {a+b+1}{2};x^{2} \biggr) \\ &{}+\frac{4ab}{a+b+1}x^{2}x^{\prime 2}F \biggl(a+1,b+1;\frac{a+b+3}{2};x^{2} \biggr) \biggr]F \biggl( \frac{1}{4},\frac{3}{4};1;x^{2} \biggr) \\ &{}-\frac{3x^{2}x^{\prime 2}}{8}F \biggl(a,b;\frac{a+b+1}{2};x^{2} \biggr)F \biggl(\frac {5}{4},\frac{7}{4};2;x^{2} \biggr). \end{aligned}$$
(2.15)

We clearly see from (1.1) that

$$x^{\prime 2}F \biggl(\frac{5}{4},\frac{7}{4};2;x^{2} \biggr)=F \biggl(\frac{1}{4},\frac {3}{4};2;x^{2} \biggr) \leq F \biggl(\frac{1}{4},\frac{3}{4};1;x^{2} \biggr) $$

for \(0< x<1\). This implies, in conjunction with (2.15), that

$$ f_{1}(x)\geq F \biggl(\frac{1}{4}, \frac{3}{4};1;x^{2} \biggr)f_{2}(x), $$
(2.16)

where

$$\begin{aligned} f_{2}(x)={}& \biggl[\frac{a+b-1}{2}- \biggl(a+b-\frac{5}{8} \biggr)x^{2} \biggr]F \biggl(a,b;\frac{a+b+1}{2};x^{2} \biggr) \\ &{}+\frac{4ab}{a+b+1}x^{2}\bigl(1-x^{2}\bigr)F \biggl(a+1,b+1;\frac{a+b+3}{2};x^{2} \biggr). \end{aligned}$$

It follows from the definition of hypergeometric function that

$$\begin{aligned} f_{2}(x)={}&\frac{a+b-1}{2}\sum _{n=0}^{\infty}\frac{(a,n)(b,n)}{(\frac {a+b+1}{2},n)}\frac{x^{2n}}{n!}- \biggl(a+b-\frac{5}{8} \biggr)\sum_{n=0}^{\infty}\frac{(a,n)(b,n)}{(\frac{a+b+1}{2},n)}\frac {x^{2n+2}}{n!} \\ &{}+\frac{4ab}{a+b+1} \Biggl[\sum_{n=0}^{\infty}\frac{(a+1,n)(b+1,n)}{(\frac {a+b+3}{2},n)}\frac{x^{2n+2}}{n!}-\sum_{n=0}^{\infty}\frac {(a+1,n)(b+1,n)}{(\frac{a+b+3}{2},n)}\frac{x^{2n+4}}{n!} \Biggr] \\ ={}&\frac{a+b-1}{2}+ \biggl[\frac{ab(a+b-1)}{a+b+1}- \biggl(a+b- \frac {5}{8} \biggr)+\frac{4ab}{a+b+1} \biggr]x^{2} \\ &{}+\frac{a+b-1}{2}\sum_{n=0}^{\infty}\frac {(a,n+2)(b,n+2)}{(\frac{a+b+1}{2},n+2)}\frac{x^{2n+4}}{(n+2)!} \\ &{}- \biggl(a+b-\frac{5}{8} \biggr)\sum _{n=0}^{\infty}\frac {(a,n+1)(b,n+1)}{(\frac{a+b+1}{2},n+1)}\frac{x^{2n+4}}{(n+1)!} \\ &{} +2 \Biggl[\sum_{n=0}^{\infty}\frac{(a,n+2)(b,n+2)}{(\frac {a+b+1}{2},n+2)}\frac{x^{2n+4}}{(n+1)!}-\sum_{n=0}^{\infty}\frac {(a,n+1)(b,n+1)}{(\frac{a+b+1}{2},n+1)}\frac{x^{2n+4}}{n!} \Biggr] \\ ={}&\frac{a+b-1}{2} \biggl[1-\frac{3x^{2}}{4(a+b+1)} \biggr]+ \frac {4ab(a+b-1)-4(a-b)^{2}+1}{4(a+b+1)}x^{2} \\ &{}+\sum_{n=0}^{\infty}\frac{(a,n+1)(b,n+1)}{(\frac{a+b+1}{2},n+2)} \frac {C_{n}}{(n+2)!}x^{2n+4}, \end{aligned}$$
(2.17)

where

$$\begin{aligned} C_{n}={}&\frac{a+b-1}{2}(a+n+1) (b+n+1)- \biggl(a+b-\frac{5}{8} \biggr) \biggl(\frac{a+b+1}{2}+n+1 \biggr) (n+2) \\ &{}+2(a+n+1) (b+n+1) (n+2)-2 \biggl(\frac{a+b+1}{2}+n+1 \biggr) (n+1) (n+2) \\ ={}& \biggl(\frac{4a+4b-7}{8} \biggr)n^{2}+ \biggl[ \frac {32ab+5(a+b)-29}{16} \biggr]n \\ &{}+\frac{4ab(a+b+3)-4(a-b)^{2}-(3a+3b+5)}{8}. \end{aligned}$$
(2.18)

If \((a,b)\in D_{0}\), namely, \(a+b\geq7/4\) and \(ab\geq a+b-31/28\), we can verify

  1. (i)
    $$\begin{aligned} &4ab(a+b-1)-4(a-b)^{2}+1\\ &\quad\geq4 \biggl(a+b- \frac{31}{28} \biggr) (a+b-1)-4(a-b)^{2}+1 \\ &\quad=\frac{1}{7} \bigl[112ab-59(a+b)+38 \bigr]\geq\frac {53}{7} \biggl(a+b-\frac{86}{53} \biggr)\geq\frac{27}{28}, \end{aligned}$$
  2. (ii)
    $$\begin{aligned} 32ab+5(a+b)-29&\geq32 \biggl(a+b-\frac{31}{28} \biggr)+5(a+b)-29 \\ &=\frac{37}{7} \biggl[7(a+b)-\frac{451}{259} \biggr]\geq \frac {9}{28}, \end{aligned}$$
  3. (iii)
    $$\begin{aligned} &4ab(a+b+3) -4(a-b)^{2} -(3 a + 3 b + 5)\\ &\quad\geq4 \biggl(a+b-\frac{31}{28} \biggr) (a+b+3) \\ &\qquad{} -4(a-b)^{2}-(3a+3b+5)=\frac{16}{7} \bigl[7ab+2(a+b)-8 \bigr] \\ &\quad\geq \frac{16}{7} \biggl[7 \biggl(a+b-\frac{31}{28} \biggr)+2(a+b)-8 \biggr]=\frac{36}{7}\bigl[4(a+b)-7)\bigr]\geq0. \end{aligned}$$

This, in conjunction with (2.17) and (2.18), implies that \(f_{2}(x)>0\) for \(0< x<1\). Therefore, \(f(x)\) is strictly increasing on \((0,1)\), which follows from (2.14) and (2.16) if \((a,b)\in D_{0}\). □

Remark 2.4

The function \(f(x)\) defined in Lemma 2.3 is not monotone on \((0,1)\) if two positive numbers \(a,b\) satisfy \(a+b<1\), since \(\lim_{x\rightarrow 0^{+}}f(x)=\lim_{x\rightarrow1^{-}}f(x)=+\infty\) and Lemma 2.1(1) shows the monotonicity of \(f(x)\) on \((0,1)\) if \(a+b=1\). In the remaining case \(a+b>1\), it follows from (2.15) that \(f_{1}(0^{+})=(a+b-1)/2>0\). This, in conjunction with (2.14), implies that \(f(x)\) is strictly increasing on \((0,x^{*})\) for a sufficiently small \(x^{*}>0\). This enables us to find a sufficient condition for \(a,b\) with \(a+b>1\) such that \(f(x)\) is strictly increasing on \((0,1)\) in Lemma 2.3.

The following corollary can be derived immediately from the monotonicity of \(f(x)\) in Lemma 2.3 and the quadratic transformation equality (1.3).

Corollary 2.5

Let \(x=x(r)=\sqrt{8r(1+r)}/(1+3r)\), if \((a,b)\in D_{0}\), then the inequality

$$ \bigl(xx'\bigr)^{\frac{a+b-1}{2}}F \biggl(a,b; \frac{a+b+1}{2};x^{2} \biggr)>\sqrt {1+3r}\bigl(rr' \bigr)^{\frac{a+b-1}{2}}F \biggl(a,b;\frac{a+b+1}{2};r^{2} \biggr) $$
(2.19)

holds for all \(r\in(0,1)\).

3 Main results

Theorem 3.1

The quadratic transformation inequality

$$ F \biggl(a,b;\frac{a+b+1}{2};\frac{8r(1+r)}{(1+3r)^{2}} \biggr)\leq \sqrt {1+3r}F \biggl(a,b;\frac{a+b+1}{2};r^{2} \biggr) $$
(3.1)

holds for all \(r\in(0,1)\) with \(a,b>0\) if and only if \((a,b)\in D_{1}\) and the reversed inequality

$$ F \biggl(a,b;\frac{a+b+1}{2};\frac{8r(1+r)}{(1+3r)^{2}} \biggr)\geq \sqrt {1+3r}F \biggl(a,b;\frac{a+b+1}{2};r^{2} \biggr) $$
(3.2)

takes place for all \(r\in(0,1)\) if and only if \((a,b)\in D_{2}\), with equality only for \((a,b)=p\textit{ or }q\).

In the remaining case \((a,b)\in D_{3}\cup D_{4}\), neither of the above inequalities holds for all \(r\in(0,1)\).

Proof

Suppose that \(x(r)=[8r(1+r)]/(1+3r)^{2}\), then we clearly see that \(x(r)>r^{2}\) for \(0< r<1\). It follows from Lemma 2.1(1) that \(\eta (x(r))<\eta(r^{2})\) for \((a,b)\in D_{1}\setminus\{p,q\}\) and \(\eta (x(r))>\eta(r^{2})\) for \((a,b)\in D_{2}\setminus\{p,q\}\). This, in conjunction with the quadratic transformation formula (1.3), implies

$$ F\bigl(x(r)\bigr)< \frac{\widehat{F}(x(r))}{\widehat{F}(r^{2})}F\bigl(r^{2}\bigr)=\sqrt{1+3r}F \bigl(r^{2}\bigr) $$

for \((a,b)\in D_{1}\setminus\{p,q\}\), and it degenerates to the quadratic transformation equality for \((a,b)=p (\text{or} q)\). This completes the proof of (3.1).

Inequality (3.2) can be derived analogously, and the remaining case follows easily from Lemma 2.2(1). □

Theorem 3.2

We define the function

$$\varphi(r)=\sqrt{1+3\sqrt{r}}F \biggl(a,b,;\frac{a+b+1}{2};r \biggr)-F \biggl(a,b;\frac{a+b+1}{2};\frac{8\sqrt{r}(1+\sqrt{r})}{(1+3\sqrt{r})^{2}} \biggr) $$

for \(r\in(0,1)\) with \(a,b>0\) and \((a,b)\neq p,q\). Let \(L_{1}=\{(a,b)| a+b=1, 0< a<\frac{1}{4}\textit{ or }\frac{3}{4}<a<1\}\) and \(L_{2}=\{ (a,b)| a+b=1, \frac{1}{4}< a<\frac{3}{4}\}\). Then the following statements hold true:

  1. 1.

    If \((a,b)\in L_{1}(\textit{or }L_{2})\), then \(\varphi(r)\) is strictly increasing (resp., decreasing) from \((0,1)\) onto \((0,[R(a,b)-\log64]/B(a,b) )\) (resp., \(([R(a,b)-\log64]/B(a,b),0)\));

  2. 2.

    If \((a,b)\in D_{1}\setminus L_{1}\), then \(\varphi(r)\) is strictly increasing from \((0,1)\) onto \((0,H(a,b))\);

  3. 3.

    If \((a,b)\in D_{2}\setminus L_{2}\), then \(\varphi(r)\) is strictly decreasing from \((0,1)\) onto \((-\infty,0)\).

As a consequence, the inequality

$$\begin{aligned} F \biggl(a,b;\frac{a+b+1}{2};\frac{8r(1+r)}{(1+3r)^{2}} \biggr)&\leq \sqrt {1+3r}F \biggl(a,b,;\frac{a+b+1}{2};r^{2} \biggr) \\ & \leq F \biggl(a,b;\frac{a+b+1}{2};\frac{8r(1+r)}{(1+3r)^{2}} \biggr)+H(a,b) \end{aligned}$$
(3.3)

holds for all \(r\in(0,1)\) if \((a,b)\in D_{1}\setminus L_{1}\), and the following inequality is valid for all \(r\in(0,1)\):

$$\begin{aligned} & F \biggl(a,b;\frac{a+b+1}{2};\frac{8r(1+r)}{(1+3r)^{2}} \biggr) \\ &\quad \leq( \geq) \sqrt{1+3r}F \biggl(a,b,;\frac{a+b+1}{2};r^{2} \biggr) \\ &\quad\leq(\geq)F \biggl(a,b;\frac{a+b+1}{2};\frac {8r(1+r)}{(1+3r)^{2}} \biggr)+ \frac{R(a,b)-\log64}{B(a,b)} \end{aligned}$$
(3.4)

if \((a,b)\in L_{1} (\textit{resp., }L_{2})\).

Proof

Let \(z=z(r)=[8\sqrt{r}(1+\sqrt{r})]/(1+3\sqrt{r})^{2}\), then we clearly see that

$$ \frac{dz}{dr}=\frac{4(1-\sqrt{r})}{\sqrt{r}(1+3\sqrt{r})^{3}}=\frac {4(1-z)}{\sqrt{r}(1-\sqrt{r})(1+3\sqrt{r})}. $$
(3.5)

Taking the derivative of \(\varphi(r)\) with respect to r and using (3.5) yields

$$\begin{aligned} \sqrt{r}(1+3\sqrt{r})\varphi'(r)={}& \frac{3\sqrt{1+3\sqrt {r}}}{4}F(r)+\sqrt{r} (\sqrt{1+3\sqrt{r}} )^{3} \frac {2ab}{a+b+1}G(r) \\ &{}-\frac{2ab}{a+b+1}\frac{4(1-z)}{1-\sqrt{r}}G(z). \end{aligned}$$
(3.6)

We substitute \(\sqrt{r}\) for r in the quadratic transformation equality (1.3), then differentiate it with respect to r to obtain

$$ \frac{4(1-z)}{1-\sqrt{r}}\widehat{G}(z)=4\sqrt{1+3\sqrt{r}}\widehat {F}(r)+\sqrt{r} ( \sqrt{1+3\sqrt{r}} )^{3}\widehat{G}(r), $$

in other words,

$$ \frac{4(1-z)}{1-\sqrt{r}}\frac{\widehat{G}(z)}{\widehat{G}(r)}=4\sqrt {1+3\sqrt{r}} \frac{\widehat{F}(r)}{\widehat{G}(r)}+\sqrt{r} (\sqrt {1+3\sqrt{r}} )^{3}. $$
(3.7)

If \((a,b)\in D_{1}\setminus\{p,q\}\), then it follows from Lemma 2.2(2) that \(G(x)/\widehat{G}(x)\) is strictly decreasing on \((0,1)\). This, in conjunction with \(z>r\), implies that \(G(z)/\widehat{G}(z)< G(r)/\widehat {G}(r)\), that is,

$$ G(z)< \frac{\widehat{G}(z)}{\widehat{G}(r)}G(r). $$
(3.8)

Combing (3.6), (3.7) with the inequality (3.8), we clearly see that

$$\begin{aligned} &\sqrt{r}(1+3\sqrt{r})\varphi'(r) \\ &\quad=\frac{3\sqrt{1+3\sqrt{r}}}{4}F(r)+\sqrt{r} (\sqrt{1+3\sqrt {r}} )^{3} \frac{2ab}{a+b+1}G(r)-\frac{2ab}{a+b+1}\frac {4(1-z)}{1-\sqrt{r}}G(z) \\ &\quad>\frac{3\sqrt{1+3\sqrt{r}}}{4}F(r)+\sqrt{r} (\sqrt{1+3\sqrt {r}} )^{3} \frac{2ab}{a+b+1}G(r)-\frac{2ab}{a+b+1}\frac {4(1-z)}{1-\sqrt{r}} \frac{\widehat{G}(z)}{\widehat{G}(r)}G(r) \\ &\quad=\frac{3\sqrt{1+3\sqrt{r}}}{4}F(r)+\sqrt{r} (\sqrt{1+3\sqrt {r}} )^{3} \frac{2ab}{a+b+1}G(r) \\ &\qquad{}-\frac{2ab}{a+b+1} \biggl[4\sqrt{1+3\sqrt{r}}\frac{\widehat {F}(r)}{\widehat{G}(r)}+\sqrt{r} ( \sqrt{1+3\sqrt{r}} )^{3} \biggr]G(r) \\ &\quad=4\sqrt{1+3\sqrt{r}} \biggl[\frac{3}{16}F(r)-\frac{2ab}{a+b+1} \frac {\widehat{F}(r)}{\widehat{G}(r)}G(r) \biggr] \\ &\quad =4\sqrt{1+3\sqrt{r}}\frac{F(r)^{2}}{\widehat{G}(r)} \biggl(\frac{\widehat {F}(r)}{F(r)} \biggr)'. \end{aligned}$$
(3.9)

It follows from Lemma 2.2(1) that \(\widehat{F}(r)/F(r)\) is strictly increasing on \((0,1)\) if \((a,b)\in D_{1}\setminus\{p,q\}\). This, in conjunction with (3.9), implies that \(\varphi(r)\) is strictly increasing on \((0,1)\) if \((a,b)\in D_{1}\).

Analogously, if \((a,b)\in D_{2}\setminus\{p,q\}\), then we obtain the following inequality:

$$ G(z)>\frac{\widehat{G}(z)}{\widehat{G}(r)}G(r). $$

By using a similar argument as above, we have

$$ \sqrt{r}\varphi'(r)< \frac{4F^{2}(r)}{\widehat{G}(r)} \biggl(\frac{\widehat {F}(r)}{F(r)} \biggr)'< 0, $$

since \(F(r)/\widehat{F}(r)\) is strictly increasing on (0,1) if \((a,b)\in D_{2}\setminus\{p,q\}\) by Lemma 2.2(1). Hence, \(\varphi(r)\) is strictly decreasing on \((0,1)\) if \((a,b)\in D_{2}\).

Notice that \(\varphi(0^{+})=0\) and

$$ \lim_{r\rightarrow1^{-}}\varphi(r)=\textstyle\begin{cases} H(a,b),&a+b< 1,\\ \frac{R(a,b)-\log64}{B(a,b)},&a+b=1,\\ -\infty,&a+b>1. \end{cases} $$
(3.10)

Therefore, we obtain the desired assertion from (3.10). □

Theorem 3.3

If we define the function

$$\phi(r)=2\mu_{a,b} \biggl(\frac{\sqrt{8r(1+r)}}{1+3r} \biggr)- \mu_{a,b}(r), $$

for \((a,b)\in D_{0}\), then \(\phi(r)\) is strictly increasing from \((0,1)\) onto \((-\infty,0)\). As a consequence, the inequality

$$2\mu_{a,b} \biggl(\frac{\sqrt{8r(1+r)}}{1+3r} \biggr)< \mu_{a,b}(r) $$

holds for all \(r\in(0,1)\) if \((a,b)\in D_{0}\).

Proof

Remark 2.4 enables us to consider the case for \(a+b>1\). Note that \(\phi (1^{-})=0\) and

$$\begin{aligned} &\lim_{r\rightarrow0^{+}}\phi(r) \\ &\quad =\lim_{r\rightarrow0^{+}}\frac{B(a,b)}{2} \biggl[2F \biggl(a,b; \frac {a+b+1}{2}; \biggl(\frac{1-r}{1+3r} \biggr)^{2} \biggr)-F \biggl(a,b;\frac {a+b-1}{2};1-r^{2} \biggr) \biggr] \\ &\quad=B(a,b)\lim_{r\rightarrow0^{+}} \biggl[ \biggl( \frac{\sqrt {8r(1+r)}}{1+3r} \biggr)^{1-a-b}F \biggl(\frac{b-a+1}{2}, \frac {a-b+1}{2};\frac{a+b+1}{2}; \biggl(\frac{1-r}{1+3r} \biggr)^{2} \biggr) \\ &\qquad{}-\frac{1}{2}r^{1-a-b}F \biggl( \frac{b-a+1}{2},\frac {a-b+1}{2};\frac{a+b+1}{2};1-r^{2} \biggr) \biggr] \\ &\quad=\frac{1}{2}B \biggl(\frac{a+b+1}{2},\frac{a+b-1}{2} \biggr)\lim_{r\rightarrow0^{+}} \biggl[2 \biggl(\frac{\sqrt{8r(1+r)}}{1+3r} \biggr)^{1-a-b}-r^{1-a-b} \biggr] \\ &\quad=-\infty. \end{aligned}$$
(3.11)

Let \(x=x(r)=\sqrt{8r(1+r)}/(1+3r)\) and \(x'=\sqrt{1-x^{2}}\). Then

$$ \frac{dx}{dr}=\frac{\sqrt{2}(1-r)}{\sqrt{r(1+r)}(1+3r)^{2}}=\frac {x'(1+3x')^{2}}{4x}. $$
(3.12)

Taking the derivative of \(\phi(r)\) and using (3.12) leads to

$$\begin{aligned} \phi'(r)={}&-2\frac{\Gamma(\frac{a+b+1}{2})^{2}}{\Gamma(a+b)} \frac {1}{x^{a+b}x^{\prime a+b+1}F(a,b;\frac{a+b+1}{2};x^{2})^{2}}\cdot\frac {x'(1+3x')^{2}}{4x} \\ &{}+\frac{\Gamma(\frac{a+b+1}{2})^{2}}{\Gamma(a+b)}\frac {1}{r^{a+b}r^{\prime a+b+1}F(a,b;\frac{a+b+1}{2};r^{2})^{2}} \\ ={}&\frac{\Gamma(\frac{a+b+1}{2})^{2}}{\Gamma(a+b)}\frac {(1+3x')^{2}}{2(1+3r)x^{a+b+1}x^{\prime a+b}F(a,b;\frac{a+b+1}{2};x^{2})^{2}} \\ &{}\times \biggl[\frac{(xx')^{a+b-1}F(a,b;\frac {a+b+1}{2};x^{2})^{2}}{(rr')^{a+b-1}F(a,b;\frac {a+b+1}{2};r^{2})^{2}}-(1+3r) \biggr]. \end{aligned}$$
(3.13)

Therefore, the monotonicity of \(\phi(r)\) follows immediately from (2.19) and (3.13). This, in conjunction with (3.11), gives rise to the desired result. □

4 Results and discussion

In the article, we establish several quadratic transformation inequalities for Gaussian hypergeometric function \(_{2}F_{1}(a,b;(a+b+1)/2;x)\) \((0< x<1)\). As applications, we provide the analogs of duplication inequalities for the generalized Grötzsch ring function

$$ \mu_{a,b}(r)=\frac{B(a,b)}{2}\frac{ F (a,b;(a+b+1)/2;1-r^{2} )}{F (a,b;(a+b+1)/2;r^{2} )} $$

introduced in [33].

5 Conclusion

We find several quadratic transformation inequalities for the Gaussian hypergeometric function and Grötzsch ring function. Our approach may have further applications in the theory of special functions.