1 Introduction

Applications of composite materials are growing vastly along with the development of research interests concerning material behavior. A large variety of new materials represents a challenge in mathematical modeling. In practice, the strengthening of the body is often achieved by reinforcement constructions on the outer edge, so it is important to study the mathematical models concerning the elastic bodies with rigid inclusions on the outer boundary. In this regard, it is of interest to investigate the contact problems for plates that are reinforced by rigid inclusions.

There are a number of works related to the modeling of contact problems for composites (see, e.g., [1–4]. It is known that the classical approach to contact problems is characterized by a given contact area [5, 6]. In contrast to this, for the mathematical models with unilateral boundary conditions of Signorini type, the contact area is not known a priori [7–14]. The power and generality of variational methods make it possible to solve various problems for elastic bodies and plates with inclusions; see, for example, [15–21]. In particular, a framework for two-dimensional elasticity problems with a thin delaminated rigid inclusion and nonlinear Signorini-type conditions on a part of boundary is proposed in [15]. The three-dimensional case is considered in [22]. The paper [23] is devoted to the analysis of the shapes of cracks and thin rigid inclusions in elastic bodies. The formula for the shape derivative of the energy functional is obtained for the equilibrium problem for an elastic body with a delaminated thin rigid inclusion [19]. For a Kirchhoff-Love plate containing a thin rigid inclusion, the cases both with and without delamination of inclusion are considered [24]. In that work, for the plate without delamination of inclusions, it is established that by passing to the limit in the equilibrium problems for volume inclusions embedded in an elastic plate as the size of the inclusions tends to zero we obtain the equilibrium problem for the plate with a thin inclusion.

In this paper, we study the nonlinear equilibrium problem for a plate subject to the Signorini condition on a part of the boundary. We consider volume inclusions defined by three-dimensional domains and thin inclusions defined by cylindrical surfaces. The present study investigates the effect of varying the inclusion size. We formulate an optimal control problem with the cost functional characterizing the deviation of the displacement vector from a given function. The control functions depend on the size parameter of the rigid inclusion. We prove the existence of an optimal inclusion size.

Additionally, we establish a qualitative connection between the contact problems for plates with rigid inclusions of varying size. In particular, we prove the strong convergence of the solutions for problems with volume inclusions to the solution of the problem for thin inclusion as the size parameter of the volume inclusion tends to zero.

2 Equilibrium problems for an elastic plate containing a rigid inclusion

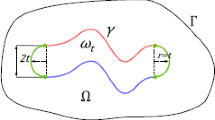
Let us formulate the family of contact problems for an elastic inhomogeneous plate containing a volume rigid inclusion. We suppose that the inhomogeneous clamped plate may come into contact with a rigid obstacle. Let \(\Omega\subset\mathbf{R}^{2}\) be a bounded domain with a smooth boundary Γ. Suppose that the smooth unclosed curves γ and \(\gamma_{0}\) lie on Γ such that \(\operatorname{meas}(\gamma)>0\), \(\operatorname{meas}(\gamma_{0})>0\), and \(\bar{\gamma}\cap\bar{\gamma}_{0}=\emptyset\).

We consider the family of simply connected domains \(\omega_{t}\subset\Omega\), \(t\in(0,t_{0}]\), with the following properties:

  1. (a)

    the boundaries \(\partial{\omega}_{t}\) are smooth such that \(\partial\omega_{t}\in C^{0,1}\);

  2. (b)

    \(\gamma=\partial\omega_{t}\cap\Gamma\) for all \(t\in(0,t_{0}]\);

  3. (c)

    \(\omega_{t}\subset\omega_{t'}\) for all \(t,t'\in(0,t_{0}]\), \(t< t'\);

  4. (d)

    for any fixed \(\hat{t}\in(0,t_{0})\) and any neighborhood \(\mathcal{O}\) of the domain \(\overline{\omega}_{t}\), there exists \(t_{\mathcal{O}}>\hat{t}\) such that \(\omega_{t}\subset \mathcal{O}\) for all \(t\in[\hat{t},t_{\mathcal{O}}]\);

  5. (e)

    for any neighborhood \(\mathcal{O}\) of the curve γ, there exists \(t_{\mathcal{O}}>0\) such that \(\omega_{t}\subset{\mathcal{O}}\) for all \(t\in (0,t_{\mathcal{O}}]\);

  6. (f)

    \(\bigcup_{t< t'}{\omega_{t}}=\omega_{t'}\) for all \(t'\in(0,t_{0}]\);

  7. (g)

    the sets \(\Omega\backslash\bar{\omega}_{t}\) are Lipschitzian domains for all \(t\in(0,t_{0}]\).

As an example of such a family, we give the following family of domains \(\omega_{t}\), \(t\in(0,t_{0}]\), restricted by the closed curves \(\partial\omega_{t}={\gamma}\cup{\gamma_{t}}\cup{\gamma_{t}^{1}}\cup{\gamma_{t}^{2}}\), where

$$\begin{aligned}& {\gamma=\bigl\{ (x_{1},x_{2}) \mid -a< x_{1}< 0, x_{2}=g(x_{1})\bigr\} }, \\& {\gamma_{t}=\bigl\{ (x_{1},x_{2}) \mid -a< x_{1}< 0, x_{2}=g(x_{1})-t\bigr\} },\quad g\in C^{1,1}[0,1], \end{aligned}$$

and \(\gamma^{1}_{t}\), \(\gamma^{2}_{t}\) are axis-parallel line segments (see Figure 1). For this example, the domain thickness along the \(Ox_{2}\) axis is equal to t.

Figure 1
figure 1

Example of the domains \(\pmb{\omega_{t}}\) .

Full size image

We define a three-dimensional Cartesian space \(\{x_{1},x_{2},z\}\) such that the set \(\{\Omega\}\times\{0\}\subset\mathbf{R}^{3}\) corresponds to the middle plane of the plate. Fix the parameter \(t\in(0,t_{0}]\). According to our arguments, the rigid inclusion is specified by the set \(\omega_{t}\times[-h,h]\), that is, the boundary of the rigid inclusion is given by the cylindrical surface \(\partial\omega_{t}\times[-h,h]\). The elastic part of the plate corresponds to the domain \(\Omega\backslash\overline{\omega}_{t}\). The thickness of the plate is considered to be constant and equal to 2h.

Denote by \(({W},w)\) the vector of mid-plane displacements (\(x\in\Omega\)), where \({W}=(w_{1},w_{2})\) are the displacements in the plane, and \(\{x_{1},x_{2}\}\) and w are the displacements along the axis z. We denote the angles of rotation of a normal fiber by \(\psi=\psi(x)=(\psi_{1},\psi_{2})\) (\(x\in\Omega\)).

Introduce the tensors describing the deformation of the transversely isotropic plate:

$$\varepsilon_{ij}(\psi)=\frac{1}{2}(\psi_{i,j}+ \psi_{j,i}),\qquad \varepsilon_{ij}(W)=\frac{1}{2}(w_{i,j}+w_{j,i}), \quad i,j=1,2\ \biggl(v,_{i}=\frac{\partial v}{\partial x_{i}}\biggr). $$

The tensors of moments \(m(\psi)=\{m_{ij}( \psi)\}\) and stresses \(\sigma( W)=\{\sigma_{ij}( W)\}\) are expressed by the formulas (summation is performed over repeated indices) [25]

$$ m_{ij}(\psi)=a_{ijrl}\varepsilon_{kl}( \psi),\qquad \sigma_{ij}(W)=3h^{-2}a_{ijkl}\varepsilon_{kl}(W), \quad i,j,k,l=1,2, $$
(1)

where the nonzero components of elasticity tensor \(A=\{a_{ijkl}\}\) are as follows:

$$ a_{iiii}=D, \qquad a_{iijj}=D{\ae},\qquad a_{ijij}=a_{ijji}={D(1-{\ae})}/{2},\quad i\neq j, i,j=1,2, $$
(2)

with constants D and æ: D is a cylindrical rigidity of the plate, and æ is the Poisson ratio, \(0<{\ae}<{1}/{2}\). The transverse forces in the Timoshenko-type model are specified by the expressions

$$ q_{i}(w,\psi)=\Lambda(w,_{i}+ \psi_{i}),\quad i=1,2, $$
(3)

where \(\Lambda=2{k'}gh\), \(k'\) is the shear coefficient, g is the shear modulus in areas perpendicular to the middle plane of the plate, and Λ is a constant [25]. Let \(B(G,\cdot ,\cdot)\) be the bilinear form defined by the equality

$$B(G,\chi,\bar{\chi})= \int _{G}\bigl\{ m_{ij}(\psi)\varepsilon_{ij}( \bar{\psi})+\Lambda(w,_{i}+\psi_{i}) (\bar{v},_{i}+ \bar{\psi}_{i})+ \sigma_{ij}(W)\varepsilon_{ij}(\bar{W})\bigr\} \,dG $$

with some Lipschitzian subdomain \(G\subset\Omega\), \(\chi=(W,w,\psi)\), \(\bar{\chi}=(\bar{W},\bar{w},\bar{\psi})\). The potential energy functional of the plate occupying the region Ω has the form

$$\Pi(\chi)=\frac{1}{2}B(\Omega,\chi,\chi)- \int _{\Omega} F\chi \,d\Omega ,\quad \chi=(W,w,\psi), $$

where \(F=(f_{1},f_{2},f_{3},\mu_{1},\mu_{2})\in L^{2}(\Omega)^{5}\) is the vector specifying the external loads [25].

Introduce the Sobolev spaces

$$H^{1,0}_{\gamma_{0}}(\Omega)= \bigl\{ v\in H^{1}(\Omega) \mid v=0 \mbox{ a.e. on } \gamma_{0} \bigr\} ,\qquad H( \Omega)=H^{1,0}_{\gamma_{0}}(\Omega)^{5} , \qquad\|\cdot\|=\| \cdot\| _{H(\Omega)}. $$

Due to presence of a rigid inclusion in the plate, restrictions of the functions describing displacements \((W,w)\) and angles of rotation ψ to the domain \(\omega_{t}\) satisfy a special kind of relations. We introduce the space that allows us to characterize the properties of volume rigid inclusion [26]:

$$\begin{aligned} R(\omega_{t})=\bigl\{ \zeta \mid \zeta(x) =(bx_{2}+c_{1},-bx_{1}+c_{2},a_{0}+a_{1}x_{1}+a_{2}x_{2},-a_{1},-a_{2}); {x}\in\omega_{t} \bigr\} , \end{aligned}$$
(4)

where \(b,c_{1},c_{2},a_{0},a_{1},a_{2}\in\mathbf{R}\).

The displacements for the Timoshenko plates along the z-axis are independent of the plate thickness, whereas the displacements \(W(x,z)=(w_{1}(x,z), w_{2}(x, z))\) along the plane \((x_{1},x_{2})\) depend on z in the following way [25]:

$$w_{i}(x,z)=w_{i}(x)+z\psi(x), \quad i=1,2, |z|\leq h. $$

Thus, the nonpenetration condition can be easily derived from the relation

$$\bigl(w_{1}(x,z),w_{2}(x,z),w\bigr)\cdot(\nu_{1}, \nu_{2},0)\leq0,\quad x\in\gamma, |z|\leq h. $$

Hence, in view of the arbitrariness of \(z\in[-h;h]\), we get

$$ -W\nu\geq h|\psi\nu| \quad \mbox{on } \gamma. $$
(5)

We formulate the contact problem of the plate with a rigid inclusion

$$ \inf_{\chi\in K_{t}}\Pi(\chi), $$
(6)

where

$$K_{t}=\bigl\{ \chi=(W,w,\psi)\in H(\Omega)\mid -W\nu\geq h|\psi\nu| \mbox{ on } \gamma, \chi|_{\omega_{t}}\in R(\omega_{t})\bigr\} $$

is the set of admissible functions. Note that the inclusion \(\chi\in H(\Omega)\) assumes that the following homogeneous boundary-value conditions hold:

$$ w=0, \qquad\psi=W=(0,0) \quad \mbox{on } \gamma_{0}. $$
(7)

It can be shown that the set \(K_{t}\) is convex and closed in the Hilbert space \(H(\Omega)\) [27]. Due to the estimate

$$B(\Omega,\chi,\bar{\chi})\leq c_{1}\|\chi\|\|\bar{\chi}\|, $$

where the constant \(c_{1}>0\) is independent of \(\chi\in H(\Omega)\) and \(\bar{\chi}\in H(\Omega)\), the symmetric bilinear form of \(B({\Omega},\chi,\bar{\chi})\) is continuous with respect to \(H(\Omega)\). The coercivity of the functional \(\Pi(\chi)\) follows from the inequality

$$ B(\Omega,\chi,\chi)\geq c\|\chi\|^{2},\quad \chi\in H( \Omega), $$
(8)

where the constants \(c>0\) are independent of χ (see [28]).

Remark 1

It should be noted that, by property (g), for fixed \(t\in(0,t_{0}]\), we have the inequalities

$$B(\Omega\backslash\bar{\omega}_{t},\chi,\chi)\geq c_{t}\| \chi\|^{2}_{H^{1}_{0}(\Omega\backslash\bar{\omega}_{t})^{5}},\quad \chi\in H^{1}_{0}(\Omega \backslash\bar{\omega}_{t})^{5}, $$

with the constant \(c_{t}>0\) independent of χ.

These properties of the energy functional \(\Pi(\chi)\), bilinear form \(B({\Omega},\cdot,\cdot)\), and set \(K_{t}\) allow us to establish the existence of a unique solution \(\xi_{t}=(U_{t},u_{t},\phi_{t})\in K_{t}\) for problem (6) (see [29]). The symmetry and continuity of the bilinear form \(B({\Omega},\cdot,\cdot)\) and the properties of the set \(K_{t}\) provide (see [29]) the equivalence of problem (6) to the variational inequality

$$ \xi_{t}\in K_{t}, \quad B(\Omega, \xi_{t},{\chi}-\xi_{t})\geq \int _{\Omega} F({\chi}-\xi_{t})\,d\Omega \quad\forall \chi=(W,w, \psi)\in K_{t}. $$
(9)

In parallel with the contact problem for a plate with a volume rigid inclusion, we also consider the contact problem for an elastic plate with a thin inclusion. Here we assume that the thin rigid inclusion is described by the cylindrical surface \({x}=(x_{1},x_{2})\in\gamma\), \(-h\le z\le h\). Let us first introduce some notation:

$$\begin{aligned} R(\gamma)=\bigl\{ \zeta \mid \zeta(x) =(bx_{2}+c_{1},-bx_{1}+c_{2},a_{0}+a_{1}x_{1}+a_{2}x_{2},-a_{1},-a_{2}); {x}\in\gamma \bigr\} , \end{aligned}$$
(10)

where \(b,c_{1},c_{2},a_{0},a_{1},a_{2}\in\mathbf{R}\); and

$$K_{0}=\bigl\{ \chi=(W,w,\psi)\in H(\Omega) \mid -W\nu\geq h|\psi \nu| \mbox{ on }\gamma; \chi|_{\gamma}\in R(\gamma)\bigr\} . $$

Consider a variational formulation of the problem. We want to find a function \(\xi_{0}=(U_{0},u_{0},\phi_{0})\in K_{0}\) such that

$$ \Pi(\xi_{0})=\inf_{\chi\in K_{0}}\Pi(\chi). $$
(11)

Bearing in mind the properties of the functional \(\Pi(\chi)\) and due to the convexity and the closeness of \(K_{0}\), we can be established that problem (11) has a unique solution \(\xi_{0}\) that satisfies the variational inequality

$$ \xi_{0}\in K_{0}, \quad B(\Omega, \xi_{0},{\chi}-{\xi}_{0})\geq \int _{\Omega}F(\chi-{\xi}_{0})\,d\Omega \quad\forall \chi\in K_{0}. $$
(12)

A detailed proof of a similar result for Timoshenko plate containing a crack along a thin rigid inclusion can be found in [30].

3 An optimal control problem

Consider the cost functional

$$J(t) = \bigl\| \xi_{t}-\xi^{*}\bigr\| _{H(\Omega)} ,\quad t\in[0,t_{0}], $$

where \(\xi^{*}\) is a prescribed element, \(\xi_{t}\) is solution of problem (6) for \(t>0\), and \(\xi_{0}\) is a solution of problem (11). We seek a solution of the maximization problem

$$ \sup_{t\in[0,t_{0}]}J(t). $$
(13)

Theorem 1

There exists a solution of the optimal control problem (13).

Proof

Let \(\{t_{n}\}\) be a minimizing sequence. By the boundedness of the segment \([0,t_{0}]\) we can extract a convergent subsequence \(\{t_{n_{k}}\}\subset\{t_{n}\}\) such that

$$t_{n_{k}}\to t^{*} \quad\mbox{as } k\to\infty, t^{*}\in[0,t_{0}]. $$

Without loss of generality, we assume that \(t_{n_{k}}\neq t^{*}\) for sufficiently large k. Otherwise, there would exist a sequence \(\{t_{n_{l}}\}\) such that \(t_{n_{l}}\equiv t^{*}\), and therefore \(J(t^{*})\) is a solution of (13). Consider the case of the subsequence \(\{t_{n_{k}}\}\) satisfying \(t_{n_{k}}\neq t^{*}\) for sufficiently large k. Now we take into account Lemma 2 that will be proved further the solutions \(\xi_{k}\) of (6) corresponding to the parameters \(t_{n_{k}}\) converge to the solution \(\xi_{t^{*}}\) strongly in \(H(\Omega)\) as \(k\to\infty\). This allows us to obtain the convergence

$$J(t_{n_{k}})\to J\bigl(t^{*}\bigr). $$

This means that

$$J\bigl(t^{*}\bigr)=\sup_{t\in[0,t_{0}]}J(t). $$

The theorem is proved. □

Before proceeding further, we first prove the following lemma.

Lemma 1

Let \(t^{*}\in[0,t_{0}]\) be a fixed real number, and let \(\{t_{n}\}\subset[t^{*},t_{0}]\) be a sequence of real numbers converging to \(t^{*}\) as \(n\to\infty\). Then for an arbitrary function \({\eta}\in K_{t^{*}}\), there exist a subsequence \(\{t_{k}\}=\{t_{n_{k}}\}\subset\{t_{n}\}\) and a sequence of functions \(\{{\eta}_{k}\}\) such that \({\eta}_{k}\in K_{t_{k}}\), \(k\in\mathbf{N}\), and \({\eta}_{k}\to{\eta}\) weakly in \(H(\Omega)\) as \(k\to\infty\).

Proof

If there exists a subsequence \(\{t_{n_{k}}\}\) such that \(t_{n_{k}}=t^{*}\), then the assertion of the lemma holds for the sequence \({\eta}_{k}\equiv{\eta}\), \(k\in\mathbf{N}\). Therefore, we further assume that \(t_{n}> t^{*}\) for sufficiently large n. Denote by \(\zeta^{*}\) the function describing the structure of η in \(\omega_{t^{*}}\) for the case \(t^{*}>0\), that is, \({\eta}=\zeta ^{*}=(bx_{2}+c_{1},-bx_{1}+c_{2},a^{*}_{0}+a^{*}_{1}x_{1}+a^{*}_{2}x_{2},-a_{1}^{*},-a_{2}^{*})\) in \(\omega_{t^{*}}\). If \(t^{*}=0\) and the function η has the specified structure on \(\gamma^{-}\), then we adopt the same notation, that is, \(\zeta^{*}={\eta}\) on \(\gamma^{-}\). We extend the definition of \(\zeta^{*}\) to the whole domain Ω by the equality

$$\zeta ^{*}(x)=\bigl(b^{*}x_{2}+c^{*}_{1},-b^{*}x_{1}+c^{*}_{2},a^{*}_{0}+a^{*}_{1}x_{1}+a^{*}_{2}x_{2},-a_{1}^{*},-a_{2}^{*} \bigr),\quad x\in\Omega. $$

Fix an arbitrary value \(t\in(0,t_{0}]\) and consider the following family of auxiliary problems:

$$ \mbox{find } {\eta}_{t}\in K_{t}' \mbox{ such that } p({\eta}_{t})=\inf_{\chi\in K_{t}'}p(\chi), $$
(14)

where \(p(\chi)=B(\Omega, \chi-{\eta},\chi-{\eta})\), and

$$K_{t}'=\bigl\{ \chi=(W,w,\psi)\in H(\Omega) \mid \chi=\eta \mbox{ on } \Gamma\backslash\gamma, \chi|_{\omega_{t}}=\zeta^{*}\bigr\} . $$

It is easy to see that the functional \(p(\chi)\) is coercive and weakly lower-semicontinuous on the space \(H(\Omega)\). It can be verified that the set \(K_{t}'\) is convex and closed in \(H(\Omega)\). These properties guarantee the existence of a solution of problem (14). Besides, the solution \({\eta}_{t}\) is unique [12, 29].

Since the functional \(p(\chi)\) is convex and differentiable on \(H(\Omega)\), problem (14) can be written in the equivalent form

$$ {\eta}_{t}\in K_{t}', \quad B( \Omega, \eta_{t}-{\eta},\chi-{\eta}_{t})\geq0\quad \forall \chi\in K_{t}'. $$
(15)

By property (c) it is evident that the solution \({\eta}_{t_{0}}\) of (15) for \(t=t_{0}\) belongs to the set \(K_{t}'\) with \(t'\in(0,t_{0}]\). Substituting \({\eta}_{t_{0}}\) as the test functions into (15), we get

$$B(\Omega,{\eta}_{t}-{\eta},{\eta}_{t_{0}})+B(\Omega,{\eta},{ \eta}_{t})\geq B(\Omega,{\eta}_{t}, {\eta}_{t}) \quad \forall t\in(0,t_{0}]. $$

Using inequality (8), we obtain from this relation the following uniform upper bound:

$$\| {\eta}_{t}\|\leq c\quad \forall t\in(0,t_{0}]. $$

Therefore, we can extract from the sequence \(\{{\eta}_{t_{n}}\}\) a subsequence \(\{{\eta}_{k}\}\), which is defined by the equalities \({\eta}_{k}={\eta}_{t_{n_{k}}}\), \(k\in\mathbf{N}\) (henceforth, we define a sequence \(\{t_{k}\}\) by the equality \(t_{k}=t_{n_{k}}\)), and \(\{{\eta}_{k}\}\) weakly converges to some function η̃ in \(H(\Omega)\).

We now show that \(\widetilde{\eta}={\eta}\). To this end, we must distinguish two cases for \(t^{*}\), namely \(t^{*}>0\) and \(t^{*}=0\). Let us first assume that \(t^{*}>0\). Then, by construction \(({\eta}_{k}-{\eta})\in H^{1}_{0}(\Omega\backslash\overline{\omega}_{t^{*}})^{5}\). Consequently, by the weak closeness of \(H^{1}_{0}(\Omega\backslash\overline{\omega}_{t^{*}})^{5}\) we have \((\widetilde{\eta}-{\eta})\in H^{1}_{0}(\Omega\backslash\overline{\omega}_{t^{*}})^{5}\). We now consider the functions of the form \(\chi_{k}^{\pm}={\eta}_{k}\pm{\theta}\), where \({\theta}\in C_{0}^{\infty}(\Omega\backslash\overline{\omega}_{t^{*}})^{5}\cap C_{0}^{\infty}(\Omega)^{5}\). Bearing in mind property (d), observe that \(\chi_{k}^{\pm}\in K_{t_{k}}\) for sufficiently large k. We next substitute the elements of these sequences \(\{\chi_{k}^{+}\}\) and \(\{\chi_{k}^{-}\}\) as test functions into inequalities (15) corresponding to \(t_{k}\). As a result, we obtain

$$ {\eta}_{k}\in K_{t_{k}}',\quad B( \Omega,{\eta}_{k}-{\eta},{\theta})=0. $$
(16)

Fix the function θ. Passing to the limit in (16), we deduce

$$B(\Omega,\widetilde {\eta}-{\eta},{\theta})=B(\Omega\backslash\overline{\omega}_{t^{*}},\widetilde {\eta}-{\eta},{\theta})=0 \quad\forall {\theta}\in C_{0}^{\infty}(\Omega\backslash\overline{\omega}_{t^{*}})^{5} \cap C_{0}^{\infty}(\Omega)^{5}. $$

Hence, by the denseness of \(C_{0}^{\infty}(\Omega\backslash\overline{\omega}_{t^{*}})\) in \(H^{1}_{0}(\Omega\backslash\overline{\omega}_{t^{*}})\) (see [31]) and Remark 1 we infer that \(\widetilde {\eta}-{\eta}=0\) in \(H^{1}_{0}(\Omega\backslash\overline{\omega}_{t^{*}})^{5}\). Finally, by construction, the equality \(\widetilde{\eta}={\eta}\) is fulfilled in \(\omega_{t^{*}}\). Therefore, \(\widetilde{\eta}={\eta}\) in \(H(\Omega)\), and there is a sequence \(\{{\eta}_{k}\}\) such that \({\eta}_{k}\in K_{t_{k}}\), \(k\in\mathbf{N,}\) and \({\eta}_{k}\to{\eta}\) weakly in \(H(\Omega)\) as \(n\to\infty\).

Let us consider the second case. Suppose that \(t^{*}=0\). By construction, we have \(({\eta}_{k}-{\eta})\in H^{1}_{0}(\Omega)^{5}\) and, consequently, the relation \((\widetilde{\eta}-{\eta})\in H^{1}_{0}(\Omega)^{5}\). We now consider functions of the form \(\chi_{k}^{\pm}={\eta}_{k}\pm{\theta}\), where \({\theta}\in C_{0}^{\infty}(\Omega)^{5}\). Observe that property (d) yields that for sufficiently large k, we have the inclusion \(\chi_{k}^{\pm}\in K_{t_{k}}\). Substituting these functions into (15) corresponding to \(t_{k}\) yields the equality

$$ {\eta}_{k}\in K_{t_{k}}', \quad B( \Omega,{\eta}_{k}-{\eta},{\theta})=0. $$
(17)

We fix the function θ in (17) and pass to the limit as \(k\to\infty\). As a result, we get

$$ B(\Omega,\widetilde{\eta}-{\eta},{\theta})=0 \quad\forall {\theta} \in C_{0}^{\infty}(\Omega)^{5}. $$
(18)

The denseness of \(C_{0}^{\infty}(\Omega)\) in \(H^{1}_{0}(\Omega)\) see [31] allows us to obtain from (18) the equality \(\widetilde{\eta}-{\eta}=0\) in \(H(\Omega)\). Thus, \(\widetilde{\eta}={\eta}\) in \(H(\Omega)\), and there exists a subsequence of functions \(\{{\eta}_{k}\}\) such that \({\eta}_{k}\in K_{t_{k}}\) and \({\eta}_{k}\to{\eta}\) weakly in \(H(\Omega)\). The lemma is proved. □

Now we can prove the following statement.

Lemma 2

Let \(t^{*}\in[0,t_{0}]\) be a fixed real number. Then \(\xi_{t}\to\xi_{t^{*}}\) strongly in \(H(\Omega)\) as \(t\to t^{*}\), where \(\xi_{t}\) is the solution of (6) corresponding to \(t\in(0,t_{0}]\), whereas \(\xi_{t^{*}}\) is the solution corresponding to (6) for \(t^{*}>0\) and to problem (11) for \(t^{*}=0\).

Proof

We will prove it by contradiction. Let us assume that there exist a number \(\epsilon_{0}>0\) and a sequence \(\{t_{n}\}\subset(0,t_{0}]\) such that \(t_{n}\to t^{*}\), \(\|\xi_{n}-\xi_{t^{*}}\|\geq\epsilon_{0}\), where \(\xi_{n}=\xi_{t_{n}}\), \(n\in\mathbf{N}\), are the solutions of (6) corresponding to \(t_{n}\).

Since \(\chi^{0}\equiv0\in K_{t}\) for all \(t\in[0,t_{0}]\), we can substitute \(\chi=\chi^{0}\) into (9) for all \(t\in(0,t_{0}]\) and into (12) for \(t=0\). This provides

$$\xi_{t}\in K_{t}, \quad B(\Omega,\xi_{t},{ \xi}_{t})\leq \int _{\Omega}F{\xi}_{t}\,d\Omega \quad\forall t \in[0,t_{0}]. $$

From here, using (8), we can deduce that for all \(t\in[0,t_{0}]\),

$$\|\xi_{t}\|\leq c $$

with some constant \(c>0\) independent of t. Consequently, replacing \(\xi_{n}\) with a subsequence if necessary, we can assume that \(\xi_{n}\) converges to some ξ̃ weakly in \(H(\Omega)\).

Now we show that \(\tilde{\xi}\in K_{t^{*}}\). Indeed, we have \(\xi_{n}|_{\omega_{t_{n}}}=\zeta_{n}\in R(\omega_{t_{n}})\). By the Sobolev embedding theorem [32] we obtain that

$$\begin{aligned}& \xi_{n}|_{\omega_{t^{*}}}\to\tilde{\xi}|_{\omega_{t^{*}}} \quad \mbox{strongly in } L_{2}(\omega_{t^{*}})^{5} \mbox{ as }n\to\infty, \end{aligned}$$
(19)
$$\begin{aligned}& \xi_{n}|\to\tilde{\xi}|_{\gamma}\quad\mbox{strongly in } L_{2}(\gamma)^{5} \mbox{ as } n\to\infty. \end{aligned}$$
(20)

Choosing a subsequence, if necessary, we assume that \(\xi_{n}\to\tilde{\xi}\) a.e. in \(\omega_{t^{*}}\) as \(n\to\infty\). This allows us to conclude that each of the numerical sequences \(\{b_{n}\}\), \(\{c_{1n}\}\), \(\{c_{2n}\}\), \(\{a_{0n}\}\), \(\{a_{1n}\}\), \(\{a_{2n}\}\) defining the structure of \(\zeta_{n}\) in domains \(\omega_{t_{n}}\) is bounded in absolute value. Thus, we can extract subsequences (retain notation) such that

$$b_{n}\to b, \qquad a_{0n}\to a_{0}, \qquad c_{in}\to c_{i},\qquad a_{in}\to a_{i}, \quad i=1,2, \mbox{as } n\to\infty. $$

Further, we must distinguish two different cases, \(t^{*}=0\) and \(t^{*}>0\). In the first case, for the sequence \(\{{\xi}_{n}\}\) corresponding to the specified convergent number sequences \(\{b_{n}\}\), \(\{c_{1n}\}\), \(\{c_{2n}\}\), \(\{a_{0n}\}\), \(\{a_{1n}\}\), \(\{a_{2n}\}\), we have

$$\begin{aligned} {\xi}_{n}|_{\gamma}\to (bx_{2}+c_{1},-bx_{1}+c_{2},a_{0}+a_{1}x_{1}+a_{2}x_{2},-a_{1},-a_{2}) \end{aligned}$$
(21)

strongly in \(L_{2}(\gamma)^{5}\) as \(n\to\infty\). The last relation with (19) leads to the equality

$$\tilde{\xi}=(bx_{2}+c_{1},-bx_{1}+c_{2},a_{0}+a_{1}x_{1}+a_{2}x_{2},-a_{1},-a_{2}) \quad\mbox{a.e. on } \gamma. $$

This means that \(\tilde{\xi}|_{\gamma}\in R(\gamma)\).

Consider the second case. If there exists a subsequence \(\{t_{k}\}\subset\{t_{n}\}\) such that \(t_{k}\geq t^{*}\) for all \(k\in\mathbf{N}\), then we can easily obtain the convergence

$$ {\xi}_{k}|_{\omega_{t^{*}}}\to (bx_{2}+c_{1},-bx_{1}+c_{2},a_{0}+a_{1}x_{1}+a_{2}x_{2},-a_{1},-a_{2}) $$
(22)

strongly in \(L_{2}(\omega_{t^{*}})^{5}\) as \(k\to\infty\). Therefore, from (22) and (19) we obtain that \(\tilde {\xi}|_{\omega_{t^{*}}}\in R(\omega_{t^{*}})\).

Suppose that there exists a subsequence \(\{t_{k}\}\subset\{t_{n}\}\) satisfying \(t_{k}< t^{*}\) for all \(k\in\mathbf{N}\) and \(t_{k}\to t^{*}\) as \(k\to\infty\). In this case, for an arbitrary fixed \(k'\in \mathbf{N}\) and the corresponding value \(t'=t_{k'}\), by property (c) we have

$$\begin{aligned} {\xi}_{k}|_{\omega_{t'}}\to (bx_{2}+c_{1},-bx_{1}+c_{2},a_{0}+a_{1}x_{1}+a_{2}x_{2},-a_{1},-a_{2}) \end{aligned}$$
(23)

strongly in \(L_{2}(\omega_{t'})^{5}\) as \(k\to\infty\). It is possible to define a function \(l=a_{0}+a_{1}x_{1}+a_{2}x_{2}\) in \(\omega_{t^{*}}\). In view of the absolute continuity of the Lebesgue integral and properties (c) and (f), for any \(\epsilon>0\), we can choose a number \(k'\in\mathbf{N}\) large enough such that

$$\|l\|_{L^{2}(\omega_{t^{*}}\backslash\omega_{t'})}< \sqrt{\epsilon}, \qquad\| \tilde{u}\|_{L^{2}(\omega_{t^{*}}\backslash\omega_{t'})}< \sqrt{ \epsilon}. $$

Further, by the triangle inequality from this it follows that

$$\begin{aligned} \|u_{k}-l\|_{L^{2}(\omega_{t^{*}}\backslash\omega_{t'})} \leq& \|u_{k} \|_{L^{2}(\omega_{t^{*}}\backslash\omega_{t'})}+\|l\|_{L^{2}(\omega _{t^{*}}\backslash\omega_{t'})} \\ \leq&\|\tilde{u}\|_{L^{2}(\omega_{t^{*}}\backslash\omega_{t'})}+\|u_{k}-\tilde{u}\|_{L^{2}(\omega_{t^{*}}\backslash\omega_{t'})}+ \|l\|_{L^{2}(\omega _{t^{*}}\backslash\omega_{t'})} \\ < & 2\sqrt{\epsilon}+\|u_{k}-\tilde{u}\|_{L^{2}(\omega_{t^{*}})}. \end{aligned}$$

Therefore, we have

$$ \begin{aligned}[b] \|u_{k}-l\|^{2}_{L^{2}(\omega_{t^{*}})}&= \|u_{k}-l\|^{2}_{L^{2}(\omega_{t^{*}}\backslash \omega_{t'})}+\|u_{k}-l \|^{2}_{L^{2}(\omega_{t'})}\\ &< \bigl(2\sqrt{\epsilon}+\|u_{k}-\tilde{u}\|_{L^{2}(\omega_{t^{*}})}\bigr)^{2}+ \|u_{k}-l\|^{2}_{L^{2}(\omega_{t'})}. \end{aligned} $$
(24)

We can see that for all sufficiently large numbers k, we have the estimates

$$\|u_{k}-\tilde{u}\|_{L^{2}(\omega_{t^{*}})}< \sqrt{\epsilon},\qquad \|u_{k}-l\|_{L^{2}(\omega_{t'})}< \sqrt{\epsilon}, $$

and the right-hand side of (24) is less than 10ϵ. Therefore, \(u_{k}\to l\) strongly in \({L^{2}(\omega_{t^{*}})}\). Consequently, taking into account (19), we get \(\tilde {u}|_{\omega_{t^{*}}}=l\) in \(\omega_{t^{*}}\).

It can be proved analogously that

$$\begin{aligned}& \tilde{U}|_{\omega_{t^{*}}}= b(x_{2},-x_{1})+(c_{1},c_{2}) \quad \mbox{a.e. in }\omega_{t^{*}}, \\& \tilde{\phi}|_{\omega_{t^{*}}}= (-a_{1},-a_{2}) \quad \mbox{a.e. in }\omega_{t^{*}}. \end{aligned}$$

Thus, we conclude that \(\tilde{\xi}|_{\omega_{t^{*}}}\in R(\omega_{t^{*}})\). Therefore, in all possible cases, we have \(\tilde{\xi}|_{\omega_{t^{*}}}\in R(\omega_{t^{*}})\).

It remains to show that ξ̃ satisfies the inequality \(-\tilde{U}\nu\geq h|\tilde{\phi}\nu|\) on γ. In view of (20), we can extract subsequences once again and obtain the convergence \(\xi_{n}|_{\gamma}\to\tilde{\xi}|_{\gamma}\) a.e. on γ. Now, passing to the limit, as \(n\to\infty\), in the inequalities

$$-U_{n}\nu\geq h|\phi_{n}\nu| \quad\mbox{on } \gamma, $$

we get that \(-\tilde{U}\nu\geq h|\tilde{\phi}\nu|\) on γ and \(\tilde{\xi}\in K_{t^{*}}\).

Observe that, as \(t_{n} \to t^{*}\), there must exist either a subsequence \(\{t_{n_{l}}\}\) such that \(t_{n_{l}}\leq t^{*}\) for all \(l\in\mathbf{N}\) or, if that is not the case, a subsequence \(\{t_{n_{m}}\}\), \(t_{n_{m}}>t^{*}\) for all \(m\in\mathbf{N}\).

For the first case, we have the subsequence \(\{t_{n_{l}}\}\subset(0,t_{0}]\) such that \(t_{n_{l}}\leq t^{*}\) for all \(l\in\mathbf{N}\). This implies that \(t^{*}>0\). For convenience, we denote this subsequence by \(\{t_{n}\}\). Since \(t_{n}\leq t^{*}\), by property (b) the arbitrary test function \(\chi\in K_{t^{*}}\) also belongs to the set \(K_{t_{n}}\). This property allows us to pass to the limit as \(n\to\infty\) in the following inequalities with the test functions \(\chi\in K_{t^{*}}\):

$$\xi_{n}\in K_{t_{n}}, \quad B(\Omega,\xi_{n},{ \chi}-{\xi}_{n})\geq \int _{\Omega}F(\chi-{\xi}_{n})\,d\Omega,\quad t_{n}\in\bigl(0, t^{*}\bigr]. $$

Taking into account the weak convergence of \(\xi_{n}\) to ξ̃, the variational inequality in the limit takes the form

$$B(\Omega,\tilde{\xi},{\chi}-\tilde{\xi})\geq \int _{\Omega}F(\chi-\tilde{\xi})\,d\Omega\quad \forall \chi\in K_{t^{*}}. $$

This means that \(\tilde{\xi}=\xi_{t^{*}}\). To complete the proof for the first case, we have to establish the strong convergence \({\xi_{n}}\to\xi_{t^{*}}\). Substituting \(\chi=2\xi_{t}\) and \(\chi=0\) into the variational inequalities (9) for \(t\in(0,t_{0}]\), we get

$$ \xi_{t}\in K_{t},\quad B(\Omega, \xi_{t},{\xi}_{t})= \int _{\Omega}F{\xi}_{t}\,d\Omega \quad\forall t \in(0,t_{0}]. $$
(25)

In view of (9), this means that the relation

$$ \xi_{t}\in K_{t},\quad B(\Omega, \xi_{t},\chi)\geq \int _{\Omega}F\chi \,d\Omega \quad\forall\chi\in K_{t} $$
(26)

holds for all \(t\in(0,t_{0}]\). Hence, by the weak convergence \(\xi_{n}\to\xi_{t^{*}}\) in \(H(\Omega)\) as \(n\to\infty\) we deduce

$$\lim_{n\to\infty} B(\Omega,\xi_{n},\xi_{n})= \lim_{n\to\infty} \int _{\Omega}F\xi _{n}\,d\Omega= \int _{\Omega}F\xi_{t^{*}}\,d\Omega=B(\Omega, \xi_{t^{*}},\xi_{t^{*}}). $$

Since we have the equivalence of norms (see Remark 1), we can see that \(\xi_{n}\to\xi_{t^{*}}\) strongly in \(H(\Omega)\) as \(n\to\infty\). Thus, in the first case, we get a contradiction to the assumption \(\|\xi_{n}-\xi_{t^{*}}\|\geq\epsilon\) for all \(n\in\mathbf{N}\).

Consider the second case, that is, we suppose that the elements of the subsequence \(\{t_{n_{m}}\}\) satisfy \(t_{n_{m}}>t^{*}\) for all \(m\in\mathbf{N}\). For convenience, we keep the same notation for the subsequence. Then we have \(t_{n}\to t^{*}\) and \(t_{n}>t^{*}\). Taking into account the results at the beginning of the proof, we have that \(\xi_{n}\to\tilde{\xi}\) weakly in \(H(\Omega)\) as \(n\to\infty\). For instance, we will prove that \(\xi_{n}\to\tilde{\xi}\) strongly in \(H(\Omega)\) as \(n\to\infty\). In view of the weak convergence \(\xi_{n}\to\tilde{\xi}\) in \(H(\Omega)\) as \(n\to\infty\), from (25) we deduce

$$ \lim_{n\to\infty} B(\Omega,{\xi}_{n}, \xi_{n})= \int _{\Omega}F\tilde{\xi}\,d\Omega. $$
(27)

Next, substituting \(\chi=\xi_{t'}\in K_{t'}\subset K_{t}\) for arbitrary fixed numbers \(t,t'\in(0,t_{0}]\) such that \(t'\geq t\) into (26) as the test function, we arrive at the inequality

$$B(\Omega,{\xi}_{t},\xi_{t'})\geq \int _{\Omega}F\xi_{t'}\,d\Omega. $$

Therefore, we conclude that for all \(t_{n}\) and \(t_{m}\) satisfying \(t_{n}\leq t_{m}\),

$$ B(\Omega,{\xi}_{n},\xi_{m})\geq \int _{\Omega}F\xi_{m} \,d\Omega. $$
(28)

Fix an arbitrary value m in (28) and pass to the limit in the last relation as \(n\to\infty\). As a result, we have

$$ B(\Omega,\tilde{\xi},\xi_{m})\geq \int _{\Omega}F\xi_{m} \,d\Omega. $$
(29)

Passing to the limit in (29) as \(m\to\infty\), we find

$$B(\Omega,\tilde{\xi},\tilde{\xi})\geq \int _{\Omega}F\tilde{\xi}\,d\Omega. $$

This inequality, the formula (27), and the weak lower semicontinuity of the bilinear form \(B(\Omega,\cdot,\cdot)\) yield the chain of relations

$$B(\Omega,\tilde{\xi},\tilde{\xi})\geq \int _{\Omega}F\tilde{\xi}\,d\Omega=\lim_{n\to\infty} B( \Omega,{\xi}_{n},{\xi}_{n})\geq B(\Omega,\tilde{\xi},\tilde{ \xi}). $$

This means that

$$B(\Omega,\tilde{\xi},\tilde{\xi})= \lim_{n\to\infty} B(\Omega,{ \xi}_{n},{\xi}_{n}). $$

Again, by the equivalence of norms (see Remark 1) we deduce that \(\xi_{n}\to\tilde{\xi}\) strongly in \(H(\Omega)\) as \(n\to\infty\).

By Lemma 1, for any \({\eta}\in K_{t^{*}}\) there exist a subsequence \(\{t_{k}\}=\{t_{n_{k}}\}\subset\{t_{n}\}\) and a sequence of functions \(\{{\eta}_{k}\}\) such that \({\eta}_{k}\in K_{t_{k}}\) and \({\eta}_{k}\to{\eta}\) weakly in \(H(\Omega)\) as \(k\to\infty\).

The properties established for the convergent sequences \(\{{\eta}_{k}\}\) and \(\{\xi_{n}\}\) allow us to pass to the limit as \(k\to\infty\) in following inequalities derived from (9) for \(t_{k}\) and with test functions \({\eta}_{k}\):

$$B(\Omega,{\xi}_{k},{\eta}_{k}-{\xi}_{k})\geq \int _{\Omega}F({\eta}_{k}-{\xi}_{k})\,d \Omega. $$

As a result, we have

$$B(\Omega,\tilde{\xi},{\eta}-\tilde{\xi})\geq \int _{\Omega}F({\eta}-\tilde{\xi})\,d\Omega\quad \forall {\eta}\in K_{t^{*}}. $$

The unique solvability of this variational inequality implies that \(\tilde{\xi}=\xi_{t^{*}}\). Therefore, in either case, there exists a subsequence \(\{t_{n_{k}}\}\subset\{t_{n}\}\) such that \(t_{k}\to t^{*}\), \(\xi_{k}\to\xi_{t^{*}}\) strongly in \(H(\Omega)\), which is a contradiction. The lemma is proved. □

4 Conclusion

The existence of a solution to the optimal control problem (13) is proved. For that problem, the cost functional \(J(t)\) characterizes the deviation of the displacement vector from a given function ξ∗, whereas the size parameter t of the rigid inclusion is chosen as the control function.

Lemmas 1 and 2 establish a qualitative connection between the contact problems for plates with rigid inclusions of varying size. In particular, it is shown that as the size parameter of volume rigid inclusion tends to zero, the solutions of the contact problems converge to the solution of the contact problem for a plate containing a thin rigid inclusion.

In contrast to the classical Kirchhoff-Love theory of plates, the Timoshenko-type plate theories take into account the transversal shear deformation and rotation inertia. Therefore, this model is more accurate, particularly, for moderately thin plates and when transverse shear plays a significant role; see [33, 34]. The reference [35] is devoted to the construction of the Timoshenko-Reissner theories by the asymptotic method. In this work, for the dynamic case, a method is suggested for the extension of the range of applicability of the Timoshenko-Reissner theory.