1 Introduction

First, we give some definitions for the main results.

Definition 1.1

Let C be a nonempty subset of a Banach space X. A mapping \(T :C \to C\) is said to be:

  1. (i)

    nonexpansive if

    $$\Vert Tx - Ty \Vert \leq \Vert x - y \Vert , $$

    for all \(x, y \in C\);

  2. (ii)

    quasi-nonexpansive if

    $$\Vert Tx - p \Vert \leq \Vert x - p \Vert , $$

    for each \(p \in F(T)\) and for all \(x\in C\), where \(F(T)= \{x \in C; Tx = x \}\) denotes the set of fixed points of T.

In 2008, Suzuki [1] introduced a class of single-valued mappings, called Suzuki-generalized nonexpansive mappings, as follows.

Definition 1.2

Let T be a mapping on a subset of a Banach space X. Then T is said to satisfy condition \((C)\) if

$$\frac{1}{2} \Vert x - T x\Vert \leq \Vert x - y \Vert \quad \text{implies} \quad \Vert Tx - Ty \Vert \leq \Vert x - y \Vert , $$

for all \(x,y \in C\).

From the following examples, we know that condition \((C)\) is weaker than nonexpansiveness and stronger than quasi-nonexpansiveness, that is, every nonexpansive mapping T satisfies condition \((C)\) and if the mapping T satisfies condition \((C)\) with \(F(T) \neq\phi\), then it is a quasi-nonexpansive.

Example 1.3

[1]

Define a mapping T on \([0,3]\) by

$$Tx = \textstyle\begin{cases} 0, &\mbox{if } x \neq3, \\ 1, &\mbox{if } x = 3. \end{cases} $$

Then T satisfies condition \((C)\), but T is not nonexpansive.

Example 1.4

[1]

Define a mapping T on \([0,3]\) by

$$Tx = \textstyle\begin{cases} 0, & \mbox{if } x \neq3, \\ 2, & \mbox{if } x = 3. \end{cases} $$

Then \(F(T)= \{0\} \neq\phi\) and T is quasi-nonexpansive, but T does not satisfy condition \((C)\).

In [1], Suzuki proved the existence of the fixed point and convergence theorems for mappings satisfying condition \((C)\) in Banach spaces. In the same space setting under certain conditions Dhompongsa et al. [2] improved the results of Suzuki [1] and obtained a fixed point result for mappings with condition \((C)\).

In 2011, Karapınar et al. [3], proposed some new classes of mappings which significantly generalized the notion of Suzuki-type nonexpansive mappings as follows.

Definition 1.5

Let C be a nonempty subset of a metric space \((X, d)\). The mapping \(T: C \to C\) is said to be:

  1. (i)

    a Suzuki-Ciric mapping SCC [3] if

    $$\frac{1}{2} d(Tx, Ty) \leq d(x, y)\quad \text{implies}\quad d(Tx, Ty) \leq M(x, y), $$

    where \(M(x, y) = \max\{d(x, y), d( x, Tx), d( y, Ty), d( x, Ty), d( y, Tx) \} \) for all \(x, y \in C\);

  2. (ii)

    a Suzuki-KC mapping SKC if

    $$\frac{1}{2} d(Tx, Ty) \leq d( x, y)\quad \text{implies}\quad d(Tx, Ty) \leq N(x, y), $$

    where \(N(x, y) = \max \{d(x, y),\frac{d(x, Tx) + d(y, Ty)}{2}, \frac {d(x, Ty)+ d(y, Tx)}{2} \} \) for all \(x, y \in C\);

  3. (iii)

    a Kannan-Suzuki mapping KSC if

    $$\frac{1}{2} d(Tx, Ty) \leq d(x, y)\quad \text{implies}\quad d(Tx, Ty) \leq \frac{d(x, Tx) + d(y, Ty)}{2} $$

    for all \(x, y \in C\);

  4. (iv)

    a Chatterjea-Suzuki mapping CSC if

    $$\frac{1}{2} d(T x, T y) \leq d(x, y)\quad \text{implies}\quad d(Tx, Ty) \leq \frac{d(y, Tx) + d(x, Ty)}{2} $$

    for all \(x, y \in C\).

From the above definition, it is clear that every nonexpansive mapping satisfies condition \(SKC\), but the converse is not true, as becomes clear from the following examples.

Example 1.6

[3]

Define a mapping T on \([0,4]\) by

$$Tx = \textstyle\begin{cases} 0, & \mbox{if } x \neq4, \\ 1, & \mbox{if } x = 4, \end{cases} $$

T satisfies both the \(SCC\) condition and the \(SKC\) condition but T is not nonexpansive.

Example 1.7

[3]

Define a mapping T on \([0,4]\) by

$$Sx = \textstyle\begin{cases} 0,& \mbox{if } x \neq4, \\ 3,& \mbox{if } x = 4, \end{cases} $$

S is quasi-nonexpansive and \(F(S) \neq\phi\) but S does not satisfy the \(SKC\) condition.

Example 1.8

Consider the space \(X= \{(0,0), (0,1), (1,1), (1,2)\}\) with \(\ell ^{\infty}\) metric,

$$d\bigl( (x_{1},y_{1}), (x_{2}, y_{2}) \bigr) =\max\bigl\{ \vert x_{1} -y_{1} \vert, \vert y_{1} - y_{2} \vert\bigr\} . $$

Define a mapping T on X by

$$T(x) = \textstyle\begin{cases} (1,1), &\text{if } (x,y) \neq(0,0),\\ (0,1), &\text{if } (x, y) =(0,0). \end{cases} $$

T obeys condition \(SKC\). Suppose that \(( x, y) =(0, 0)\) and \((x, y) = (1,1)\), then

$$\frac{1}{2} d\bigl(T(0,0), (0,0) \bigr) \leq d\bigl((0,0), (1,1) \bigr) $$

and

$$\begin{aligned} \begin{aligned} N\bigl((0,0), (1,1)\bigr) = {}& \max \biggl\{ d\bigl((0,0), (1,1)\bigr), \frac{1}{2} \bigl[d\bigl(T(0,0), (0,0)\bigr) + d\bigl(T(1,1),(1,1)\bigr) \bigr], \\ &{} \frac{1}{2} \bigl[d\bigl(T (1,1),(0,0)\bigr) + d\bigl(T(0,0), (1,1) \bigr) \bigr] \biggr\} \\ ={}& 1, \end{aligned} \end{aligned}$$

thus

$$d\bigl(T(0,0), T(1,1)\bigr) =1 \leq N\bigl((0,0), (1,1)\bigr)=1. $$

One can check that the condition of the \(SKC\)-mapping holds for the other point of the space X. Note that \(F(T) = \{(1,1)\} \neq\phi\), and \(F(T)\) is closed and convex.

In the framework of \(\operatorname {CAT}(0)\) spaces one gave some characterization of existing fixed point results for mappings with condition \((C)\). In [4], Abbas et al. extended the result of Nanjaras et al. [5] for the class of \(SKC\)-mappings and proved some strong and Δ-convergence results for a finite family of \(SKC\)-mappings using an Ishikawa-type iteration process in the framework of \(\operatorname {CAT}(0)\) spaces (see [4]).

On the other hand, the following fixed point iteration processes have been extensively studied by many authors for approximating either fixed points of nonlinear mappings (when these mappings are already known to have fixed points) or solutions of nonlinear operator equations.

(M) The Mann iteration process (see [6, 7]) is defined as follows:

For C, a convex subset of Banach space X, and a nonlinear mapping T of C into itself, for each \(x_{0}\in C\), the sequence \(\{ x_{n}\} \) in C is defined by

$$\begin{aligned} x_{n+1} =& ( 1- \alpha_{n}) x_{n} + \alpha_{n} Tx_{n} = M(x_{n}, \alpha _{n}, T),\quad n \in\mathbb{N}, \end{aligned}$$
(1.1)

where \(\{\alpha_{n}\}\) is a real sequence in \([0, 1]\) which satisfies the following conditions:

(M1):

\(0 \leq\alpha_{n} <1 \),

(M2):

\(\lim_{n\to \infty} \alpha_{n} = 0\),

(M3):

\(\sum_{n =1}^{\infty} \alpha_{n} = \infty\).

In some applications condition (M3) is replaced by the condition \(\sum_{n=1}^{\infty} \alpha_{n} ( 1-\alpha_{n}) = \infty\).

(I) The Ishikawa iteration process (see [6, 8]) is defined as follows:

With C, X, and T as in (M), for each \(x_{0}\in C\), the sequence \(\{ x_{n} \}\) in C is defined by

$$\begin{aligned} x_{n+1} = &( 1- \alpha_{n}) x_{n} + \alpha_{n} T\bigl[(1-\beta_{n}) x_{n} + \beta_{n} Tx_{n}\bigr],\quad n \in\mathbb{N}, \end{aligned}$$
(1.2)

where \(\{\alpha_{n}\}\) and \(\{\beta_{n}\}\) are sequences in \([0,1]\) which satisfy the following conditions:

(I1):

\(0\leq\alpha_{n} \leq \beta_{n} < 1\),

(I2):

\(\lim_{n \to\infty} \beta_{n} =0\),

(I3):

\(\sum_{n =1}^{\infty} \alpha_{n} \beta_{n} = \infty\).

It is clear that the process (M) is not a special case of the process (I) because of condition (I1). In some papers (see [9–13]) condition (I1) \(0\leq\alpha_{n} \leq\beta_{n} < 1\) has been replaced by the general condition (\(\mathrm{I}_{1}^{'}\)) \(0< \alpha _{n}, \beta_{n} <1\). With this general setting, the process (I) is a natural generalization of the process (M). It is observed that, if the process (M) is convergent, then the process (I) with condition (\(\mathrm{I}_{1}^{'}\)) is also convergent under suitable conditions on \(\alpha_{n}\) and \(\beta_{n}\).

Recently, Agarwal et al. [14] introduced the S-iteration process as follows. For C, a convex subset of a linear space X, and T be a mapping of C into itself, the iterative sequence \(\{x_{n}\}\) of the S-iteration process is generated from \(x_{0} \in C\) is defined by

$$ \textstyle\begin{cases} x_{n+1} = ( 1- \alpha_{n}) Tx_{n} + \alpha_{n} Ty_{n}, \\ y_{n} = ( 1- \beta_{n}) x_{n} + \beta_{n} Tx_{n},\quad n \in\mathbb{N}, \end{cases} $$
(1.3)

where \(\{\alpha_{n}\}\) and \(\{\beta_{n}\}\) are sequences in \((0, 1)\) satisfying the condition

$$\sum_{n =0}^{\infty} \alpha_{n} \beta_{n} ( 1-\beta_{n})= \infty. $$

It is easy to see that neither the process (M) nor the process (I) reduces to an S-iteration process and vice versa. Thus, the S-iteration process is independent of the Mann [7] and Ishikawa [8] iteration processes (see [6, 14, 15]).

It is observed that the rate of convergence of the S-iteration process is similar to the Picard iteration process, but faster than the Mann iteration process for a contraction mapping (see [6, 14, 15]).

On the other hand, in [16], Leuştean proved that \(\operatorname {CAT}(0)\) spaces are uniformly convex hyperbolic spaces with a modulus of uniform convexity \(\eta(r, \varepsilon) = \frac{\varepsilon^{2}}{8}\) quadratic in ε. Therefore, we know that the class of uniformly convex hyperbolic spaces is a generalization of both uniformly convex Banach spaces and \(\operatorname {CAT}(0)\) spaces.

We consider the following definition of a hyperbolic space introduced by Kohlenbach [17], and, also, Zhao et al. [18] and Kim et al. [19] got some convergence results in a hyperbolic space setting.

Definition 1.9

A hyperbolic space \((X, d, W)\) is a metric space \((X, d)\) together with a convexity mapping \(W: X^{2} \times[0,1] \to X\) satisfying:

  1. (W1)

    \(d( u, W(x, y, \alpha)) \leq\alpha d( u, x) + ( 1-\alpha ) d( u, y)\);

  2. (W2)

    \(d(W(x, y, \alpha), W(x, y,\beta)) = \vert\alpha- \beta \vert d( x, y)\);

  3. (W3)

    \(W(x, y, \alpha) = W(y, x, 1-\alpha)\);

  4. (W4)

    \(d( W(x, z, \alpha), W(y, w, \alpha))\leq(1-\alpha) d(x, y)+\alpha d(z, w)\),

for all \(x, y, z, w \in X\) and \(\alpha, \beta\in[0,1]\).

A metric space is said to be a convex metric space in the sense of Takahashi [20], where a triple \((X, d, W) \) satisfies only (W1) (see [21]). We get the notion of the space of hyperbolic type in the sense of Goebel and Kirk [22], where a triple \((X, d, W)\) satisfies (W1)-(W3). Condition (W4) was already considered by Itoh [23] under the name of ‘condition III’ and it is used by Reich and Shafrir [24] and Kirk [25] to define their notions of hyperbolic spaces.

The class of hyperbolic spaces include normed spaces and convex subsets thereof, the Hilbert space ball equipped with the hyperbolic metric [26], the Hadamard manifold, and the \(\operatorname {CAT}(0)\) spaces in the sense of Gromov (see [27]).

A subset C of hyperbolic space X is convex if \(W( x, y, \alpha) \in C\) for all \(x, y \in C\) and \(\alpha\in[0,1]\). If \(x, y \in X\) and \(\lambda\in[0,1]\), then we use the notation \((1-\lambda)x \oplus\lambda y\) for \(W(x, y, \lambda)\). The following holds even for the more general setting of a convex metric space [20, 21]: for all \(x, y\in X\) and \(\lambda\in[0,1]\),

$$d\bigl( x, (1-\lambda)x \oplus\lambda y\bigr) = \lambda d( x, y) $$

and

$$d\bigl( y, (1-\lambda)x \oplus\lambda y\bigr)= ( 1-\lambda) d( x, y). $$

A hyperbolic space \((X, d, W)\) is uniformly convex [16] if, for any \(r > 0\) and \(\varepsilon\in(0, 2]\), there exists \(\delta \in(0, 1]\) such that, for all \(a, x, y \in X\),

$$\begin{aligned} d \biggl(\frac{1}{2} x \oplus\frac{1}{2} y, a \biggr) \leq& ( 1- \delta ) r, \end{aligned}$$

provided \(d(x, a) \leq r\), \(d(y, a) \leq r\), and \(d(x, y) \geq \varepsilon r\).

A mapping \(\eta: (0, \infty) \times(0, 2] \to(0,1]\) providing such a \(\delta= \eta(r, \varepsilon)\) for given \(r>0\) and \(\varepsilon \in(0, 2]\), is called a modulus of uniform convexity. We say that η is monotone if it decreases with r for fixed ε.

The purpose of this paper is to prove some strong and Δ-convergence theorems of the S-iteration process which is generated by \(SKC\)-mappings in uniformly convex hyperbolic spaces. Our results can be viewed as an extension and a generalization of several well-known results in Banach spaces as well as \(\operatorname {CAT}(0)\) spaces (see [1–6, 15, 21, 28–30]).

2 Preliminaries

First, we give the concept of Δ-convergence and some of its basic properties.

Let C be a nonempty subset of metric space \((X, d)\) and let \(\{ x_{n}\}\) be any bounded sequence in X. Let \(\operatorname {diam}(C)\) denote the diameter of C. Consider a continuous functional \(r_{a}(\cdot, \{x_{n}\}): X \to\mathbb{R^{+}}\) defined by

$$r_{a}\bigl( x, \{x_{n}\}\bigr) = \limsup _{n \to\infty} d( x_{n}, x),\quad x \in X. $$

Then the infimum of \(r_{a} (\cdot, \{x_{n}\})\) over C is said to be the asymptotic radius of \(\{x_{n}\}\) with respect to C and is denoted by \(r_{a}(C, \{x_{n}\})\).

A point \(z \in C\) is said to be an asymptotic center of the sequence \(\{x_{n}\}\) with respect to C if

$$r_{a} \bigl( z, \{x_{n}\}\bigr) = \inf \bigl\{ r_{a} \bigl( x, \{x_{n}\}\bigr): x \in C \bigr\} , $$

the set of all asymptotic centers of \(\{x_{n}\}\) with respect to C is denoted by \(\operatorname {AC}(C, \{x_{n}\})\). This is the set of minimizers of the functional \(r(\cdot,\{x_{n}\})\) and it may be empty or a singleton or contain infinitely many points.

If the asymptotic radius and the asymptotic center are taken with respect to X, then these are simply denoted by \(r_{a}( X, \{x_{n}\}) = r_{a}( \{x_{n}\})\) and \(\operatorname {AC}(X, \{x_{n}\})= \operatorname {AC}(\{x_{n}\})\), respectively. We know that, for \(x \in X\), \(r_{a}( x, \{x_{n}\}) = 0 \) if and only if \(\lim_{n \to\infty} x_{n} = x\).

It is well known that every bounded sequence has a unique asymptotic center with respect to each closed convex subset in uniformly convex Banach spaces and even \(\operatorname {CAT}(0)\) spaces.

The following lemma is due to Leuştean [31] and we know that this property also holds in a complete uniformly convex hyperbolic space.

Lemma 2.1

[31]

Let \((X, d, W)\) be a complete uniformly convex hyperbolic space with monotone modulus of uniform convexity η. Then every bounded sequence \(\{x_{n}\}\) in X has a unique asymptotic center with respect to any nonempty closed convex subset C of X.

Definition 2.2

A sequence \(\{x_{n}\}\) in a hyperbolic space X is said to be Δ-convergent to \(x \in X\), if x is the unique asymptotic center of \(\{u_{n}\}\) for every subsequence \(\{u_{n}\}\) of \(\{x_{n}\}\). In this case, we write Δ-\(\lim_{n} x_{n} = x\) and we call x the Δ-limit of \(\{x_{n}\}\).

Recall that a bounded sequence \(\{x_{n}\}\) in a complete uniformly convex hyperbolic space with a monotone modulus of uniform convexity η is said to be regular if \(r_{a}(X, \{x_{n}\}) = r_{a}(X, \{ u_{n}\})\) for every subsequence \(\{u_{n}\}\) of \(\{x_{n}\}\).

It is well known that every bounded sequence in a Banach space (or complete \(\operatorname {CAT}(0)\) space (see [28])) has a regular subsequence. Since every regular sequence Δ-converges, we see immediately that every bounded sequence in a complete uniformly convex hyperbolic space with a monotone modulus of uniform convexity η has a Δ-convergent subsequence. Notice that (see [32], Lemma 1.10) given a bounded sequence \(\{x_{n}\} \subset X\), where X is a complete uniformly convex hyperbolic space with a monotone modulus of uniform convexity η, such that Δ-\(\lim_{n} x_{n} = x\) and for any \(y \in X\) we have \(y \neq x\), then

$$\lim_{n \to\infty} d( x_{n}, x) < \lim_{n \to\infty} d( y_{n}, y). $$

Clearly, X satisfies the above condition, which is known in Banach space theory as the Opial property.

Lemma 2.3

[33]

Let \((X, d, W)\) be a uniformly convex hyperbolic space with monotone modulus of uniform convexity η. Let \(x \in X\) and \(\{t_{n}\}\) be a sequence in \([a, b]\) for some \(a, b \in(0,1)\). If \(\{x_{n}\}\) and \(\{ y_{n}\}\) are sequences in X such that

$$\begin{aligned}& \limsup_{ n \to\infty} d( x_{n}, x) \leq c,\qquad \limsup_{ n \to \infty} d( y_{n}, x) \leq c, \\& \lim_{ n \to\infty} d\bigl(W(x_{n}, y_{n}, t_{n} ), x \bigr) =c, \end{aligned}$$

for some \(c \geq0\), then \(\lim_{ n \to\infty} d( x_{n}, y_{n} ) =0\).

3 Main results

Now we will give the definition of \(Fej\acute{e}r\) monotone sequences.

Definition 3.1

Let C be a nonempty subset of hyperbolic space X and let \(\{x_{n}\}\) be a sequence in X. Then \(\{x_{n}\}\) is \(Fej\acute{e}r\) monotone with respect to C if for all \(x \in C\) and \(n \in\mathbb{N}\),

$$d(x_{n+1}, x) \leq d(x_{n}, x). $$

Example 3.2

Let C be a nonempty subset of X and let \(T : C \to C\) be a quasi-nonexpansive (in particular, nonexpansive) mapping such that \(F(T) \neq\phi\). Then the Picard iterative sequence \(\{x_{n}\}\) is \(Fej\acute{e}r\) monotone with respect to \(F(T)\).

Proposition 3.3

[19]

Let C be a nonempty subset of X and let \(\{x_{n}\}\) be a \(Fej\acute{e}r\) monotone sequence with respect to C. Then we have the following:

  1. (1)

    \(\{x_{n}\}\) is bounded;

  2. (2)

    the sequence \(\{d(x_{n}, p)\}\) is decreasing and convergent for all \(p \in F(T)\).

We now define the S-iteration process in hyperbolic spaces (see [19]):

Let C be a nonempty closed convex subset of a hyperbolic space X and let T be a mapping of C into itself. For any \(x_{1} \in C\), the sequence \(\{x_{n}\}\) of the S-iteration process is defined by

$$ \textstyle\begin{cases} x_{n+1} = W(Tx_{n}, Ty_{n}, \alpha_{n}), \\ y_{n} = W(x_{n}, Tx_{n}, \beta_{n}), \quad n \in\mathbb{N}, \end{cases} $$
(3.1)

where \(\{\alpha_{n}\}\) and \(\{\beta_{n}\}\) are real sequences such that \(0 < a \leq\alpha_{n} \), \(\beta_{n} \leq b < 1\).

We can easily prove the following lemma from the definition of \(SKC\)-mapping.

Lemma 3.4

Let C be a nonempty closed convex subset of a hyperbolic space X and let \(T :C \to C\) be an \(SKC\)-mapping. If \(\{x_{n}\}\) is a sequence defined by (3.1), then \(\{x_{n}\}\) is \(Fej\acute{e}r\) monotone with respect to \(F(T)\).

Proof

Let \(p \in F(T)\). Then by (3.1), we have

$$\begin{aligned} d( y_{n}, p) =& d\bigl( W(x_{n}, Tx_{n}, \beta_{n}), p\bigr) \\ \leq& ( 1- \beta_{n}) d( x_{n}, p) + \beta_{n} d(Tx_{n}, p) \\ \leq& ( 1- \beta_{n}) d( x_{n}, p) + \beta_{n} \bigl[5 d( p, Tp) + d( x_{n}, p) \bigr] \\ \leq& d(x_{n}, p). \end{aligned}$$
(3.2)

Again, using (3.1) and (3.2), we have

$$\begin{aligned} d( x_{n+1}, p ) =& d\bigl(W(Tx_{n}, Ty_{n}, \alpha_{n}), p\bigr) \\ \leq& ( 1- \alpha_{n})d( Tx_{n} , p) + \alpha_{n} d( T y_{n} , p) \\ \leq& ( 1- \alpha_{n})d( Tx_{n} , p) + \alpha_{n} \bigl[5 d( p, TP) + d( y_{n} , p)\bigr] \\ \leq& ( 1- \alpha_{n})d( x_{n} , p) + \alpha_{n} d( y_{n} , p) \\ \leq& ( 1- \alpha_{n})d( x_{n} , p) + \alpha_{n} d( x_{n} , p) \\ = & d(x_{n}, p), \end{aligned}$$
(3.3)

for all \(p \in F(T)\). Thus, \(\{x_{n}\}\) is \(Fej\acute{e}r\) monotone with respect to \(F(T)\). □

Lemma 3.5

Let C be a nonempty closed convex subset of a complete uniformly convex hyperbolic space with monotone modulus of uniform convexity η and let \(T :C \to C\) be an \(SKC\)-mapping. If \(\{x_{n}\}\) is the sequence defined by (3.1), then \(F(T)\) is nonempty if and only if \(\{x_{n}\}\) is bounded and \(\lim_{n \to\infty}d(x_{n}, Tx_{n}) = 0\).

Proof

Let \(F(T)\) be nonempty and \(p \in F(T)\). Then by Lemma 3.4, \(\{ x_{n}\}\) is \(Fej\acute{e}r\) monotone with respect to \(F(T)\). Hence, by Proposition 3.3, \(\{x_{n}\}\) is bounded and \(\lim_{n \to\infty}d(x_{n}, p)\) exists. Let \(\lim_{n \to\infty }d(x_{n}, p) = c \geq0\). If \(c =0\), then we obviously have

$$\begin{aligned} d( x_{n} , Tx_{n}) \leq& d( x_{n}, p) + d( Tx_{n} , p) \\ \leq& d( x_{n} , p) + 5 d( p , Tp) + d( x_{n} , p) \\ \leq& 2 d( x_{n}, p). \end{aligned}$$

Taking the limit supremum on both sides of above inequality, we have

$$\lim_{n \to\infty} d( x_{n} , Tx_{n}) = 0. $$

Let \(c>0\). Since T is an \(SKC\)-mapping, we have

$$d(Tp, Ty_{n}) \leq d(p, y_{n}) $$

and

$$d(Tp, Tx_{n}) \leq d(p, x_{n}). $$

Therefore,

$$\begin{aligned} d( Tx_{n}, p ) \leq& d(Tx_{n}, Tp) \\ \leq& d(x_{n}, p) \end{aligned}$$

for all \(n \in\mathbb{N}\). Taking the limit supremum on both sides, we get

$$\begin{aligned} \limsup_{n \to\infty} d(Tx_{n}, p) \leq c, \end{aligned}$$
(3.4)

for \(c>0\). Similarly, we have

$$\begin{aligned} \limsup_{n \to\infty} d(Ty_{n}, p) \leq c. \end{aligned}$$
(3.5)

Taking the limit supremum on both sides (3.2), we have

$$\begin{aligned} \limsup_{n \to\infty} d(y_{n}, p) \leq c. \end{aligned}$$
(3.6)

Since

$$\begin{aligned} c =& \limsup_{n \to\infty} d( x_{n+1} , p) \\ =& \limsup_{n \to\infty} \bigl\{ d \bigl(W(Tx_{n} , Ty_{n}, \alpha_{n}),p \bigr) \bigr\} \\ \leq& \limsup_{ n \to\infty} \bigl\{ (1-\alpha_{n}) d(Tx_{n} , p) + \alpha_{n} d( T y_{n}, p) \bigr\} \\ \leq& ( 1- \alpha_{n}) \limsup_{ n \to\infty} d(Tx_{n} , p) + \alpha_{n} \limsup_{ n \to\infty} d( T y_{n}, p), \end{aligned}$$

from (3.4) and (3.5), we have

$$\begin{aligned} c \leq& \bigl((1-\alpha_{n}) c + \alpha_{n} c \bigr)=c. \end{aligned}$$

Thus,

$$\begin{aligned} \lim_{n \to\infty} \bigl\{ d \bigr(W(Tx_{n} , Ty_{n}, \alpha_{n}),p \bigl) \bigr\} = c, \end{aligned}$$

for \(c>0\). Hence, it follows from Lemma 2.3 that

$$\begin{aligned} \lim_{n \to\infty} d(Tx_{n}, Ty_{n}) = 0. \end{aligned}$$
(3.7)

Next,

$$\begin{aligned} d(x_{n+1}, Tx_{n} ) & = d \bigl(W(Tx_{n}, Ty_{n}, \alpha_{n}), Tx_{n}\bigr) \\ & \leq b d(Ty_{n}, Tx_{n}) \\ & \to 0, \quad \text{as } n \to\infty. \end{aligned}$$
(3.8)

Hence, from (3.7) and (3.8), we have

$$\begin{aligned} d(x_{n+1}, Ty_{n}) & \leq d(x_{n+1}, Tx_{n}) + d(Tx_{n}, Ty_{n}) \\ & \to 0, \quad \text{as } n \to\infty. \end{aligned}$$
(3.9)

Now we observe that

$$\begin{aligned} d(x_{n+1}, p) \leq& d(x_{n+1}, Ty_{n}) + d(Ty_{n}, p) \\ \leq& d(x_{n+1}, Ty_{n}) + d(y_{n}, p), \end{aligned}$$

which yields

$$\begin{aligned} c \leq\liminf_{n \to\infty} d(y_{n}, p). \end{aligned}$$
(3.10)

From inequalities (3.6) and (3.10), we have

$$\begin{aligned} \lim_{n \to\infty} d(y_{n}, p) = c. \end{aligned}$$

Thus, from (3.1), we have

$$\begin{aligned} \lim_{n \to\infty} d\bigl(W(x_{n}, Tx_{n}, \beta_{n}), p\bigr) = c, \end{aligned}$$

which implies

$$\begin{aligned} \lim_{n \to\infty} d(x_{n}, Tx_{n}) = 0. \end{aligned}$$
(3.11)

Conversely, suppose that \(\{x_{n}\}\) is bounded and \(\lim_{n \to\infty} d(x_{n}, Tx_{n}) = 0\).

Let \(\operatorname {AC}(C, \{x_{n}\})= \{x\}\) be a singleton. Then, by Lemma 2.1, \(x \in C\). Since T is an \(SKC\)-mapping,

$$d(x_{n}, Tx) \leq5 d(x_{n}, Tx_{n}) + d(x_{n}, x), $$

which implies that

$$\begin{aligned} r_{a}\bigl(Tx, \{x_{n}\}\bigr) =& \limsup _{ n \to\infty} d( x_{n} , Tx) \\ \leq& \limsup_{ n \to\infty} \bigl\{ 5 d( x_{n}, Tx_{n}) + d( x_{n} , x) \bigr\} \\ \leq& \limsup_{ n \to\infty} d( x_{n} , x) \\ =& r_{a}\bigl( x, \{x_{n}\} \bigr). \end{aligned}$$

By using the uniqueness of the asymptotic center, \(Tx = x\), so x is a fixed point of T. Hence, \(F(T)\) is nonempty. □

Now, we are in a position to prove the Δ-convergence theorem.

Theorem 3.6

Let C be a nonempty closed convex subset of a complete uniformly convex hyperbolic space X with monotone modulus of uniform convexity η and let \(T : C \to C\) be an \(SKC\)-mapping with \(F(T) \neq\phi\). If \(\{x_{n}\}\) is the sequence defined by (3.1), then the sequence \(\{x_{n}\}\) is Δ-convergent to a fixed point of T.

Proof

From Lemma 3.5, we observe that \(\{x_{n}\}\) is a bounded sequence. Therefore, \(\{x_{n}\}\) has a Δ-convergent subsequence. We now prove that every Δ-convergent subsequence of \(\{x_{n}\}\) has a unique Δ-limit in \(F(T)\). For this, let u and v be Δ-limits of the subsequences \(\{u_{n}\}\) and \(\{ v_{n}\}\) of \(\{x_{n}\}\), respectively. By Lemma 2.1, \(\operatorname {AC}(C, \{ u_{n}\})= \{u\}\) and \(\operatorname {AC}(C, \{v_{n}\})= \{v\}\). Since \(\{u_{n}\}\) is a bounded sequence, from Lemma 3.5, \(\lim_{ n \to\infty} d( u_{n} Tu_{n}) =0\). We have to show that u is a fixed point of T. Since T is an \(SKC\)-mapping,

$$d(u_{n}, Tu) \leq5 d(u_{n}, Tu_{n}) + d(u_{n}, u). $$

Taking the limit supremum on both sides, we have

$$\begin{aligned} r_{a}\bigl(\{u_{n}\}, Tu\bigr) = & \limsup _{n \to\infty} d( u_{n} ,Tu) \\ \leq& \limsup_{n \to\infty} \bigl\{ 5 d(u_{n}, Tu_{n}) + d(u_{n}, u) \bigr\} \\ \leq& \limsup_{n \to\infty} d(u_{n}, u) \\ = & r_{a} \bigl( \{u_{n}\} , u\bigr). \end{aligned}$$

Hence, we have

$$\begin{aligned} r_{a} \bigl( \{u_{n}\}, Tu\bigr) \leq& r_{a} \bigl( \{u_{n}\}, u\bigr). \end{aligned}$$

By uniqueness of the asymptotic center, \(Tu=u\).

Similarly, we can prove that \(Tv=v\). Thus, u and v are fixed points of T. Now we show that \(u =v\). If not, then by the uniqueness of the asymptotic center,

$$\begin{aligned} \limsup_{n \to\infty} d(x_{n},u) = & \limsup _{n \to \infty} d(u_{n}, u) \\ < & \limsup_{n \to\infty} d(u_{n}, v) \\ = & \limsup_{n \to\infty} d(x_{n}, v) \\ = & \limsup_{n \to\infty} d(v_{n}, v) \\ < & \limsup_{n \to\infty} d(v_{n}, u), \\ =& \limsup_{n \to\infty} d( x_{n}, u), \end{aligned}$$

which is a contradiction. Hence \(u =v \). □

Remark 3.7

Theorem 3.6 is an extension of Theorem 3.3 of Abbas et al. [4] from \(\operatorname {CAT}(0)\) space to a uniformly convex hyperbolic space. Theorem 3.6 also holds for the \(KSC\), \(SCC\), and \(CSC\)-mappings.

Now, we will introduce the strong convergence theorems in hyperbolic spaces.

Theorem 3.8

Let C be a nonempty closed convex subset of a complete uniformly convex hyperbolic space X with monotone modulus of uniform convexity η and let \(T : C \to C\) be an \(SKC\)-mapping. If \(\{x_{n}\}\) is the sequence defined by (3.1), then the sequence \(\{x_{n}\}\) converges strongly to some fixed point of T if and only if

$$\liminf_{n \to\infty} D\bigl(x_{n}, F(T)\bigr) = 0, $$

where \(D( x_{n} , F(T)) = \inf_{ x \in F(T)} d( x_{n} , x)\).

Proof

Necessity is trivial. We have to prove only the sufficient part. First, we show that \(F(T)\) is closed, let \(\{x_{n}\}\) be a sequence in \(F(T)\) which converges to some point \(z \in C\). Since T is an \(SKC\)-mapping, we have

$$d(x_{n}, Tz)\leq5 d(Tx_{n}, Tz)+ d( x_{n} , z) \leq d(x_{n}, z). $$

By taking the limit on both sides, we have

$$\lim_{n \to\infty}d(x_{n}, Tz) \leq\lim_{n \to\infty}d(x_{n}, z) = 0. $$

Then, from the uniqueness of the limit, we have \(z = Tz\), so that \(F(T)\) is closed.

Suppose that

$$\begin{aligned} \liminf_{n \to\infty} D\bigl(x_{n}, F(T)\bigr) = 0. \end{aligned}$$

Then, from inequality (3.3), we get

$$\begin{aligned} D\bigl(x_{n+1}, F(T)\bigr) \leq D\bigl(x_{n}, F(T)\bigr). \end{aligned}$$

It follows from Lemma 3.4 and Proposition 3.3 that \(\lim_{n \to\infty}d(x_{n}, F(T))\) exists. Hence we know that

$$\lim_{ n \to\infty} D\bigl(x_{n} , F(T)\bigr) =0. $$

Hence, we can take a subsequence \(\{x_{n_{k}}\}\) of \(\{x_{n}\}\) such that

$$d(x_{n_{k}}, p_{k}) < \frac{1}{2^{k}},\quad \text{for all } k \geq1, $$

where \(\{p_{k}\}\) is in \(F(T)\). By Lemma 3.4, we have

$$d(x_{n_{k+1}}, p_{k}) \leq d(x_{n_{k}}, p_{k}) < \frac{1}{2^{k}}, $$

which implies that

$$\begin{aligned} d(p_{k+1}, p_{k}) \leq& d(p_{k+1}, x_{n_{k+1}}) + d(x_{n_{k+1}}, p_{k}) \\ < & \frac{1}{2^{k+1}} + \frac{1}{2^{k}} \\ < & \frac{1}{2^{k-1}}. \end{aligned}$$

This means that \(\{p_{k}\}\) is a Cauchy sequence. Since \(F(T)\) is closed, \(\{p_{k}\}\) is a convergent sequence. Let \(\lim_{k \to\infty}p_{k} = p\). Then we have to show that \(\{x_{n}\}\) converges to p. In fact, since

$$d(x_{n_{k}} , p) \leq d(x_{n_{k}} , p_{k}) + d(p_{k}, p) \to0 \quad \text{as } k \to\infty, $$

we have

$$\lim_{k \to\infty} d(x_{n_{k}} , p) = 0. $$

Since \(\lim_{n \to\infty} d(x_{n} , p)\) exists, the sequence \(\{x_{n}\}\) is convergent to p. □

Next, we will give one more strong convergence theorem by using Theorem 3.8. We recall the definition of condition (I) introduced by Senter and Doston [34].

Let C be a nonempty subset of a metric space \((X, d)\). A mapping \(T : C\to C\) is said to satisfy condition (I), if there is a nondecreasing function \(f [0, \infty) \to[0, \infty)\) with \(f(0) = 0\), \(f(t) > 0 \) for all \(t \in(0, \infty)\) such that

$$d(x, Tx) \geq f\bigl(D\bigl(x, F(T)\bigr)\bigr), $$

for all \(x \in C\), where \(D( x, F(T)) = \inf\{d(x, p) : p \in F(T)\}\).

Theorem 3.9

Let C be a nonempty closed convex subset of a complete uniformly convex hyperbolic space X with monotone modulus of uniform convexity η and let \(T : C \to C\) be an \(SKC\)-mapping with condition (I) and \(F(T) \neq\phi\). Then the sequence \(\{x_{n}\}\) which is defined by (3.1) converges strongly to some fixed point of T.

Proof

We know that \(F(T)\) is closed from the proof of Theorem 3.8, and from Lemma 3.5 we have \(\lim_{n \to \infty}d(x_{n}, Tx_{n}) = 0\). It follows from condition (I) that

$$\begin{aligned} \lim_{n \to\infty} d( x_{n} , T x_{n}) \geq\lim _{n \to\infty} f\bigl( D\bigl(x_{n} , F(T)\bigr)\bigr), \end{aligned}$$

for a nondecreasing function \(f [0, \infty) \to[0, \infty)\) with \(f(0) = 0\), \(f(t) > 0 \) for all \(t \in(0, \infty)\). Hence, we have

$$\lim_{n \to\infty}f\bigl(D\bigl(x_{n}, F(T)\bigr)\bigr) = 0. $$

Since f is a nondecreasing mapping satisfying \(f (0) = 0\) for all \(t \in(0, \infty)\), we have

$$\lim_{n \to\infty}D\bigl(x_{n}, F(T)\bigr) = 0. $$

Therefore, we can get the desired result from Theorem 3.8. □

Remark 3.10

Theorems 3.6, 3.8, and 3.9 improve and extend the previous known results from Banach spaces and \(\operatorname {CAT}(0)\) spaces to uniformly convex hyperbolic spaces (see [1–6, 15, 21, 28–30], in particular, Theorems 3.1, 3.2, 3.3, and 3.4 in [4]). In our results, we considered the S-iteration which is faster than the other iteration process to approximate the fixed point of underlying mapping in the framework of uniformly convex hyperbolic spaces.

4 Numerical example

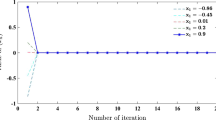
Example 4.1

Let \((X,d) = \mathbb{R}\) with \(d( x, y) = \vert x - y \vert\) and \(C = [0, 4] \subset\mathbb{R}\). Denote

$$\begin{aligned} W( x, y , \alpha) = & \alpha x + ( 1- \alpha) y,\quad \text{for all } x, y \in C, \end{aligned}$$
(4.1)

then \((X, d,W)\) is a complete uniformly convex hyperbolic space with a monotone modulus of uniform convexity and C is a nonempty closed and convex subset of X. Let T be a mapping as defined in Example 1.6.

It is easy to see that T satisfies the \(SKC\) condition and \(0 \in C\) is a fixed point of T. It is observed that it satisfies all conditions in Theorem 3.6. Let \(\{\alpha_{n}\}\) and \(\{\beta_{n}\}\) be constant sequences such that \(\alpha_{n} = \beta_{n} = \frac{1}{2}\) for all \(n \geq0\). From the definition of T the following cases arise.

Case 1: Consider \(x \neq4\), for the sake of simplicity, we can assume that \(x_{0} = 1\). Then by the iteration process (3.1) and the definition of W (4.1), we have

$$\begin{aligned} y_{0} =& W \biggl(x_{0}, Tx_{0}, \frac{1}{2}\biggr) \\ =& \frac{1}{2} (x_{0} + Tx_{0} )= \frac{1}{2} \end{aligned}$$

and

$$\begin{aligned} x_{1} =& W \biggl(Tx_{0}, Ty_{0}, \frac{1}{2}\biggr) \\ =& \frac{1}{2} \biggl(T(1) + T\biggl(\frac{1}{2}\biggr) \biggr) =0 \in F(T). \end{aligned}$$

Case 2: Consider \(x =4\), for the sake of simplicity, we can assume that \(x_{0} = 4\). Then by the iteration process and the definition of W

$$\begin{aligned} y_{0} =& W \biggl(x_{0}, Tx_{0}, \frac{1}{2}\biggr) \\ =& \frac{1}{2} (x_{0} + Tx_{0} )= \frac{1}{2}(4 + 1 ) \\ =& \frac{5}{2} \end{aligned}$$

and

$$\begin{aligned}& x_{1} = W \biggl(Tx_{0}, Ty_{0}, \frac{1}{2}\biggr)= \frac{1}{2} \biggl(T(4) + T\biggl(\frac {5}{2}\biggr) \biggr) \\& \hphantom{x_{1} } = \frac{1}{2} (1 + 0) = \frac{1}{2}, \\& y_{1} = W\biggl(x_{1}, Tx_{1}, \frac{1}{2}\biggr) = \frac{1}{2} \biggl(\frac{1}{2} +T\biggl( \frac{1}{2}\biggr) \biggr)= \frac{1}{4}, \\& x_{2} = W\biggl(Tx_{1} , Ty_{1}, \frac{1}{2}\biggr) = \frac{1}{2}(0+0 ) = 0. \end{aligned}$$

Hence, the sequence \(\{x_{n}\}\) converges to \(0 \in F(T)\).