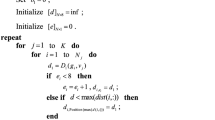1 Introduction

In the field of computer vision, signal, image, and video processing, noise is unfortunately inevitable during data acquisition and transmission. The accuracy of many algorithms significantly relies on well hand-tuned parameter adjustments to account for variations in noise [1–3]. To automate the process and achieve reliable procedures, the capability for accurate noise estimation is essential to motion estimation, edge detection, super-resolution, restoration, shape-from-shading, feature extraction, and object recognition [4–9]. In particular, image noise having a Gaussian-like distribution is quite often encountered, and it is characterized by adding to each pixel a random value obtained from a zero-mean Gaussian distribution, whose variance determines the magnitude of the corrupting noise. This zero-mean property enables such noise to be removed by locally averaging neighboring pixel values [10, 11].

Indeed, many noise reduction algorithms incorporate the knowledge of the noise level in the denoising process and assume that it is known a priori [12–15]. Accordingly, estimation for the amount of noise is critical in these methods, because it enables the process to adapt to the level of noise rather than using fixed values and thresholds. The challenge of noise estimation is to determine whether local image variations are due to color, texture, and lighting changes of images themselves, or caused by the noise. Nevertheless, existing noise estimation algorithms can be broadly classified into three major categories: filtered-based, block-based, and transform-based approaches [4, 5, 11, 16, 17].

In filtered-based methods, an input image is first filtered by a low-pass filter to smooth the structures and suppress the noise in the image [4]. The noise variance is then estimated from the difference between the noisy image and the filtered image. One fundamental problem of filtered-based methods is that the difference image is assumed to be the noise, but this assumption is not always true in general. This is because the low-pass filtered image is not equivalent to the original noise-free image, particularly when the image is with strong structures and complicated details. To minimize the influence and obtain a realistic basis for noise level estimation, Rank et al. [18] proposed to use the vertical and horizontal information of an image to extract the noise detail and histogram information in the corresponding components. However, it has a relatively higher computation load and many user-defined parameters to be set.

For block-based algorithms, an image is tessellated into a number of blocks followed by noise variance computation in a set of homogeneous blocks [5, 17, 19]. The philosophy underlying this approach is that a homogeneous block in an image is treated as a perfectly smooth image block with added noise, which has a relatively higher chance to contain useful visual activities. Consequently, the block with a smaller standard deviation has a weaker variation in intensity, leading to a smoother block. One main difficulty of block-based approaches is how to efficiently identify the homogeneous blocks. Lee and Hoppel [20] estimated noise level by assuming that the smallest standard deviation of a block is equivalent to additive white Gaussian noise. This method is simple but tends to produce overestimation results for small noise cases. Shin et al. [5] split an image into a number of blocks, which were further classified by the standard deviation in intensity. An adaptive Gaussian filtering process was then applied to relatively flat blocks, where the noise was estimated from the difference of the selected blocks between the noisy image and its filtered image.

While noise estimation methods in the first two categories work directly on the pixel intensity in the spatial domain, transform-based methods seek particular features in the transformed domain [21]. For example, the median absolute deviation method [22–24] used wavelet coefficients to estimate noise standard deviation based on the assumption that wavelet coefficients in the diagonal subband HH1 are dominated by noise. This approach provides good estimations for large noise cases, but it can overestimate the noise in small noise cases. The reason for overestimation is that wavelet coefficients in the diagonal subband contain not only added noise but also image details. Subsequently, Li et al. [25] proposed a modified noise estimation algorithm based on the wavelet coefficients in the HH1 subband. Better results were obtained by reducing the estimated original image contribution from HH1 comparing to the traditional methods. Liu and Lin [17] investigated the possibility to estimate noise in the singular value decomposition (SVD) domain. The authors used the tail of singular values to alleviate the influence of the signal in the noise estimation process and demonstrated the effectiveness of their method over wavelet-based approaches. However, due to the use of SVD twice in the estimation procedure, the computation time is more expensive.

Alternatively, there are other methods that estimate noise in various manners [26]. Immerkaer [27] proposed a Laplacian-based noise estimation algorithm, which computes the noise variance by convolving the image with a Laplacian-like mask with zero mean. This approach is fast and performs well on images that are corrupted by high level noise. However, for highly textured images, it perceives thin lines as noise, leading to overestimation. Tai and Yang [28] extended Immerkaer’s work by introducing the Sobel operator for edge detection to exclude the edge pixels. Salmeri et al. [29] introduced different weights to various subregions based on a similarity measure followed by a fuzzy procedure to estimate the variance of noise. Zoran and Weiss [30] proposed a statistical model to estimate the variance of noise and showed the effectiveness on images with low-level noise. Their assumption is that adding noise to images results in changes to kurtosis values throughout the scales. In their approach, the image was first convolved by the DCT filter to produce a response image, from which the variance and kurtosis were estimated. Aja-Fernández et al. [16] presented a noise estimation method based on the mode of local statistics (MLS). The authors demonstrated the efficiency of using the mode of the local sample statistical distribution for the variance estimation of additive noise provided that a great amount of low-variability areas exist in the image.

Among existing noise estimation methods, block-based algorithms are relatively simple and straightforward. Nonetheless, one main issue of this approach is how to effectively identify the homogeneous regions while alleviating the dependence of various noise levels. To address this major challenge and overcome the drawbacks in the existing methods, this paper proposes a new noise estimation algorithm that automatically and efficiently divides an image into a number of homogeneous subregions, which are called superpixels. To reduce noise influences, a statistical decision is then made to select the best superpixel, from which the noise variance is estimated. The ambition is to improve the estimation accuracy in low level noise while maintaining precision for higher level noise comparing to existing methods. The remainder of this paper is organized as follows. In Section 2, the noise model along with the probability density function of the Gaussian noise is described. Section 3 introduces the proposed algorithm that consists of three major phases: superpixel classification, local variance computation, and statistical determination. In Section 4, the performance of this new noise estimation method using a wide variety of images with various scenarios is evaluated and compared with many state-of-the-art methods. Finally, Section 5 discusses the results and Section 6 summarizes the contributions of the current work.

2 Noise model

The fundamental assumption of the noise model is that the image is corrupted by additive, zero-mean white Gaussian noise with an unknown variance given by

$$ I\left(x,\ y\right) = f\left(x,\ y\right) + n\left(x,\ y\right) $$
(1)

where (x, y) represents the coordinates of a pixel under consideration, I(x, y) is the observed image, f(x, y) is the intact image, and n(x, y) is the Gaussian noise, whose probability density function (PDF) can be written as follows:

$$ p(z) = \frac{1}{\sqrt{\ 2\pi}\sigma }{e}^{\hbox{-} {\left(z-\overline{\mathrm{z}}\ \right)}^2/2{\sigma}^2} $$
(2)

where z represents the intensity, \( \overline{\mathrm{z}} \) is the mean of z, and σ is the standard deviation used to control the shape of the distribution.

Figure 1 illustrates two eight-bit images corrupted by additive Gaussian noise with σ = 10 and the corresponding histogram maps. The original image in Fig. 1a has two uniform subregions with intensity values equal to 50 and 200, respectively. It is observed that the histogram distribution has two similar shapes correspondingly centered at the original intensity values after corruption. This is because the Gaussian noise model (Eq. (2)) is actually a normal distribution so that the histogram follows the normal distribution with the same standard deviation in each individual region provided that no influences occur. If the image is further divided into more subregions and the process is repeated as shown in Fig. 1b, the same observation will be obtained as illustrated in the region enclosed by the red box. Rather than estimating the noise level globally in the entire image, this paper proposes to classify the image into several subregions and compute the noise variance locally in each individual region to minimize the influence caused by color, texture, and lighting changes [1, 16, 17, 24].

Fig. 1
figure 1

Two images (a, b) corrupted by Gaussian noise with σ = 10 and the corresponding histogram maps

Full size image

3 Methods

The proposed noise estimation algorithm can be divided into three major phases as shown in Fig. 2 and described as follows.

Fig. 2
figure 2

Flowchart of the proposed noise estimation algorithm

Full size image

3.1 Superpixel classification

The first step in our noise estimation framework is to divide a noisy image into several subregions. Unlike conventional block-based methods, each subregion is not necessary to be a rectangular block and it is usually not. In essence, each region is expected to have similar gray-level, color, and texture characteristics regardless of its geometry. To do this, the normalized cut algorithm [31] is adopted to achieve this goal. The basic idea is to use the theoretic criteria of graph to measure the goodness of an image partition. More specifically, it measures both the total dissimilarity between different groups as well as the total similarity within groups. The optimization of this criterion can be formulated as a generalized eigenvalue problem that can be efficiently solved. The concept of this perceptual grouping technique is briefly described as follows.

Given an image of N pixels, the set of pixels can be represented as a weighted undirected graph G = (V, E), where V represents nodes of the graph corresponding to the pixels in the feature space, E represents edges that are formed between every pair of nodes. A weight w(i, j) is assigned to each edge that captures the similarity between nodes i and j. In grouping, the goal is to partition the set of vertices into m disjoint sets V 1 , V 2 ,…, V m , where, by some measure, the similarity among the vertices in a set V i is high while it is low across different sets.

For simplicity, a graph partitioned into two disjoint sets, A and B, is considered by simply removing edges connecting these two parts that satisfies A ∪ B = V, A ∩ B = Φ. The degree of dissimilarity between these two sets can be computed as a total weight of the edges that have been removed, which is called the cut:

$$ \mathrm{cut}\left(A,B\right) = {\varSigma}_{u\in A,\ \mathrm{v}\in B}w\left(u,v\right), $$
(3)

where the graph edge weight connecting two nodes i and j is defined as follows:

$$ w\left(i,j\right)= exp\left(\frac{-{\left\Vert I(i)-I(j)\right\Vert}_2^2}{\sigma_I^2}\right)\times \left\{\begin{array}{l} exp\left(\frac{-{\left\Vert X(i)-X(j)\right\Vert}_2^2}{\sigma_X^2}\right)\hfill \\ {}0,\kern2.75em \mathrm{otherwise}\hfill \end{array}\right.,\mathrm{if}\ {\left\Vert X(i)-X(j)\right\Vert}_2^2<r $$
(4)

where X(i) and X(j) are the spatial coordinates of nodes i and j, respectively. In Eq. (4), r is a prescribed threshold, I(i)  and I(j) are the intensity values at the corresponding locations, and σ I and σ X are the standard deviations for the intensity component and the spatial component, respectively.

The normalized cut (Ncut) between two sets, A and B, is proposed to solve the problem of unnatural bias based on Eq. (3) in such a way to partition out small sets of pixels using the following:

$$ \mathrm{Ncut}\left(A,B\right)=\frac{\mathrm{cut}\left(A,B\right)}{\mathrm{assoc}\left(A,V\right)}+\frac{\mathrm{cut}\left(A,B\right)}{\mathrm{assoc}\left(B,V\right)}, $$
(5)

where cut(A, B) is the total weight of the edges that have been removed after a graph is partitioned into two disjoint sets A and B, assoc(A, V) = ∑ u ∈ A,t ∈ V w(u, t) is the total connection from nodes in A to all nodes in the graph, and assoc(B, V) is similarly defined. The challenge is to find optimal sets A and B such that Ncut(A, B) in Eq. (5) is minimized. Unfortunately, minimizing the normalized cut is exactly NP-complete, even for the special case of graphs on grids. Based on the spectral graph theory, an approximately discrete solution can be efficiently obtained by thresholding the eigenvector corresponding to the second smallest eigenvalue λ 2 of the generalized eigenvalue system with

$$ \left(D-W\right)y=\lambda Dy, $$
(6)

where D is a diagonal matrix with entries D ii given as

$$ {D}_{ii}=d(i)={\displaystyle {\sum}_{j\in V}w\left(i,j\right)} $$
(7)

which is the total connection from node i to all other nodes in the graph.

As illustrated in Fig. 3, the input image in Fig. 3a is classified into several subregions using the normalized cut algorithm as shown in Fig. 3b. Herein, each subregion is referred to as a “superpixel.” The concept of superpixel is based on over-segmentation results, and a superpixel is local and coherent that preserves most of the structure at the scale of interest [32]. After the classification procedure, a set of regions R representing the superpixel map is obtained. Note that the histogram distribution of intensity in each superpixel is approximately a normal distribution centered at different intensity values as illustrated in Fig. 3b, comparing to the overall histogram distribution shown in Fig. 3a.

Fig. 3
figure 3

Superpixel classification and the associated histograms of a input image and b superpixel map image

Full size image

3.2 Local variance computation

After the superpixel classification procedure and obtaining R, local variance computation is performed inside each superpixel using

$$ {\mu_R}_i={\displaystyle {\sum}_{x=1}^{n_i}I\left({R}_i,\ x\right)/{n}_i,\kern1em i=1,\ 2, \dots,\ N} $$
(8)

and

$$ {\sigma_R}_i^2={\displaystyle {\sum}_{x=1}^{n_i}{\left(I\left({R}_i,x\right)-{\mu_R}_i\right)}^2/{n}_i,\kern0.75em i=1,\ 2, \dots,\ N}, $$
(9)

where I(R i , x) is the intensity of pixel x in superpixel R i , μ Ri is the mean intensity in R i , n i is the number of all pixels in R i , σ Ri 2 is the variance in R i , and N is the total number of superpixel regions in R.

3.3 Statistical determination

By now, the noise variance values for all superpixel regions in R are obtained. Intuitively, the smallest variance value should be selected for the noise variance estimation result. Practically, however, the variance is somewhat affected by the size, detail, and texture of each individual superpixel so that underestimation could occur. Since the probability distribution of the Gaussian noise is normal, the region that is most close to normal distribution is chosen as an estimation candidate. The Jarque–Bera (JB) test [33, 34], which is a goodness-of-fit test, is used to decide whether sample data match a normal distribution based on the skewness and kurtosis. The statistical JB test is defined as follows:

$$ \mathrm{J}\mathrm{B} = \frac{n}{6}\left({S}^2+\frac{1}{4}{\left(K-3\right)}^2\right) $$
(10)

where n is the number of observations (or degree of freedom in general).

In Eq. (10), S is the sample skewness and K is the sample kurtosis respectively defined as follows:

$$ S=\frac{{\widehat{\mu}}_3}{{\widehat{\sigma}}_3}=\frac{\frac{1}{n}{\displaystyle {\sum}_{i=1}^n}{\left({x}_i-\overline{x}\right)}^3}{{\left(\frac{1}{n}{\displaystyle {\sum}_{i=1}^n}{\left({x}_i-\overline{x}\right)}^2\right)}^{3/2}} $$
(11)

and

$$ K=\frac{{\widehat{\mu}}_4}{{\widehat{\sigma}}_4}=\frac{\frac{1}{n}{\displaystyle {\sum}_{i=1}^n}{\left({x}_i-\overline{x}\right)}^4}{{\left(\frac{1}{n}{\displaystyle {\sum}_{i=1}^n}{\left({x}_i-\overline{x}\right)}^2\right)}^2}, $$
(12)

where \( {\widehat{\mu}}_3 \) and \( {\widehat{\mu}}_4 \) are, respectively, the estimates of the third and fourth central moments; \( \overline{x} \) is the sample mean; and \( {\widehat{\sigma}}^2 \) is the estimate of the second central moment, i.e., the variance. If the data present a normal distribution, the JB statistic will have a chi-squared distribution with 2 degrees of freedom asymptotically. The null hypothesis is a joint hypothesis with both the skewness and the excess kurtosis being 0. Any deviation from this condition will increase the JB statistic. Accordingly, the null hypothesis based on the JB test is defined as follows:

$$ {{\mathrm{JB}}_R}_i=\left\{\begin{array}{l}0,\kern0.75em \mathrm{accept}\ \mathrm{null}\ \mathrm{hypothesis}\hfill \\ {}1,\kern0.75em \mathrm{reject}\ \mathrm{null}\ \mathrm{hypothesis}\hfill \end{array}\right.. $$
(13)

In other words, the JB value equals to 0 if the corresponding superpixel region is examined as a normal distribution; otherwise, it is set to 1.

After the JB test procedure in each individual superpixel region in R, the final noise estimation result is produced based on the following rules:

  1. 1.

    Sort R i based on the standard deviation \( {\sigma}_{R_i} \) in ascending order.

  2. 2.

    Exclude the superpixel region whose JB value equals to 1.

  3. 3.

    Exclude the superpixel region whose pixel number is less than \( 10\times \min \left({\sigma}_{R_i}\right) \), where \( \min \left({\sigma}_{R_i}\right) \) is the smallest value of \( {\sigma}_{R_i} \) in region R.

  4. 4.

    Choose the smallest value of \( {\sigma}_{R_i} \) from the remaining regions as the noise estimation result.

The reason for excluding the regions with a small pixel number in rule 3 is due to the fact that these regions may not have an enough sample quantity to reflect the real noise distribution, leading to poor estimations. As the region size is somewhat related to the value of \( {\sigma}_{R_i} \), the threshold is thus defined as it is and scaled by an experimental constant.

4 Experimental results

To evaluate the proposed algorithm, a wide variety of photographic images (512 × 512) were tested, and some representative images are shown in Fig. 4. In addition, the Berkeley image database [35] was adopted to evaluate the performance of the algorithm. The Berkeley database is a public domain that contains hundreds of images (481 × 321 or 321 × 481) of plants, animals, persons, landscapes, and architectures as partly illustrated in Fig. 5. Different levels of additive Gaussian noise were superimposed on those images to generate various noisy images for experiments. To assess the performance quantitatively, the relative error in terms of the standard deviation was computed as given in the following equation:

Fig. 4
figure 4

Representative images for the experiments. The image dimension is 512 × 512

Full size image
Fig. 5
figure 5

Some of the 100 images obtained from the Berkeley image database for the experiments. The image dimension is 481 × 321 or 321 × 481

Full size image
$$ {\varepsilon}_r=\frac{\left|{\upsigma}_e-{\sigma}_a\right|}{\sigma_a} \times 100\kern0.5em \%, $$
(14)

where σ e represents the standard deviation of the estimated noise, σ a represents the standard deviation of the added noise, and ε r represents the relative percentage error between the added and estimated noise levels.

As the proposed algorithm was insensitive to parameter settings, all experiments were conducted using the same fixed parameters in the process. All compared methods were executed with appropriate parameter settings as suggested by the corresponding authors, if any. The robustness of the superpixel classification procedure based on the normalized cut algorithm with respect to different levels of additive Gaussian noise was first investigated. As illustrated in Fig. 6, the superpixel maps with different noise standard deviations varying from σ a  = 1 to σ a  = 40 were approximately similar from the perspective of smooth regions. Figure 7 shows the estimation results of using the proposed algorithm on the Bird and Countryroad images, whose noise levels were quite widespread with σ a  = 1, 3, 5, 7, 10, and 15. It is obvious that the estimated values of σ e are quite accurate and close to the corresponding values of σ a in all levels of noise in both images. Table 1 summarizes the quantitative analysis in estimating various noise levels on the Bird image using the JI96 [27], Z&W09 [30], MLS09 [16], SVD13 [17], and the proposed algorithm. For σ a  = 1 and σ a  = 3, the proposed framework produced much higher accuracy than all other methods. For σ a  = 5 and σ a  ≥ 7, the MLS09 and SVD13 methods outperformed all other methods, respectively. However, both MLS09 and SVD13 methods severely overestimated small noise levels that resulted in the augmentation of the overall error. While the JI96 method overestimated and the Z&W09 method underestimated all noise levels, the proposed method provided consistent accuracy that achieved a small average error of 6.22 %.

Fig. 6
figure 6

Superpixel maps of Bird with different levels of Gaussian noise. a σ a  = 1. b σ a  = 5. c σ a  = 10. d σ a  = 20. e σ a  = 30. f σ a  = 40

Full size image
Fig. 7
figure 7

Noise estimation results with various levels: a Bird. b Countryroad

Full size image
Table 1 Quantitative analysis in noise level estimation with σ a  = 1, 3, 5, 7, 10, 15, 20 on the Bird image using different methods
Full size table

Table 2 presents the statistical comparison in noise level estimation on all six representative images in Fig. 4 between JI96, Z&W09, MLS09, SVD13, and the proposed algorithm. The JI96 continued to overestimate the noise levels with σ a  ≤ 20, which were particularly worse in low-level noise cases. Not only did the Z&W09 method underestimate all noise levels with σ a  ≤ 25, but it also generated no results in larger noise levels with σ a  ≥ 30 (not shown). Other three methods alternately produced the best estimation results on different noise levels. The proposed method and MLS09 achieved similar accuracy with the average error less than 12 %. Although MLS09 had slightly smaller error than our framework, it was not statistically significant based on only six images. For completeness, Table 3 shows the quantitative results of noise estimation using the JI96, Z&W09, MLS09, SVD13, and the proposed algorithm on 100 images, which were randomly selected from the Berkeley database [35], some of which are shown in Fig. 5. The JI96 method severely overestimated the Gaussian noise levels until the standard deviation σ a  > 15. On the other hand, the Z&W09 method performed better in lower level noise with σ a  < 5, but it was unable to handle noise with σ a  > 25. Both MLS09 and SVD13 methods provided higher accuracy in larger noise levels but achieved worse estimations in small noise levels, particularly for σ a  = 1. Nevertheless, the proposed scheme produced better accuracy in smaller noise levels and compatible estimations in large noise levels that resulted in a smaller overall error than all other methods.

Table 2 Statistical comparison of noise level estimation on the six representative images in Fig. 4 between different methods
Full size table
Table 3 Statistical comparison of noise level estimation on 100 images obtained from the Berkeley image database between different methods
Full size table

5 Discussion

A new superpixel-based algorithm was proposed to estimate the additive Gaussian noise level in images. The approach relied on the normalized cut algorithm to classify the image in order to obtain the superpixel map, from which the local variance was computed and selected. As illustrated in Fig. 6, each superpixel region had similar gray-level, color, and texture characteristics such that it provided great flexibility for subsequent statistical analysis. Since the Gaussian noise obeys a normal distribution, we proposed to use the Jarque–Bera test [33, 34] to separate those superpixel regions that follow a Gaussian distribution from all other regions based on the skewness and kurtosis. After excluding the superpixel regions that had a relatively small number of pixels, the remaining smallest local standard deviation was selected as the noise estimation result.

The proposed framework was applied on a wide variety of images and compared with four state-of-the-art methods, namely JI96 [27], Z&W09 [30], MLS09 [16], and SVD13 [17]. As illustrated in Fig. 7, our technique provided high accuracy for both simple (Countryroad) and complicated (Bird) texture images, particularly for low-level noise estimations. This great capability of excellent accuracy in low-level noise estimation can also be observed from Tables 1 and 2, which were experimented on the images shown in Fig. 4. In addition, the algorithm was extensively evaluated on 100 randomly selected images from the Berkeley database, which contained a wide diversity of photographic images. In comparison with the JI96, Z&W09, MLS09, and SVD13 methods, the proposed approach provided more accurate estimations for low-level noise images as well as smaller overall estimation errors as presented in Table 3. In general, the JI96 method performs better in images with high-level noise but inadequately for images with low-level noise. In contrast, the Z&W09 method performs better in images with lower level noise, but it fails to produce estimation results for larger noise levels with σ a  > 25. Both MLS09 and SVD13 methods can provide satisfactory results in larger noise level estimation but they may notably overestimate small noise levels.

While our algorithm strikes a good compromise between the JI96, Z&W09, MLS09, and SVD13 methods in providing better estimation results across various noise levels. One limitation of this new noise estimation algorithm is that it could overestimate small noise levels when the image is with high details and complicated textures as illustrated in Fig. 8. Table 4 summarizes the performance of the proposed algorithm along with the JI96, Z&W09, MLS09, and SVD13 methods in estimating the noise levels using the image in Fig. 8. Note that all five methods overestimated the noise levels when σ a  ≤ 20 due to the highly sandy pattern over the entire image. In particular, the poor performance of SVD13 (see Tables 3 and 4) may be due to the singular value decomposition of rectangle images. Lastly, the computation time of our framework was expensive comparing with other tested methods as presented in Table 5. Nevertheless, the proposed algorithm still outperformed all other methods with closer standard deviation and smaller average error across various noise levels.

Fig. 8
figure 8

Image with high details and complicated textures (Berkeley image database: 86016)

Full size image
Table 4 Performance analysis in noise level estimation on the image in Fig. 8 using different methods
Full size table
Table 5 Comparison of computation time in seconds between tested methods based on different dimensions of images
Full size table

6 Conclusions

In summary, a new algorithm for additive Gaussian noise level estimation is described, which consists of three major phases: superpixel classification, local variance computation, and statistical determination. Th e algorithm strikes a good compromise between low-level and high-level noise estimations. Hundreds of images with various subjects, scenes, textures, and structures were used to evaluate the proposed framework. Experimental results demonstrated the feasibility and effectiveness of the algorithm in providing accurate estimation results across a wide range of noise levels. This robust noise estimation framework is advantageous to automating denoising algorithms that require noise variance information. Moreover, the proposed noise estimation algorithm is of potential and promising in computer vision, image, and video processing applications. Further research is needed to more effectively divide the image into appropriate superpixels, to investigate the incorporation of filtered-based techniques, and to accelerate the computation for real-time applications.