1 Introduction

The explosion of data traffic over wireless communication has brought a huge demand for spectrum resources. Cognitive radio has arisen as a promising technology for efficiently utilizing the limited spectrum [1, 2]. The key principle behind the functionality of a spectrum sharing approach (also known as underlay strategy) in cognitive radio networks (CRNs) is that unlicensed secondary users are allowed to access the licensed spectrum as long as the interference from the secondary transmitters is harmless to the primary receivers [3]. In order words, the secondary transmitters need to set their transmit powers in order to not cause any interference to the primary network that is above a predefined level. This power adjustment implies a reduction in the coverage area of the secondary network. Fortunately, cooperative relay schemes, which can enhance the coverage of wireless networks by deploying helping nodes to transfer information from the source to the destination, have been introduced in CRNs with spectrum-sharing environment (see, for instance, [4–8]). Specifically, different relay selection schemes assuming amplify-and-forward (AF) and decode-and-forward (DF) relaying protocols, were studied in [6–8], and the results showed that by applying appropriate cooperative schemes, cognitive relay networks can significantly attain improved performance.

However, the aforementioned studies employed half-duplex (HD) relays, which are inefficient from the spectrum usage point of view. Note that a conventional relay uses two time-slots for two operating phases, i.e., listening to messages from the information source node and relaying message to the destination. To tackle this spectral inefficiency, full-duplex (FD) techniques have been proposed for relay networks [9, 10], which enable relay nodes to transmit and receive signals simultaneously at the price of self-interference. Although self-interference is an undesirable effect in practice, the developments in signal processing and antenna technologies have proven that FD techniques are a promising solution for efficient spectrum usage in the next generation of wireless communication [11–13]. Moreover, the effect of FD techniques on relay networks has attracted wide attention recently [14–16]. The authors in [17–19] investigated a FD, dual-hop, AF system, in which the self-interference variance was modeled as a function of transmit power. In [20], the authors studied different relay selection policies based on the availability of system’s channel state information (CSI) at the source node of a multiple AF FD relay system. In [21], motivated by incremental-DF protocol, the authors proposed a new cooperative protocol for FD relays named as incremental-selective-DF and compared its performance with selective-DF protocol in Nakagami-m fading environment. In [9], the authors examined the outage probability (OP) of a DF relay network to find the optimal duplex mode of the considered system. However, in all these aforementioned studies, the influence of spectrum-sharing environment on FD relay networks is not well understood. Motivated by this observation, in this paper, we study the performance of cognitive FD relay networks in the presence of multiple FD relays and multiple primary receivers. The contributions of the paper can be summarized as follows:

  • Two relay selection schemes, namely, optimal relay selection (ORS) and partial relay selection (PRS), based on the availability of the system CSI at the secondary information source are proposed.

  • Due to the existence of the common random variables (RVs), i.e., the channels from the source and/or selected relay to multiple primary receivers, the signal-to-noise-ratios (SNRs) of all links become correlated which makes the analysis troublesome. To get around this challenge, we first apply the conditional probability on these RVs and then derive the analytical expressions for the OP of the considered system. Specifically, the exact and asymptotic expressions of OP in PRS and ORS schemes are also obtained.

  • The derived results reveal several insights. For instance, it is shown that the primary network’s parameters, i.e., the peak interference constraint, the distance from the primary receivers to the secondary transmitters, and the number of primary receivers, have a high impact on the performance of the secondary network and should be carefully designed. In addition, ORS strategy outperforms PRS 1 in terms of OP, and increasing the number of FD relays can significantly improve the system performance.

The rest of this paper is organized as follows. The system and channel models are introduced in Section 2. Exact and asymptotic expressions for the OP assuming ORS and PRS policies are derived in Sections 3 and 4, respectively. Numerical results are presented in Section 5, which are corroborated through Monte Carlo simulations. Finally, the main conclusions are outlined in Section 6. Appendices A, B, C, and D present the proofs of four Lemmas.

2 System and channel models

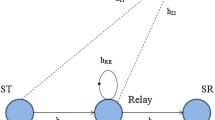
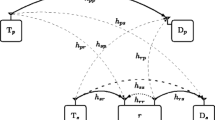
We consider a cognitive relay network consisting of one secondary transmitter S, K secondary FD DF relays R k , k∈{1,…,K}, one secondary receiver D, and M primary receivers P m , m∈{1,…,M}, as shown in Fig. 1. We assume that the primary transmitters are located sufficiently far away from the secondary nodes so as not to impinge any interference upon the received signals at the relays and destination and not to cause perturbation on the relay selection process. The node S is equipped with a single antenna and employs a transmit power \(\mathcal {P}_{\mathsf {S}}\). Meanwhile, R k is equipped with two antennas (one receive antenna and one transmit antenna) for operating in FD mode1. All the channels are assumed to experience Rayleigh fading, in which the respective channel power gains are exponentially distributed.

Fig. 1
figure 1

Cognitive spectrum sharing network

Full size image

Since a spectrum sharing approach is adopted and R k is in full-duplex mode, the transmit power from S and R k is constrained by the primary network’s peak interference parameter \(\mathcal {I}_{p}\) as follows:

$$\begin{array}{*{20}l} \mathcal{I}_{p} \geq \mathcal{P}_{\mathsf{S}} \max\limits_{m=1,\ldots,M}|h_{\mathsf{S} \mathsf{P}_{m}}|^{2} + \mathcal{P}_{\mathsf{R}} \max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{k} \mathsf{P}_{m}}|^{2} \end{array} $$
(1)

From (1), non-optimal condition for \(\mathcal {P}_{\mathsf {S}}\) and \(\mathcal {P}_{\mathsf {R}}\) can be selected as follows:

$$\begin{array}{*{20}l} \mathcal{P}_{\mathsf{S}} = \frac{\mathcal{I}_{p}}{2\max\limits_{m=1,\ldots,M}|h_{\mathsf{S} \mathsf{P}_{m}}|^{2}}, \end{array} $$
(2)
$$\begin{array}{*{20}l} \mathcal{P}_{\mathsf{R}} = \frac{\mathcal{I}_{p}}{2\max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{k} \mathsf{P}_{m}}|^{2}}, \end{array} $$
(3)

where \(\mathcal {P}_{\mathsf {S}}\) and \(\mathcal {P}_{\mathsf {R}}\) are the transmit powers of S and R k , respectively, \(h_{\mathsf {S} \mathsf {P}_{m}}\phantom {\dot {i}\!}\) and \(\phantom {\dot {i}\!}h_{\mathsf {R}_{k} \mathsf {P}_{m}}\) denote the channel coefficients pertaining to the S→P m and R k →P m links, respectively. The CSI of the channel gains from the source and relays to primary users can be obtained from direct feedback from PU-Rx or indirect feedback from band manager [22].

The transmission is performed in two hops. In the first hop, S transmits information to \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}}\), where the subscript k ∗ indicates the aiding relay that is chosen in the relay selection process, which will be detailed next. Because \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}}\) simultaneously receives and forwards information, self-interference occurs at the receive antenna of \(\mathsf {R}_{k^{*}}\phantom {\dot {i}\!}\). Furthermore, although \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}}\) applies self-interference cancellation techniques, the self-interference channel at \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}}\), i.e., \(\phantom {\dot {i}\!}h_{\mathsf {R}_{k^{*}}}\), cannot be fully mitigated and is modeled as an independent Rayleigh distributed channel [23]. In addition, we assume that the impact of interference from the primary transmitter on secondary network is neglected when the primary transmitter is located far away from secondary receiver [24, 25]. Thus, the received signal at \(\mathsf {R}_{k^{*}}\phantom {\dot {i}\!}\) is given by

$$\begin{array}{*{20}l} y_{\mathsf{R}_{k^{*}}} = \sqrt{\mathcal{P}_{\mathsf{S}}}h_{\mathsf{S} \mathsf{R}_{k^{*}}} x_{\mathsf{S}} + \sqrt{\mathcal{P}_{\mathsf{R}}}h_{\mathsf{R}_{k^{*}}} x_{\mathsf{R}} + n_{\mathsf{R}}, \end{array} $$
(4)

where x S and x R represent the transmitted signals from S and \(\mathsf {R}_{k^{*}}\phantom {\dot {i}\!}\), respectively, \(h_{\mathsf {S} \mathsf {R}_{k^{*}}}\phantom {\dot {i}\!}\) is the channel coefficient from S to \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}}\), and \(\phantom {\dot {i}\!}n_{\mathsf {R}} \sim \mathcal {N}(0,N_{0})\) is the additive white Gaussian noise (AWGN) at \(\mathsf {R}_{k^{*}}\phantom {\dot {i}\!}\).

After decoding the received information from S, \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}}\) forwards the decoded message to D in the second hop. The received information at D can be expressed as

$$\begin{array}{*{20}l} y_{\mathsf{D}} = \sqrt{\mathcal{P}_{\mathsf{R}}}h_{\mathsf{R}_{k^{*}} \mathsf{D}} x_{\mathsf{R}} + n_{\mathsf{D}}, \end{array} $$
(5)

where \(h_{\mathsf {R}_{k^{*}} \mathsf {D}}\phantom {\dot {i}\!}\) denotes the channel coefficient from \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}}\) to D and \(\phantom {\dot {i}\!}n_{\mathsf {D}} \sim \mathcal {N}(0,N_{0})\) stands for the AWGN term at D.

The signal-to-interference-plus-noise-ratio (SINR) at \(\phantom {\dot {i}\!}\mathsf {R}_{k^{*}} \) and SNR at D can be written, respectively, as

$$\begin{array}{*{20}l} \gamma_{1k^{*}} &= \frac{\mathcal{P}_{\mathsf{S}}|h_{\mathsf{S} \mathsf{R}_{k^{*}}}|^{2}}{\mathcal{P}_{\mathsf{R}}|h_{\mathsf{R}_{k^{*}}}|^{2} + N_{0}}, \end{array} $$
(6)
$$\begin{array}{*{20}l} \gamma_{2k^{*}} &= \frac{\mathcal{P}_{\mathsf{R}}|h_{\mathsf{R}_{k^{*}} \mathsf{D}}|^{2}}{N_{0}}. \end{array} $$
(7)

In the considered system, we assume that R k employs a DF protocol thanks to its better performance in the presence of self-interference compared to that of AF protocol [26]. Thus, the end-to-end SNR can be computed as [5]

$$\begin{array}{*{20}l} \gamma_{k^{*}}=\min(\gamma_{1k^{*}},\gamma_{2k^{*}}). \end{array} $$
(8)

From (8), the capacity of the overall transmission S→R k →D can be expressed as

$$\begin{array}{*{20}l} C = \log_{2}\left[1+ \gamma_{k^{*}}\right]. \end{array} $$
(9)

Knowing that the OP is defined as the probability that the channel capacity of the considered system falls below a given threshold, such a metric can be formulated as

where denotes probability, \(F_{\gamma _{k^{*}}}(\cdot)\phantom {\dot {i}\!}\) represents the cumulative distribution function (CDF) of \(\phantom {\dot {i}\!}\gamma _{k^{*}}\), \(\phantom {\dot {i}\!}\beta = 2^{R_{\text {th}}}-1\), and R th is the target rate of the secondary network.

3 Outage probability analysis

3.1 Partial relay selection (PRS)

In some networks, such as wireless sensor networks, the energy and computational resources are limited. Therefore, utilizing aiding relay based on full global CSI is infeasible. Motivated by this fact, in PRS scheme, the node S uses the CSI solely of the channels pertaining to first-hop transmission to select the aiding relay R p that has the best link from S, i.e.,

$$\begin{array}{*{20}l} k^{\ast}_{\mathsf{PRS}} = \arg \max\limits_{k=1,\ldots,K}\left(|h_{\mathsf{S} \mathsf{R}_{k}}|^{2}\right). \end{array} $$
(10)

From (2), (3), (6), and (7), the SINR of the first hop and the SNR of the second hop are formulated, respectively, as

$$\begin{array}{*{20}l} \gamma_{1k^{\ast}}^{\mathsf{PRS}} &= \frac{\frac{\mathcal{I}_{p}}{2\max\limits_{m=1,\ldots,M}|h_{\mathsf{S} \mathsf{P}_{m}}|^{2}}\max\limits_{k=1,\ldots,K}|h_{\mathsf{S} \mathsf{R}_{k}}|^{2}}{ \left(\frac{\mathcal{I}_{p}}{2\max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{p} \mathsf{P}_{m}}|^{2}}|h_{\mathsf{R}_{p}}|^{2}+ N_{0} \right)} \\ &=\frac{\frac{\gamma_{1}}{\max\limits_{m=1,\ldots,M}|h_{\mathsf{S} \mathsf{P}_{m}}|^{2}}\max\limits_{k=1,\ldots,K}|h_{\mathsf{S} \mathsf{R}_{k}}|^{2}}{ \frac{\gamma_{1}}{\max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{p} \mathsf{P}_{m}}|^{2}}|h_{\mathsf{R}_{p}}|^{2}+ 1 }, \end{array} $$
(11)
$$\begin{array}{*{20}l} \gamma_{2k^{\ast}}^{\mathsf{PRS}} &= \frac{\mathcal{I}_{p}|h_{\mathsf{R}_{p}\mathsf{D}}|^{2}}{2\max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{p} \mathsf{P}_{m}}|^{2} N_{0}} \\ &= \frac{\gamma_{1}|h_{\mathsf{R}_{p}\mathsf{D}}|^{2}}{\max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{p} \mathsf{P}_{m}}|^{2}}, \end{array} $$
(12)

where \(\gamma _{1} = \frac {\mathcal {I}_{p}}{2N_{0}}\). From (8), (11), and (12), the end-to-end SNR of the considered PRS policy is given by

$$\begin{array}{*{20}l} \gamma_{k^{\ast}}^{\mathsf{PRS}} = \min\left(\gamma_{1k^{\ast}}^{\mathsf{PRS}},\gamma_{2k^{\ast}}^{\mathsf{PRS}}\right). \end{array} $$
(13)

From (11)–(13), we have the following lemma.

Lemma 1

The OP of the considered PRS scheme is given as follows:

where 2 F 1(·,·;·;·) symbolizes the Gaussian hypergeometric function ([27], Eq. (9.14.1)) and \(\lambda _{X}^{-1}\) is the mean value of exponential random variable |h X |2, X∈{SR k ,R k D,SP m ,R k P m ,R k }.

Proof

The proof is given in Appendix A. □

3.2 Optimal relay selection (ORS)

In ORS scheme, the node S is assumed to be a stationary base station that has rich energy and powerful computational resources. Therefore, S is able to collect and process all the system CSI to choose the aiding relay that can maximize the capacity of the considered system. In this case, the aiding relay R o is selected according to the following rule:

$$\begin{array}{*{20}l} k^{\ast}_{\mathsf{ORS}} = \arg \max\limits_{k=1,\ldots,K} \min\left(\gamma_{1k},\gamma_{2k}\right) \end{array} $$
(14)

The end-to-end SNR is given by

$$\begin{array}{*{20}l} \gamma_{k^{\ast}}^{\mathsf{ORS}} = \max\limits_{k=1,\ldots,K} \min\left(\gamma_{1k},\gamma_{2k}\right), \end{array} $$
(15)

where γ 1k and γ 2k denote the SINR of the first hop and the SNR of the second hop, respectively, and are expressed as

$$\begin{array}{*{20}l} \gamma_{1k} &=\frac{\frac{\gamma_{1}}{\max\limits_{m=1,\ldots,M}|h_{\mathsf{S} \mathsf{P}_{m}}|^{2}}|h_{\mathsf{S} \mathsf{R}_{k}}|^{2}}{ \frac{\gamma_{1}}{\max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{p} \mathsf{P}_{m}}|^{2}}|h_{\mathsf{R}_{p}}|^{2}+ 1 }, \end{array} $$
(16)
$$\begin{array}{*{20}l} \gamma_{2k} &= \frac{\gamma_{1}|h_{\mathsf{R}_{k}\mathsf{D}}|^{2}}{\max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{k} \mathsf{P}_{m}}|^{2}}, \end{array} $$
(17)

From (15)–(17), we have the following lemma.

Lemma 2

The OP of the considered ORS scheme is given as follows:

where

$$\begin{array}{*{20}l}{} \Delta_{1} &= 1-\sum\limits_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}m \lambda_{\mathsf{R}\mathsf{P}} \exp\left(-\frac{\beta\lambda_{\mathsf{S}\mathsf{R}} }{\gamma_{1}}y \right)\\ &\quad\left\lbrace \frac{\beta\lambda_{\mathsf{S}\mathsf{R}} }{\lambda_{\mathsf{R}}} y \exp\left(\frac{\beta\lambda_{\mathsf{S}\mathsf{R}} \left(\frac{\beta \lambda_{\mathsf{R}\mathsf{D}}}{\gamma_{1}} + m \lambda_{\mathsf{R}\mathsf{P}} \right)}{\lambda_{\mathsf{R}}}y \right) \right. \\ &\quad\left. \times \text{Ei}\!\left(\!-\frac{\beta \lambda_{\mathsf{S}\mathsf{R}}}{\lambda_{\mathsf{R}}}\left(\!\frac{\beta \lambda_{\mathsf{R}\mathsf{D}}}{\gamma_{1}} + m \lambda_{\mathsf{R}\mathsf{P}}\!\!\right)\!y\!\right) \!+ \frac{\gamma_{1}}{\beta \lambda_{\mathsf{R}\mathsf{D}} + m \lambda_{\mathsf{R}\mathsf{P}}\gamma_{1}} \right\rbrace \end{array} $$
(18)

Proof

The proof is given in Appendix B. □

4 Asymptotic outage analysis

In this section, an asymptotic outage analysis is carried out in order to gain further insights into the system performance. As will be shown, the considered system has null diversity order because of the self-interference effect inherent to the FD technique2. In addition, from the asymptotic expressions, we can observe that in the high SNR regime, the performance of the considered system does not depend on the channel of the second hop. In other words, to enhance the performance of the considered system, the performance of the first hop must be strengthen.

4.1 Partial relay selection

Lemma 3

In the high SNR regime, the OP of the considered system with PRS scheme can be expressed as

Proof

The proof is given in Appendix C. □

4.2 Optimal relay selection

Lemma 4

In the high SNR regime, the OP of the considered system with ORS scheme can be expressed as

where

$$\begin{array}{*{20}l}{} \Delta_{2}&= \sum\limits_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}\frac{m\beta\lambda_{\mathsf{S}\mathsf{R}}\lambda_{\mathsf{R}\mathsf{P}} y}{\lambda_{\mathsf{R}}} \exp\left(\frac{m\beta\lambda_{\mathsf{S}\mathsf{R}} \lambda_{\mathsf{R}\mathsf{P}} }{\lambda_{\mathsf{R}}}y \right)\\ &\quad\mathbf{Ei}\left(-\frac{m \beta \lambda_{\mathsf{S}\mathsf{R}}\lambda_{\mathsf{R}\mathsf{P}}}{\lambda_{\mathsf{R}}} y\right). \end{array} $$
(19)

Proof

The proof is given in Appendix D. □

5 Numerical results and discussions

In this section, numerical examples are presented to show the impact of the network’s parameters on the overall system performance. The accuracy of our analysis is attested by Monte Carlo simulations, in which a perfect agreement between the analytical and simulated curves is observed. Without loss of generality, we adopt a two-dimensional topology in which the coordinates (x,y) of S, R, and D are (0,0), (2,0), and (3,0), respectively. Thus, the Euclidian distance between the nodes can be calculated as \(d_{AB} = \sqrt {(x_{A}-x_{B})^{2} + (y_{A}-y_{B})^{2}}\), where A is placed at (x A ,y A ) and B has the coordinate (x B ,y B ). In order to take the path-loss into account, we assume \(\lambda _{X} = d_{X}^{-\alpha }\), where α denotes the path-loss exponent and λ X ∈{λ SP ,λ SR ,λ RP ,λ RD ,}. Without loss of generality, in the plots, we set α=4 and the target rate of the secondary network R th=0.4 bits/s/Hz, and λ R =22.

Figures 2 and 3 show the effect of the primary users’ locations on the system OP for the PRS and ORS schemes, respectively. From these figures, one can observe that as the primary receivers move farther from the secondary transmitters, the performance of the secondary network improves. The reason is that the longer the distance between the primary receiver and the secondary transmitter results in the higher the transmit power of the secondary transmitter, which implies a better secondary transmission. In addition, the effects of the primary network’s peak interference constraint on the secondary network are also revealed. Note that, if the peak interference constraint is too small, the secondary transmitters will not have sufficient transmit power to ensure good transmissions. On the other hand, if the peak interference constraint is too high, the transmit power at the FD relays will be large, resulting in high levels of self-interference. Besides, these two figures also show that the ORS scheme outperforms PRS one.

Fig. 2
figure 2

Effect of primary users’ positions on system OP for PRS scheme

Full size image
Fig. 3
figure 3

Effect of primary users’ positions on the system OP for ORS scheme

Full size image

In Fig. 4, the effect of the number of primary receivers on system OP is investigated. As can be seen, when the SNR is low, increasing the number of primary receivers decreases the performance of the considered system. However, at high SNR regions, increasing the number of primary receivers will force the secondary transmitters to reduce their transmit powers, reducing the self-interference at the relay and consequently the OP.

Fig. 4
figure 4

OP for different numbers of primary receivers

Full size image

Figures 5 and 6 illustrate the influence of self-interference on the secondary network’s performance by varying the mean power of self-interference channel, i.e., \(\frac {1}{\lambda _{\mathsf {R}}}\). As expected, the worse the quality of the self-interference channel is, the better the system performance is. Particularly, as the SNR of the considered system is high, the smaller the mean power of self-interference channel is, the higher the system diversity gain is. In addition, the results show that applying ORS scheme can restraint the effect of self-interference better than PRS scheme.

Fig. 5
figure 5

Effect of self-interference on the system OP with PRS scheme

Full size image
Fig. 6
figure 6

Effect of self-interference on the system OP with ORS scheme

Full size image

Figure 7 demonstrates the influence of the number of relays on the system OP. When the number of relays increases, the performance of the considered system is enhanced. Particularly, a more significant improvement can be witnessed in ORS scheme than in PRS scheme.

Fig. 7
figure 7

OP for different numbers of FD relays

Full size image

Figure 8 shows the comparison in system’s capacity between FD and HD relays. We can observe that applying FD relays can help the system achieve a higher capacity. The reason is that FD relays can listen and transmit information simultaneously while HD relays have two phases of operation, i.e., listening to the information source and relaying signal to the destination.

Fig. 8
figure 8

Comparison between FD and HD relays

Full size image

6 Conclusions

In this paper, the system performance in terms of outage probability of a cognitive FD relay network in the presence of multiple primary receivers has been evaluated. In particular, two relay selection strategies, namely ORS and PRS, have been proposed to enhance the performance of the system. New exact and asymptotic expressions for the OP of the PRS and ORS schemes were derived. The results showed that the ORS scheme has a better performance than PRS scheme. In addition, increasing the number of FD relays can enhance the system performance. Primary network designing parameters, i.e., the peak interference constraint, the number of primary receivers, and their locations, have great influences on the performance of the secondary network and should be mindfully considered.

7 Endnotes

1 Dual-antenna FD implementation is one of many ways to deploy FD mode, including single-antenna FD implementation.

2 In the considered system, the transmit power at the full-duplex relay is non-optimal. A transmit power optimization scheme at full-duplex relay can be considered to restrain the self-interference effect.

8 Appendix A: Proof of Lemma 1

Let

$$\begin{array}{*{20}l} \mathcal{X}_{1} &=\max\limits_{k=1,\ldots,K}|h_{\mathsf{S} \mathsf{R}_{k}}|^{2}, \\ \mathcal{X}_{2} &= \max\limits_{m=1,\ldots,M}|h_{\mathsf{S} \mathsf{P}_{m}}|^{2}, \\ \mathcal{X}_{3} &= |h_{\mathsf{R}_{p}}|^{2}, \\ \mathcal{X}_{4} &= \max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{p} \mathsf{P}_{m}}|^{2}, \\ \mathcal{X}_{5} &= |h_{\mathsf{R}_{p}\mathsf{D}}|^{2}. \end{array} $$
(20)

The CDF and the probability density function (PDF) of \(\mathcal {X}_{1}\) can be expressed as

$$\begin{array}{*{20}l} F_{{\mathcal{X}_{1}}}\left({x}\right) &= 1-\sum_{k=1}^{K}\left(\begin{array}{c}K\\ {k}\end{array}\right)(-1)^{k+1}\exp(-k\lambda_{\mathsf{S}\mathsf{R}} x), \end{array} $$
(21)
$$\begin{array}{*{20}l} f_{{\mathcal{X}_{1}}}\left({x}\right) &= \sum_{k=1}^{K}\left(\begin{array}{c}K\\ {k}\end{array}\right)(-1)^{k+1}k\lambda_{\mathsf{S}\mathsf{R}}\exp(-k\lambda_{\mathsf{S}\mathsf{R}} x). \end{array} $$
(22)

In the same way, the CDF and PDF of \(\mathcal {X}_{2}\) are given by

$$\begin{array}{*{20}l} F_{{\mathcal{X}_{2}}}\left({x}\right) &= 1-\sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}\exp(-m\lambda_{\mathsf{S}\mathsf{P}} x), \end{array} $$
(23)
$$\begin{array}{*{20}l} f_{{\mathcal{X}_{2}}}\left({x}\right) &= \sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}m\lambda_{\mathsf{S}\mathsf{R}}\exp(-m\lambda_{\mathsf{S}\mathsf{P}} x), \end{array} $$
(24)

and the CDF and PDF of \(\mathcal {X}_{4}\) can be written as

$$\begin{array}{*{20}l} F_{{\mathcal{X}_{4}}}\left({x}\right) &= 1-\sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}\exp(-m\lambda_{\mathsf{R}\mathsf{P}} x), \end{array} $$
(25)
$$\begin{array}{*{20}l} f_{{\mathcal{X}_{4}}}\left({x}\right) &= \sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}m\lambda_{\mathsf{R}\mathsf{P}}\exp(-m\lambda_{\mathsf{R}\mathsf{P}} x). \end{array} $$
(26)

Finally, the CDF and PDF of \(\mathcal {X}_{3}\) are given by

$$\begin{array}{*{20}l} F_{{\mathcal{X}_{3}}}\left({x}\right) &= 1- \exp(-\lambda_{\mathsf{R}} x), \end{array} $$
(27)
$$\begin{array}{*{20}l} f_{{\mathcal{X}_{3}}}\left({x}\right) &= \lambda_{\mathsf{R}}\exp(-\lambda_{\mathsf{R}} x), \end{array} $$
(28)

and the CDF and PDF of \(\mathcal {X}_{5}\) are given by

$$\begin{array}{*{20}l} F_{{\mathcal{X}_{5}}}\left({x}\right) &= 1- \exp(-\lambda_{\mathsf{R}\mathsf{D}} x), \end{array} $$
(29)
$$\begin{array}{*{20}l} f_{{\mathcal{X}_{5}}}\left({x}\right) &= \lambda_{\mathsf{R}\mathsf{D}}\exp(-\lambda_{\mathsf{R}\mathsf{D}} x). \end{array} $$
(30)

From (11) and (12), \( \gamma _{1k^{\ast }}^{\mathsf {PRS}}\) and \( \gamma _{2k^{\ast }}^{\mathsf {PRS}}\) can be rewritten as follows:

$$\begin{array}{*{20}l} \gamma_{1k^{\ast}}^{\mathsf{PRS}} &=\frac{\gamma_{1}\frac{\mathcal{X}_{1}}{\mathcal{X}_{2}}}{\gamma_{1}\frac{\mathcal{X}_{3}}{\mathcal{X}_{4}}+1}, \end{array} $$
(31)
$$\begin{array}{*{20}l} \gamma_{2k^{\ast}}^{\mathsf{PRS}} &=\gamma_{1}\frac{\mathcal{X}_{5}}{\mathcal{X}_{4}}. \end{array} $$
(32)

Since \( \gamma _{1k^{\ast }}^{\mathsf {PRS}}\) and \( \gamma _{2k^{\ast }}^{\mathsf {PRS}}\) depend on \(\mathcal {X}_{4}\), the CDF of \(\gamma _{k^{\ast }}^{\mathsf {PRS}}\) can be expressed as

$$\begin{array}{*{20}l}{} F_{{\gamma_{k^{\ast}}^{\mathsf{PRS}}}}\left({\beta}\right)&=\int_{0}^{\infty} \left[1-\left(1-F_{\gamma_{1k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}(\beta)\right) \right.\\ &\quad\left. \left(1-F_{\gamma_{2k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}(\beta)\right)\right] f_{\mathcal{X}_{4}}(x)dx. \end{array} $$
(33)

In order to derive \(F_{\gamma _{k^{\ast }}^{\mathsf {PRS}}}(\beta)\), we need to determine \({F_{\gamma _{1k^{\ast }}^{\mathsf {PRS}}|\mathcal {X}_{4}}}{\beta }\) and \(F_{\gamma _{2k^{\ast }}^{\mathsf {PRS}}|\mathcal {X}_{4}}(\beta)\). In this case, \(F_{\gamma _{1k^{\ast }}^{\mathsf {PRS}}|\mathcal {X}_{4}}(\beta)\) can be written as

Similarly, \(F_{\gamma _{1k^{\ast }}^{\mathsf {PRS}}|\mathcal {X}_{4}}(\beta)\) can be calculated as

where Ei(·) denotes the exponential integral function and (??) is obtained with the help of ([27], Eq. (3.351)). By substituting (??) and (??) into (33), (??) is attained.

9 Appendix B: Proof of Lemma 2

Let

$$\begin{array}{*{20}l} \mathcal{Y}_{1k}&=|h_{\mathsf{S} \mathsf{R}_{k}}|^{2},\\ \mathcal{Y}_{3k}&= |h_{\mathsf{R}_{k}}|^{2},\\ \mathcal{Y}_{4k}&= \max\limits_{m=1,\ldots,M}|h_{\mathsf{R}_{k} \mathsf{P}_{m}}|^{2},\\ \mathcal{Y}_{5k}&=|h_{\mathsf{R}_{k}\mathsf{D}}|^{2},\\ \Psi_{k} &= \min(\gamma_{1k},\gamma_{2k}). \end{array} $$

The CDF and PDF of \(\mathcal {Y}_{4k}\) are given by

$$\begin{array}{*{20}l} F_{{\mathcal{Y}_{4k}}}\left({x}\right) &= 1-\sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}\exp(-m\lambda_{\mathsf{R}\mathsf{P}} x), \end{array} $$
(34)
$$\begin{array}{*{20}l} f_{{\mathcal{Y}_{4k}}}\left({x}\right) &= \sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}m\lambda_{\mathsf{R}\mathsf{P}}\exp(-m\lambda_{\mathsf{R}\mathsf{P}} x). \end{array} $$
(35)

From (16) and (17), γ 1k and γ 2k can be rewritten as

$$\begin{array}{*{20}l} \gamma_{1k} &=\frac{\gamma_{1}\frac{\mathcal{Y}_{1k}}{\mathcal{X}_{2}}}{\gamma_{1}\frac{\mathcal{Y}_{3k}}{\mathcal{Y}_{4k}}+1}, \end{array} $$
(36)
$$\begin{array}{*{20}l} \gamma_{2k} &= \gamma_{1}\frac{\mathcal{Y}_{5k}}{\mathcal{Y}_{4k}}. \end{array} $$
(37)

Since Ψ k , for k∈{1,…,K}, depends on \(\mathcal {X}_{2}\), the CDF of \(\gamma _{k^{\ast }}^{\mathsf {ORS}}\) can be expressed as

$$\begin{array}{*{20}l} F_{{\gamma_{k^{\ast}}^{\mathsf{ORS}}}}\left({\beta}\right)=\int_{0}^{\infty}\left[F_{{\Psi_{k}|\mathcal{X}_{2}}}\left({\beta}\right)\right]^{K} f_{{\mathcal{X}_{2}}}\left({y}\right) dy, \end{array} $$
(38)

From (36) and (37), note that γ 1k and γ 2k depend on \(\mathcal {Y}_{4k}\). Therefore, the CDF of Ψ k conditioned on \(\mathcal {X}_{2}\) can be calculated by

$$\begin{array}{*{20}l}{} F_{{\Psi_{k}|\mathcal{X}_{2}}}\!\left({\beta}\right)&=\!\! \int_{0}^{\infty}\! \left[\!1\,-\,\left(\!1\,-\,F_{{\gamma_{1k}|\mathcal{X}_{2},\mathcal{Y}_{4k}}}\left({\beta}\right)\right) \right.\\ &\quad\!\left.\left(1-F_{\gamma_{2k}|\mathcal{Y}_{4k}}(\beta)\right) \right] f_{{\mathcal{Y}_{4k}}}\left({x}\right) dx. \end{array} $$
(39)

On the other hand, the CDF of γ 2k conditioned on \(\mathcal {Y}_{4k}\) can be calculated as

Finally, the CDF of γ 1k conditioned on \(\mathcal {X}_{2}\) and \(\mathcal {Y}_{4k}\) can be calculated as

where \(F_{{\mathcal {Y}_{1k}}}\left ({x}\right) = 1- \exp \left (-\lambda _{\mathsf {S}\mathsf {R}} x\right) \) and \(f_{{\mathcal {Y}_{3k}}}\left ({x}\right) = \lambda _{\mathsf {R}} \exp \left (-\lambda _{\mathsf {R}} x\right) \).

Thus, from (??), (??), and (35), the CDF of Ψ k conditioned on \(\mathcal {X}_{2}\) can be calculated as

$$\begin{array}{*{20}l}{} F_{{\Psi_{k}|\mathcal{X}_{2}}}\left({\beta}\right) &= 1 - \int_{0}^{\infty} \sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right) \frac{(-1)^{m+1}m\lambda_{\mathsf{R}\mathsf{P}}\lambda_{\mathsf{R}}}{\lambda_{\mathsf{R}}+\beta\lambda_{\mathsf{S}\mathsf{R}}\frac{\mathcal{X}_{2}}{x}} \\ &\quad\exp\!\left(-\frac{\beta\lambda_{\mathsf{S}\mathsf{R}}\mathcal{X}_{2}}{\gamma_{1}}\right)\! \exp\!\left(-\frac{\beta\lambda_{\mathsf{R}\mathsf{D}} x}{\gamma_{1}}-m\lambda_{\mathsf{R}\mathsf{P}} x\right)dx \\ &= 1\! -\!\! \sum\limits_{m=1}^{M}\!\!\left(\!\!\begin{array}{c}M\\ {m}\end{array}\!\right)\!(-1)^{m+1}m \lambda_{\mathsf{R}\mathsf{P}} \exp\! \left(\!-\frac{\beta\lambda_{\mathsf{S}\mathsf{R}} }{\gamma_{1}}\mathcal{X}_{2} \!\right)\\ &\quad\left\{\frac{\beta\lambda_{\mathsf{S}\mathsf{R}} }{\lambda_{\mathsf{R}}} \mathcal{X}_{2} \exp\left(\frac{\beta\lambda_{\mathsf{S}\mathsf{R}} \left(\frac{\beta \lambda_{\mathsf{R}\mathsf{D}}}{\gamma_{1}} + m \lambda_{\mathsf{R}\mathsf{P}} \right)}{\lambda_{\mathsf{R}}}\mathcal{X}_{2} \right) \right. \\ &\quad \times \text{Ei}\left(-\frac{\beta \lambda_{\mathsf{S}\mathsf{R}}}{\lambda_{\mathsf{R}}}\left(\frac{\beta \lambda_{\mathsf{R}\mathsf{D}}}{\gamma_{1}} + m \lambda_{\mathsf{R}\mathsf{P}}\right)\mathcal{X}_{2}\right)\\ &\left.\qquad\!\!\!\!\mathsf{+} \frac{\gamma_{1}}{\beta \lambda_{\mathsf{R}\mathsf{D}} + m \lambda_{\mathsf{R}\mathsf{P}}\gamma_{1}} {\vphantom{\frac{\beta\lambda_{\mathsf{S}\mathsf{R}} }{\lambda_{\mathsf{R}}} \mathcal{X}_{2} \exp\left(\frac{\beta\lambda_{\mathsf{S}\mathsf{R}} \left(\frac{\beta \lambda_{\mathsf{R}\mathsf{D}}}{\gamma_{1}} + m \lambda_{\mathsf{R}\mathsf{P}} \right)}{\lambda_{\mathsf{R}}}\mathcal{X}_{2} \right)}}\right\}, \end{array} $$
(40)

where (40) is obtained with the help of ([27], Eq. (3.352.4)). Now, by substituting (40) and

$$\begin{array}{*{20}l} f_{{\mathcal{X}_{2}}}\left({x}\right) = \sum_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}m\lambda_{\mathsf{S}\mathsf{R}}\exp(-m\lambda_{\mathsf{S}\mathsf{P}} x) \end{array} $$

into (38), (??) is attained.

10 Appendix C: Proof of Lemma 3

At high SNR regions, i.e., assuming high γ 1, (16) can be rewritten as

$$\begin{array}{*{20}l} \gamma_{1k^{\ast}}^{\mathsf{PRS}} &= \frac{\gamma_{1}\frac{\mathcal{X}_{1}}{\mathcal{X}_{2}}}{\gamma_{1}\frac{\mathcal{X}_{3}}{\mathcal{X}_{4}}+1} \mathop\approx^{\text{large }\gamma_{1}} \frac{\mathcal{X}_{1}\mathcal{X}_{4}}{\mathcal{X}_{2}\mathcal{X}_{3}}. \end{array} $$
(41)

Thus, the CDF of \(\gamma _{1k^{\ast }}^{\mathsf {PRS}}\) conditioned on \(\mathcal {X}_{4}\) is given by

$$\begin{array}{*{20}l}{} F_{{\gamma_{1k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}}\left({\beta}\right)&= 1+ \sum\limits_{m_{1}=1}^{M}\sum\limits_{k=1}^{K}(-1)^{m_{1}+k}\left(\begin{array}{c}M\\ {m_{1}}\end{array}\right)\left(\begin{array}{c}K\\ {k}\end{array}\right) \\ &\quad\;\frac{m_{1}\lambda_{\mathsf{R}} \lambda_{\mathsf{S}\mathsf{P}} \mathcal{X}_{4}}{k\beta\lambda_{\mathsf{S}\mathsf{R}}}\! \exp\!\left(\!\frac{m_{1} \lambda_{\mathsf{S}\mathsf{P}}}{k\beta \lambda_{\mathsf{S}\mathsf{R}}}\mathcal{X}_{4} \!\right)\!\text{Ei}\!\left(\!-\frac{m_{1} \lambda_{\mathsf{S}\mathsf{P}}}{k\beta \lambda_{\mathsf{S}\mathsf{R}}}\mathcal{X}_{4}\!\!\right) \end{array} $$
(42)

Now, analyzing \(F_{\gamma _{2k^{\ast }}^{\mathsf {PRS}}|\mathcal {X}_{4}}(\beta)\) at high γ 1, we have that

$$\begin{array}{*{20}l} F_{{\gamma_{2k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}}\left({\beta}\right)&=1-\exp\left(-\frac{\lambda_{\mathsf{R}\mathsf{D}}\mathcal{X}_{4}\beta}{\gamma_{1}}\right), \mathop\approx^{(a)} \frac{\lambda_{\mathsf{R}\mathsf{D}}\mathcal{X}_{4}\beta}{\gamma_{1}}, \end{array} $$
(43)

where step (a) is obtained by using the McLaurin expansion of exp(x) and neglecting the high order items for small x.

Making use of the above results, it can be shown that the CDF of \(\gamma _{k^{\ast }}^{\mathsf {PRS}}\) is given by

$$\begin{array}{*{20}l}{} F_{{\gamma_{k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}}\!\left({x}\right)\! &=\! \!1\,-\,\left[\!1\,-\,F_{\gamma_{1k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}{(x)}\right]\!\left[\!F_{\!\gamma_{2k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}{(x)}\right]\! \mathop\approx^{(b)}\! F_{{\gamma_{1k^{\ast}}^{\mathsf{PRS}}|\mathcal{X}_{4}}}\!\left({x}\right)\!, \end{array} $$
(44)

where step (b) is performed by neglecting the high order terms. By substituting (42) into (44), and after some mathematical manipulations, (??) is obtained.

11 Appendix D: Proof of Lemma 4

For high γ 1, \(F_{\gamma _{2k}|\mathcal {X}_{2}|\mathcal {Y}_{4k}}\) and \( F_{\gamma _{1k}|\mathcal {X}_{2}|\mathcal {Y}_{4k}} \) can be rewritten as follows:

$$\begin{array}{*{20}l} F_{\gamma_{2k}|\mathcal{Y}_{4k}}(\beta)&=1-\exp\left(-\frac{\beta\lambda_{\mathsf{R}\mathsf{D}}\mathcal{Y}_{4k}}{\gamma_{1}}\right) \\ &\mathop\approx^{(c)}\frac{\beta\lambda_{\mathsf{R}\mathsf{D}}\mathcal{Y}_{4k}}{\gamma_{1}}, \end{array} $$
(45)
$$\begin{array}{*{20}l} F_{\gamma_{1k}|\mathcal{X}_{2},\mathcal{Y}_{4k}}(\beta)&= 1-\frac{\lambda_{\mathsf{R}}}{\lambda_{\mathsf{R}}+\beta\lambda_{\mathsf{S}\mathsf{R}}\frac{\mathcal{Y}_{2k}}{\mathcal{Y}_{4k}}}\exp\left(-\frac{\beta\lambda_{\mathsf{S}\mathsf{R}}\mathcal{Y}_{2k}}{\gamma_{1}}\right) \\ &\mathop\approx^{(d)}1-\frac{\lambda_{\mathsf{R}}}{\lambda_{\mathsf{R}}+\beta\lambda_{\mathsf{S}\mathsf{R}}\frac{\mathcal{Y}_{2k}}{\mathcal{Y}_{4k}}}, \end{array} $$
(46)

where steps (c) and (d) are performed by using the McLaurin expansion of exp(x) and neglecting the high order terms for small x.

In addition, the CDF of Ψ k conditioned on \(\mathcal {X}_{2}\) and \(\mathcal {Y}_{4k}\) can be formulated as

$$\begin{array}{*{20}l}{} F_{{\Psi_{k}|\mathcal{X}_{2},\mathcal{Y}_{4k}}}\left({\beta}\right) &= 1-\left[1\,-\,F_{{\gamma_{1k}|\mathcal{X}_{2},\mathcal{Y}_{4k}}}\left({\beta}\right)\right]\left[1-F_{{\gamma_{2k}|\mathcal{Y}_{4k}}}\left({\beta}\right)\right] \\ &\mathop\approx^{(e)}F_{{\gamma_{1k}|\mathcal{X}_{2},\mathcal{Y}_{4k}}}\left({\beta}\right), \end{array} $$
(47)

where step (e) is performed by neglecting the high order terms. From (46) and (47), the CDF of Ψ k conditioned on \(\mathcal {X}_{2}\) can be found as

$$\begin{array}{*{20}l}{} F_{{\Psi_{k}|\mathcal{X}_{2}}}\left({\beta}\right) &= \sum\limits_{m=1}^{M}\left(\begin{array}{c}M\\ {m}\end{array}\right)(-1)^{m+1}\frac{m\beta\lambda_{\mathsf{S}\mathsf{R}}\lambda_{\mathsf{R}\mathsf{P}}}{\lambda_{\mathsf{R}}} \mathcal{X}_{2}\\ &\quad\exp\left(\frac{m\beta\lambda_{\mathsf{S}\mathsf{R}}\lambda_{\mathsf{R}\mathsf{P}}}{\lambda_{\mathsf{R}}}\mathcal{X}_{2} \right)\text{Ei}\left(-\frac{m \beta \lambda_{\mathsf{S}\mathsf{R}}\lambda_{\mathsf{R}\mathsf{P}}}{\lambda_{\mathsf{R}}} \mathcal{X}_{2}\right). \end{array} $$
(48)

Finally, by replacing (48) and

$$\begin{array}{*{20}l} f_{{\mathcal{X}_{2}}}\left({y}\right)= \sum\limits_{n=1}^{M} (-1)^{n+1} \left(\begin{array}{c}M\\ {n}\end{array}\right)n \lambda_{\mathsf{S}\mathsf{P}} \exp(-n\lambda_{\mathsf{S}\mathsf{P}} y) \end{array} $$

into (38), (??) is obtained.