Robust transmit design for secure AF relay networks with imperfect CSI

Abstract

This paper studies robust transmit design for secure AF relay networks with imperfect channel state information (CSI). Two CSI error models, deterministically bounded error model and stochastic error model, are considered. In order to use the power at relays more efficiently, a joint cooperative relaying and jamming scheme is considered, where relays cooperate to forward the source signal and simultaneously they cooperate to send jamming signals to confuse the eavesdroppers. In this joint cooperative relaying and jamming framework, we address the robust joint optimization of the relay weights and the input covariance matrix of jamming signals for secrecy rate maximization (SRM), under both total and individual relay power constraints. Specifically, for the case of deterministically bounded error model, where the CSI error can be specified by an uncertainty set, we maximize the worst-case secrecy rate. While for the case of stochastic error model, where the probability distribution of the CSI error is Gaussian, we maximize the outage constrained secrecy rate. The challenge of these considered SRM-based optimizations lies in their non-convexity. This paper shows that such SRM-based optimization can be solved in a convex fashion and via solving a sequence of semidefinite programs (SDPs). Numerical results are presented to show the efficacy of the proposed scheme.

1 Introduction

In the classical three-node wiretap channel, secrecy capacity is typically zero when the source-destination link is weaker than the source-eavesdropper link [1, 2]. One way to achieve non-zero secrecy rate in this case is to introduce multi-antenna nodes [3–11], wherein multi-antenna techniques can enable directional transmission, thus allowing secret communication even when the eavesdropper’s channel has a much better quality. However, due to the cost or size limitations, multi-antenna nodes may not be available in some practical applications. In this case, node cooperation is an alternative way to enable single-antenna nodes to enjoy the benefits brought by multi-antenna nodes [12–23].

Generally, there are two kinds of cooperation schemes. One is cooperative relaying [14–16], where relays cooperate to improve the source destination channel quality. The other is cooperative jamming (CJ) [13–15], where relays cooperate to send jamming signals to confuse the eavesdroppers.

In [13–16], cooperative relaying and cooperative jamming were considered independently. In contrast, the works of [18–26] considered a joint cooperative relaying and jamming scheme, where some of the relays cooperate to forward the source signal and simultaneously the other relays cooperate to send jamming signals to confuse the eavesdroppers. Such joint scheme is especially useful when the number of relays is large. Later, in [27, 28], a more general joint cooperative relaying and jamming scheme was proposed, where each relay forwards the source signal and transmits jamming signals simultaneously. Due to noise amplification at relays, there exists a rate performance ceiling for the source-relay-destination (SRD) link, thus spending extra power in relaying will not help increase the secrecy rate after a certain point is reached. In contrast, distributing a portion of power to transmit jamming signals to confuse the eavesdropper may be more helpful.

Most of the works mentioned above assume the availability of a perfect channel state information (CSI) at relays. In practice, the CSI available at relays is usually imperfect due to different factors such as estimation error, quantization, and feedback delay. In addition, the rate performance of the relay designs obtained under the assumption of perfect CSI degrades in the presence of CSI errors. Hence, it is important to develop relay designs that are robust to CSI errors. Works along these lines include [29–35] which consider the scenario with no relays and [24–27] which consider the scenario with relays. As compared with the transmission design in the former scenario, the robust secure relay design is more difficult due to noise amplification at relays. Moreover, to the best of the authors’ knowledge, existing robust designs for secure AF relay networks are few. For example, the works [24, 25] considered the stochastic CSI error model which is applicable when the imperfect CSI is mainly due to errors in channel estimation and tried to minimize the outage probability of the secrecy rate. The works [26, 27] considered the deterministically bounded CSI error model which is applicable when the CSI error is dominated by quantization errors and tried to compute the maximal achievable worst-case secrecy rate.

In this paper, we aim to give a more general framework which applies to both the deterministically bounded CSI error model and the stochastic CSI error model. For the case of deterministically bounded error model, we maximize the worst-case secrecy rate. While for the case of stochastic error model, we maximize the outage constrained secrecy rate. As in our conference paper [27], we consider a more general joint cooperative relaying and jamming scheme, where each relay forwards the source signal and transmits jamming signals simultaneously. We should note that the works [24–26] considered a different joint cooperative relaying and jamming scheme, where some of the relays cooperate to forward the source signal while the other relays cooperate to send jamming signals to confuse the eavesdroppers.

Our main contributions are summarized below.

• 1. Robust joint optimization of the relay weights and the input covariance matrix of jamming signals for secrecy rate maximization (SRM) is addressed, under both total and individual relay power constraints. The challenge of these SRM-based optimizations lies in their non-convexity. In this paper, we provide a unified approach for solving these SRM-based optimizations. The key insight is to recast the SRM-based problem as a two-level optimization problem: an outer problem and an inner problem. We show that the outer problem can be dealt with a one-dimensional search, while the inner problem admits a tight convex relaxation and hence can be exactly solved in an efficient manner.

• 2. The crux of our approach is to construct a tight convex relaxation of the inner problem. To deal with this issue, we first introduce an alternative secrecy rate constrained (SRC) power minimization problem, i.e., minimizing the total relay power, under constraints on the achievable worst-case secrecy rate or the achievable outage constrained secrecy rate. We solve the SRC power minimization problem with semidefinite relaxation (SDR) techniques, and we prove that the relaxation here is tight. We then prove that the optimal relay weights and input covariance matrix of jamming signals in the SRC power minimization problem also constitute an optimal solution to our inner problem. In this way, we provide a tight convex relaxation of our inner problem.

We should note that in the practical implementation of any coherent wireless communication systems, the issue of synchronization needs to be addressed. In this paper, the relay transmissions are assumed to be synchronized, by resorting to global positioning system (GPS) satellite signals [36] or the master-slave scheme [37]. Imperfect synchronization can also be overcome by employing carrier frequency offset (CFO) compensation [38]. Since our goal is to give the fundamental limit of the secrecy transmission rate from a theoretic perspective, and also due to the lack of space, in this paper, we do not go into the detailed analysis of the impact of imperfect synchronization.

This paper is organized as follows. In Section 2, we describe the system model. In Section 3, we consider the deterministically bounded CSI error model and compute the maximal achievable worst-case secrecy rate. In Section 4, we consider the stochastic CSI error model and compute the maximal achievable outage constrained secrecy rate. Numerical results are provided in Section 5, and conclusions are drawn in Section 6.

Notation.

A ^H, tr{A}, and rank{A} represent the hermitian transpose, trace, and rank of a matrix A, respectively; diag{A} denotes a diagonal matrix with the same main diagonal elements as the matrix A; [A] _k,k denotes the kth diagonal element of the matrix A; diag{a} represents a diagonal matrix with a on the main diagonal. I is an identity matrix with appropriate size; A≽0 means A is a hermitian positive semidefinite matrix; ${\mathbf {A}} \in {\mathbb {H}}^{n }$ means A is a n×n complex hermitian matrix. $x\sim \mathcal {CN}(0,\Sigma)$ means x is a random variable following a complex circular Gaussian distribution with mean zero and covariance Σ; E{·} is the expectation operator. $\mathbb {C}^{N \times M}$ represents a N×M complex matrix set.

2 System model

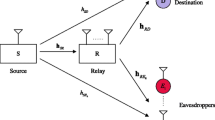
As depicted in Fig. 1, a source node aims to send confidential messages to the destination in the presence of M eavesdroppers, with the help of N relays. Each node is equipped with one antenna. Two phases including the broadcasting phase and the relaying phase are required. In the broadcasting phase, the source broadcasts its message and the received signal at relays is given by

$$ {\mathbf{y}_{\mathrm{R}}} = {\mathbf{h}_{\text{SR}}}s + {\mathbf{n}_{\mathrm{R}}}, $$

(1)

Fig. 1

AF relay network with single-antenna nodes

where s, E{|s|²}=P _s , is the data to be transmitted. $\mathbf {h}_{\text {SR}}\in \mathbb {C}^{N \times 1}$ represents the channel vector from the source to the relay. n _R is the noise vector at relays, with i.i.d. entries distributed as $\mathcal {CN}(0,{\sigma }_{\mathrm {R}}^{2})$. In the relaying phase, the relay forwards a weighted version of the received signal. Simultaneously, the relay transmits jamming signals, n _J, to confuse the eavesdropper. The signal transmitted by relays can thus be expressed as

$$ \mathbf{x} = {\text{diag}}\{\mathbf{v}\} ({\mathbf{h}_{\text{SR}}}s + {\mathbf{n}_{\mathrm{R}}}) + {\mathbf{n}_{\mathrm{J}}}, $$

(2)

where v is the relaying weight vector.

Denote $\mathbf {h}_{\text {RD}}^{H}\in \mathbb {C}^{1\times N}$ and $\mathbf {g}_{\text {RE},m}^{H}\in \mathbb {C}^{1 \times N}$ as the channel vector from the relays to the destination and the mth eavesdropper, respectively. The signals received at the destination and the mth eavesdropper can be respectively expressed as

$$ {y_{D}} = \mathbf{h}_{\text{RD}}^{H}{\text{diag}}\{ \mathbf{v}\} ({\mathbf{h}_{\text{SR}}}s + {\mathbf{n}_{\mathrm{R}}}) + \mathbf{h}_{\text{RD}}^{H}{\mathbf{n}_{J}} + {n_{D}}, $$

(3)

$$ {y_{E,m}} = \mathbf{g}_{\text{RE},m}^{H}{\text{diag}}\{ \mathbf{v}\} ({\mathbf{h}_{\text{SR}}}s + {\mathbf{n}_{R}}) + \mathbf{g}_{\text{RE},m}^{H}{\mathbf{n}_{J}} + {n_{E,m}}, $$

(4)

where ${n_{D}}\sim \mathcal {CN}(0,{\sigma }_{D}^{2})$ and ${n_{E,m}}\sim \mathcal {CN}(0,{\sigma }_{E}^{2})$ are the AWGN at each receiver.

Denote h=diag{h _SR}h _RD and g _m =diag{h _SR}g _RE,m the channel from the source to the destination and the mth eavesdropper, respectively. For a given relaying weight vector v and input covariance matrix of jamming signals Q _J , the received signal-to-noise (SNR) at the destination and the mth eavesdropper are, respectively,

$$\begin{array}{@{}rcl@{}} {\gamma_{D}} &=& \frac{{{P_{s}}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}}\mathbf{h}}}{{{\sigma_{D}^{2}} + \mathbf{h}_{\text{RD}}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{h}_{\text{RD}}}}}, \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}} {\gamma_{E,m}} & =& \frac{{{P_{s}}\mathbf{g}_{m}^{H}{\mathbf{Q}_{\mathbf{v}}}{\mathbf{g}_{m}}}}{{{\sigma_{E}^{2}} + \mathbf{g}_{\text{RE},m}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{g}_{\text{RE},m}}}}, \end{array} $$

(6)

where Q _v =v v ^H. The transmitted power of the kth relay, k=1,⋯,N, is t _k (Q _v ,Q _J )=ζ _k (Q _v ,Q _J ), where

$$\begin{array}{@{}rcl@{}} \zeta_{k}(\mathbf{A}, \mathbf{B})\triangleq {\left[ {{P_{s}}{\text{diag}}\{{\mathbf{h}_{\text{SR}}}{\mathbf{h}_{\text{SR}}^{H}}\}\mathbf{A} + {\sigma_{R}^{2}}\mathbf{A} + \mathbf{B}} \right]_{k,k}}. \end{array} $$

In this paper, we aim to address the robust joint optimization of the relay weights and the input covariance matrix of jamming signals for SRM, under both total and individual relay power constraints. Two CSI error models, the deterministically bounded error model and the stochastic error model, are considered. For the case of deterministically bounded error model, we aim to maximize the worst-case secrecy rate. While for the case of stochastic error model, we aim to maximize the outage constrained secrecy rate. The challenge of these SRM-based optimizations lies in their non-convexity. In the following sections, we provide a unified approach for solving these SRM-based optimizations.

3 Robust joint relaying and jamming design with norm-bounded CSI error

In this section, we study the case where the CSI of the eavesdropping channel is partially known. The deterministically bounded error model is considered, and we aim to maximize the worst-case secrecy rate. To this end, we first solve the SRC power minimization problem. We then study the relationship between the solutions of the SRC power minimization problem and the worst-case SRM problem. By exploiting this relationship, we provide an approach for solving the worst-case SRM in a convex fashion.

3.1 Channel uncertainty

The channel vector from the relays to the eavesdroppers are modeled as [30]

$$ {\mathbf{g}_{\text{RE},m}}= {\hat{\mathbf{g}}_{\text{RE},m}}{\mathrm{+ }}\Delta {\mathbf{g}_{\text{RE},m}}, m=1,\dots,M, $$

(7)

where ${\hat {\mathbf {g}}_{\text {RE},m}}$ is the channel information known at the source node. We should note that the estimation of the eavesdropper’s channel is possible in situations in which the eavesdropper is an active member of the network, and thus, its whereabouts and behavior can be monitored. Δ g _RE,m denotes the channel uncertainties. The deterministically bounded error model is considered in this section.

Thus, the actual channel coefficients g _RE,m is contained in a certain sphere, i.e.,

$$ \Omega_{m}= \{ \mathbf{g}_{\text{RE},m} | \|{\mathbf{g}_{\text{RE},m}}-{\hat{\mathbf{g}}_{\text{RE},m}}\|_{F} \le \beta_{m} \}, $$

(8)

where β _m is a known constant.

3.2 Worst-case secrecy rate constrained power minimization

In this subsection, we consider the SRC power minimization problem, i.e., minimizing the total relay power, under the constraint on the achievable worst-case secrecy rate.

$$ \begin{aligned} {\mathop {\min}\limits_{\{\mathbf{v},{\mathbf{Q}_{J}}\}} } & \quad {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \\ \mathrm{s.t.} & \quad \gamma_{D} \ge \delta_{1}, \\ & \quad \gamma_{E,m}\le \delta_{2},\forall \mathbf{g}_{\text{RE},m} \in \Omega_{m}, m=1,\cdots,M, \\ & \quad \zeta_{k}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}})\le {P_{k}}, k=1,\cdots, N, \\ & \quad \mathbf{Q}_{\mathbf{v}}=\mathbf{vv}^{H},\mathbf{Q}_{J}\succeq \mathbf{0}. \end{aligned} $$

(9)

where δ ₁ and δ ₂ denote the SNR constraints on the legitimate receiver and the eavesdropper, respectively.

By dropping the rank 1 constraint on Q _v , we reformulate (9) as

$$ \begin{aligned} &\mathop{\min}\limits_{\{\mathbf{Q}_{\mathbf{v}},{\mathbf{Q}_{J}}\}} {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}(\mathbf{Q}_{\mathbf{v}},{\mathbf{Q}_{J}}) \\ &\mathrm{s.t.} \frac{{P_{s}}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}\mathbf{h}}}{{{\sigma_{D}^{2}} + \mathbf{h}_{\text{RD}}^{H}({\sigma_{R}^{2}}{\text{diag}}\{\mathbf{Q}_{\mathbf{v}}\} + {\mathbf{Q}_{J}}){\mathbf{h}_{\text{RD}}}}} \ge \delta_{1} \\ & \quad\frac{P_{s}\mathbf{g}_{m}^{H}\mathbf{Q}_{\mathbf{v}}{\mathbf{g}_{m}}}{{{\sigma_{E}^{2}} + \mathbf{g}_{\text{RE},m}^{H}({\sigma_{R}^{2}}{\text{diag}}\{\mathbf{Q}_{\mathbf{v}}\} + {\mathbf{Q}_{J}}){\mathbf{g}_{\text{RE},m}}}}\le \delta_{2} \\ &\quad\quad\quad\quad\quad\quad \forall \mathbf{g}_{\text{RE},m} \in \Omega_{m}, \quad m=1,\cdots,M \\ & \quad {\zeta_{k}}(\mathbf{Q}_{\mathbf{v}},{\mathbf{Q}_{J}}) \le {P_{k}}, k=1,\cdots,N \\ & \quad \mathbf{Q}_{\mathbf{v}}\succeq {\mathbf{0}},{\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(10)

Proposition 1.

The optimization (10) can be reformulated into a SDP and solved by CVX.

Proof.

To handle the imperfect-CSI induced constraints in (10), we need the following lemma (please see [39] for more details).

Lemma 1.

Let ${\varphi _{k}}(\mathbf {x})={\mathbf {x}^{H}}{\mathbf {A}_{k}}\mathbf {x} + 2{\mathop {\Re }\nolimits } \{ \mathbf {b}_{k}^{H}\mathbf {x}\} + {c_{k}}$, where ${\mathbf {A}_{k}} \in {\mathbb {H}}^{n }$, $\mathbf {b}_{k} \in {\mathbb {C}}^{n \times 1}$, $c_{k} \in {\mathbb {R}}$. Assume that there exists a point $\hat {\mathbf {x}}$ such that ${\varphi _{1}}(\hat {\mathbf {x}}) < 0$. Then, the implication φ ₁(x)≤0⇒φ ₂(x)≤0 holds if and only if there exists a ϱ≥0 such that

$$\varrho \left[ {\begin{array}{cc} {{\mathbf{A}_{1}}}&{{\mathbf{b}_{1}}}\\ {\mathbf{b}_{1}^{H}}&{{c_{1}}} \end{array}} \right] - \left[ {\begin{array}{cc} {{\mathbf{A}_{2}}}&{{\mathbf{b}_{2}}}\\ {\mathbf{b}_{2}^{H}}&{{c_{2}}} \end{array}} \right] \succeq \mathbf{{0}}, $$

For ease of exposition, we first rewrite the second constraint in (10) as

$$ \mathbf{g}_{\text{RE},m}^{H}\mathbf{\Theta} {\mathbf{g}_{\text{RE},m}} - \delta_{2} {\sigma_{E}^{2}} \le 0 $$

(11)

where $\boldsymbol {\Theta } = {P_{s}}{\text {diag}}{\{ {\mathbf {h}_{\text {SR}}}\}^{H}}{{\mathbf {Q}}}_{\mathbf {v}}{\text {diag}}\{ {\mathbf {h}_{\text {SR}}}\} - {\sigma _{R}^{2}} \delta _{2} {\text {diag}}\{{{\mathbf {Q}}}_{\mathbf {v}}\} - \delta _{2} {{{\mathbf {Q}}}_{J}}$. Substituting (7) into (11) yields

$$ \begin{aligned} {\Delta\mathbf{g}_{\text{RE},m}^{H}}\boldsymbol{\Theta} {\Delta\mathbf{g}_{\text{RE},m}}+2{\Re} \{ {\hat{\mathbf{g}}_{\text{RE},m}^{H}}\boldsymbol{\Theta} {\Delta\mathbf{g}_{\text{RE},m}}\} \\ +{\hat{\mathbf{g}}_{\text{RE},m}}^{H}\boldsymbol{\Theta} \hat{\mathbf{g}}_{\text{RE},m}- \delta_{2} {\sigma_{E}^{2}} \le 0. \end{aligned} $$

(12)

According to Lemma 1, $\|\Delta \mathbf {g}_{\text {RE},m}\|_{F}^{2} \le {\beta }_{m}^{2} \Rightarrow$(12) if and only if for some μ _m ≥0,

$$ \begin{aligned} \left[ \begin{array}{*{20}{c}} {\mu}_{m} \mathbf{I} - \boldsymbol{\Theta}& - {\boldsymbol{\Theta}^{H}}\hat{\mathbf{g}}_{\text{RE},m}\\ -\hat{\mathbf{g}}_{\text{RE},m}^{H}\boldsymbol{\Theta}&-{\beta_{m}^{2}}{\mu}_{m} - \hat{\mathbf{g}}_{\text{RE},m}^{H}\boldsymbol{\Theta} \hat{\mathbf{g}}_{\text{RE},m} + \delta_{2} {\sigma_{E}^{2}} \end{array} \right] \succeq \mathbf{{0}}. \end{aligned} $$

Therefore, the optimization (10) can be re-expressed as

$$ \begin{aligned} &{\mathop{\min}\limits_{\{ {\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}},{\mu}_{1},\cdots,{\mu}_{M} \}} } {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \\ & \mathrm{s.t.}~ {P_{s}}{\text{tr}}\{ \mathbf{h}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}}\} \ge \delta_{1}{\sigma_{D}^{2}} +\delta_{1} \bar \xi ({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \\ & \left[ \begin{array}{cc} {\mu}_{m} \mathbf{I} - \boldsymbol{\Theta}&- {\boldsymbol{\Theta}^{H}}{{\hat{\mathbf{g}}}_{\text{RE},m}}\\ -\hat{\mathbf{g}}_{\text{RE},m}^{H}\boldsymbol{\Theta}&-\beta_{m}^{2}{\mu}_{m} - \hat{\mathbf{g}}_{\text{RE},m}^{H}\boldsymbol{\Theta} \hat{\mathbf{g}}_{\text{RE},m} + \delta_{2} {\sigma_{E}^{2}} \end{array} \right] \succeq \mathbf{{0}} \\ & \quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad m=1,\cdots,M \\ & \ {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \le {P_{k}}, k=1,\cdots,N \\ & \ {\mu}_{m} \ge 0, {\mathbf{Q}_{\mathbf{v}}}\succeq {\mathbf{0}},{\mathbf{Q}_{J}}\succeq {\mathbf{0}}, \end{aligned} $$

(13)

where we define $\bar {\xi }({{{\mathbf {Q}}}_{\mathbf {v}}},{{{\mathbf {Q}}}_{J}})=\text {{tr}}\{ {\sigma _{R}^{2}} {\text {diag}}\{ {\mathbf {h}_{\text {RD}}}\mathbf {h}_{\text {RD}}^{H}\} \mathbf {Q}_{\mathbf {v}} + {\mathbf {h}_{\text {RD}}}\mathbf {h}_{\text {RD}}^{H}{\mathbf {Q}_{J}}\}$.

According to [39], the optimization (13) is a SDP and can be solved by CVX. This completes the proof.

Proposition 2.

Denote the optimal solution to (10) as $\{\hat {\mathbf {Q}}_{\mathbf {v}},{\hat {\mathbf {Q}}}_{J} \}$. Then, $\hat {\mathbf {Q}}_{\mathbf {v}}$ is rank 1, provided that a positive secrecy rate is achieved.

Proof.

See Appendix 6.

By applying the matrix decomposition, we get ${\hat {\mathbf {Q}}}_{\mathbf {v}}=\hat {\mathbf {v}}{\hat {\mathbf {v}}}^{H}$. From Proposition 2, the rank 1 constraint relaxation in (10) is tight. Therefore, $\{\hat {\mathbf {v}},\hat {\mathbf {Q}}_{J}\}$ is the optimal solution to (9).

3.3 Worst-case secrecy rate maximization

In this subsection, we aim to maximize the worst-case achievable secrecy rate subject to both total and individual relay power constraints, i.e.,

$$ \begin{aligned} \mathop{\max}\limits_{\{\mathbf{v},{\mathbf{Q}_{J}}\} }&\mathop{\min}\limits_{\stackrel{m \in \{ 1, \cdots,\,M\}} {\mathbf{g}_{\text{RE},m} \in \Omega_{m}}} \frac{1}{2}\log (1 + {\gamma_{D}}) - \frac{1}{2}\log (1 + {\gamma_{E,m}}) \\ \mathrm{s.t.}&\quad {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{r}} \\ &\quad {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{k}}, k=1,\cdots,N \\ & \quad {\mathbf{Q}_{\mathbf{v}}}=\mathbf{v}\mathbf{v}^{H},{\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(14)

In general, the optimization problem in (14) is non-convex and challenging to solve directly. To deal with this issue, the two-layer idea in [13] is adopted. The key insight is to recast the original optimization problem in (14) as a two-level optimization problem. The inner-level part is dealt with the SDR technique, and the outer-level part is handled by a one-dimensional search. Specifically, the outer-level part is

$$ \quad\quad\quad{\mathop{\max}\limits_{\tau \in [{\tau_{lb}},{\tau_{ub}}]} \frac{{1 + {\bar{f}}(\tau)}}{{1 + \tau }}}, $$

(15)

where $\bar {f}(\tau)$ is obtained through solving the following inner-level part optimization problem for a given τ

$$ \begin{aligned} \bar{f} (\tau)&={\mathop{\max}\limits_{\{\mathbf{v},{\mathbf{Q}_{J}}\}} } \frac{{{P_{s}}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}}\mathbf{h}}}{{{\sigma_{D}^{2}} + \mathbf{h}_{\text{RD}}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{h}_{\text{RD}}}}} \\ \mathrm{s.t.} & \frac{{{P_{s}}\mathbf{g}_{m}^{H}{\mathbf{Q}_{\mathbf{v}}}{\mathbf{g}_{m}}}}{{{\sigma_{E}^{2}} + \mathbf{g}_{\text{RE},m}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{g}_{\text{RE},m}}}}\le \tau \\ &\quad\quad\quad\quad\quad \forall \mathbf{g}_{\text{RE},m} \in \Omega_{m}, \quad m=1,\cdots,M \\ & \ {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{r}} \\ & \ {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{k}}, k=1,\cdots,N \\ & \ {\mathbf{Q}_{\mathbf{v}}}=\mathbf{v}\mathbf{v}^{H}, {\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(16)

By dropping the rank 1 constraint on Q _v , we reformulate the optimization (16) as

$$ \begin{aligned} \bar{g}(\tau)&= {\mathop{\max}\limits_{\{{\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}\}}} \frac{{{P_{s}}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}}\mathbf{h}}}{{{\sigma_{D}^{2}} + \mathbf{h}_{\text{RD}}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{h}_{\text{RD}}}}} \\ \mathrm{s.t.} & \frac{{{P_{s}}\mathbf{g}_{m}^{H}{\mathbf{Q}_{\mathbf{v}}}{\mathbf{g}_{m}}}}{{{\sigma_{E}^{2}} + \mathbf{g}_{\text{RE},m}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{g}_{\text{RE},m}}}}\le \tau \\ &\quad\quad\quad\quad\quad\quad \forall \mathbf{g}_{\text{RE},m} \in \Omega_{m}, \quad m=1,\cdots,M \\ & \ {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{r}} \\ & \ {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{k}}, k=1,\cdots,N \\ & \ {\mathbf{Q}_{\mathbf{v}}}\succeq {\mathbf{0}}, {\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(17)

Proposition 3.

The optimization (17) can be reformulated into a SDP and solved by CVX.

Proof.

By letting $\eta = \frac {1}{{{\sigma _{D}^{2}} + \mathbf {h}_{RD}^{H}({\sigma _{R}^{2}}{\text {diag}}\{ {\mathbf {{Q}}_{\mathbf {v}}}\} + {\mathbf {Q}_{J}}){\mathbf {h}_{RD}}}}$, $\tilde {\mathbf {Q}}_{\mathbf {v}} = \eta {\mathbf {Q}_{\mathbf {{v}}}}$, $\tilde {\mathbf {Q}}_{J}=\eta {\mathbf {Q}_{J}}$, and using the Charnes-Cooper transformation, we recast the optimization (17) as

$$ \begin{aligned} \bar{g}(\tau)&= \mathop{\max}\limits_{\{ \tilde{\mathbf{Q}}_{\mathbf{v}},\tilde{\mathbf{Q}}_{J},\eta \}} {P_{s}}\text{tr}\{\mathbf{h}{\mathbf{h}^{H}} {\tilde{\mathbf{Q}}_{\mathbf{v}}}\} \\ \mathrm{s.t.}~&{\sigma_{D}^{2}}\eta + \text{tr} \{{\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}\} {\tilde{\mathbf{Q}}_{\mathbf{v}}} + {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}{\tilde{\mathbf{Q}}_{J}}\}=1 \\ &\frac{{{P_{s}}\mathbf{g}_{m}^{H}{\tilde{\mathbf{Q}}_{\mathbf{v}}}\mathbf{g}_{m}}}{{{\sigma_{E}^{2}} \eta+ \mathbf{g}_{\text{RE},m}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\tilde{\mathbf{Q}}_{\mathbf{v}}}\} + {\tilde{\mathbf{Q}}_{J}}){\mathbf{g}_{\text{RE},m}}}}\le \tau \\ &\quad\quad\quad\quad\quad\quad \forall \mathbf{g}_{\text{RE},m} \in \Omega_{m}, \quad m=1,\cdots,M \\ \quad &{\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}(\tilde{\mathbf{Q}}_{\mathbf{v}}, {\tilde{\mathbf{Q}}_{J}}) \le \eta {P_{r}} \\ & {\zeta_{k}}(\tilde{\mathbf{Q}}_{\mathbf{v}}, \tilde{\mathbf{Q}}_{J})\le \eta {P_{k}},k=1,\cdots,N \\ & \tilde{\mathbf{Q}}_{\mathbf{v}}\succeq {\mathbf{0}},{\tilde{\mathbf{Q}}_{J}}\succeq {\mathbf{0}},\eta >0. \end{aligned} $$

(18)

Applying the same derivation from (11) to (12) and applying Lemma 1, we re-express the optimization (18) as

$$ \begin{aligned} \bar{g}&(\tau)= \mathop{\max }\limits_{\{{\mathbf{Q}_{v}},{\mathbf{Q}_{J}},\eta, {\mu}_{1},\cdots,{\mu}_{M} \}} {P_{s}}\text{tr}\{\mathbf{hh}^{H} {\tilde{\mathbf{Q}}_{\mathbf{v}}}\} \\ \mathrm{s.t.}~& {\sigma_{D}^{2}}\eta + \text{tr} \{{\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}\} {\tilde{\mathbf{Q}}_{\mathbf{v}}} + {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}{\tilde{\mathbf{Q}}_{J}}\}=1 \\ &\left[ \begin{array}{cc} {\mu}_{m} \mathbf{I} - \mathbf{\Phi}& - {\mathbf{\Phi}^{H}}{\hat{\mathbf{g}}_{\text{RE},m}}\\ -\hat{\mathbf{g}}_{\text{RE},m}^{H}\mathbf{\Phi}&-{\beta_{m}^{2}}{\mu}_{m} - \hat{\mathbf{g}}_{\text{RE},m}^{H}\mathbf{\Phi} {\hat{\mathbf{g}}_{\text{RE},m}} + \tau \eta {\sigma_{E}^{2}} \end{array}\! \right] \succeq \mathbf{{0}} \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \quad m=1,\cdots,M \\ \quad &{\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}(\tilde{\mathbf{Q}}_{\mathbf{v}}, {\tilde{\mathbf{Q}}_{J}}) \le \eta {P_{r}} \\ & {\zeta_{k}}(\tilde{\mathbf{Q}}_{\mathbf{v}}, {\tilde{\mathbf{Q}}_{J}})\le \eta {P_{k}},k=1,\cdots,N \\ & {\tilde{\mathbf{Q}}_{\mathbf{v}}}\succeq {\mathbf{0}},{\tilde{\mathbf{Q}}_{J}}\succeq {\mathbf{0}}, \eta >0, {\mu}_{m}\ge 0, \end{aligned} $$

(19)

where $\mathbf {\Phi } = {P_{s}}{\text {diag}}{\{ {\mathbf {h}_{\text {SR}}}\}^{H}}{\tilde {\mathbf {Q}}_{\mathbf {v}}}{\text {diag}}\{ {\mathbf {h}_{\text {SR}}}\} - {\sigma _{R}^{2}} \tau {\text {diag}}\{ {\tilde {\mathbf {Q}}_{\mathbf {v}}}\} - \tau {\tilde {\mathbf {Q}}_{J}}$.

According to [39], the optimization (19) is a SDP and can be efficiently solved by CVX. This completes the proof.

Proposition 4.

Go back to the optimization problem (10), and let $\delta _{1}=\bar {g}(\tau)$, δ ₂=τ. Then, the optimal solution to (10), $\{{\hat {\mathbf {Q}}}_{\mathbf {v}},{{\hat {\mathbf {Q}}}_{J}} \}$, constitutes an optimal solution to (17).

Proof.

Denote by $\{ {{\bar {\mathbf {Q}}}_{\mathbf {v}}},{{\bar {\mathbf {Q}}}_{J}} \}$ the optimal solution to (17). Because $\{ {{\bar {\mathbf {Q}}}_{\mathbf {v}}},{{\bar {\mathbf {Q}}}_{J}} \}$ is feasible to the optimization (17), it is also feasible to (10). In addition, $\{ {{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_{J}} \}$ is the optimal solution to (10), thus

$$ {\sum\nolimits}_{k = 1}^{N} {\zeta({\hat{\mathbf{Q}}}_{\mathbf{v}},{\hat{\mathbf{Q}}}_{J})} \le {\sum\nolimits}_{k = 1}^{N} {\zeta({\bar{\mathbf{Q}}}_{\mathbf{v}},{\bar{\mathbf{Q}}}_{J})} \le P_{r}, $$

which indicates the point $\{ {{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_{J}} \}$ is feasible to the optimization (17).

For notional simplicity, let

$$ \Psi ({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}})=\frac{{{P_{s}}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}}\mathbf{h}}}{{{\sigma_{D}^{2}} + \mathbf{h}_{\text{RD}}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{h}_{\text{RD}}}}}. $$

From the definition of $\bar g(\tau)$, $\Psi ({\hat {\mathbf {Q}}_{\mathbf {v}}},{\hat {\mathbf {Q}}_{J}})\le \bar {g}(\tau)$. Moreover, from (10), $\Psi ({\hat {\mathbf {Q}}_{\mathbf {v}}},{\hat {\mathbf {Q}}_{J}})\ge \bar {g}(\tau)$, Thus, we have

$$ \Psi({\hat{\mathbf{Q}}_{\mathbf{v}}},{\hat{\mathbf{Q}}_{J}})=\bar{g}(\tau), $$

which implies that the point $\{{{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_{J}}\}$ achieves the maximal value of the optimization (17). This completes the proof.

Remark.

According to Proposition 4, $\{{{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_{J}}\}$ constitutes an optimal solution to (17). In addition, according to Proposition 2, ${\text {rank}}\{{{\hat {\mathbf {Q}}}_{\mathbf {v}}}\}=1$, thus, the optimization (17) is indeed a tight approximation of (16). Besides, $\{\hat {\mathbf {v}},{{\hat {\mathbf {Q}}}_{J}}\}$ is the optimal solution to (16) and $\bar {f}(\tau)=\bar {g}(\tau)$.

So far, the inner-level part is solved and $\bar {f}(\tau)$ is determined for any given τ. The remaining issue now is to resolve the optimal τ ^⋆ maximizing the objective function in (15). In (15), τ _lb and τ _ub denote the lower and upper bound of γ _E,m , respectively. Firstly, γ _E,m is no less than 0, thus, we set τ _lb =0. Secondly, according to the security requirement, γ _E,m should be no more than γ _D . Thus, we set ${\tau _{ub}}=P_{s}P_{r}|\mathbf {h}|^{2}/{\sigma _{D}^{2}}$. By performing one-dimensional search over [τ _lb ,τ _ub ], the optimal τ ^⋆ which maximizes the objective function in (15) could be found. Correspondingly, the optimal solution $\{\mathbf {v}^{\star },{\mathbf {Q}_{J}^{\star }}\}$ to the original optimization (14) can be obtained. In Table 1, we summarize our proposed algorithm for maximizing the worst-case secrecy rate.

Table 1 An algorithm for determining the optimal solution $\{\mathbf {v}^{\star },{\mathbf {Q}_{J}^{\star }}\}$ which maximizes the worst-case secrecy rate

4 Robust joint relaying and jamming design with stochastic CSI error

In this section, we extend our joint cooperative relaying and jamming scheme in Section 3 to the stochastic CSI error model case, and we maximize the outage constrained secrecy rate. In particular, we first solve the SRC power minimization problem. We then study the relationship between the solutions of the SRC power minimization problem and the outage constrained secrecy rate maximization problem. By exploiting this relationship, we provide an approach for solving the outage constrained secrecy rate maximization problem in a convex fashion.

4.1 Channel uncertainty

The channel vector from the relays to the eavesdroppers are modeled as [35]

$$ {\mathbf{g}_{\text{RE},m}}= {\hat{\mathbf{g}}_{\text{RE},m}}+\Delta {\mathbf{g}_{\text{RE},m}}, m=1,\dots,M, $$

(20)

where ${\bar {\mathbf {g}}_{\text {RE},m}}$ denotes the presume part at source node and Δ g _RE,m is the error channel vectors. We assume that each channel error vector has a circularly symmetric complex Gaussian distribution

$$ {\mathbf{g}_{\text{RE},m}}\sim\mathcal{CN}(\hat{\mathbf{g}}_{\text{RE},m},{\mathbf{C}_{m}}) \quad m=1,\dots,M. $$

(21)

4.2 Secrecy outage constrained power minimization

In this subsection, we consider the secrecy outage constrained power minimization problem, i.e., minimizing the total relay power, under the constraint on the achievable secrecy outage rate.

$$ \begin{aligned} \mathop{\min}\limits_{\{\mathbf{v},{\mathbf{Q}_{J}}\}} &{\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \\ \mathrm{s.t.}~\quad & {\gamma_{D}}\ge \delta_{1} \\ &{\text{Prob}}\{\gamma_{E,m}\le{\delta_{2}}\}\ge1-\rho, \forall m \\ & {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \le {P_{k}}, \forall k \\ &{\mathbf{Q}_{\mathbf{v}}}=\mathbf{v}\mathbf{v}^{H},{\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(22)

By letting $\bar {\xi } ({{{\mathbf {Q}}}_{\mathbf {v}}},{{{\mathbf {Q}}}_{J}})=\text {{tr}}\{ {\sigma _{R}^{2}} {\text {diag}}\{ {\mathbf {h}_{\text {RD}}}\mathbf {h}_{\text {RD}}^{H}\} {\mathbf {Q}_{\mathbf {v}}} + {\mathbf {h}_{\text {RD}}}\mathbf {h}_{\text {RD}}^{H}{\mathbf {Q}_{J}}\}$, and dropping the rank 1 constraint on Q _v , we rewrite (22) as

$$ \begin{aligned} \mathop{\min}\limits_{\{{\mathbf{Q}_{v}},{\mathbf{Q}_{J}}\} } &{\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \\ \mathrm{s.t.}~\quad & {P_{s}}{\text{tr}}\{ \mathbf{hh}^{H}{\mathbf{Q}_{\mathbf{v}}}\} \ge \delta_{1}{\sigma_{D}^{2}} +\delta_{1} \bar{\xi} ({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \\ & {\text{Prob}}\{\gamma_{E,m}\le{\delta_{2}}\}\ge1-\rho, \forall m \\ &{\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \le {P_{k}}, \forall k \\ & {\mathbf{Q}_{\mathbf{v}}}\succeq {\mathbf{0}}, {\mathbf{Q}_{J}}\succeq {\mathbf{0}}, \end{aligned} $$

(23)

which is not known to be computationally tractable due to its rate outage probability constraints.

Proposition 5.

The optimization (23) can be safely approximated with a SDP.

Proof.

Our strategy for tackling the rate outage constraints is to find a convex set to approximate them. To this end, we first rewrite the rate outage probability constraints as

$$ {\text{Prob}}\{-\mathbf{g}_{\text{RE},m}^{H}\boldsymbol{\Theta}{\mathbf{g}_{\text{RE},m}} +\delta_{2} {\sigma_{E}^{2}} \ge 0\}\ge1-\rho, $$

(24)

with $\boldsymbol {\Theta } ={P_{s}}{\text {diag}}{\{ {\mathbf {h}_{\text {SR}}}\}^{H}}{{\mathbf {Q}}_{\mathbf {v}}}{\text {diag}}\{ {\mathbf {h}_{\text {SR}}}\} -{\sigma _{E}^{2}} \delta _{2}{\text {diag}}\{ {{\mathbf {Q}}_{\mathbf {v}}}\} - \delta _{2} {{\mathbf {Q}}_{J}}$. Combining (20) with (21), we arrive at

$$ {\mathbf{g}_{\text{RE},m}}= {\hat{\mathbf{g}}_{\text{RE},m}}+ \mathbf{C}^{1/2}_{m}{\mathbf{e}_{m}}, $$

(25)

where ${\mathbf {e}_{m}}\sim \mathcal {CN}({\mathbf {0}},{\mathbf {I}_{N}})$.

Substituting (25) into (24), we then arrive at

$$ {\text{Prob}}\{\mathbf{e}_{m}^{H} \mathbf{Q}_{m} \mathbf{e}_{m}+2{\Re}\{\mathbf{e}_{m}^{H}\mathbf{r} \}+c_{m}\ge 0\}\ge1-\rho, $$

(26)

in which $\mathbf {Q}_{m}=-\mathbf {C}^{1/2}_{m} \boldsymbol {\Theta } \mathbf {C}^{1/2}_{m}$, $\mathbf {r}_{m}=-\mathbf {C}^{1/2}_{m} \boldsymbol {\Theta }{\hat {\mathbf {g}}}_{\text {RE},m}$, and $c_{m}=\delta _{2}{\sigma _{E}^{2}}-{\hat {\mathbf {g}}}_{\text {RE},m}^{H}\boldsymbol {\Theta }{\hat {\mathbf {g}}}_{\text {RE},m}$.

Applying the Sphere Bounding method in [40], we obtain a convex restriction of (26) as follows:

$$ \left[ {\begin{array}{*{20}{c}} {{\mu}_{m} \mathbf{I} + \mathbf{Q}_{m}}& \mathbf{r}_{m}\\ {\mathbf{r}_{m}^{H}}&{c_{m}-\mu_{m} d^{2} } \end{array}} \right] \succeq \mathbf{{0}}, \forall m, $$

(27)

where μ _m ≥0, $d=\sqrt {\mathbf {\Xi }_{\chi _{2N}^{2}}^{{-1}}(1-\rho)/2}$ is the ball radius and ${\boldsymbol {\Xi }_{{\chi _{m}^{2}}}^{{-1}}}(.)$ is the inverse cumulative distribution function of the (central) chi-square random variable with m degrees of freedom.

By replacing the rate outage probability constraints in (23) with (27), we obtain

$$ \begin{aligned} &{\mathop {\min }\limits_{\{ {\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}},{\mu}_{1},\cdots,{\mu}_{M} \}} } {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \\ & \mathrm{s.t.}~ {P_{s}}{\text{tr}}\{ \mathbf{h}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}}\} \ge \delta_{1}{\sigma_{D}^{2}} +\delta_{1} \bar{\xi} ({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \\ &\quad \left[ \begin{array}{cc} {{\mu}_{m} \mathbf{I} + \mathbf{Q}_{m}}& \mathbf{r}_{m}\\ {\mathbf{r}_{m}^{H}}&{c_{m}-\mu_{m} d^{2} } \end{array} \right] \succeq \mathbf{{0}}, \forall m \\ & \quad \ {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}},{\mathbf{Q}_{J}}) \le {P_{k}}, \forall k \\ &\quad \ {\mu}_{m} \ge 0, {\mathbf{Q}_{\mathbf{v}}}\succeq {\mathbf{0}},{\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(28)

According to [39], the optimization (28) is a SDP and can be solved by CVX. This completes the proof.

Proposition 6.

Denote the optimal solution to (23) as $\{ {{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_{J}} \}$. Then ${{\hat {\mathbf {Q}}}_{\mathbf {v}}}$ is rank 1, provided that a positive secrecy rate is achieved.

Proof.

The KKT conditions of (28) are the same as that of (13), with the exception of ${\mathbf {G}_{m}} = \left [{\mathbf {C}_{m}^{1/2}},\ {{\hat {\mathbf {g}}_{RE,m}}} \right ]$. Following the proof in Appendix 6, it is easy to verify $\text {rank}({{\hat {\mathbf {Q}}}_{\mathbf {v}}})=1$. This completes the proof.

By applying the matrix decomposition, we get ${\hat {\mathbf {Q}}}_{\mathbf {v}}=\hat {\mathbf {v}}{\hat {\mathbf {v}}}^{H}$. From Proposition 5, the rank 1 constraint relaxation in (23) is tight. Therefore, $\{\hat {\mathbf {v}},{{\hat {\mathbf {Q}}}_{J}}\}$ is the optimal solution to (22).

4.3 Outage constrained secrecy rate maximization

In this subsection, we aim to maximize the achievable outage constrained secrecy rate, subject to both total and individual relay power constraints, i.e.,

$$ \begin{aligned} \mathop{\max}\limits_{\{r, \mathbf{v, Q}_{J}\}}& \quad r \\ \mathrm{s.t.}&\quad{\text{Prob}}\{{R_{d}}-{R_{e,m}}\ge{r}\}\ge1-\rho, \forall m \\ &\quad {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{r}} \\ &\quad {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{k}}, \forall k \\ & \quad {\mathbf{Q}_{\mathbf{v}}}=\mathbf{v}\mathbf{v}^{H},{\mathbf{Q}_{J}}\succeq {\mathbf{0}}, \end{aligned} $$

(29)

where $R_{d}=\frac {1}{2}\log (1 + {\gamma _{D}})$, $R_{e,m}=\frac {1}{2}\log (1 + {\gamma _{E,m}})$. Letting r _e =R _d −r, we reformulate (29) as

$$ \begin{aligned} \mathop{\max}\limits_{\{r_{e}, \mathbf{v,Q}_{J}\}}& \quad R_{d}-r_{e} \\ \mathrm{s.t.}~&\quad{\text{Prob}}\{{R_{e,m}} \le r_{e}\}\ge 1-\rho, \forall m \\ &\quad {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{r}} \\ &\quad {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{k}}, \forall k \\ & \quad {\mathbf{Q}_{\mathbf{v}}}=\mathbf{v}\mathbf{v}^{H},{\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(30)

By applying the two-layer idea in [13], we recast (30) as a two-level optimization problem. Specifically, the outer-level problem is

$$ {\mathop{\max}\limits_{\tau \in [{\tau_{lb}},{\tau_{ub}}]} \frac{1}{2}\log\left(\frac{{1 + {\bar{f}}(\tau)}}{{1 + \tau }}\right)}, $$

(31)

where ${\bar {f}}(\tau)$ is obtained through solving the following inner-level part optimization problem for a given τ,

$$ \begin{aligned} \bar{f}(\tau)= &{\mathop{\max }\limits_{\{\mathbf{v,Q}_{J}\}}} \frac{{{P_{s}}{\mathbf{h}^{H}}{\mathbf{Q}_{\mathbf{v}}}\mathbf{h}}}{{{\sigma_{D}^{2}} + \mathbf{h}_{\text{RD}}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{h}_{\text{RD}}}}} \\ \mathrm{s.t.}~ & \quad {\text{Prob}}\{{\gamma_{E,m}}\le \tau\}\ge 1-\rho,\quad \forall m \\ & \quad {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{r}} \\ & \quad {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{k}}, \forall k \\ & \quad {\mathbf{Q}_{\mathbf{v}}}=\mathbf{vv}^{H}, {\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(32)

By dropping the rank 1 constraint on Q _v , we obtain

$$ \begin{aligned} \bar{g}(\tau)= &{\mathop{\max}\limits_{\{{\mathbf{Q}_{v}},{\mathbf{Q}_{J}}\}} } \frac{P_{s}\mathbf{h}^{H}\mathbf{Q}_{\mathbf{vh}}}{{\sigma_{D}^{2} + \mathbf{h}_{\text{RD}}^{H}({\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{Q}_{\mathbf{v}}}\} + {\mathbf{Q}_{J}}){\mathbf{h}_{\text{RD}}}}} \\ \mathrm{s.t.}~ & \quad {\text{Prob}}\{{\gamma_{E,m}}\le \tau\}\ge 1-\rho,\forall m \\ & \quad {\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{r}} \\ & \quad {\zeta_{k}}({\mathbf{Q}_{\mathbf{v}}}, {\mathbf{Q}_{J}}) \le {P_{k}}, \forall k \\ & \quad {\mathbf{Q}_{v}}\succeq {\mathbf{0}}, {\mathbf{Q}_{J}}\succeq {\mathbf{0}}. \end{aligned} $$

(33)

Proposition 7.

The optimization (33) can be safely approximated with a SDP.

Proof.

By letting $\eta =\frac {1}{{{\sigma _{D}^{2}} + \mathbf {h}_{\text {RD}}^{H}({\sigma _{R}^{2}}{\text {diag}}\{ {\mathbf {{Q}}_{\mathbf {v}}}\} + {\mathbf {Q}_{J}}){\mathbf {h}_{\text {RD}}}}}$, ${\tilde {\mathbf {Q}}_{\mathbf {v}}} = \eta {\mathbf {Q}_{\mathbf {{v}}}}$, ${\tilde {\mathbf {Q}}_{J}}= \eta {\mathbf {Q}_{J}}$, and using the Charnes-Cooper transformation, we recast the optimization (33) as

$$ \begin{aligned} \bar{g}(\tau)&= \mathop{\max}\limits_{\{ {\tilde{\mathbf{Q}}_{\mathbf{v}}},{{\tilde{\mathbf{Q}}}_{J}},\eta \}} {P_{s}}\text{tr}\{\mathbf{h}{\mathbf{h}^{H}} {\tilde{\mathbf{Q}}_{\mathbf{v}}}\} \\ \mathrm{s.t.} ~ &{\sigma_{D}^{2}}\eta + \text{tr} \{{\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}\} {{\tilde{\mathbf{Q}}}_{\mathbf{v}}} + {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}{{\tilde{\mathbf{Q}}}_{J}}\}=1 \\ &{\text{Prob}}\{-\mathbf{g}_{\text{RE},m}^{H}\mathbf{\Phi}{\mathbf{g}_{\text{RE},m}} +\tau \eta {\sigma_{E}^{2}} \ge 0\}\ge1-\rho, \forall m \\ \quad &{\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\tilde{\mathbf{Q}}_{\mathbf{v}}}, {\tilde{\mathbf{Q}}_{J}}) \le \eta {P_{r}} \\ & {\zeta_{k}}({\tilde{\mathbf{Q}}_{\mathbf{v}}}, {\tilde{\mathbf{Q}}_{J}})\le \eta {P_{k}},\forall k \\ & {\tilde{\mathbf{Q}}_{\mathbf{v}}}\succeq {\mathbf{0}},{\tilde{\mathbf{Q}}_{J}}\succeq {\mathbf{0}},\eta >0, \end{aligned} $$

(34)

where $\boldsymbol {\Phi } = {P_{s}}{\text {diag}}{\{ {\mathbf {h}_{\text {SR}}}\}^{H}}{{\tilde {\mathbf {Q}}}_{\mathbf {v}}}{\text {diag}}\{ {\mathbf {h}_{\text {SR}}}\} - {\sigma _{R}^{2}} \tau {\text {diag}}\{ {{\tilde {\mathbf {Q}}}_{\mathbf {v}}}\} - \tau {\tilde {\mathbf {Q}}_{J}}$.

Applying the same derivation from (26) to (28), we safely approximate the rate outage constraint with LMIs, and reformulate the optimization (34) as

$$ \begin{aligned} \bar{g}(\tau)&= \mathop{\max} \limits_{\{ {{\tilde{\mathbf{Q}}}_{\mathbf{v}}},{{\tilde{\mathbf{Q}}}_{J}},\eta,\mu_{1},\cdots,\mu_{m} \}} {P_{s}}\text{tr}\{\mathbf{h}{\mathbf{h}^{H}} {{\tilde{\mathbf{Q}}}_{\mathbf{v}}}\} \\ \mathrm{s.t.}~ &{\sigma_{D}^{2}}\eta + \text{tr} \{{\sigma_{R}^{2}}{\text{diag}}\{ {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}\} {{\tilde{\mathbf{Q}}}_{\mathbf{v}}} + {\mathbf{h}_{RD}} \mathbf{h}_{RD}^{H}{{\tilde{\mathbf{Q}}}_{J}}\}=1 \\ &\left[ {\begin{array}{cc} {\mu_{m} \mathbf{I} - \mathbf{C}^{1/2}_{m}\mathbf{\Phi}\mathbf{C}^{1/2}_{m} }&{ -\mathbf{C}^{1/2}_{m} {\mathbf{\Phi}}{{\hat{\mathbf{g}}}_{\text{RE},m}}}\\ - (\mathbf{C}^{1/2}_{m} {\mathbf{\Phi}}{{\hat{\mathbf{g}}}_{\text{RE},m}})^{H}&c_{m}-{\mu}_{m} d^{2} \end{array}} \right] \succeq \mathbf{{0}}, \forall m \\ \quad &{\sum\nolimits}_{k = 1}^{N} {\zeta_{k}}({\tilde{\mathbf{Q}}_{\mathbf{v}}}, {\tilde{\mathbf{Q}}_{J}}) \le \eta {P_{r}} \\ & {\zeta_{k}}({\tilde{\mathbf{Q}}_{\mathbf{v}}}, {\tilde{\mathbf{Q}}_{J}})\le \eta {P_{k}},\forall k \\ & {\tilde{\mathbf{Q}}_{\mathbf{v}}}\succeq {\mathbf{0}},{\tilde{\mathbf{Q}}_{J}}\succeq {\mathbf{0}},\eta >0,\mu_{m} \ge 0, \end{aligned} $$

(35)

where $c_{m}={\tau \eta \sigma _{E}^{2}}-\hat {\mathbf {g}}_{\text {RE},m}^{H}\mathbf {\Phi } {{\hat {\mathbf {g}}}_{\text {RE},m}}$. According to [39], the optimization (35) is a SDP and can be solved by CVX. This completes the proof.

Proposition 8.

Go back to the optimization problem (23), and let $\delta _{1}=\bar {g}(\tau)$, δ ₂=τ. Then, the optimal solution to (23), $\{ {{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_{J}}\}$, constitutes an optimal solution to (33).

Proof.

The proof is similar with that of Proposition 4 and thus omitted here. This completes the proof.

Remark.

We should note that ${\text {rank}}\{{{\hat {\mathbf {Q}}}_{\mathbf {v}}}\}=1$ according to Proposition 6. Thus, the solution, $\{ {{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_{J}} \}$, is indeed a tight approximation of (32). Moreover, $\bar {f}(\tau)=\bar {g}(\tau)$.

So far, the inner-level part is solved and $\bar {f}(\tau)$ is determined for any given τ. The remaining issue now is to resolve the optimal τ ^⋆ maximizing the objective function in (31). In (31), τ _lb and τ _ub denote the lower and upper bounds of γ _E,m , respectively. Firstly, γ _E,m is no less than 0, thus we set τ _lb =0. Secondly, according to the security requirement, γ _E,m should be no more than γ _D . Thus, we set ${\tau _{ub}}=P_{s}P_{r}|\mathbf {h}|^{2}/{\sigma _{D}^{2}}$. By performing a one-dimensional search over [τ _lb ,τ _ub ], the optimal τ ^⋆ which maximizes the objective function in (31) could be found. Correspondingly, the optimal solution $\{\mathbf {v}^{\star },{\mathbf {Q}_{J}^{\star }}\}$ to the original optimization (29) can be obtained. In Table 2, we summarize our proposed algorithm for maximizing the outage constrained secrecy rate.

Table 2 An algorithm for determining the optimal solution $\{\mathbf {v}^{\star },{\mathbf {Q}_{J}^{\star }}\}$ which maximizes the outage constrained secrecy rate

5 Numerical results

In this section, we present the numerical results to validate the secrecy rate performance of the proposed joint cooperative relaying and jamming scheme. The transmit power at the source node P _s =10 dB. The covariance of noise at receivers ${\sigma _{D}^{2}}={\sigma _{E}^{2}}={\sigma _{R}^{2}}=1$. The number of relays N=10. The individual relay power budget P _k =0.5P _r /N for k=1,⋯,N/2, and P _k =2P _r /N for k=N/2+1,⋯,N. For ease of exposition, ∀m, we set $\beta _{m} /\sqrt {{N}}=\varepsilon$ for the case of deterministically bounded CSI error model and set C _m =ε I for the case of stochastic CSI error model. At each trial, the entries of the channels h _SR and h _RD, $\hat {\mathbf {g}}_{\text {RE},i}$ are randomly generated following an independent and identically distributed (i.i.d.) complex Gaussian distribution with zero mean and unit variance. Results are averaged over 1000 independent channel trials.

In the following figures, the lines labeled as “SRD link without Eaves” show the maximal achievable rate of the no-eavesdropper case, which provides an upper bound on the secrecy rate of all security schemes. The lines labeled as “Proposed CR and CJ” and “Relaying without jamming” illustrate the worst-case or the outage constrained secrecy rate achieved by the proposed joint cooperative relaying and jamming scheme (also referred to as the proposed scheme in the sequel) and the relaying without jamming scheme, respectively. We should note that for the relaying without jamming scheme, we set $\mathbf {Q}_{J}^{\star }=0$ and compute the relaying weights v ^⋆ according to Tables 1 and 2. The lines labeled as “Jamming Power” denote the power ratio allocated to jamming signals, i.e.,

$$ \delta={\text{tr}}\{\mathbf{Q}_{J}\}/({\text{tr}}\{\mathbf{Q}_{\mathbf{v}}\}+{\text{tr}}\{\mathbf{Q}_{J}\}). $$

The maximal achievable secrecy rate results versus the total relay power budget are plotted in Fig. 2. Here, we set the number of eavesdroppers M=2 and assume that CSI is perfectly known. That is, let ε=0 or let C=0 and compute the optimal input parameter $\{\mathbf {v}^{\star },\mathbf {Q}_{J}^{\star }\}$ according to Table 1 or Table 2. It can be observed that there exists a rate performance ceiling on the SRD link. This is because the signal received at relays contains both the signal transmitted from the source and the unavoidable additive noise. Amplifying the received signal will also amplify the additive noise. We should note that the gap between the maximal secrecy rate that can be achieved by any security schemes and the maximal achievable rate of the SRD link is caused by the secrecy constraint. Obviously, the proposed scheme gets a smaller gap than the relaying without jamming scheme. Moreover, when the power budget at relays is large enough, the secrecy rate achieved by the proposed scheme approaches the maximal achievable rate of the SRD link.

Fig. 2

Secrecy rate and transmit power fraction versus total relay power budget

The worst-case secrecy rate results of different schemes versus the number of eavesdroppers are plotted in Fig. 3. Here, the total relay power budget P _r =20 dB and the channel mismatch ε=0.2. It can be observed that both the secrecy rate achieved by the proposed scheme and that achieved by the relaying without jamming scheme decline with the increasing number of eavesdroppers. However, the secrecy rate achieved by the proposed scheme always outperforms that achieved by the relaying without jamming scheme. Moreover, the secrecy rate achieved by the proposed scheme declines gently while that achieved by the relaying without jamming scheme decreases dramatically. When the number of eavesdropper becomes larger, the power allocated to jamming signals becomes larger, and the benefits of using cooperative jamming is more obvious.

Fig. 3

Worst-case secrecy rate and transmit power fraction versus the number of eavesdroppers when ε=0.2

The channel mismatch impact on the worst-case secrecy rate of different schemes is plotted in Fig. 4. Here, the total relay power budget P _r =20 dB and the number of eavesdroppers M=2. It can be observed that both the worst-case secrecy rate achieved by the proposed scheme and that achieved by the relaying without jamming scheme decline with the increasing of channel uncertainties. However, the robustness of the proposed scheme is more obvious. In particular, the worst-case secrecy rate achieved by the proposed scheme always outperforms that achieved by the relaying without jamming scheme. Moreover, the worst-case secrecy rate achieved by the proposed scheme declines gently, while that achieved by the relaying without jamming scheme decreases dramatically. The power allocated to jamming signals increases as the channel mismatch becomes larger.

Fig. 4

Worst-case secrecy rate and transmit power fraction versus channel mismatch

The number of eavesdroppers impact or the channel mismatch impact on the achievable outage constrained secrecy rate are plotted in Figs. 5 and 6, respectively. We set the secrecy rate outage probability ρ=0.1, the total relay power budget P _r =20 dB. In Fig. 5, we set the channel mismatch C _m =0.02I and let the number of eavesdroppers vary from 1 to 6. In Fig. 6, we set the number of eavesdroppers M=2 and let the channel mismatch vary from 0 to 0.2. Similar to the behavior in Figs. 3 and 4, both the outage constrained secrecy rate achieved by the proposed scheme and that achieved by the relaying without jamming scheme decline with the increasing number of eavesdroppers or the channel uncertainties. However, the outage constrained secrecy rate achieved by the proposed scheme declines gently, while that achieved by the relaying without jamming scheme decreases dramatically. The outage constrained secrecy rate achieved by the proposed scheme always outperforms that achieved by the relaying without jamming scheme. Besides, the power ratio allocated to the jamming signals increases as the number of eavesdroppers increases or the channel mismatch becomes larger. Based on these observations, we verify the robustness of the proposed joint cooperative relaying and jamming scheme.

Fig. 5

Outage constrained secrecy rate and transmit power fraction versus the number of eavesdroppers

Fig. 6

Outage constrained secrecy rate and transmit power fraction versus channel mismatch

6 Conclusions

This paper addressed robust joint optimization of the relay weights and the input covariance matrix of jamming signals for secrecy rate maximization (SRM), under both total and individual relay power constraints. Two CSI error models, deterministically bounded error model and stochastic error model, were considered. For the case of deterministically bounded error model, we maximized the worst-case secrecy rate. While for the case of stochastic error model, we maximized the outage constrained secrecy rate. The challenge of these SRM-based optimizations lies in their non-convexity. In this paper, we provided a unified approach for solving these SRM-based optimizations. Specifically, we recast the original non-convex optimization problem into a sequence of convex optimization problems, via two-level reformulation and semidefinite relaxation techniques. Numerical results showed that the secrecy rate achieved by the proposed joint cooperative relaying and jamming scheme outperforms that achieved by the relaying without jamming scheme. Especially, when the CSI is perfectly known and the power is large enough, the secrecy rate achieved by the proposed scheme approaches that achieved by the SRD link. Moreover, with the increasing of the total relay power budget, the number of eavesdroppers, or the channel uncertainties, distributing part of the total relay power to transmit jamming signals becomes more necessary in order to improve the secrecy rate performance.

7 \thelikesection Appendix A: Proof of Proposition 2

Proposition 2: Denote the optimal solution to (10) as $\{ {{\hat {\mathbf {Q}}}_{\mathbf {v}}},{{\hat {\mathbf {Q}}}_J} \}$. Then ${{\hat {\mathbf {Q}}}_{\mathbf {v}}}$ is rank-one, provided that a positive secrecy rate is achieved.

Proof.

According to Section III, solving the optimization (10) equals to solving the optimization (13) which is convex with part of the KKT conditions as follows

$$\begin{array}{@{}rcl@{}} {\mathbf{Y}} &=& {P_s}{\text{diag}}\{ {{\mathbf{h}}_{SR}}{\mathbf{h}}_{SR}^{H}\} + \sigma _{R}^{2}{\mathbf{I}} \\ && + \lambda [\sigma _{R}^{2}{f(\tau)} {\text{diag}}\{ {{\mathbf{h}}_{RD}}{\mathbf{h}}_{RD}^{H}\} - {P_s}{\mathbf{h}}{{\mathbf{h}}^{H}}] \\ & & + {\sum\nolimits}_{m = 1}^{M} {{\text{diag}}\{ {{\mathbf{h}}_{SR}}\} {{\mathbf{G}}_m}{{\mathbf{B}}_m}{\mathbf{G}}_{m}^{H}{\text{diag}}{{\{ {{\mathbf{h}}_{SR}}\} }^{H}}} \\ & & - {\sum\nolimits}_{m = 1}^{M} {\sigma _{R}^{2}\tau {\text{diag}}\{ {{\mathbf{G}}_m}{{\mathbf{B}}_m}{\mathbf{G}}_{m}^{H}\} }\\ && + {\sum\nolimits}_{k = 1}^{N} {{v_k}[{P_s}{\text{diag}}\{ {{\mathbf{E}}_k}{{\mathbf{h}}_{SR}}{\mathbf{h}}_{SR}^{H}\} + \sigma _{R}^{2}{{\mathbf{E}}_k}]}, \end{array} $$

(36a)

$$\begin{array}{@{}rcl@{}} {\mathbf{X}} &=& {\mathbf{I}} + \lambda {f(\tau)} {{\mathbf{h}}_{RD}}{\mathbf{h}}_{RD}^{H} - {\sum\nolimits}_{m = 1}^{M} {\tau {{\mathbf{G}}_m}{{\mathbf{B}}_m}{\mathbf{G}}_{m}^{H}} \\ && + {\sum\nolimits}_{k = 1}^{N} {{v_k}{{\mathbf{E}}_k}}, \end{array} $$

(36b)

$$\begin{array}{@{}rcl@{}} &{\mathbf{Y}}{\hat{\mathbf{Q}}_{\mathbf{v}}}& = {\mathbf{0}}, \end{array} $$

(36c)

$$\begin{array}{@{}rcl@{}} &{\mathbf{Y}} \succeq& {\mathbf{0}}, {\mathbf{X}} \succeq {\mathbf{0}}, {\mathbf{B}}_{m} \succeq {\mathbf{0}}, \forall m, {v_k}\ge 0, \forall k, \lambda \ge 0, \end{array} $$

(36d)

in which ${{\mathbf {G}}_m} = \left [{\mathbf {I}},\ {{{{\hat {\mathbf {g}}}}_{RE,m}}} \right ]$. Y and X are dual variables associated with $\hat {\mathbf {Q}}_{\mathbf {v}}$ and $\hat {\mathbf {Q}}_{J}$, respectively. In addition, λ, B _m and v _k are dual variables associated with corresponding inequalities in (13).

Combining (36a) and (36b), we arrive at the following equality

$$ \begin{aligned} {\mathbf{ Y}}=& {P_s}{\text{diag}}\{ {{\mathbf{h}}_{SR}}{\mathbf{h}}_{SR}^{H}\} + \sigma _{R}^{2}{\text{diag}}\{ {\mathbf{X}}\} \\ & + {\sum\nolimits}_{m = 1}^{M} {{\text{diag}}\{ {{\mathbf{h}}_{SR}}\} {{\mathbf{G}}_m}{{\mathbf{B}}_m}{\mathbf{G}}_{m}^{H}{\text{diag}}{{\{ {{\mathbf{h}}_{SR}}\} }^{H}}} \\ & + {\sum\nolimits}_{k = 1}^{N} {{v_k}[{P_s}{\text{diag}}\{ {{\mathbf{E}}_k}{{\mathbf{h}}_{SR}}{\mathbf{h}}_{SR}^{H}\} ]} \\ & - \lambda {P_s}{\mathbf{h}}{{\mathbf{h}}^{H}}. \end{aligned} $$

Let

$$ \begin{aligned} {\tilde{\mathbf{Y}}}=& {P_s}{\text{diag}}\{ {{\mathbf{h}}_{SR}}{\mathbf{h}}_{SR}^{H}\} + \sigma _{R}^{2}{\text{diag}}\{ {\mathbf{X}}\} \\ & + {\sum\nolimits}_{m = 1}^{M} {{\text{diag}}\{ {{\mathbf{h}}_{SR}}\} {{\mathbf{G}}_m}{{\mathbf{B}}_m}{\mathbf{G}}_{m}^{H}{\text{diag}}{{\{ {{\mathbf{h}}_{SR}}\} }^{H}}} \\ & + {\sum\nolimits}_{k = 1}^{N} {{v_k}[{P_s}{\text{diag}}\{ {{\mathbf{E}}_k}{{\mathbf{h}}_{SR}}{\mathbf{h}}_{SR}^{H}\} ]}. \end{aligned} $$

Then we have

$$ {\mathbf{Y}}={\tilde{\mathbf{Y}}}- \lambda {P_s}{\mathbf{h}}{{\mathbf{h}}^{H}}. $$

(37)

Generally, ${\text {diag}}\{ {{\mathbf {h}}_{SR}}{\mathbf {h}}_{SR}^{H}\}\succ {\mathbf {0}}$. And the other two terms in the sum expression of ${\tilde {\mathbf {Y}}}$ are non-negative hermite matrices. On the other hand, from (36d), X≽0, so diag{x _d }≽0. Therefore, we arrive at ${\tilde {\mathbf {Y}}} \succ {\mathbf {0}}$.

According to [41], we have ${\text {rank}}\{\lambda {P_s}{\mathbf {h}}{{\mathbf {h}}^{H}}{\hat {\mathbf {Q}}_{\mathbf {v}}}\} \le 1$. Substituting (37) into (36c), we arrive at ${\tilde {\mathbf {Y}}}{\hat {\mathbf {Q}}_{\mathbf {v}}}=\lambda {P_s}{\mathbf {h}}{{\mathbf {h}}^{H}}{\hat {\mathbf {Q}}_{\mathbf {v}}}$. Thus, ${\text {rank}}\{{\tilde {\mathbf {Y}}}{\hat {\mathbf {Q}}_{\mathbf {v}}}\} = {\text {rank}}\{\lambda {P_s}{\mathbf {h}}{{\mathbf {h}}^{H}}{\hat {\mathbf {Q}}_{\mathbf {v}}}\} \le 1$. In addition, ${\tilde {\mathbf {Y}}} \succ {\mathbf {0}}$, so ${\text {rank}}\{{\hat {\mathbf {Q}}_{\mathbf {v}}}\}={\text {rank}}\{{\tilde {\mathbf {Y}}}{\hat {\mathbf {Q}}_{\mathbf {v}}}\} \le 1$. On the other hand, ${\text {rank}}\{{\hat {\mathbf {Q}}_{\mathbf {v}}}\} =0$ implies ${\hat {\mathbf {Q}}_{\mathbf {v}}}={\mathbf {0}}$ which contradicts with the positive secrecy rate requirement. Thus, ${\text {rank}}\{{\hat {\mathbf {Q}}_{\mathbf {v}}}\} =1$. The completes the proof.