1 Introduction

An efficient signal constellation has always been an active research area since 1960s for the purpose of wired and wireless communication. Quadrature amplitude modulation (QAM) has become the dominant modulation scheme in terms of power and bandwidth efficiency. It was first suggested by C. R. Cahn in 1960 [1]. Since then, many developments have been made in the geometry of QAM. The constellation was named QAM. Hancock and Lucky [2] expanded the work of Cahn. They suggested constellations with signal points taken on concentric circles, with outer ring having more points than on the inner ring. Idea behind this was to remove errors due to phase shift. Later in 1962, Campopiano and Glazer [3] introduced a well-organized structure of even-bit signal constellation, which is presently known as square QAM (SQAM). In 1960s and 1970s, progressive research on the structure of a potent 16-ary constellation had been carried out. Since Square QAM retains a high minimum distance between constellation points and has simple detection technique, plenty of the digital communication systems using high modulation orders with 16 or greater number of constellation points have been utilizing the SQAM. Little literature on constellation designs defeating the SQAM in terms of good transmission capability is available since its birth. In [4], a honeycomb-like architecture of constellation whose signal points are taken at the origin and on the first and the second concentric hexagon has been advised. The authors named this constellation as Honeycomb Signal Set. In 1989, Shinjiro Oshita et al. [5] proposed another structure which had hexagonal packing; it was analyzed and named as triangular-shaped signal set (TSSS). In spite of the structures of constellations suggested in [4, 5] which give improved performance over the SQAM, they are not practicable because of the increase in detection complexity at the receiver end.

Recently, in 2007, Sung-Joon Park [6] presented a novel symmetrical structure named as triangular quadrature amplitude modulation (TQAM) in which vertices of the equilateral triangles were taken as constellation signal points. TQAM has a proven efficiency against SQAM in terms of error probability performance and detection complexity in [6, 7]. TQAM uses even number of bits to represent a signal point in the constellation. The key reason behind the efficiency of TQAM constellation is its compact geometry. In 2010, symbol error probability (SEP) of TQAM was evaluated by K. Cho, J. Lee, and D. Yoon for additive white Gaussian noise (AWGN) channel [8] and also, an approximation of SEP expression for TQAM was derived for AWGN and fading channels by T. T. DUY and H. Y. KONG [9], in which maximal-ratio combining (MRC) was used to analyze TQAM over Rayleigh fading channel with multipath reception. In [10], θ-QAM was introduced to incorporate SEP of SQAM and TQAM in a single analytical expression over AWGN and Nakagami-m channels; however, J. Lee et al. [11] proved their work incorrect for higher modulation order and presented their own equations for exact SEP and bit error probability (BEP) over AWGN channel and also paved way for exact BEP over Rayleigh, Rician, and Nakagami-m channels. However, the SEP expressions provided in [10] are valid only for modulation order 16. In 2012, Sung-Joon Park analyzed the SEP performance of TQAM in AWGN channel using an approximate expression for the SEP [7]. Though an exact generalized mathematical SEP expression in the presence of AWGN channel is provided in [11], the mathematical model we provide in this article can be implemented easily when dealing with TQAM not only in AWGN, but also this model is extended to Rayleigh, Nakagami-m, Nakagami-n, and Nakagami-q channels. To the best of author’s knowledge, generalized SEP expressions for fading channels incorporating diversity reception have not been presented before in [7–11].

In this paper, TQAM has been analyzed in single-input multi-output (SIMO) environment with spatial diversity. We use spatial diversity to mitigate fading. Diversity combining is the most powerful way to cater the aftermaths of multipath fading. These combining techniques were introduced by Brennan [12]. Diversity is available whenever multiple, independently fading channels link the transmitter and receiver. Such multiple channels naturally occur in multi-input multi-output (MIMO) applications for which the transmitter or receiver use an antenna array. These diversity combining techniques are actually the operations performed on an antenna array. The idea behind using diversity reception scheme is that, as the signal paths are independent, all of them have very low probability to experience deep fades simultaneously. Thus, we transmit same signal over independently fading paths in diversity reception scheme. In this article, at receiving end these paths are then combined using MRC algorithm that the fading amount of the combined received signal decreases and consequently its signal-to-noise ratio (SNR) improves. MRC was first proposed by Kahn [13]. In MRC, if there are total L antennas at the receiving end, the received signals from all of the L branches are weighted according to their individual SNR and then summed together to provide single output.

The performance of M-ary QAM with space diversity in various fading channels has been analyzed in [9, 14–24], on which light, is shredded in terms of comparison in Section 5. Recently in 2010, Xi-chun Zhang et al. [25] utilized the MGF-based approach to evaluate the performance of cross QAM over fading channels, and later in 2013, their work was extended by Hua Yu et al. [26] to SIMO systems with MRC reception. Here, based on the moment-generating function (MGF) method, average SEP of M-ary TQAM is analyzed, whereas, MRC is used as the spatial diversity technique at the receiving end. The fading channels considered in this article are Rayleigh, Nakagami-m, Nakagami-n (Rice), and Nakagami-q (Hoyt). The results presented are valid for slow flat fading channels only. Moreover, we consider a coherent general order TQAM signal assuming perfect channel estimation. We are using finite integral form of Gaussian Q-function and the unified MGF-based approach to reach the final expressions. SEP closed-form expression provided here consists of single finite range integrals, and the integrand is composed of elementary functions which provide easy numerical evaluation. Moreover, the mathematical expressions are valid for general modulation order TQAM and are accurate and elementary enough that it becomes conducive and fast to quantify the SEP performance of TQAM with MRC.

The remaining article is organized in six sections. In Section 2, we show the SEP expression for AWGN channel. In Section 3, we present the channel model for MRC spatial diversity. In Section 4, we pursue the derivation of SEP expression for M-ary TQAM with MRC. Section 5 presents numerical results with brief discussion. An example has been simulated in Section 6, which validates our results derived in Section 4, whereas, conclusion is given in Section 7.

2 SEP of TQAM over AWGN channel

From Fig. 1, it is observed that unlike SQAM, in TQAM, all the nearest neighbors to any signal point in constellation are equidistant. This is the key reason that SEP expressions provided here give exact fit over the simulation curves. Point P is taken at Euclidean distance d/2 from the origin at an angle of 60°, where d is the length of one side of the triangle, or we can say distance between any two adjacent signal points is d. M-ary TQAM is an even-bit representation of constellation points, i.e., M = 22m where m = 2, 3, 4, …, and M is the modulation order of the constellation.

Fig. 1
figure 1

Signal constellation for 16-TQAM

Full size image

In Fig. 2, dots p j represents jth signal point, where j = 1, 2, 3, …, M and the lines show decision boundaries for 16-TQAM. Now here, four of the innermost signal points have hexagonal decision regions which resemble like honeycomb. The decision boundary lines for all the signal points are drawn based on the Campopiano-Glazer construction rule ([27]: Article 9.9.2). For 64-TQAM, [7: Fig. 1b] is referred. We assume here that all the signal points are equally probable and Re(p j ) and Im(p j ) are the real and imaginary values of signal point p j , respectively. Average energy per symbol E s for M-ary TQAM can be evaluated as:

Fig. 2
figure 2

Decision boundaries for 16-TQAM

Full size image
$$ {E}_s=\frac{1}{M}\left[{\displaystyle \sum_{j=1}^M{\left\{\mathrm{R}\mathrm{e}\left({p}_j\right)\right\}}^2+{\displaystyle \sum_{j=1}^M{\left\{\mathrm{I}\mathrm{m}\left({p}_j\right)\right\}}^2}}\right] $$
(1)
$$ {E}_s=\frac{4}{M}\left[\frac{\sqrt{M}}{4}{\displaystyle \sum_{i=1}^{\sqrt{M}}{\left\{\left(2i-1\right)\frac{d}{2} cos{60}^o\right\}}^2+\frac{\sqrt{M}}{2}{\displaystyle \sum_{i=1}^{\raisebox{1ex}{$\sqrt{M}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\left\{\left(2i-1\right)\frac{d}{2} sin{60}^o\right\}}^2}}\right] $$
(2)

In (2), upper limit of the summation is always a positive integer. Solving summation of polynomial expressions using Faulhaber’s formula ([28]: p. 106):

$$ {E}_s=\frac{\left(7M-4\right){d}^2}{48} $$
(3)

This leads us to minimum Euclidean distance d expression,

$$ d=\sqrt{\frac{48{E}_s}{7M-4}} $$
(4)

since symbol’s signal-to-noise ratio γ can be written as:

$$ \gamma =\frac{E_s}{N_o}=\frac{\left(7M-4\right)}{24}{\left(\frac{d}{2\sigma}\right)}^2=\frac{\left(7M-4\right){\beta}^2}{24} $$
(5)

where σ 2 = N O /2 is the variance of Gaussian probability distribution function and β is the normalized least distance between adjacent symbols. Thus:

$$ \beta =\sqrt{\frac{24\gamma }{\left(7M-4\right)}}=\sqrt{2D\gamma } $$
(6)
$$ D=\frac{12}{7M-4} $$
(7)

The SEP expressions in this section and Section 4 are derived in terms of β.

The main reason for using the MGF-based approach is to utilize the technique of writing Gaussian Q-function with finite integration limits. Now in this constellation, there are five types of signal points based on the number of neighbors each point has, and unlike SQAM, for this particular constellation, each symbol has all the neighbors as the nearest neighbors. Table 1 tells us about the number of nearest neighbors for M-ary TQAM, where S N means number of signal points having N nearest neighbors.

Table 1 Signal points S N having N nearest neighbors
Full size table

Probability of correct symbol reception P C, N for a symbol having N nearest neighbors is written as:

$$ {P}_{C,2}={\left(1-Q\left(\beta \right)\right)}^2=1-2Q\left(\beta \right)+{Q}^2\left(\beta \right) $$
(8)
$$ {P}_{C,3}={\left(1-Q\left(\beta \right)\right)}^3=1-3Q\left(\beta \right)+3{Q}^2\left(\beta \right)-{Q}^3\left(\beta \right) $$
(9)
$$ {P}_{C,4}={\left(1-Q\left(\beta \right)\right)}^4=1-4Q\left(\beta \right)+6{Q}^2\left(\beta \right)-4{Q}^3\left(\beta \right)+{Q}^4\left(\beta \right) $$
(10)
$$ {P}_{C,5}={\left(1-Q\left(\beta \right)\right)}^5=1-5Q\left(\beta \right)+10{Q}^2\left(\beta \right)-10{Q}^3\left(\beta \right)+5{Q}^4\left(\beta \right)-{Q}^5\left(\beta \right) $$
(11)
$$ {P}_{C,6}={\left(1-Q\left(\beta \right)\right)}^6=1-6Q\left(\beta \right)+15{Q}^2\left(\beta \right)-20{Q}^3\left(\beta \right)+15{Q}^4\left(\beta \right)-6{Q}^5\left(\beta \right)+{Q}^6\left(\beta \right) $$
(12)

where Q(β) is the Gaussian Q-function and to evaluate it numerically, [29]: equation (9)] is used, which is its finite limit integral form. The exact probability of correct receiving symbol for M-ary TQAM is given as:

$$ {P}_C\left(\beta \right)=\frac{1}{M}\left[{S}_2{P}_{C,2}+{S}_3{P}_{C,3}+{S}_4{P}_{C,4}+{S}_5{P}_{C,5}+{S}_6{P}_{C,6}\right] $$
(13)
$$ \begin{array}{l}{P}_C\left(\beta \right)=1-\left(\frac{2}{M}-\frac{8}{\sqrt{M}}+6\right)Q\left(\beta \right)+\left(\frac{18}{M}-\frac{35}{\sqrt{M}}+15\right){Q}^2\left(\beta \right)\\ {}-\left(\frac{44}{M}-\frac{61}{\sqrt{M}}+20\right){Q}^3\left(\beta \right)+\left(\frac{46}{M}-\frac{53}{\sqrt{M}}+15\right){Q}^4\left(\beta \right)\\ {}-\left(\frac{22}{M}-\frac{23}{\sqrt{M}}+6\right){Q}^5\left(\beta \right)+\left(\frac{4}{M}-\frac{4}{\sqrt{M}}+1\right){Q}^6\left(\beta \right)\end{array} $$
(14)

since P e (β) = 1 − P C (β):

$$ \begin{array}{l}{P}_e\left(\beta \right)=6\left(1+\frac{1}{3M}-\frac{4}{3\sqrt{M}}\right)Q\left(\beta \right)-15\left(1+\frac{6}{5M}-\frac{7}{3\sqrt{M}}\right){Q}^2\left(\beta \right)\\ {}+20\left(1+\frac{11}{5M}-\frac{61}{20\sqrt{M}}\right){Q}^3\left(\beta \right)-15\left(1+\frac{46}{15M}-\frac{53}{15\sqrt{M}}\right){Q}^4\left(\beta \right)\\ {}+6\left(1+\frac{11}{3M}-\frac{23}{6\sqrt{M}}\right){Q}^5\left(\beta \right)-\left(1+\frac{4}{M}-\frac{4}{\sqrt{M}}\right){Q}^6\left(\beta \right)\end{array} $$
(15)

Equation (15) gives us the exact SEP of M-ary TQAM in the presence of AWGN channel. In Section 4, using (15), we evaluate the SEP over various fading channels with MRC reception after presenting channel model in Section 3.

3 MRC spatial diversity channel models

In SIMO system, the signal is transmitted over L diversity paths where each copy of the signal struggles through individual fading amplitude. The multipath receiver uses the algorithm of MRC diversity reception scheme to increase the SNR of the combined received signal by decreasing the SEP. For MRC, SNR of the combined output signal γ ∑ at the receiver is expressed as ([30]: equation (5.98)):

$$ {\gamma}_{\sum }=\frac{E_s}{N_o}{\displaystyle \sum_{i=1}^L{\alpha_i}^2}={\displaystyle \sum_{i=1}^L{\gamma}_i}\kern0.6em \mathrm{where}\ i = 1,\ 2,\ 3, \dots,\ L $$
(16)
$$ {\gamma}_i=\frac{E_s}{N_0}{\alpha_i}^2 $$
(17)

where γ i is the instantaneous received SNR per symbol and α i is the instantaneous fading amplitude at the ith diversity path. SEP evaluation of TQAM over fading channels while using MRC diversity receiver demands knowledge of probability density function (pdf) of SNR γ ∑ of the combined signal at output. Before that, we take a look at the pdf of the instantaneous received SNR per symbol γ i of the ith diversity path over Rayleigh, Nakagami-m, Nakagami-n and Nakagami-q channels respectively, provided from [31] as:

$$ {p}_{\gamma_i,\mathrm{Rayleigh}}\left(\gamma \right)=\frac{1}{\overline{\gamma_i}} exp\left(-\frac{\gamma }{\overline{\gamma_i}}\right),{\gamma}_i\ge 0 $$
(18)
$$ {p}_{\gamma_i,{m}_i}\left(\gamma \right)=\frac{{m_i}^{m_i}{\gamma}^{m_i-1}}{{\overline{\gamma_i}}^{m_i}\varGamma (m)} exp\left(-\frac{m_i\gamma }{\overline{\gamma_i}}\right),{\gamma}_i\ge 0,{m}_i\ge 0.5 $$
(19)
$$ {p}_{\gamma_i,{n}_i}\left(\gamma \right)=\frac{\left(1+{n_i}^2\right){e}^{-{n_i}^2}}{\overline{\gamma_i}} exp\left(-\frac{\left(1+{n_i}^2\right)\gamma }{\overline{\gamma_i}}\right){I}_0\left(2{n}_i\sqrt{\frac{\left(1+{n}_2\right)\gamma }{\overline{\gamma_i}}}\right),{\gamma}_i\ge 0,{n}_i\ge 0 $$
(20)
$$ {p}_{\gamma_i,{q}_i}\left(\gamma \right)=\frac{\left(1+{q_i}^2\right)}{2{q}_i\overline{\gamma_i}} exp\left(-\frac{{\left(1+{q_i}^2\right)}^2\gamma }{4{q_i}^2\overline{\gamma_i}}\right){I}_0\left(\frac{\left(1-{q_i}^4\right)\gamma }{4{q_i}^2\overline{\gamma_i}}\right),{\gamma}_i\ge 0,{q}_i\in \left[0,1\right] $$
(21)

where \( \overline{\gamma_i}=E\left[{\gamma_i}^2\right] \) is the average received SNR per symbol. E[.] is the expectation operator and I 0 (.) is the modified Bessel function of the first kind and zero order. Using (18)–(21) along with (22), the MGFs of Rayleigh, Nakagami-m, Nakagami-n, and Nakagami-q fading channels are respectively given in [31] as:

$$ {M}_{\gamma_i}(s)={\displaystyle {\int}_0^{\infty }{e}^{s\gamma }{p}_{\gamma_i}\left(\gamma \right)}d\gamma $$
(22)
$$ {M}_{\gamma_i,\mathrm{Rayleigh}}(s)={\left(1+\overline{\gamma_i}s\right)}^{-1} $$
(23)
$$ {M}_{\gamma_i,{m}_i}(s)={\left(1+\frac{\overline{\gamma_i}}{m_i}s\right)}^{-{m}_i},{m}_i\ge 0.5 $$
(24)
$$ {M}_{\gamma_i,{n}_i}(s)=\frac{\left(1+{n_i}^2\right)}{1+{n_i}^2+s\overline{\gamma_i}} exp\left(\frac{{n_i}^2s\overline{\gamma_i}}{1+{n_i}^2+s\overline{\gamma_i}}\right),{n}_i\ge 0 $$
(25)
$$ {M}_{\gamma_i,{q}_i}(s)={\left(1+2s\overline{\gamma_i}+\frac{{\left(2s\overline{\gamma_i}\right)}^2{q_i}^2}{{\left(1+{q_i}^2\right)}^2}\right)}^{-1/2},{q}_i\in \left[0,1\right] $$
(26)

From (23) to (26), we can observe that these are MGFs of the individual ith diversity path. As we are considering multiple channels which are independent but not necessarily identical, then the MGF of the γ ∑ is written as the product of the individual MGFs of γ i :

$$ {M}_{\gamma_{\sum }}(s)={\displaystyle \prod_{i=1}^L{M}_{\gamma_i}(s)} $$
(27)

Equation (27) gives us the MGF of the SNR of the combined signal at the output of the receiver.

4 SEP of TQAM with MRC spatial diversity

Now we attend our main objective, i.e., to find the SEP expression for M-ary TQAM in MRC diversity scheme. This is achieved by averaging the SEP formula (15) over the pdf of the SNR \( {p}_{\gamma_{\sum }}\left(\gamma \right) \) of the combined signal at the output.

$$ {P}_{\mathrm{diversity}}={\displaystyle \underset{0}{\overset{\infty }{\int }}{P}_e\left(\gamma \right)}{p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma $$
(28)

P e (γ) is the exact SEP for M-ary TQAM in AWGN channel as provided in (15), whereas, from (6) we know that β is a function of γ.

$$ \begin{array}{l}{P}_{\mathrm{diversity}}=6\left(1+\frac{1}{3M}-\frac{4}{3\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}Q\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma }-15\left(1+\frac{6}{5M}-\frac{7}{3\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^2\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma}\\ {}+20\left(1+\frac{11}{5M}-\frac{61}{20\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^3\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma }-15\left(1+\frac{46}{15M}-\frac{53}{15\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^4\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma}\\ {}+6\left(1+\frac{11}{3M}-\frac{23}{6\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^5\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma }-\left(1+\frac{4}{M}-\frac{4}{\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^6\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma}\end{array} $$
(29)

Ignoring the higher order terms Q i, i > 4, the average symbol error probability is approximately given as:

$$ \begin{array}{l}{P}_{\mathrm{diversity}}\approx 6\left(1+\frac{1}{3M}-\frac{4}{3\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}Q\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma }-15\left(1+\frac{6}{5M}-\frac{7}{3\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^2\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma}\\ {}+20\left(1+\frac{11}{5M}-\frac{61}{20\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^3\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma }-15\left(1+\frac{46}{15M}-\frac{53}{15\sqrt{M}}\right){\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^4\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma}\end{array} $$
(30)

In (30), we remove the infinite upper limit in the integrals by using a few mathematical tools. From [32: equation (2)], we can write \( Q\left(\beta \right)=2{Q}_a\left(\beta, \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right) \) and from [33: equation (12)], we can write \( {Q}^2\left(\beta \right)=2{Q}_a\left(\beta, \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$4$}\right.\right) \), both for β ≥ 0. Where,

$$ {Q}_a\left(\beta, \varphi \right)=\frac{1}{2\pi }{\displaystyle {\int}_0^{\varphi } exp\left[-\frac{\beta^2}{2{sin}^2\theta}\right]}d\theta $$
(31)

The form in (31) simplifies the evaluation of SEP performance over fading channels. For higher powers of the Gaussian Q-function, we refer to [31: Article 4.1.4]. The following relationships are applied:

$$ Q\left(\beta \right)=2{Q}_a\left(\beta, \frac{\pi }{2}\right) $$
(32)
$$ {Q}^2\left(\beta \right)=2{Q}_a\left(\beta, \frac{\pi }{4}\right) $$
(33)
$$ \begin{array}{l}{Q}^3\left(\beta \right)=Q\left(\beta \right){Q}^2\left(\beta \right)\\ {}{Q}^3\left(\beta \right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]} exp\left(-\frac{\beta^2}{2{sin}^2\theta}\right)d\theta \\ {}+\frac{1}{2{\pi}^2}{\displaystyle \underset{0}{\overset{sin^{-1}\left(1/\sqrt{3}\right)}{\int }}\left\{\pi -{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]\right\}} exp\left(-\frac{\beta^2}{2{sin}^2\theta}\right)d\theta \end{array} $$
(34)
$$ \begin{array}{l}{Q}^4\left(\beta \right)={Q}^2\left(\beta \right){Q}^2\left(\beta \right)\\ {}{Q}^4\left(\beta \right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]} exp\left(-\frac{\beta^2}{2{sin}^2\theta}\right)d\theta \end{array} $$
(35)

Still we have not eliminated the infinite upper limit in the integrals of (30). We have only simplified the evaluation of higher powers of the Gaussian Q-function yet. Now, if

$$ I\left(\beta, \varphi \right)={\displaystyle \underset{0}{\overset{\infty }{\int }}Q\left(\beta \right)}{p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma $$
(36)

then from relationships provided in (6) and (32), we can write

$$ I\left(D,\varphi \right)=2{\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}_a\left(\sqrt{2D\gamma },\varphi \right)}{p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma $$
(37)

This integral can be expressed in terms of MGF of γ (22). Using (31), we get

$$ I\left(D,\varphi \right)={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\varphi }{\int }} exp\left[-\frac{D\gamma }{sin^2\theta}\right]d\theta }}{p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma $$
(38)
$$ I\left(D,\varphi \right)={\displaystyle \underset{0}{\overset{\varphi }{\int }}\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }} exp\left[-\frac{D\gamma }{sin^2\theta}\right]}}{p}_{\gamma_{\sum }}\left(\gamma \right) d\gamma d\theta $$
(39)
$$ I\left(D,\varphi \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\varphi }{\int }}{M}_{\gamma}\left(\frac{D}{sin^2\theta}\right)}d\theta $$
(40)

Now (40) is applicable to 1st and 2nd power of the Gaussian Q-function. For 3rd and 4th power of the Gaussian Q-function, we define I Q3 (D, φ) and I Q4(D, φ) as:

$$ \begin{array}{l}{I}_{Q3}\left(D,\frac{\pi }{6}\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^3\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma}\\ {}{I}_{Q3}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{M}_{\gamma}\left(\frac{D}{sin^2\theta}\right)d\theta \\ {}+\frac{1}{2{\pi}^2}{\displaystyle \underset{0}{\overset{sin^{-1}\left(1/\sqrt{3}\right)}{\int }}\left\{\pi -{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]\right\}}{M}_{\gamma}\left(\frac{D}{sin^2\theta}\right)d\theta \end{array} $$
(41)
$$ \begin{array}{l}{I}_{Q4}\left(D,\frac{\pi }{6}\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^4\left(\beta \right){p}_{\gamma_{\sum }}\left(\gamma \right)d\gamma}\\ {}{I}_{Q4}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{M}_{\gamma}\left(\frac{D}{sin^2\theta}\right)d\theta \end{array} $$
(42)

Now (30) can be expressed as:

$$ \begin{array}{l}{P}_{\mathrm{diversity}}\approx 6\left(1+\frac{1}{3M}-\frac{4}{3\sqrt{M}}\right)I\left(D,\frac{\pi }{2}\right)-15\left(1+\frac{6}{5M}-\frac{7}{3\sqrt{M}}\right)I\left(D,\frac{\pi }{4}\right)\\ {}+20\left(1+\frac{11}{5M}-\frac{61}{20\sqrt{M}}\right){I}_{Q3}\left(D,\frac{\pi }{6}\right)-15\left(1+\frac{46}{15M}-\frac{53}{15\sqrt{M}}\right){I}_{Q4}\left(D,\frac{\pi }{6}\right)\\ {}\end{array} $$
(43)

The difference in (30) and (43) is that we have overcome the infinite limits of integration. The SEP expression (43) is used to measure performance of M-ary TQAM in diversity systems using MRC technique. On substituting MGF from (27) in (40), we get following four integrals with finite limits for Rayleigh, Nakagami-m, Nakagami-n, and Nakagami-q fading mediums, respectively as:

$$ {I}_{\mathrm{Rayleigh}}\left(D,\varphi \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\varphi }{\int }}{\displaystyle \prod_{i=1}^L\left[\frac{sin^2\theta }{sin^2\theta +D\overline{\gamma_i}}\right]}}d\theta $$
(44)
$$ {I}_m\left(D,\varphi \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\varphi }{\int }}{\displaystyle \prod_{i=1}^L{\left(1+\frac{\overline{\gamma_i}}{m_i}\frac{D}{sin^2\theta}\right)}^{-{m}_i}}}d\theta $$
(45)
$$ {I}_n\left(D,\varphi \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\varphi }{\int }}{\displaystyle \prod_{i=1}^L\left(\frac{\left(1+{n_i}^2\right)}{1+{n_i}^2+D\overline{\gamma_i}{ \csc}^2\theta } exp\left(\frac{{n_i}^2D\overline{\gamma_i}}{sin^2\theta +{n_i}^2{sin}^2\theta +D\overline{\gamma_i}}\right)\right)}}d\theta $$
(46)
$$ {I}_q\left(D,\varphi \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\varphi }{\int }}{\displaystyle \prod_{i=1}^L{\left(1+\frac{2\overline{\gamma_i}D}{sin^2\theta }+{\left(\frac{2{q}_i\overline{\gamma_i}}{1+{q_i}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}}}d\theta $$
(47)

Similarly, on substituting MGF from (27) in (41), we get following four integrals with finite limits for Rayleigh, Nakagami-m, Nakagami-n, and Nakagami-q fading mediums, respectively as:

$$ \begin{array}{l}{I}_{Q3,\mathrm{Rayleigh}}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L\left[\frac{{ \sin}^2\theta }{{ \sin}^2\theta +D\overline{\gamma_i}}\right]}d\theta \\ {}+\frac{1}{2{\pi}^2}{\displaystyle \underset{0}{\overset{{ \sin}^{-1}\left(1/\sqrt{3}\right)}{\int }}\left\{\pi -{cos}^{-1}\left[\frac{3 \cos 2\theta -1}{2{cos}^32\theta }-1\right]\right\}}{\displaystyle \prod_{i=1}^L\left[\frac{{ \sin}^2\theta }{{ \sin}^2\theta +D\overline{\gamma_i}}\right]}d\theta \end{array} $$
(48)
$$ \begin{array}{l}{I}_{Q3,m}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L{\left(1+\frac{\overline{\gamma_i}}{m_i}\frac{D}{sin^2\theta}\right)}^{-{m}_i}}d\theta \\ {}+\frac{1}{2{\pi}^2}{\displaystyle \underset{0}{\overset{sin^{-1}\left(1/\sqrt{3}\right)}{\int }}\left\{\pi -{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]\right\}}{\displaystyle \prod_{i=1}^L{\left(1+\frac{\overline{\gamma_i}}{m_i}\frac{D}{sin^2\theta}\right)}^{-{m}_i}}d\theta \end{array} $$
(49)
$$ \begin{array}{l}{I}_{Q3,n}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L\left(\frac{\left(1+{n_i}^2\right)}{1+{n_i}^2+D\overline{\gamma_i}{csc}^2\theta } exp\left(\frac{{n_i}^2D\overline{\gamma_i}}{sin^2\theta +{n_i}^2{sin}^2\theta +D\overline{\gamma_i}}\right)\right)}d\theta \\ {}+\frac{1}{2{\pi}^2}{\displaystyle \underset{0}{\overset{sin^{-1}\left(1/\sqrt{3}\right)}{\int }}\left\{\pi -{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]\right\}}{\displaystyle \prod_{i=1}^L\left(\frac{\left(1+{n_i}^2\right)}{1+{n_i}^2+D\overline{\gamma_i}{csc}^2\theta } exp\left(\frac{{n_i}^2D\overline{\gamma_i}}{sin^2\theta +{n_i}^2{sin}^2\theta +D\overline{\gamma_i}}\right)\right)}d\theta \end{array} $$
(50)
$$ \begin{array}{l}{I}_{Q3,q}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L{\left(1+\frac{2\overline{\gamma_i}D}{sin^2\theta }+{\left(\frac{2{q}_i\overline{\gamma_i}}{1+{q_i}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}}d\theta \\ {}+\frac{1}{2{\pi}^2}{\displaystyle \underset{0}{\overset{sin^{-1}\left(1/\sqrt{3}\right)}{\int }}\left\{\pi -{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]\right\}}{\displaystyle \prod_{i=1}^L{\left(1+\frac{2\overline{\gamma_i}D}{sin^2\theta }+{\left(\frac{2{q}_i\overline{\gamma_i}}{1+{q_i}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}}d\theta \end{array} $$
(51)

Treating (42) in similar fashion with (27), we get I Q4(D, φ) for the stated fading mediums.

$$ {I}_{Q4,\mathrm{Rayleigh}}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L\left[\frac{sin^2\theta }{sin^2\theta +D\overline{\gamma_i}}\right]}d\theta $$
(52)
$$ {I}_{Q4,m}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L{\left(1+\frac{\overline{\gamma_i}}{m_i}\frac{D}{sin^2\theta}\right)}^{-{m}_i}}d\theta $$
(53)
$$ {I}_{Q4,n}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L\left(\frac{\left(1+{n_i}^2\right)}{1+{n_i}^2+D\overline{\gamma_i}{csc}^2\theta } exp\left(\frac{{n_i}^2D\overline{\gamma_i}}{sin^2\theta +{n_i}^2{sin}^2\theta +D\overline{\gamma_i}}\right)\right)}d\theta $$
(54)
$$ {I}_{Q4,q}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}{\displaystyle \prod_{i=1}^L{\left(1+\frac{2\overline{\gamma_i}D}{sin^2\theta }+{\left(\frac{2{q}_i\overline{\gamma_i}}{1+{q_i}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}}d\theta $$
(55)

Since the four integrals from (44) to (55) are finite range, single integrals and integrand composed of elementary functions only; using (43), the average SEP of general modulation order TQAM with MRC spatial diversity over fading channels can be conveniently assessed through numerical integration methods.

5 Numerical results and discussion

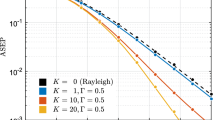
Here, we verify our analytical formulas using computer simulations. In Fig. 3, (15) is compared with the SEP approximation provided in ([7]: equation (5)). Figure 3 shows the SEP of 16-TQAM and 64-TQAM against SNR in AWGN channel, and it is observed that our expression for exact SEP (15) completely agrees with the simulation curve. Figures 4 and 5 show symbol error rate performance of 16-TQAM and 64-TQAM over Rayleigh fading channel using MRC diversity scheme, respectively. In Fig. 4, comparison has been made with the SQAM results provided in [15]. We investigate the effect of m, the Nakagami-m fading parameter (m ≥ 0.5), in Figs. 6 and 7, which displays the SEP performance of M = 16 and M = 64 for Nakagami-m channel against SNR with MRC reception, where m = 2, 4. Figure 6 shows comparison with SQAM [16]. Figures 8 and 9 explain the SEP performance in Nakagami-n channel, where K = n 2 and various values of K considered are K = 1 dB, 7 dB. Here, n is the Nakagami-n fading parameter, which ranges from 0 to ∞. For comparison with SQAM, we apply the results of [17] in Fig. 8. Similarly from Figs. 10 and 11, we confirm analytical expression for Nakagami-q fading channel derived in (43) along with (47), (51), and (55) for q = 0, 0.3, where q is the Nakagami-q fading parameter (0 ≤ q ≤ 1). Comparison with SQAM [22] is shown in Fig. 10 for Nakagami-q medium.

Fig. 3
figure 3

SEP performance of M-TQAM in AWGN channel

Full size image
Fig. 4
figure 4

SEP performance of 16-TQAM in Rayleigh channel

Full size image
Fig. 5
figure 5

SEP performance of 64-TQAM in Rayleigh channel

Full size image
Fig. 6
figure 6

SEP Performance of 16-TQAM in Nakagami-m Channel

Full size image
Fig. 7
figure 7

SEP performance of 64-TQAM in Nakagami-m channel

Full size image
Fig. 8
figure 8

SEP performance of 16-TQAM in Nakagami-n channel

Full size image
Fig. 9
figure 9

SEP performance of 64-TQAM in Nakagami-n channel

Full size image
Fig. 10
figure 10

SEP performance of 16-TQAM in Nakagami-q channel

Full size image
Fig. 11
figure 11

SEP performance of 64-TQAM in Nakagami-q channel

Full size image

Table 2 provides power gains achieved because of using antenna array instead of single antenna in MRC scenario. We observe quite significant power gain, as L increases. The highest gain is obtained by going from single antenna to two-branch diversity. Now, as the diversity paths are increased from two to three, the power gain lessens as it was for going from one to two, generally as we keep on increasing L, the power gain diminishes. The gains for Nakagami-m, m = 1, and Nakagami-q, q = 1, are same as for the Rayleigh fading channel. It is clearly observed that the system performance improves as the diversity order increases. The results illustrate the advantage of diversity as a means for combating the fading phenomena.

Table 2 Power gains for TQAM with MRC diversity scheme at P e = 10−2
Full size table

6 Example

To further validate the analytical SEP expressions (43) to (55) for M-ary TQAM in MRC, we simulate an example. We take five diversity branches, each with different type of channel fading. The experiment is performed over both 16-TQAM and 64-TQAM, respectively. Following are the channel fadings being considered over different diversity branches:

  • First branch: Rayleigh fading

  • Second branch: Nakagami-m fading (m = 2)

  • Third branch: Nakagami-m fading (m = 4)

  • Fourth branch: Nakagami-q fading (q = 0)

  • Fifth branch: Nakagami-q fading (q = 0.3)

Now to evaluate the analytical expression for this experiment, we use (43); however, the integrals are evaluated using (56), (57), and (58) as below:

$$ \begin{array}{l}I\left(D,\varphi \right)=\frac{1}{\pi }{\displaystyle \underset{0}{\overset{\varphi }{\int }}\left[\frac{sin^2\theta }{sin^2\theta +D\overline{\gamma}}\right]\left[{\left(1+\frac{\overline{\gamma}}{2}\frac{D}{sin^2\theta}\right)}^{-2}\right]\left[{\left(1+\frac{\overline{\gamma}}{4}\frac{D}{sin^2\theta}\right)}^{-4}\right]}\\ {}\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta}\right)}^{-\frac{1}{2}}\right]\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta }+{\left(\frac{2(0.3)\overline{\gamma}}{1+{0.3}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}\right]d\theta \end{array} $$
(56)
$$ \begin{array}{l}{I}_{Q3}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}\left[\frac{sin^2\theta }{sin^2\theta +D\overline{\gamma}}\right]\left[{\left(1+\frac{\overline{\gamma}}{2}\frac{D}{sin^2\theta}\right)}^{-2}\right]\\ {}\left[{\left(1+\frac{\overline{\gamma}}{4}\frac{D}{sin^2\theta}\right)}^{-4}\right]\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta}\right)}^{-\frac{1}{2}}\right]\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta }+{\left(\frac{2(0.3)\overline{\gamma}}{1+{0.3}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}\right]d\theta \\ {}+\frac{1}{2{\pi}^2}{\displaystyle \underset{0}{\overset{sin^{-1}\left(1/\sqrt{3}\right)}{\int }}\left\{\pi -{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]\right\}}\left[\frac{sin^2\theta }{sin^2\theta +D\overline{\gamma}}\right]\left[{\left(1+\frac{\overline{\gamma}}{2}\frac{D}{sin^2\theta}\right)}^{-2}\right]\\ {}\left[{\left(1+\frac{\overline{\gamma}}{4}\frac{D}{sin^2\theta}\right)}^{-4}\right]\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta}\right)}^{-\frac{1}{2}}\right]\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta }+{\left(\frac{2(0.3)\overline{\gamma}}{1+{0.3}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}\right]d\theta \end{array} $$
(57)
$$ \begin{array}{l}{I}_{Q4}\left(D,\frac{\pi }{6}\right)=\frac{1}{\pi^2}{\displaystyle \underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$6$}\right.}{\int }}{cos}^{-1}\left[\frac{3 cos2\theta -1}{2{cos}^32\theta }-1\right]}\left[\frac{sin^2\theta }{sin^2\theta +D\overline{\gamma}}\right]\left[{\left(1+\frac{\overline{\gamma}}{2}\frac{D}{sin^2\theta}\right)}^{-2}\right]\\ {}\left[{\left(1+\frac{\overline{\gamma}}{4}\frac{D}{sin^2\theta}\right)}^{-4}\right]\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta}\right)}^{-\frac{1}{2}}\right]\left[{\left(1+\frac{2\overline{\gamma}D}{sin^2\theta }+{\left(\frac{2(0.3)\overline{\gamma}}{1+{0.3}^2}\right)}^2\frac{D^2}{sin^4\theta}\right)}^{-\frac{1}{2}}\right]d\theta \\ {}\end{array} $$
(58)

The simulation result for this example is shown in Fig. 12. A good fit of SEP simulation curve over the theoretical curve adds to the validity of our analytical expressions derived in Section 4.

Fig. 12
figure 12

SEP performance of M-ary TQAM in various fading channels, L = 5

Full size image

7 Conclusion

In this article, the SEP performance of TQAM with MRC spatial diversity over independent but not necessarily identical multi-branch fading channels, including Rayleigh, Nakagami-m, Nakagami-n, and Nakagami-q channels, have been evaluated based on the unified MGF-based approach. The SEP expressions are simple and accurate and can be applied to any even-bit general modulation order TQAM. These SEP expressions consist of single integrals with finite limits and integrand composed of elementary functions only, which can be accurately evaluated numerically. The simulation results, along with the example, also confirm the efficacy of numerical expressions obtained for the abovementioned channels. So, by choosing only the modulation order of the constellation and the diversity order of MRC, we can study the impact of diversity reception, which removes the need for Monte Carlo simulations to optimize any wireless system parameters using TQAM.