1 Introduction

The past decade has seen a lot of research in the area of distributed estimation for wireless sensor networks [1–4]. The diffusion scheme using the least mean square (LMS) algorithm was first introduced by Lopes and Sayed in [2]. The first algorithm to propose a variable step-size for the diffusion LMS algorithm was proposed by Saeed et al. in [5] and extended by Saeed et al. in [6]. Since then, several variable step-size algorithms have been proposed [7–12].

While each algorithm improves in performance, the improvement comes at the cost of increased computational complexity. The variable step-size strategy proposed by Kwong and Johnston in [13] was extended to the distributed network scenario by Saeed et al. in [5, 6]. This work was further expanded by Saeed and Zerguine in [7] by using the distributed nature of the network to improve performance. A noise constraint was introduced by Saeed et al. in [8] for improved performance. An optimal step-size for the distributed scenario was derived by Ghazanfari-Rad and Labeau in [9], based on which they derived a variable step-size for each iteration. A variable step-size as well as combination weights were derived using an upper bound for the mean square deviation (MSD) by Jung et al. in [10]. Lee et al. derived an individual step-size for each sensor by minimizing the local MSD in [11]. Saeed et al. proposed a variable step-size strategy for distributed estimation in a compressible system in [12].

While all these algorithms provide excellent performance, they are all based on the l2-norm, except for the algorithm in [12]. This means that the power of the instantaneous error is the key factor for all these algorithms. This means that the performance of these algorithms suffers significantly in low signal-to-noise ratio (SNR) scenarios. Furthermore, there is significant increase in computational complexity as a trade-off for improved performance.

This work proposes a method where the step-size is varied using a quotient of the filtered error power. The algorithm is inspired from the work of Zhao et al. in [14]. The quotient form combined with the windowing effect reduces the effect of the power of the instantaneous error, making the algorithm more robust to low SNR scenarios. The quotient form of [14] is combined with the diffusion scheme in this work. A theoretical analysis of the algorithm has been presented. The energy conservation approach used for the analysis in this work was not used in [14]. Saeed presented a generalized analysis for variable step-size schemes using the energy conservation approach in [15]. This work was extended to the diffusion scheme by Saeed et al. in [16]. However, the variable step-size using the quotient form was not included in [16]. The analysis presented here utilizes the approach of [16] and gives stability, transient, and steady-state analyses for the proposed algorithm. Simulation comparisons with the variable step-size diffusion LMS (VSSDLMS) algorithm of [6] show that the proposed algorithm achieves significant improvement with a reasonably acceptable increase in computational complexity.

The rest of the paper is divided as follows. Section 2 presents the system model and defines the problem statement. Section 3 proposes the new algorithm. The theoretical analysis is given in Section 4, followed by simulation results in Section 5. Section 6 concludes this work.

2 System model

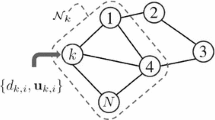
A geographical area of N sensor nodes, each connected to its closest neighbors as shown in Fig. 1, is being considered. The unknown parameters are modeled as a vector, wo, of size (M×1). The input to a node at any given time instant, i, is a (1×M) regressor vector, uk(i), where k∈N is the node index. The resulting observed output for the node is a noise corrupted scalar, dk(i), given by

$$ d_{k}(i) = \mathbf{u}_{k}(i)\mathbf{w}^{o} + v_{k}(i), $$
(1)
Fig. 1
figure 1

An illustration of an adaptive network of N nodes

Full size image

where vk(i) is the zero-mean additive noise.

The generic form of the Adapt-then-Combine (ATC) variable step-size diffusion LMS (VSDLMS) algorithm is given by [16]

$$\begin{array}{@{}rcl@{}} \boldsymbol{\Psi}_{k}(i+1) &=& \mathbf{w}_{k} (i) + \mu_{k}(i) e_{k}(i) \mathbf{u}_{k}^{T} (i), \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} \mathbf{w}_{k} (i+1) &=& \sum_{l \in \mathcal{N}_{k}} {c_{lk} \boldsymbol{\Psi}_{l} (i+1)}, \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} \mu_{k} (i+1) &=& f\{\mu_{k}(i)\}, \end{array} $$
(4)

where wk(i) is the estimate of the unknown vector at time instant i for node k, bfΨk(i) is the intermediate update for node k, ek(i)=dk(i)−uk(i)wk(i) is the instantaneous error, clk is the combination weight for the data transmitted from node l to node k, \(\mathcal {N}_{k}\) is the neighborhood of node k and (.)T is the transpose operator. The step-size is denoted by μk(i) and f{.} is the function that updates the step-size at every iteration.

The main objective of this work is to propose a new function, f{.}, for the VSDLMS algorithm defined by (2)–(4). The new function is derived in the next section, followed by theoretical analysis and experimental results.

3 Proposed algorithm

The proposed update equation for the step-size is given by

$$\begin{array}{@{}rcl@{}} \mu_{k} (i+1) &=& \alpha \mu_{k} (i) + \gamma \theta_{k} (i), \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \theta_{k} (i) &=& \frac{\sum_{m=0}^{i} {a^{m} e_{k}^{2} (i-m)}}{\sum_{n=0}^{i} {b^{n} e_{k}^{2} (i-n)}}, \end{array} $$
(6)

where α and γ are positive parameters such that 0<α<1 and γ>0 and a and b are forgetting factors for the decaying exponential windows in the numerator and denominator and are bounded as 0<a<b<1. Although (6) represents the complete window for both the numerator and denominator, a more suitable and iterative representation is given by

$$\begin{array}{@{}rcl@{}} A_{k}(i) &=& \sum_{m=0}^{i} {a^{m} e_{k}^{2} (i-m)} = a A_{k} (i-1) + e_{k}^{2} (i), \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} B_{k}(i) &=& \sum_{n=0}^{i} {b^{n} e_{k}^{2} (i-n)} = b B_{k} (i-1) + e_{k}^{2} (i), \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} \theta_{k} (i) &=& \frac{A_{k}(i)}{B_{k}(i)} = \frac{a A_{k}(i-1) + e_{k}^{2} (i)}{b B_{k}(i-1) + e_{k}^{2} (i)}. \end{array} $$
(9)

Combining (5) and (9) with (2) and (3) gives the proposed variable step-size diffusion LMS algorithm with a quotient form (VSQDLMS).

4 Theoretical analysis

Recently, the authors of [16] proposed a unified theoretical analysis for VSDLMS algorithms. Following the same procedure as [16], the following global variables are introduced to represent the entire network:

$$\begin{array}{@{}rcl@{}} \mathbf{w}(i) &=& \text{col} \left\{ {\mathbf{w}_{1}(i),\mathbf,\mathbf{w}_{N}(i)} \right\}, \\ \boldsymbol{\Psi}(i) &=& \text{col} \left\{ {\boldsymbol{\Psi}_{1}(i),\ldots,\boldsymbol{\Psi}_{N}(i)} \right\}, \\ \mathbf{U}(i) &=& \text{diag} \left\{ {\mathbf{u}_{1}(i),\ldots,\mathbf{u}_{N}(i)} \right\}, \\ \mathbf{D}(i) &=& \text{diag} \left\{ {\mu_{1}(i) {\mathbf{I}}_{M},\ldots,\mu_{N}(i) {\mathbf{I}}_{M}} \right\}, \\ \boldsymbol{\Theta}(i) &=& \text{diag} \left\{ {\theta_{1}(i) {\mathbf{I}}_{M},\ldots,\theta_{N}(i) {\mathbf{I}}_{M}} \right\}, \\ \bar{\mathbf{A}}(i) &=& \text{diag} \left\{ {A_{1}(i) {\mathbf{I}}_{M},\ldots,A_{N}(i) {\mathbf{I}}_{M}} \right\}, \\ \bar{\mathbf{B}}(i) &=& \text{diag} \left\{ {B_{1}(i) {\mathbf{I}}_{M},\ldots,B_{N}(i) {\mathbf{I}}_{M}} \right\}, \\ \mathbf{d}(i) &=& \text{col} \left\{ {d_{1} \left(i \right),\ldots,d_{N} \left(i \right)} \right\}, \\ \mathbf{v}(i) &=& \text{col} \left\{ {v_{1} \left(i \right),\ldots,v_{N} \left(i \right)} \right\}. \end{array} $$

The combination weight matrix is given by {C}lk=clk. When expanded to the entire network, this becomes G=C⊗IM, where ⊗ represents the Kronecker product. The unknown parameters vector wo is expanded for the entire network using w(o)=Qwo, where Q=col{IM,IM,…,IM} is a (MN×M) sized matrix. The resulting global set of equations representing the VSQDLMS algorithm are given by

$$\begin{array}{@{}rcl@{}} \mathbf{d}(i) &=& \mathbf{U}(i) \mathbf{w}^{\left(o \right)} + \mathbf{v}(i), \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} \boldsymbol{\Psi}\left(i+1\right) &=& \mathbf{w}(i) + \mathbf{D}(i) \mathbf{U}^{T}(i) \left({\mathbf{d}(i) - \mathbf{U}(i) \mathbf{w}(i)} \right), \\ \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} \mathbf{w}\left(i+1\right) &=& \mathbf{G}\boldsymbol{\Psi}\left(i+1\right), \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} \boldsymbol{\Theta} (i) &=& \frac{\bar{\mathbf{A}} (i)}{\bar{\mathbf{B}} (i)}, \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \mathbf{D}\left(i+1\right) &=& \alpha \mathbf{D} (i) + \gamma \boldsymbol{\Theta} (i). \end{array} $$
(14)

4.1 Mean analysis

Introducing the global weight-error vector as

$$ \tilde{\mathbf{w}}(i) = \mathbf{w}^{\left(o \right)} - \mathbf{w}(i). $$
(15)

Using (15), the update in (2) is rewritten as

$$ \tilde{\boldsymbol{\Psi}}_{k}(i+1) = \tilde{\mathbf{w}}_{k} (i) - \mu_{k}(i) e_{k}(i) \mathbf{u}_{k}^{T} (i), $$
(16)

where the relation in (15) is extended for Ψk(i). Expanding the error term, ek(i), and rearranging gives

$$\begin{array}{@{}rcl@{}} \tilde{\boldsymbol{\Psi}}_{k}(i+1) &=& \left[ \mathbf{I}_{M} - \mu_{k} (i) \mathbf{u}_{k}^{T} (i) \mathbf{u}_{k} (i) \right] \tilde{\mathbf{w}}_{k} (i) \\ &&- \mu_{k}(i) \mathbf{u}_{k}^{T} (i) v_{k} (i). \end{array} $$
(17)

Applying the expectation operator to (17) and using the independence assumption gives, after simplification

$$ \mathsf{E} \left[ \tilde{\boldsymbol{\Psi}}_{k}(i+1) \right] = \left[ \mathbf{I}_{M} - \mathsf{E} \left[ \mu_{k} (i) \right] \mathbf{R}_{\mathbf{u}_{k}} \right] {\mathsf{E}} \left[ \tilde{\mathbf{w}}_{k} (i) \right], $$
(18)

where \(\mathbf {R}_{\mathbf {u}_{k}} = {\mathsf {E}} \left [ \mathbf {u}_{k}^{T} (i) \mathbf {u}_{k} (i) \right ]\) is the autocorrelation of the input data at node k.

The algorithm will be stable in the mean sense if the term \(\left [ \mathbf {I}_{M} - {\mathsf {E}} \left [ \mu _{k} (i) \right ] \mathbf {R}_{\mathbf {u}_{k}} \right ]\) is bounded. This means that the algorithm will not diverge if this term is bounded. Thus, for the algorithm to be stable in the mean, the following condition needs to be satisfied:

$$ 0 < {\mathsf{E}}\left[ {\mu_{k}(i)} \right] < \frac{2}{{\lambda_{\max} \left({\mathbf{R}_{\mathbf{u},k}} \right)}}, \hspace{0.5cm} 1 \le k \le N, $$
(19)

where λmax(Ru,k) is the maximum eigenvalue of the auto-correlation matrix Ru,k.

4.2 Mean-square analysis

The mean-square analysis in [16] assumes Gaussian input data. The auto-correlation matrix is decomposed into its component eigenvector and eigenvalue matrices as RU=TΛTT, with Λ being the diagonal eigenvalue matrix and T being the eigenvector matrix, such that TTT=I. The eigenvector matrix T is then used to transform the remaining variables as follows:

$$\begin{array}{*{20}c} {\overline{\mathbf{w}}(i) = \mathbf{T}^{T} \tilde{\mathbf{w}}(i)} & {\overline{\mathbf{U}}(i) = \mathbf{U}(i) \mathbf{T}} \\ {\overline{\mathbf{G}} = \mathbf{T}^{T} {\mathbf{G}\mathbf{T}}} & {\overline{\boldsymbol{\Sigma}} = \mathbf{T}^{T} \boldsymbol{\Sigma} \mathbf{T}} \\ {\overline{\boldsymbol{\Sigma}} ' = \mathbf{T}^{T} \boldsymbol{\Sigma} '\mathbf{T}} & \overline{\mathbf{D}}(i) = \mathbf{T}^{T} \mathbf{D}(i) \mathbf{T} = \mathbf{D}(i), \end{array} $$

where Σ and \(\phantom {\dot {i}\!}\boldsymbol {\Sigma }^{'}\) are weighting matrices. The final iterative update equation for the mean-square transient analysis is given by [16]

$$\begin{array}{@{}rcl@{}} {\mathsf{E}} \left[ \left\| \overline{\mathbf{w}}(i+1) \right\|^{2}_{\overline{\boldsymbol{\sigma}}} \right] &=& {\mathsf{E}} \left[ \left\| \overline{\mathbf{w}}(i) \right\|^{2}_{\bar{\boldsymbol{\sigma}}} \right] + \mathbf{b}^{T}\left(i \right) \overline{\boldsymbol{\sigma}} \\ &&+ \left\| \overline{\mathbf{w}}^{(o)} \right\|^{2}_{\mathcal{\mathbf{A}}(i)\left[\mathbf{F}(i) - \boldsymbol{I}_{M^{2} N^{2}} \right] \overline{\boldsymbol{\sigma}}} \\ &&+ \mathcal{B} (i) \left[\mathbf{F}(i) - \boldsymbol{I}_{M^{2} N^{2}} \right] \overline{\boldsymbol{\sigma}}, \end{array} $$
(20)

where

$$\begin{array}{@{}rcl@{}} \mathbf{b} (i) &=& \text{bvec} \left\{ \mathbf{R}_{\mathbf{v}} {\mathsf{E}} \left[ \mathbf{D}^{2} (i) \right] \boldsymbol{\Lambda} \right\}, \\ \mathbf{F}(i) &=& \left[ {\mathbf{I}_{M^{2} N^{2}} - \left({\mathbf{I}_{MN} \odot \boldsymbol{\Lambda} {\mathsf{E}}\left[ {\mathbf{D}} \left(i \right) \right]} \right)} \right. \\ &&- \left({\boldsymbol{\Lambda} {\mathsf{E}}\left[ {\mathbf{D}} \left(i \right) \right] \odot \mathbf{I}_{MN}} \right) \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} &&\left. + \left({{\mathsf{E}}\left[ {\mathbf{D}\left(i \right) \odot \mathbf{D}\left(i \right)} \right]} \right)\mathbf{A} \right].\left({\mathbf{G}^{T} \odot \mathbf{G}^{T}} \right), \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} \mathcal{\mathbf{A}}(i+1) &=& \mathcal{\mathbf{A}}(i) \mathbf{F}(i), \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} {\mathcal{B}}(i+1) &=& {\mathcal{B}} (i) \mathbf{F}(i) + \mathbf{b}^{T} (i) \boldsymbol{I}_{M^{2} N^{2}}, \end{array} $$
(24)

where ⊙ denotes the block Kronecker product, Rv=Λv⊙IM, Λv is a diagonal noise variance matrix for the network and \({\overline {\boldsymbol {\sigma }}} = \text {bvec} \left \{ \overline {\boldsymbol {\Sigma }} \right \}\). The matrix A is given in [2, 16] as A=diag{A1,A2,…,AN}, with each component matrix defined as

$$\begin{array}{@{}rcl@{}} \mathbf{A}_{k} = \text{diag} &&\left\{ {\boldsymbol{\Lambda}_{1} \otimes \boldsymbol{\Lambda}_{k},\ldots,\boldsymbol{\lambda}_{k} \boldsymbol{\lambda}_{k}^{T} + 2\boldsymbol{\Lambda}_{k} \otimes \boldsymbol{\Lambda}_{k},} \right. \\ &&\left. {\ldots,\boldsymbol{\Lambda}_{N} \otimes \boldsymbol{\Lambda}_{k}} \right\}, \end{array} $$
(25)

where Λk is the diagonal eigenvalue matrix and λk is the corresponding eigenvalue vector for node k.

In order to find the mean square deviation (MSD), the weighting matrix is chosen as \(\overline {\boldsymbol {\Sigma }} = \mathbf {I}_{N^{2} M^{2}}\). To get the excess mean square error (EMSE), the weighting matrix is chosen as \(\overline {\boldsymbol {\Sigma }} = \boldsymbol {\Lambda }\).

4.3 Steady-state analysis

At steady-state, (20) becomes

$$ {\textsf{E}}\left[ {\left\| {\overline{\mathbf{w}}_{ss}} \right\|_{\overline{\boldsymbol{\sigma}} }^{2}} \right] = {\textsf{E}}\left[ {\left\| {\bar{\mathbf{w}}_{ss}} \right\|_{\textbf{F}_{ss} \overline{\boldsymbol{\sigma}} }^{2}} \right] + \textbf{b}_{ss}^{T} \overline{\boldsymbol{\sigma}}, $$
(26)

where

$$\begin{array}{@{}rcl@{}} \mathbf{F}_{ss} &=& \left[ {\mathbf{I}_{M^{2} N^{2}} - \left({\mathbf{I}_{MN} \odot \Lambda {\mathsf{E}}\left[ {\mathbf{D}_{ss}} \right]} \right) - \left({\Lambda {\mathsf{E}}\left[ {\mathbf{D}_{ss}} \right] \odot \mathbf{I}_{MN}} \right)} \right. \\ &&+ \left.{\left({{\mathsf{E}}\left[ {\mathbf{D}_{ss} \odot \mathbf{D}_{ss}} \right]} \right)\mathbf{A}} \right].\left({\mathbf{G}^{T} \odot \mathbf{G}^{T}} \right), \end{array} $$
(27)
$$\begin{array}{@{}rcl@{}} \mathbf{b}_{ss} &=& \mathbf{R}_{\mathbf{v}} \mathbf{D}_{ss}^{2} \boldsymbol{\Lambda}. \end{array} $$
(28)

To get the steady-state MSD, we choose \({\overline {\boldsymbol {\sigma }}} = \text {bvec} \left \{ \mathbf {I}_{N^{2} M^{2}} \right \}\), and to get the steady-state EMSE, we choose \({\overline {\boldsymbol {\sigma }}} = \text {bvec} \left \{ \boldsymbol {\Lambda } \right \}\).

4.4 Steady-state step-size analysis

The step-size matrices, Dss=diag{μk,ssIM} and \(\mathbf {D}_{ss}^{2} = \text {diag} \left \{ \mu _{k,ss}^{2} \mathbf {I}_{M} \right \}\), are defined by the individual node values for the steady-state step-size. The step-size update for the proposed algorithm is defined by (5), (7)-(9). Taking the expectation gives

$$\begin{array}{@{}rcl@{}} {\mathsf{E}} \left[ A_{k} (i) \right] &=& a {\mathsf{E}} \left[ A_{k} (i-1) \right] + {\mathsf{E}} \left[ e_{k}^{2} (i) \right] \\ &=& a {\mathsf{E}} \left[ A_{k} (i-1) \right] + \text{EMSE} (i) + \sigma^{2}_{v,k}, \end{array} $$
(29)
$$\begin{array}{@{}rcl@{}} {\mathsf{E}} \left[ B_{k} (i) \right] &=& b {\mathsf{E}} \left[ B_{k} (i-1) \right] + \text{EMSE} (i) + \sigma^{2}_{v,k}, \end{array} $$
(30)
$$\begin{array}{@{}rcl@{}} {\mathsf{E}} \left[ \theta_{k} (i) \right] &\approx& \frac{{\mathsf{E}} \left[ A_{k} (i) \right]}{{\mathsf{E}} \left[ B_{k} (i) \right]}, \end{array} $$
(31)
$$\begin{array}{@{}rcl@{}} {\mathsf{E}} \left[ \mu_{k} (i+1) \right] &=& \alpha {\mathsf{E}} \left[ \mu_{k} (i) \right] + \gamma {\mathsf{E}} \left[ \theta_{k} (i) \right]. \end{array} $$
(32)

At steady-state, the EMSE value is assumed to go to 0, the expectation operator is removed and after simple manipulations, we get

$$\begin{array}{@{}rcl@{}} A_{k,ss} &=& \frac{1}{1-a} \sigma^{2}_{v,k}, \end{array} $$
(33)
$$\begin{array}{@{}rcl@{}} B_{k,ss} &=& \frac{1}{1-b} \sigma^{2}_{v,k}, \end{array} $$
(34)
$$\begin{array}{@{}rcl@{}} \theta_{k,ss} &=& \frac{A_{k,ss}}{B_{k,ss}} = \frac{1-b}{1-a}, \end{array} $$
(35)
$$\begin{array}{@{}rcl@{}} \mu_{k,ss} &=& \frac{\gamma (1-b)}{(1-\alpha)(1-a)}, \end{array} $$
(36)

where the term ss indicates steady-state value. Thus, the steady-state step-size value is given by (36) and the value for \(\mu _{k,ss}^{2}\) is simply the square of (36).

5 Results and discussion

This section presents experimental results for the proposed algorithm. The algorithm is tested in four different scenarios. First, the proposed algorithm is compared with the algorithm from [6] as well with the no cooperation case, in which each sensor applies the variable step-size quotient strategy for estimation without cooperating with any other sensor. The reason for the comparison with only the algorithm of [6] is that the computational complexity for both algorithms is similar. However, it is shown that with a small increase in computational complexity, the proposed algorithm performs much better. Next, the theoretical transient analysis of (20) is compared with simulation results. In the third experiment, the steady-state results from (26) are compared with steady-state simulation results. Finally, the performance of the proposed algorithm is tested in a scenario where the exact value of M is unknown.

5.1 Experiment I

In the first experiment, the proposed VSQDLMS algorithm is compared with the variable step-size diffusion LMS (VSSDLMS) algorithm from [6]. A comparison of computational complexity is given in Table 1. As can be seen, the increase in computations is small. The performance of the two algorithms is compared through simulations. The no cooperation case has been added to compare the performance of the proposed algorithm with the scenario where each sensor operates as if it were acting in a stand-alone environment. The size of wo is chosen as M=5. The size of the network is N = 20. The SNR value is varied from 0 dB to 20 dB. The parameters defining the step-size update equations are shown in Table 2. The values of the parameters are chosen such that the convergence speed is the same for all algorithms and the performance is measured on the basis of the steady-state MSD, as shown in the figures. Results are shown for white Gaussian input regressor data as well as colored input regressor data, with the correlation factor of 0.5. As can be seen from Figs. 2 and 3, the proposed algorithm clearly outperforms the VSSDLMS algorithm from [6]. At low SNR, the performance of the proposed algorithm at 0 dB is even better than the performance of the VSSDLMS algorithm at 10 dB. The steady-state results for these experiments are given in Table 3. As can be seen, the proposed algorithm gives an improvement in performance of almost 10 dB for the case of white input and 5 dB for the case of colored input. This significant improvement in performance clearly justifies the trade-off between complexity and performance.

Fig. 2
figure 2

Performance comparison for the proposed VSQDLMS vs VSSDLMS [6] algorithms for white input

Full size image
Fig. 3
figure 3

Performance comparison for the proposed VSQDLMS vs VSSDLMS [6] algorithms for correlated input

Full size image
Table 1 Computational complexity comparison for step-size update equations
Full size table
Table 2 Parameter values for Experiment 1
Full size table
Table 3 Steady-state results for Figs. 1 and 2
Full size table

5.2 Experiment II

In this experiment, the performance of the proposed algorithm is tested for different network sizes with a fixed unknown vector length, M=5. The performance of the proposed algorithm is then tested for a fixed network size, N=20, while the length of the unknown vector, M is varied. Finally, the performance of the algorithm is compared for Gaussian and Uniform input data. The results are shown in Figs. 4, 5, and 6. For varying N and M, the steady-state MSD results are plotted. As expected, performance improves as N increases as each sensor has more neighboring nodes for sharing data and improving its estimate. However, the performance degrades with increase in M as it becomes difficult to obtain an accurate estimate as the number of unknown parameters increases. The results shown use the same control parameters as in Experiment I.

Fig. 4
figure 4

Steady-state results for varying N with M = 5 and SNR 20 dB

Full size image
Fig. 5
figure 5

Steady-state results for varying M with N = 20 and SNR 20 dB

Full size image
Fig. 6
figure 6

Performance comparison for Gaussian and uniform input data

Full size image

5.3 Experiment III

The next experiment compares the transient behavior of the proposed algorithm obtained from (20) with the simulation results. For this experiment, the network size is chosen as N = 5 and N = 10. The length of the unknown parameter vector is taken to be M = 2 and M = 5. The SNR is fixed at 20 dB. The step-size control parameters are set as α=a=0.99, γ=10−3 and b = 1−10−3. The results are shown in Figs. 7 and 8. As can be seen, the theoretical results closely match the simulation results. The mismatch during the transient stage is a result of the assumptions from [16]. However, this is expected, as shown in the results of [16], and is acceptable as the two curves are closely matched at steady-state.

Fig. 7
figure 7

Theory (20) vs simulation for a network of size N = 5

Full size image
Fig. 8
figure 8

Theory (20) vs simulation for a network of size N=10

Full size image

5.4 Experiment IV

Next, we compare the steady-state results obtained using (26) with the steady-state results obtained through simulations. The SNR values are varied from 0 dB to 30 dB. The network size is varied from N = 5 to N = 20. The results are shown in Figs. 9, 10, 11, and 12. There is a very close match for all results. For an exact comparison, some of these results have been tabulated in Tables 4 and 5. As can be seen, the results for the theory match closely with those obtained through simulation.

Fig. 9
figure 9

Steady-state theory (26) vs simulation for a network of size N=5

Full size image
Fig. 10
figure 10

Steady-state theory (26) vs simulation for a network of size N = 10

Full size image
Fig. 11
figure 11

Steady-state theory (26) vs simulation for a network of size N = 15

Full size image
Fig. 12
figure 12

Steady-state theory (26) vs simulation for a network of size N = 20

Full size image
Table 4 Steady-state results for N = 5 and N = 10
Full size table
Table 5 Steady-state results for N = 15 and N = 20
Full size table

5.5 Experiment V

In the last experiment, the robustness of the proposed algorithm is tested in the case that the exact number of unknown parameters are not known. This means that the exact value for M is unknown. In such a case, there are three possible scenarios. First, an underdetermined case, where the value of M is chosen as less than the actual value. Second, an overdetermined case, where the value of M is chosen as more than the actual value. Finally, the case where the value of M is chosen correctly. For this experiment, the network size is chosen as N = 10 and the unknown parameter vector length as M = 10. The range for M is varied between 5 and 15, and the steady-state results are compared for SNR values of 0 dB, 10 dB, and 20 dB. The results are shown in Fig. 13. It can be seen that for the underdetermined case, the value of SNR does not matter, as the algorithm converges very quickly to give a large error. The best result is achieved for an exact match, as expected. However, the results for the overdetermined case are very close to the best result. As the value of M increases, the value of the steady-state error also increases. However, it is clear from these results that in case of a mismatch, it is better to have an overdetermined system rather than an underdetermined system.

Fig. 13
figure 13

Steady-state results for a mismatch in the value of M for a network of size N = 10

Full size image

6 Conclusion

This work proposes a new variable step-size diffusion least mean square algorithm, based on the quotient form, for distributed estimation in adaptive networks. The mean, mean-square, and steady-state analyses have presented. The proposed algorithm has been compared with the algorithm from [6], and a computational complexity analysis has been shown to justify this comparison. It has been shown that the proposed algorithm easily outperforms the algorithm from [6] and provides a much better trade-off between complexity and performance. Results show an improvement in steady-state MSD of almost 10 dB for white input data and almost 5 dB for correlated input. Results are also shown for different network sizes as well as for different sizes of the unknown vector. A comparison between theoretical and simulation results has been shown and the two were found to be closely matched, as shown by the figures as well as the tables. Finally, the performance of the algorithm has been tested in case of a mismatch in the value of M. The proposed algorithm has been shown to perform well in a Gaussian noise environment. However, for non Gaussian environments, a variable step-size algorithm based on the least mean fourth algorithm be developed.