1 Introduction

In the last decades nanotechnologies made possible the production of innovative devices with promises of high density integration, for an exponential increasing of electronic systems complexity. Nanostructures and nanotechnologies are reaching important breakthroughs in single molecule sensing and manipulation, with fundamental applications. In particular, among these nanostructures, silicon nanowires (SiNW) are largely investigated for the central role assumed by Silicon (Si) in the semiconductor industry. Such device can be used as transistors [1, 2], logic devices [3], and thermoelectric coolers [4, 5], but also for other application fields such as biological and nanomechanical sensors [6, 7]. When the physical size of the system becomes smaller, quantum effects on electronic properties become important and then a description via quantum mechanics is required. These quantum effects arise in systems which confine electrons to regions comparable to their de Broglie wavelength.

In a nanowire (NW) the electronic states become subject to quantization in the two-dimensional transversal section, and the transport is due to the one-dimensional electron gas in the longitudinal dimension.

2 Methods

Charge transport in SiNWs, under reasonable hypotheses on the device’s dimensions, can be tackled using the 1-D Multiband Boltzmann Transport Equation (MBTE) coupled self-consistently with the 3-D Poisson and 2-D Schrödinger equations, in order to obtain the self-consistent potential and subband energies and wavefunctions. However, solving the MBTE numerically is not an easy task, because it forms an integro-differential system in two dimensions in the phase-space and one in time, with a complicate collisional operator. An alternative is to take the moments of the MBTE to obtain hydrodynamic-like models where the resulting system of balance equations can be closed by resorting to the Maximum Entropy Principle (MEP).

In the following we shall focus primarily on the mathematical method itself, whereas a minor emphasis will be given to the physical model, because some simplifications will be made which could lead to doubtful results.

3 Transport physics in SiNWs

In SiNWs the band structure is altered with respect to the bulk silicon, depending on the cross-section wire dimension, the atomic configuration, and the crystal orientation. Atomistic simulations are able to capture the nanowire band structure, including information about band coupling and mass variations as functions of quantization [8,9,10,11,12,13]. In this paper we shall limit ourselves to the results obtained via the empirical Tight-Binding (TB) model [9].

For a rectangular SiNW with longitudinal direction along the [100] crystal orientation, confined in the plane \((y,z)\), the 1-D Brillouin zone is 1/2 as long as the length of the bulk Si Brillouin zone along the Δ line (i.e. \(\pi /a _{0}\)). In SiNW the six equivalent Δ conduction valleys of the bulk Si are split into two groups because of the quantum confinement. The subbands related to the four unprimed valleys \(\Delta_{4}\) ([0 ± 10] and [00 ± 1] orthogonal to the wire axis) are projected into a unique valley in the Γ point of the one-dimensional Brillouin zone. The subbands related to the primed valleys \(\Delta_{2}\) ([±100] along the wire axis) are found at higher energies and exhibit a minimum located at \(k _{x}=\pm 0.37\pi /a _{0}\). The SiNW band gap, as well as the energy splitting between the \(\Delta_{2}\)–\(\Delta_{4}\) valleys increases with decreasing diameter of the nanowire. Moreover the subband isotropy break down at energies of the order of 150 meV above the (bulk) conduction-band maximum. From the energy dispersion relation \(E(k)\) obtained from the TB, one can evaluate the effective mass \(m ^{*}\) in the parabolic spherical band approximation. In this paper we shall consider the parameters obtained in [9] (see Table 1), which are valid for diameters greater then 3 nm. These values will certainly be affected by non-parabolic corrections.

Table 1 Silicon nanowire constants
Full size table

The main quantum transport phenomena in SiNWs at room temperature, such as the source-to-drain tunneling, and the conductance fluctuation induced by the quantum interference, become significant only when the channel lengths are smaller than 10 nm [14]. For longer longitudinal lengths, which is the case we are going to simulate, semiclassical formulations based on the 1-D BTE can give reliable terminal characteristics when it is solved self-consistently by adding the Schrödinger–Poisson equations in the transversal direction.

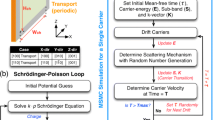
In the following, we shall consider a SiNW having rectangular cross section (with dimensions \(L _{y}\), \(L _{z}\)) in which electrons are spatially confined in the y–z plane by a SiO2 layer which gives rise to a deep potential barrier having \(U= 3.2\mbox{ eV}\), and free to move in the orthogonal x direction, having dimension \(L _{x}\) (see Fig. 1). Hence, it is natural to assume the following ansatz for the electron wave function

$$\begin{aligned}& \phi(x, y, z)=\chi_{l}^{\mu}(y, z) \frac{e^{ik_{x}x}}{\sqrt{L_{x}}}, \end{aligned}$$
(1)

where μ is the valley index (one \(\Delta_{4}\) valley and two \(\Delta_{2}\) valleys), \(l= 1\), \(N _{\mathrm{sub}}\) the subband index, \(\chi ^{\mu } _{l}(y,z)\) is the subband wave function of the \(\sqrt{ l}\)th subband and μth valley, and the term \(e ^{ \mathit{ik_{x}x}}/ L _{x}\) describes an independent plane wave in x-direction, with wave-vector \(k _{x}\). The spatial confinement in the \((y,z)\) plane is governed by the Schrödinger–Poisson system (SP)

$$\begin{aligned}& \textstyle\begin{cases} H[V]\chi_{lx}^{\mu}[V]=\varepsilon_{lx}^{\mu}[V]\chi_{lx}^{\mu}[V], \\ H[V]=-\frac{\hbar^{2}}{2m_{\mu}^{*}} (\frac{\partial^{2}}{\partial y^{2}}+ \frac{\partial^{2}}{\partial z^{2}})+V_{\mathrm{tot}}(x, y, z), \\ \nabla\cdot[\epsilon_{0}\epsilon_{r}\nabla V(x,y,z)]=-e(N_{D}-N_{A}-n[V]), \\ n[V](x, y, z,t)=\sum_{\mu}\sum_{l}\rho_{l}^{\mu}(x,t) \vert \chi_{lx}^{\mu}[V](y, z, t) \vert ^{2}, \end{cases}\displaystyle \end{aligned}$$
(2)

where \(N _{D}\), \(N _{A}\) are the assigned doping profiles (due to donors and acceptors), and \(V_{ \mathrm{tot}}(x,y,z) = U(y,z) - eV (x,y,z)\) (in the Hartree approximation). The electron density \(n[V ]\) is given by (2)4, where \(\rho_{l}^{\mu}(x, t)\) is the linear density in the μ-valley and l-subband which must be evaluated by the transport model (hydrodynamic/kinetic) in the free movement direction. We emphasize that the use of the effective mass approximation (2)1 is probably valid for semiconductor nanowires down to 5 nm in diameter, below which atomistic electronic structure models need to be employed [15, 16]. The SP system forms a set of coupled nonlinear Partial Differential Equations, which are usually solved by an iteration between Poisson and Schrödinger equations. Since a simple iteration by itself does not converge, it is necessary to introduce an adaptive iteration scheme [17], where the Poisson equation has been solved by the finite-difference scheme proposed in [18], which can be used for every cross-section shape of the wire with complex geometries of the boundary/interface.

Figure 1
figure 1

SiNW transistor. Cross sections of the Gate-All-Around SiNW transistor

Full size image

Transport in the free direction is described by the multisubband Boltzmann Transport Equation (MBTE) [19]

$$\begin{aligned}& \frac{\partial f_{l}^{\mu}}{\partial t}+v_{\mu}(k_{x}) \frac{\partial f_{l}^{\mu}}{\partial x} - \frac{1}{\hbar}\frac{\partial\varepsilon^{\mu}_{l}}{\partial x} \frac{\partial f_{l}^{\mu}}{\partial k_{x}}= \sum _{\eta l'}\mathcal{C}_{\eta}\bigl[f_{l}^{\mu},f_{l'}^{\mu} \bigr] +\sum_{\mu}\sum_{\mu'\neq\mu} \sum_{l'}\mathcal{C}_{\eta}\bigl[f_{l}^{\mu}, f_{l'}^{\mu'}\bigr], \end{aligned}$$
(3)

where \(f_{l}^{\mu}= f_{l}^{\mu}(x,k_{x}, t)\) is the electron distribution function, \(v _{\mu }={\sim} k _{x} /m ^{*} _{\mu }\) is the electron group velocity. The RHS of equation (3) is the collisional operator, which is split into two terms modeling respectively scattering in the same valley (i.e. intra-valley with \(\mu =\mu^{0}\)) and into different valleys (i.e. inter-valley with \(\mu 6= \mu^{0}\)). In the low density approximation (not degenerate case), the collisional term for the ηth scattering rate is:

$$\begin{aligned}& \mathcal{C}_{\eta}\bigl[f_{l}^{\mu},f_{l'}^{\mu'} \bigr] \\& \quad =\frac{L_{x}}{2\pi} \int dk_{x}' \bigl\{ w_{\eta} \bigl(k_{x}', \mu', l', k_{x}, \mu, l\bigr) f_{l'}^{\mu'}\bigl(x, k_{x}', t\bigr) -w_{\eta}\bigl(k_{x}, \mu, l, k_{x}', \mu', l' \bigr)f_{l}^{\mu}(x, k_{x}, t)\bigr\} , \end{aligned}$$
(4)

where \(w_{\eta}(k_{x}', \mu', l', k_{x}, \mu, l)\) is the ηth scattering rate. Phonon scattering has been tackled following the bulk Si scattering selection rules [12] whose details are given in [20]. But this is no more than a simplification, because major differences in the transport properties can appear including confined phonons [21] and anisotropic deformation potentials [22].

Finally, another key scattering mechanism in SiNW is the Surface Roughness (SR) scattering. This is due to the random fluctuations of the boundaries that nominally form the confining potential in such a low-dimensional system. It depends on quantum confinement as well as it also depends very strongly on the charge density. The SR scattering can be in principle intra-valley or intervalley. However, its dependence on the transfer crystal momentum usually renders intervalley processes weaker. This scattering mechanism can be treated at very different levels of approximation, from fully atomistic models to semi-phenomenological models (see [23, 24]). In the following we shall use a very simple model introduced in [21], where imagecharge effects (due to the mismatch of the dielectric constants between Si and SiO2), and exchange-correlation energy (due to the electron–electron interaction) are neglected, which is reasonable for silicon thickness greater than 8 nm [25]. Moreover corner effects [26] have been neglected. In this case the SR scattering rate along the y-direction is

$$\begin{aligned}& w_{\mathrm{sr}}\bigl(k_{x}, \mu, l, k_{x}', \mu,l', E_{y}\bigr) \\& \quad =\frac{4\sqrt{2}e^{2}m_{\mu}^{*}}{ \hbar^{3}L_{x}} \frac{H(a)}{\sqrt{a}} \bigl[ \mathcal{F}_{ll'}^{\mu\mu}(E_{y}) \bigr]^{2} \frac{\lambda_{\mathrm{sr}}\Delta_{\mathrm{sr}}^{2}}{ (k_{x}-k_{x}')^{2}\lambda_{\mathrm{sr}}^{2}+2} \bigl[\delta\bigl(k_{x}'- \sqrt{a}\bigr)+\delta\bigl(k_{x}'+\sqrt{a}\bigr)\bigr], \end{aligned}$$
(5)

where \(H(x)\) is the Heaviside function, \(E_{y}(x,y, z) = -\frac{\partial V}{\partial y}\), \(\Delta_{\mathrm{sr}}\) and \(\lambda_{\mathrm{sr}}\) are the rms (root mean square) height and the correlation length of the fluctuations at the Si–SiO2 interface

$$\begin{aligned}& a=k_{x}^{2}+ \frac{2m_{\mu}^{*}}{\hbar} \bigl( \varepsilon^{\mu}_{l}-\varepsilon_{l'}^{\mu} \bigr) , \qquad \mathcal{F}_{ll}^{\mu\mu}(E_{y})= \int\bigl(\chi^{\mu}_{l}\bigr)^{\star}(y,z)E_{y}(x,y,z) \chi^{\mu}_{l'}(y,z)\,dy\,dz \end{aligned}$$
(6)

and \(\chi^{\mu } _{l}\), \(\varepsilon^{\mu } _{l}\) are given by solving equation (2). All parameters are listed in Table 1.

4 Extended hydrodynamic model

One of the most popular approaches is to solve the MBTE in a stochastic sense by Monte Carlo (MC) methods [21, 27,28,29] or by using deterministic numerical solvers [27, 30]. However, the extensive computations required by both methods as well as the noisy results obtained with MC simulations, make them impractical for device design on a regular basis.

Another alternative is to obtain from the MBTE hydrodynamic models that are a good engineering-oriented approach. This can be achieved by obtaining a set of balance equations by means the so called moment method. The idea is to investigate only some moments of interest of the distribution function. In this way a hierarchy of balance equations is obtained, which can be truncated at some order, supposing to determine the (unknowns) higher-order moments as well as the production terms (i.e., the moments on the collisional operator). In the last two decades, the Maximum Entropy Principle (MEP) has been successfully employed to close this hierarchy of balance equations. Important results have also been obtained for the description of charge/thermal transport in devices made both of elemental and compound semiconductors, in cases where charge confinement is present and the carrier flow is two- or one-dimensional (see [31] for a review). By multiplying both sides of the MBTE equation (3) by the weight functions

$$\overrightarrow{\psi}=(1,v_{\mu}, \mathcal{E}_{\mu}, \mathcal{E}_{\mu}v_{\mu}),\qquad v_{\mu} = \frac{\hbar k_{x}}{ m_{\mu}^{*}},\qquad \mathcal{E}_{\mu} =\frac{\hbar^{2}k^{2}_{x}}{ 2m^{*}_{\mu}} $$

and integrating with respect to \(k _{x}\), balance equations are obtained in the moment unknowns \((\rho^{\mu } _{l},V _{l} ^{\mu },W _{l} ^{\mu },S _{l} ^{\mu })\), from which one can evaluate

$$\begin{aligned}& \rho=\sum_{\mu,l}\rho_{l}^{\mu} \quad \mbox{total linear density}, \end{aligned}$$
(7)
$$\begin{aligned}& V=\frac{\sum_{\mu,l}\rho_{l}^{\mu}V_{l}^{\mu}}{\rho}\quad \mbox{mean velocity}, \end{aligned}$$
(8)
$$\begin{aligned}& W=\frac{\sum_{\mu,l}\rho_{l}^{\mu}W_{l}^{\mu}}{\rho}\quad \mbox{mean energy}, \end{aligned}$$
(9)
$$\begin{aligned}& S=\frac{\sum_{\mu,l}\rho_{l}^{\mu}S_{l}^{\mu}}{\rho}\quad \mbox{mean energy flux}. \end{aligned}$$
(10)

By exploiting the MEP, constitutive relations for the higher-order moments and the production can be obtained (see [32] for the details). In this way a physics-based hydrodynamic model is obtained, consistent with thermodynamics principles, valid in a larger neighborhood of local thermal equilibrium, and free of any tunable parameters.

5 Results and discussion

The main goal of this paper is to check if the above mentioned Extended hydrodynamic model is able to describe the quasi-equilibrium regime. Taking advantage of examples present in literature, we have considered a Gate-All-Around (GAA) SiNW transistor, with quadratic cross section. This is a Silicon nanowire with an added gate wrapped around it, in such a way we have a three contact device with source, drain, and gate. The device length is \(L _{x} = 120\) nm, the transversal dimensions \(L _{y}=L _{z} \leq 10\) nm, and the oxide thickness tox is 1 nm. The device is undoped, at room temperature and its cross sections are shown in Fig. 1.

An important parameter characterizing the quasi-equilibrum regime, useful for benchmarking different technology options and device architectures, is the low-field mobility [33, 34]. It is defined as the ratio between the average electron velocity, evaluated in the stationary regime, and a driving low electric field E, i.e.,

$$ \mu^{\mathrm{low}}=\frac{\sum_{A}\rho^{A}\mu^{A}}{\sum_{A}\rho^{A}}, \qquad \mu^{A}= \frac{\sum_{l}V_{l}^{A}}{E}, \qquad \rho^{A}=\sum_{l} \rho_{l}^{A}, $$
(11)

where \(\mu^{A}\) are the mobilities in the respective valleys, evaluated as function of the gate voltage \(V _{G}\). The subband densities \(\rho_{l}^{A}\) and velocities \(V_{l}^{A}\) are determined by solving the former hydrodynamic model with the following steps:

  1. (i)

    equilibrium solution

First of all, let us consider the thermal equilibrium regime where no voltage is applied to the contacts, i.e., \(V _{S}=V _{D}=V _{G} = 0\) and no current flows. Hence, the electron distribution function is the Maxwellian:

$$\begin{aligned}& f_{l}^{\mu(e q)}(k_{x})=N_{0} \exp \biggl(- \frac {\frac{\hbar^{2}k_{x}^{2}}{2m_{\mu}^{*}} +\varepsilon_{lx}^{\mu}+\varepsilon_{\mu}^{0}-\nu}{ k_{B}T}\biggr), \end{aligned}$$
(12)

where ν is the Fermi level, \(\varepsilon_{\mu}^{0}\) the valley energy minimum, and T the electron temperature, which we shall assume to be the same in each subband and equal to the lattice temperature \(T _{L}\). The condition of zero net current requires that the Fermi level must be constant throughout the sample, and it can be determined by imposing that the total electron number equals the total donor number in the wire. Then, the linear electron density at equilibrium is:

$$\begin{aligned}& \rho_{l}^{\mu(e,q)}(x)= \frac{N_{D}L_{y}L_{z}\sqrt{m_{\mu}^{*}}}{ \mathcal{Z}^{(eq)}} \exp \biggl[\frac{-\varepsilon_{lx}^{\mu(eq)}-\varepsilon_{\mu}^{0}}{ k_{B}T}\biggr], \end{aligned}$$
(13)
$$\begin{aligned}& \mathcal{Z}^{(eq)}=\sum_{\mu,l} \sqrt{m_{\mu}^{*}}\exp\biggl[\frac {-\varepsilon_{lx}^{\mu(eq)}-\varepsilon_{\mu}^{0}}{ k_{B}T}\biggr], \end{aligned}$$
(14)

where the subband energies \(\varepsilon_{lx}\) are obtained by solving the SP system (2).

  1. (ii)

    quasi-equilibrium solution

Now, we consider the quasi-equilibrium regime, where a very small axial electric field frozen along the channel (\(E= 1000\) V/cm) is applied, and we turn on the gate. The system is still in local thermal equilibrium, the distribution function is the Maxwellian, but some charge flows in the wire. The linear density can be written as

$$\begin{aligned}& \rho_{l}^{\mu}= \frac{N_{D}L_{y}L_{z}\sqrt{m_{\mu}^{*}}}{ \mathcal{Z}^{(eq)}} \exp\biggl[ \frac{-\varepsilon_{lx}^{\mu}-\varepsilon_{\mu}^{0}}{ k_{B}T}\biggr], \end{aligned}$$
(15)

where the only difference between equations (13) and (15) is in the energy subbands \(\varepsilon^{\mu } _{lx}\), which now are obtained solving the SP system (2) with \(V _{S} = 0.012\) V, \(V _{D} = 0\) V, and \(V _{G}\) variable. Once the solution has been obtained, the energies \(\varepsilon^{\mu } _{lx}\) and wave functions \(\chi^{\mu } _{lx}\) for each subband are fixed and exported into the hydrodynamic model.

  1. (iii)

    low-field mobility determination

Since the wire is undoped, with a frozen electric field along its x-axis, we can skip the spatial dependence in the hydrodynamic model, which reduces to a system of Ordinary Differential Equations. The energies \(\varepsilon^{\mu } _{lx}\) and wave functions \(\chi^{ \mu } _{lx}\) for each subband are imported from the previous steps (and kept fixed), as well as the linear density (15) which is used as initial condition. The other initial conditions are

$$\begin{aligned}& V_{l}^{\mu}(0)=0,\qquad W_{l}^{\mu}(0)= \frac{1}{2}k_{B}T_{L}, \qquad S_{l}^{\mu}(0)=0. \end{aligned}$$
(16)

The hydrodynamic system has been solved using a standard Runge–Kutta algorithm. The simulation stops when the stationary regime has been reached obtaining the subband densities and velocities, and finally the low-field mobility (11) has been evaluated.

As a case study, we have fixed \(L _{x}=L _{y} = 8\) nm and run the code, changing \(V _{G}\). The numerical experiments indicate that it is sufficient to take into account only the first four subbands, since the other ones are very scarcely populated. For the solution of step (ii), the Schrödinger–Poisson block has been solved with a maximum of 25 iterations, with a CPU time of few minutes. The subband energies \(\varepsilon^{\mu } _{lx}\) and wave functions \(\chi ^{\mu } _{l}(y,z)\) for the \(\Delta_{4}\) valley and the first four subbands are shown in Figs. 2–6 for \(V _{G} = 0.6\) V. We notice from Fig. 2 that, for \(\mu = 1\), the subband energies \(\varepsilon^{\mu } _{lx}\) coincide for \(l= 2\) and \(l= 3\) (see dot green and blue circle curves in Fig. 2), and the corresponding wave functions \(\chi ^{\mu } _{l} (y,z)\) show a symmetry (see Figs. 4 and 5). This behaviour is due to the quadratic cross section, in accordance to the infinitely deep quantum wire case [35].

Figure 2
figure 2

Subband energies. Subband energies \(\varepsilon ^{\mu } _{lx}\) versus longitudinal dimension x, for \(V _{G} = 0.6\) V

Full size image
Figure 3
figure 3

Subband Wave function. Subband wave function \(\chi ^{ \mu } _{l}(y,z)\) for \(\mu = 1\) (\(\Delta_{4}\) valley), subband \(l= 1\) in the cross section \(x= 60\) nm, for \(V _{G} = 0.6\) V

Full size image
Figure 4
figure 4

Subband Wave function. Subband wave function \(\chi ^{ \mu } _{l} (y,z)\) for \(\mu= 1\) (\(\Delta_{4}\) valley), subband \(l= 2\) in the cross section \(x= 60\) nm, for \(V _{G} = 0.6\) V

Full size image
Figure 5
figure 5

Subband Wave function. Subband wave function \(\chi ^{ \mu } _{l} (y,z)\) for \(\mu= 1\) (\(\Delta_{4}\) valley), subband \(l= 3\) in the cross section \(x= 60\) nm, for \(V _{G} = 0.6\) V

Full size image
Figure 6
figure 6

Subband Wave function. Subband wave function \(\chi ^{ \mu } _{l} (y,z)\) for \(\mu= 1\) (\(\Delta_{4}\) valley), subband \(l= 4\) in the cross section \(x= 60\) nm, for \(V _{G} = 0.6\) V

Full size image

About step (iii), the stationary regime of the hydrodynamic system has been reached in some ps, and the CPU effort varies according to the voltage \(V _{G}\) with a maximum of one hour.

The electron density (2)4 in the cross section \(x= 60\) nm, perpendicular to the transport direction, is shown in the Figs. 7, 8, 9 for \(V _{G} = 0.16,0.6,1\) V respectively. For small gate voltage, the volume charge is peaked in the center of the wire as shown in Fig. 7. As the gate voltage increases, the electron density is peaked close to the oxide interface (see Figs. 8 and 9). This phenomenon can be seen also in Fig. 10 where we plot the electron density (2)4 and total potential \(V _{\mathrm{tot}}\) in the cross section \(y= 0\) nm and \(x= 60\) nm, for \(V _{G} = 0.6\) V. In particular one can observe the effect of the wave function penetration in the oxide and the formation of a surface inversion layer, similar to a usual MOSFET channel.

Figure 7
figure 7

Density. Electron density (2)4 in the cross section perpendicular to the transport direction (\(x= 60\) nm), for \(V _{G} = 0.16\) V

Full size image
Figure 8
figure 8

Density. Electron density (2)4 in a cross section perpendicular to the transport direction (\(x= 60\) nm), for \(V _{G} = 0.6\) V

Full size image
Figure 9
figure 9

Density. Electron density (2)4 in a cross section perpendicular to the transport direction (\(x= 60\) nm), for \(V _{G} = 1\) V

Full size image
Figure 10
figure 10

Density and potential. Electron density (2)4 and total potential \(V_{\mathrm{tot}}\) in the cross sections \(y= 0\) nm and \(x= 60\) nm, for \(V _{G} = 0.6\) V

Full size image

In Fig. 11 we show the low-field mobility as function of the effective field, obtained by including/excluding the SR scattering mechanism. From this figure it is clear how the SR is the key scattering mechanism as it yields a very strong dependence of the low-field electron mobility on the effective field. The obtained results are very similar to those obtained by means of Monte Carlo simulations [21].

Figure 11
figure 11

Low-field mobility. Low-field mobility versus the Effective Field, obtained with/without Surface Roughness Scattering mechanism, for a 8 × 8 nm2 SiNW

Full size image

Finally in Fig. 12 we show the low-field mobility as function of the wire cross section (\(L _{x}=L _{y}\)), for some values of the effective field. We observe that the mobility decreases with shrinking of the wire cross section, in qualitative accordance to the results obtained by MC simulations by Ramayya et al. [21].

Figure 12
figure 12

Low-field mobility. Low-field mobility versus wire width and thickness (\(L _{x}=L _{y}\)), obtained with Surface Roughness Scattering mechanism, for some values of the Effective Field

Full size image

The presented results have been obtained using MATLAB running in an AMD Phenom II X6 1090T 3.2 GHz and 8 Gb RAM.

6 Conclusions

We present a theoretical study of low-field electron mobility in a Gate-All-Around silicon nanowires, having rectangular cross section, based on a hydrodynamic model coupled to the Schrödinger–Poisson equations. The hydrodynamic model has been formulated by taking the moments of the multisubband Boltzmann equation, and by closing the obtained hierarchy of balance equations with the use of the Maximum Entropy Principle. The most relevant scattering mechanisms, such as scattering of electrons with acoustic and non-polar optical phonons and surface roughness, have been included. The results show a good qualitative agreement with data available from the literature, confirming that this hydrodynamic model is valid in the quasiequilibrium regime limit. The study of off-equilibrium transport phenomena as well as of thermoelectric effects for such structures, using also circular cross-sections of the wire, will be the subjects of future researches.