1 Introduction

With the increasing demand for driving comfort, it is becoming more important to insulate the engine and road to transmit vibrations in the vehicle. The hydraulic mount is a passive absorber that is attached to the damping mechanism, which can provide varying dynamic characteristics under different driving conditions. This is an important reason for replacing the traditional rubber mount with a hydraulic mount.

At present, research on the dynamic characteristics of hydraulic mounts is not perfect and remains in the early stages. Many scholars have invested substantial effort into studying hydraulic mounts in different manners, including early experimental methods [1,2,3,4] and more recent software analysis methods. Experimental methods can accurately obtain the dynamic characteristics of the hydraulic mount [5,6,7,8]. However, such experiments require a large number of different physical samples [9, 10], which results in a long time cycle and a large amount of investment, and it is difficult to guide the design directly. Software analysis is an effective solution to this problem. At the beginning of the design, the dynamic characteristics of the hydraulic mounts are predicted according to the 3D mathematical model or key characteristic parameters. Software analysis methods can be divided into several types. The first is based on a 3D mathematical model and the USES finite element method for simulation analysis [11,12,13,14]. The advantage of this approach is that the simulated model is closest to the real part and can best guide the design, but the cycle is long and the requirement for computer hardware is high. The second is the use of AMESIM or ADAMS software, which offers the advantage that it can better consider the motion of liquid in the simulation process, but the calculation cycle is relatively long [15]. The third is the use of MATLAB software [16,17,18,19,20] or other software [21,22,23,24] to establish a parametric model of the hydraulic mount, which can rapidly predict the dynamic characteristics according to parameter changes. Moreover, the ISIGHT software can be easily integrated for optimization design.

Based on the central parameter model, the central parameter of the structural parameters relating to the structure was optimized in this study. Specifically, through the establishment of a mechanical model, theoretical derivation, and evolution, the dynamic stiffness and loss angle of the dimensionless expressions were innovatively proposed. The model had a very good effect on the control of key performance indicators and the curves exhibited fast convergence. The accuracy of the theory was verified experimentally. Through structural parameter sensitivity analysis, the correspondence between the structural parameters and peak frequency was established, and the performance of the hydraulic mount was optimized for a certain project.

2 Mechanical Model of Hydraulic Mount

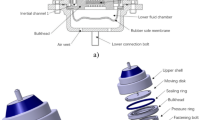
Based on the structure of the hydraulic mount, analysis and simplicity are necessary. The mechanical model was obtained when the upper end of the hydraulic cavity was stimulated in the vertical direction, as illustrated in Figure 1.

Figure 1
figure 1

Schematics of hydraulic mount mechanical model

Full size image

In Figure 1, \({c}_{s}\) is the main spring damping of the hydraulic mount, \({k}_{s}\) is the main spring stiffness of the hydraulic mount, \(\kappa\) is the volume flexibility of the upper chamber, \(A\) is the equivalent piston area, \({A}_{k}\) is the cross-sectional area of the inertial channel, \({z}_{k}\) is the displacement of fluid motion, \({p}_{0}\) is the upper chamber pressure, and \({p}_{u}\) is the lower chamber pressure.

When the upper end of the hydraulic mount is subjected to vibration from the power train, the response equation of the overhanging body can be obtained using the damping characteristics of the hydraulic suspension.

$$F_{iso} = k_{s} \cdot z + c_{s} \cdot \dot{z} + A\left( {p - p_{u} } \right).$$
(1)

According to the Laplace transform, the following equation is obtained:

$$\frac{{F_{iso} }}{z} = k_{s} + c_{s} \cdot s + A\frac{{\left( {p - p_{u} } \right)}}{z} .$$
(2)

When the pressure changes in the upper fluid, the volume change equation is expressed as follows:

$$\begin{gathered} \dot{V} = \dot{z} \cdot A = \dot{z}_{k} \cdot A_{k} + \frac{\Delta V}{{\Delta t}}, \hfill \\ \dot{V} = \dot{z} \cdot A = \dot{z}_{k} \cdot A_{k} + \frac{\Delta V}{{\Delta p}} \cdot \frac{\Delta p}{{\Delta t}}. \hfill \\ \end{gathered}$$

The following formula is used to define the volume flexibility \(\kappa\):

$$\kappa = \frac{\Delta V}{{\Delta p}}$$

Figure 2 presents a flow diagram of the inertial channel. When the upper chamber body receives a vertical excitation vibration, there is a pressure difference between the upper and lower cavities, which combines the change in the inertia channel displacement with the change in the volume flexibility.

$$\begin{gathered} A \cdot \smallint \dot{z} = A_{k} \cdot \smallint \dot{z}_{k} + \kappa \cdot \mathop \smallint \limits_{{p_{u} }}^{{p_{0} }} \frac{\partial p}{{\partial t}}, \hfill \\ z \cdot A = z_{k} \cdot A_{k} + \kappa \cdot \left( {p_{0} - p_{u} } \right), \hfill \\ p_{0} - p_{u} = \frac{z \cdot A}{{\upkappa }}\left( {1 - \frac{{z_{k} }}{z} \cdot \frac{{A_{k} }}{A}} \right). \hfill \\ \end{gathered}$$
(3)
Figure 2
figure 2

Inertial channel diagram

Full size image

The mass of the inertial channel is set as \({m}_{k}\). The transformation of the differential equation of motion is as follows:

$${m}_{k}={A}_{k}\cdot {L}_{k}\cdot \rho$$
$${m}_{k}\ddot{{z}_{k}}+{k}_{k}\cdot \dot{{z}_{k}}={A}_{k}\left({p}_{0}-{p}_{u}\right),$$
$${m}_{k}{s}^{2}{z}_{k}+{k}_{k}\cdot \text{s}\cdot {z}_{k}={A}_{k}\left({p}_{0}-{p}_{u}\right),$$
$${m}_{k}{s}^{2}{z}_{k}+{k}_{k}\cdot \text{s}\cdot {z}_{k}={A}_{k}\cdot \frac{z\cdot A}{\upkappa }\left(1-\frac{{z}_{k}}{z}\cdot \frac{{A}_{k}}{A}\right),$$
$${\kappa \cdot m}_{k}{s}^{2}\frac{{z}_{k}}{z}+\kappa \cdot {k}_{k}\cdot \text{s}\cdot \left(\frac{{z}_{k}}{z}\right)$$
$$={A}_{k}\cdot A-{A}_{k}\cdot A\cdot \left(\frac{{z}_{k}}{z}\right)\cdot \frac{{A}_{k}}{A},$$
$$\frac{{z}_{k}}{z}=\frac{A}{{A}_{k}}\cdot \frac{{\omega }^{2}}{{\omega }_{k}^{2}+2{\zeta }_{k}{\omega }_{k}\cdot j\omega -{\omega }^{2}},$$
(4)

\({\omega }_{k}^{2}=\frac{{A}_{k}^{2}}{\upkappa \bullet {m}_{k}}=\frac{{c}_{k}}{{m}_{k}}{\zeta }_{k}=\frac{{k}_{k}}{2\sqrt{{c}_{k}{m}_{k}}}\), where \({\omega }_{k}\) is the fluid vibration element frequency of the inertial channel, \({k}_{k}\) is the fluid column stiffness of the inertial channel, \({\zeta }_{k}\) is the damping ratio, and \({\zeta }_{k}\) is a physical quantity that varies with the frequency and is related to the amplitude. The formula is derived as follows:

\(\zeta _{c} = 0.35*\left( {\left( {2\frac{{A\delta X}}{{A_{c} l_{c} }}} \right)^{2} + \frac{{\left( {1 - \lambda ^{2} } \right)^{4} }}{{\lambda ^{4} }}} \right)^{{1/4}}\).

Based on Eqs. (2)‒(4), the following equations can be obtained:

$$C_{dy} \left( \omega \right) = k_{s} + c_{s} \cdot \omega + \frac{{A^{2} }}{{\upkappa }} \cdot \left( {1 - \frac{{z_{k} }}{z} \cdot \frac{{A_{k} }}{A}} \right)$$
(5)
$$\left| {{\text{C}}_{dyn} \left( \omega \right)} \right|{ } = \sqrt {{\text{Re}}\left( \omega \right)^{2} + {\text{Im}}\left( \omega \right)^{2} } ,$$
(6)
$$\left| {\varphi \left( \omega \right)} \right| = {\text{tan}}\left( {\frac{{{\text{Im}}\left( \omega \right)}}{{{\text{Re}}\left( \omega \right)}}} \right)^{ - 1 } .$$
(7)

The above is the expression of the dynamic stiffness. To simplify the formula, the trend of the dynamic stiffness and loss angle is obtained. The dimensionless expression is introduced to make the data more convenient and the program converge faster.

$$C_{dyn} \left( \omega \right) = \frac{{C_{dy} \left( \omega \right)}}{{k_{s} }}$$

The following parameters are defined:

$$\lambda = \frac{\omega }{{\omega_{k} }},N = \frac{{A^{2} }}{{k_{s} \kappa }},$$

where \(\lambda\) is the frequency ratio and \(N\) is the coefficient of the hydraulic mount. In general, the coefficient of a good hydraulic mount is approximately 0.5 to 0.8.

$$\begin{gathered} C_{dyn} \left( \lambda \right) = 1 + N \cdot \left( {1 - \frac{1}{{\left( {1 - \lambda^{2} } \right)}}} \right), \hfill \\ \varphi \left( \lambda \right) = {\text{tan}}\left( {\frac{0}{{{\text{Re}}\left( \lambda \right)}}} \right)^{ - 1} . \hfill \\ \end{gathered}$$

The above expression is first discussed, followed by the synthesized curves.

For feature point 1, when the frequency ratio \(\lambda\) is 0, the following parameter is obtained:

$$C_{dyn} \left( 0 \right) = 1; \varphi \left( 0 \right) = 0^{^\circ } .$$

For feature point 2, when the magnification factor \({C}_{dyn}\) is 0, the following parameter is obtained:

$$\begin{gathered} C_{dyn} \left( \lambda \right) = 0, \hfill \\ \lambda_{1,2} = \pm \frac{1}{{\sqrt {1 + N} }}\varphi \left( {\lambda_{1,2} } \right) = \left\{ {\begin{array}{*{20}c} {0,} \\ {180^{^\circ } .} \\ \end{array} } \right. \hfill \\ \end{gathered}$$

For feature point 3, when the frequency ratio \(\lambda\) is 1; that is, at the resonance point, the following parameter is obtained:

$$C_{dyn} \left( 1 \right) = \infty ; \varphi \left( 0 \right) = 180^{^\circ } .$$

For feature point 4, when the frequency ratio \(\lambda\) is \(+\infty\), the following parameter is obtained:

$$\mathop {\lim }\limits_{\lambda \to \infty } C_{dyn} \left( \lambda \right) = 1 + N; \varphi \left( 0 \right) = 0^{^\circ } .$$

The change rules of the dynamic stiffness and loss angle are depicted in Figures 3 and 4. The dynamic stiffness changes with an increasing frequency ratio, as follows: first a decrease, then an increase to the maximum value, and then a decrease. When the dynamic stiffness reaches the minimum value, the maximum phase angle of the loss angle appears. After the resonance frequency, where \(\lambda\) is 1, the minimum value appears. The dynamic stiffness and loss angle can be clearly distinguished using this method.

Figure 3
figure 3

Dynamic stiffness dimensionless simulation curve

Full size image
Figure 4
figure 4

Loss angle dimensionless simulation curve

Full size image

3 Simulation and Verification of Dynamic Characteristics

3.1 Acquired Parameters of Hydraulic Mount

The main parameters of the hydraulic mount can be obtained by measurement and CAE analysis according to the data model. Through numerous of experimental validations and accumulations, this method can be conveniently used to guide the preliminary design and it can be corrected in subsequent tests, which plays a decisive role in the positive development of hydraulic mounts. The concept of the parameter design is shown in Figure 5.

Figure 5
figure 5

Parameter acquisition process

Full size image

The fluid density is obtained through the actual filling material, the area and length of the inertial passage are determined by measurement, and the equivalent piston area of the upper chamber \(A\) can be obtained by the middle section.

$$A = \frac{1}{2} \times \left( {A_{1} + A_{2} } \right),$$

where \({A}_{1}\,{\text{and}\,A}_{2}\) are the upper and lower sections of the upper chamber, respectively.

The calculation of the volume flexibility is relatively complicated because the rubber material is nonlinear. First, based on the general simplified principle in the analysis, it is assumed that the rubber material in each direction is incompressible hyperelastic. Only the nonlinearity of the rubber is considered, whereas its viscoelasticity is excluded. In this case, the function expression of the Mooney–Rivlin material model is used for the calculation. The function is as follows:

$$U = \mathop \sum \limits_{i + j = 1}^{N} C_{ij} \left( {I_{1} - 3} \right)^{i} \left( {I_{2} - 3} \right)^{j} + \mathop \sum \limits_{i = 1}^{N} \frac{1}{D}\left( {\sqrt {I_{3} } - 1} \right)^{2i} .$$

Owing to the bidirectional decoupling diaphragm pressure, the deformation of the decoupling diaphragm is ignored. The decoupling diaphragm is simplified to an elastic sheet without holes, which is connected to the rubber of the main spring by a common node. The material is the same as that of the main spring. The connection between the bottom of the decoupled diaphragm, and the housing of the main spring and upper and lower cases is constrained. The calculation model is depicted in Figure 6.

Figure 6
figure 6

Finite elements of calculation grid model

Full size image

When the volume and pressure changes of the upper chamber are known, the volume flexibility can be obtained by Eq. (2), where the key parameters required are listed in Table 1.

$$C = \Delta V/\Delta P.$$
(8)
Table 1 Key parameters of finite element analysis
Full size table

The fitting curve is presented in Figure 7. It should be noted that the lower cavity is free to deform and is connected to the outside world owing to its small thickness, which means that the fluctuation of the pressure is small and it is ignored here.

Figure 7
figure 7

Volume compliance fitting curve

Full size image

3.2 Verification of Dynamic Simulation

Hydraulic mounts can reflect unique features under low-frequency, larges amplitudes [25,26,27,28,29]. With an amplitude of 1 mm as the excitation source, the variation laws of the dynamic stiffness and loss angle were investigated and compared with the measured data, as shown in Figures 8 and 9. The test curve was a real measurement result of the hydraulic mount, and the simulation curve was obtained from the simulation analysis.

Figure 8
figure 8

Dynamic stiffness vs. frequency curves

Full size image
Figure 9
figure 9

Loss angle vs. frequency curves

Full size image

It can be observed from Figures 8 and 9 that the difference between the experimental and simulation curves was small. The reason for this error is that the main spring was properly simplified, and its real state was strongly nonlinear, which could not be avoided in the simulation analysis. The relative error between 10% and 20% could meet the requirements of the project, and the accuracy of the simulation model was verified.

4 Analysis of Influence of Parameter Variation on Hydraulic Performance

4.1 Influence of Equivalent Piston Area on Dynamic Characteristics

As illustrated in Figures 10 and 11, the peaks of the dynamic stiffness and loss angle increased gradually with an increase in the equivalent piston area. However, the increase in the frequency was not obvious.

Figure 10
figure 10

Dynamic stiffness vs. frequency curves in different piston areas

Full size image
Figure 11
figure 11

Loss angle vs. frequency curves in different piston areas

Full size image

4.2 Influence of Liquid Column Length on Dynamic Characteristics

As illustrated in Figures 12 and 13, as the cross-sectional area increased, the peaks of the dynamic stiffness and loss angle increased slightly. However, the peak frequency increase was more obvious, which was caused by the greater inertia effect.

Figure 12
figure 12

Dynamic stiffness vs. frequency curves in different inertial channel areas

Full size image
Figure 13
figure 13

Loss angle vs. frequency curves in different inertial channel areas

Full size image

4.3 Influence of Liquid Column Length on Dynamic Characteristics

As illustrated in Figures 14 and 15, as the length increased, the peaks of the dynamic stiffness and loss angle increased, but the frequency decreased continuously. This is because the increase in the length corresponded to an increase in the mass and a decrease in the fixed frequency.

Figure 14
figure 14

Dynamic stiffness vs. frequency curves for different inertial channel lengths

Full size image
Figure 15
figure 15

Loss angle vs. frequency curves for different inertial channel lengths

Full size image

4.4 Influence of Volume Flexibility on Dynamic Characteristics

As illustrated in Figures 16 and 17, the peaks of the dynamic stiffness and loss angle decreased with an increase in the volume flexibility, whereas the frequency decreased.

Figure 16
figure 16

Dynamic stiffness vs. frequency curves for different volume compliances

Full size image
Figure 17
figure 17

Loss angle vs. frequency curves for different volume compliances

Full size image

The change was owing to the increase in the volume flexibility, which means that the volume stiffness decreased and the motion displacement increased. In the case of a constant vibration source, the dynamic stiffness decreased and the loss angle changes followed the same rule.

According to the influence of the hydraulic mount parameters on its dynamic performance, the vibration of the dynamic stiffness and loss angle peaks can be controlled by optimizing the equivalent piston area. The peak and frequency can be optimized through the port area, length, and volume flexibility simultaneously.

5 Application of Case

To improve the driving experience and comfort, it was necessary to adjust the vibration characteristics of the hydraulic mount at a test site during the course of the project.

The test condition was to pass a specific road at a constant speed at the test site. The vertical vibration of the real vehicle was obvious and the driving performance was poor, as illustrated in Figure 18.

Figure 18
figure 18

Suspension tuning

Full size image

During the adjustment process, the PCB acceleration sensor, Devesoft data acquisition instrument, and other equipment were tested objectively. The results were optimized, as indicated in Figure 19. The peak vibration was large before optimization and was consistent with the subjective feeling. The structural parameters were modified and the sample test was executed again. The peak acceleration and peak frequency were significantly reduced. The optimized curve is presented in Figure 19.

Figure 19
figure 19

Acceleration vs. frequency curves

Full size image

The key parameters of the hydraulic mount are displayed in Table 2.

Table 2 Key parameters of hydraulic mount.
Full size table

6 Conclusions

A mechanical model of a hydraulic mount was established by means of fluid mechanics and mechanical structures. The parameterization of the structural variables and the establishment of dimensionless formulas were of significant help in the early stages of design. The specific research results demonstrate the following.

  1. 1.

    Based on the mechanical model, the dimensionless and concrete expressions of the dynamic stiffness and loss angle were derived, which could lay a solid foundation for the study of dynamic characteristics.

  2. 2.

    Through the impact analysis of the parameter variation, the structural parameters and frequency peaks were established with a one-to-one correspondence. This is of guiding significance for the matching of mounts.

  3. 3.

    Real vehicle tests demonstrated that the dynamic performance of liquid resistance can be improved by optimizing reasonable structural parameters, which may contribute to the overall performance of the vehicle, and reduce the research and development cycle.