1 Introduction

The wave maker is one of the most important facilities in the research field of ocean engineering and hydraulic engineering. Its performance of wave simulation has an effect on the testing of sea keeping. As the wave maker plays an extremely important role in engineering research, the theory and implementation of wave generation have been attracting extensive attention for years. Scientists often perform laboratory experiments on the basis of push-type wave makers, which move a wave plate to generate waves [1, 2]. Refs. [3, 4] facilitates the generation of arbitrary finite-amplitude waves at any distance from the wave maker. Moronkeji [5] performed experimental studies using electrically driven wave plates to improve plate amplitude. Teng et al. [6] reported a variation of the commonly used push-type wave maker principle. By varying the speed and distance between the carriage and plate, waves of different amplitudes were generated. This method resolved the problem related to limiting the plate amplitude of push-type wave makers. The study of Wu et al. [7] on long waves generated by a push-type wave maker concludes that the method proposed by Wu et al. [8] was effective for generating solitary waves of stable height. The technology of generating white noise wave requires that wave amplitudes remain stable in a certain plate frequency range. White noise wave spectrum is basically flat in the floating objects test and this technology makes frequency response function more reliable in experiment analysis in a large frequency range [9].

The wave generator driven by electric motor is widely used in low load; for example, rocker flap wave maker. Conversely, the hydraulic wave generator could produce high torque with quick-response and high-accuracy, thus it can be applied in push-type wave maker in heavy load. Electro-hydraulic servo technology was frequently adopted as a solution of high-power and high-accuracy vibration systems in recent years [10, 11]. To obtain the high flow, thrust, and frequency in these driving systems, a variety of electro-hydraulic excitation devices with high thrust and high frequency were studied by many scholars, as a result, the AC servo hydraulic vibration technology, as well as the new electro-hydraulic digital control technology, etc. were presented [12, 13]. Many scholars have been seeking new control elements to satisfy specific engineering requirements. For example, Hao et al. [14] utilized rotary valve structure to increase the wave frequency of exciter, and applied it to coal industry, metallurgical industry, construction industry, etc. Ruan et al. [15] proposed a high frequency electro-hydraulic exciter with rotary valve and studied the frequency characteristic of electro-hydraulic exciter, high frequency signal acquisition and control of typical excited wave forms. Ren et al. [16] studied vibration waveforms excited by an electro-hydraulic exciter with a two-dimensional rotary valve theoretically and experimentally. Other similar progresses include equilibrium hydraulic rotary valve with high pressure, large flow and electro-hydraulic rotary valve studied at Zhejiang University [17, 18] and rotating shaft hydraulic rotary valve with good manufacturability designed by Marcus [19]. A fluid driven PWM valve based on a unidirectional rotary spool was presented, and it was found that the rotary valve reduced actuation power from a cubic dependence to a square dependence by eliminating motion reversals during transition [20]. Liu et al. [21, 22] designed a single stage rotary valve for application to high energy and variable-frequency vibration condition. The single stage rotary valve can be used to obtain the required vibration frequency and waveform by controlling the rotary velocity of spool, and thus meet different working requirements of tamping device.

In this paper, to make it easier to generate waves and improve wave amplitude in a certain plate frequency range, a simple push-type wave generating method using digital rotary valve control was proposed [23] and developed, and the control system model was established, and different wave amplitudes and lengths were generated and further analyzed.

2 Working Principle and Test Rig

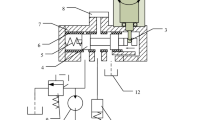
The working principle of the novel digital rotary valve-controlled cylinder system is shown in Figure 1. It is composed mainly of a double-acting hydraulic servo cylinder, a digital rotary valve, an electro-hydraulic proportional axial variable piston pump, and a proportional relief valve. The wave experiment rig, as shown in Figure 1, includes a water tank (0.6 m wide×1.2 m high×12 m long), an electro-hydraulic control system, a wave generation mechanism and a wave height meter.

Figure 1
figure 1

Working principles of electro-hydraulic control system and wave experiment rig

Full size image

The working principle and structure of the designed rotary valve are shown in Figure 2. It can be seen that 4 shoulders with same structure are designed and manufactured on the rotary valve spool. The rotary frequency of the spool can be controlled by a servo motor, and the axial displacement of the spool can be controlled by a linear stepper motor, thus the opening of the spool as well as the flow through the opening can be controlled. The valve ports are designed symmetrical, so that the opening area of the valve ports on the front shoulder 1 can change from zero to the maximum, and from the maximum to zero, then so can the opening area of the corresponding valve ports on the nearby shoulder 4 do. On the other hand, when one valve port is closed, another valve port on the opposite side of the same shoulder is just open, keeping the valve on working order.

Figure 2
figure 2

Working principles of digital rotary valve

Full size image

When the valve core rotates to the specific angle as shown in Figure 2(a), oil flows from port P to port B, and then from port A to port T. In this case, the cylinder moves to the right. When the valve core rotates to another angle as shown in Figure 2(b), oil flows from P to A, and then from B to T, driving the cylinder to the left. With the change of servo motor’s speed, the frequency of the rotary valve core changes, leading to the change of wave maker’s working frequency. To meet higher flow for cylinder motion, linear flow and pressure control requirements, grooves in the valve core and windows in the sleeve are designed to be rectangular accordingly.

A test rig of wave experiment was established to validate the new working principle. By adjusting the stepper motor and the servo motor, we can control the axial displacement and the rotational speed of valve core respectively. Supply oil pressure can be set through the proportional relief valve. Consequently, the amplitude of wave plate becomes adjustable and the frequency of wave plate changeable. The experimental instruments are shown in Table 1. The main parameters of the new wave maker system are listed in Table 2. The operation parameters with instruments are listed in Table 3.

Table 1 Experimental instruments
Full size table
Table 2 Main parameters of new wave maker system
Full size table
Table 3 Operation parameters with instruments
Full size table

3 Mathematical Modelling

According to the Figure 1, the hydraulic transmission model is shown in Figure 3. The bottom of water tank is smooth and the hydrostatic depth is d. In the distal wave trough, there is no reflection, wave completely absorbed by the wave damper. Assume that the wave propagation direction is the positive x axis, the vertical direction is the positive z axis, the origin of the coordinate is on the surface of the water. The wave amplitude is much less than the wave length. Φ is the velocity potential function. The boundary value problem for the wave maker in the wave tank follows directly from the boundary value problem for two-dimensional waves propagating in an inviscid, incompressible, irrotational fluid. Boundary value problem specification for periodic water waves is shown in Figure 3. According to the above assumptions, the potential flow theory and small amplitude wave theory [24,25,26], the equation of wave amplitude of the front plate a0 and plate amplitude e in different cycles is expressed as follows:

$$ \begin{aligned} T (\omega ,d ) & = \frac{{a_{0} }}{{e_{1} }} = \frac{{H_{0} }}{{2e_{1} }} = \frac{4{\sinh}{kd}}{\sinh{2kd} + 2kd} \hfill \\ & \quad \times (\frac{{1 - e_{2} /e_{1} }}{{1 - d_{2} /d_{1} }}\frac{d}{{d_{1} }}\sinh{kd} + \frac{{e_{2} /e_{1} - d_{2} /d_{1} }}{{1 - d_{2} /d_{1} }}\sinh{kd} \hfill \\ & \quad + \frac{{1 - e_{2} /e_{1} }}{{1 - d_{2} /d_{1} }}\frac{1}{{kd_{1} }} - \frac{1}{{kd_{1} }}\frac{{1 - e_{2} /e_{1} }}{{1 - d_{2} /d_{1} }}\cosh{kd}), \hfill \\ \end{aligned} $$
(1)

where H0 is the wave height, d is the depth of water, e1, e2 are the amplitudes of plate motion distance from the bottom d1, d2, respectively, e is the amplitude of plate motion at water surface.

Figure 3
figure 3

Hydraulic transmission model

Full size image

For push-type wave maker, \( e_{1} = e_{2} = e,d_{1} = d,d_{2} = 0 \). According to the cylinder connection point of Figure 1, e (namely, the amplitude of wave plate) is equal to the motion displacement of hydraulic cylinder yp, so:

$$ T_{1} \left( {\omega ,d} \right) = \frac{{a_{0} }}{e} = \frac{{a_{0} }}{{y_{\text{p}} }} = \frac{{H_{0} }}{{2y_{\text{p}} }} = \frac{{4\sinh^{2} kd}}{2kd + \sinh2kd}. $$
(2)

The relation of the wave number k and the angular velocity of wave ω meets the dispersion formula: ω2 = 4π2 f2j = gktanh(kd) [1], where fj is the working frequency of the wave plate, namely the hydraulic cylinder working frequency. k cannot be directly obtained from the above formula, where k can be solved by means of Matlab software tool . The parameter values of k and T1 used in the calculation are listed in Table 4.

Table 4 Corresponding parameters of hydraulic transmission
Full size table

The equivalent bridge of the rotary valve-controlled cylinder system is shown in Figure 4. It is assumed that the system pressure ps is constant, the total supply flow is qs, qL is the flow through the load and pL is the pressure drop across the load.

Figure 4
figure 4

Equivalent bridge of the rotary valve-controlled cylinder system

Full size image

The equations of flow through the orifices 1, 2, 3 and 4 are expressed as follows:

$$ q_{\text{v1}} = C_{\text{d}} S_{\text{v1}} \sqrt {\frac{{2(p_{\text{s}} - p_{1} )}}{\rho }} , $$
(3)
$$ q_{\text{v2}} = C_{\text{d}} S_{\text{v2}} \sqrt {\frac{{2 (p_{1} - p_{0} )}}{\rho }} , $$
(4)
$$ q_{\text{v3}} = C_{\text{d}} S_{\text{v3}} \sqrt {\frac{{2 (p_{2} - p_{0} )}}{\rho }} , $$
(5)
$$ q_{\text{v4}} = C_{\text{d}} S_{\text{v4}} \sqrt {\frac{{2(p_{\text{s}} - p_{2} )}}{\rho }} , $$
(6)

where p1 and p2 are the pressure of hydraulic cylinder two cavity respectively, Cd is the flow rate coefficient, ρ is the oil density, and Svi (i = 1, 2, 3, 4) are orifice area of valve ports on the correspondent shoulder i.

Firstly, it is assumed that the connecting pipeline between rotary valve and hydraulic cylinder is short, thick and symmetrical enough, the dynamic loss and the pressure loss of the pipe can be ignored, the oil temperature and bulk modulus of hydraulic oil are constant, and the leakage of hydraulic cylinder is zero. When the cylinder moves to the right, the flow rate continuity equations of the chamber of the cylinder can be used.

The left chamber is

$$ q_{\text{v1}} - q_{\text{v2}} = \frac{{{\text{d}}y_{\text{p}} }}{{{\text{d}}t}}A_{\text{p}} + \frac{{V_{1} }}{{\beta_{\text{e}} }}\frac{{{\text{d}}p_{1} }}{{{\text{d}}t}}, $$
(7)

whereas the right chamber is

$$ q_{\text{v3}} - q_{\text{v4}} = \frac{{{\text{d}}y_{\text{p}} }}{{{\text{d}}t}}A_{\text{p}} - \frac{{V_{2} }}{{\beta_{\text{e}} }}\frac{{{\text{d}}p_{2} }}{{{\text{d}}t}}, $$
(8)

where V1 is the volume of forward chamber, V1 = Vo1+Apyp, Vo1 is the initial volume of forward chamber, V2 is the volume of return chamber, V2 = Vt – (Vo1+Apyp), Vt is the total volume of cylinder chambers, βe is the effective bulk modulus of oil and is assumed to be as constant in Low pressure test, Ap is the area of piston.

As the orifices are both matched and symmetrical, the flows in diagonally opposite arms of the bridge, as shown in Figure 4, are equal. Therefore, \( S_{{{\text{v}}1}} \left( \theta \right) = S_{{{\text{v}}3}} \left( {\theta +\uppi} \right), \) \( S_{{{\text{v}}4}} (\theta ) = S_{{{\text{v}}2}} (\theta +\uppi). \)

The equations of the flow through the orifices in a cycle are expressed as follows:

$$ \left\{ \begin{aligned} q_{\text{v1}} = q_{\text{v3}} = C_{\text{d}} S_{\text{v1}} \sqrt {\frac{{2(p_{\text{s}} - p_{1} )}}{\rho }} = C_{\text{d}} S_{\text{v3}} \sqrt {\frac{{2(p_{2} - p_{0} )}}{\rho }} , \hfill \\ q_{\text{v2}} = q_{\text{v4}} = 0, \hfill \\ \end{aligned} \right. (\uppi - \theta \ge 0), $$
(9)
$$ \left\{ \begin{aligned} q_{\text{v1}} = q_{\text{v3}} = 0, \hfill \\ q_{\text{v2}} = q_{\text{v4}} = C_{\text{d}} S_{\text{v2}} \sqrt {\frac{{2(p_{1} - p_{0} )}}{\rho }} = C_{\text{d}} S_{\text{v4}} \sqrt {\frac{{2(p_{\text{s}} - p_{2} )}}{\rho }} , \hfill \\ \end{aligned} \right. (\uppi - \theta \le 0). $$
(10)

If the external leakage and internal leakage are zero, and ps = p1+p2, pL = p1−p2, the load flow of the cylinder is \( q_{\text{L}} = q_{\text{v1}} - q_{\text{v2}} \). That is,

$$ \begin{aligned} q_{\text{L}} = {\text{sign}}(\uppi - \theta )\frac{{C_{\text{d}} S_{\text{vi}} }}{\sqrt \rho }\sqrt {p_{\text{s}} - {\text{sign}}(\uppi - \theta )p_{\text{L}} } \hfill \\ = \left\{ \begin{aligned} \, C_{\text{d}} S_{\text{v1}} \sqrt {\frac{{p_{\text{s}} - p_{\text{L}} }}{\rho }} , { }\uppi - \theta \ge 0, \hfill \\ - C_{\text{d}} S_{\text{v2}} \sqrt {\frac{{p_{\text{s}} + p_{\text{L}} }}{\rho }} , { }\uppi - \theta \le 0. \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned} $$
(11)

The total open area is Svi = 2xvyvi, where xv is the axial opening width of the valve.

It is assumed that the opening circumferential conduction width of B and A are yv1 and yv4, respectively. If yv1 is from zero to the maximum, then from the maximum to zero, after that, to enter the next opening port of nearby shoulder subsequently, yv4 is also from zero to the maximum, then from the maximum to zero, so the equations of yv1 and yv4 are:

$$ y_{\text{v1}} = \left\{ \begin{aligned} &2R\sin \frac{{\omega_{1} t}}{2} , { }0 \le \omega_{1} t< \frac{\uppi}{4} , { } \hfill \\ & 2R\sin \left[ {\frac{\uppi}{4} - \frac{{\omega_{1} t}}{2}} \right] , { }\frac{\uppi}{4} \le \omega_{1} t < \frac{\uppi}{2}, \hfill \\ & 0, \, \frac{\uppi}{2} \le \omega_{1} t < \frac{{3\uppi}}{4}, \hfill \\ & 0, \, \frac{{3\uppi}}{4} \le \omega_{1} t \le\uppi ,\hfill \\ \end{aligned} \right. $$
(12)
$$ y_{\text{v4}} = \left\{ \begin{aligned} &0, \, 0 \le \omega_{1} t < \frac{\uppi}{4}, \hfill \\ &0 , { }\frac{\uppi}{4} \le \omega_{1} t < \frac{\uppi}{2}, \hfill \\ &2R\sin \left[ {\frac{{\omega_{1} t}}{2} - \frac{\uppi}{4}} \right] , { }\frac{\uppi}{2} \le \omega_{1} t < \frac{{3\uppi}}{4} ,\hfill \\ &2R\sin \left[ {\frac{\uppi}{2} - \frac{{\omega_{1} t}}{2}} \right] , { }\frac{{3\uppi}}{4} \le \omega_{1} t <\uppi ,\hfill \\ \end{aligned} \right. \, $$
(13)

where R is the radius of the spool shoulder, f is the rotational frequency of spool, and ω1 is the rotational angular velocity of valve spool.

Figure 2 shows that a single complete cycle of spool and the twice of oil reversing make hydraulic cylinder oscillating back and forth twice, so the relation between the working frequency of hydraulic cylinder and the rotational frequency of spool is\( f_{\text{j}} = 2f \).

The equation of motion for the cylinder is

$$ A_{\text{P}} (p_{1} - p_{2} ) = m_{\text{t}} \ddot{y}_{\text{p}} + B_{\text{c}} \dot{y}_{\text{p}} + F_{\text{L}}. $$
(14)

where mt is the equivalent mass, Bc is the total damping coefficient, and FL is the force by the action of water on the plate. The system is greatly affected by the mass inertial force and the force by the action of water on the plate, the effect of other forces are so little that can be neglected when conducting actual calculation.

The wavefront equation of the two-dimensional small amplitude propulsion wave with constant depth is

$$ \eta = a_{0} \cos\theta = a_{0} \cos\left( {kx - \omega t} \right), $$
(15)

where \( \theta \) is the phase of the wave. The determination of the constants \( k \) and \( \omega \) is as follows:

(1) When x is increased or decreased by one wave length L, the wavefront height η should be constant. This must make

$$ kL = 2\pi . $$
(16)

(2) When the time increments by one cycle T, the wave surface height of the same point should be constant, that is

$$ \omega T = 2\pi . $$
(17)

Based on the above dispersion formula: ω2 = gktanh(kd) [1], substitute into Eqs. (16) and (17), so:

$$ L = \frac{{gT^{2} }}{2\pi }{\text{tanh}}kd. $$
(18)

The relation between the working frequency of hydraulic cylinder and the rotational frequency of spool is \( f_{\text{j}} = 2f \), so: T = 1/\( f_{\text{j}} = 1/2f \).

4 Theoretical and Experimental Results

Figure 5 show the wave experiment and acquisition interface system of wave height meter. The distance between the wave height meter is X, the time difference of initial wave height data is \( \Delta t \). We can get L from the equation \( L = {X \mathord{\left/ {\vphantom {X {\Delta tf_{j} }}} \right. \kern-0pt} {\Delta tf_{j} }} \) with the experimental data.

Figure 5
figure 5

Wave experiment

Full size image

Test values in the wave experiment were compared with those obtained in the numerical analysis. It was assumed that the initial point of cylinder piston is in the middle with the maximum opening of valve port, and the cylinder to the right direction is positive to correspond to the hydraulic transmission model. The main factors and the control parameters for wave experiment can be obtained by continuously adjusting different input parameters (xv, ps and fj), and analyzing output curves (yp, L and a0) in the solution process of mathematical models by means of Simulink software tool.

In the actual operation, because no feedbacks were used in the hydraulic control system, the cylinder piston rod was set to the leftmost position in each experiment and the valve port was set to closed at the same time. Therefore, the motion displacement of hydraulic cylinder in a cycle was 2yp. The wave height H0 (2a0max) of experimental data was measured by the wave height meter.

4.1 Influence of Different x v and f j on Wave Simulation

Figure 6 and Figure 7(a) show the yp-t and a0-t curves under different xv at the working frequency of 1 Hz. From equation S = 2xvyvi, Figure 6 and Figure 7(a), Sv is determined by xv, directly affecting yp and a0, Thus, xv is the crucial factor for the motion amplitude of hydraulic cylinder and wave amplitude, and the bigger xv is, the bigger Sv, yp and a0 will be. Under the condition of 1.0 MPa (oil supply pressure), 1 Hz (Plate motion frequency, T1 = 1.54), 2.0 mm (Axial opening width), the maximum wave amplitude can reach to 64 mm. It can be seen from Figure 6 and Table 5 that test value and theoretical value in the maximum wave amplitude a0max agree relatively well.

Figure 6
figure 6

yp theoretical curve under different xv

Full size image
Figure 7
figure 7

Influence of different xv and fj

Full size image
Table 5 Main comparison between theoretical and test values of a0max (L) (ps = 1 MPa) (mm)
Full size table

Figure 7(b) shows a0 and yp under different work frequencies at 1.0 MPa oil supply pressure. From Figure 7(b), it can be seen that when work frequency is 1.6 Hz (T1 = 2), the maximum amplitude of the cylinder is 16 mm (xv is set to 1 mm) or 21 mm (xv is set to 2 mm), and a0max is 32 mm (xv is set to 1 mm) or 42 mm (xv is set to 2 mm). When work frequency is 2 Hz (T1 = 2), the maximum amplitude of the cylinder is 12 mm (xv is set to 1 mm) or 15 mm (xv is set to 2 mm), and a0max is 24 mm (xv is set to 1 mm) or 30 mm (xv is set to 2 mm). It can be also drawn from the curve of different work frequencies that the value of a0 can be determined by xv. A larger value of xv will lead to larger a0.

Figure 7(c) shows the relationship between the working frequency and a0max (H0/2) under different xv. The wave amplitude descends with the increase of the plate working frequency, the higher the working frequency, the smaller the wave amplitude. a01 (xv is set to 2 mm) is higher than a02 (xv is set to 1.5 mm), and a02 (xv is set to 1.5 mm) is higher than a03 (xv is set to 1 mm). The main comparison between theoretical and test values of a0max under the same pressure are shown in Table 5. The test results under different xv are in accordance with the theoretical calculation results, but the test values are slightly lower than the theoretical values.

Figure 7(d) shows the relationship between the working frequency and L under different xv. The wave length descends with the increase of the plate working frequency, the higher the working frequency, the smaller the wave length. At the same frequency, the wave length remains unchanged with the axial opening width change. The main comparison between theoretical and test values of L under the same pressure are shown in Table 5. The test results under different xv are in accordance with the theoretical calculation results.

4.2 Influence of Different p s and f j on Wave Simulation

Figure 8(a) shows yp and a0 curves under different oil supply pressure. It can be seen from Figure 8(a), when fj is set to 1 Hz, xv is set to 1 mm, the maximum amplitude of the cylinder can reach to 25 mm under the pressure of 0.9 MPa, 31 mm under the pressure of 1.0 MPa, 36 mm under the pressure of 1.2 MPa, and a0max can reach to 39 mm under the pressure of 0.9 MPa, 48 mm under the pressure of 1.0 MPa, 55 mm under the pressure of 1.2 MPa. Numerical curve shows that a0 can be controlled by the oil supply pressure. The higher the oil supply pressure, the larger the wave plate amplitudes and wave amplitudes. It can be seen from Figure 8 and Table 6 that test value and theoretical value in the maximum wave amplitude agree relatively well.

Figure 8
figure 8

Influence of different ps and fj

Full size image
Table 6 Main comparison between theoretical and test values of a0max (L) (xv = 1 mm) (mm)
Full size table

Figure 8(b) shows a0 at different work frequencies when xv is set to 1 mm. It can be seen from the Figure 8(b) that when the work frequency is 1.6 Hz (T1 = 2), the maximum amplitude of the cylinder is 15 mm (ps is set to 1.0 MPa) or 18 mm (ps is set to 1.2 MPa), and a0max is 30 mm (ps is set to 1.0 MPa) or 36 mm (ps is set to 1.2 MPa). When the work frequency is 2 Hz (T1 = 2), the maximum amplitude of the cylinder is 12 mm (ps is set to 1.0 MPa) or 14 mm (ps is set to 1.2 MPa), and a0max is 24 mm (ps is set to 1.0 MPa) or 28 mm (ps is set to 1.2 MPa). It can be also drawn from the curve of different work frequencies that the value of a0 can be determined by ps. The higher the ps, the greater the a0.

Figure 8(c) shows the relationship between the working frequency and the a0max (H0/2) under different supply pressure. a01 (ps is set to 1.2 MPa) is higher than a02 (ps is set to 1.0 MPa). The test results under different ps are in accordance with the theoretical calculation results. It can be seen from Figure 7(c) and Figure 8(c), a0 descends with the increasing of working frequency. The main comparison between theoretical and test values of a0max under the same xv are shown in Table 6. Test values are slightly lower than the theoretical values. The differences between the test and theoretical values in Table 5 and Table 6 are mainly caused by water leaks from the gaps at both sides of the wave paddle.

Figure 8(d) shows the relationship between the working frequency and L under different supply pressure. At the same frequency, the wave length remains unchanged with the supply pressure change. The main comparison between theoretical and test values of L under the same xv are shown in Table 6. The test results under different supply pressure are in accordance with the theoretical calculation results.

5 Conclusions

The experiment and analysis results show that the motion frequency and amplitude of push-type wave maker can be continuously adjusted and the various required regular waves can be obtained conveniently. The axial opening width of the valve is the crucial factor for the plate amplitude and the wave amplitude. A larger value of the axial opening width lead to larger the wave plate amplitude and wave amplitude. The wave amplitude also depends on oil supply pressure, the higher the oil supply pressure, the greater the plate amplitude and the wave amplitude. At the same water depth, the working frequency of push plate determines wave number and wave length. Wave length is not affected by the axial opening width and the oil supply pressure. Although the wave amplitude and length descends with the increase of the working frequency, the wave amplitude can be easily improved by setting the axial opening width of the valve and the oil supply pressure of the system. These results indicate that different regular waves can be obtained conveniently by the new wave generating method, and the wave amplitude can be further improved in a certain plate frequency range. These facilitate convenient implementation of wave experiment. Based on the characteristics of high power electro-hydraulic system, the new approach demonstrates its potential application to achieve high-power wave experiment with high-power wave maker system.

Considering the feasibility and practicability of the rotary valve-controlled cylinder system applied to high-power wave experiment, future efforts will focus on practical application of the high-power wave maker. Future work includes vibration cylinder bias compensation with feedbacks, optimized and integrated design of the device.