1 Introduction

Conventional articulated truss structures are composed of mechanical hinges which can meet accuracy and stiffness requires of space mission. But those structures have some disadvantages, such as large weight, high friction and energy-wasting features. Tape-spring hyperelastic (TSH) hinges, which are folded elastically can self-deploy by releasing stored strain energy, which consist of a fewer component parts, can be manufactured conveniently [1, 2]. Flexible hinges have several advantages for space applications, including a low mass-to-deployed-stiffness ratio, cost, and self-latch [3]. With the increasing demand, flexible hinges have been widely used as folding and deployment mechanisms in deployable structures, such as synthetic aperture radars (SARs) [4,5,6], solar arrays and antenna booms. Tape-spring hinges have been used in the Japanese Mars orbiter PLANT-B for bar-like deployment structures of the thermal plasma analyzer [7,8,9].

The U.S. Air Force Research Laboratory (AFRL) [10] used TSH hinge in the main truss’s folding longeron elements, which provided considerable snap-through force to drive and lock the main truss. Imperial College London Santer [11] proposed a concertina-folded magnetometer boom with TSH hinges for CubeSat use. Watt et al. [12] proposed a TSH hinge with two sets of wheels held together by wires wrapped around them, and deploying impact is reduced for the added damp. The Mars Advanced Radar Express spacecraft [13, 14] consisted of two 20 m dipoles and a 7 m monopole which were slotted at certain intervals to stow them in a much small size. Silver et al. [15] proposed an integral folding hinge to deploy camera and investigated axial loading, bending induced buckling response. Schioler et al. and Seffen et al. [16, 17] analyzed buckling properties of single layer TSH hinge based on Timoshenko theory. Seffen et al. [18] got sample points by finite element method and obtained fitting nonlinear mechanical models by single value decomposition method of TSH hinge. Guan et al. [19, 20] designed a TSH hinge for solar sail and investigated its buckling properties by finite element method. Bai et al. [21], Yan et al. [22], Wang et al. [23] investigated geometrical and mechanical properties of ultra-thin-walled lenticular collapsible composite tube in fold deformation. Yang et al. [24, 25] optimized the geometric parameters of TSH hinge to improve driving moment and reduce deploying impact, and established two different theoretical models to analyze the stability of deployment status for the TSH hinges. However, there are still some engineering problems for the TSH hinge applying to a deployable mechanism.

This paper proposed a new ten-module triangular prism mast (TPM) with TSH hinges. Static bending stiffness and compression stiffness theoretical models are established. The compression stiffness tests are performed to verify the accuracy of the static theoretical models of the TPM. Finite element model of ten-module TPM are establish by ABAQUS and geometrical parameter study are analyzed for bending and twisted modal frequencies. Two-module TPM is developed to test the fundamental frequencies and related modal shapes which are used to verify the accuracy of the ten-module TPM (Additional file 1).

2 Design and Static Analysis

2.1 Structures Design

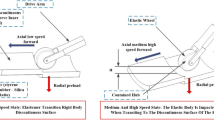
One module TPM with tape-spring hinges is shown in Figure 1. Adjacent two-module is connected by triangular frame. The length of triangular frame is 469 mm, stowed and deployed longitudinal lengths of ten-module prism mast are 475.2 mm and 5278 mm respectively. All components except standard parts are manufactured by duralumin 2A12. Each modulus TPM with TSH hinge contains three longitudinal links and two triangular frames. The TSH hinges are used to drive and lock TPM. Lateral area of each modulus has a series of flexible Kevlar rope with tensile force 30 N which ensures high stiffness of the deployed prism mast and reduces deploying impact. There is one resin-based carbon fiber drive pipe one each end of the tensile lock which prevent involvement during deploying process.

Figure 1
figure 1

One modulus TPM with Hyperelastic hinges

Full size image

The TSH hinge folded with 180°, the two triangular frame close to each other, and three longitudinal links folded between the two triangular frames when the mast stowed. The tape-spring drive the mast to deploy. After deploying, the TSH hinge restore original shape, the Kevlar ropes tensile and the TPM was rigidified to a structure.

2.2 Static Analysis

Bending stiffness analysis has been analyzed in Ref. [8]. Thus, stretching stiffness and compression stiffness will be derived in this paper.

2.2.1 Stretching Stiffness

Axial force F0 is applied on each point A, B and C. Circumcircle radius of cross section is \(R_{1} = {{l_{b} } \mathord{\left/ {\vphantom {{l_{b} } {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}\). Stretch force diagram is shown as Figure 2.

Figure 2
figure 2

Stretched diagram of TPM

Full size image

By resolving the forces in the x-direction at point A, the equation is obtained as follows.

$$2F_{r0} \sin \beta_{0} + F_{l} = F_{0} ,$$
(1)

where F l is axial force of longitudinal link, Fr0 is initial pretension of the rope, l b is the cross link length, β0 is the angle between line GD and line ED.

When the TPM is under stretching, deformation of longitudinal link and diagonal rope has following related equation based on geometric deformation condition.

$$\delta_{r}^{i} = \delta_{l}^{i} \sin \beta_{0} ,$$
(2a)
$$\delta_{r}^{i} = \frac{{F_{r} l_{r} }}{{E_{r} A_{r} }},$$
(2b)
$$\delta_{l}^{i} = \frac{{2F_{l} l_{1} }}{{E_{1} A_{1} }} + \frac{{F_{l} l_{2} }}{{n_{1} a_{11} }},$$
(2c)

where δ i r is rope deformation in each modulus, δ i l is longitudinal stretch deformation of each modulus, l r is rope length, F r is the force in rope, E r is the material Young modulus for rope, A r is cross section area of the rope, l1 is the length of longitudinal rigid link, l2 is the length of the TSH hinge, F l is the force in the longitudinal link, E1 is the material Young modulus for longitudinal link, A1 is the cross-section area of the longitudinal link, n1 is the number of the tape spring, a11 is the unit stretching stiffness of the TSH hinge.

Stretch deformation δl of the TPM is

$$\delta_{l} = \frac{{n_{2} \cdot 3F_{0} \left( {2l_{1} + l_{2} } \right)}}{EA},$$
(3a)
$$\delta_{l} = n_{2} \delta_{l}^{i} ,$$
(3b)

where n2 is the module number of the TPM, EA is the stretching stiffness of the TPM.

Simultaneous Eqs. (1), (2) and (3), stretching stiffness of the TPM is obtained as follows:

$$EA = 6E_{r} A_{r} \sin^{3} \beta_{0} + \frac{{3\left( {2l_{1} + l_{2} } \right)}}{{\frac{{2l_{1} }}{{E_{1} A_{1} }} + \frac{{l_{2} (1 - \nu^{2} )}}{{n_{1} Et}}}}.$$
(4)

If the TPM has no rape, the stretching stiffness is rearranged as follows:

$$EA = \frac{{3\left( {2l_{1} + l_{2} } \right)}}{{\frac{{2l_{1} }}{{E_{1} A_{1} }} + \frac{{l_{2} (1 - \nu^{2} )}}{{n_{1} Et}}}}.$$

2.2.2 Compression Stiffness

One end of the TPM is fixed and a compressive force 3F0 is applied on the other end. Due to initial tension Fr0 of rope initial deformation is δr0 = Fr0l r /(E r A r ), which leads to a critical compress value 3F0′ on the end. Based on the geometric deformation conditions longitudinal link deformation of each module is written as follows:

$$\delta_{l}^{i} = \frac{{\delta_{r0} }}{{\sin \beta_{0} }}.$$
(5)

When compressive force is applied at point A, equilibrium equation is gotten as follows:

$$- 2F_{r} \sin \beta_{0} + F_{l} = F_{0} .$$
(6)

Simultaneous Eq. (2c), Eq. (5) and Eq. (6), critical unloaded compressive force is expressed as follows:

$$F^{\prime} = \frac{{3F_{r0} l_{r} }}{{E_{r} A_{r} \sin \beta_{0} \left( {\frac{{2l_{1} }}{{E_{1} A_{1} }} + \frac{{l_{2} }}{{n_{1} a_{11} }}} \right)}}.$$
(7)

If axial compressive force is no less than the critical unloaded compressive force, unloaded compressive stiffness equals to sum total compression stiffness of longitudinal rigid links and hyperelastic tape-spring hinges, that is

$$EA = \frac{{3\left( {2l_{1} + l_{2} } \right)}}{{\frac{{2l_{1} }}{{E_{1} A_{1} }} + \frac{{l_{2} }}{{n_{1} a_{11} }}}}.$$
(8)

If axial compressive force is more than the critical unloaded compressive force, the total deformation of the rope is

$$\delta_{r} = \delta_{r0} - \delta_{r}^{\prime } ,$$
(9a)
$$\delta_{r}^{\prime } = \frac{{F_{r}^{\prime } l_{r} }}{{E_{r} A_{r} }},$$
(9b)

where δ ′ r is deformation of the rope with only axial compress force, δr0 is deformation of the rope under initial pretension force.

Single module longitudinal link and rope deformation meets the geometric deformation conditions. When 3F0 is lower than F′, simultaneous Eq. (2), Eq. (3), Eq. (6) and Eq. (9) equivalent compression stiffness of the TPM is

$$EA = 6E_{r} A_{r} \sin^{3} \beta_{0} + 3\left( {1 - \frac{{2F_{r0} \sin \beta_{0} }}{{F^{\prime}_{l} }}} \right)\frac{{\left( {2l_{1} + l_{2} } \right)}}{{\frac{{2l_{1} }}{{E_{1} A_{1} }} + \frac{{l_{2} (1 - \nu^{2} )}}{{n_{1} Et}}}}.$$
(10)

It is found that when 3F0 is more than F′ the compression stiffness is related to the compression stiffness of the longitudinal link and the TSH hinges; when 3F0 is lower than F′, the compression stiffness changed with axial load. If the end compress load 3F0 is much small, that is

$$3F_{0} = 12F_{0} \sin^{3} \beta_{0} \cdot \left[ {\frac{{2l_{1} }}{{E_{1} A_{1} }} + \frac{{l_{2} (1 - \nu^{2} )}}{{n_{1} Et}}} \right] \cdot \frac{{E_{r} A_{r} }}{{l_{r} }}.$$
(11)

The compression stiffness can be written as follows

$$EA = 6E_{r} A_{r} \sin^{3} \beta_{0} .$$
(12)

The compression stiffness is only related to the rope stiffness E r A r and initial angle β0.

3 Deploying State Modal Analysis

3.1 Modal Analysis

Due to nonlinear characteristics of the TSH hinge modal analysis of the TPM is performed by ABAQUS. In finite element model x-axis is along direction of transverse link, y-axis is along longitudinal link and z-axis points from section center of transverse links to point of the other two transverse links. Materials of the TSH hinge, rigid link, transverse link and rope are Ni36CrTiAl, stainless steel, aluminum alloy and Kevlar respectively. Longitudinal link, transverse link and the TSH hinge are set up with four nodes that are fully integrated to reduce shell elements (S4R). Rope is modeled by two nodes and three dimensional elements (T3D2). Weld is defined to model connection between ropes and transverse links. Reference point (RP) is established at each joint which are given mass and inertial properties. Multi-point coupling is applied to model the connection of transverse links. The joint hinges are modeled by defining Hinge connection. Contact of tape springs are modeled by defining Tie constraint.

Six reference points at the root of the TPM restrain three translational Degree of Freedoms (DOFs) and the TPM is in the state of cantilever. Firstly, the TPM is performed on static analysis with 30 N pretension force and deformation is got. Then, modal analysis is done by subspace method with rope prestress deformation. Total length for ten-module TPM is 5.26 m. Figure 3 shows the FEM of the ten-module TPM with TSH hinges.

Figure 3
figure 3

Finite element model of TPM with TSH hinges

Full size image

The five order modal shapes of ten modules TPM with TSH hinge are shown in Figure 4. The five order mode frequencies and mode shape description are listed in Table 1.

Figure 4
figure 4

Five order modal shapes of the ten-module TPM with the TSH hinges

Full size image
Table 1 Five order mode frequencies and mode shape description of the ten-module TPM with TSH hinges
Full size table

3.2 Parameter Study

Compared to conventional rigid deployable mechanism the TSH hinge introduces flexible influence. Thus, it is necessary to analyze the effect of geometric parameters, such as thickness t, cross-section radius R, center angle φ and separation distance s, to mode frequency and propose method of increasing stiffness. Table 2 lists frequencies of ten-module TPM under different thickness. It is shown that bend frequency increases 3.695%–11.84% and twist frequency increases 0.186%–0.221% when the thickness changes from 0.12 mm to 0.14 mm.

Table 2 Frequencies of ten-module TPM under different thicknesses
Full size table

Table 3 lists ten-module mast frequencies under different tape central angles. It can be seen that the bend frequency increases by 3.654%–6.156% and twist frequency increases by 0.393%–0.434% when the central angle changes from 80° to 100°.

Table 3 Frequencies of ten-module TPM under different tape central angles
Full size table

Frequencies of the ten-module TPM under different radiuses are listed in Table 4. It can be seen that bend frequencies increase by 2.674%–5.343% and twist frequencies increase by 0.372%–0.41% when radius change from 18 mm to 22 mm.

Table 4 Frequencies of ten-module TPM under different radiuses
Full size table

Frequencies of ten-module TPM under different separations are listed in Table 5. It can be seen that bend frequencies decrease by 0.0428%–0.0919% and twist frequencies increase by 0.134%–0.141% when the separation changes from 16 mm to 20 mm.

Table 5 Frequencies of ten-module TPM under different separations
Full size table

It can be concluded that geometric parameters have greater influence on bend stiffness than twist stiffness. Sensitivity of the geometric parameter is from large to small as follows: thickness, central angle, radius and separation. What’s more, front three parameters have enhanced effect on bend stiffness and the last one has induced effect.

4 Experiment Investigation

4.1 Two-module TPM

To validate the precision of static stiffness theoretical model, two units triangular prism mast is developed. Figure 5 is folding and deployment configurations of triangular prism mast with hyperelastic hinges.

Figure 5
figure 5

Folded and deployed states of TPM with TSH hinges

Full size image

Two adjacent units triangular prism mast are closed to each other by locating pins and fastened to a work holder by a rope when it is folded. At this time, the longitudinal links are stowed into the prism frames and tension ropes are located to grooves. After releasing the tension ropes, the triangular prism mast is deploying by the driving of the TSH hinges. Spherical wheels support the mast to reduce the influence of gravity.

4.2 Compression Stiffness Test

Figure 6 is compression stiffness test diagram of the TPM. Weights are applied at the end of the TPM for 10 kg at each time. Compress load and displacement for the two-modulus TPM are listed in Table 6.

Figure 6
figure 6

Compression stiffness test diagram

Full size image
Table 6 Compress load and displacement for the two-modulus TPM
Full size table

It can be calculated that experimental compression stiffness is 2.324 × 106 N/m and theoretical value is 2.167 × 106 N/m. Relative error between the experimental and theoretical value is 7.08%. The main reason for the phenomenon is that equivalent stiffness of the TSH hinges is much smaller, contact stiffness between the tape springs should be considered.

4.3 Deploying Repeat Accuracy Test

Figure 7 shows deploying configuration for the two modulus TPM. High-speed camera is employed to capture deploying process of the TPM. Spherical hinges and elastic rope are used to eliminate the effect of weight and friction. Figure 8 shows longitudinal displacement-time relationship for five times deploying processes. Table 7 lists compress load and displacement for the two-modulus TPM.

Figure 7
figure 7

Deploying configuration for the two-modulus TPM

Full size image
Figure 8
figure 8

Longitudinal displacement–time relationship for five times deploying processes

Full size image
Table 7 Longitudinal displacement for five times deployment
Full size table

Based on longitudinal displacement for five times deploying test standard deviation of the experimental value is 1.688 mm. Thus, deploying repeat accuracy is 1.688 mm.

4.4 Modal Analysis of Cantilever Position

LMS multi-channel vibration test and analysis system is employed to measure fundamental frequencies and mode shapes which consists of exciting hammer, acceleration sensor which can test three directional accelerations, dynamic signal acquisition system and data processor. The longitudinal direction of the TPM is set as x-axis, outer normal direction of cross section is set as y-axis and vertical downward direction is set as z-axis which is selected as force hammer stimulating direction. The measurements of three acceleration sensors, which are located at three nodes on the crossbeam, are divided into three groups. Then, integral modal superposition is carried out. The exciting point is set at one end of the crossbeam. Test apparatus and geometry diagram of cantilever position are shown in Figure 9. Three vertexes on the bottom are constrained points. Alphabets a and b stand for the order of two times measurement. Location of point b3 is closest to the exciting point. Vibration test curves of six nodes for two-module TPM at cantilever position are shown in Figure 10. Modal shapes for the TPM at cantilever position are shown in Figure 11. Modal test results for the two-modulus TPM at cantilever position are listed in Table 8. It can be seen that acceleration sensor at point b3 has a larger response at initial phase; response curves of two group acceleration sensors are concentrated on middle- and low frequency. The first order frequency of the TPM at cantilever position is 13.02 Hz and corresponding mode shape is bending.

Figure 9
figure 9

Test apparatus and geometry diagram of cantilever position

Full size image
Figure 10
figure 10

Vibration test curves of six nodes for two-module TPM at cantilever position

Full size image
Figure 11
figure 11

Modal shapes for the TPM at cantilever position

Full size image
Table 8 Modal test results for the two-modulus TPM at cantilever position
Full size table

Then, modal analysis of the two-module TPM at cantilever position and the modeling method is identical to the ten-module TPM by ABAQUS. Modal shape simulation results for the two-module TPM at cantilever position are shown in Figure 12.

Figure 12
figure 12

Modal shape simulation results for the two-module TPM at cantilever position

Full size image

The model with black lines is undeformed configuration and the model with colored lines is deformed configuration. Comparison between modal test and simulation results for the two-modulus TPM at cantilever position is listed in Table 9. It can be seen that the mode shapes between simulated and experimental results are consistent compared to Figures 11, 12 and Table 9. The relative errors between simulated and experimental results for frequencies are no more than 5.501%. It indicates that the finite element model for the ten-module TPM is accurate.

Table 9 Comparison between modal test and simulation results for the two-modulus TPM at cantilever position
Full size table

5 Conclusions

Structure design and deploying modal analysis of the ten-modulus TPM are performed. The two-modulus TPM is processed and its mechanical properties are investigated by experiment.

  1. (1)

    The experimental and theoretical compression stiffness static models are 2.324 × 106 N/m and theoretical value is 2.167 × 106 N/m. It verifies the accuracy of the static theoretical models.

  2. (2)

    Geometric parameters have greater influence on bend stiffness than twist stiffness. Sensitivity of the geometric parameter is from large to small as follows: thickness, central angle, radius and separation.

  3. (3)

    The deploying repeat accuracy of the two-module TPM is 1.688 mm which is tested by the high-speed camera.

  4. (4)

    The veracity of the finite element model of the ten-module TPM at cantilever position is validated by modal test of the two-module TPM. The first fundamental frequency of the ten-module TPM is 2.561 Hz and the corresponding mode shape is bending.