Modelling the effects of chemotherapy and relapse on the transmission dynamics of leprosy

Abstract

Purpose

Although there is a declining trend in the global burden of leprosy, there are 15 countries in Asia and Africa which account for 94% of the global total of the new-case detection rate. Here, we assess the impact of different intervention strategies aimed at leprosy eradication through targeting non-symptomatic and symptomatic individuals.

Methods

We develop a mathematical model of leprosy transmission and treatment amongst symptomatic and non-symptomatic, in order to investigate the effects of leprosy relapse cases, case finding of non-symptomatic individuals and compliance to therapy of individuals administered with treatment. Comparison theory has been qualitatively used to analyze the global stability of the disease-free equilibrium. With the aid of centre manifold theory, the local stability of the endemic equilibrium has been investigated. Population-level effects of increased case findings and high treatment rate (guaranteed by compliance and completion of therapy via educational campaigns) are evaluated through numerical simulations and presented in support of the analytical results.

Results

Comprehensive and qualitative mathematical analysis of the model reveals that, the disease-free equilibrium is globally, asymptotically stable whenever the reproductive number is less than unity. Further, we have established that the model has a locally, asymptotically stable endemic equilibrium when the reproductive number is greater, but close to unity. Numerical simulation suggests that case finding of non-symptomatic leprosy carriers, greater that 40% is necessary for reducing leprosy prevalence and maybe useful on attaining leprosy eradication.

Conclusions

At its best, the study suggests that high level of case finding targeting non-symptomatic and symptomatic individuals, together with high level of compliance by individuals on treatment, may have a substantial effect on controlling leprosy relapses and possible may assist on attaining leprosy eradication.

Background

Although documented for many years, leprosy currently remains endemic in some developing parts of the world [1]. Leprosy is curable, and treatment provided in the early stages averts disability. According to official reports received from 121 countries and territories, the global registered prevalence of leprosy at the beginning of 2009 stood at 213,036 cases, while the number of new cases during 2008 was 30,055 cases and 31,037 cases in 2007 [2] for a disease which appeared to be vanishing in the seventeenth and eighteenth centuries [3]. In 1991, the World Health Organization (WHO) and its member states committed themselves to eliminate leprosy as a public health problem by the year 2000 [4]. Elimination was defined as a prevalence of less than 1 case per 10,000 persons. At the end of the year 2000, the deadline of the program, 597,232 leprosy cases were registered for treatment, and 719,330 cases were newly detected in the world [5]. Despite these tremendous efforts by the World Health Organization to eradicate leprosy, pockets of high endemicity still remain in some developing countries around the subtropical and tropical zone where the social and economic resources have not been sufficient to support the living standards needed to limit the disease. Here, we list the highest registered prevalences as of 2008: Angola (1,184 cases), Brazil (39,914 cases), Democratic Republic of Congo (6,114 cases), Ethiopia (4,187 cases), India (134,184 cases), Madagascar (1,763 cases), Mozambique (1,313 cases), Nepal (4,708 cases), Sudan (1,901 cases), Nigeria (4,899 cases), Sri-Lanka (1,979 cases) and the United Republic of Tanzania (3,276 cases) [2].

Mathematical models have become invaluable management tools for epidemiologists, both shedding light on the mechanisms underlying the observed dynamics as well as making quantitative predictions on the effectiveness of different control measures. The literature and development of mathematical epidemiology are well documented and can be found in [6–8].

This study intends to investigate the effects of early therapy to latently infected individuals and the role of non-compliance to leprosy dynamics. Adhering to a treatment schedule and successfully completing it are crucial to the control of any disease [5, 9]. Poor adherence to self-administration of treatment of a chronic disease is a common behavioral problem, [9, 10] including TB [11, 12] and leprosy [13].

The paper is structured as follows. The model is formulated in the ‘Methods’ section and comprehensively analyzed in the section ‘Analytical results’. Expected population effects from improved public health practices are investigated in the section ‘Results and discussion’ through numerical simulations of the model using a set of plausible parameter values abound in literature. A brief conclusion rounds up the paper.

Analytical results

In this section, we derive the equilibrium states, disease-free (DFE) and endemic (EE), of system (11) and investigate their stability using the reproductive number.

Disease-free equilibrium

Model system (11) has an evident DFE given by

$${\mathcal{E}}^0=\left(S^0,E^0,E_{\mathrm{D}}^0,P^0,M^0,R^0\right)=\left(\frac{\Lambda }{\mu },0,0,0,0,0\right).$$

(1)

The linear stability of ${\mathcal{E}}^0$ is governed by the basic reproduction number, which is defined as the spectral radius of the next generation matrix [14]. Following the next generation approach and the notation defined therein [14], the matrices F and V for model system (11) are respectively given by

$$\begin{array}{l}F=\left[\begin{array}{lllll}0& 0& \beta & \mathrm{\beta \theta }& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\end{array}$$

(2)

and

$$\begin{array}{l}V=\left[\begin{array}{lllll}{\gamma }_{\mathrm{P}}+{\gamma }_{\mathrm{M}}+\varphi +\mu & \hfill 0\hfill & \hfill -f{\alpha }_{\mathrm{P}}\hfill & \hfill -f{\alpha }_{\mathrm{M}}\hfill & \hfill 0\hfill \\ \hfill -\varphi \hfill & \kappa +\sigma +\mu & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\gamma }_{\mathrm{P}}\hfill & \hfill -\mathrm{\sigma \delta }\hfill & {\alpha }_{\mathrm{P}}+{\nu }_{\mathrm{P}}+\mu & \hfill 0\hfill & \hfill -q_{\mathrm{P}}\hfill \\ \hfill -{\gamma }_{\mathrm{M}}\hfill & -\sigma (1-\delta )& \hfill 0\hfill & {\alpha }_{\mathrm{M}}+\mu +{\nu }_{\mathrm{M}}& \hfill -q_{\mathrm{M}}\hfill \\ \hfill 0\hfill & \hfill -\kappa \hfill & -(1-f){\alpha }_{\mathrm{P}}& -(1-f){\alpha }_{\mathrm{M}}& q_{\mathrm{P}}+q_{\mathrm{M}}+\mu \end{array}\right].\end{array}$$

(3)

Thus, the reproductive number is given by

$$\begin{array}{lll}{\mathcal{R}}_{\mathrm{PM}}\hfill & =\hfill & \frac{\beta ({\mathcal{A}}_1-{\mathcal{A}}_2)}{{\mathcal{A}}_3+{\mathcal{A}}_4},\hfill \\ \text{where}\hfill & {\mathcal{A}}_1>{\mathcal{A}}_2,\hfill \\ \text{and}\hfill \\ {\mathcal{A}}_1\hfill & =\hfill & (1-f)(\theta {\alpha }_{\mathrm{P}}-{\alpha }_{\mathrm{M}})\left[q_{\mathrm{P}}\right((1-\delta )\mathrm{\sigma \varphi }+{\hslash }_1{\gamma }_{\mathrm{M}})\hfill \\ \hfill -q_{\mathrm{M}}(\mathrm{\delta \sigma \varphi }+{\hslash }_1{\gamma }_{\mathrm{P}})],\hfill \\ {\mathcal{A}}_2\hfill & =\hfill & {\hslash }_2[\mathrm{\kappa \varphi }{q}_{\mathrm{P}}+{\hslash }_3(\mathrm{\delta \sigma \varphi }+{\hslash }_1{\gamma }_{\mathrm{P}}\left)\right]+\theta (\mu +{\alpha }_{\mathrm{P}}+{\nu }_{\mathrm{P}})\hfill \\ \times [\mathrm{\kappa \varphi }{q}_{\mathrm{M}}+{\hslash }_3((1-\delta )\mathrm{\sigma \varphi }+{\hslash }_1{\gamma }_{\mathrm{M}}\left)\right)],\hfill \\ {\mathcal{A}}_3\hfill & =\hfill & f\left[{\hslash }_2{\alpha }_{\mathrm{P}}\right(\mathrm{\kappa \varphi }{q}_{\mathrm{P}}+{\hslash }_2(\mathrm{\delta \sigma \varphi }+{\hslash }_1{\gamma }_{\mathrm{P}}))\hfill \\ +{\alpha }_{\mathrm{M}}{\hslash }_4(\mathrm{\kappa \varphi }{q}_{\mathrm{M}}+{\hslash }_2((1-\delta )\mathrm{\sigma \varphi }+{\hslash }_1{\gamma }_{\mathrm{M}}\left)\right],\hfill \\ {\mathcal{A}}_4\hfill & =\hfill & {\hslash }_2(\mu +\varphi +{\gamma }_{\mathrm{P}}+{\gamma }_{\mathrm{M}})\left[\right(1-f){\hslash }_1{q}_4{\alpha }_{\mathrm{P}}{q}_{\mathrm{P}}\hfill \\ +{\hslash }_4\left(\right(1-f){\alpha }_{\mathrm{M}}{q}_{\mathrm{M}}-{\hslash }_2{\hslash }_3)],\hfill \\ \text{with}\hfill \\ {\hslash }_1\hfill & =\hfill & \mu +\kappa +\sigma ,{\hslash }_2=\mu +{\alpha }_{\mathrm{M}}+{\nu }_{\mathrm{M}},\hfill \\ {\hslash }_3\hfill & =\hfill & \mu +q_{\mathrm{P}}+q_{\mathrm{M}},{\hslash }_4=(\mu +{\alpha }_{\mathrm{P}}+{\nu }_{\mathrm{P}}).\hfill \end{array}$$

(4)

The threshold quantity ${\mathcal{R}}_{\mathrm{PM}}$ measures the average number of new secondary cases generated by a single infectious individual in a population where the aforementioned control measures are in place. Using Theorem 2 in [14], the following result is established.

Lemma 1

The disease-free equilibrium ${\mathcal{E}}^0$ of system (11) is locally, asymptotically stable if ${\mathcal{R}}_{\mathrm{PM}}<1$ and unstable if ${\mathcal{R}}_{\mathrm{PM}}>1$.

Global stability of the disease-free

We claim the following result.

Lemma 2

The disease-free equilibrium $\left({\mathcal{E}}^0\right)$ of model system (11) is globally, asymptotically stable (GAS) if ${\mathcal{R}}_{\mathrm{PM}}<1$ and unstable if ${\mathcal{R}}_{\mathrm{PM}}>1$.

Proof

The proof is based on using a comparison theorem [15]. Note that the equations of the infected components in system (11) can be written as

$$\begin{array}{c}\left[\begin{array}{l}{E}^{\prime }\\ E_{\mathrm{D}}^{\prime }\\ P^{\prime }\\ M^{\prime }\end{array}\right]=[F-V]\left[\begin{array}{l}E\\ E_{\mathrm{D}}\\ P\\ M\end{array}\right]\hfill \\ -\beta \left[1-\frac{S}{N}\right]\left[\begin{array}{lllll}0& 0& 1& \theta & 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{l}E\\ E_{\mathrm{D}}^{\prime }\\ P\\ M\end{array}\right]\end{array}$$

where F and V are as defined earlier on Equations 2 and 3, respectively. Since S ≤ N, (for all t ≥ 0) in Φ, it follows that

$$\begin{array}{l}\left[\begin{array}{l}{E}^{\prime }\\ E_{\mathrm{D}}^{\prime }\\ P^{\prime }\\ M^{\prime }\end{array}\right]\le [F-V]\left[\begin{array}{l}E\\ E_{\mathrm{D}}\\ P\\ M\end{array}\right]\end{array}$$

(5)

Using the fact that the eigenvalues of the matrix F − V all have negative real parts, it follows that the linearized differential inequality system (5) is stable whenever ${\mathcal{R}}_{\mathrm{PM}}<1.$ Consequently, (E,E_DP, M, R) → (0, 0, 0, 0, 0) as $t\to \mathrm{\infty .}$ Thus, by comparison theorem [15], (E,E_DP, M, R) →(0, 0, 0, 0, 0) as $t\to \infty$, and evaluating system (11) at E =E_D= P = M = 0 gives $S\to S^0$ for ${\mathcal{R}}_{\mathrm{PM}}<1.$ Hence, the DFE $\left({\mathcal{E}}^0\right)$ is GAS for ${\mathcal{R}}_{\mathrm{PM}}<1.$ □

Sensitivity analysis of ${\mathcal{R}}_{\mathrm{PM}}$

Due to the complexity nature of the expression which defines ${\mathcal{R}}_{\mathrm{PM}}$, we shall apply numerical simulations to investigate the impact of (a) disease relapse when both strains co-exist, (b) reduction in treatment compliance and (c) role of leprosy case findings at latent stage. From Figure 1, trend line (a) shows the effects of disease relapse on the reproductive number ${\mathcal{R}}_{\mathrm{PM}}$, and series (b) shows the effects of decreasing treatment compliance level. Figure 1 suggests that an increase in relapse rate and a decrease in treatment compliance level will result in an increase in ${\mathcal{R}}_{\mathrm{PM}}$, thus increasing leprosy prevalence in the community, which is a negative impact on the WHO campaign to eradicate leprosy epidemic. However, from series (c), we note that an increase in the leprosy case findings at the latent stage may have a positive impact on the leprosy eradication campaign since the increase in the case finding level results in a marked decrease of ${\mathcal{R}}_{\mathrm{PM}}$. Further analysis of Figure 1 suggests that if q ≥ 0.05, then ${\mathcal{R}}_{\mathrm{PM}}>1.$

Figure 1

Simulations showing the impact of disease relapse, reduction in treatment compliance and leprosy case findings. Simulation of model system (11) showing (curve a) disease relapse when both strains co-exist, (curve b) reduction in treatment compliance and (curve c) role of leprosy case findings at latent stage. Parameter values used are as in Table 1, with either q, f or ϕ varying in steps of 0.1.

Table 1 Model parameters and their interpretations

Endemic equilibrium and stability analysis

Model system (11) has an endemic state given by ${\mathcal{E}}^{\ast }=(S^{\ast },E^{\ast },E^{\ast }\mathrm{D},P^{\ast },M^{\ast },R^{\ast })$. In order to analyze the stability of this equilibrium point (${\mathcal{E}}^{\ast }$), we make use of the centre manifold theory [16] as described in Theorem 4.1 of Castillo-Chavez and Song [16]. To establish the local stability, we defineS = x₁E = x₂,E_D = x₃,P = x₄, M = x₅, R = x₆ so that $N=\sum _{i=1}^6{x}_i.$ Using the vector notation $X={(x_1,x_2,x_3,x_4,x_5,x_6)}^T,$ model system (11) under these conditions can be written in the form $\frac{\mathrm{dX}}{\mathrm{dt}}=F={(f_1,f_2,f_3,f_4,f_5,f_6)}^T,$ such that

$$\begin{array}{c}{x}_1^{\prime }=f_1=\Lambda -\frac{\beta (x_4+\theta x_5)x_1}{\sum _{i=1}^6{x}_i}-\mu x_1,\hfill \\ x_2^{\prime }=f_2=\frac{\beta (x_4+\theta x_5)x_1}{\sum _{i=1}^6{x}_i}+f{\alpha }_{\mathrm{P}}{x}_4+f{\alpha }_{\mathrm{M}}{x}_5\hfill \\ -({\gamma }_{\mathrm{P}}+\varphi +{\gamma }_{\mathrm{M}}+\mu )x_2,\\ x_3^{\prime }=f_3=\varphi x_2-(\kappa +\sigma +\mu )x_3,\hfill \\ x_4^{\prime }=f_4={\gamma }_{\mathrm{P}}{x}_2+\mathrm{\sigma \delta }{x}_3+q_{\mathrm{p}}{x}_6-({\alpha }_{\mathrm{P}}+\mu +{\nu }_{\mathrm{P}})x_4,\hfill \\ x_5^{\prime }=f_5={\gamma }_{\mathrm{M}}{x}_2+\sigma (1-\delta )x_3+q_{\mathrm{M}}{x}_6\hfill \\ -({\alpha }_{\mathrm{M}}+\mu +{\nu }_{\mathrm{M}})x_5,\hfill \\ x_6^{\prime }=f_6=\kappa x_3+(1-f){\alpha }_{\mathrm{P}}{x}_4+(1-f){\alpha }_{\mathrm{M}}{x}_5\hfill \\ -(q_{\mathrm{P}}+q_{\mathrm{M}}+\mu )x_6.\hfill \end{array}$$

(6)

We now evaluate the Jacobian $J\left({\mathcal{E}}^0\right)$ of system (6) at the disease-free $\left({\mathcal{E}}^0\right)$ in order for us to find the right and left eigenvalues, which are necessary for determining the existence and the nature of the bifurcation for ${\mathcal{R}}_0>1$.

$$\begin{array}{c}J\left({\mathcal{E}}^0\right)=\left[\begin{array}{cccccc}-\mu & 0& 0& -\beta & -\mathrm{\beta \theta }& 0\\ 0& -\mu -{\gamma }_{\mathrm{P}}-\varphi -{\gamma }_{\mathrm{M}}& 0& \beta +f{\alpha }_{\mathrm{P}}& \mathrm{\beta \theta }+f{\alpha }_{\mathrm{M}}& 0\\ 0& \varphi & -\kappa -\sigma -\mu & 0& 0& 0\\ 0& {\gamma }_{\mathrm{P}}& \mathrm{\sigma \delta }& -\mu -{\alpha }_{\mathrm{P}}-{\nu }_{\mathrm{P}}& 0& q_{\mathrm{P}}\\ 0& {\gamma }_{\mathrm{M}}& \sigma (1-\delta )& 0& -\mu -{\alpha }_{\mathrm{M}}-{\nu }_{\mathrm{M}}& q_{\mathrm{M}}\\ 0& 0& \kappa & (1-f){\alpha }_{\mathrm{P}}& (1-f){\alpha }_{\mathrm{M}}& -\mu -q_{\mathrm{p}}-q_{\mathrm{M}}\end{array}\right]\end{array}$$

(7)

From Equation 7, it follows that the reproductive number is given by

$${\mathcal{R}}_{\mathrm{PM}}=\frac{\beta ({\mathcal{A}}_1-{\mathcal{A}}_2)}{{\mathcal{A}}_3+{\mathcal{A}}_4},$$

(8)

with ${\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_4$ as defined in Equation 4.

If β is taken as the bifurcation parameter, solving for β = β^∗when ${\mathcal{R}}_{\mathrm{PM}}=1$, we obtain

$$\beta ={\beta }^{\ast }=\frac{{\mathcal{A}}_3+{\mathcal{A}}_4}{{\mathcal{A}}_1-{\mathcal{A}}_2}.$$

(9)

Thus, the linearized system of the transformed system (6) with β = β^∗ chosen as a bifurcation parameter has a simple zero eigenvalue. Hence, it can be shown that the Jacobian (Equation 7) at β = β^∗ has a right and left eigenvector given below.

Eigenvectors of $J\left({\mathcal{E}}^0\right)$

It can be shown that the Jacobian $J\left({\mathcal{E}}^0\right)$ of system (6) at β = β^∗has a right eigenvector (corresponding to the zero eigenvalue) given by u = ${(u_1,u_2,u_3,u_4,u_5,u_6)}^T$, where

$$\mathbf{\text{u}}\left\{\begin{array}{c}{u}_1=-\frac{{\beta }^{\ast }(u_4+\theta u_5)}{\mu },u_2>0,u_3=\frac{\varphi u_2}{\kappa +\sigma +\mu },\\ u_4=\frac{{\gamma }_{\mathrm{P}}{u}_2+\mathrm{\sigma \delta }{u}_3+q_{\mathrm{P}}{u}_6}{\mu +{\alpha }_{\mathrm{P}}+{\nu }_{\mathrm{p}}},\hfill \\ u_4=\frac{{\gamma }_{\mathrm{M}}{u}_2+\sigma (1-\delta )u_3+q_{\mathrm{M}}{u}_6}{\mu +{\alpha }_{\mathrm{M}}+{\nu }_{\mathrm{M}}},\hfill \\ u_5=\frac{\kappa u_3+(1-f)[{\alpha }_{\mathrm{P}}{u}_4+{\alpha }_{\mathrm{M}}{u}_5]}{\mu +q_{\mathrm{p}}+q_{\mathrm{M}}}.\hfill \end{array}\right.$$

Furthermore, the Jacobian $J\left({\mathcal{E}}^0\right)$ has a left eigenvector (associated with the zero eigenvalue) given by z = ${(z_1,z_2,z_3,z_4,z_5,z_6)}^T$, where

$$\mathbf{\text{z}}\left\{\begin{array}{c}{z}_1=0,z_2>0,z_3=\frac{\mathrm{\sigma \delta }{z}_4+\sigma (1-\delta )z_5+\kappa z_6}{\kappa +\mu +\sigma },\hfill \\ z_4=\frac{({\beta }^{\ast }+f{\alpha }_{\mathrm{P}})z_2+(1-f){\alpha }_{\mathrm{P}}{z}_6}{\mu +{\alpha }_{\mathrm{P}}+{\nu }_{\mathrm{P}}},\hfill \\ z_5=\frac{(\theta {\beta }^{\ast }f{\alpha }_{\mathrm{M}}+)z_2+(1-f){\alpha }_{\mathrm{M}}{z}_6}{\mu +{\alpha }_{\mathrm{M}}+{\nu }_{\mathrm{M}}},z_6=\frac{q_{\mathrm{p}}{z}_4+q_{\mathrm{M}}{z}_5}{\mu +q_{\mathrm{P}}+q_{\mathrm{M}}}.\end{array}\right.$$

Computations of the bifurcation coefficients a and b

It can be shown, after some algebraic manipulations (involving the associated non-zero partial derivative of F (at the DFE) to be used in the expression (for a) and (b) defined in centre manifold theorem [16]), that

$$\begin{array}{ll}a& =z_2\sum _{i,j=1}^6{u}_{\mathrm{i}}{u}_{\mathrm{j}}\frac{{\partial }^2{f}_2}{\partial x_{\mathrm{i}}\partial x_{\mathrm{j}}}\\ =-\frac{2{\beta }^{\ast }\mu (u_2+u_3+u_4+u_5+u_6)(u_4+\theta u_5)z_2}{\Lambda }<0,\\ b& =(u_4+\theta u_4)z_2>0.\end{array}$$

(10)

We summarise the result in Lemma 3 below.

Lemma 3

The endemic equilibrium (${\mathcal{E}}^{\ast }$) is locally, asymptotically stable for ${\mathcal{R}}_{\mathrm{PM}}>1,$ but close to 1, as guaranteed by Theorem 4.1 [16].

Results and discussion

Population-level effects

In order to illustrate the results of the foregoing analysis in this study, we carry out detailed numerical simulations using MATLAB ODE solver, ode 45 programming language and parameter values summarized in Table 1. Unfortunately, the scarcity of data on the transmission dynamics of leprosy limits our ability to calibrate, but nevertheless, we assume some of the parameters in the realistic range for illustrating the dynamics. These parsimonious assumptions reflect the lack of information currently available on the transmission dynamics of the leprosy epidemic. Since this theoretical study is seemingly the first of its kind, it should be seen as a template for future research, especially in data collection in this section.

Figure 2a demonstrates the effects of increasing leprosy relapse cases over a period of 100 years. If there are leprosy relapse cases, then the annual incidence of active leprosy decreases sharply in the presence of case finding of non-symptomatic carriers together with treatment of symptomatic carriers. Simulations, suggest that increasing relapse cases may result in increased leprosy prevalence. Figure 2b clearly demonstrates the impact of different treatment compliance levels for leprosy patients on therapy. We observe that a decrease in treatment compliance level may increase leprosy prevalence in the community.

Figure 2

Effects of leprosy relapse cases and treatment compliance. Simulations of model system (11) showing the effects of leprosy relapse cases (a) and treatment compliance (b) over a period of 100 years. Parameters are fixed on their baseline values from Table 1.

The final set of simulations (Figure 3) depicts the dynamics of the cumulative new infections over a period of 100 years. It suggests that if the case finding rate for non-symptomatic individuals is less than 40%, then leprosy eradication will be difficult to attain. However, case finding for any level (ϕ ≥ 40%) predicts that leprosy can be eradicated from the community. Simulation confirms the analytical observation discussed earlier in this study. This makes it clear that the case finding for non-symptomatic carriers is necessary for leprosy eradication.

Figure 3

Dynamics of the cumulative new infections. Effects of control measures on leprosy incidence (modeled by the parameter ϕ) are demonstrated over a period of 80 years. The rest of the parameters are fixed on their baseline values from Table 1.

Conclusions

The number of leprosy patients registered worldwide has fallen from a peak of 10 to 15 million to a current total of less than 1 million. However, the transmission of leprosy continues unabated in high-burden countries, with the number of new leprosy cases registered each year remaining relatively constant [20]. India is one of the countries where at least 1,000 new cases of leprosy were reported during 2006 [5]. A mathematical model for the transmission dynamics of leprosy in the context of disease relapse was set up; case findings of non-symptomatic carriers and compliance for individuals on treatment were formulated; mathematical properties were investigated in order to assess the impact of disease relapse, case findings of non-symptomatic individuals and treatment compliance on the dynamics of leprosy. Qualitative analysis of the model suggests that maintaining low levels extremely close to zero or exactly zero percentage for leprosy relapse cases, coupled with a high level of case finding of non-symptomatic leprosy carriers together with high level of treatment compliance, may have a substantial effect on controlling a leprosy epidemic.

Methods

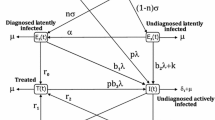
In this section, we introduce a mathematical model for investigating the transmission dynamics of leprosy in human population. We consider a population N whose demography is regulated by a constant birth/recruitment rate Λ and a natural mortality rate μ. Based on epidemiological status, the population is subdivided into the following classes: susceptible (S), individuals who are not yet infected by the disease and can be infected by Mycobaterium leprae and join a latently infected class (E). To account for case findings, we define ϕ as the rate at which leprosy cases are detected at latent stage. Once detected, these individuals move into the detected latent class where they may receive chemoprophylaxis. Individuals who receive effective chemoprophylaxis are assumed to recover at a rate κ while those who do not receive treatment become infectious at a rate σ, with a fraction δ progressing to paucibacillary leprosy (P), and the complementary fraction (1−δ) progressing to multibacillary (M). Undetected latently infected individuals who progress to active disease do so in two different ways. They can develop localized, paucibacillary leprosy, with a strong cell-mediated response, which may resolve spontaneously, affects host survival only minimally, and is much less transmissible [3, 21]. Alternatively, they can develop disseminated multibacillary disease (M), which will somewhat reduce average survival time and is more contagious. The pathway taken (paucibacillary (PB) or multibacillary (MB)) seems to be dependent not on the strain of the organism but on the host response [3, 21]. Because borderline cases will often progress over time to either paucibacillary or multibacillary forms, for the purposes of simplifying our study, we have included only these two pathways. This division of the active states of leprosy into two discrete forms has been used in other studies [3]. Infectious individuals are assumed to be administered treatment and join the recovery class (R) at rates _{α P} and _{α M} for those infected with paucibacillary or multibacillary, respectively. Thus, the total population (N) at a time t is given by

$$N=S+E+E_{\mathrm{D}}+P+M+\mathrm{R.}$$

Assuming homogeneous mixing of the population, the susceptible acquire leprosy infection at a rate $\lambda =\frac{\beta (P+\mathrm{\theta M})}{N},$ where β denotes the effective contact rate for leprosy transmission. Since PB is less transmissible in comparison to MB [3], parameter θ is the enhancement factor for assumed transmission of MB strain compared to PB strain. Latent individuals progress to active leprosy at ratesγ_P andγ_M for P and M, respectively. To capture the impact of treatment compliance, we assume that a fraction f will fail to complete treatment after 3 to 4 weeks, and the complementary fraction (1 − f) will successfully complete treatment. Some individuals in the R class relapse back into the infective state at ratesq_P andq_M for P and M cases, respectively. Infectious individuals suffer an additional mortality at ratesν_P andν_M, respectively, due to the disease. The model flow diagram is shown in Figure 4.

Figure 4

Model flow diagram.

The deterministic compartmental model provides a means of obtaining insight into the dynamics of leprosy. As with most models for disease transmission and control, our model is based on the simple susceptible-infected-recovered (SIR) model [22]. The main parameter of the SIR model is the basic reproduction number, ${\mathcal{R}}_0$. If this parameter is below unity, then the disease dies out, whereas if this parameter is above unity, any small introduction of infected individuals in the population results in an oscillatory approach to an endemic equilibrium. Mathematically, there is a trivial equilibrium, known as the disease-free equilibrium, which is globally asymptotically stable w henever ${\mathcal{R}}_0<1$[14]. The aforementioned assumptions and description above give rise to the following system of ordinary differential equations:

$$\begin{array}{c}{S}^{\prime }=\Lambda -(\lambda +\mu )S,\hfill \\ E^{\prime }=\mathrm{\lambda S}+f{\alpha }_{\mathrm{P}}P+f{\alpha }_{\mathrm{M}}M-({\gamma }_{\mathrm{P}}+{\gamma }_{\mathrm{M}}+\varphi +\mu )E,\hfill \\ E_{\mathrm{D}}^{\prime }=\mathrm{\varphi E}-(\kappa +\sigma +\mu )E_{\mathrm{D}},\hfill \\ P^{\prime }={\gamma }_{\mathrm{P}}E+\mathrm{\sigma \delta }{E}_{\mathrm{D}}+q_{\mathrm{P}}R-({\alpha }_{\mathrm{P}}+\mu +{\nu }_{\mathrm{P}})P,\hfill \\ M^{\prime }={\gamma }_{\mathrm{M}}E+\sigma (1-\delta )E_{\mathrm{D}}+q_{\mathrm{M}}R-({\alpha }_{\mathrm{M}}+\mu +{\nu }_{\mathrm{M}})M,\hfill \\ R^{\prime }=\kappa E_{\mathrm{D}}+(1-f){\alpha }_{\mathrm{P}}P+(1-f){\alpha }_{\mathrm{M}}M\hfill \\ -(q_{\mathrm{P}}+q_{\mathrm{M}}+\mu )\mathrm{R.}\hfill \end{array}$$

(11)

For system (11), the first octant in the state space is positively invariant and attracting, that is, solutions that start where all the variables are non-negative remain there. Thus, system (11) will be analyzed in a suitable region $\Phi \subset {ℝ}_{+}^6$, the region

$$\Phi =\left\{(S,E,E_{\mathrm{D}},P,M,R)\in {ℝ}_{+}^6:N\le \frac{\Lambda }{\mu }\right\},$$

(12)

which is positively invariant and attracting. Existence, uniqueness and continuation results for system (11) hold in this region.

Author’s contributions

The authors contributed equally to this work. All authors read and approved the final manuscript.