Mathematical methods for a reliable treatment of the (2+1)-dimensional Zoomeron equation

Abstract

Purpose

This paper investigates an analytical solution to a physical model called (2 + 1)-dimensional Zoomeron equation.

Methods

The solutions of Zoomeron are obtained using direct methods such as the extended tanh, the exponential function and the sech^p−tanh^pfunction methods.

Results

Several soliton solutions are obtained using the proposed methods.

Conclusions

The obtained solutions are new, and each has its own structure.

Background

It is well known that many models in mathematics and physics are described by nonlinear partial differential equations (NPDEs). The theory of solitons, ‘the most important side in applications to NPDEs’, has contributed to understanding many experiments in mathematical physics. Thus, it is of interest to evaluate new solutions of these equations. A problem of real interest for applications consists in constructing explicit traveling wave solutions of an incognito evolution equation that is called Zoomeron equation:

$${\left(\frac{u_{\mathit{\text{xy}}}}{u}\right)}_{\mathit{\text{tt}}}-{\left(\frac{u_{\mathit{\text{xy}}}}{u}\right)}_{\mathit{\text{xx}}}+2{(u^2)}_{\mathit{\text{xt}}}=0,$$

(1)

where u(x,y,t) is the amplitude of the relevant wave mode. In the literature, there are a few articles about this equation. We only know that this equation was introduced by Calogero and Degasperis[1]. Recently, Reza[2] obtained periodic and soliton solutions to Zoomeron equation by means of G^′/G method.

Recently, the powerful direct methods, tanh[3] and exponential function methods[4], have been developed to find special solutions of nonlinear equation. Our aim in this paper is to present tanh, exponential function and sech^p-tanh^pmethods to Equation 1. In what follows, we highlight the main features of the proposed methods where more details and examples can be found in[3, 5–7].

Results and discussion

In this section, we solve the (2+1)-dimensional Zoomeron equation

$${\left(\frac{u_{\mathit{\text{xy}}}}{u}\right)}_{\mathit{\text{tt}}}-{\left(\frac{u_{\mathit{\text{xy}}}}{u}\right)}_{\mathit{\text{xx}}}+2{(u^2)}_{\mathit{\text{xt}}}=0.$$

(2)

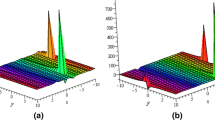
First, by means of the extended tanh method (Figure1), we use the wave variable ζ = x + cy − wt that transforms Equation 2 into the ODE:

$$c(1-w^2)u^{\prime \prime }-2w{u}^3+\mathit{\text{Ru}}=0,$$

(3)

where R is the integration constant.

Figure 1

Propagations of the solution of Zoomeron equation. Propagations vary over t = 0.01, 0.1, 0.2 and 0.5, where R = 1, w = 4 and μ = 1 using the extended tanh method.

Balancing the linear term u⁽²⁾ and the nonlinear term u³ gives M + 2 = 3M, and thus, M = 1. The tanh method allows us to use the finite expansion:

$$u(x,t)=S\left(Y\right)=a_{-1}{Y}^{-1}+a_0+a_{1}Y,$$

(4)

where Y = tanh(μζ). Substituting Equation 4 in Equation 3 yields

$$\begin{array}{l}0=B^{2}w+c(-1+w^2){\mu }^2\\ 0=R-6\mathit{\text{BCw}}+2c(-1+w^2){\mu }^2\\ 0=R-6\mathit{\text{BCw}}+2c(-1+w^2){\mu }^2\\ 0=C^{2}w+c(-1+w^2){\mu }^2.\end{array}$$

(5)

Solving the above system, we get the following:

$$C=-B=\mp \frac{\sqrt{R}}{2\sqrt{2}\sqrt{w}};c=-\frac{R}{8(-1+w^2){\mu }^2};A=0,$$

(6)

where R, w and μ are free parameters with R > 0, w > 0, w ≠ 1 and μ ≠ 0. Therefore, the solution of Equation 2 is given by the following:

$$\begin{array}{ll}u(x,y,t)=& \mp \frac{\sqrt{R}}{2\sqrt{2}\sqrt{w}}\text{coth}\left(x+\frac{R}{8(-1+w^2){\mu }^2}y-\mathit{\text{wt}}\right)\\ \pm \frac{\sqrt{R}}{2\sqrt{2}\sqrt{w}}\text{tanh}\left(x+\frac{R}{8(-1+w^2){\mu }^2}y-\mathit{\text{wt}}\right).\end{array}$$

(7)

Second, by means of the exponential method (Figure2), we substitute Equation 24 in Equation 3 to obtain the following algebraic system:

$$\begin{array}{ll}0& =A_3^{2}R-2w\\ 0& =-A_5^{2}R+2A_2^{2}w\\ 0& =A_3{A}_4(2R+c(-1+w^2\left){\mu }^2\right)\\ +A_1(-6w+A_3^2(R-c(-1+w^2){\mu }^2\left)\right)\\ 0& =A_4^{2}R+2A_3{A}_{5}R-6A_1^{2}w+A_4^{2}c{\mu }^2-4A_3{A}_{5}c{\mu }^2\\ -A_4^{2}c{w}^2{\mu }^2+4A_3{A}_{5}c{w}^2{\mu }^2+A_1{A}_3{A}_4(2R\\ +c(-1+w^2){\mu }^2)+A_2(-6w+A_3^2(R-4c(-1\\ +w^2\left){\mu }^2\right))\\ 0& =-2A_1^{3}w+A_4{A}_5(2R-3c(-1+w^2\left){\mu }^2\right)\\ +A_2(-12A_{1}w+A_3{A}_4(2R-3c(-1+w^2){\mu }^2\left)\right)\\ +A_1(A_4^{2}R+2A_3{A}_5(R+3c(-1+w^2){\mu }^2\left)\right)\\ 0& =-6A_2^{2}w+A_5\left(A_5\right(R-4c(-1+w^2){\mu }^2)\\ +A_1{A}_4(2R+c(-1+w^2\left){\mu }^2\right))+A_2(-6A_1^{2}w\\ +A_4^2(R-c(-1+w^2\left){\mu }^2\right)+2A_3{A}_5(R+2c(-1\\ +w^2\left){\mu }^2\right))\\ 0& =-6A_1{A}_2^{2}w+A_1{A}_5^2(R-c(-1+w^2\left){\mu }^2\right)\\ +A_2{A}_4{A}_5(2R+c(-1+w^2\left){\mu }^2\right).\end{array}$$

(8)

Solving the above system yields the following:

$$\begin{array}{l}{A}_1=\mp \sqrt{\frac{R\left(A_4^2-4\sqrt{2}{A}_5\sqrt{\frac{w}{R}}\right)}{2w}},A_2=-\frac{A_5\sqrt{R}}{\sqrt{2w}},\\ A_3=\frac{\sqrt{2w}}{\sqrt{R}},c=-\frac{2R}{{\mu }^2(w^2-1)}.\end{array}$$

(9)

From Equation 9, we conclude that a solution of Zoomeron equation exists if the following conditions on the parameters are satisfied:

$$w>0,w\ne 1,\mu \ne 0,R>0,A_4^2-4\sqrt{2}{A}_5\sqrt{\frac{w}{R}}>0.$$

(10)

Therefore, the solution is given by the following:

$$u(x,y,t)=\frac{e^{-\mu (x+\frac{2R}{{\mu }^2(w^2-1)}y-\mathit{\text{wt}})}+\sqrt{\frac{R\left(A_4^2-4\sqrt{2}{A}_5\sqrt{\frac{w}{R}}\right)}{2w}}-\frac{A_5\sqrt{R}}{\sqrt{2w}}{e}^{\mu (x+\frac{2R}{{\mu }^2(w^2-1)}y-\mathit{\text{wt}})}}{\frac{\sqrt{2w}}{\sqrt{R}}{e}^{-\mu (x+\frac{2R}{{\mu }^2(w^2-1)}y-\mathit{\text{wt}})}+A_4+A_5{e}^{\mu (x+\frac{2R}{{\mu }^2(w^2-1)}y-\mathit{\text{wt}})}},$$

(11)

Figure 2

Propagations of the solution of Zoomeron equation. Propagations vary over t = 0.1, 0.5, 0.9, 1.9, 2.9 and 3.5, where w = 4, μ = 1, A₄ = 4,$A_5=\sqrt{2}$ and R = 1 using exponential method.

where R, w, A₄, A₅ and μ are free parameters being chosen and satisfying conditions given in Equation 10.

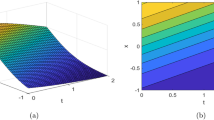
Third, we substitute ansatz 25 in Equation 3 to get the following (Figure3):

$$\begin{array}{ll}0& =(-\mathit{\text{Acq}}{\mu }^2-\mathit{\text{Ac}}{q}^2{\mu }^2+\mathit{\text{Acq}}{w}^2{\mu }^2\\ +\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2)\text{cosh}{\left(z\mu \right)}^{-2-q}-2A^{3}w\text{cosh}{\left(z\mu \right)}^{-3q}\\ +(\mathit{\text{AR}}+\mathit{\text{Ac}}{q}^2-\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2)\text{cosh}{\left(z\mu \right)}^{-q}.\end{array}$$

(12)

By equating the exponents and the coefficients of each pair of the cosh function, we obtain the following algebraic system:

$$\begin{array}{l}0=-2-q+3q\\ 0=-\mathit{\text{Acq}}{\mu }^2-\mathit{\text{Ac}}{q}^2{\mu }^2+\mathit{\text{Acq}}{w}^2{\mu }^2\\ +\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2-2A^{3}w\\ 0=\mathit{\text{AR}}+\mathit{\text{Ac}}{q}^2-\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2.\end{array}$$

(13)

Solving the above system yields the following:

$$\begin{array}{l}q=1\\ A=\mp \frac{\sqrt{R}}{\sqrt{w}}\\ c=\frac{R}{(w^2-1){\mu }^2}.\end{array}$$

(14)

Therefore, the solution of Zoomeron equation is

$$u(x,y,t)=\mp \frac{\sqrt{R}}{\sqrt{w}}\text{sech}\left(\mu (x-\frac{R}{(w^2-1){\mu }^2}y-\mathit{\text{wt}})\right),$$

(15)

provided that w > 0, w ≠ 1 and μ ≠ 0.

Figure 3

Propagations of the solution of Zoomeron equation. Propagations vary over t = 0.1, 0.6, 1.1, 1.6 and 2.1, where R = 1, w = 2 and μ = 1 using cosh^q-ansatz.

Finally, we substitute ansatz 26 in Equation 3 to get the following (Figure4):

$$\begin{array}{ll}0=& (-\mathit{\text{Acq}}{\mu }^2+\mathit{\text{Ac}}{q}^2{\mu }^2+\mathit{\text{Acq}}{w}^2{\mu }^2\\ -\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2)\text{tanh}{\left(z\mu \right)}^{-2+q}\\ +(\mathit{\text{AR}}-2\mathit{\text{Ac}}{q}^2{\mu }^2+2\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2)\text{tanh}{\left(z\mu \right)}^q\\ -2A^{3}w\text{tanh}{\left(z\mu \right)}^{3q}\\ +(\mathit{\text{Acq}}{\mu }^2+\mathit{\text{Ac}}{q}^2{\mu }^2-\mathit{\text{Acq}}{w}^2{\mu }^2\\ -\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2)\text{tanh}{\left(z\mu \right)}^{2+q}.\end{array}$$

(16)

Figure 4

Propagations of the solution of Zoomeron equation. Propagations vary over t = 0.01, 0.1 and 0.5, where R = 0.01, w = 4 and μ = 0.3 using tanh^q-ansatz.

By equating the exponents and the coefficients of each pair of the tanh function, we obtain the following algebraic system:

$$\begin{array}{l}0=-2+q-3q\\ 0=-\mathit{\text{Acq}}{\mu }^2+\mathit{\text{Ac}}{q}^2{\mu }^2+\mathit{\text{Acq}}{w}^2{\mu }^2-\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2-2A^{3}w\\ 0=\mathit{\text{AR}}-2\mathit{\text{Ac}}{q}^2{\mu }^2+2\mathit{\text{Ac}}{q}^2{w}^2{\mu }^2.\end{array}$$

(17)

Solving the above system yields the following:

$$\begin{array}{l}q=-1\\ A=\mp \frac{\sqrt{R}}{\sqrt{2w}}\\ c=-\frac{R}{2(w^2-1){\mu }^2}.\end{array}$$

(18)

Therefore, the solution of Zoomeron equation is

$$u(x,y,t)=\mp \frac{\sqrt{R}}{\sqrt{2w}}\text{coth}\left(\mu (x+\frac{R}{2(w^2-1){\mu }^2}y-\mathit{\text{wt}})\right),$$

(19)

provided that w > 0, w ≠ 1 and μ ≠ 0.

Conclusion

In this paper, a physical model called (2 + 1)-dimensional Zoomeron equation is discussed. Mathematical methods such as the extended tanh, the exponential function and the sech^p−tanh^p function methods are used for analytical treatment of this model. By means of these methods, we have the advantage of reducing the nonlinear problem to a system of algebraic equations that can be solved by any computerized packages. The proposed methods are straightforward, concise and effective, and can be applied to many nonlinear equations arise in applied sciences.

Methods

In this section, we will highlight briefly the main steps of each of the three methods that will be used in this paper. We first unite the independent variables x, y and t into one wave variable ζ = x − cy − wt to convert the PDE

$$P(u,u_t,u_x,u_{\mathit{\text{xy}}},u_{\mathit{\text{xyt}}},\dots )$$

(20)

into an ODE

$$Q(u,-c{u}^{\prime },u^{\prime },-w{u}^{\prime \prime },\mathit{\text{cw}}{u}^{\prime \prime \prime },\dots ).$$

(21)

Equation 21 is then integrated as long as all terms contain derivatives.

The extended tanh method

The extended tanh technique is based on the assumption that the traveling wave solutions can be expressed in terms of the tanh function[8, 9]. We therefore introduce a new independent variable

$$Y=\text{tanh}\left(\mu \zeta \right).$$

(22)

Then, the solution can be proposed a finite power series in Y in the form:

$$u\left(\mu \zeta \right)=S\left(Y\right)=\sum _{i=-M}^M{a}_i{Y}^i,$$

(23)

limiting them to solitary and shock wave profiles. The parameter M is a positive integer, in most cases, that will be determined using a balance procedure, whereby comparing the behavior of Yⁱ in the highest derivative against its counterpart within the nonlinear terms. With M determined, we collect all coefficients of powers of Y in the resulting equation where these coefficients have to vanish; hence, the coefficients a _i can be determined.

The exponential method

Using the wave variable ζ = x − cy − wt, the exponential method admits the use of the ansatz

$$u(x,y,t)=\frac{e^{-\mu \zeta }+A_1+A_2{e}^{\mu \zeta }}{A_3{e}^{-\mu \zeta }+A_4+A_5{e}^{\mu \zeta }},$$

(24)

where A₁, A₂, A₃, A₄, A₅, μ, w and c are parameters that will be determined by collecting all coefficients of powers of e^μζ in the resulting equation where these coefficients have to vanish.

Solitary ansatz in terms of cosh^pand tanh^p

The solitary wave ansatz in terms of cosh^pis assumed as Equation 25 (see[7, 10, 11]).

$$u(x,t)=\frac{A}{{\text{cosh}}^q\left(\mu \zeta \right)}.$$

(25)

The solitary wave ansatz in terms of tanh^pis assumed as Equation 26 (see[7, 10]).

$$u(x,t)=A{\text{tanh}}^q\left(\mu \zeta \right).$$

(26)

The unknown index q as well as A and μ is to be determined during the course of derivation of the solution of Equation 21.