An analytic algorithm of Lane-Emden-type equations arising in astrophysics - a hybrid approach

Abstract

A new analytic algorithm for Lane-Emden equations is proposed in this paper. The proposed algorithm is obtained by using a new iterative method. The new iterative method is a hybrid of variational iteration method and the Adomian decomposition method and further refined by introducing a new correction functional. This new correction functional is obtained from the standard correction functional of variational iteration method by introducing an auxiliary parameter γ in it. Further, a sequence$G_n\left(x\right)$, with suitably chosen support, is also introduced in the new correction functional. The algorithm is easy to implement and gives fairly accurate solutions. Several test examples are given establishing the accuracy and the efficiency of the algorithm.

Background

The study of singular initial value problems modelled by second-order nonlinear ordinary differential equations has attracted many mathematicians and physicists. One of the equations in this category is the following Lane-Emden-type equation:

$$y\text{'}\text{'}\left(x\right)+\frac{\alpha }{x}y\text{'}\left(x\right)+f\left(x,y\right)=g\left(x\right),\alpha x\ge 0\text{,}$$

(1)

with the initial conditions (IC)

$$y\left(0\right)=a,y\text{'}\left(0\right)=0\text{,}$$

(2)

where the prime denotes the differentiation with respect to x, α is a constant, f(x,y) is a nonlinear function of x and y. It is well known that an analytic solution of the Lane-Emden-type equation (Equation 1) is always possible[1] in the neighbourhood of the singular point x=0 for the above IC. It is named after the astrophysicists Jonathan H. Lane and Robert Emden[2] as it was studied by them.

Taking α=2, f(x,y)=yⁿ, g(x)=0 and α=1 in Equations 1 and 2, respectively, we get

$$y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)+y^n=0,x\ge 0\text{,}$$

(3)

which may also be written as

$$\frac{1}{x^2}\frac{d}{dx}\left(x^2\frac{dy}{dx}\right)+y^n=0,$$

(4)

subject to IC

$$y\left(0\right)=1,y\text{'}\left(0\right)=0.$$

(5)

Classically, Equations 4 and 5 are known as the Lane-Emden equation. In astrophysics, this equation is Poisson's equation for the gravitational potential θ of a self-gravitating, spherically symmetric polytropic fluid. Physically, hydrostatic equilibrium connects the gradient of the potential, the density and the gradient of the pressure, whereas Poisson's equation connects the potential with the density.

Its solution provides the run of pressure P and density ρ with radius r_, where x and y are interpreted as$x=r{\left(\frac{4\pi G{\rho }_0^2}{\left(n+1\right)P_0}\right)}^{1/2}$ and$y={\left(\frac{\rho }{{\rho }_0}\right)}^{1/n}=\frac{\theta }{{\theta }_0}\text{,}$ respectively.

The subscript ‘0’ refers to the values at the centre of the sphere. It is assumed that θ₌0 when ρ=0 (at the surface of the sphere). If m(r) is the mass of the sphere at radius r, then$\frac{d\theta }{dr}=\frac{Gm\left(r\right)}{r^2}=g\text{,}$ where g is the acceleration due to gravity and G is the universal gravitational constant. The number n is the polytropic index in which the pressure and density of the gas are related by the well-known polytropic equation$P=K{\rho }^{1+1/n}\text{,}$ where K is a constant. The gravitational potential of the degenerate white-dwarf stars can be modelled by the so-called white-dwarf equation[3] obtained from Equations 1 and 2 by choosing α=2,$f\left(x,y\right)={\left(y^2-C\right)}^{3/2}$ and α=1. Similarly, isothermal gas spheres[1] are modelled by

$$\begin{array}{cc}y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)+e^{y\left(x\right)}\hfill & =0,x\ge 0,withICy\left(0\right)\hfill \\ =0,y\text{'}\left(0\right)=0.\hfill \end{array}$$

(6)

The solutions of the Lane-Emden equation for a given index n are known as polytropes of index n. In Equation 3, the parameter n has physical significance in the range 0≤n≤5, and Equation 3 with IC (Equation 5) has analytical solutions for n=0, 1, 5[3], and for other values of n, numerical solutions are sought.

However, the singularity at x=0 poses a challenge to the numerical solution of not only the Lane-Emden equation but also to a variety of non-linear problems in quantum mechanics and astrophysics such as the scattering length calculations in the variable phase approach. The series solution can be found by perturbation techniques and the Adomian decomposition method (ADM). However, these solutions are often convergent in restricted regions. Thus, some techniques such as Pade's method is required to enlarge the convergent regions[1, 4, 5].

Recently, a number of algorithms have been proposed to solve Equation 1 with$\alpha =2\text{,}$$f\left(x,y\right)=f\left(y\right)\text{,}$ a function of y alone and$g\left(x\right)=0$. They are the quasilinearization method[6–8], reducing the second-order Lane-Emden equation to a first order by Lie group analysis and then determining the power series solution of the resulting reduced equation[9], the homotopy analysis method (HAM)[10] and a variational approach using a semi-inverse method to obtain variational principle[11] and may employ the Ritz technique to obtain approximate solutions[12]. Later, Ramos[13] obtained series solutions of the Lane-Emden equation (Equation 3) based on either Volterra integral equation formulation or the expansion of the dependent variable in the original ordinary differential equation and compared them with series solutions obtained by means of integral or differential equations based on a transformation of the dependent variables.

In the same year, Youseffi[14], using the integral operator,$L_{\alpha }\left(·\right)={\displaystyle \underset{0}{\overset{x}{\int }}{x}^{-\alpha }}{\displaystyle \underset{0}{\overset{x}{\int }}{t}^{\alpha }}\left(·\right)dtdx\text{,}$ converted the Lane-Emden equation (Equation 1) to an integral equation and then, using Legendre wavelets, obtained an approximate solution for$0\le x\le 1$.

Dehghan and Shakeri[15] applied the transformation$x=e^t$ to Equation 1 (with$\alpha =2\text{,}$$f\left(x,y\right)=f\left(y\right)$ and$g\left(x\right)=0$) to get

$$\ddot{y}\left(t\right)+\dot{y}\left(t\right)+e^{2t}f\left(y\left(t\right)\right)=0,$$

(7)

subject to the conditions

$$\underset{t\to -\infty }{\text{lim}}y\left(t\right)=a,\underset{t\to -\infty }{\text{lim}}{e}^{-t}y\left(t\right)=0\text{,}$$

(8)

where the symbol  · denotes the differentiations with respect to t. Equation 7 is free of singularity at the origin. Then, they applied variational iteration method (VIM) to Equation 7 to obtain an approximate solution in [0,1], for special cases when$f\left(y\right)=y^n,n=0,1,5$.

Singh et al.[16] proposed an efficient analytic algorithm for Lane-Emden equations using modified homotopy analysis method (MHAM), which is different from other analytic techniques as it itself provided a convenient way to adjust convergence regions even without the Pade technique.

Recently, Parand et al.[17] proposed an approximation algorithm for the solution of Lane-Emden-type equations using Hermite collocation method. This method reduces the solution of a problem to the solution of a system of algebraic equations.

The aim of the present paper is to propose a new analytic algorithm based on the hybrid of variational iteration method, an auxiliary parameter γ and the Adomian polynomials to solve Lane-Emden-type equations. Some illustrative examples are given to demonstrate the efficiency of the proposed algorithm. The analytic approximate solutions obtained by the proposed method contain Shawagfeh's[4], Wazwaz's[5] and Ramos's[13] solutions given by ADM and series expansion, respectively. Moreover, they are convergent in considerably larger regions even without the Pade technique.

Results and discussion

In this section, we apply our proposed algorithm to solve Lane-Emden-type equations arising in astrophysics and discuss our results. In the following examples,$y_n\left(x\right)$ will denote the approximate solution of the problem under consideration, obtained by truncating series (52) at level n. Also, the absolute error is defined as$E_n\left(\gamma \right)=\left|y_{\text{exact}}\left(x\right)-y_n\left(x\right)\right|$ and${E_n}^{*}\left(\gamma \right)=10E_n\left(\gamma \right)$.

Example 1. The thermal behaviour of a spherical cloud of a gas under the mutual attraction of its molecules and subject to classical laws of thermodynamics is modelled by the Lane-Emden equation[1, 4]:

$$\begin{array}{cc}y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)+y^{\mu }\left(x\right)\hfill & =0,withICy\left(0\right)\hfill \\ =a,y\text{'}\left(0\right)\hfill \\ =0;x\ge 0,\mu \ge 0\hfill \end{array}$$

(9)

By choosing$y_0\left(x\right)=u_0\left(x\right)=a\text{,}$$g\left(x\right)=0$ and$\varphi \left(y\right)=y^{\mu }$ in Equation 59, we get

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\left(\frac{s^2}{x}-s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ +\frac{2}{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\hfill \\ +\left.{\displaystyle \sum _{i=0}^n{A}_i\left(u_0,u_1,\cdots ,u_i\right)}\right]\hfill \end{array}$$

(10)

where$A_n$s are calculated by the formula

$$A_n\left(u_0,u_1,\cdots ,u_n\right)=\frac{1}{n!}{\left[\frac{d^n}{d{\eta }^n}{\left({\displaystyle \sum _{k=0}^n{\eta }^k{u}_k}\right)}^{\mu }\right]}_{\eta =0},n\ge 0\text{.}$$

(11)

The first few polynomials are given as follows:

$$\begin{array}{cc}{A}_0\hfill & =u_0^{\mu },A_1=\mu u_0^{\mu -1}{u}_1,\hfill \\ A_2\hfill & =\frac{1}{2}\mu u_0^{\mu -2}((\mu -1)u_1^2+2u_0{u}_2),\hfill \\ A_3\hfill & =\frac{1}{6}\mu u_0^{\mu -3}((2-3\mu +{\mu }^2)u_1^3+6(\mu -1)u_0{u}_1{u}_2\hfill \\ +6u_0^2{u}_3),\cdots \text{.}\hfill \end{array}$$

Solving Equation 10 and using Equation 11, the various iterations are

$$u_1\left(x\right)=-\frac{1}{6}{a}^{\mu }{x}^2\gamma \text{,}$$

$$u_2\left(x\right)=\frac{1}{120}{a}^{\mu -1}{x}^2\gamma \left(20a\left(\gamma -1\right)+\mu a^{\mu }{x}^2\gamma \right)\text{,}$$

$$\begin{array}{cc}{u}_3\left(x\right)\hfill & =-\frac{1}{15,120}{a}^{\mu -2}{x}^2\gamma \left(2,520a^2{\left(\gamma -1\right)}^2\right)\hfill \\ +252\mu a^{\mu +1}{x}^2\left(\gamma -1\right)\gamma \hfill \\ +\mu a^{2\mu }\left(8\mu -5\right)x^4{\gamma }^2,\cdots \text{.}\hfill \end{array}$$

Hence, the solution$y\left(x\right)$ is given by

$$\begin{array}{cc}y(x)\hfill & =a-\frac{1}{6}{a}^{\mu }{x}^2\gamma +\frac{1}{120}{a}^{\mu -1}{x}^2\gamma \left(20a\left(\gamma -1\right)+\mu a^{\mu }{x}^2\gamma \right)\hfill \\ -\frac{1}{15,120}{a}^{\mu -2}{x}^2\gamma (2,520a^2{\left(\gamma -1\right)}^2+252\mu a^{\mu +1}\hfill \\ \times x^2\left(\gamma -1\right)\gamma +\mu a^{2\mu }\left(8\mu -5\right)x^4{\gamma }^2)+\cdots .\hfill \end{array}$$

(12)

Taking$a=1$ and$\gamma =1$, the solution (12) reduces to the solution obtained by Wazwaz[5] using ADM. Thus, we can say that our solution (12) of the problem (9) contains the solution of the problem (9) obtained by using ADM.

Case (i)

For$\mu =0$ and$a=1$, the solution series (12) reduces to

$$y\left(x\right)=1-\frac{\gamma x^2}{6}+{\displaystyle \sum _{m=1}^{\infty }\left(\gamma -1\right)u_m\left(x\right)}\text{,}$$

(13)

which converges to the exact solution$1-\frac{x^2}{6}$ for$\gamma =1$.

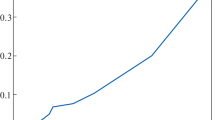
The solution series (13) is truncated at$m=20$ and the dependence of the associated error$E_n\left(\gamma \right)$ on γ is shown in Figure1. Our solution compares very well with that of MHAM solution[16] at the same level of truncation, obvious from Figures three and four of[16]. The region of convergence of the solution series (13) truncated at$m=20$ depends on the convergence-control parameter γ, so we plot the γ-curve for$y_{20}\left(1\right)$ in Figure2. As discussed in[18–20], the interval of convergence is determined by the flat portion of the γ-curve. It is clear from Figure2 that the admissible values of γ are contained in$\left[0.3,1.7\right]\text{.}$

Figure 1

Errors E ₂₀ (0.88) and E ₂₀ (0.83).

Figure 2

γ -curve for the 20th-order approximation.

Case (ii)

For$\mu =1$ and$a=1\text{,}$ the solution is given by

$$\begin{array}{cc}y(x)\hfill & =1-\frac{1}{6}{x}^2\gamma +\frac{1}{120}{x}^2\gamma \left(20\left(1-\gamma \right)+x^2\gamma \right)\hfill \\ -\frac{1}{15,120}{x}^2\gamma (2,520{\left(\gamma -1\right)}^2\hfill \\ +252x^2(\gamma -1)\gamma +3x^4{\gamma }^2)+\cdots \hfill \end{array}$$

$$\to {\displaystyle \sum _{m=0}^{\infty }\frac{{\left(-1\right)}^m}{\left(2m+1\right)!}{x}^{2m}}=\frac{\mathit{\text{sin}}x}{x},\text{as}\gamma \to 1\text{,}$$

(14)

which is the exact solution. Dehghan and Shakeri[15] obtained an approximate solution (not exact) valid only for$0\le x<1\text{,}$ using VIM. Truncating the solution series (14) at level$m=18\text{,}$ the dependence of regions of convergence$R\left(\gamma \right)$ is shown in Figure3 and error$E_n\left(\gamma \right)$ on γ is shown in Figures4 and5. The 18th-order solution from our method converges to the exact solution in the interval$\subseteq \left[0,19\right]$ as shown in Figure5, whereas the 19th-order solution from MHAM converges to the exact solution in the interval$\subseteq \left[0,10\right]$ (cf. Figure five in[16]). From Figure5, we see that our solution is more accurate than that of MHAM (cf. Figure six in[16]).

Figure 3

Exact and approximate solutions y ( x ) and y ₁₈ ( x ).

Figure 4

Error E ₁₈ (1).

Figure 5

Error E ₁₈ (0.892).

Case (iii)

In this case, we analyze the effect of IC (Equation 9) on the convergence region$R\left(\gamma \right)$ of the solution of Equation 9 when$\mu =2\text{,}$ through Figures6,7 and8. Figures6,7 and8 depict the approximate solution$y_{12}\left(x\right)$ at$a=1,a=5$ and$a=10$, respectively. From the figures, it is observed that when the value of a increases monotonically, the region of convergence decreases monotonically.

Figure 6

Approximate solution y ₁₂ ( x ) when a = 1, μ = 2.

Figure 7

Approximate solution y ₁₂ ( x ) when a = 5, μ = 2.

Figure 8

Approximate solution y ₁₂ ( x ) when a = 10, μ = 2.

Case (iv)

In this case, we study the effect of γ on the convergence region$R\left(\gamma \right)$ of the solution of Equation 9 for$\mu =2.5$ and$\mu =3.5$ through Figures9 and10, respectively, for$a=1$. Liao[10] has also solved the above two problems. For$\mu =2.5$, the 10th-order approximate solution from our method converges in the interval$\subseteq \left[0,7.5\right]$ and the same order approximate solution from HAM converges in the interval$\subseteq \left[0,5.4\right]$ (cf. Figure one in[10]). For$\mu =3.5$, the 20th-order approximate solution from our method converges in the interval$\subseteq \left[0,10\right]$, whereas the 24th-order approximate solution from HAM converges in the interval$\subseteq \left[0,9.8\right]$ (cf. Figure two in[10]).

Figure 9

Approximate solution y ₁₀ ( x ),  μ  = 2.5.

Figure 10

Approximate solution y ₂₀ ( x ), μ = 3.5.

Case (v)

In this case, we compare the solution of Equation 9 to the solution obtained by Parand et al.[17] for$\mu =3$ and$\mu =4$ through Tables1 and2, respectively. Tables1 and2 show that the solution obtained by our proposed algorithm is more accurate as compared to that obtained by Parand et al.[17].

Table 1 Comparison between the solutions obtained by the proposed method and Parand et al. for μ=3

Table 2 Comparison between the solutions obtained by the proposed method and Parand et al. for μ=4

Case (vi)

For$\mu =5\text{,}$ and$a=1$, the solution series (12) reduces to

$$\begin{array}{cc}y\left(x\right)\hfill & =1-\frac{1}{6}{x}^2\gamma +\gamma \left(-\frac{x^2}{6}+\frac{\gamma x^2}{6}+\frac{\gamma x^4}{24}\right)\hfill \\ +\gamma \left(-\frac{x^2}{6}+\frac{\gamma x^2}{3}+\frac{\gamma x^4}{12}-\frac{{\gamma }^2{x}^2}{6}-\frac{{\gamma }^2{x}^4}{12}-\frac{5{\gamma }^2{x}^6}{432}\right)\hfill \\ +\cdots \hfill \end{array}$$

$$\begin{array}{c}\to 1-\frac{x^2}{6}+\frac{x^4}{24}-\frac{5x^6}{432}+\frac{35x^8}{10,368}+\cdots \hfill \\ ={\left(1+\frac{x^2}{3}\right)}^{-1/2},\text{as}\gamma \to 1\text{,}\hfill \end{array}$$

(15)

which is the exact solution, whereas Dehghan and Shakeri[15] obtained an approximate solution using VIM valid for a restricted region$0\le x\le 1$. Figure11 shows the admissible values of γ for$\mu =3\text{,}$$y\left(0\right)=a,y\text{'}\left(0\right)=0\text{,}$ and 5.

Figure 11

γ -curves for the eighth-order approximation for μ=3(red), 4(blue) and 5(green).

Example 2. (Isothermal gas sphere equation). The isothermal gas spheres are modelled by Davis[1, 9]:

$$\begin{array}{cc}y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)+e^{y\left(x\right)}\hfill & =0,withICy\left(0\right)\hfill \\ =0,y\text{'}\left(0\right)=0\text{,}\hfill \end{array}$$

(16)

By choosing$y_0\left(x\right)=u_0\left(x\right)=0\text{,}$$g\left(x\right)=0$ and applying the proposed hybrid algorithm, we get

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\left(\frac{s^2}{x}-s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ +\frac{2}{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\hfill \\ \left.+{\displaystyle \sum _{i=0}^n{A}_i\left(u_0,u_1,\cdots ,u_i\right)}\right]ds\text{.}\hfill \end{array}$$

(17)

The$A_n$s are calculated by the formula

$$A_n\left(u_0,u_1,\cdots ,u_n\right)=\frac{1}{n!}{\left[\frac{d^n}{d{\eta }^n}\left\{Exp\left({\displaystyle \sum _{k=0}^n{\eta }^k{u}_k}\right)\right\}\right]}_{\eta =0},n\ge 0\text{.}$$

(18)

Solving Equation 17 and using Equation 18, the various iterations are

$$\begin{array}{cc}{u}_1\left(x\right)\hfill & =-\frac{1}{6}{x}^2\gamma \text{,}\hfill \end{array}$$

$$\begin{array}{cc}{u}_2\left(x\right)\hfill & =\gamma \left(-\frac{1}{6}{x}^2+\frac{1}{6}{x}^2\gamma +\frac{1}{120}{x}^4\gamma \right)\text{,}\hfill \end{array}$$

$$\begin{array}{cc}{u}_3\left(x\right)\hfill & =\gamma \left(-\frac{1}{6}{x}^2+\frac{1}{3}{x}^2\gamma +\frac{1}{60}{x}^4\gamma -\frac{1}{6}{x}^2{\gamma }^2-\frac{1}{60}{x}^4{\gamma }^2\right.\hfill \\ \left.-\frac{1}{1,890}{x}^6{\gamma }^2\right),\cdots \text{.}\hfill \end{array}$$

Hence, the solution$y\left(x\right)$ is given by

$$\begin{array}{ll}y(x)& =-\frac{1}{6}{x}^2\gamma +\gamma \left(-\frac{1}{6}{x}^2+\frac{1}{6}{x}^2\gamma +\frac{1}{120}{x}^4\gamma \right)\hfill \\ +\gamma (-\frac{1}{6}{x}^2+\frac{1}{3}{x}^2\gamma +\frac{1}{60}{x}^4\gamma -\frac{1}{6}{x}^2{\gamma }^2\hfill \\ -\frac{1}{60}{x}^4{\gamma }^2-\frac{1}{1,890}{x}^6{\gamma }^2)+\cdots \text{.}\hfill \end{array}$$

(19)

$$\begin{array}{c}\to -\frac{1}{6}{x}^2+\frac{1}{120}{x}^4-\frac{1}{1,890}{x}^6+\frac{61}{1,632,960}{x}^8\hfill \\ +\cdots ,\text{as}\gamma \to 1\text{,}\hfill \end{array}$$

(20)

which is the same as the solution obtained by Wazwaz[5], Liao[10], Ramos[13] and Singh et al.[16] by using ADM, HAM, series expansion and MHAM, respectively. However, Equation 20 is valid in the restricted region$0\le x<3.5$. By choosing suitable values of$\gamma \text{,}$ the region of convergence of Equation 20 may be enlarged as shown in Figure12. Liao[10] has also solved this problem. The 20th-order solutions from our method and HAM (cf. Figure seven in[10]) both converges in the interval$\subseteq \left[0,14\right]$. Thus, the solution obtained by our method is comparable with that obtained by HAM[10].

Figure 12

Approximate solution y ₂₀ ( x ).

Example 3. (The white-dwarf equation)[3].

$$\begin{array}{c}y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)+{\left(y^2-C\right)}^{3/2}=0,withICy\left(0\right)\hfill \\ =1,y\text{'}\left(0\right)=0\text{,}\hfill \end{array}$$

(21)

models the gravitational potential of the degenerate white-dwarf stars.

By choosing$y_0\left(x\right)=u_0\left(x\right)=1\text{,}$$g\left(x\right)=0$ and applying the proposed algorithm, we get

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\left(\frac{s^2}{x}-s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ \left.+\frac{2}{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)+{\displaystyle \sum _{i=0}^n{A}_i\left(u_0,u_1,\cdots ,u_i\right)}\right]ds\text{.}\hfill \end{array}$$

(22)

The$A_n$ s are calculated by the formula

$$A_n\left(u_0,u_1,\cdots ,u_n\right)=\frac{1}{n!}{\left[\frac{d^n}{d{\eta }^n}\left\{{\left({\displaystyle \sum _{k=0}^n{\eta }^k{u}_k}\right)}^2-C\right\}\right]}_{\eta =0},n\ge 0\text{.}$$

(23)

The first few polynomials are given as follows:

$$\begin{array}{cc}{A}_0\hfill & ={\left(u_0^2-C\right)}^{3/2},A_1=\frac{3}{2}{u}_1{\left(u_0^2-C\right)}^{1/2},\hfill \\ A_2\hfill & =\frac{3}{2}{u}_2{\left(u_0^2-C\right)}^{1/2}+\frac{3}{8}{u}_1^2{\left(u_0^2-C\right)}^{-1/2},\hfill \\ A_3\hfill & =\frac{3}{2}{u}_3{\left(u_0^2-C\right)}^{1/2}+\frac{3}{4}{u}_1{u}_2{\left(u_0^2-C\right)}^{-1/2}\hfill \\ -\frac{1}{16}{u}_1^3{\left(u_0^2-C\right)}^{-3/2},\cdots \text{.}\hfill \end{array}$$

Solving Equation 22 and using Equation 23, the various iterations are

$$u_1\left(x\right)=-\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2\gamma \text{,}$$

$$u_2\left(x\right)=-\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2\gamma \left(1-\gamma \right)+\frac{1}{40}{\left(1-C\right)}^2{x}^4{\gamma }^2\text{,}$$

$$\begin{array}{c}{u}_3(x)=-\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2\gamma +\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2{\gamma }^2(2-\gamma )+\frac{1}{20}{\left(1-C\right)}^2{x}^4{\gamma }^2(1-\gamma )\hfill \\ -\frac{1}{5,040}{\left(1-C\right)}^{5/2}{x}^6{\gamma }^3\left(5\left(1-C\right)+14\right),\cdots \text{.}\end{array}$$

Hence, the solution$y\left(x\right)$ is given by

$$\begin{array}{ll}y(x)\hfill & =1-\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2\gamma -\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2\gamma (1-\gamma )\hfill \\ +\frac{1}{40}{\left(1-C\right)}^2{x}^4{\gamma }^2-\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2\gamma \hfill \\ +\frac{1}{6}{\left(1-C\right)}^{3/2}{x}^2{\gamma }^2(2-\gamma )+\frac{1}{20}{\left(1-C\right)}^2{x}^4{\gamma }^2(1-\gamma )\hfill \\ -\frac{1}{5,040}{\left(1-C\right)}^{5/2}{x}^6{\gamma }^3\left(5\left(1-C\right)+14\right)+\cdots .\hfill \end{array}$$

(24)

As$\gamma \to 1\text{,}$ we have

$$y\left(x\right)=1-\frac{1}{6}{q}^3{x}^2+\frac{1}{40}{q}^4{x}^4-\frac{1}{5,040}{q}^5{x}^6\left(5q^2+14\right)+\cdots \text{,}$$

(25)

where$q=\sqrt{1-C}$ in Equation 25.

Equation 25 is the same as obtained by[5, 10, 13]. Figure13 shows the approximate solution$y_{10}\left(x\right)$ for$C=0.4$, whereas Figure14 shows the approximate solution$y_{18}\left(x\right)$ for$C=0$. Note that for a small value of C, Equation 25 is not valid in the whole region with$y\left(x\right)\ge \sqrt{C}$ as shown in Figures13 and14. Liao[10] has also solved this problem for C = 0.4 and C = 0. For C = 0.4, the 10th-order approximate solution from our method converges in the interval ⊆ [0, 4.5], whereas the same order approximate solution from HAM (cf. Figure four in[10]) converges in the interval ⊆ [0, 4]. Similarly, for C = 0, the 18th-order solution from our method and that from HAM (cf. Figure five in[10]) both converge in the interval ⊆ [0, 10]. Thus, the solution obtained by our method for C = 0 is comparable with that obtained by HAM[10].

Figure 13

Approximate solution y ₁₀ ( x ), C = 0.4.

Figure 14

Approximate solution y ₁₈ ( x ), C = 0.

Example 4. Consider the following Lane-Emden-type equation:

$$\begin{array}{c}y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)-6y\left(x\right)-4y\left(x\right)\mathit{\text{ln}}\left(y\left(x\right)\right)\hfill \\ =0,withICy\left(0\right)=1,y\text{'}\left(0\right)=0,x\ge 0\hfill \end{array}$$

(26)

having$y\left(x\right)=e^{x^2}$ as the exact solution.

Choosing the initial approximation y₀(x) = u₀(x) = 1, g(x) = 0 and applying the proposed hybrid algorithm, the correction functional for Equation 26 is

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\left(\frac{s^2}{x}-s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ +\frac{2}{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)-6{\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\hfill \\ \left.-4{\displaystyle \sum _{i=0}^n{A}_i\left(u_0,u_1,\cdots ,u_i\right)}\right]ds\text{.}\hfill \end{array}$$

(27)

The A _n s are calculated by the formula

$$\begin{array}{cc}{A}_n\left(u_0,u_1,\cdots ,u_n\right)\hfill & =\frac{1}{n!}\left[\frac{d^n}{d{\lambda }^n}\left\{\left({\displaystyle \sum _{k=0}^n{\eta }^k{u}_k}\right)\right.\right.\hfill \\ {\left.\left.\mathit{\text{ln}}\left({\displaystyle \sum _{k=0}^n{\eta }^k{u}_k}\right)\right\}\right]}_{\eta =0},n\ge 0\text{.}\hfill \end{array}$$

(28)

Solving Equation 27 and using Equation 28, the various iterations are

$$u_1\left(x\right)=x^2\gamma \text{,}$$

$$u_2\left(x\right)=\left(1-\gamma \right)u_1\left(x\right)+\frac{1}{2}{x}^4{\gamma }^2\text{,}$$

$$u_3\left(x\right)={\left(1-\gamma \right)}^2{u}_1\left(x\right)+2\left(1-\gamma \right)u_2\left(x\right)+\frac{1}{6}{x}^6{\gamma }^3,\cdots \text{.}$$

Hence, the solution y(x) is given by

$$\begin{array}{cc}y\left(x\right)\hfill & =1+x^2\gamma +x^2\gamma \left(1-\gamma \right)+\frac{1}{2}{x}^4{\gamma }^2\hfill \\ +x^2\gamma {\left(1-\gamma \right)}^2+x^4{\gamma }^2\left(1-\gamma \right)+\frac{1}{6}{x}^6{\gamma }^3\hfill \\ +\cdots .\hfill \end{array}$$

(29)

As γ  → 1, we have

$$y\left(x\right)=1+x^2+\frac{1}{2}{x}^4+\frac{1}{6}{x}^6+\cdots =e^{x^2}\text{.}$$

(30)

which is the exact solution.

Table3 shows that the solution obtained by the proposed hybrid approach is more accurate in comparison to that obtained by Parand et al.[17].

Table 3 Comparison between the solutions obtained by proposed method and Parand et al. for Example 4

Example 5. Consider the following problem[14, 16, 21]:

$$\begin{array}{c}y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)-2\left(2x^2+3\right)y\left(x\right)\hfill \\ =0,withICy\left(0\right)=1,y\text{'}\left(0\right)=0,0\le x\angle 1\hfill \end{array}$$

(31)

having$y\left(x\right)=e^{x^2}$ as the exact solution.Choosing the initial approximation y₀(x)=μ₀(x)=1, g(x)=0 and applying the proposed hybrid algorithm, the correction functional for Equation 31 is

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\left. (\frac{s^2}{x}-s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ \left.+\frac{2}{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)-2\left(2s^2+3\right){\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right]ds\text{.}\hfill \end{array}$$

(32)

Solving Equation 32, we obtain

$$\begin{array}{cc}{u}_1\left(x\right)\hfill & =\gamma \left(x^2+\frac{x^4}{5}\right)\text{,}\hfill \end{array}$$

$$\begin{array}{cc}{u}_2\left(x\right)\hfill & =\gamma \left(x^2+\frac{x^4}{5}-x^2\gamma +\frac{x^4\gamma }{10}+\frac{13x^6\gamma }{105}+\frac{x^8\gamma }{90}\right)\text{,}\hfill \end{array}$$

$$\begin{array}{cc}{u}_3(x)\hfill & =\gamma \left(x^2+\frac{x^4}{5}-2x^2\gamma +\frac{x^4\gamma }{5}+\frac{26x^6\gamma }{105}+\frac{x^8\gamma }{45}+x^2{\gamma }^2\right.\hfill \\ \left.-\frac{2x^4{\gamma }^2}{5}-\frac{43x^6{\gamma }^2}{210}+\frac{x^8{\gamma }^2}{210}+\frac{59x^{10}{\gamma }^2}{11,550}\right)+⋮\text{.}\hfill \end{array}$$

Hence,

$${\left(\lambda \text{'}\text{'}\left(s\right)-\alpha \frac{s\lambda \text{'}\left(s\right)-\lambda \left(s\right)}{s^2}\right)|}_{s=x}=0$$

$$\begin{array}{c}+\frac{x^8\gamma }{45}+x^2{\gamma }^2-\frac{2x^4{\gamma }^2}{5}-\frac{43x^6{\gamma }^2}{210}+\frac{x^8{\gamma }^2}{210}\hfill \\ +\frac{59x^{10}{\gamma }^2}{11,550}+\frac{x^{12}{\gamma }^2}{3,510})+\cdots \hfill \end{array}$$

$$\to 1+x^2+\frac{x^4}{2!}+\cdots =e^{x^2}$$

(33)

γ = 1which is the exact solution of Equation 31. Thus, our algorithm gives the exact solution of the problem. Yousefi[14] obtained an approximate solution of the above problem using Legendre wavelets. The error E₇(1.0099) is of the order 10e − 11, whereas that of the Legendre wavelet method is 10e − 10, so our algorithm gives better approximation even at the truncation level m=7. The dependence of error E _n (γ) on γ is shown in Figure15. Table4 shows that the eighth-order approximate solution obtained by the proposed hybrid approach for the optimal value of γ = 1.01294 is more accurate in comparison to that obtained by Parand et al.[17]. The optimal value of γ = 1.01294 is obtained from minimizing the eighth-order square residual J₈(γ) using Equations 49 to 51.

Figure 15

Errors E ₇ (1) and E ₇ ^* (1.0099).

Table 4 Comparison between the solutions obtained by the proposed method and Parand et al. for Example 5

In the next two examples, we consider the non-homogeneous Lane-Emden equations.

Example 6. Consider the following non-homogeneous Lane-Emden equation[14, 16]:

$$y\text{'}\text{'}\left(x\right)+\frac{2}{x}y\text{'}\left(x\right)+y\left(x\right)=6+12x+x^2+x^3,0\le x<1$$

(34)

with IC y(0) = 0, y’(0) = 0, having y(x) = x² + x³ as the exact solution.

By choosing y₀(x) = u₀(x) = 0, g₀(x) = 6, g₁(x) = 12x + x², g₂(x) = x³ and g _i (x) = 0, 3 ⩽ i ⩽ m, and applying our proposed algorithm, we get

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\left(\frac{s^2}{x}-s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ \left.+\frac{2}{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)+{\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}-G_n\left(s\right)\right]ds\text{.}\hfill \end{array}$$

(35)

Solving Equation 35, the various iterations are

$$\begin{array}{cc}{u}_1\left(x\right)\hfill & =x^2\gamma \text{,}\hfill \end{array}$$

$$\begin{array}{cc}{u}_2\left(x\right)\hfill & =\gamma \left(-\left(\gamma -1\right)x^2+x^3+\left(\gamma -1\right)\frac{x^4}{20}\right)\text{,}\hfill \end{array}$$

$$\begin{array}{cc}{u}_3\left(x\right)\hfill & =\frac{1}{840}{x}^2\gamma \left(\gamma -1\right)\left(-840x-28x^3+840\left(\gamma -1\right)\right.\hfill \\ \left.+x^4\gamma +42x^2\left(2\gamma -1\right)\right),\cdots \text{.}\hfill \end{array}$$

Hence, the solution y(x) of Equation 34 is given by

$$\begin{array}{cc}y(x)\hfill & =x^2\gamma +\gamma \left(-\left(\gamma -1\right)x^2+x^3+\left(\gamma -1\right)\frac{x^4}{20}\right)\hfill \\ +\frac{1}{840}{x}^2\gamma (\gamma -1)(-840x-28x^3+840\left(\gamma -1\right)\hfill \\ +x^4\gamma +42x^2\left(2\gamma -1\right))+\cdots \text{.}\hfill \end{array}$$

(36)

Choosing the auxiliary parameter γ = 1, in Equation 36, we get the exact solution y(x) = x² + x³. Thus, we obtain the exact solution at level m = 2, when γ = 1.

Example 7. Consider the following non-homogeneous Lane-Emden equation[14, 16]:

$$\begin{array}{cc}y\text{'}\text{'}\left(x\right)+\frac{8}{x}y\text{'}\left(x\right)+xy\left(x\right)\hfill & =x^5-x^4+44x^2-30x,\hfill \\ 0\le x<1\hfill \end{array}$$

(37)

with IC y(0) = 0, y’(0) = 0, having y(x) = x⁴ − x³ as the exact solution.

By choosing y₀(x) = u₀(x) = 0, g₀(x) = 30x − 44x², g₁(x) = x⁴ − x⁵ and g _i (x) = 0, 2 ⩽ i ⩽ m, and applying the proposed hybrid algorithm, we get

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\left(\frac{s^2}{x}-s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right]\hfill \\ \left.+\frac{8}{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)+s{\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}-G_n\left(s\right)\right]ds\text{.}\hfill \end{array}$$

(38)

Solving Equation 38, the various iterations are

$$u_1\left(x\right)=\left(x^4-x^3\right)\gamma \text{,}$$

$$u_2\left(x\right)=\gamma \left(x^4-x^3-\frac{x^6}{78}+\frac{x^7}{98}+x^3\gamma -x^4\gamma +\frac{x^6\gamma }{78}-\frac{x^7\gamma }{98}\right)\text{,}$$

a = 10

Hence, the solution y(x) of Equation 37 is given by

$$\begin{array}{cc}y\left(x\right)\hfill & =\left(x^4-x^3\right)\gamma \hfill \\ +\gamma \left(x^4-x^3-\frac{x^6}{78}+\frac{x^7}{98}+x^3\gamma -x^4\gamma +\frac{x^6\gamma }{78}-\frac{x^7\gamma }{98}\right)\hfill \\ +\to \left(x^4-x^3\right),as\gamma \to 1\text{,}\hfill \end{array}$$

(39)

which is the exact solution of Equation 37. Thus, we obtain the exact solution at level m = 1, when γ  → 1.

Conclusions

A new hybrid algorithm is proposed to solve nonlinear differential equations. The algorithm is applied to solve Lane-Emden-type equations. The equation has a singularity at x = 0, thus poses a challenge to its numerical solution. VIM has been applied to solve nonlinear differential equations, but it has its own limitations since the series solution obtained by VIM has a relatively smaller region of convergence and noise terms appear in the successive approximations. To overcome these difficulties, we introduce an auxiliary parameter γ (as suggested by Geng[22]) and expand the nonlinear terms using the Adomian polynomials to propose our algorithm. This algorithm has advantages over the previous ones as (1) it increases the region of convergence (of the solution series) even without the Pade technique and (2) the computation of various iterates becomes much simpler since the nonlinear terms are replaced by their Adomian polynomial representations.

The accuracy and efficiency of the algorithm is established by means of several examples given in the ‘Results and discussion’ section. These examples show that we can enlarge the convergence region of the solution by the auxiliary parameter γ even without the Pade technique. From the illustrative examples, we conclude that the results obtained from the proposed algorithm are better than those obtained from ADM, HAM, series expansion, Legendre wavelet methods and Hermite collocation method. Figures2 and11 illustrate that the region of admissible values of γ shrinks as nonlinearity increases.

Methods

The VIM is well established[23]. The main drawbacks of the solution obtained by standard VIM is that it is convergent in a small region and noise terms appear in the successive approximations as shown in[15, 21]. To enlarge the convergence region and remove the noise terms appearing in the sequence of successive approximations, we modify the standard VIM by introducing an auxiliary parameter γ, expanding the nonlinear term Ny _n in terms of the Adomian polynomials and decomposing g(x) as finite sum. This idea was motivated by the work of Liao[10, 18–20] and Singh et al.[16].

Consider the following differential equation:

$$Ly+Ny=g\left(x\right),x\in \Omega \text{,}$$

(40)

where L and N are linear and nonlinear differential operators, respectively, and g(x) is the source term.

Decomposing the source term g(x) as$g\left(x\right)={\displaystyle \sum _{i=0}^m{g}_i\left(x\right)}\text{,}$ we construct a sequence {G _n (x)}, where

$$G_n\left(x\right)={\displaystyle \sum _{i=0}^m{\chi }_{n-i+2}{g}_i\left(x\right)}\text{,}$$

(41)

and

$${\chi }_n=\{\begin{array}{l}0n\le 1\\ 1n>1.\end{array}$$

(42)

The sequence G _n (x)  → g(x) as n  → ∞.

Geng[22] introduced an auxiliary parameter γ ≠ 0 by adding and subtracting Ly in Equation (40) as follows:

$$Ly-Ly+\gamma \left[Ly+Ny-g\left(x\right)\right]=0\text{.}$$

(43)

The addition and subtraction of Ly is done to facilitate the computation of λ(s).

We construct the correction functional for Equation (43) as follows:

$$\begin{array}{cc}{y}_{n+1}\left(x\right)\hfill & =y_n\left(x\right)+{\displaystyle \underset{0}{\overset{x}{\int }}\lambda \left(s\right)}\left\{L{y}_n-L{\tilde{y}}_n+\gamma \left[L{\tilde{y}}_n\left(s\right)\right.\right.\hfill \\ \left.\left.+N{\tilde{y}}_n\left(s\right)-{\tilde{G}}_n\left(s\right)\right]\right\}ds\text{,}\hfill \end{array}$$

(44)

where λ(s) is a general Lagrange multiplier which is identified optimally via variational theory[18], the subscript n denotes the n th approximation, and ỹ _n is considered as a restricted variation, i.e. δỹ _n  = 0.

Once the λ(s) is computed, we discard the added and subtracted terms from Equation 44 to get

$$\begin{array}{cc}{y}_{n+1}\left(x\right)\hfill & =y_n\left(x\right)+\gamma {\displaystyle \underset{0}{\overset{x}{\int }}\lambda \left(s\right)}\left\{\left[L{y}_n\left(s\right)+N{y}_n\left(s\right)\right]\right\}\hfill \\ \left.\left.-G_n\left(s\right)\right]\right\}ds,n=0,1,2,\cdots \text{.}\hfill \end{array}$$

(45)

In our proposed algorithm, this will be called as the first step.

Following Abbasbandy[24], we decompose y _n (x) as

$$y_n\left(x\right)={\displaystyle \sum _{i=0}^n{u}_i\left(x\right)}\text{,}$$

(46)

and expand nonlinear terms Ny _n (x) in terms of Adomian's polynomials as

$$N{y}_n\left(x\right)=N\left({\displaystyle \sum _{i=0}^n{u}_i\left(x\right)}\right)={\displaystyle \sum _{i=0}^n{A}_i\left(u_0,u_1,\cdots ,u_i\right)}\text{,}$$

(47)

where A _i s are Adomian's polynomials which are calculated by the algorithm (Equation 48) constructed by Adomian[25, 26]:

$$A_n\left(u_0,u_1,\cdots ,u_n\right)=\frac{1}{n!}{\left[\frac{d^n}{d{\eta }^n}N\left({\displaystyle \sum _{k=0}^n{\eta }^k{u}_k}\right)\right]}_{\eta =0},n\ge 0\text{.}$$

(48)

Expressing the nonlinear term Ny _n (x) by Equation 47 will be referred as the second step.

Substituting Equations 46 and 47 in Equation 45 and solving, we get the various iterates u _i (x)

These iterates u _i (x) are now substituted in Equation 46 to obtain the n th-order approximate solution y _n (x). Substituting the n th-order approximate solution y _n (x) in Equation 40, we obtain the following residual:

$$R_n\left(x,\gamma \right)=L\left(y_n\left(x\right)\right)+N\left(y_n\left(x\right)\right)-g\left(x\right)\text{.}$$

(49)

In order to find the optimal value of γ, we first construct the functional (called the square residual error),

$$J_n\left(\gamma \right)={\displaystyle \underset{\Omega }{\int }{R_n}^2\left(x,\gamma \right)}dx$$

(50)

and then minimizing it, we get

$$\frac{\partial J_n}{\partial \gamma }=0.$$

(51)

Substituting the optimal values of γ obtained from Equation 51 into Equation 46, the n th-order approximate solution y _n is obtained. Now, taking the limit as n  → ∞, we obtain the following series representation of the solution:

$$y\left(x\right)=\underset{n\to \infty }{\text{lim}}{y}_n\left(x\right)=\underset{n\to \infty }{\text{lim}}{\displaystyle \sum _{i=0}^n{u}_i\left(x\right)}\text{.}$$

(52)

The novelty of our proposed algorithm is that (1) we decompose the source term as a finite sum and construct a sequence (Equation 42) converging to g(x), (2) using the sequence {G _n (x)}, a new correction functional (Equation 45) is constructed and (3) we combine the first and second steps to yield a new hybrid algorithm for nonlinear differential equations.

For the Lane-Emden-type equations (Equation 1), we construct the correction functional as follows:

$$\begin{array}{cc}{y}_{n+1}\left(x\right)\hfill & =y_n\left(x\right)+\underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left\{\left(\frac{d^2{y}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{y}_n}{ds}\right)\right.\hfill \\ -\left(\frac{d^2{\tilde{y}}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{\tilde{y}}_n}{ds}\right)+\gamma \left[\left(\frac{d^2{\tilde{y}}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{\tilde{y}}_n}{ds}\right)\right.\hfill \\ \left.\left.+f\left(s,{\tilde{y}}_n\right)-{\tilde{G}}_n\left(s\right)\right]\right\}ds\text{,}\hfill \end{array}$$

(53)

The optimal value of λ(s) is calculated from Equation 53 as shown in the following steps:

$$\begin{array}{cc}\delta y_{n+1}\left(x\right)\hfill & =\delta y_n\left(x\right)+\delta \left(\underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left\{\left(\frac{d^2{y}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{y}_n}{ds}\right)\right.\right.\hfill \\ -\left(\frac{d^2{\tilde{y}}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{\tilde{y}}_n}{ds}\right)+\gamma \left[\left(\frac{d^2{\tilde{y}}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{\tilde{y}}_n}{ds}\right)\right.\hfill \\ \left.\left.\left.+f\left(s,{\tilde{y}}_n\right)-{\tilde{G}}_n\left(s\right)\right]\right\}ds\right)\text{,}\hfill \end{array}$$

$$=\delta y_n\left(x\right)+\delta {\displaystyle \underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left[\frac{d^2{y}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{y}_n}{ds}\right]}ds$$

Integration by parts yields

$$\begin{array}{cc}\delta y_{n+1}\left(x\right)\hfill & ={\left(1-\lambda \text{'}\left(s\right)+\frac{\alpha }{s}\lambda \left(s\right)\right)|}_{s=x}\delta y_n\left(x\right)+{\lambda \left(s\right)|}_{s=x}\hfill \\ \cdot \delta {\left(\frac{d{y}_n}{ds}\right)|}_{s=x}+{\displaystyle \underset{0}{\overset{x}{\int }}\delta y_n\left[\lambda \text{'}\text{'}\left(s\right)-\alpha \frac{s\lambda \text{'}\left(s\right)-\lambda \left(s\right)}{s^2}\right]}\hfill \\ \times ds=0.\hfill \end{array}$$

Thus, the stationary conditions are obtained as

$$\begin{array}{c}{\left(1-\lambda \text{'}\left(s\right)+\frac{\alpha }{s}\lambda \left(s\right)\right)|}_{s=x}=0,\lambda \left(s\right){|}_{s=x}=0,\hfill \\ \times \left(\lambda "\left(s\right)-\alpha \frac{s\lambda \text{'}\left(s\right)-\lambda \left(s\right)}{s^2}\right){|}_{s=x}=0\hfill \end{array}$$

(54)

Solving Equation 54, the Lagrange multiplier is obtained and given by Equation 55:

$$\lambda \left(s\right)=\{\begin{array}{l}s\mathit{\text{ln}}\left(\frac{s}{x}\right)\alpha =1,\\ \frac{s}{\left(1-\alpha \right)}-\frac{s^{\alpha }}{\left(1-\alpha \right)x^{\alpha -1}}\alpha \ne 1.\end{array}$$

(55)

Hence, the iteration formula (53) reduces to

$$\begin{array}{cc}{y}_{n+1}\left(x\right)\hfill & =y_n\left(x\right)\hfill \\ +\gamma {\displaystyle \underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left[\frac{d^2{y}_n}{d{s}^2}+\frac{\alpha }{s}\frac{d{y}_n}{ds}+f\left(s,y_n\right)-G_n\left(s\right)\right]}ds\hfill \end{array}$$

(56)

where λ(s) is given by Equation 55.

Applying the second step of the proposed algorithm, Equation 56 becomes

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)+\frac{\alpha }{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ \left.+f\left(s,{\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)-G_n\left(s\right)\right]ds\hfill \end{array}$$

(57)

We restrict ourselves to three different choices of the function f(x, y) = h(x), ϕ(y) and h(x)ϕ(y). Their respective correction functionals, obtained from Equation 57, are given as

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)+\frac{\alpha }{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ \left.+h\left(s\right)-G_n\left(s\right)\right]ds\text{,}\hfill \end{array}$$

(58)

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)+\frac{\alpha }{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ \left.+{\displaystyle \sum _{i=0}^n{A}_i\left(u_0,u_1,\cdots ,u_i\right)}-G_n\left(s\right)\right]ds\text{,}\hfill \end{array}$$

(59)

and

$$\begin{array}{cc}{u}_{n+1}\left(x\right)\hfill & =\gamma \underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left[\frac{d^2}{d{s}^2}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)+\frac{\alpha }{s}\frac{d}{ds}\left({\displaystyle \sum _{i=0}^n{u}_i\left(s\right)}\right)\right.\hfill \\ \left.+h\left(s\right){\displaystyle \sum _{i=0}^n{A}_i\left(u_0,u_1,\cdots ,u_i\right)}-G_n\left(s\right)\right]ds\text{,}\hfill \end{array}$$

(60)

where

$$A_n\left(u_0,u_1,\cdots ,u_n\right)=\frac{1}{n!}{\left[\frac{d^n}{d{\eta }^n}\varphi \left({\displaystyle \sum _{i=0}^n{\eta }^i{u}_i}\right)\right]}_{\eta =0}\text{.}$$

(61)

Theorem: Taking u₀(x) = a and assuming that the series$y\left(x\right)={\displaystyle \sum _{i=0}^{\infty }{u}_i\left(x\right)}$ converges, where u_n+1(x) are given by either Equations 58, 59 or 60, then it must be the solution of the Lane-Emden equation (Equation 1).

Proof: As limit n  → ∞, Equations 58, 59 and 60 will reduce to

$$0=\gamma {\displaystyle \underset{0}{\overset{x}{\int }}\lambda \left(s\right)\left[\frac{d^{2}y}{d{s}^2}+\frac{\alpha }{s}\frac{dy}{ds}+f\left(s,y\right)-g\left(s\right)\right]}ds\text{,}$$

thus proving the theorem since y(0) = u₀(0) = a and u _n (0) = 0, n ≥ 1.

Authors’ information

VKB and RKP are senior research fellows in the Department of Applied Mathematics, Indian Institute of Technology (BHU), Varanasi, India. MPT is an assistant professor in the Department of Mathematics, U.P. College, Varanasi, India. OPS is a professor in the Department of Applied Mathematics, Indian Institute of Technology (BHU), Varanasi, India.