Multiple vacation policy for M^X/H_k/1 queue with un-reliable server

Abstract

This paper studies the operating characteristics of an M^X/H_k/1 queueing system under multiple vacation policy. It is assumed that the server goes for vacation as soon as the system becomes empty. When he returns from a vacation and there is one or more customers waiting in the queue, he serves these customers until the system becomes empty again, otherwise goes for another vacation. The breakdown and repair times of the server are assumed to follow a negative exponential distribution. By using a generating function, we derive various performance indices. The approximate formulas for the probability distribution of the waiting time of the customers in the system by using the maximum entropy principle (MEP) are obtained. This approach is accurate enough for practical purposes and is a useful method for solving complex queueing systems. The sensitivity analysis is carried out by taking a numerical illustration.

Background

Server vacation models are useful for queueing systems in which the server wants to utilize his idle time for different purposes. The vacation mechanism considered in this paper is termed as ‘multiple vacation policy’. That is, the server upon returning from a vacation leaves immediately for another one if the system is empty at that moment. Applications of the server with multiple vacation models can be found in manufacturing systems, designing of computer and communication systems, etc. Queueing systems with multiple server vacations have attracted the attention of numerous researchers. Baba (1986) studied batch-arrival M^X/G/1 queueing systems with multiple vacations. A discrete-time Geo/G/1 queue with multiple vacations was studied by Tian and Zhang (2002). An M^X/G(a,b)/1 queue with multiple vacations including closedown time has been studied by Arumuganathan and Jeykumar (2004). Kumar and Madheswari (2005) analyzed a Markovian queue with two heterogeneous servers and multiple vacations. By using the matrix geometric method, they derived the stationary queue length distribution and mean system size. Wu and Takagi (2006) investigated an M/G/1 queue with multiple vacations and exhaustive service discipline such that the server works with different rates rather than completely stopping the service during vacation. Ke (2007) studied an M^X/G/1 queueing system under a variant vacation policy where the server takes at most j vacations. He derived the system size distribution as well as waiting time distribution in the queue. Ke and Chang (2009) considered an M^X/(G₁,G₂)/1 retrial queue with general retrial times, where the server provides two phases of heterogeneous service to all customers under Bernoulli vacation schedules. They constructed the mathematical model and derived the steady-state distribution of the server state and the number of customers in the system/orbit. Ke et al. (2009) studied the vacation policy for a finite buffer M/M/c queueing system with an un-reliable server. Threshold N-policy for an M^X/H₂/1 queueing system with an un-reliable server and vacations was studied by Sharma (2010). Moreover, Singh et al. (2012) investigated an M/G/1 queueing model with vacation and used the generating function method for obtaining various performance measures. Very recently, an un-reliable bulk queue with state-dependent arrival rates was examined by Singh et al. (2013).

Queueing models with an un-reliable server under multiple vacation policy are more realistic representation of the systems. The service of the components may be interrupted when the operator encounters unpredicted breakdowns, and it is to be immediately recovered with a random time. When the repair is completed, the server immediately returns for service. Wang et al. (1999) extended Wang's model to the N-policy for an M/H₂/1 queueing system and focused on single-arrival Erlangian service time queueing model with an un-reliable server. Wang et al. (2004) considered an M/H_k/1 queueing system with a removable and un-reliable server under N-policy and presented the optimal operating policy. Wang (2004) considered an M/G/1 queue with an un-reliable server and second optional service. Using the supplementary variable method, he obtained transient and steady-state solutions for both queueing and reliability measures of interest. Ke (2005) studied a modified T vacation policy for an M/G/1 queueing system where an un-reliable server may take at most J vacations repeatedly until at least one customer appears in the queue upon returning from vacation, and the server needs a startup time before starting each of his service periods. Li et al. (2007) proposed a single-server vacation queue with two policies, working vacation and service interruption. Choudhury and Deka (2008) studied an M/G/1 retrial queue with an additional second phase of optional service subject to breakdowns occurring randomly at any instant while serving the customers. Further, Wang and Xu (2009) obtained the solution of an M/G/1 queue with second optional service and server breakdown using the method of functional analysis. The work on an M/G/1 queue with second optional service and server breakdown has been done by Choudhury and Tadj (2009). They derived the Laplace-Stieltjes transform of busy period distribution and waiting time distribution. Further, an un-reliable server queue with multi-optional services and multi-optional vacations was analyzed by Jain et al. (2013).

Approximate results of many complex queueing models have been developed by several authors by applying the technique of maximum entropy principle. Jain and Singh (2000) used the principle of maximum entropy to analyze the optimal flow control of a G/G/c finite capacity queue. Jain and Dhakad (2003) provided the steady-state queue size distribution of an M^X/G/1 queue using the maximum entropy approach in which the constraints are expressed in terms of mean arrival rates, mean service rates, and mean number of customers in the system. Further, Ke and Lin (2006) employed the principle of maximum entropy to derive the approximate formulas for the steady-state probability distributions of the queue length. Ke and Lin (2008) suggested the maximum entropy principle to examine the M^X/G/1 queueing system in different frameworks. Omey and Gulck (2008) did maximum entropy analysis of an M^X/M/1 queueing model with multiple vacations and server breakdowns. Wang and Huang (2009) analyzed a single removable and un-reliable server M/G/1 queue under the (p,N)-policy. They did the maximum entropy analysis to obtain the approximate formulas for the probability distributions of the number of customers and the expected waiting time in the system. Maximum entropy approach has been applied for an un-reliable server vacation queueing model by Jain et al. (2012).

The main objective of our study is to develop an M^X/H_k/1 queueing model with an un-reliable server under multiple vacation policy. In this paper, an M^X/H_k/1 queue has been analyzed including more features, namely (1) bulk arrival, (2) server breakdown, and (3) multiple vacation. The various approximate results for waiting time distribution have been analyzed using the maximum entropy principle which was not considered in the previous study. Now, we cite a real-life situation of a given model wherein all the features are encountered simultaneously. To highlight the application, we cite an example of production of heat transfer equipment. In the production of these equipment, the raw material of these equipment arrives in group (batch arrival). The production of these equipment has been done by the machine in phases (called k-type hyper-exponential distribution). During the production, the production of the equipment may be interrupted due to some machinery faults called server breakdown. After interruption in the service, the machine is immediately sent for repairing. After repairing, the machine renews and works as a new one. As the raw material of these equipment is finished, the operator may take multiple vacations till the raw material arrives again. More realistic assumptions incorporated in our model provide a new dimension in the area of queueing systems.

Our main objective of this paper is to develop an M^X/H_k/1 queueing model with an un-reliable server under multiple vacation policy. Further, we intend to determine the approximate results for the steady-state probability distributions of the queue length using the maximum entropy approach. The rest of the paper is organized as follows. In the ‘Model description’ section, we describe the model and construct the steady-state equations governing the model. Afterwards, in the ‘Probability generating function’ section, we obtain the queue size distribution by using the probability generating function technique. In the ‘Performance measures’ section, we derive various performance indices. The principle of maximum entropy is described in the ‘Maximum entropy principle’ section to establish the approximate results for the expected system size and expected waiting time. In the ‘Numerical illustration and sensitivity analysis’ section, numerical illustrations and sensitivity analysis are presented to validate the analytical results. Finally, conclusion has been drawn in the ‘Conclusion’ section.

Model description

Consider a single un-reliable, removable server queue with state-dependent rates. We assume that the states of the system are described by the triplet (i,j,n), where i = 0, 1,…, k; j = V, B, D; and n = 0, 1, 2,…. Here i = 0 denotes that the customer is not in service, and i = 1, 2,…, k denotes that the customer is in the i th phase service; j = V, B, D represents that the server is on vacation, busy, and under repair after failure, respectively; and n denotes the number of customers present in the system. The service time is assumed to follow the k-type hyper-exponential distribution. It is assumed that μ _i (i = 1, 2,…, k) is the service rate of i th phase service. Let the probability that the next customer to enter in the service is of type i be q _i (i = 1, 2,…, k) and ${\displaystyle \sum _{i=1}^k{q}_i=1.}$ Other assumptions made to construct the mathematical model are as follows:

• The customers arrive in batches according to the Poisson process with state-dependent arrival rate λ _j given by

  $${\lambda }_j=\left\{\begin{array}{l}{\lambda }_0,\mathrm{if}\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{on}\mathrm{vacation}\\ {\lambda }_1,\mathrm{if}\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{turned}\mathrm{on}\mathrm{and}\mathrm{is}\mathrm{in}\mathrm{operation}\\ {\lambda }_2,\mathrm{if}\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{turned}\mathrm{on}\mathrm{and}\mathrm{is}\mathrm{under}\mathrm{repair}\end{array}\right.$$

• Let A be the random variable denoting the batch size, and then the batch size distribution is given by

  $$c_j=\mathrm{Pr}\left[A=j\right],j=1,2,\dots ,d$$

• Furthermore, the generating function for the batch size distribution is $A\left(z\right)={\displaystyle \sum _{j=1}^{\infty }{c}_j{z}^j}$. It follows that E(A) = A′(1) and E[A(A − 1)] = A″(1).

• When the breakdown occurs, the server is unable to render service to the customers, but after completing repair provided by a repairman, it works as efficiently as before the failure. The life time and repair time of the server are negative exponentially distributed with mean 1/α and 1/β, respectively.

• The customers are served according to the first come, first served (FCFS) discipline.

Let us denote the steady-state probabilities depicting the system status as follows:

• P_0,V(n): Probability that there are n (n = 0, 1,…) customers in the system and the server is on vacation.

• P_i,B(n): Probability that there are n (n = 1, 2,…) customers in the system and the customer in service is in phase i (i = 1, 2,…, k), when the server is turned on and is in busy state.

• P_i,D(n): Probability that there are n (n = 1, 2,…) customers in the system and the customer in service is in phase i (i = 1, 2,…, k), when the server is turned on and is in a breakdown state.

The steady-state equations governing the model are given as follows:

$$\left({\lambda }_0+\nu \right)P_{0,V}\left(n\right)={\lambda }_0{\displaystyle \sum _{k=1}^n{P}_{0,V}\left(n-k\right)c_k;n\ge 1}$$

(1)

$${\lambda }_0{P}_{0,V}\left(0\right)={\displaystyle \sum _{j=1}^k{\mu }_j{P}_{0,V}\left(1\right)}$$

(2)

$$\left({\lambda }_1+\alpha +{\mu }_i\right)P_{i,B}\left(1\right)=q_i{\displaystyle \sum _{j=1}^k{\mu }_j{P}_{j,B}\left(2\right)}+\beta P_{i,D}\left(1\right);1\le i\le k$$

(3)

$$\begin{array}{ll}\left({\lambda }_1+\alpha +{\mu }_i\right)P_{i,B}\left(n\right)& =q_i{\displaystyle \sum _{j=1}^k{\mu }_j{P}_{j,B}\left(n+1\right)}+\beta P_{i,D}\left(n\right)\\ +{\lambda }_1{\displaystyle \sum _{k=1}^{n-1}{P}_{i,B}\left(n-k\right)c_k};n\ge 2,1\le i\le k\end{array}$$

(4)

$$\left({\lambda }_2+\beta \right)P_{i,D}\left(1\right)=\alpha P_{i,B}\left(1\right);1\le i\le k$$

(5)

$$\left({\lambda }_2+\beta \right)P_{i,D}\left(n\right)=\alpha P_{i,B}\left(n\right)+{\lambda }_2{\displaystyle \sum _{k=1}^{n-1}{P}_{i,D}\left(n-k\right)c_k};n\ge 2,1\le i\le k$$

(6)

Probability generating function

In this section, we present the probability generating function (PGF) technique to obtain the analytical solution of Equations 1 to 6. Let us define the following partial generating functions:

$$G_{0,V}\left(z\right)={\displaystyle \sum _{n=0}^{\infty }{z}^n{P}_{0,V}\left(n\right)},\left|z\right|\le 1$$

(7)

$$G_{i,B}\left(z\right)={\displaystyle \sum _{n=1}^{\infty }{z}^n{P}_{i,B}\left(n\right)},1\le i\le k,\left|z\right|\le 1$$

(8)

$$G_{i,D}\left(z\right)={\displaystyle \sum _{n=1}^{\infty }{z}^n{P}_{i,D}\left(n\right)},1\le i\le k,\left|z\right|\le 1$$

(9)

Lemma 1. The expressions for the partial generating functions are obtained as follows:

$$G_{0,V}\left(z\right)=\frac{1}{1-{\rho }_{\nu }A\left(z\right)}{P}_{0,V}\left(0\right)$$

(10)

$$G_{i,B}\left(z\right)=\frac{N_i\left(z\right)}{D\left(z\right)}{P}_{0,V}\left(0\right),i=1,2,\dots ,k$$

(11)

$$G_{i,D}\left(z\right)=\frac{\alpha }{\left({\lambda }_2+\beta -{\lambda }_{2}A\left(z\right)\right)}{G}_{i,B}\left(z\right),1\le i\le k$$

(12)

where

$${\rho }_{\nu }=\frac{{\lambda }_0}{{\lambda }_0+\nu };D\left(z\right)={\displaystyle \prod _{i=1}^k{\theta }_i\left(z\right)}+{\displaystyle \sum _{i=1}^k\left[q_i{\mu }_i{\displaystyle \prod _{j\ne i}^k{\theta }_j\left(z\right)}\right]}$$

$$N_i\left(z\right)={\displaystyle \prod _{j\ne i}^k{\theta }_j\left(z\right)}{q}_i{\lambda }_{0}z;$$

$${\theta }_i\left(z\right)=\left[{\lambda }_1\mathit{zA}\left(z\right)-\left({\lambda }_1+\alpha +{\mu }_i+\frac{\mathit{\alpha \beta }}{\left({\lambda }_2\mathrm{C}\left(z\right)-{\lambda }_2-\beta \right)}\right)z\right],i=1,2,\dots ,k$$

Proof. For proof, see ‘Proof of Lemma 1’ in the Appendix.

Lemma 2. The probability P _0,V (0) is

$$P_{0,V}\left(0\right)={\left[\frac{1}{1-{\rho }_{\nu }}+{\displaystyle \sum _{i=1}^k\frac{{\rho }_i{q}_i\left(1+\frac{\alpha }{\beta }\right)\left[\mathit{i\beta }-\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right)\right]{\displaystyle \sum _{i=1}^{k-1}\frac{1}{{\mu }_i}]}}{\left[\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right){\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}-\beta }\right]}}\right]}^{-1}$$

(13)

Also, the stability condition is given by

$$\frac{\alpha }{\beta }<\frac{\left(1-{\lambda }_{1}E\left[A\right]\right){\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}}}{{\lambda }_{2}E\left[A\right]{\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}}}$$

(14)

Proof. For proof, see ‘Proof of Lemma 2’ in the Appendix.

Theorem 1. The probability generating function of the number of customers in the system is given by

$$G\left(z\right)=\left[\frac{1}{1-{\rho }_{\nu }\mathrm{C}\left(z\right)}+{\displaystyle \sum _{i=1}^k\left[1+\frac{\alpha }{\left({\lambda }_2+\beta -{\lambda }_2\mathrm{C}\left(z\right)\right)}\right]\frac{N_i\left(z\right)}{D\left(z\right)}}\right]P_{0,V}\left(z\right)$$

(15)

Proof. For proof, see ‘Proof of Theorem 1’ in the Appendix.

Performance measures

In order to predict the system characteristics under variant circumstances, it is worthwhile to explore key aspects by establishing analytical formulae. In this section, some performance measures in terms of steady-state probabilities are obtained. The long-run probabilities of the server being on vacation, busy, and breakdown are denoted by P _V , P _B , and P _D , respectively. Thus, we obtain

$$P_V={\displaystyle \sum _{n=1}^{\infty }{z}^n{P}_{0,V}\left(n\right)}=G{}_{0,V}\left(1\right)=\frac{1}{1-{\rho }_{\nu }}{P}_{0,V}\left(0\right)$$

(16)

$$\begin{array}{l}{P}_B={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{z}^n{P}_{i,B}\left(n\right)}}={\displaystyle \sum _{i=1}^k{G}_{i,B}\left(1\right)}\\ ={\displaystyle \sum _{i=1}^k\frac{{\rho }_i{q}_i\left(1+\frac{\alpha }{\beta }\right)\left[\mathit{i\beta }-\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right){\displaystyle \sum _{i=1}^{k-1}\frac{1}{{\mu }_i}}\right]}{\left[\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right){\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}-\beta }\right]}}{P}_{0,V}\left(0\right)\end{array}$$

(17)

$$\begin{array}{l}{P}_D={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{z}^n{P}_{i,D}\left(n\right)}}={\displaystyle \sum _{i=1}^k{G}_{i,D}\left(1\right)}\\ ={\displaystyle \sum _{i=1}^k\frac{\alpha {\rho }_i{q}_i\left(1+\frac{\alpha }{\beta }\right)\left[\mathit{i\beta }-\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right){\displaystyle \sum _{i=1}^{k-1}\frac{1}{{\mu }_i}}\right]}{\beta \left[\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right){\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}-\beta }\right]}{P}_{0,V}\left(0\right)}\end{array}$$

(18)

Theorem 2. The expected number of customers in the system (L _N ) is given by

$$\begin{array}{ll}{L}_N=G^{\prime }\left(1\right)& =\left[\frac{{\rho }_{\nu }E\left[A\right]}{{\left(1-{\rho }_{\nu }\right)}^2}\right.\\ +{\displaystyle \sum _{i=1}^k\left[\frac{\left(\alpha +\beta \right)(N_i^{″}\left(1\right)D^{\prime }\left(1\right)-N_i^{\prime }\left(1\right)D^{″}\left(1\right)}{2\beta D^{\prime }{\left(1\right)}^2}\right.}\\ \left.\left.+\frac{N_i^{\prime }\left(1\right){\lambda }_{2}E\left[A\right]}{D^{\prime }\left(1\right){\beta }^2}\right]\right]P_{0,V}\left(0\right)\end{array}$$

(19)

where

$$N_i^{\prime }\left(1\right)={\displaystyle \prod _{j\ne i}^k{\left(1\right)}^{i+1}{\lambda }_0{\mu }_j{q}_i\left(1-{\displaystyle \sum _{i=1}^k{a}_i}\right),i=1,2,\dots ,k}$$

$$\begin{array}{ll}{N}_i^{″}\left(1\right)=& {\left(-1\right)}^i{q}_i{\lambda }_0\left[b{\displaystyle \sum _{i=1}^{k-1}}\right.{\displaystyle \underset{k-1}{\prod _{j=1}^{j\ne i}}{\mu }_j}\\ \left.+2{\displaystyle \prod _{i=1}^{k-1}{\mu }_i}\left\{{\displaystyle \sum _{i=1}^{k-1}{a}_i}-{\displaystyle \sum _{i=1}^{k-1}{a}_i}{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{k-1}{a}_j}\right\}\right],\\ i=1,2,\dots ,k\end{array}$$

$$D\mathit{\text{'}}\left(1\right)={\displaystyle \prod _{i=1}^k{\mu }_i{\displaystyle \sum _{i=1}^k{a}_i{q}_i,}}i=1,2,\dots ,k$$

$$D^{″}\left(1\right)=b{\displaystyle \sum _{i=1}^k{q}_i{\displaystyle \prod _{j\ne i}^k{\mu }_j}-2{\displaystyle \prod _{i=1}^k{\mu }_i{a}_i{\displaystyle \sum _{i=1}^k\frac{1-q_i}{a_i},i=1,2,\dots ,k}}}$$

$$a_i=\frac{{\lambda }_{1}E\left[A\right]+\delta }{{\mu }_i}-1,i=1,2,\dots ,k,\delta =\frac{\alpha {\lambda }_{2}E\left[A\right]}{\beta }$$

$$b=2{\lambda }_{1}E\left[A\right]+2\delta +E\left[A\left(A-1\right)\right]\left({\lambda }_1+\frac{\alpha }{\beta }{\lambda }_2\right)-\frac{2}{\alpha }{\delta }^2$$

Proof. For proof, see ‘Proof of Theorem 2’ in the Appendix.

Maximum entropy principle

Exact probabilities of the system states of an M^X/H_k/1 queueing system with multiple vacations and an un-reliable server have not been found earlier to the best information of the authors. In order to evaluate approximate results for the steady-state probabilities, we employ the maximum entropy approach. It is well established that the principle of maximum entropy can be used for estimating probabilistic information measures which is further used to obtain the queue size distribution of various complex queueing systems in different frameworks. In order to obtain the steady-state probabilities P _0,V (n), P _i,B (n), and P _i,D (n) by using the principle of maximum entropy, we formulate the maximum entropy model as follows.

The maximum entropy model

Following El-Affendi and Kouvatsos (1983), the entropy function y can be mathematically formulated as

$$\begin{array}{l}y=-{\displaystyle \sum _{n=0}^{\infty }{P}_{0,V}\left(n\right)log{P}_{0,V}\left(n\right)}-{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,B}\left(n\right)log{P}_{i,B}\left(n\right)}}\\ -{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,D}\left(n\right)log{P}_{i,D}\left(n\right)}}\end{array}$$

(20)

subject to the following constraints:

• 1. Normalizing condition

  $${\displaystyle \sum _{n=0}^{\infty }{P}_{0,V}\left(n\right)}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,B}\left(n\right)}}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,D}\left(n\right)=1}}$$

  (21)

• 2. The probability that the server being busy

  $${\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,B}\left(n\right)}}={\displaystyle \sum _{i=1}^k{G}_{i,B}\left(1\right)={\displaystyle \sum _{i=1}^k{A}_i}}$$

  (22)

• 3. The probability that the server is in a breakdown state

  $${\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,D}\left(n\right)}}={\displaystyle \sum _{i=1}^k{G}_{i,D}\left(1\right)={\displaystyle \sum _{i=1}^k{E}_i}}$$

  (23)

• 4. The expected number of customers in the system

  $${\displaystyle \sum _{n=0}^{\infty }n{P}_{0,V}\left(n\right)}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^{k}n{P}_{i,B}\left(n\right)}}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^{k}n{P}_{i,D}\left(n\right)=L_N}}$$

  (24)

where A _i  = G _i,B (1), E _i  = G _i,D (1), (1 ≤ i ≤ k), and L _N are given by Equations 17, 18, and 19, respectively.

After introducing Lagrange's multipliers corresponding to constraints (21) to (24), we construct Lagrange's function as

$$\begin{array}{l}y=-{\displaystyle \sum _{n=0}^{\infty }{P}_{0,V}\left(n\right)log{P}_{0,V}\left(n\right)}-{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,B}\left(n\right)log{P}_{i,B}\left(n\right)}}\\ -{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,D}\left(n\right)log{P}_{i,D}\left(n\right)}}\\ -{\theta }_1\left[{\displaystyle \sum _{n=0}^{\infty }{P}_{0,V}\left(n\right)}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,B}\left(n\right)}}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{P}_{i,D}\left(n\right)-1}}\right]\\ -{\displaystyle \sum _{i=1}^k{\eta }_i\left[{\displaystyle \sum _{n=1}^{\infty }{P}_{i,B}\left(n\right)-A_i}\right]}\\ -{\displaystyle \sum _{i=1}^k{\xi }_i\left[{\displaystyle \sum _{n=1}^{\infty }{P}_{i,D}\left(n\right)-E_i}\right]}\\ -{\xi }_{k+1}\left[{\displaystyle \sum _{n=0}^{\infty }n{P}_{0,V}\left(n\right)}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^{k}n{P}_{i,B}\left(n\right)}}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^{k}n{P}_{i,D}\left(n\right)-L_N}}\right]\end{array}$$

(25)

where θ₁, η _i  (1 ≤ i ≤ k) and ξ _i  (1 ≤ i ≤ k + 1) are Lagrange's multipliers corresponding to constraints (21) to (24), respectively.

The maximum entropy analysis

The maximum entropy results are obtained by taking the partial derivatives of y w.r.t. P _0,V (n), P _i,B (n), and P _i,D (n) and equating to zero. Thus, we get

$$\frac{\partial y}{\partial P_{0,V}\left(n\right)}=-log{P}_{0,V}\left(n\right)-1-{\theta }_1-{\xi }_{k+1}n=0$$

(26)

$$\begin{array}{l}\frac{\partial y}{\partial P_{i,B}\left(n\right)}=-log{P}_{i,B}\left(n\right)-1-{\theta }_1-{\eta }_i-{\xi }_{k+1}n\\ =0,1\le i\le k\end{array}$$

(27)

$$\begin{array}{l}\frac{\partial y}{\partial P_{i,D}\left(n\right)}=-log{P}_{i,D}\left(n\right)-1-{\theta }_1-{\xi }_i-{\xi }_{k+1}n\\ =0,1\le i\le k\end{array}$$

(28)

From Equations 26 to 28, we get

$$P_{0,V}\left(n\right)=e^{-\left(1+{\theta }_1\right)}{e}^{-{\xi }_{k+1}n},n=0,1,\dots$$

(29)

$$\begin{array}{l}{P}_{i,B}\left(n\right)=e^{-\left(1+{\theta }_1+{\eta }_i\right)}{e}^{-{\xi }_{k+1}n},n\\ =1,2,\dots ,1\le i\le k\end{array}$$

(30)

$$\begin{array}{l}{P}_{i,D}\left(n\right)=e^{-\left(1+{\theta }_1+{\xi }_i\right)}{e}^{-{\xi }_{k+1}n},n\\ =1,2,\dots ,1\le i\le k\end{array}$$

(31)

Denote

$${\phi }_1=e^{-\left(1+{\theta }_1\right)},{\psi }_i=e^{-{\eta }_i},1\le i\le k\mathit{and}{\delta }_i=e^{-{\xi }_i},1\le i\le k+1.$$

Then, Equations 29 to 31 can be written as

$$P_{0,V}\left(n\right)={\phi }_1{\delta }_{k+1}^n,n=0,1,\dots$$

(32)

$$P_{i,B}\left(n\right)={\phi }_1{\psi }_i{\delta }_{k+1}^n,n=1,2,\dots ,1\le i\le k$$

(33)

$$P_{i,D}\left(n\right)={\phi }_1{\delta }_i{\delta }_{k+1}^n,n=1,2,\dots ,1\le i\le k$$

(34)

On substituting the values of P _0,V (n), P _i,B (n), and P _i,D (n) from Equations 32 to 34 into Equations 21 to 23, we obtain

$${\displaystyle \sum _{n=0}^{\infty }{\phi }_1{\delta }_{k+1}^n=\frac{{\phi }_1}{1-{\delta }_{k+1}}=1-{\displaystyle \sum _{i=1}^k\left(A_i+E_i\right)}}$$

(35)

$${\displaystyle \sum _{n=1}^{\infty }{\phi }_1{\psi }_i{\delta }_{k+1}^n=\frac{{\phi }_1{\psi }_i{\delta }_{k+1}}{1-{\delta }_{k+1}}=A_i,1\le i\le k}$$

(36)

$${\displaystyle \sum _{n=1}^{\infty }{\phi }_1{\delta }_i{\delta }_{k+1}^n=\frac{{\phi }_1{\delta }_i{\delta }_{k+1}}{1-{\delta }_{k+1}}=E_i,1\le i\le k}$$

(37)

It follows from Equations 35 to 37 that

$${\phi }_1=\left(1-\rho \right)\left(1-{\delta }_{k+1}\right)$$

(38)

$${\psi }_i=\frac{A_i}{\left(1-\rho \right){\delta }_{k+1}},1\le i\le k$$

(39)

$${\delta }_i=\frac{E_i}{\left(1-\rho \right){\delta }_{k+1}},1\le i\le k$$

(40)

where

$$\rho ={\displaystyle \sum _{i=1}^k\left(A_i+E_i\right)}.$$

On substituting the values of φ₁,  ψ _i  and δ _i (1 ≤ i ≤ k) from Equations 38 to 40 into Equation 24 and after doing some algebraic manipulations, we obtain

$${\delta }_{k+1}=\frac{L_N-\rho }{1+L_N-\rho }$$

(41)

On substituting the values of φ₁, ψ _i , andδ _i from Equations 38 to 40 into Equations 32 to 34 and using Equation 40, we finally get

$$\begin{array}{l}{P}_{0,V}\left(n\right)=\left(\frac{1-\rho }{1+L_{N_1}-\rho }\right){\left(\frac{L_N-\rho }{1+L_N-\rho }\right)}^n,n\\ =0,1,\dots \end{array}$$

(42)

$$\begin{array}{l}{P}_{i,B}\left(n\right)=\left(\frac{A_i}{1+L_{N_1}-\rho }\right){\left(\frac{L_N-\rho }{1+L_N-\rho }\right)}^{n-1},n\\ =1,2,\dots ,1\le i\le k\end{array}$$

(43)

$$\begin{array}{l}{P}_{i,D}\left(n\right)=\left(\frac{E_i}{1+L_{N_1}-\rho }\right){\left(\frac{L_N-\rho }{1+L_N-\rho }\right)}^{n-1},n\\ =1,2,\dots ,1\le i\le k\end{array}$$

(44)

The expected waiting time in the system

Let $W_S\mathit{and}{\widehat{W}}_S$ denote the exact and the expected waiting time in the system, respectively. Then,

$$W_S=\frac{L_N}{{\lambda }_{\mathit{eff}}}$$

(45)

where λ _eff  = [λ₀P _V  + λ₁P _B  + λ₂P _D ]E[A].

Following the work of Wang et al. (2007), the approximate expected waiting time in the system is given by the approximate expected waiting time in

$$\begin{array}{l}{\widehat{W}}_S={\displaystyle \sum _{i=1}^k{\displaystyle \sum _{n=1}^{\infty }\left[\frac{n{q}_i}{{\mu }_i}+\frac{1}{\nu }+\frac{q_i}{2{\mu }_i}\left(\frac{E\left[A^2\right]}{E\left[A\right]}-1\right)\right]}}{P}_{0,V}\left(n\right)\\ +{\displaystyle \sum _{i=1}^k{\displaystyle \sum _{n=0}^{\infty }\left[\frac{n{q}_i}{{\mu }_i}+\frac{q_i}{2{\mu }_i}\left(\frac{E\left[A^2\right]}{E\left[A\right]}-1\right)\right]}{P}_{i,B}\left(n\right)}\\ +{\displaystyle \sum _{i=1}^k{\displaystyle \sum _{n=0}^{\infty }\left[\frac{n{q}_i}{{\mu }_i}+\frac{1}{\beta }+\frac{q_i}{2{\mu }_i}\left(\frac{E\left[A^2\right]}{E\left[A\right]}-1\right)\right]}{P}_{i,D}\left(n\right)}\end{array}$$

(46)

Substituting the values of P_0,V(n), P_i,B(n) and P_i,D(n)  from Equations 42 to 44 into Equation 46, the approximate expected waiting time in the system is given by

$$\begin{array}{l}{\widehat{W}}_S=\frac{1-{\displaystyle \sum _{i=1}^k{A}_i}-{\displaystyle \sum _{i=1}^k{E}_i}}{\nu }\\ +{\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}\left[L_N+\frac{1}{2}\left(\frac{E\left[A^2\right]}{E\left[A\right]}-1\right)\right]}+\frac{{\displaystyle \sum _{i=1}^k{E}_i}}{\beta }\end{array}$$

(47)

Numerical illustration and sensitivity analysis

In this section, we present a numerical simulation by taking the illustration of production of heat transfer equipment (HTE) discussed in the ‘Background’ section. For developing the code of computational program, we have used the ‘MATLAB’ software. For computation purposes, we assume that the raw materials arrive in batches of fixed batch size k = 3. The arrival rates are chosen as λ₁ = 0.5, λ₂ = 0.9, and λ₃ = 0.7. The service times of the machine when producing these equipment are μ₁ = 1, μ₂ = 2, and μ₃ = 3. The processing of the equipment may be interrupted with rate α = 0.8 and again becomes available for processing with rate β = 2. Further, the server may go for multiple vacations with rate v = 0.09. The expected number of these equipment in the system is obtained by using Equations 1 to 19 as L _N  = 36.

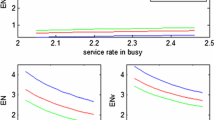
Now, we present the numerical results to demonstrate the effects of different parameters on various performance indices. The accuracy of numerical results is examined by comparing the exact waiting time (W _S ) obtained in the ‘Maximum entropy principle’ section using the probability generating function approach with the approximate waiting time (${\widehat{W}}_S$) obtained by the maximum entropy principle (MEP) of the M^X/H_K/1 queueing system under multiple vacation policy. Relative percentage error is tabulated for this purpose. The variations of different parameters on the average queue length are shown in Figures 1 and 2 graphically.

Figure 1

Average queue length vs. (a) α , (b) β , and (c) v for homogeneous and heterogeneous arrival rates.

Figure 2

Average queue length vs. (a) α , (b) β , and (c) v for different batch sizes.

Table 1 summarizes the numerical results for long-run fraction of time of the server being in different states by varying the parameters λ, μ, α, β, and v for two different cases of q _i (case 1: (q₁, q₂, q₃) = (0.6, 0.3, 0.1) and case 2: (q₁, q₂, q₃) = (0.7, 0.2, 0.1)). For the sake of convenience, we choose the default parameters λ₁ = 0.9, λ₂ = 0.8, λ₃ = 0.7, μ = 1, μ₁ = 1 μ, μ₂ = 2 μ, μ₃ = 3 μ, α = 0.2, β = 1, and v = 0.9. It is noticed that P _V shows a decreasing trend with respect to the increasing values of λ, α, and v, but an increasing trend has been found with other parameters for both cases. Similarly, P _B and P _D increase as we increase the values of λ, α, and v and decrease with increasing values of μ and β for both cases. Table 2 presents the comparison between W _S and ${\widehat{W}}_S$ for case 1: (q₁, q₂, q₃) = (0.5, 0.1, 0.4) and case 2: (q₁, q₂, q₃) = (0.4, 0.3, 0.3). We fix default parameters for numerical results summarized in Table 2 as λ₁ = 0.8, λ₂ = 0.7, λ₃ = 0.6, μ = 1, μ₁ = 1 μ, μ₂ = 2 μ, μ₃ = 3 μ, α = 0.2, β = 3, and v = 0.01. For both cases, W _S increases as we increase the values of λ₁ and α but decreases with increasing values of λ₀, μ, β, and v. As we increase the values of λ₁, μ, β, and v, it is seen that ${\widehat{W}}_S$ decreases but increases with λ₀ and α for both cases. It can be observed easily from Table 2 that the relative percentage error varies from 0 % to 3 % which is reasonably less.

Table 1 Effect of various parameters on long-run fraction of time of the server being in different states

Table 2 Comparison between the exact and the approximate results of waiting times

Figure 1a,b,c depicts the effect of different parameters on average queue length for various sets of heterogeneous arrival rate (λ₀ = 1.8λ, λ₁ = 0.5λ, λ₂ = 0.6λ) shown by discrete lines and homogeneous arrival rate (λ₀ = λ₁ = λ₂ = λ) shown by continuous lines. We observe that the average queue length is higher for the heterogeneous arrival rate in comparison to the homogeneous arrival rate on increasing the breakdown rate of the server. The queue length shows a gradual decreasing trend on increasing the repair rate and the vacation rate. Further, Figure 2a,b,c visualizes the effect of batch size on the average queue length. It is observed that the average queue length reveals an increasing trend with increasing values of α and β while shows a decreasing trend with increasing values of v. The tractability of numerical results shows that our model can be easily implemented for the quantitative assessment of the performance of many real-time congestion systems.

Methods

In this paper, an M^X/H_k/1 queue under multiple vacations and an un-reliable server with varying arrival rates is studied. The probability generating function technique is used to determine various performance measures in explicit form. Then, MEP is further employed to compare the approximate results with exact results. For validating the analytical results, the sensitivity analysis is also carried out.

Results and discussion

The role of queueing analysis based on MEP lies in the fact that it helps basically system designers and managers to take decisions based on the performance indices determined using the probability distribution of the system size in terms of available information by MEP approach. The numerical illustration presented demonstrates that maximum entropy analysis is a simple approach to deal with complex scenarios for real-life congestion situations and can be easily applied to complex queueing scenarios for which performance measures are not easily obtained by using a classical approach. Based on the numerical experiment and sensitivity analysis carried out, we overall conclude that the comparative analysis of approximate results with exact results has demonstrated that the results obtained by MEP are reasonably good. The average queue length is higher for heterogeneous arrival rate in comparison to homogeneous arrival rate. The trends are more perceptible for larger batch size, which is quite obvious as the congestion increases significantly if the batch size of arriving customers is large.

Conclusion

In this paper, an M^X/H_k/1 queue with multiple vacations and an un-reliable server has been studied in order to facilitate various performance indices in explicit form by using an analytical approach based on the generating function method and maximum entropy principle. The incorporation of some more realistic features such as multiple vacations, un-reliable server, and batch arrival makes our model closer to real-life congestion situations. This model depicts many real-time embedded systems, namely production system, computer system, data communication system, etc. The numerical results and sensitivity analysis obtained provide an insight into how the system can be made more efficient by controlling the sensitive parameters. The queueing model studied can be further extended by taking the concept of k-phase optional repair. The concept of working vacation, N-policy, and multi-repair can also be included which is the topic of our future research work.

Appendix

Proof of Lemma 1

Multiplying Equation 1 by appropriate powers of z and then summing over n, we get

$$\left({\lambda }_0+\nu -{\lambda }_0\mathrm{A}\left(z\right)\right)G_{0,V}\left(z\right)=\left({\lambda }_0+\nu \right)P_{0,V}\left(0\right)$$

(48)

Substituting ${\rho }_{\nu }=\frac{{\lambda }_0}{{\lambda }_0+\nu }$ in Equation 48, we have

$$G_{0,V}\left(z\right)=\frac{1}{1-{\rho }_{\nu }\mathrm{A}\left(z\right)}{P}_{0,V}\left(0\right)$$

(49)

Multiplying Equation 2 by q _i z, Equation 3 by z², and Equation 4 by zⁿ⁺¹ and then adding these equations term by term for all possible values of n, finally, we obtain

$$\begin{array}{l}\left[{\lambda }_{1}z\mathrm{A}\left(z\right)-\left({\lambda }_1+\alpha +{\mu }_i\right)z\right]G_{i,B}\left(z\right)\\ +q_i{\displaystyle \sum _{j=1}^k{\mu }_j}{G}_{j,B}\left(z\right)+\mathit{\beta z}{G}_{i,D}\left(z\right)\\ =q_{i}z{\lambda }_{0}P{}_{0,V}\left(0\right),1\le i\le k\end{array}$$

(50)

After multiplying Equation 5 by z and Equation 6 by zⁿ and then adding these equations term by term for all possible values of n, thus, we obtain

$$\begin{array}{ll}\left({\lambda }_2+\beta \right)G_{i,D}\left(z\right)& =\alpha G_{i,B}\left(z\right)\\ +{\lambda }_2\mathrm{A}\left(z\right)G_{i,D}\left(z\right),1\le i\le k\end{array}$$

(51)

Using Equation 51, we have

$$G_{i,D}\left(z\right)=\frac{\alpha }{\left({\lambda }_2+\beta -{\lambda }_2\mathrm{A}\left(z\right)\right)}{G}_{i,B}\left(z\right),1\le i\le k$$

(52)

Now put i = 1 in Equation 50 and using Equation 52 into Equation 50, we have

$$\begin{array}{l}\left[{\lambda }_1\mathit{zA}\left(z\right)-\left({\lambda }_1+\alpha +{\mu }_1+\frac{\mathit{\alpha \beta }}{\left({\lambda }_{2}A\left(z\right)-{\lambda }_2-\beta \right)}\right)z+q_1{\mu }_1\right]G_{1,B}\left(z\right)\\ +q_1{\displaystyle \sum _{j=2}^k{\mu }_j}{G}_{j,B}\left(z\right)=q_{1}z{\lambda }_{0}P{}_{0,V}\left(0\right)\end{array}$$

(53)

Again put i = 2 in Equation 50 and using Equation 52 into Equation 50, we obtain

$$\begin{array}{l}{q}_2{\mu }_1{G}_{1,B}\left(z\right)+\left[{\lambda }_1\mathit{zA}\left(z\right)-\left({\lambda }_1+\alpha +{\mu }_2+\frac{\mathit{\alpha \beta }}{\left({\lambda }_{2}A\left(z\right)-{\lambda }_2-\beta \right)}\right)z+q_2{\mu }_2\right]G_{2,B}\left(z\right)\\ +q_2{\displaystyle \sum _{j=3}^k{\mu }_j}{G}_{j,B}\left(z\right)=q_{2}z{\lambda }_{0}P{}_{0,V}\left(0\right)\end{array}$$

(54)

Similarly, repeating this process for i = k, we get

$$\begin{array}{l}{q}_k{\displaystyle \sum _{j=1}^{k-1}{\mu }_j}{G}_{j,B}\left(z\right)\\ +\left[{\lambda }_1\mathit{zA}\left(z\right)-\left({\lambda }_1+\alpha +{\mu }_k+\frac{\mathit{\alpha \beta }}{\left({\lambda }_{2}A\left(z\right)-{\lambda }_2-\beta \right)}\right)z+q_k{\mu }_k\right]G_{k,B}\left(z\right)=q_{k}z{\lambda }_{0}P{}_{0,V}\left(0\right)\end{array}$$

(55)

We use Cramer's rule to solve Equations 53 to 55. Now we get

$$G_{i,B}\left(z\right)=\frac{N_i\left(z\right)}{D\left(z\right)}{P}_{0,V}\left(0\right),i=1,2,\dots ,k$$

(56)

Proof of Lemma 2

Using Lemma 1, we obtain

$$G_{0,V}\left(1\right)={lim}_{z\to 1}{G}_{0,V}\left(z\right)=\frac{1}{1-{\rho }_{\nu }}{P}_{0,V}\left(0\right)$$

(57)

$$\begin{array}{l}{G}_{i,B}\left(1\right)={lim}_{z\to 1}{G}_{i,B}\left(z\right)\\ =\frac{{\rho }_i{q}_i\left[\mathit{i\beta }-\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right){\displaystyle \sum _{i=1}^{k-1}\frac{1}{{\mu }_i}}\right]}{\left[\left({\lambda }_1\mathit{\beta E}\left[A\right]+\alpha {\lambda }_{2}E\left[A\right]\right){\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}-\beta }\right]}{P}_{0,V}\left(0\right),i=1,2,\dots ,k\end{array}$$

(58)

$$\begin{array}{l}{G}_{i,D}\left(1\right)={lim}_{z\to 1}{G}_{i,D}\left(z\right)=\frac{\alpha }{\beta }{G}_{i,B}\left(1\right),i\\ =1,2,\dots ,k\end{array}$$

(59)

where

$${\rho }_i=\frac{{\lambda }_0}{{\mu }_i}.$$

The L-Hospital rule has been applied to compute the above results.

To determine P_0,V(0), we use the normalizing condition given by

$$\mathrm{G}\left(1\right)=G_{0,V}\left(1\right)+{\displaystyle \sum _{i=1}^k\left(G_{i,B}\left(1\right)+G_{i,D}\left(1\right)\right)}$$

(60)

On substituting the values of G_0,V(1), G_i,B(1), and G_i,D(1) from Equations 57 to 59 into Equation 60, we obtain the value of P_0,V(0).

For finding the result of the stable condition, we use the condition

$$0<P_{0,V}\left(0\right)<1.$$

(61)

Using Equation 13 into Equation 61, we have

$$0<\left({\lambda }_1\beta +\alpha {\lambda }_2\right)E\left[A\right]{\displaystyle \sum _{i=1}^k\frac{q_i}{{\mu }_i}}-\beta <1.$$

(62)

After some algebraic manipulations, Equation 62 provides the result given in Equation 14.

Proof of Theorem 1

In order to prove Equation 15, we have

$$\begin{array}{l}\mathrm{G}\left(z\right)={\displaystyle \sum _{n=0}^{\infty }{z}^n{P}_{0,V}\left(n\right)}+{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{z}^n{P}_{i,B}\left(n\right)}}\\ +{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{i=1}^k{z}^n{P}_{i,D}\left(n\right)}}\\ =G_{0,V}\left(z\right)+{\displaystyle \sum _{i=1}^k\left[G_{i,B}\left(z\right)+G_{i,D}\left(z\right)\right]}\end{array}$$

(63)

On substituting the values of G_0,V(z), G_i,B(z), and G_i,D(z) from Lemma 1 into Equation 63, we get Equation 15.

Proof of Theorem 2

The average system size is computed using

$$L_N={lim}_{z\to 1}{G}^{\prime }\left(z\right).$$

The L-Hospital rule is applied twice to compute the results given in Equation 19.