Investigation of Solitary wave solutions for Vakhnenko-Parkes equation via exp-function and Exp(−ϕ(ξ))-expansion method

Abstract

In this paper, we have described two dreadfully important methods to solve nonlinear partial differential equations which are known as exp-function and the exp(−ϕ(ξ)) -expansion method. Recently, there are several methods to use for finding analytical solutions of the nonlinear partial differential equations. The methods are diverse and useful for solving the nonlinear evolution equations. With the help of these methods, we are investigated the exact travelling wave solutions of the Vakhnenko- Parkes equation. The obtaining soliton solutions of this equation are described many physical phenomena for weakly nonlinear surface and internal waves in a rotating ocean. Further, three-dimensional plots of the solutions such as solitons, singular solitons, bell type solitary wave i.e. non-topological solitons solutions and periodic solutions are also given to visualize the dynamics of the equation.

1. Introduction

The effort in finding exact solutions to nonlinear equations is witnessed significant curiosity and progress in finding solutions to nonlinear partial differential equations (NPDEs) that resemble physical phenomena. The nonlinear wave phenomena observed in fluid dynamics, plasma and optical fibers are often modeled by the bell (i.e. non-topological solitons) shaped sech solutions and the kink (i.e. topological solitons) shaped tanh solutions. Both mathematicians and physicists have devoted considerable effort of research regarding this matter. A peek at the literature reveals a lot of effective methods that solve this type of NPDEs.

For instance the inverse scattering transform (Ablowitz and Clarkson 1991; Vakhnenko and Parkes 2002; Vakhnenko and Parkes 2012a; Vakhnenko and Parkes 2002b), the complex hyperbolic function method (Zayed et al. 2006; Chow 1995), the rank analysis method (Feng 2000), the ansatz method (Hu 2001a; Hu 2001b; Majid et al. 2012), the (G′/G) -expansion method (Wang et al. 2008; Roshid et al. 2013a; Bekir 2008; Roshid et al. 2013b; Zhang 2008; Alam 2013), the modified simple equation method (Jawad et al. 2010), the exp-functions method (He and Wu 2006), the Hirota method (Hirota 1971), the sine-cosine method (Wazwaz 2004), the tanh-function method (Parkes and Duffy 1996), extended tanh-function method (Fan 2000; Parkes 2010a; Parkes 2010b), the Jacobi elliptic function expansion method (Liu 2005; Chen and Wang 2005), the F-expansion method (Wang and Zhou 2003; Wang and Li 2005), the Backlund transformation method (Miura 1978), the Darboux transformation method (Matveev and Salle 1991), the homogeneous balance method (Wang 1995; Zayed et al. 2004; Wang 1996), the Adomian decomposition method (Adomain 1994; Wazwaz 2002), the auxiliary equation method (Sirendaoreji and Sun 2003; Sirendaoreji 2007), the exp(−ϕ(ξ)) -expansion method (Khan and Akbar 2013) and so on.

Recently, a remarkable and important discover has been made by Vakhnenko and Parkes (Vakhnenko and Parkes 1998), who have confirmed an integrable equation as follows:

$$u{u}_{xxt}-u_x{u}_{xt}+u^2{u}_t=0$$

(1)

The traveling wave solutions of this Vakhnenko-Parkes equation was investigated in (Kangalgil and Ayaz 2008; Parkes 2010b; Gandarias and Bruzon 2009; Yasar 2010; Abazari 2010; Liu and He 2013, Ostrovsky 1978) and Liu (Liu and He 2013) found traveling wave solutions of this equations by improved (G′/G) -expansion method with auxiliary equation GG″ = AG² + BGG′ + C(G′)².

In this paper, we investigate the traveling wave solutions of the Vakhnenko-Parkes equation (1) via two methods namely the Exp-function and the exp(−ϕ(ξ)) -expansion methods.

The rest of the paper is organized as follows: In section 2, we build up an introduction of exp-function and the exp(−ϕ(ξ)) -expansion method. By these methods, we gain the exact solutions of Vakhnenko-Parkes equation in section 3. In section 4, we out line results and discussion of the achieved solutions. Finally, some conclusions are drawn in the section 5.

2. The methodologies

In this section, we will go over the main points of the exp-function method and the exp(−ϕ(ξ)) -expansion method to raise the rational solitary wave and periodic wave solutions for the Vakhnenko-Parkes equation which have been paid attention by many researchers in mathematical physics.

Consider a nonlinear equation with two independent variable x and t, is given by

$$P\left(U,U_x,U_t,U_{xx},U_{xt},U_{tt},\dots \dots \right)=0$$

(2)

where U = U(x,t) is an unknown function, P is a polynomial in U = U(x,t) and its partial derivatives, in which the highest order derivatives term and nonlinear terms are involved.

Combining the independent variable x and t into one traveling wave variable ξ = x ± wt, we suppose that

$$U\left(x,t\right)=u\left(\xi \right),\xi =x\pm \mathit{wt}\text{,}$$

(3)

The travelling wave variable (3) permits us to convert the Eq. (2) to an ODE for u = u(ξ) is

$$P\left(u,u^{\prime },u^{″},\cdots \cdots \cdots \right)=0$$

(4)

2.1. The exp-function method

We now discuss the exp-function method to solve partial differential equation Eq. (1).

Step-2.1.1. Assume the solution of the Eq. (1) can be expressed in the following form (He and Wu, 2006):

$$\begin{array}{l}u\left(\xi \right)=\frac{\sum _{n=-c}^d{a}_{n}exp\left(n\xi \right)}{\sum _{m=-p}^q{b}_{n}exp\left(n\xi \right)}\\ =\frac{a_{-c}exp\left(-c\xi \right)+\cdots \cdots +a_{d}exp\left(d\xi \right)}{b_{-p}exp\left(-p\xi \right)+\cdots \cdots +b_{q}exp\left(q\xi \right)}\end{array}$$

(5)

where c, d, p and q are positive unknown integers that could be determine subsequently, a _n and b _m are unknown constants, Eq. (5) can be re-written in the following form:

$$u\left(\xi \right)=\frac{a_{c}exp\left(c\xi \right)+\cdots \cdots +a_{-d}exp\left(-d\xi \right)}{b_{p}exp\left(p\xi \right)+\cdots \cdots +b_{-q}exp\left(-q\xi \right)}$$

(6)

Step-2.1.2: To determine the values of c and p, we balance the highest order linear term with the highest order nonlinear term in Equation Eq. (4). Similarly, to determine the values of d and q, we have to balance the lowest order linear term with the lowest order nonlinear term in Equation Eq. (4). This confirms the determination of the values of c, d, p and q.

Step-2.1.3: Inserting the values of c, d, p and q into Eq. (6) and then substituting Eq. (6) into Eq. (4) and simplifying, we attain;

$$\sum _j{C}_{j}exp\left(j\xi \right)=0$$

(7)

Then collecting all coefficient Cj and setting each of them to zero, yields a system of algebraic equations for a _c ’s and b _p ’s. Then unknown a _c ’s and b _p ’s can be evaluated by solving the system of algebraic equations with the help of maple-13. Substituting these values into Eq. (6), we gain traveling wave solutions of the Eq. (1).

2.2. The exp(−ϕ(ξ)) -expansion method

Step 2.2.1. Assume that the solution of ODE (4) can be expressed by a polynomial in exp(−ϕ(ξ)) as follows:

$$u={\displaystyle \sum _{i=0}^m{l}_{i}exp{\left(-\varphi \left(\xi \right)\right)}^i}$$

(8)

where ϕ′(ξ) satisfies the ODE

$${\varphi }^{\prime }\left(\xi \right)=exp\left(-\varphi \left(\xi \right)\right)+\mu exp\left(\varphi \left(\xi \right)\right)+\lambda \text{,}$$

(9)

The well-known solutions of the ODE (9) are as follows:

$$\begin{array}{l}\mathrm{When}{\lambda }^2-4\mu >0,\mu \ne 0,\mathrm{then}\varphi \left(\xi \right)\\ =ln\left(\frac{-\sqrt{{\lambda }^2-4\mu }tanh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\xi +C\right)\right)-\lambda }{2\mu }\right)\end{array}$$

(10)

$$\begin{array}{l}\mathrm{When}{\lambda }^2-4\mu <0,\mathrm{then}\varphi \left(\xi \right)\\ =ln\left(\frac{\sqrt{4\mu -{\lambda }^2}tan\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\xi +C\right)\right)-\lambda }{2\mu }\right)\end{array}$$

(11)

$$\begin{array}{l}\mathrm{When}{\lambda }^2-4\mu >0,\mu =0,\mathrm{then}\varphi \left(\xi \right)\\ =-ln\left(\frac{\lambda }{exp\left(\lambda \left(\xi +C\right)\right)-1}\right)\end{array}$$

(12)

$$\begin{array}{l}\mathrm{When}{\lambda }^2-4\mu =0,\mu \ne 0,\lambda \ne 0,\mathrm{then}\varphi \left(\xi \right)\\ =ln\left(-\frac{2\left(\lambda \left(\xi +C\right)+2\right)}{{\lambda }^2\left(\xi +C\right)}\right)\end{array}$$

(13)

$$\begin{array}{l}\mathrm{When}{\lambda }^2-4\mu =0,\mu =\lambda =0,\mathrm{then}\varphi \left(\xi \right)\\ =ln\left(\xi +C\right)\end{array}$$

(14)

l _i , w, λ; i = 0, ⋯ ⋯, m and μ are constants to be determined later, l _m  ≠ 0, the positive integer m can be determined by considering the homogeneous balance between the highest order derivatives and nonlinear terms arising in the ODE(4).

Step 2.2.2. By substituting Eq. (8) into Eq. (4) and using the ODE (9), and then collecting all terms with the same order of exp(−ϕ(ξ)) together, the left hand side of Eq. (4) is converted into new polynomial in exp(−ϕ(ξ)). Setting each coefficient of this polynomial to zero, yields a system of algebraic equations for l _i , ⋯ w, λ; i = 0, ⋯ ⋯, m and μ. Solving the system of algebraic equations and substituting l _i , ⋯ w; i = 0, ⋯ ⋯, m, and the general solutions of Eq. (9) into Eq. (8). We have more traveling wave solutions of nonlinear evolution equation Eq. (1).

3. Application

In this section, we exert the exp-function method and the exp(−ϕ(ξ)) -expansion method to construct the rational solitary wave, non-topological soliton, periodic wave solutions for some nonlinear evolution equations in mathematical physics via the Vakhnenko-Parkes equation Eq. (1).

Inserting Eq. (3) into Eq. (1), we amend the Eq. (1) into the ODE:

$$u{u}^{‴}-u^{\prime }{u}^{″}+u^2{u}^{\prime }=0$$

(15)

Integrating Eq. (15) with respect to ξ and setting the integration constant equal to zero yields

$$3u{u}^{″}-3{\left(u^{\prime }\right)}^2+u^3=0$$

(16)

3.1. Solution of Vakhnenko- Parkes equation via the exp-function method

Now, we apply the Exp-function method to create the generalized traveling wave solutions of the Vakhnenko- Parkes Eq. (1).

According to Step 2.1.1 in the Exp-function method, the solution of Eq. (16) can be written in the form of Eq. (6). To determine the values of c and p, according to Step 2.1.2, we balance the term of the highest order in uu″ and the highest nonlinear terms u³ in Eq. (16). With the aid of computational software Maple 13, yields p = c. To find out the values of q and d, we balance the term of lowest order uu″ in Eq. (16) with lowest order nonlinear term u³, with the aid of computational software Maple 13, yields to result q = d. The parameters are free, so we can arbitrarily prefer the values of c and d, but the ultimate solution does not depend upon the choices of them.

Case 1: Suppose p = c = 1 and q = d = 1.

$$u\left(\xi \right)=\frac{a_1{e}^{\xi }+a_0+a_{-1}{e}^{-\xi }}{b_1{e}^{\xi }+b_0+b_{-1}{e}^{-\xi }}$$

(17)

Since there are some free variables, for simplicity, we presume b₁ = 1.

$$u\left(\xi \right)=\frac{a_1{e}^{\xi }+a_0+a_{-1}{e}^{-\xi }}{e^{\xi }+b_0+b_{-1}{e}^{-\xi }}$$

(18)

Now, substituting Eq. (18) into Eq. (16) and by employing the computer algebra, such as Maple 13, we gain

$$\begin{array}{l}\frac{1}{A}(C_1{e}^{8\xi }+C_2{e}^{7\xi }+C_3{e}^{6\xi }+C_4{e}^{5\xi }+C_5{e}^{4\xi }+C_6{e}^{3\xi }\\ +C_7{e}^{2\xi }+C_8{e}^{\xi }+C_9)=0\end{array}$$

Where A = (e^2ξ + b₀e^ξ + b_‒ 1)⁴,

$$\begin{array}{l}{C}_1=a_1^3,C_2=a_1^3{b}_0+3a_0{a}_1^2+3a_0{a}_1-3a_1^2{b}_0,\\ C_3=3a_0^2{a}_1+3a_{-1}{a}_1^2+a_1^3{b}_{-1}+3a_0{a}_1^2{b}_0-12a_1^2{b}_{‒1}+12a_{-1}{a}_1,\\ C_4=18a_{-1}{a}_1{b}_0+6a_0{a}_1{a}_{-1}+3a_0{a}_1^2{b}_{-1}+3a_0{a}_{-1}-3a_1^2{b}_{-1}{b}_0+a_0^3\\ +3a_{-1}{a}_1^2{b}_0-18a_0{a}_1{b}_{-1}+3a_0^2{a}_1{b}_0-3a_0^2{b}_0+3a_0{a}_1{b}_0^2,\\ C_5=a_0^3{b}_0+3a_0^2{a}_1{b}_{-1}+6a_0{a}_1{a}_{-1}{b}_0+12a_{-1}{a}_1{b}_0^2+3a_0^2{a}_{-1}-12a_0^2{b}_{-1}+3a_1^2{a}_{-1}{b}_{‒1}+3a_1{a}_{-1}^2\\ C_6=-18a_0{a}_{-1}{b}_{-1}+3a_0{a}_1{b}_{-1}^2+3a_1{a}_{-1}^2{b}_0+18a_{-1}{a}_1{b}_0{b}_{-1}+3a_0{a}_{-1}^2\\ +6a_0{a}_{-1}{a}_1{b}_{-1}+a_0^3{b}_{-1}-3a_{-1}^2{b}_0-3a_0^2{b}_{-1}{b}_0+3a_0^2{a}_{-1}{b}_0+3a_0{a}_1{b}_0^2,\\ C_7=12a_{-1}{a}_1{b}_{-1}^2+3a_0^2{a}_{-1}{b}_{-1}+a_{-1}^3+3a_0{a}_{-1}^2{b}_0+3a_{-1}^2{a}_1{b}_{‒1}-12a_{-1}^2{b}_{-1},\\ C_8=3a_0{a}_{-1}{b}_{-1}^2+3a_0{a}_{-1}^2{b}_{-1}+a_{-1}^3{b}_0-3a_{-1}^2{b}_{-1}{b}_0\mathrm{and}{C}_9=a_{-1}^3{b}_{-1}\end{array}$$

Setting these equations to zero and solving the system of algebraic equations with the aid of commercial software Maple-13, we achieve the following solution.

$$a_{-1}=0,a_0=3b_0,a_1=0,b_0=\mathit{const}\mathrm{and}{b}_{-1}=b_0^2/4$$

Setting these values in the Eq. (18) we acquire the solution

$$\begin{array}{l}u\left(\xi \right)=\frac{3b_0}{e^{\xi }+b_0+b_0^2{e}^{-\xi }/4}\\ =\frac{12b_0}{4e^{\xi }+4b_0+b_0^2{e}^{-\xi }}\\ =\frac{12b_0}{\left(4+b_0^2\right)cosh\xi +\left(4-b_0^2\right)sinh\xi +4b_0},\mathrm{where}\xi =x-\mathit{wt}\end{array}$$

(19)

If we set

If we choose

$$b_0=2,u\left(\xi \right)=\frac{3}{cosh\xi +1}$$

(20)

Case 2: Suppose p = c = 2 and q = d = 1.

$$u\left(\xi \right)=\frac{a_2{e}^{2\xi }+a_1{e}^{\xi }+a_0+a_{-1}{e}^{-\xi }}{b_2{e}^{2\xi }+b_1{e}^{\xi }+b_0+b_{-1}{e}^{-\xi }}$$

(21)

Since there are some free parameters, for simplicity, we imagine b₂ = 1, b_− 1 = 0.

$$u\left(\xi \right)=\frac{a_2{e}^{2\xi }+a_1{e}^{\xi }+a_0+a_{-1}{e}^{-\xi }}{e^{2\xi }+b_1{e}^{\xi }+b_0}$$

(22)

Executing the same procedure as described in case-1, we gain

$$\begin{array}{l}{a}_{-1}=a_0=a_2=0,a_1=3b_1,b_1=\mathit{const}\mathrm{and}{b}_0\\ =b_1^2/4\text{.}\end{array}$$

Setting these values in the Eq. (22) we acquire the solution

$$\begin{array}{l}u\left(\xi \right)=\frac{12b_1}{\left(4+b_1^2\right)cosh\xi +\left(4-b_1^2\right)sinh\xi +4b_1}\mathrm{where}\xi \\ =x-\mathit{wt}\end{array}$$

(23)

which is same obtain in the previous case-1.

Case 3: Suppose p = c = 2 and q = d = 2.

$$u\left(\xi \right)=\frac{a_2{e}^{2\xi }+a_1{e}^{\xi }+a_0+a_{-1}{e}^{-\xi }+a_{-2}{e}^{-2\xi }}{b_2{e}^{2\xi }+b_1{e}^{\xi }+b_0+b_{-1}{e}^{-\xi }+b_{-2}{e}^{-2\xi }}$$

(24)

Since there are some free parameters, for simplicity, we presume a_− 2 = a_− 1 = 0, b_− 2 = b_− 1 = 0, b₁ = 1_.

$$u\left(\xi \right)=\frac{a_2{e}^{2\xi }+a_1{e}^{\xi }+a_0}{b_2{e}^{2\xi }+e^{\xi }+b_0}$$

(25)

Executing the same procedure as described in the case-1 and in the case-2, we attain

$$\begin{array}{l}{a}_0=0,a_1=3,a_2=0,b_0=\mathit{const},b_1\\ =\mathit{const}\mathrm{and}{b}_2={\left(4b_0\right)}^{-1}\end{array}$$

Hence require solution is

$$u\left(\xi \right)=\frac{12b_0}{\left(1+4b_0^2\right)cosh\xi +\left(1-4b_0^2\right)sinh\xi +4b_0}$$

(26)

where ξ = x − wt.

This is also similar solutions achieved in the previous cases and so we should not repeat the procedure again and again for different values of the parameters. Actually the solution is a bell shape soliton solution which referred to as non-topological solitons solution. But in generally, we can obtain all of the above solutions and another family of solutions in case 4.

Case 4: Suppose p = c = 1 and q = d = 1.

$$u\left(\xi \right)=\frac{a_1{e}^{\xi }+a_0+a_{-1}{e}^{-\xi }}{b_1{e}^{\xi }+b_0+b_{-1}{e}^{-\xi }}$$

(27)

Now, substituting Eq. (27) into Eq. (15) and by employing the computer algebra, such as Maple 13, we gain

$$\begin{array}{l}\frac{e^{\xi }}{A}(C_1{e}^{8\xi }+C_2{e}^{7\xi }+C_3{e}^{6\xi }+C_4{e}^{5\xi }+C_5{e}^{4\xi }+C_6{e}^{3\xi }\\ +C_7{e}^{2\xi }+C_8{e}^{\xi }+C_9)=0\end{array}$$

Where A = (b₁e^2ξ + b₀e^ξ + b_‒ 1)⁵, others are omitted for simplicity and setting these equations to zero and solving the system of algebraic equations with the aid of commercial software Maple-13, we achieve the following solution.

• (i)
  $$\begin{array}{l}{a}_{-1}=0,a_0=3b_0,a_1=0,b_0=\mathit{const}\mathrm{and}{b}_{-1}=\\ b_0^2/4b_1\text{.}\end{array}$$
• (ii)
  $$\begin{array}{l}{a}_{-1}=-b_0^2/4b_1,a_0=2b_0,a_1=-b_1,\mathrm{and}{b}_{-1}=\\ b_0^2/4b_1\text{.}\end{array}$$

The solution (i) is same obtained in case 1.

Setting these values of (ii) in the Eq. (18) we acquire the solution

$$\begin{array}{l}u\left(\xi \right)=\frac{-b_1{e}^{\xi }+2b_0-b_0^2{e}^{-\xi }/4b_1}{b_1{e}^{\xi }+b_0+b_0^2{e}^{-\xi }/4b_1},\mathrm{where}\xi \\ =x-\mathit{wt}\end{array}$$

(28)

If we choose

$$b_0=2b_1,u\left(\xi \right)=-1+\frac{3b_0}{b_1{e}^{\xi }+b_0+b_0^2{e}^{-\xi }/4b_1}$$

(29)

Or if choose

$$b_0=1,b_1=1/2,u\left(\xi \right)=-1+\frac{3}{cosh\xi +1}$$

(30)

Remark-1: We have the solution (19) in the form via Exp-function method, $u\left(\xi \right)=\frac{12b_0}{4e^{\xi }+4b_0+b_0^2{e}^{-\xi }}$

It note that if b₀ > 0 and exp(−x₀) = 2/b₀ then it can be written $u\left(\xi \right)=\frac{3}{2}sec{h}^2\left(\frac{1}{2}\left(x-\mathit{wt}-x_0\right)\right)$ and if b₀ <0 and exp(−x₀) = 2/|b₀| then it can be written $u\left(\xi \right)=-\frac{3}{2}cosec{h}^2\left(\frac{1}{2}\left(x-\mathit{wt}-x_0\right)\right)$. These two solutions are just solutions u₁₁ and u₁₂ in Parkes (Parkes 2010b) with k = 1/2.

And for the solution (29) in the form via Exp-function method, $u\left(\xi \right)=-1+\frac{3b_0}{b_1{e}^{\xi }+b_0+b_0^2{e}^{-\xi }/4b_1}$

It note that if b₁/b₀ > 0 and exp(−x₀) = 2b₁/b₀ then it can be written $u\left(\xi \right)=-1+\frac{3}{2}sec{h}^2\left(\frac{1}{2}\left(x-\mathit{wt}-x_0\right)\right)$ and if b₁/b₀ < 0 and exp(−x₀) = 2b₁/|b₀| then it can be written $u\left(\xi \right)=-1-\frac{3}{2}cosec{h}^2\left(\frac{1}{2}\left(x-\mathit{wt}-x_0\right)\right)$. These two solutions are just solutions u₂₁ and u₂₂ in Parkes (Parkes 2010b) with k = 1/2.

3.2. Solutions of Vakhnenko- Parkes equation via the exp(−ϕ(ξ)) -expansion method

Balance the highest order derivate term uu″ with the highest nonlinear terms u³ in Eq. (16), we obtain m = 2, so assume the equation Eq. (1) has the solution

$$u\left(\xi \right)=l_0+l_1\left(exp\left(-\varphi \left(\xi \right)\right)\right)+l_2{\left(exp\left(-\varphi \left(\xi \right)\right)\right)}^2$$

(31)

Inserting Eq. (31) into Eq. (16) and using the ODE (9), and then collecting all terms with the same order of exp(−ϕ(ξ)) together, Eq. (16) is converted into new polynomial in exp(−ϕ(ξ)). Setting each coefficients of this polynomial is to zero, yields a system of algebraic equations for l₀, l₁, l₂ , λ; and μ which are as follows:

$$\begin{array}{l}3l_0{l}_1\lambda \mu +6l_0{l}_2{\mu }^2-3l_1^2{\mu }^2+l_0^3=0,\\ 3l_0^2{l}_1+6l_0{l}_1\mu -3l_1^2\mu \lambda -6l_1{l}_2{\mu }^2+3l_0{l}_1{\lambda }^2+18l_0{l}_2\lambda \mu =0,\\ 24l_0{l}_2\mu -3l_1{l}_2\lambda \mu -6l_2^2{\mu }^2+3l_0{l}_1^2+9l_0{l}_1\lambda +12l_0{l}_2{\lambda }^2+3l_0^2{l}_2=0,\\ 6l_0{l}_1{l}_2+l_1^3+3l_1^2\lambda +6l_1{l}_2\mu +6l_0{l}_1-6l_2^2\lambda \mu +30l_0{l}_2\lambda +3l_1{l}_2{\lambda }^2=0,\\ 3l_1^2{l}_2+15l_1{l}_2\lambda +3l_1^2+3l_0{l}_2^2+18l_0{l}_2=0,\\ 3l_1{l}_2^2+12l_1{l}_2+6l_2^2\lambda =0,6l_2^2+l_2^3=0\end{array}$$

Solving the system of algebraic equations and we obtained l₀ = − 6μ, l₁ = − 6λ, l₂ = − 6. Substituting the values of l₀, l₁, l₂ in the general solutions of Eq. (9) achieve more traveling wave solutions of nonlinear evolution equation Eq. (1) as follows:

When λ² − 4μ > 0, μ ≠ 0, then

$$\begin{array}{l}\therefore u\left(\xi \right)=-6\mu +6\lambda \left(\frac{2\mu }{\sqrt{{\lambda }^2-4\mu }tanh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\xi +C\right)\right)+\lambda }\right)\\ -6{\left(\frac{2\mu }{\sqrt{{\lambda }^2-4\mu }tanh\left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\xi +C\right)\right)+\lambda }\right)}^2\end{array}$$

(32)

When λ² − 4μ < 0, then

$$\begin{array}{l}\therefore u\left(\xi \right)=-6\mu -6\lambda \left(\frac{2\mu }{\sqrt{4\mu -{\lambda }^2}tan\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\xi +C\right)\right)-\lambda }\right)\\ -6{\left(\frac{2\mu }{\sqrt{4\mu -{\lambda }^2}tan\left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\xi +C\right)\right)-\lambda }\right)}^2\end{array}$$

(33)

When λ² − 4μ > 0, μ = 0, then

$$\therefore u\left(\xi \right)=-6\lambda \left(\frac{\lambda }{exp\left(\lambda \left(\xi +C\right)\right)-1}\right)-6{\left(\frac{\lambda }{exp\left(\lambda \left(\xi +C\right)\right)-1}\right)}^2$$

(34)

When λ² − 4μ = 0, μ ≠ 0, λ ≠ 0, then

$$\therefore u\left(\xi \right)=-6\mu +6\lambda \left(\frac{{\lambda }^2\left(\xi +C\right)}{2\left(\lambda \left(\xi +C\right)+2\right)}\right)-6{\left(\frac{{\lambda }^2\left(\xi +C\right)}{2\left(\lambda \left(\xi +C\right)+2\right)}\right)}^2$$

(35)

$$\begin{array}{l}\mathrm{When}{\lambda }^2-4\mu =0,\mu =\lambda =0,\mathrm{then}\therefore u\left(\xi \right)\\ =-6{\left(\frac{1}{\xi +C}\right)}^2\end{array}$$

(36)

Remark-2: All of the solutions presented in this latter have been checked with Maple by putting them back into the original equations.

4. Results and discussion

In this paper we exerted the exp-function methods and the exp(−ϕ(ξ)) -expansion method as useful mathematical tools to construct topological soliton, non-topological soliton, periodic wave solutions for the Vakhnenko- Parkes equation. The methods have successfully handled with the aid of commercial software Maple-13 that greatly reduces the volume of computation and improves the results of the equation. We have achieved a family of solutions via exp-function method. It is worth declaring that some of our obtained solutions via the exp(−ϕ(ξ)) -expansion method is in good agreement with already published results which is presented in the Tables 1 and 2. The others are completely new solutions achieved by exp(−ϕ(ξ)) -expansion method.

Table 1 Comparison between Liu and He’s (Liu and He 2013 ) solutions and our solutions

Table 2 Comparison between Parkes’s (Parkes 2010b ) solutions and our solutions

4.1. Physical interpretation

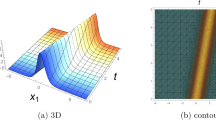
In this subsection, we describe the physical interpretation of the solutions for the Vakhnenko- Parkes equation. Solitons are solitary waves with stretchy dispersion possessions, which described many physical phenomena in soliton physics. Soliton preserve their shapes and speed after colliding with each other. Soliton solutions also give ascend to particle-like structures, such as magnetic monopoles etc. The solution (19) in Figure 1 of the equation (1) is represented the exact Bell type solitary (non-topological soliton) wave solution for the parameters b₀ = 4, w = 1 with − 3 ≤ x, t ≤ 3 via exp-function method. Since second family Eq. (30) has a constant different with first family it figure is also the exact Bell type solitary (non-topological soliton) wave solution. Others solutions via exp-function method are similar to this solution or can be obtained from this solution which profiles are similar to the Figure 1. The solution (32) obtained by the exp(−ϕ(ξ)) -expansion method is cuspon whose shape is depicted in the Figure 2 for the parameters λ = 3, μ = c = w = 1 with − 3 ≤ x, t ≤ 3.

Figure 1

Bell shape (non-topological) soliton solution of the Eq. ( 19 ) for the parameters b ₀ = 4, w = 1.

Figure 2

Cuspon soliton solution of the Eq. ( 32) for the parameters λ  = 3, μ  =  c  =  w  = 1 .

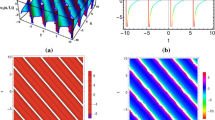
The solution (33) of the equation Eq. (11) is presented the periodic travelling wave solution for various values of the physical parameters. The Figure 3 has been shown the shape of the solution (33) for the parameters λ = 1, μ = c = 2, w = 1 with − 3 ≤ x, t ≤ 3.

Figure 3

Periodic solution of the Eq. ( 33) for the parameters λ = 1, μ = c = 2, w = 1 .

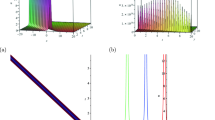
Solutions (34) of the equation Eq. (1) represent singular soliton solution for the parameters λ = w = 1, μ = c = 0 with − 3 ≤ x, t ≤ 3 whose shape is given by the Figure 4.

Figure 4

Singular soliton solution of the Eq. ( 34) for the parameters λ = w = 1, μ = c = 0 .

Finally, solution (35) and (36) are similar type solutions and they represent the multiple soliton solution. Omitting one figure we depicted the Figure 5 of the Eq. (35) for the parameters λ = w = 1, μ = c = 0 with − 3 ≤ x, t ≤ 3.

Figure 5

Multiple soliton solution of the Eq. ( 35) for the parameters λ = c = 2, μ = c = 1 .

4.2. Graphical representations

The graphical illustrations of the solutions are given below in the figures (Figures 1, 2, 3, 4 and 5) with the aid commercial software of Maple-13.

5. Conclusion

In this research some new solitary wave solutions of the Vakhnenko-Parkes equation is found using the exp-function method and the exp(−ϕ(ξ)) -expansion method. As a results two family of bell type solitary wave solutions Eq. (19) or Eq. (26) and Eq. (30) using exp-function method and five solutions Eq. (32)-Eq. (36) including cuspon, singular soliton, multiple soliton and periodic solutions are achieved via exp(−ϕ(ξ)) -expansion method of the Vakhnenko- Parkes equation exist for real sense depends on different relevant physical parameters. Numerical results of the solutions for real sense by using Maple software have been shown graphically and discussed. This will have a good sense to encourage the extensive application of the equations.