Abstract
Exact solutions of nonlinear evolution equations (NLEEs) play a vital role to reveal the internal mechanism of complex physical phenomena. In this work, the exact traveling wave solutions of the Boussinesq equation is studied by using the new generalized (G′/G)-expansion method. Abundant traveling wave solutions with arbitrary parameters are successfully obtained by this method and the wave solutions are expressed in terms of the hyperbolic, trigonometric, and rational functions. It is shown that the new approach of generalized (G′/G)-expansion method is a powerful and concise mathematical tool for solving nonlinear partial differential equations in mathematical physics and engineering.
PACS
05.45.Yv, 02.30.Jr, 02.30.Ik
Similar content being viewed by others
Introduction
Large varieties of physical, chemical, and biological phenomena are governed by nonlinear partial differential equations. One of the most exciting advances of nonlinear science and theoretical physics has been the development of methods to look for exact solutions of nonlinear partial differential equations. Exact solutions to nonlinear partial differential equations play an important role in nonlinear science, especially in nonlinear physical science since they can provide much physical information and more insight into the physical aspects of the problem and thus lead to further applications. Nonlinear wave phenomena of dispersion, dissipation, diffusion, reaction and convection are very important in nonlinear wave equations. In recent years, quite a few methods for obtaining explicit traveling and solitary wave solutions of nonlinear evolution equations have been proposed. A variety of powerful methods, such as, the inverse scattering transform method (Ablowitz and Clarkson 1991), the homogeneous balance method (Fan 2000a), the Exp-function method (He and Wu 2006; Akbar and Ali 2012), the modified simple equation method (Jawad et al. 2010; Khan et al. 2013), the novel (G′/G)-expansion method (Alam et al. 2014; Alam and Akbar 2014), the improved (G′/G)- expansion method (Zhang et al. 2010), the (G′/G)- expansion method (Wang et al. 2008; Bekir 2008; Zayed 2009; Zhang et al. 2008; Akbar et al. 2012), the tanh-function method (Wazwaz 2005), the extended tanh-function method (Fan 2000b; El-Wakil and Abdou 2007), the sine-cosine method (Wazwaz 2004), the modified Exp-function method (Usman et al. 2013), the generalized Riccati equation method (Yan and Zhang 2001), the Jacobi elliptic function expansion method (Liu 2005; Chen and Wang 2005), the Hirota’s bilinear method (Wazwaz 2012), the Miura transformation method (Bock and Kruskal 1979), the new generalized (G′/G)-expansion method (Naher and Abdullah 2013; Alam et al. 2013a; Alam and Akbar 2013a; Alam and Akbar 2013b; Alam et al. 2013b), the Cole-Hopf transformation method (Salas and Gomez 2010), the Adomian decomposition method (Adomain 1994; Wazwaz 2002), the ansatz method (Hu 2001a; Hu 2001b), the exp(–Ф(η))-expansion method (Khan and Akbar 2013), the method of bifurcation of planar dynamical systems (Li and Liu 2000; Liu and Qian 2001), and so on.
The objective of this article is to apply the new generalized (G'/G) expansion method to construct the exact traveling wave solutions of the Boussinesq equation.
The outline of this paper is organized as follows: In Section Description of the new generalized (G'/G)-expansion method, we give the description of the new generalized (G'/G) expansion method. In Section Application of the method, we apply this method to the Boussinesq equation, results and discussions and graphical representation of solutions. Conclusions are given in the last section.
Description of the new generalized (G′/G)-expansion method
Let us consider a general nonlinear PDE in the form
where v=v(x,t) is an unknown function, Ф is a polynomial in v(x,t) and its derivatives in which highest order derivatives and nonlinear terms are involved and the subscripts stand for the partial derivatives.
Step 1: We combine the real variables x and t by a complex variable η
where V is the speed of the traveling wave. The traveling wave transformation (2) converts Eq. (1) into an ordinary differential equation (ODE) for v=v(η):
where ψ is a polynomial of v and its derivatives and the superscripts indicate the ordinary derivatives with respect to η.
Step 2: According to possibility, Eq. (3) can be integrated term by term one or more times, yields constant(s) of integration. The integral constant may be zero, for simplicity.
Step 3. Suppose the traveling wave solution of Eq. (3) can be expressed as follows:
where either α N or β N may be zero, but could be zero simultaneously, α i (i= 0,1,2…,N) and β i (i= 1,2,…,N) and d are arbitrary constants to be determined and M(η) is
where G=G(η) satisfies the following auxiliary nonlinear ordinary differential equation:
where the prime stands for derivative with respect to η; A, B, C and E are real parameters.
Step 4: To determine the positive integer N, taking the homogeneous balance between the highest order nonlinear terms and the derivatives of the highest order appearing in Eq. (3).
Step 5: Substitute Eq. (4) and Eq. (6) including Eq. (5) into Eq. (3) with the value of N obtained in Step 4, we obtain polynomials in (d+M)N (N=0,1,2,…) and (d+M)-N (N=0,1,2,…). Subsequently, we collect each coefficient of the resulted polynomials to zero, yields a set of algebraic equations for α i (i=0,1,2,…,N) and β i (i=1,2,…,N), d and V.
Step 6: Suppose that the value of the constants α i (i=0,1,2,…,N), β i (i=1,2,…,N), d and V can be found by solving the algebraic equations obtained in Step 5. Since the general solutions of Eq. (6) are known to us, inserting the values of α i (i=0,1,2,…,N), β i (i=1,2,…,N), d and V into Eq. (4), we obtain more general type and new exact traveling wave solutions of the nonlinear partial differential Equation (1).
Step 7: Using the general solution of Eq. (6), we have the following solutions of Eq. (5):
Family 1: When B ≠ 0, ω=A-C and Ω =B2 + 4E(A-C) > 0,
Family 2: When B ≠ 0, ω=A-C and Ω =B2 + 4E(A-C) < 0,
Family 3: When B ≠ 0, ω = A-C and Ω = B2 + 4 E(A-C) = 0,
Family 4: When B = 0, ω = A-C and Δ=ωE>0,
Family 5: When B = 0, ω = A-C and Δ = ωE < 0,
Application of the method
In this section, we will put forth the new generalized (G'/G) expansion method to construct many new and more general traveling wave solutions of the Boussinesq equation. Let us consider the Boussinesq equation,
Now, we will use the traveling wave transformation Eq. (2) into the Eq. (12), which yields:
Eq. (13) is integrable, therefore, integrating with respect to η once yields:
where K is an integration constant which is to be determined.
Taking the homogeneous balance between highest order nonlinear term v2 and linear term of the highest order v″ in Eq. (14), we obtain N=2. Therefore, the solution of Eq. (14) is of the form:
where α0, α1, α2, β1, β2 and d are constants to be determined.
Substituting Eq. (15) together with Eqs. (5) and (6) into Eq. (14), the left-hand side is converted into polynomials in (d+M)N (N=0,1,2,.......) and (d+M)-N (N=1,2,…). We collect each coefficient of these resulted polynomials to zero yields a set of simultaneous algebraic equations (for simplicity, the equations are not presented) for α0, α 1 , α 2 , β1, β2d, K and V. Solving these algebraic equations with the help of computer algebra, we obtain following:
Set 1:
where n1 = ( - A2 + V2A2 - 12d2ω2 + 8Eω - 12Bdω - B2), n2 = ( - 2Edω + 3Bd2ω + 2d3ω2 - EB + B2d), n3 = - ( - 2Ed2ω + d4ω2 + 2Bd3ω + E2 + B2d2 - 2BdE), n4 = - ( - 8EB2ω + V4A4 - 2V2A4 - 16E2ω2 + A4 - B4), ω = A - C, V, d, A, B, C, E are free parameters.
Set 2:
Where ω = A-C, V, d, A, B, C, E are free parameters.
Set 3: , V=V, , , α1=0,
where n5 = ((V2 - 1)A2 + 8Eω + 2B2), n6 = - (16E2ω2 + 8EB2ω + B 4), n7 = ((V2 - 1)2A4 - 256E2ω2 - 128B2Eω -16B4), ω = A - C, V, A, B, C, E are free parameters.
For set 1, substituting Eq. (16) into Eq. (15), along with Eq. (7) and simplifying, yields following traveling wave solutions, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (16) into Eq. (15), along with Eq. (8) and simplifying, our exact solutions become, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (16) into Eq. (15), together with Eq. (9) and simplifying, our obtained solution becomes:
Substituting Eq. (16) into Eq. (15), along with Eq. (10) and simplifying, we obtain following traveling wave solutions, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (16) into Eq. (15), together with Eq. (11) and simplifying, our obtained exact solutions become, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
where η = x-Vt.
Again for set 2, substituting Eq. (17) into Eq. (15), along with Eq. (7) and simplifying, our traveling wave solutions become, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (17) into Eq. (15), along with Eq. (8) and simplifying yields exact solutions, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (17) into Eq. (15), along with Eq. (9) and simplifying, our obtained solution becomes:
Substituting Eq. (17) into Eq. (15), together with Eq. (10) and simplifying, yields following traveling wave solutions, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (17) into Eq. (15), along with Eq. (11) and simplifying, our exact solutions become, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
where η = x-Vt.
Similarly, for set 3, substituting Eq. (18) into Eq. (15), together with Eq. (7) and simplifying, yields following traveling wave solutions, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (18) into Eq. (15), along with Eq. (8) and simplifying, we obtain following solutions, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (18) into Eq. (15), along with Eq. (9) and simplifying, our obtained solution becomes:
Substituting Eq. (18) into Eq. (15), along with Eq. (10) and simplifying, yields following exact traveling wave solutions, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
Substituting Eq. (18) into Eq. (15), along with Eq. (11) and simplifying, our obtained exact solutions become, if C1 = 0 but C2 ≠ 0; C2 = 0 but C1 ≠ 0 respectively:
where η = x-Vt.
Results and discussions
It is worth declaring that some of our obtained solutions are in good agreement with already published results which are presented in the following tables (Table 1).
Beside this table, we obtain further new exact traveling wave solutions , , , , in this article, which have not been reported in the previous literature.
Graphical representation of the solutions
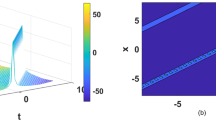
The graphical illustrations of the solutions are given below in the figures with the aid of Maple (Figures 1, 2, 3, 4 and 5).
The solutions corresponding to , , is identical to the solution , the solution corresponding to is identical to the solution , the solution corresponding to is identical to the solution , the solution corresponding to , is identical to the solution and the solution corresponding to , is identical to the solution .
Conclusion
In this paper, we obtain the traveling wave solutions of the Boussinesq equation by using the new approach of generalized (G'/G) -expansion method. We apply the new approach of generalized (G'/G)-expansion method for the exact solution of this equation and constructed some new solutions which are not found in the previous literature. This study shows that the new generalized (G'/G)-expansion method is quite efficient and practically well suited to be used in finding exact solutions of NLEEs. Also, we observe that the new generalized (G'/G)-expansion method is straightforward and can be applied to many other nonlinear evolution equations.
References
Ablowitz MJ, Clarkson PA: Soliton, nonlinear evolution equations and inverse scattering. New York: Cambridge University Press; 1991.
Adomain G: Solving frontier problems of physics: The decomposition method. Boston: Kluwer Academic Publishers; 1994.
Akbar MA, Ali NHM: New Solitary and Periodic Solutions of Nonlinear Evolution Equation by Exp-function Method. World Appl Sci J 2012, 17(12):1603-1610.
Akbar MA, Ali NHM, Zayed EME: A generalized and improved ( G′/G )-expansion method for nonlinear evolution equations. Math Prob Engr 2012., 2012(2012): doi: 10.1155/2012/459879
Alam MN, Akbar MA: Exact traveling wave solutions of the KP-BBM equation by using the new generalized ( G′/G )-expansion method. Springer Plus 2013, 2(1):617. doi: 10.1186/2193-1801-2-617 10.1186/2193-1801-2-617
Alam MN, Akbar MA: Traveling wave solutions of nonlinear evolution equations via the new generalized ( G′/G )-expansion method. Univ J Comput Math 2013, 1(4):129-136. doi: 10.13189/ujcmj.2013.010403
Alam MN, Akbar MA: Traveling wave solutions of the nonlinear (1 + 1)-dimensional modified Benjamin-Bona-Mahony equation by using novel ( G′/G )-expansion. Phys Rev Res Int 2014, 4(1):147-165.
Alam MN, Akbar MA, Khan K: Some new exact traveling wave solutions to the (2 + 1)-dimensional breaking soliton equation. World Appl Sci J 2013, 25(3):500-523.
Alam MN, Akbar MA, Roshid HO: Study of nonlinear evolution equations to construct traveling wave solutions via the new approach of generalized ( G′/G )-expansion method. Math Stat 2013, 1(3):102-112. doi: 10.13189/ms.2013.010302
Alam MN, Akbar MA, Mohyud-Din ST: A novel ( G′/G )-expansion method and its application to the Boussinesq equation. Chin Phys B 2014, 23(2):020203-020210. doi: 10.1088/1674-1056/23/2/020203 10.1088/1674-1056/23/2/020203
Bekir A: Application of the ( G′/G )-expansion method for nonlinear evolution equations. Phys Lett A 2008, 372: 3400-3406. 10.1016/j.physleta.2008.01.057
Bock TL, Kruskal MD: A two-parameter Miura transformation of the Benjamin-One equation. Phys Lett A 1979, 74: 173-176. 10.1016/0375-9601(79)90762-X
Chen Y, Wang Q: Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic functions solutions to (1 + 1)-dimensional dispersive long wave equation. Chaos, Solitons Fractals 2005, 24: 745-757. 10.1016/j.chaos.2004.09.014
El-Wakil SA, Abdou MA: New exact travelling wave solutions using modified extended tanh-function method. Chaos, Solitons Fractals 2007, 31(4):840-852. 10.1016/j.chaos.2005.10.032
Fan EG: Two new applications of the homogeneous balance method. Phys Lett A 2000, 265: 353-357. 10.1016/S0375-9601(00)00010-4
Fan E: Extended tanh-function method and its applications to nonlinear equations. Phys Lett A 2000, 277(4–5):212-218.
He JH, Wu XH: Exp-function method for nonlinear wave equations, Chaos. Solitons Fract 2006, 30: 700-708. 10.1016/j.chaos.2006.03.020
Hu JL: Explicit solutions to three nonlinear physical models. Phys Lett A 2001, 287: 81-89. 10.1016/S0375-9601(01)00461-3
Hu JL: A new method for finding exact traveling wave solutions to nonlinear partial differential equations. Phys Lett A 2001, 286: 175-179. 10.1016/S0375-9601(01)00291-2
Jawad AJM, Petkovic MD, Biswas A: Modified simple equation method for nonlinear evolution equations. Appl Math Comput 2010, 217: 869-877. 10.1016/j.amc.2010.06.030
Khan K, Akbar MA: Application of exp(–Ф( η ))-expansion method to find the exact solutions of modified Benjamin-Bona-Mahony equation. World Appl Sci J 2013, 24(10):1373-1377.
Khan K, Akbar MA, Alam MN: Traveling wave solutions of the nonlinear Drinfel’d-Sokolov-Wilson equation and modified Benjamin-Bona-Mahony equations. J Egyptian Math Soc 2013, 21: 233-240. http://dx.doi.org/10.1016/j.joems.2013.04.010 10.1016/j.joems.2013.04.010
Li JB, Liu ZR: Smooth and non-smooth traveling waves in a nonlinearly dispersive equation. Appl Math Model 2000, 25: 41-56. 10.1016/S0307-904X(00)00031-7
Liu D: Jacobi elliptic function solutions for two variant Boussinesq equations. Chaos, Solitons Fractals 2005, 24: 1373-1385. 10.1016/j.chaos.2004.09.085
Liu ZR, Qian TF: Peakons and their bifurcation in a generalized Camassa-Holm equation. Int J Bifur Chaos 2001, 11: 781-792. 10.1142/S0218127401002420
Naher H, Abdullah FA: New approach of ( G′/G )-expansion method and new approach of generalized ( G′/G )-expansion method for nonlinear evolution equation. AIP Adv 2013, 3: 032116. doi: 10.1063/1.4794947 10.1063/1.4794947
Neyrame A, Roozi A, Hosseini SS, Shafiof SM: Exact travelling wave solutions for some nonlinear partial differential equations. J King Saud Univ (Sci) 2010, 22: 275-278. 10.1016/j.jksus.2010.06.015
Salas AH, Gomez CA: Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation. Math Probl Eng 2010., 2010: Art. ID 194329 14 pages
Usman M, Nazir A, Zubair T, Rashid I, Naheed Z, Mohyud-Din ST: Solitary wave solutions of (3 + 1)-dimensional Jimbo Miwa and Pochhammer-Chree equations by modified Exp-function method. Int J Modern Math Sci 2013, 5(1):27-36.
Wang ML, Li XZ, Zhang J: The ( G′/G )-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics. Phys Lett A 2008, 372: 417-423. 10.1016/j.physleta.2007.07.051
Wazwaz AM: Partial Differential equations: Method and Applications. London: Taylor and Francis; 2002.
Wazwaz AM: A sine-cosine method for handle nonlinear wave equations. Appl Math Comput Model 2004, 40: 499-508. 10.1016/j.mcm.2003.12.010
Wazwaz AM: The tanh method for generalized forms of nonlinear heat conduction and Burgers–Fisher equations. Appl Math Comput 2005, 169: 321-338. 10.1016/j.amc.2004.09.054
Wazwaz AM: Multiple-soliton solutions for a (3 + 1)-dimensional generalized KP equation. Commun Nonlin Sci Numer Simulat 2012, 17: 491-495. 10.1016/j.cnsns.2011.05.025
Yan Z, Zhang H: New explicit solitary wave solutions and periodic wave solutions for Whitham Broer-Kaup equation in shallow water. Phys Lett A 2001, 285(5–6):355-362.
Zayed EME: The ( G′/G )-expansion method and its applications to some nonlinear evolution equations in the mathematical physics. J Appl Math Comput 2009, 30: 89-103. 10.1007/s12190-008-0159-8
Zhang S, Tong J, Wang W: A generalized ( G′/G )-expansion method for the mKdV equation with variable coefficients. Phys Lett A 2008, 372: 2254-2257. 10.1016/j.physleta.2007.11.026
Zhang J, Jiang F, Zhao X: An improved ( G′/G )-expansion method for solving nonlinear evolution equations. Int J Com Math 2010, 87(8):1716-1725. 10.1080/00207160802450166
Acknowledgements
The authors would like to express their sincere thanks to the anonymous referees for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors, viz MNA, MAA and HOR with the consultation of each other carried out this work and drafted the manuscript together. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Alam, M.N., Akbar, M.A. & Roshid, HO. Traveling wave solutions of the Boussinesq equation via the new approach of generalized (G′/G)-expansion method. SpringerPlus 3, 43 (2014). https://doi.org/10.1186/2193-1801-3-43
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2193-1801-3-43