Probabilistic failure modelling of reinforced concrete structures subjected to chloride penetration

Abstract

Structural durability is an important criterion that must be evaluated for every type of structure. Concerning reinforced concrete members, chloride diffusion process is widely used to evaluate durability, especially when these structures are constructed in aggressive atmospheres. The chloride ingress triggers the corrosion of reinforcements; therefore, by modelling this phenomenon, the corrosion process can be better evaluated as well as the structural durability. The corrosion begins when a threshold level of chloride concentration is reached at the steel bars of reinforcements. Despite the robustness of several models proposed in literature, deterministic approaches fail to predict accurately the corrosion time initiation due the inherent randomness observed in this process. In this regard, structural durability can be more realistically represented using probabilistic approaches. This paper addresses the analyses of probabilistic corrosion time initiation in reinforced concrete structures exposed to chloride penetration. The chloride penetration is modelled using the Fick's diffusion law. This law simulates the chloride diffusion process considering time-dependent effects. The probability of failure is calculated using Monte Carlo simulation and the first order reliability method, with a direct coupling approach. Some examples are considered in order to study these phenomena. Moreover, a simplified method is proposed to determine optimal values for concrete cover.

Introduction

Concrete structures, especially reinforced concrete structures, are one of the most used types of structures around world. When it is located in non-aggressive environments, these types of structures respect, in general, its structural life predicted. However, the structural durability can be strongly reduced by degradation processes of environmental and/or functional origins (Angst et al.2009; Guzmán et al.2011). Among these processes, it is worth to mention the chloride penetration, carbonation, fatigue, and creep. Durability can be measured as a period of time in which the structure maintains, at least, minimal functional conditions, resistance, and external aspects required in its design.

Considering reinforced concrete structures, durability and service life should be parameters with major importance on rational design. In these cases, analyses and criteria based on environmental aspects, prediction of repairs, and maintenance costs should be required on design stage (Nogueira et al.2012). These types of analyses are accurately performed considering probabilistic approaches, due the large randomness contained in environmental phenomena. In this regard, the requirement of time-variant reliability assessment of structural durability has becoming increasingly accepted (Xiang and Zhao2007; Sarveswaran and Roberts1999; Kong et al.2002).

Reinforcement's corrosion is directly responsible by durability and failure of reinforced concrete structures. Moreover, chloride ingress is identified as one of the major factors that cause reinforcement's corrosion. When the corrosion begins, the structure is affected by several phenomena like reduction of reinforcement's cross-section, bursting of concrete, and adherence loss between steel and concrete (Kirkpatrick et al.2002; Jung et al.2003), all of them reduce the structural durability.

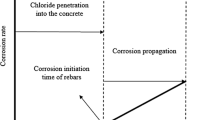
The deterioration process of reinforced concrete structures due to steel's corrosion can be divided into two stages: the initiation and the propagation periods. During the initiation period, chlorides diffuse through concrete toward the reinforcements. The chloride concentration along the concrete cover grows until reaches a threshold value, which triggers the corrosion of steel. The propagation period includes the period of time from the start of corrosion to a critical steel loss. Compared with the first stage, the propagation period is relatively short. Therefore, the chloride diffusion process is frequently used to indicate the durability and service life conditions of concrete structures (Tuutti1982).

Several models have been proposed in literature to deal properly with the corrosion phenomenon in reinforced concrete structures. Most of them propose deterministic approaches in order to model this structural problem. However, due to the large number of uncertainties, which are inherent at this problem, it can only be accurately analyzed considering probabilistic approaches. Among these models and formulations, it is worth to mention the research of Thirumalai et al. (2006); Enright and Frangopol (1998), DuraCrete (2000), Vu and Stewart (2000), and Balaji Rao et al. (2004), where the corrosion process was studied, considering several conditions and parameters. Based on these probabilistic models, durability and service life assessment analyses in reinforced concrete structures exposed to chloride penetration can be accurately performed (Stewart and Rosowsky1998; Estes and Frangopol2003; Suo and Stewart2009). Moreover, considering its results, maintenance and inspection plans, as well as the concrete cover, can be designed taking into account the randomness of each variable and the cost involved on each procedure.

The penetration of chlorides in concrete is controlled by complex interactions among physical and chemical mechanisms, where several sources of uncertainties are observed (Nogueira et al.2012). This phenomenon is often simplified, without significant representation loss, by a process governed only by diffusion process. In this regard, these problems can be modelled using Fick's diffusion law (Tuutti1982; Crank1975). This classical approach of diffusion considers the apparent coefficient of diffusion as constant along time and homogeneous in space. Moreover, this law assumes the concentration of chlorides on the environment as constant and admits the concrete in saturated condition. By coupling Fick's diffusion law with reliability algorithms, probabilistic analyses of chloride ingress in concrete structures can be performed.

In this paper, a coupled model based on mechanical behavior simulation and reliability algorithms is developed in order to allow probabilistic analyses of reinforced concrete structures subjected to chloride ingress. This model aims at quantifying the probability of corrosion start in reinforced concrete structures based on reliability algorithms. The mechanical model is based on Fick's diffusion law, which is capable to simulate the chloride penetration process in porous materials, as well as simulate the chloride concentration growth along time. Therefore, the chloride concentration at a given cover depth and time can be evaluated with this model. The probabilistic model is developed based on reliability algorithms. In order to determine the probability of failure, two reliability algorithms are considered: first order reliability method (FORM), by coupling directly the mechanical model with FORM, and Monte Carlo simulation. Both algorithms determine the probability of failure considering the failure scenarios achieved by the mechanical model based on Fick's diffusion law.

The coupled model developed is applied to the analysis of probabilistic chloride penetration problem in reinforced concrete structures. Some specific scenarios are considered, which differ by the environmental aggressiveness and concrete properties, and the results obtained are discussed. Considering the developed model, a simplified method is proposed in order to obtain optimal values for concrete cover and time intervals for periodic inspection procedures. This simplified method is the main contribution of this paper.

Methods

The mechanical model

Corrosion of reinforcements induced by chlorides occurs in the presence of oxygen and moisture when the chloride build-up within the structure exceeds a threshold value. Even for carefully constructed concrete structures, with negligible or practically non-chloride inherited at the construction stage, the gradual buildup of chloride content takes place slowly through ingress of chlorides from external sources.

The transport phenomenon associated with the movement of chlorides along structures exposed to aggressive environments is attributed, in most part, to diffusion of chloride ions into concrete pores under a concentration gradient. The coefficient of chloride diffusion, which depends upon the pore structure of concrete, characterizes this flow under a given external concentration of chloride. This parameter is assumed as a characteristic property of hardened concrete.

In order to simulate the chloride ingress and its transport into concrete pores, Fick's diffusion law (Crank1975) has been widely applied and considered as an acceptable model. Fick's laws for diffusion are applicable for homogeneous, isotropic, and inert materials (Dhir et al.1998). Moreover, the mechanical properties related to diffusion process are assumed to be identical along all directions and kept constants along time. Considering concrete, these hypotheses are not completely satisfied, because concrete is well known as heterogeneous, anisotropic, and chemically reactive (continued hydration and micro-cracking process) material. However, the methods commonly adopted for chloride transportation modelling in concrete consider this process as governed only by ionic diffusion. Then, it assumes that the concrete cover is completely saturated. Therefore, it makes the hypotheses of Fick's laws acceptable for chloride ingress modelling, because, in this case, the material is assumed completely saturated, with unidirectional chloride flux, i.e., from the exterior surface into the concrete depth. When chloride diffuses into porous concrete, a change in chloride concentration, C, occurs at any time, t, in every point, x, of the concrete structure, i.e., it is a non-steady state of diffusion. In order to simplify its analysis, the diffusion problem is considered as one-dimensional. Many engineering problems of chloride ingress, as those discussed in this paper, can be solved considering this simplification.

The assumption of Fick's diffusion theory is that the transport of chlorides into concrete though a unit section area of concrete per unit of time (the flux F) is proportional to the gradient concentration of chlorides measured at normal direction of section. Then:

$$F=-D\frac{\partial C}{\partial x}.$$

(1)

The negative sign on the equation above arises because the diffusion of chlorides occurs in the opposite direction of the increasing concentration of chlorides. The constant of proportionality D, presented in Equation 1, is called chloride diffusion coefficient. In general, D is not constant but depends on many parameters as the time for which diffusion has taken place, location in the concrete, and composition of the concrete among other factors. If the chloride diffusion coefficient is constant, Equation 1 is usually referred as Fick's first diffusion law. If this is not the case, the relation is usually referred as Fick's first general diffusion law.

There are some cases where this simple relation should not be applied. In this regard, it is worth to mention the cases where the diffusion process may be irreversible or has a history dependence. In such cases, Fick's diffusion law is not valid, and the diffusion process is referred as anomalous. However, non-observation so far indicates that the chloride diffusion into concrete should be characterized as an anomalous diffusion. Fick's second law can be derived considering the mass balance principle. Therefore:

$$\frac{\partial C}{\partial t}=\frac{\partial }{\partial x}\left(-D\frac{\partial C}{\partial x}\right).$$

(2)

In order to apply Fick's second diffusion law, in this form, for concrete exposed to chloride during a long period of time, one ought to know the variation of the chloride diffusion coefficient along time t. If only few observations exist in a specific case, it is possible to estimate upper and lower boundaries for the variation of D in time. Despite this dependence, an especial case can be considered where the chloride diffusion coefficient is independent of location, x, time, t, and chloride concentration, C. In this case, Fick's second law can be written in the simple form:

$$\frac{\partial C}{\partial t}=-D_0\frac{{\partial }^{2}C}{\partial x^2},$$

(3)

in which D₀ is the constant coefficient of diffusion.

The solution of the differential equation presented above, for a semi-infinite domain with a uniform concentration at the structural surface, is given by:

$$C\left(x,t\right)=C_0\mathit{erfc}\left[\frac{x}{2\sqrt{D_{0}t}}\right],$$

(4)

where C₀ is the chloride concentration at the structural surface supposed constant in the time; erfc is the complementary error function.

In this paper, Equation 4 is used to evaluate the chloride concentration, C(x, t), at a given depth and time into reinforced concrete structure. Therefore, Equation 4 is an analytical solution which composes the mechanical model. Based on the chloride concentration values at a given structural depth, it is possible to assess the structural safety. However, in order to allow the safety assessment, a coupling among the described mechanical model and reliability algorithms has to be considered. These coupling models take into account the randomness that emerges on the diffusion process.

Based on these models, the structural safety variation along time can be assessed. Therefore, one of the most important products of these coupling is the possibility to choose the time of structural maintenance based on a given reliability index target. Moreover, these models allow the determination of the cover depth, considering a structural safety level target. The determination of the cover depth and time for maintenance considering uncertainties related to mechanical structural behavior is the main contribution of this paper.

Reliability concepts and methods of analysis

General concepts

The reliability analyses aim at computing the probability of failure regarding a specific failure scenario known as limit state. The first step in the reliability assessment is to identify the basic set of random variables X = [x₁, x₂,…, x _n ]^T from which uncertainties have to be considered. For all these variables, probability distributions are attributed in order to model its randomness. These probability distributions can be defined by physical observations, statistical studies, laboratory analysis, and expert's opinion. The number of random variables is an important parameter to determine the computing time consumed during the reliability analysis. In order to reduce the size of the random variable space, it is strongly recommended to consider all variables as deterministic, the uncertainties of which lead to minor effects on the value of probability of failure.

The second step consists of defining a number of potentially critical failure modes. For each of them, a limit state function, G(X), separates the space into two regions as described in Figure 1: the safe domain where G(X) > 0, and the failure domain where G(X) < 0. The boundary between these two domains is defined by G(X) = 0, known as the limit state itself. It is worth to mention that an explicit expression of the limit state function is usually not possible. When numerical mechanical models are used, it can be computed only at a desired number of points. In this paper, the limit state is defined using the critical failure modes calculated using Equation 4.

Figure 1

Domains of failure and safety for two random variables.

The probability of failure is evaluated by integrating, over the failure domain, the joint density function as presented by (Ditlevsen and Madsen1996):

$$P_{\mathrm{f}}={\displaystyle {\int }_{G\le 0}{f}_X\left(x_1,x_2,\dots ,x_n\right)d{x}_1,d{x}_2,\cdots d{x}_n},$$

(5)

in which f _X (X) is the joint density function of the variables, X.

As the evaluation of the integral defined by Equation 5 is almost impossible in practice, alternative procedures have been developed on the basis of reliability index concept, β, (Hasofer and Lind1974). This parameter is defined by the distance between the mean point and the failure point placed at the limit state function G(X) = 0 in the normalized space of random variables. The reliability index allows us to calculate the probability of failure using the FORM as follows:

$$P_{\mathrm{f}}=\Phi \left(-\beta \right),$$

(6)

in which Φ(·) is the standard Gaussian cumulated distribution function.

There are some alternative procedures, available in the reliability theory, which allow the evaluation of probabilities of structural failure. These procedures are based on numerical simulation techniques. The most important approach, among them, is the Monte Carlo simulation method. However, when numerical mechanical models (expensive in terms of computational work) are adopted, this approach may be unreliable due to the large sampling required for simulation, especially when the probability of failure to be assessed is small, i.e., 10⁻³ or lesser.

In this study, two reliability approaches are adopted. The first is known as direct method, as it is the result of the direct coupling of a mechanical model at the FORM. The second approach used is the classical Monte Carlo simulation. In both cases, the models are used to evaluate the probabilities of failure considering the chloride ingress process in reinforced concrete structures. These approaches will be discussed in the following sections.

Direct method

The basic procedure in this approach consists of directly coupling the reliability model FORM with the mechanical model given by Equation 4. This approach has demonstrated to be accurate and robust for analysis of many complex engineering problems, as discussed by Leonel et al. (2010,2011a,2012).

As described in the previous section, the limit state function defines the boundary between safe and failure domains. Considering chloride penetration problem, the limit state function can be written in terms of time for corrosion initiation:

$$G\left(X\right)=t_{\mathrm{R}}\left(X\right)-t_{\mathrm{a}},$$

(7)

in which t_R is the time for corrosion initiation that depends on the group of random variables X; t_a is the structural life-time expected in design which was considered as a deterministic parameter.

The time t_R is evaluated using Equation 4 assuming the chloride concentration C(x, t) as known at a given position x inside the concrete. Actually, C(x, t) is assumed to be equal to the chloride concentration threshold over which the steel corrosion is triggered on failure condition. The range of x position, in this case, is the concrete cover. It assumes zero at the external surface of the structural member and the cover value at the reinforcement's surface inside the concrete. In this regard, the time for corrosion initiation can be determined explicitly from Equation 4 as:

$$t_{\mathrm{R}}=\frac{1}{D_0}{\left\{\frac{x}{2\mathit{erfc}\left[C\left(x,t\right)/C_0\right]}\right\}}^2.$$

(8)

In order to include invariance measure of safety, the random variables, defined on physical space, are transformed into independent standard Gaussian variables (Hasofer and Lind1974) using appropriate probabilistic transformations. The limit state function, defined on physical space, G(X) = 0, is transformed into H(U) = 0 on standard normalized space, where U = u₁, u₂, …, u _n ^T denotes the standard Gaussian variables.

In this standard space, the reliability index β is given by the minimum distance between the failure domain and the origin of the standard space. The reliability index can be evaluated by solving a constrained optimization problem, as described below:

Find P*

which minimizes

$$\beta =\sqrt{U^T·U}$$

(9)

subject to H(U) = 0.

The solution of this problem converges to the failure point nearest to the space origin, known as design point or the most probable failure point P*. In standard space, the distance between this point and the origin is known as reliability index, as shown in Figure 2. The reliability index β can be achieved by applying any optimization algorithm. A particular algorithm, which is efficient in this case, to solve reliability problems is the HLRF algorithm (Rackwitz and Fiessler1978). This optimization algorithm can be coupled directly to the mechanical model. As the time for corrosion initiation is known point-by-point, the resistance t_R is known. Consequently, the limit state function is determined point-by-point. Then, the gradient of the limit state function can be determined using any numerical procedure. In this paper, the forward finite differences technique for this proposal was adopted.

Figure 2

Reliability index and design point.

Some difficulties arise from Equation 8, particularly its gradients evaluation, due to the presence of the complementary error function. A natural barrier that can be remarked in this type of approach is the numerical error due to the finite difference procedure, which may affect the convergence of the coupled procedure, as well as the precision of the solution, especially for nonlinear transient phenomena. However, for all problems studied in this paper, numerical problems related to finite differences method were not observed. Moreover, it was verified that the direct coupling procedure gives accurate results and stable convergence rate with low number of mechanical analyses.

Monte Carlo simulation

Monte Carlo method is a numerical simulation approach widely used in reliability problems (Nowak and Collins2000). In this method, a sampling of random variables is used to construct a set of values aiming to describe the failure and safe spaces, and calculate Equation 5. The sampling is constructed based on the statistical distributions assigned for each random variable introduced in the problem. As this method deals with simulations of the limit state function, the bigger the sampling adopted, the more accurate will be the description of spaces and the probability of failure achieved.

The kernel of this method is the construction of a sampling for each random variable involved in the problem. Then, the domain of safety and failure points are prospected by simulating Equation 7, as described in Figure 3. The probability of failure is calculated, for Monte Carlo simulation, using the following expression:

$$P_{\mathrm{f}}={\displaystyle {\int }_{G\le 0}{f}_X\left(x_i\right)d{x}_i}={\displaystyle {\int }_{G\le 0}I\left(x_i\right)f_X\left(x_i\right)d{x}_i=E\left[I\left(x_i\right)\right]}.$$

(10)

Figure 3

Monte Carlo's sampling for two random variables.

The function I(x _i ) can be written as:

$$I\left(x_i\right)=\{\begin{array}{c}\hfill 1\to G\le 0\hfill \\ \hfill 0\to G>0\hfill \end{array}$$

(11)

By simulating the limit state function for a convenient range of sampling, the mean value of I(x _i ) will be an estimator for the probability of failure. Then:

$$\overline{P_f}=E\left[I\left(x_i\right)\right]=\frac{1}{N}{\displaystyle \sum }_{i=1}^{N}I\left(x_i\right).$$

(12)

The disadvantage of this method is related to the large amount of simulations required to compute accurately the probability of failure. Normally, in order to estimate accurately the probability of failure of 10⁻ⁿ, the number of simulations must be higher than 10^{n + 2} or 10^{n + 3}. It means, in civil engineering structures, where the probabilities of failure are in between 10⁻³ to 10⁻⁶, at least 10⁵ to 10⁹ realizations of the limit state function is required. When complex numerical mechanical models are involved, which lead to high computational work, this method may be not reliable. However, theoretically, this method leads to the real probability of failure when the sampling range becomes infinite.

Methodology of analysis

The corrosion phenomenon modelling in reinforced concrete structures has to take into account two different stages, as illustrated in Figure 4. The first one is related to chloride ingress into porous concrete. In this stage, the chloride concentration, along the cover depth, increases as the time passes. Then, the corrosion starts when the chloride concentration surrounding the reinforcements reaches a threshold level, leading to the loss of the concrete chemical passive protection. At the end of this stage, the steel of reinforcements remains undamaged. The second stage, called propagation stage, is characterized by the reduction of the reinforcement's cross-sections, which generates the loss of structural strength along the time.

Figure 4

Corrosion process of the reinforcement cross-section area.

Compared with the first stage, the propagation period is relatively short. Therefore, the time for corrosion initiation has been widely adopted for structural durability and safety assessments (Nogueira et al.2012). In this regard, the objective of this paper is to assess the probability of failure considering the failure scenario predicted by initiation stage. Therefore, the failure is observed when the chloride concentration at the reinforcement's depth reaches the threshold level. The main parameters considered for all reliability analyses performed are the following:

• Chloride concentration threshold at the interface between concrete and reinforcement bars, which defines the beginning of the corrosion process, C(x, t). This parameter was studied experimentally by Vu and Stewart (2000).

• Chloride concentration at the structural surface, C₀. This parameter is related to the environment aggressiveness, and its reference's values may be determined by experimental observations, as presented by Vu and Stewart (2000), or defined using an international concrete standard design (Brazilian Association of Technical Standards2003).

• Concrete diffusion coefficient, D₀, which has been studied by Papadakis et al. (1996).

• Structural depth, which in this study, is defined as the reinforcement concrete cover, x.

It is worth to stress that initial cracks due concrete cure and/or bending/shear effects and longitudinal cracking have not been considered in the formulation presented in this paper. These phenomena affect the corrosion process, and its modelling can be accurately performed using numerical methods as finite element method and boundary element method (Leonel and Venturini2011; Leonel et al.2011b).

According to Vu and Stewart (2000), the chloride concentration at structural surfaces is a function of the atmosphere (environment) where these elements are located. The cover depth is also defined according to the environment, which is stated by international concrete standard designs in categories of aggressiveness. In particular, the values shown in Brazilian Association of Technical Standards (2003) have been used in this paper. The coefficient of diffusion of concrete, which represents the material resistance against chloride ingress, depends on the water/cement ratio (w/c). If the proportion of water is high, the empty volumes inside the matrix due to the cure process of the concrete will also be high. Consequently, the material permeability will be high, and the material resistance against the chloride penetration will be low. Therefore, in regions close to the coast, it is strongly recommended to construct reinforced concrete structures with lower water/cement ratio and/or large covers.

The proposed probabilistic model allows the evaluation of the probability of structural failure, taking into account the random variables previously presented. Moreover, this model is capable to describe the dependency relation between the probability of failure and time. Then, the proposed model can be used to solve an interesting structural problem which relates the determination of time intervals for structural maintenance plans based on structural safety.

In order to apply the proposed model on this problem, a given safety level, say target, must be defined. The mentioned safety level may be determined using the standard of JCSS (2001), where the prevention against structural failures is measured based on a target reliability index. As the chloride concentration at the structural cover increases along time, the safety against this failure mode reduces along time. Therefore, the intervals of time for periodic structural maintenance procedures, based on structural safety, are achieved when the reliability index calculated using the proposed model reaches the target reliability index stated by analyst. It is worth to mention that the repair procedures are assumed as perfect, i.e., after the maintenance the structure recovers its initial integrity conditions without chlorides. These intervals are determined as long as the parameters related to material, cover depth, and environment aggressiveness can be defined a priori.

Another application of the proposed model relates to the definition of values for cover depth and concrete properties (w/c ratio) based on a given safety level and the expected structural lifetime. When the intervals of time for structural maintenance and/or the expected structural lifetime are stated a priori, the w/c ratio and the cover depth values can be obtained by simulating the proposed model in order to define the couple of these values which lead the structure to maintain a safety level at least equal to the target reliability index during the specified period of time. In this application, the values of w/c ratio and cover depth are achieved when the reliability index given by the proposed model is equal to the target reliability index.

It is important to emphasize that these procedures do not take into account the costs involved neither in the maintenance procedure nor in the concrete production. However, these applications of the proposed model can be performed if analysts are interested in design considering, exclusively, safety criterion.

Results and discussion

In order to illustrate the applicability of the proposed model, probabilistic analyses were performed considering different scenarios and material properties aiming to evaluate the influence of the environment aggressiveness, w/c ratio and cover depth on the probability of structural failure due to chloride penetration. Four applications are considered, and in each of them, some specific aspects of the problem are explored.

Example 1

In this example, the probabilistic model is applied to the assessment of uncertainties related to chloride ingress in reinforced concrete structures. The results were obtained using direct method and Monte Carlo simulation approaches. Considering the direct method, the tolerance for convergence was verified in terms of reliability index and design point coordinate change, which have to be smaller than 10⁻⁴. It is worth to mention that considering this approach, only 65 limit state function runs were required in order to achieve the convergence. Moreover, this number of mechanical model runs is the highest observed among all scenarios considered. It confirms the good performance of direct method approach, which is capable to achieve the convergence with low computational work even in reliability problems involving non-Gaussian random variables and non-linear mechanical model. The analyses performed using Monte Carlo simulation considered a sampling of 10⁵ values for each random variable. It leads to 10⁵ simulations of the limit state function. Table 1 presents the statistical parameters adopted for all random variables considered in this application, which are based on the work of Vu and Stewart (2000) and of Suo and Stewart (2009).

Table 1 Statistical data for all random variables

According to the Brazilian Association of Technical Standards (2003), categories of aggressiveness (C.A.) II (moderate) and III (high) represent urban regions and coast/industrial areas, respectively. For each one of these C.A., there is a recommended concrete cover depth, x, which was adopted for the probabilistic analyses of each category.

The evolutions of the probability of corrosion initiation along the time, for both categories of aggressiveness considered in this application, are presented in Figures 5 and6. The results illustrate a considerable growth of the probability of corrosion initiation as time increases. Moreover, a strong dependency between the probability of corrosion initiation and the w/c ratio was also verified. This dependency was expected because the higher the w/c ratio, the higher the concrete permeability and, consequently, easier the chloride ingress will be.

Figure 5

Probability of failure versus time for C.A. II.

Figure 6

Probability of failure versus time for C.A. III.

Considering the horizon of time analyzed, for concretes with w/c ratio values higher than 0.5, the probability of failure, after 15 years of structural service life, tends to increase slower than in the first 15 years. Therefore, the derivative of probability of corrosion initiation after 15 years is smaller than in the first 15 years. This behavior reflects the chloride concentration evolution along time, which tends to saturate after 15 years. It is important to stress that this behavior was observed in both C.A. analyzed.

Example 2

This application aims at studying the influence of cover depth values on the probability of corrosion initiation considering two different scenarios of environment aggressiveness. The analyses were performed considering concretes composed of w/c ratios varying from 0.40 to 0.70. The analyses involved cover depth in the range of 10 to 60 mm. For each value of w/c, the mean value of cover depth was also varied, but its coefficient of variation was kept constant. This procedure was adopted because this study aims at describing the dependency of probability of failure with respect to w/c and cover depth parameters. The time was assumed as deterministic in this analysis. In order to consider all the combinations, 240 numerical reliability analyses were carried out. The direct method and Monte Carlo simulation were adopted for the evaluation of probability of failure and reliability indexes. Considering the direct method, the convergence is assumed when the difference, into two successive iterations, in terms of reliability index and design point coordinates is smaller than 10⁻⁴. Considering Monte Carlo simulation, a sampling of 10⁵ values for each random variable was adopted.

The computational time consumed in this analysis is relatively lower. Considering the direct method, the most expensive case required 65 limit state function calls, corresponding to less than 1 s of computational work. The Monte Carlo analyses required 10⁵ limit state function evaluation due to the sampling range adopted. However, it took less than 3 s of computational time process. The values adopted for all random variables considered in this application, as well its statistical information, are presented in Table 2, which are based on the work of Vu and Stewart (2000) and of Suo and Stewart (2009).

Table 2 Statistical data for all random variables

The evolution of probability of corrosion initiation in function of cover depth and w/c ratio, considering C.A. II, is presented in Figures 7,8, and9.

Figure 7

Evolution for probability of corrosion initiation. C.A. II structural lifetime equal to 5 years.

Figure 8

Evolution for probability of corrosion initiation. C.A. II structural lifetime equal to 15 years.

Figure 9

Evolution for probability of corrosion initiation. C.A. II structural lifetime equal to 25 years.

As presented on the three figures above, the probability of corrosion initiation reduces faster when the cover thickness increases from 10 to 40 mm. However, this reduction tends to stabilize when the cover depth is larger. Then, these results show that by increasing the cover thickness, an effective improvement on the structural safety is not observed from a certain value of depth. From this value, the structural cost grows faster than the structural safety against the corrosion initiation failure. However, this type of behavior is different for each value of w/c ratio adopted and the time considered. For concretes with low value of w/c, 0.4 to 0.5 for instance, the stabilization process is observed faster than in the permeable concretes, with w/c ratio of 0.6 or 0.7. Considering permeable concretes, thicker covers are required in order to achieve the stabilization on the reliability index value. The analyses aiming the determination of the evolution of probability of corrosion initiation in the function of cover depth and w/c ratio, involving C.A. III, are presented in Figures 10,11, and12.

Figure 10

Evolution for probability of corrosion initiation. C.A. III structural lifetime equal to 5 years.

Figure 11

Evolution for probability of corrosion initiation. C.A. III structural lifetime equal to 15 years.

Figure 12

Evolution for probability of corrosion initiation. C.A. III structural lifetime equal to 25 years.

The behavior of curves observed in the above three figures is similar to those presented for C.A. II. However, due to the high environment aggressiveness, the probability of corrosion initiation tends to be higher than in C.A. II for the same structural lifetime and cover depth. The stabilization of the probability of corrosion initiation values, observed on previous analyses, also occurs for C.A. III. However, this process, for C.A. III, is observed for cover depth values thicker than in C.A. II case.

Another important aspect that should be mentioned is the time dependency considered on time corrosion initiation analyses. As long is the time desired to avoid the corrosion initiation or even though to reduce the probability of corrosion initiation process, the covers adopted must be thicker to reach the condition of reliability index stabilization. Thus, this type of analysis gives an interesting parameter which can be used to establish periods of structural maintenance according the type of concrete used and the environment where the structure is located.

The results presented in this application demonstrate the importance of stating correctly a value for the cover depth. As seen in this example, the cover depth is essential for structural durability, especially in reinforced concrete structures.

Example 3

The proposed probabilistic model can be used to determine the intervals of time in order to plan inspection and maintenance procedures in reinforced concrete structures as function of w/c ratio adopted. For each w/c value adopted for concrete design, an abacus can be constructed using the probabilistic model. These abacuses allow the choice of an optimum value of concrete cover in order to perform maintenance procedures in fixed time intervals. It is important to stress that these intervals are based on safety criterion. Then, the costs involved in maintenance and repair costs are not considered.

For this proposal, a reference value (named target) of reliability index was chosen, which was assumed as minimum requirement of safety. Then, when the structure has a reliability index lower than the target one, maintenance is required. According to JCSS (2001), the reliability index target expresses the requirements of structural safety, which guarantees acceptable values of structural failure risk considering a given scenario. In this regard, JCSS (2001) defines a set of values for reliability index target considering failure and serviceability limit state scenarios. The corrosion time initiation is considered as a serviceability limit state scenario. In this study, the loss of reinforcement cross-sections have not been considered, which is a failure limit state. Therefore, the reliability index target adopted is 1.3, leading a probability of failure approximately equal to 10%. Other values of target reliability index can, evidently, be adopted as function of the structural risk desired.

The analyses in this application were carried out considering the random variables presented in Table 2, as well as its statistical properties. Two classes of aggressiveness, C.A. II and C.A. III, were considered. The abacuses involving reliability index, time, and cover depth for C.A. II are presented in Figures 13 and14. It is worth to mention that only w/c ratios of 0.4 and 0.5 were analyzed since higher w/c ratio led to reliability indexes lower than the target. Consequently, it indicates that these w/c ratios should not be used in reinforced concrete applications.

Figure 13

Abacus reliability index required for C.A. II and w/c ratio of 0.4.

Figure 14

Abacus reliability index required for C.A. II and w/c ratio of 0.5.

Figure 13 presents the behavior of the reliability index in function of time for concretes with w/c ratio equal to 0.4 and C.A. II. According to these results, cover depth value of 10 mm is not recommended because it indicates failure (reliability index lower than the target) even for short time after construction. For cover depth of 20 mm, the maintenance procedures should be performed 10 years after construction. At this time, the structural reliability index is equal to the target. After this time, the structural reliability becomes lower than the target, indicating failure. It is worth to mention that cover depth values higher than 30 mm lead maintenance time interval of higher than 25 years. In these cases, analysts should study the possibility of change of w/c ratio in order to allow, at least, one inspection in the first 25 years of structural lifetime.

Similar behavior can be observed in Figure 14, where concretes with w/c ratio of 0.5 and C.A. II were considered. In this case, the minimum cover required is 30 mm which lead to maintenance procedures of 8 years after construction. Otherwise, considering cover depth equal to 50 mm, the maintenance procedure should be performed 21 years after construction in order to keep the structural safety at a desired level. Therefore, by changing the cover depth from 30 to 50 mm, or increasing the cover in 20 mm, the maintenance can be performed 13 years later.

On the other hand, considering cover depth of 30 mm, the maintenance time for concretes with w/c ratios of 0.4 and 0.5 are 23 and 8 years, respectively, for C.A. II. Then, an increment of 187.5% on the maintenance time interval can be verified by slightly changing the w/c ratio. Moreover, keeping the w/c ratio (0.5 for instance) constant and changing the cover depth from 30 to 40 mm, the maintenance times are 8 and 14 years, respectively, for C.A. II. Therefore, by changing the cover thickness by 10 mm, it results an improvement of 75% on the maintenance time. The abacuses involving the reliability index in function of w/c ratio and cover depth values for category of aggressiveness III are presented in Figures 15 and16.

Figure 15

Abacus reliability index required for C.A. III and w/c ratio of 0.4.

Figure 16

Abacus reliability index required for C.A. III and w/c ratio of 0.5.

Considering the two figures above, the same remarks discussed for C.A. II can be performed. However, in this case, the intervals of time for maintenance are considerable reduced due to the aggressiveness of the environment analyzed, which is higher than that observed for C.A. II.

It is important to emphasize that when the w/c ratio increases, small values of cover depth tend to be prohibitive regarding the corrosion time initiation failure. Moreover, in this case, the time interval for maintenance procedures will be drastically reduced. Therefore, regarding concretes with high values of w/c ratio, maintenance procedures in short periods of time and high values of cover depth have to be used in order to prevent reinforcement's corrosion.

Based on the results presented in this application, optimum concrete mixtures and cover depth values can be obtained in order to guarantee the durability of reinforced concrete structures. Moreover, these parameters can be allied aiming the evaluation of construction, maintenance, and reparation costs. Therefore, the global structural cost, taking into account the corrosion failure scenario, can be accurately achieved.

Example 4

As last part of this study, sensitivity analysis involving all random variables present on the probabilistic problem was performed. This example aims, therefore, at verifying which variables have more influence on the probability of corrosion initiation for each failure scenario considered. This example considers the random variables, as well as its statistical properties (presented on Table 2 and used in examples 2 and 3. Figures 17,18,19, and20 show the influence of each random variable on the probability of corrosion initiation for C.A II, w/c ratios of 0.4 and 0.7, and structural lifetimes 5 and 25 years. These values of w/c ratio and structural lifetime were chosen because they are on the boundary of all analyses previously performed. The intermediate values of w/c and structural lifetime were not presented since they describe the transition behavior between the results obtained and shown below.

Figure 17

Sensitivity factors for C.A. II, w/c = 0.4 at 5 years of structural lifetime.

Figure 18

Sensitivity factors for C.A. II, w/c = 0.4 at 25 years of structural lifetime.

Figure 19

Sensitivity factors for C.A. II, w/c = 0.7 at 5 years of structural lifetime.

Figure 20

Sensitivity factors for C.A. II, w/c = 0.7 at 25 years of structural life time.

Regarding the C.A. II, it can be observed that for concretes with low w/c ratio, the more influent parameter is the cover depth, especially when thick covers are analyzed. The chloride concentration at the structural surface is another influent parameter. Its influence appears when thin covers are considered. Moreover, as the w/c ratio grows, the influence of C₀ tends to become higher even for thick covers. This behavior was expected since the concrete resistance against chloride ingress reduces when w/c ratio grows. Then, the structural resistance depends, in most part, on the concrete cover, which is required in order to equilibrate the effects of C₀.

The sensibility results for all random variables analyzed, considering C.A. III, are presented in Figures 21,22,23, and24. These figures show that the cover depth has major importance when the environment aggressiveness increases. This influence is observed for all range of values considered for cover thickness.

Figure 21

Sensitivity factors for C.A. III, w/c = 0.4 at 5 years of structural lifetime.

Figure 22

Sensitivity factors for C.A. III, w/c = 0.4 at 25 years of structural lifetime.

Figure 23

Sensitivity factors for C.A. III, w/c = 0.7 at 5 years of structural lifetime.

Figure 24

Sensitivity factors for C.A. III, w/c = 0.7 at 25 years of structural lifetime.

Based on the results presented in this example, the improvement on constructive techniques applied to reduce the randomness on the cover depth is justified. When the uncertainties present on this variable are reduced, the probability of corrosion initiation can be considerable improved. Then, the durability assessment can be performed accurately.

It is worth to mention that the blank spaces (no columns) presented in these four last figures indicate that the probabilistic analyses were carried out using Monte Carlo simulation. Then, in these cases, the sensibility quantification is not possible.

Conclusions

This paper presented a study of probabilistic corrosion initiation in reinforced concrete structures using the coupling among Fick's diffusion law and reliability algorithms. In this case, the corrosion starts when the chemical protection surrounding the steel bars is lost due to chloride ingress. The analyses involving the determination of probability of corrosion initiation along time were carried out considering two different categories of environment aggressiveness and several combinations of cover depth and concrete properties (w/c ratio).

As verified on the results presented, the corrosion initiation depends on several parameters. However, the chloride concentrations at the structural surface and the cover depth values have demonstrated to have major importance on probabilistic analysis. Equally, the coefficient of diffusion is also important in order to measure the material resistance against the chloride ingress, and it can be determinant for choosing the optimal values for concrete cover.

According the results achieved in this paper, the durability of reinforced concrete structures has to be associated with more fair values of cover depth, which are, in general, based only on international concrete standard design. This parameter is more realistically evaluated using probabilistic approaches, in order to take into account the inherent randomness present on degradation phenomenon, which affects structural durability.

Regarding the choice of optimum values of cover depth, it was observed that this parameter strongly depends on the concrete quality against porosity, which is reflected by w/c ratio, as well as on the period of time attributed for structural interventions for maintenance procedures. Evidently, the determination of optimum combination among concrete material mixture, cover depth value, and construction/maintenance/reparation costs is the next question to be answered in order for the structural design to become more economic, safe, and rational.

Based on the abacuses achieved using the proposed probabilistic model, which are based only on safety criterion, it can be observed that the use of strong concretes (i.e., with low w/c ratio) may become more interesting alternatives against simply cheaper concretes with high w/c ratio, where thick covers have to be adopted in order to prevent corrosion initiation. Therefore, based on the results presented, advanced analyses can be performed considering the conception, maintenance, and reparation costs in order to take into account the engineering solution which allies the w/c ratio and the cover depth value that lead an adequate level of structural safety.

Authors’ information

CGN is a civil engineer, and nowadays, he works and in the post-doctorate level at the University of São Paulo. EDL is an assistant professor at the same university and a member of the editorial board of Engineering Analysis with Boundary Elements. HBC is a full professor at the same university and the head of GMEC research group.