Schedule-based sequential localization in asynchronous wireless networks

Abstract

In this paper, we consider the schedule-based network localization concept, which does not require synchronization among nodes and does not involve communication overhead. The concept makes use of a common transmission sequence, which enables each node to perform self-localization and to localize the entire network, based on noisy propagation-time measurements. We formulate the schedule-based localization problem as an estimation problem in a Bayesian framework. This provides robustness with respect to uncertainty in such system parameters as anchor locations and timing devices. Moreover, we derive a sequential approximate maximum a posteriori (AMAP) estimator. The estimator is fully decentralized and copes with varying noise levels. By studying the fundamental constraints given by the considered measurement model, we provide a system design methodology which enables a scalable solution. Finally, we evaluate the performance of the proposed AMAP estimator by numerical simulations emulating an impulse-radio ultra-wideband (IR-UWB) wireless network.

1 Introduction

Localization of nodes in wireless networks is required in various applications[1]. In many scenarios, it is important for the nodes to know their own position and the position of other nodes in the network. As an example, the first responder situation considered in[2] benefits from self-localization and localization of other members by each member of the team.

Research done to address the above issues provides a variety of practical techniques. Extensive surveys of such techniques are provided in[3, 4]. In time-of-arrival (TOA)-based systems, in particular, measuring time delays with the knowledge of anchor positions provides localization. The common challenges in location estimation are measurement noise, availability of accurate timing models and anchor uncertainty. Authors in[5–8] have proposed estimation methods and algorithms which are robust to anchor and timing uncertainty.

Cooperation between the nodes is used in position estimation solutions, as described in, e.g.,[9–13]. Specifically, in[11], a distributed localization method is presented which is based on factor graphs and relies on cooperation and message-passing between nodes. The method enables accurate and robust localization in networks which are not fully connected and its performance is studied in a numerical simulation scenario based on experimental measurements. In[12], a cooperative localization algorithm is derived, which extends the non-parametric belief propagation (NBP) message-passing method first introduced in[13]. The method, which is based on approximating the junction-tree, improves performance with a reduced number of particles with respect to other NBP algorithms in the literature. The algorithm is validated by simulation and by applying it to experimental indoor ranging data acquired independently by[14].

The concept of schedule-based localization was introduced in[15–17]. It consists in the adoption of a common transmission sequence, known throughout the network. This concept achieves cooperative positioning in a decentralized manner even without communication overhead required for message passing[11–13]. Since the transmissions are event-driven, the schedule-based localization concept provides other advantages, such as asynchronous operation and high update rate. The concept can be realized with low complexity hardware[18–21]. The importance of removing communication overhead is particularly high in systems like the tactical locator system, TOR, described in[22]. In the TOR system, the inter-agent ranging device is an ‘intelligent sensor’, among others, with an internal update rate which is high compared with the 1-Hz pace of the overall system. Such a system is employed in polluted RF environments where communication resources have to be used for voice and video communication. Therefore, the use of schedule-based localization is motivated from a robust communication perspective, because it allows to replace all unnecessary communication/RF waveforms with predetermined internal sequences to ensure maximum robustness.

In this paper, we provide a general Bayesian framework for schedule-based localization which takes into account uncertainty in anchor location and in timing devices. The contribution of this paper is the extension of previous works in[15–17]. Here, we derive a new sequential estimator that, unlike previous works, is scalable to an arbitrary number of nodes and can be implemented online rather than processing large records of collected samples offline. The estimator also has an inherent robustness with respect to varying levels of measurement noise. In addition to this, we provide insight on the fundamental constraints of the considered problem. Based on this analysis, we develop a methodology to obtain a scalable solution, which achieves identifiability of individual nodes in a sequential manner. The methodology assists the formulation of the common transmission sequence.

Moreover, we evaluate the performance of the proposed estimator by numerical simulations in a case study consisting of a network of wireless nodes. For this scenario, numerous time-based localization technologies have been applied in the literature, including commercial communication infrastructure, such as wireless local area networks[23] and personal area networks[24, 25], as well as specialized ranging and positioning systems such as chirp spread spectrum[26]. In this context, the impulse-radio ultra-wideband (IR-UWB) technology, cf.[27], is widely studied in the literature and has been considered for the implementation of cooperative localization methods in[11, 28]. The sub-nanosecond time resolution property of IR-UWB, in fact, allows for centimeter-level measurement accuracy when applying time-of-arrival methods[29–31]. The characterization and modeling of the indoor UWB propagation channel are outside of the scope of the present paper and have been extensively studied in[32, 33]. The method proposed in this paper is based on several assumptions that are valid in an IR-UWB set-up, which is our main interest. Therefore, here, we present numerical simulation results obtained using a network of IR-UWB nodes, where we set the parameters of the network configuration and error based on previous experimental work[18–21]. We highlight however that the method is applicable for a plurality of other localization technologies, mutatis mutandis, yielding varying degrees of accuracy depending on the ability to resolve time signatures. Furthermore, we compare the performance of the proposed estimator to the fundamental limitations provided by a Cramér-Rao bound.

The remainder of this paper is organized as follows: Section 2 provides the problem formulation. Then, the sequential AMAP estimator is derived in section 3 along with a methodology for sequence construction. A numerical evaluation of the AMAP performance is provided in section 4. Finally, section 5 reports conclusions.

2 Problem formulation

We consider a fully connected wireless network of N - 1 transceiving nodes and an indefinite number of passive receiving nodes. The transceiving nodes transmit according to a given sequence, denoted, which is known across the network. When a node transmits a signal, it is received by the other nodes, then the next node in the sequence transmits, making the process event-driven. Delays at all nodes are assumed to be analog as mentioned in[16–18]. On the basis of observed time intervals between received signals at an arbitrary node n, the goal is to achieve both self-localization and localization of other transceiving nodes participating in the sequence, at node n without the need for clock synchronization or additional communication.

Moreover, for the purposes of this paper, the passive receiving nodes are defined as non-transmitting nodes, which therefore do not take part in the transmission sequence. In this context, the goal of such nodes is self-localization and localization of the transceiving nodes.

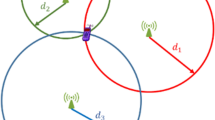
The signals are assumed to have a resolvable temporal signature that allows for timing events, e.g., pulses, symbol boundaries, etc. and the propagation velocity c is known. Let${\mathbf{x}}_i\in {\mathbb{R}}^d$ denote the position of node i, where d = 2 or 3, and${\rho }_{i,j}\triangleq {\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }_2$ denote the range between nodes i and j. Figure1 illustrates the ranges between three different nodes i,j, and n.

Figure 1

Example network setup involving the three nodes i , j , and n .

Now suppose node i initiates the transmission sequence and node j is the next node in the sequence. When it receives the signal, it transmits in return after a certain delay δ _j . The signal events at all nodes are then illustrated in Figure2.

Figure 2

Timing diagram for the example network setup in Figure1. Here, the solid black dots denote transmission events, whereas the arrows denote reception events.

Using the relations to the ranges, the observed time interval at node n can be expressed as[17, 34, 35]

$$y^{(i,j)}=\frac{1}{c}{\rho }_{i,j}+{\delta }_j+\frac{1}{c}{\rho }_{j,n}-\frac{1}{c}{\rho }_{i,n}+w^{(i,j)},$$

(1)

where w^(i,j) is modeled as zero-mean Gaussian noise with unknown variance. The noise may not be stationary or may be range-dependent[36]. For any given variance, the additive Gaussian noise model results in the least favorable Cramér-Rao bound for parameter estimation. Under the model, therefore, any estimator that attains the lower bound can be considered min-max optimal[37].

If the next node in the sequence is denoted k, then the next observed time interval is

$$y^{(j,k)}=\frac{1}{c}{\rho }_{j,k}+{\delta }_k+\frac{1}{c}{\rho }_{k,n}-\frac{1}{c}{\rho }_{j,n}+w^{(j,k)},$$

(2)

which uses one timing measurement from the previous observation y^(i,j). Therefore, there is a correlation between all consecutive measurements. In addition to the random noise, the delay δ _j is subject to uncertainty due to hardware imperfections and is modeled as${\delta }_j\sim \mathcal{N}({\mu }_{\delta },{\sigma }_{\delta }^2)$, where μ _δ is the nominal delay and the standard deviation σ _δ is assumed to be known. To avoid signal collisions, it is necessary that the delays exceed ρ_max/c, where ρ_max is the maximum range between any pair of transceivers and can easily be ensured in any bounded localization scenario.

Prior knowledge about the node positions in the network is modeled as${\mathbf{x}}_i\sim \mathcal{N}({\mathit{\mu }}_i,{\mathbf{C}}_i)$, where the nominal position μ _i and error covariance matrix C _i is set for all i[5–7]. With${\mathbf{C}}_i^{-1}=\mathbf{0}$ we can also model complete ignorance of a node position.

The goal is to formulate an estimator for any node n that performs self-localization as well as localization of an arbitrary number of transceiving nodes, by processing batches of observed time intervals sequentially.

3 Proposed estimator

Let$\mathit{\theta }={[{\mathbf{x}}_1^{\top },\cdots ,{\mathbf{x}}_{N-1}^{\top }{\mathbf{x}}_N^{\top }]}^{\top }\in {\mathbb{R}}^{\mathit{\text{dN}}}$ denote the positions of all N - 1 transceiving nodes and the position of a passive receiver node N. Note that a necessary condition for x _N to be identifiable is that localization is performed at node N since, clearly, other nodes cannot localize the passive receiver nodes. For notational simplicity, let$\mathit{\vartheta }\triangleq {[{\mathit{\theta }}^{\top }{\mathit{\delta }}^{\top }]}^{\top }\in {\mathbb{R}}^T$ denote the sought parameters, where δ contains the delays at the N-1 transceiving nodes and T = dN + N - 1.

We aim to formulate a sequential estimator that processes the observations in batches of B samples. The batches are indexed by b = 1,2,…, so that we can write

$${\mathbf{y}}_b={\mathbf{h}}_b(\mathit{\vartheta })+{\mathbf{w}}_b\in {\mathbb{R}}^B,$$

(3)

where

$${\mathbf{h}}_b(\mathit{\vartheta })=c^{-1}{\mathbf{S}}_b\mathbf{g}(\mathit{\vartheta }).$$

(4)

The nonlinear mapping is g(ϑ) = [ρ^⊤(θ) δ^⊤]^⊤, where ρ(θ) contains the N(N - 1)/2 unique ranges ρ_i,j in a fixed order. Here, the integer matrix S _b is determined by the transmission sequence for batch b, cf. (1). The noise follows${\mathbf{w}}_b\sim \mathcal{N}(\mathbf{0},{\mathbf{R}}_b)$ and

$${\mathbf{R}}_b=\left[\begin{array}{cc}{r}_{1,1}& r_{2,1}\\ r_{2,1}& r_{2,2}& r_{2,3}\\ r_{2,3}& r_{3,3}& r_{3,4}\\ \ddots & \ddots & r_{B,B-1}\\ r_{B,B-1}& r_{B,B}\end{array}\right]$$

(5)

is an unknown band-diagonal matrix, as consecutive samples are correlated.

In the next subsection, we derive an estimator$\widehat{\mathit{\vartheta }}$ which solves an approximate MAP problem using the observation model in (3). Subsequently, in subsection 3.3, we provide a schedule construction approach to achieve parameter identifiability. In this subsection, we will also discuss how the sequential formulation of the estimation problem allows for robustness to random link failures in the network.

3.1 Approximate sequential MAP estimator

Suppose that, at batch b, we have a prior estimate${\widehat{\mathit{\vartheta }}}_{b-1}$. We model the errors of${\widehat{\mathit{\vartheta }}}_{b-1}$ as zero-mean Gaussian with error covariance matrix P_b-1. For b = 1,${\widehat{\mathit{\vartheta }}}_0={[{\mathit{\mu }}_1^{\top },\cdots ,{\mathit{\mu }}_N^{\top }{\mu }_{\delta }{\mathbf{1}}^{\top }]}^{\top }$ and${\mathbf{P}}_0=\text{diag}({\mathbf{C}}_1,\cdots ,{\mathbf{C}}_N,{\sigma }_{\delta }^2{\mathbf{I}}_{N-1})$. The maximum a posteriori estimator of ϑ and R _b is given by the maximization of

$$\begin{array}{ll}J(\mathit{\vartheta },{\mathbf{R}}_b)& \triangleq lnp({\mathbf{y}}_b|\mathit{\vartheta },{\mathbf{R}}_b)+lnp({\mathbf{R}}_b)+lnp(\mathit{\vartheta })\\ =-\frac{1}{2}ln|{\mathbf{R}}_b|+lnp({\mathbf{R}}_b)-\frac{1}{2}{\parallel \mathbf{y}-{\mathbf{h}}_b(\mathit{\vartheta })\parallel }_{{\mathbf{R}}_b^{-1}}^2\\ -\frac{1}{2}{\parallel {\widehat{\mathit{\vartheta }}}_{b-1}-\mathit{\vartheta }\parallel }_{{\mathbf{P}}_{b-1}^{-1}}^2+K,\end{array}$$

(6)

where K is a constant. For tractability, we approximate${\mathbf{R}}_b\simeq {\sigma }_b^2{\mathbf{I}}_B$. Using a noninformative prior, we have$p({\mathbf{R}}_b)=p({\sigma }_b^2)\propto 1/{\sigma }_b^2$[38]. Then the approximated log-posterior is

$$\begin{array}{ll}{J}^{\prime }(\mathit{\vartheta },{\sigma }_b^2)& =-\frac{B+2}{2}ln{\sigma }_b^2-\frac{1}{2{\sigma }_b^2}{\parallel {\mathbf{y}}_b-{\mathbf{h}}_b(\mathit{\vartheta })\parallel }_2^2\\ -\frac{1}{2}{\parallel {\widehat{\mathit{\vartheta }}}_{b-1}-\mathit{\vartheta }\parallel }_{{\mathbf{P}}_{b-1}^{-1}}^2+K^{\prime },\end{array}$$

(7)

where the maximizing noise variance is${\widehat{\sigma }}_b^2={\parallel {\mathbf{y}}_b-{\mathbf{h}}_b(\mathit{\vartheta })\parallel }_2^2/(B+2)$. Inserting the estimate back into (7), the approximate MAP estimator, denoted AMAP, can be written as

$$\begin{array}{l}{\widehat{\mathit{\vartheta }}}_b=\underset{\mathit{\vartheta }\in {\mathbb{R}}^b}{\text{arg min}}{V}_b(\mathit{\vartheta }),\end{array}$$

(8)

where

$$\begin{array}{l}{V}_b(\mathit{\vartheta })\triangleq \frac{1}{2}ln{\parallel {\mathbf{y}}_b-{\mathbf{h}}_b(\mathit{\vartheta })\parallel }_2^2+\frac{{\gamma }_b^{-1}}{2}{\parallel {\widehat{\mathit{\vartheta }}}_{b-1}-\mathit{\vartheta }\parallel }_{{\mathbf{P}}_{b-1}^{-1}}^2\end{array}$$

(9)

and γ _b  = B + 2.

After solving (8), the estimate${\widehat{\mathit{\vartheta }}}_b$ can be used for the next batch b + 1. An approximate error covariance matrix P _b can be derived using the information matrix${\mathbf{\Lambda }}_b\triangleq {\mathbf{P}}_b^{-1}\succcurlyeq \mathbf{0}$. Then using the approximation${\mathbf{R}}_b\simeq {\sigma }_b^2{\mathbf{I}}_B$, the information is additive${\mathbf{\Lambda }}_b={\mathbf{\Lambda }}_{b-1}+{\sigma }_b^{-2}{\partial }_{\vartheta }{\mathbf{h}}_b^{\top }{\partial }_{\vartheta }{\mathbf{h}}_b$[39]. Inserting the estimates, the latter term becomes${\widehat{\sigma }}_b^{-2}{\mathbf{G}}_b^{\top }{\mathbf{G}}_b$, where${\mathbf{G}}_b=c^{-1}{\mathbf{S}}_b\mathbf{\Gamma }({\widehat{\mathit{\vartheta }}}_b)$ and$\mathbf{\Gamma }(\mathit{\vartheta })\triangleq {\partial }_{\vartheta }\mathbf{g}(\mathit{\vartheta })$. Then we have the recursive update of the approximate error covariance matrix

$$\begin{array}{ll}{\mathbf{P}}_b& ={\left({\mathbf{\Lambda }}_{b-1}+{\widehat{\sigma }}_b^{-2}{\mathbf{G}}_b^{\top }{\mathbf{G}}_b\right)}^{-1}\\ ={\mathbf{P}}_{b-1}-{\mathbf{P}}_{b-1}{\mathbf{G}}_b^{\top }{\left({\widehat{\sigma }}_b^2{\mathbf{I}}_B+{\mathbf{G}}_b{\mathbf{P}}_{b-1}{\mathbf{G}}_b^{\top }\right)}^{-1}{\mathbf{G}}_b{\mathbf{P}}_{b-1}.\end{array}$$

(10)

3.2 Iterative solution

To solve (8) iteratively, we linearize g(ϑ) around an initial estimate${\widehat{\mathit{\vartheta }}}_b^{(\ell )}$, i.e.,$\mathbf{g}(\mathit{\vartheta })\simeq \mathbf{g}({\widehat{\mathit{\vartheta }}}_b^{(\ell )})+{\mathbf{\Gamma }}_{\ell }\tilde{\mathit{\vartheta }}$, where${\mathbf{\Gamma }}_{\ell }=\mathbf{\Gamma }({\widehat{\mathit{\vartheta }}}_b^{(\ell )})$ and the increment is denoted$\tilde{\mathit{\vartheta }}\triangleq \mathit{\vartheta }-{\widehat{\mathit{\vartheta }}}_b^{(\ell )}$ for notational simplicity. Then the cost function (9) is approximated by

$$V_b^{(\ell )}(\tilde{\mathit{\vartheta }})\triangleq \frac{1}{2}ln{\parallel {\tilde{\mathbf{y}}}_{b,\ell }-c^{-1}{\mathbf{S}}_b{\mathbf{\Gamma }}_{\ell }\tilde{\mathit{\vartheta }}\parallel }_2^2+\frac{{\gamma }_b^{-1}}{2}{\parallel {\mathbf{z}}_{\ell }-\tilde{\mathit{\vartheta }}\parallel }_{{\mathbf{P}}_{b-1}^{-1}}^2,$$

(11)

where${\tilde{\mathbf{y}}}_{b,\ell }={\mathbf{y}}_b-c^{-1}{\mathbf{S}}_b\mathbf{g}({\widehat{\mathit{\vartheta }}}_b^{(\ell )})$ and${\mathbf{z}}_{\ell }={\widehat{\mathit{\vartheta }}}_{b-1}-{\widehat{\mathit{\vartheta }}}_b^{(\ell )}$. The initial estimate is updated by the optimal increment${\widehat{\mathit{\vartheta }}}_b^{(\ell +1)}={\widehat{\mathit{\vartheta }}}_b^{(\ell )}+\tilde{\mathit{\vartheta }}$.

To compute the optimal$\tilde{\mathit{\vartheta }}$, we find a stationary point of$V_b^{(\ell )}(\tilde{\mathit{\vartheta }})$ using the gradient

$$\begin{array}{ll}{\delta }_{\tilde{\vartheta }}{V}_b^{(\ell )}(\tilde{\mathit{\vartheta }})& ={\kappa }^{-1}(\tilde{\mathit{\vartheta }}){\mathbf{G}}_{\ell }^{\top }{\mathbf{G}}_{\ell }^{\top }-{\kappa }^{-1}(\tilde{\mathit{\vartheta }}){\mathbf{G}}_{\ell }^{\top }{\tilde{\mathbf{y}}}_{b,\ell }\\ +{\gamma }_b^{-1}{\mathbf{P}}_{b-1}^{-1}(\tilde{\mathit{\vartheta }}-{\mathbf{z}}_{\ell }),\end{array}$$

(12)

where$\kappa (\tilde{\mathit{\vartheta }})\triangleq {\parallel {\tilde{\mathbf{y}}}_{b,\ell }-c^{-1}{\mathbf{S}}_b{\mathbf{\Gamma }}_{\ell }\tilde{\mathit{\vartheta }}\parallel }_2^2$. Holding$\kappa (\tilde{\mathit{\vartheta }})$ fixed we solve${\delta }_{\tilde{\vartheta }}{V}_b^{(\ell )}(\tilde{\mathit{\vartheta }})=\mathbf{0}$, and update$\kappa (\tilde{\mathit{\vartheta }})$ resulting in a fixed-point iteration

$$\begin{array}{ll}\tilde{\mathit{\vartheta }}& :={\left({\kappa }^{-1}(\tilde{\mathit{\vartheta }}){\mathbf{G}}_{\ell }^{\top }(\tilde{\mathit{\vartheta }}){\mathbf{G}}_{\ell }+{\gamma }_b^{-1}{\mathbf{P}}_{b-1}^{-1}\right)}^{-1}\\ \times ({\kappa }^{-1}(\tilde{\mathit{\vartheta }}){\mathbf{G}}_{\ell }^{\top }{\tilde{\mathbf{y}}}_{b,\ell }+{\gamma }_b^{-1}{\mathbf{P}}_{b-1}^{-1}{\mathbf{b}}_{\ell })\\ ={\mathbf{z}}_{\ell }+{\gamma }_b{\mathbf{P}}_{b-1}{\mathbf{G}}_{\ell }^{\top }{\left({\gamma }_b{\mathbf{G}}_{\ell }{\mathbf{P}}_{b-1}{\mathbf{G}}_{\ell }^{\top }+\kappa (\tilde{\mathit{\vartheta }}){\mathbf{I}}_B\right)}^{-1}\\ \times ({\tilde{\mathbf{y}}}_{b,\ell }-{\mathbf{G}}_{\ell }{\mathbf{z}}_{\ell }).\end{array}$$

(13)

Starting with$\tilde{\mathit{\vartheta }}=\mathbf{0}$, we converge to a stationary point. As a standard analysis of the convergence properties does not appear to be tractable, we provide a numerical evaluation of convergence in a practical scenario in section 4. The sequential estimator is summarized in Algorithm 1. Note that when B is small, the computational complexity of processing a batch is low as the computation of${\widehat{\mathit{\vartheta }}}_b$ only involves the nodes participating in the batch b and therefore G _ℓ is a sparse matrix. Further, the matrix inversion on Line 12 in Algorithm 1 scales with the size of the batch B rather than the total number of nodes N.

Algorithm 1 Sequential approximate MAP estimator

3.3 Sequence construction

To achieve identifiability, it is required that a subset of the transceiving nodes have highly informative priors. We denote such nodes as anchors. The other transceiving nodes are denoted as auxiliary nodes.

We propose a strategy to localize sequentially an arbitrary number of auxiliary nodes at node n. First, we exploit the anchors to enable self-localization of node n. Subsequently, we devote each batch to the localization of one auxiliary node at a time. To achieve it, we interleave the transmissions of the auxiliary node with those of the anchors.

As an example, assume that nodes 1, 2, and 3 are anchors and node N as a passive receiving node. Then, given the sequence${\mathcal{T}}_1=\{1,2,3,1\}$, the proposed estimator operation is described in Figure3 for batch sizes B = 1 and B = 2, where the cost function V _b (ϑ) in (9) is plotted. From the figures, it can be seen that, when B = 1, node N cannot perform self-localization unambiguously, based only on the hyperbolic constraint imposed by a single time-difference measurement of (1), cf. time-difference-of-arrival localization[40, 41]. However, when B = 2, node N can perform self-localization using a single batch due to the joint imposition of two hyperbolic constraints^a.

Figure 3

Cost function V _b ( ϑ ) with respect to variables x _N , using sequence${\mathcal{T}}_{\mathbf{1}}\mathbf{=}\mathbf{\{}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{,}\mathbf{1}\mathbf{\}}$. Anchor nodes are denoted by crosses and the passive receiving node N is denoted by an asterisk. (a) Batch size B = 1, batch index b = 1. (b) Batch size B = 2, batch index b = 1.

Now, let us assume that node 4 is an auxiliary node with a noninformative prior. Then, given the sequence${\mathcal{T}}_2=\{1,2,3,1,4,2,4\}$, the cost function V _b (ϑ) in (9) is illustrated in Figure4. For batch size B = 1, node N cannot localize auxiliary node 4 unambiguously, based only on the elliptical constraint imposed by a single time-difference measurement of (1), cf.[42]. However, as node 4 is interleaved with anchor nodes in the sequence and node N has self-localized, (1) produces elliptical and hyperbolic constraints alternatingly depending on whether node i is an anchor or auxiliary node, respectively. Hence for B = 3, node N can localize the auxiliary node due to the joint imposition of two elliptical and one hyperbolic constraint.

Figure 4

Cost function V _b ( ϑ ) with respect to variables x ₄ , using sequence${\mathcal{T}}_{\mathbf{2}}\mathbf{=}\mathbf{\{}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{,}\mathbf{1}\mathbf{,}\mathbf{4}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{4}\mathbf{\}}$. Here, anchor nodes are denoted by crosses, the auxiliary node 4 is denoted by a triangle, and the passive receiving node N is denoted by an asterisk. (a) Batch size B = 1, batch index b = 4. (b) Batch size B = 3, batch index b = 2.

The above example can easily be extended to N _a anchor nodes. Let the anchor nodes be indexed as 1,2,…,N _a and the auxiliary nodes as N _a  + 1,N _a  + 2,…. Then a generic sequence can be constructed on the form

$$\begin{array}{l}{\mathcal{T}}_g=\{\underset{\text{enable self-localization}}{\underbrace{1,2,\dots ,N_a}},\dots ,\underset{k\text{th auxiliary node localized in this batch}}{\underbrace{1,N_a+k,2,N_a+k,\dots }},\dots \},\end{array}$$

where the k th auxiliary node is localized as long as it is interleaved by at least two anchor nodes in its corresponding batch. Thus, for a given batch size B, the sequence${\mathcal{T}}_g$ will be padded by interleaving anchor nodes to fulfill this constraint. Once all auxiliary nodes have been localized, the sequence is simply repeated which improves the estimates in the next round of measurements.

Finally, note that the sequential nature of the estimator allows for robustness to random link failures. In fact, in the event of a lost measurement, the corresponding batch is discarded and the estimator proceeds with the subsequent batches.

4 Numerical results

In this section, we provide a numerical performance evaluation of the estimator derived in section 3. As a case study, we consider the two-dimensional localization of nodes in an IR-UWB wireless sensor network[11, 18, 28]. In such a scenario, the timing information is obtained by measuring the propagation time of subnanosecond UWB pulses. The measurement noise is generated according to numerical values that are consistent with this scenario, i.e. subnanosecond- to nanosecond-order standard deviation, based on the experimental characterization in[18–21].

We analyze the localization of all nodes in the network performed at a passive receiver node. The analysis is applicable in a straightforward manner to any transceiver node which participates in the sequence.

Reproducible research: Code for reproducing results in this section is provided at the webpage of KTH Signal Processing, under ‘reproducible research’http://www.kth.se/en/ees/omskolan/organisation/avdelningar/sp/research/reproducibleresearch-1.433797.

4.1 Setup

We consider a fully connected network of N nodes consisting of N _a  = 4 anchors and N _u  = N - N _a unknown position nodes. The latter includes one passive receiver node, which we denote as self-localizing node, and N _u  - 1 auxiliary nodes, i.e., transceiver nodes with noninformative prior which participate in the transmission sequence. We assume that the anchors are deployed according to nominal positions affected by a Gaussian error with a known covariance${\mathbf{P}}_{{\theta }_a}={\sigma }_a^2{\mathbf{I}}_{2N_a}$. The remaining nodes have noninformative priors, i.e.,${\mathbf{P}}_{{\theta }_u}^{-1}=\mathbf{0}$, and the delay δ _i has a nominal value of μ _δ  = 10^-6 s with known error variance${\sigma }_{\delta }^2$.

In the numerical simulations, we consider a total of M samples. Except where otherwise indicated, the noise is generated as$\mathbf{w}\sim \mathcal{N}(\mathbf{0},{\sigma }^2\mathbf{Q})$, where

$$\mathbf{Q}=\left[\begin{array}{cc}{q}_1& 1/3\\ 1/3& q_2& 1/3\\ 1/3& q_3& 1/3\\ \ddots & \ddots & 1/3\\ 1/3& q_M\end{array}\right]\in {\mathbb{R}}^{M\times M}$$

(14)

and q _i  = 1, ∀i.

The transmission sequence is constructed by interleaving the transmissions from the auxiliary nodes with those of anchors, according to the approach described in section 3.3. Furthermore, the batch length is set to B = 7, which enables localization using all N _a  = 4 anchors within the same batch.

We initialize the AMAP estimator of Algorithm 1 with$\mathit{\mu }={[{\mathit{\mu }}_1^{\top }\cdots {\mathit{\mu }}_{N_a}^{\top }{\bar{\mathit{\mu }}}_1^{\top }\cdots {\bar{\mathit{\mu }}}_{N_u}^{\top }{\mu }_{\delta }{\mathbf{1}}_{N-1}^{\top }]}^{\top }$, where μ _i s are the nominal anchor positions and${\bar{\mathit{\mu }}}_i\equiv (1/N_a){\sum }_{j=1}^{N_a}{\mathit{\mu }}_j$ is the centroid of the nominal anchor positions. Furthermore, we set the termination criterion ε = 10^-2N _u except where otherwise indicated.

The average RMSE of the position and delay estimates is given by

$$\begin{array}{l}{\text{RMSE}}_{\xi }\triangleq \frac{1}{N_{\xi }}\sqrt{\text{tr}\left\{{\mathbf{C}}_{\tilde{\xi }}\right\}},\end{array}$$

where ξ can be either θ _u , in which case N _ξ  = N _u , or δ, and N _ξ  = N - 1. Here${\mathbf{C}}_{\tilde{\xi }}$ is the MSE matrix of ξ. We estimated the RMSE from 10³ Monte Carlo iterations.

4.2 Cramér-Rao bound

The mean square error when using the complete set of M samples,$\mathbf{y}=\mathbf{h}(\mathit{\vartheta })+\mathbf{w}\in {\mathbb{R}}^M$, is constrained by the Cramér-Rao bound[39]. Here we derive the bound when the noise covariance matrix equals σ²Q as of (14)[17]. Note, however, that the covariance structure Q is not given in the AMAP estimator; hence, the bound is optimistic and may not be attainable. Nevertheless, the bound provides a benchmark for evaluating the performance of the proposed estimator.

Let$\mathit{\eta }\triangleq {[{\mathit{\theta }}^{\top }{\mathit{\delta }}^{\top }{\sigma }^2]}^{\top }\in {\mathbb{R}}^{T+1}$, then we treat the parameters with noninformative priors as deterministic quantities. Suppose$\widehat{\mathit{\eta }}$ be any estimator that is conditionally unbiased with respect to the deterministic parameters. Then its mean square error (MSE) matrix is constrained by the hybrid Cramér-Rao bound (HCRB)[43],${\mathbf{C}}_{\tilde{\eta }}\succcurlyeq {\mathbf{J}}_{\eta }^{-1}$, where${\mathbf{J}}_{\eta }={\mathbf{J}}_{\eta }^D+{\mathbf{J}}_{\eta }^P\in {\mathbb{R}}^{(T+1)\times (T+1)}$.

Here,${\mathbf{J}}_{\eta }^D={\text{E}}_{\bar{\eta }}[{\mathbf{J}}^D(\mathit{\eta })]$ is the expected Fisher information matrix, where$\bar{\mathit{\eta }}$ denotes the subset of parameters that are modeled as random quantities and

$${[{\mathbf{J}}^D(\mathit{\eta })]}_{i,j}=\frac{c^{-2}}{{\sigma }^2}\frac{\partial {\mathbf{g}}^{\top }}{\partial {\eta }_i}{\mathbf{H}}^{\top }{\mathbf{Q}}^{-1}\mathbf{H}\frac{\partial \mathbf{g}}{\partial {\eta }_j}+\frac{M}{2{\sigma }^4}\frac{\partial {\sigma }^2}{\partial {\eta }_i}\frac{\partial {\sigma }^2}{\partial {\eta }_j},$$

as given in[39]. As the expectation does not have a closed form solution, we evaluate it by the Monte Carlo simulation. If a subset of node positions, θ _u , and the noise level, σ², are treated as deterministic and unknown parameters, and the remaining parameters, θ _a and δ, are random Gaussian, then the prior information matrix is given by

$${\mathbf{J}}_{\eta }^P=\left[\begin{array}{cccc}{\mathbf{P}}_{{\theta }_a}^{-1}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\sigma }_{\delta }^{-2}{\mathbf{I}}_{N-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& 0\end{array}\right]\in {\mathbb{R}}^{(T+1)\times (T+1)},$$

where${\mathbf{P}}_{{\theta }_a}$ is the covariance matrix of θ _a . In the following, we use this division between deterministic and random parameters to study practical configurations where we lack prior knowledge on the position of a subset of nodes.

4.3 Error analysis

We analyze the node deployment shown in Figure5, where the nominal positions of the anchors are the corners of a 10 × 10 m² area. The positions of the five auxiliary nodes and of the self-localizing nodes are randomly generated according to a uniform distribution within this area. Here, N _u  = 6 and we use a transmission sequence with$\left|\mathcal{T}\right|=71$.

Figure 5

True node positions and error ellipses for all nodes estimated at self-localizing node indicated by an asterisk. The anchor nominal positions are indicated by crosses, the auxiliary nodes by triangles and the centroid of the nominal anchor positions by a square. The solid black ellipses indicate the HCRB and the dashed red ellipses indicate the MSE performance of the proposed AMAP estimator. Here, σ _a  = 3 cm and σ = 1 ns. The average RMSE of the position estimate is 7.3 cm and the HCRB is 6.2 cm.

The performance of the proposed estimator is compared with the HCRB by means of error ellipses. For visual clarity, the sizes of the ellipses have been scaled to correspond to 99% confidence ellipses of a zero-mean Gaussian distribution[16].

In Figure5, a highly informative prior on the anchor positions, of centimeter level, is used. Further, in Figure6, a relatively less informative prior is employed, i.e., a decimeter-level prior, to model uncertainty in the deployment of the anchors in a practical scenario. It can be seen that the proposed AMAP estimator is close to the HCRB in both cases. In both cases, the gap between the average RMSE and the HCRB is less than 2 cm. Thus, the estimator is inherently robust with respect to anchor position uncertainty.

Figure 6

True node positions and error ellipses for the same node deployment as that in Figure5. Here, σ _a  = 30 cm and σ = 1 ns. The average RMSE of the position estimate is 13.2 cm and the HCRB is 11.5 cm.

In Figures5 and6, the ellipses related to the self-localizing node are considerably smaller than those of the auxiliary nodes, and are of the same order of magnitude as the prior on the anchor positions. Further, the minor axes of the ellipses of the auxiliary nodes are approximately aligned along the direction connecting to the self-localizing node. This phenomenon, previously observed in[16], is due to the fact that the self-localizing node performs an independent measurement of its own distance to a generic node i every time node i transmits. Therefore, the self-localization performance is improved at every measurement, and the error variance of the position estimate for node i is reduced along the direction connecting it to the self-localizing node.

Moreover, from the magnified comparison for an auxiliary node in Figure7, it is possible to visually analyze the effect of the anchor position priors on the performance. In particular, the ratio between the major and minor axes of both the HCRB and MSE ellipses decreases when the the prior becomes less informative. This is due to the increased error in the estimate of the self-localizing node position, which causes poorer performance in the direction connecting every auxiliary node and the self-localizing node.

Figure 7

Error ellipses of a single auxiliary node in the scenario of Figure5, under two different values of priors of anchor positions. The solid black ellipse is the HCRB for σ _a  = 3 cm whereas the dashed red ellipse indicates the performance of the AMAP estimator in the same scenario. The larger dash-dotted black ellipse and the dotted red ellipse indicate the HCRB and the performance of the AMAP estimator, respectively, in the σ _a  = 30 cm case. Here, σ = 1 ns.

4.4 Error statistics

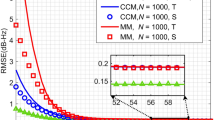
We now provide a statistical performance evaluation of the position and delay estimates as a function of the noise level, which is parameterized by σ. The simulation results, obtained using the same network configuration as that of Figure5, are shown in Figures8,9,10, and11, where different priors for the anchor positions and the delay are used.

Figure 8

Average RMSE of the position estimate vs noise level under different anchor position priors. Here, σ _δ  = 100 ps.

Figure 9

Average RMSE of the delay estimate vs noise level under different anchor position priors. Here, σ _δ  = 100 ps.

Figure 10

Average RMSE of the position estimate vs noise level under different delay priors. Here, σ _a  = 3 cm.

Figure 11

Average RMSE of the delay estimate vs noise level under different delay priors. Here, σ _a  = 3 cm.

Specifically, in Figures8 and9, the uncertainty of the anchor positions, parameterized by σ _a , is varied from centimeter-level to decimeter-level. It is possible to notice that, in low noise conditions, the RMSE of the position estimation is of the same order of magnitude as the uncertainty of the anchor positions. Also, as shown in Figure9, the delay estimator achieves a performance close to the HCRB, and is robust with respect to parameter uncertainty in the anchor positions.

Moreover, the parameter σ _δ , related to the uncertainty in the delay, is varied over two orders of magnitude in Figures10 and11. The results show that the proposed AMAP estimator is also robust with respect to uncertainty in the delay.

The behavior of the estimator with respect to the length of the transmission sequence is shown in Figure12. The different sequence lengths in the figure are obtained by repeating. Two values of the batch length B are reported. As expected, the performance improves as the length of the sequence increases. It can also be noticed that the performance of the proposed AMAP estimator improves as the batch length increases, given a fixed sequence length. This improvement establishes a performance trade-off since it comes at the expense of a reduced update rate of the system.

Figure 12

Average RMSE of the position estimate vs sequence length, in number of transmissions. Each point represents one repetition of a sequence.

4.5 Convergence evaluation

In order to analyze the convergence behavior of the proposed estimator, we evaluate simulation results obtained in the loose-prior scenario of Figure6, where we set the termination threshold ε = 10^-5N _u . Figure13a shows the behavior of the proposed estimator in a realization of the transmission sequence. It can be noticed that the error decreases at each batch within the sequence, as each auxiliary node is successfully localized.

Figure 13

Error behavior of proposed AMAP estimator, in sample realization. With respect to (a) batch index b within sequence and (b) iteration index ℓ for b = 1. Here, the average error is defined as$1/N_u∥{\mathbf{\theta }}_u-{\widehat{\mathbf{\theta }}}_u∥$.

Furthermore, Figure13b shows a sample realization of the iteration at line 3 of Algorithm 1 during the first batch. The error decreases monotonically with the number of iterations ℓ.

A histogram of the number of iterations until convergence for the first batch is shown in Figure14a. The average number of iterations is 5.54. With ε = 10^-2N _u , which yields negligible RMSE performance loss, the histogram is shown in Figure14b and we observe an average number of iterations of 3.71. Finally, simulation results show that the inner loop of line 8 in Algorithm 1 exhibits a fast convergence behavior with an average of approximately 1.23 iterations.

Figure 14

Convergence behavior for two values of stopping criterion ε : (a) ε = 10^-5N _u . (b) ε = 10^-2N _u .

4.6 Large-scale setup

In order to provide insight on the scalability of the proposed estimator, we present an extensive scenario in Figure15. We consider N = 29 nodes, including N _a  = 4 anchors in the same nominal positions as the previous scenario of Figure5, and N _u  = 25 unknown position nodes. The positions of the latter are generated by adding noise uniformly distributed in a square region with an area of 1 m² to a fixed 5 × 5 grid of evenly distributed nodes. A transmission sequence${\mathcal{T}}^{\prime }$, with$\left|{\mathcal{T}}^{\prime }\right|=337$ is used, and the batch size is set to B = 7. The figure shows that the proposed method is capable of localizing 24 auxiliary nodes with an accuracy of the same order of magnitude as the considered anchors position prior.

Figure 15

Large-scale setup on a 5 × 5 grid of unknown position nodes. Each of the nominal positions is randomized by adding a random variable which is uniformly distributed in a square region with an area of 1 m². Here, σ = 1 ns, σ _a  = 3 cm, and σ _δ  = 100 ps. The average RMSE is 3.8 cm and the HCRB is 3.3 cm.

4.7 Noise outliers

To evaluate the effect of varying noise levels on the proposed AMAP estimator, we generate noise as${\mathbf{w}}^{\prime }\sim \mathcal{N}(\mathbf{0},{\sigma }^2\mathbf{Q})$, where Q is fixed and given by (14), but in which we set

$$q_i=\left\{\begin{array}{rr}1& \text{with probability 0.9}\\ 100& \text{with probability 0.1}\end{array}\right.\forall i$$

(15)

Such a noise model is equivalent to randomly picking 10% of the observations and assigning a standard deviation σ_outl = 10σ to the noise affecting those observations. As an illustrative example, one realization of w^′ is shown in Figure16.

Figure 16

Realization of Gaussian noise having a standard deviation of σ = 1 ns, which is affected by 10% of outliers with σ _outl  = 10σ.

Figure17 shows the behavior of the AMAP estimator when the outlier measurement noise model is considered, whereas a magnification of the error ellipses for one auxiliary node is shown in Figure18. The results show that the proposed estimator is still operational and capable of providing accurate results even in the presence of relatively large outliers.

Figure 17

HCRB and MSE ellipses in the presence of outliers. The RMSE of the proposed AMAP estimator is 9.3 cm and the HCRB is 4.7 cm.

Figure 18

Error ellipses of single auxiliary node. Ellipses show effect of error outliers on HCRB and AMAP performance in scenario of Figure5. Solid black and dashed red ellipses and for the outliers case, dash-dotted black ellipse and dotted red ellipse.

5 Conclusion

We considered the schedule based network localization concept, proposed in[15–17]. This concept does away with the need for synchronization among nodes and does not involve communication overhead. It utilizes a common transmission sequence, which enables each node to perform joint self- and network localization, based on noisy propagation time measurements. The schedule-based localization problem has been posed as an estimation problem with probabilistic prior information. We derived a sequential estimator, AMAP, which is fully decentralized and copes with varying noise levels. The estimator is robust with respect to uncertainty in anchor locations and delay.

The measurement model we considered contains well-established constraints in the positioning literature, i.e., circular, hyperbolic, and elliptical constraints. The analysis of such constraints provides a schedule design methodology which enables a scalable solution. Specifically, the system can localize a large number of transceiving nodes with unknown positions by building transmission sequence batches in which such nodes are interleaved with anchor nodes. Numerical results in an IR-UWB network scenario show that AMAP provides localization accuracy close to a HCRB matched to the problem. Furthermore, AMAP is shown to be robust with respect to noise outliers.

Endnote

^a If node N is participating in the sequence, it also gives rise to circular constraints which are analogous to those provided by the two-way TOA technique[29].